Онлайн калькулятор длина дуги: Онлайн калькулятор: Калькулятор длины дуги

Онлайн калькулятор | онлайн калькулятор

Онлайн калькулятор для расчета материалов на забор.

Онлайн калькулятор / конструктор лестниц с легкостью произведет все нужные расчеты для производства и установки лестницы.

Закон Гей-Люссака гласит, что давление фиксированного объем газа при фиксированном объеме прямо пропорционально его температуры в градусах Кельвина.

При решении химических задач часто требуется узнать молярную массу газа.Для определения молярных масс у химиков существуют разные способы.

Закон Бойля утверждает, что объем газа увеличивается при уменьшении давления при постоянной температуре.

Закон идеального газа (уравнение Идеального газа) является уравнением состояния гипотетического идеального газа. Рассчитайте давление, объем, температура и моля газа.

Классическая теория тяготения Ньютона — закон, описывающий гравитационное взаимодействие в рамках классической механики.

Онлайн калькулятор для расчета процентов.

Золотое сечение – гармоническая пропорция.
В математике пропорцией называют равенство двух отношений: a : b = c : d.

Онлайн калькулятор дней, рассчитывает какое число будет через заданное количество дней.

Тетраэдр простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер.

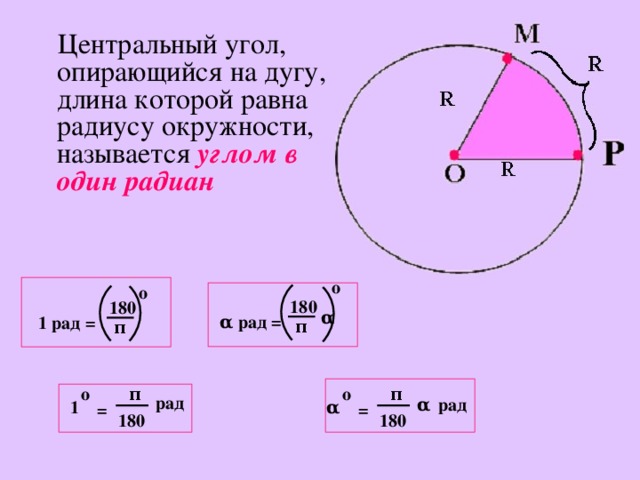
Длина дуги, пропорциональна ее радиусу и величине центрального угла.

Параллелограмм с равными сторонами называется ромбом.

Четырехугольник представляет собой геометрическую фигуру, обладающую четырьмя сторонами и таким же количеством углов.

Четырёхугольник с параллельными двумя противолежащими сторонами называется трапецией.

Параллелограмм это четырехугольник, противоположные стороны которого попарно параллельны. Противоположные стороны параллелограмма равны.

В квадрате периметр – это длина всех четырех, причем одинаковых, сторон.

Прямоугольником называется параллелограмм с прямыми углами. Периметр прямоугольника равен удвоенной сумме 2-х его сторон.

Периметр треугольника равен сумме всех трех сторон треугольника.

Площадь любого четырехугольника равна половине произведения диагоналей умноженной на синус угла между ними.

• « первая
• ‹ предыдущая
• …
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• …
• следующая ›
• последняя »

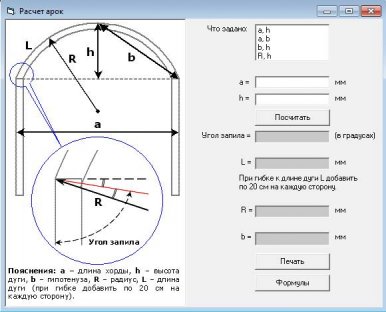
Расчет арки онлайн калькулятор. Параметрическое уравнение циклоиды и уравнение в декартовых координатах Длина дуги одной арки циклоиды

ЛЕМНИСКАТЫ
Уравнение в полярных координатах:
r 2 = a 2 cos2θ

(x 2 + y 2) 2 = a 2 (x 2 — y 2)

Угол между AB» или A»B и осью x = 45 o

Площадь одной петли = a 2 /2

ЦИКЛОИДА

Площадь одной дуги = 3πa 2

Длина дуги одной арки = 8a

Это кривая, описываемая точкой Р на окружности радиусом а, которая катится вдоль оси х.

ГИПОЦИКЛОИДЫ С ЧЕТЫРЬМЯ ОСТРИЯМИ
Уравнение в прямоугольных координатах:
x 2/3 + y 2/3 = a 2/3

Уравнения в параметрической форме:

Площадь, ограниченная кривой = 3πa 2 /8

Длина дуги целой кривой = 6a

Это кривая, описываемая точкой Р на окружности радиусом a/4, которая катится внутри окружности радиусом a.

КАРДИОИДА
Уравнение: r = a(1 + cosθ)

Площадь, ограниченная кривой = 3πa 2 /2

Длина дуги кривой = 8a

Это кривая, описываемая точкой Р на окружности радиусом a, которая катится снаружи окружности радиусом a. Эта кривая также является частным случаем улитки Паскаля.

ЦЕПНАЯ ЛИНИЯ
Уравнение:
y = a(e x/a + e -x/a)/2 = acosh(x/a)

Это кривая, по которой бы повисла цепь, подвешенная вертикально от точки А к В.

ТРЕХЛЕПЕСТКОВАЯ РОЗА
Уравнение: r = acos3θ

Уравнение r = acos3θ подобно кривой, полученной вращением против часовой стрелки по кривой 30 o или π/6 радиан.

В общем, r = acosnθ или r = asinnθ имеет n лепестков если n является нечетным.

ЧЕТЫРЕХЛЕПЕСТКОВАЯ РОЗА
Уравнение: r = acos2θ

Уравнение r = asin2θ подобно кривой, полученной вращением против часовой стрелки по кривой 45 o или π/4 радиан.

В общем r = acosnθ или r = asinnθ имеет 2n лепестков если n — четное.

ЭПИЦИКЛОИДА
Параметрические уравнения:

Это кривая, описываемая точкой Р на окружности радиуса b, когда она катится по внешней стороне окружности радиусом а. Кардиоида является частным случаем эпициклоиды.

ОБЩАЯ ГИПОЦИКЛОИДА
Параметрические уравнения:

Это кривая, описываемая точкой Р на окружности радиуса b, когда она катится по внешней стороне окружности радиусом а.

Если b = a/4, кривая является гипоциклоидой с четырьмя остриями.

ТРОХОИДА
Параметрические уравнения:

Это кривая, описываемая точкой Р на дистанции b от центра окружности с радиусом а, когда она катится по оси x.
Если b укороченной циклоидой.
Если b > a, кривая имеет форму, показанную на рис. 11-11 и называется троходой.
Если b = a, кривая есть циклоидой.

ТРАКТРИСА
Параметрические уравнения:

Это кривая, описываемая конечной точкой Р натянутой струны длиной PQ, когда другой конец Q перемещается вдоль оси х.

ВЕРЗЬЕРА (ВЕРЗИЕРА) АНЬЕЗИ (ИНОГДА ЛОКОН АНЬЕЗИ)

Уравнение в прямоугольных координатах: y = 8a 3 /(x 2 + 4a 2)

Параметрические уравнения:

В. На рисунке переменная линия OA пересекающая y = 2a и круг с радиусом a с центром (0,a) в A и B соотвественно. Любая точка P на «локоне» определяется построением линий, параллельных к осям x и y, и через B и A соответственно и определяющие точку пересечения P.

ДЕКАРТОВ ЛИСТ
Уравнение в прямоугольных координатах:
x 3 + y 3 = 3axy

Параметрические уравнения:

Площадь петли 3a 2 /2

Уравнение асимптоты: x + y + a = 0.

ЭВОЛЬВЕНТА ОКРУЖНОСТИ
Параметрические уравнения:

Эта кривая, описанная конечной точкой P струны, когда она разматывается с круга с радиусом a.

ЭВОЛЬВЕНТА ЭЛЛИПСА
Уравнение в прямоугольных координатах:
(ax) 2/3 + (by) 2/3 = (a 2 — b 2) 2/3

Параметрические уравнения:

Эта кривая является огибающей нормалью к эллипсу x 2 /a 2 + y 2 /b 2 = 1.

ОВАЛЫ КАССИНИ
Полярное уравнение: r 4 + a 4 — 2a 2 r 2 cos2θ = b 4 .

Это кривая, описываемая такой точкой P, что произведение ее расстояния от двух фиксированных точек [ расстояние 2a в сторону] есть постоянной b 2 .

Кривая, как на фигурах внизу, когда b a соответственно.

Если b = a, кривая есть лемниската

УЛИТКА ПАСКАЛЯ
Полярное уравнение: r = b + acosθ

Пусть OQ будет линией, соединяющей центр O с любой точкой Q на окружности диаметром a проходящей через O. Тогда кривая есть фокусом всех точек P, таких, что PQ = b.

Кривая, показанная на рисунках внизу когда b > a или b

ЦИССОИДА ДИОКЛА
Уравнение в прямоугольных координатах: y 2 = x 3 /(2a — x)

Параметрические уравнения:

Это кривая, описываемая такой точкой P, что расстояние OP = расстоянию RS. Используется в задаче

удвоения куба , т.e. нахождения стороны куба, который имеет удвоенный объем заданного куба

СПИРАЛЬ АРХИМЕДА
Полярное уравнение: r = aθ

Длина дуги циклоиды впервые была вычислена английским архитектором и математиком Реном в 1658 году. Рен исходил из механических соображений, напоминающих первые работы Торричелли и Роберваля. Он рассматривал поворот катящегося круга на весьма малый угол около «нижней» точки производящей окружности. Чтобы придать наводящим соображениям Рена доказательную силу, пришлось бы рассмотреть целый ряд вспомогательных теорем, соответственно пришлось бы затратить слишком много труда.

Гораздо удобнее воспользоваться более длинным, но пологим путем. Для этого нужно рассмотреть особую кривую, которая есть у каждой пологой кривой — ее развёрткой.

Рассмотрим выпуклую дугу АВ кривой линии (рис. 4.1). Представим себе, что к дуге АВ в точке А прикреплена гибкая нерастяжимая нить такой же длины, как сама дуга АВ, причем эта нить «навёрнута» на кривую и плотно к ней прилегает, так что её конец совпадает с точкой В. Будем «развертывать» — распрямлять нить, держа ее натянутой, так что свободная часть СМ нити будет все время направлена по касательной к дуге АВ. При этих условиях конец нити опишет некоторую кривую.

Вот эта-то кривая и называется разверткой или, по-латыни, эвольвентой исходной кривой.

Если дуга кривой не всюду выпукла в одну сторону, если она, подобно кривой АВ на рис. 4.2, имеет точку С, в которой касательная к кривой переходит с одной ее стороны на другую (такая точка называется точкой перегиба), то и в этом случае можно говорить о развертке кривой, но рассуждения придется немного усложнить.

Представим себе, что нить закреплена как раз в точке перегиба С (рис. 4.2). Нить, сматываясь с дуги ВС, опишет кривую ВМР — развертку.

Теперь представим себе нить, намотанную на дугу АС исходной кривой, но эта нить уже удлиненная: в точке С к ней привязан кусочек нити СР. Сматывая удлиненную нить АСР с кривой СА, мы получим дугу РНК, образующую вместе с дугой ВМР единую непрерывную кривую — непрерывную, но не везде плавную: точке прогиба С исходной кривой будет соответствовать острие (точка возврата) кривой ВМРНК: кривая ВМРНК и будет эвольвентой (разверткой) кривой ВСА.

Эти примеры помогли нам привыкнуть к новым понятиям эволюты и эвольвенты. Теперь займёмся исследованием разверток циклоидальных кривых.

Изучая ту или иную кривую, мы нередко строили вспомогательную кривую — «спутницу» данной кривой. Так, мы стоили синусоиду — спутницу циклоиды. Теперь, исходя из данной циклоиды, мы постоим неразрывно связанную с ней вспомогательную циклоиду же. Оказывается, совместное изучение такой пары циклоид в некоторых отношениях проще, чем изучение одной отдельно взятой циклоиды. Такую вспомогательную циклоиду мы будем называть сопровождающей циклоидой.

Рассмотрим половину арки циклоиды АМВ (рис. 4.3). Нас не должно смущать, что циклоида эта расположена непривычным образом («вверх ногами»). Проведем 4 прямые, параллельные направляющей прямой АК на расстояниях a , 2a , 3a и 4a . Построим производящий круг в положении, соответствующем точке М (на рис. 4.3 центр этого круга обозначен буквою О). Угол поворота МОН обозначим через ц. Тогда отрезок АН будет равен бц (угол ц выражен в радианах).

Диаметр НТ производящего круга продолжим за точку Т до пересечения (в точке Е) с прямой РР. На ТЕ как на диаметре построим окружность (с центром О 1). Построим касательную в точке М к циклоиде АМВ. Для этого точку М нужно, как мы знаем, соединить с точкой Т. Продолжим касательную МТ за точку Т до пересечения со вспомогательной окружностью, и точку пересечения назовем М 1 . Вот этой-то точкой М 1 мы и хотим теперь заняться.

Угол МОН мы обозначили через ц. Поэтому угол МТН будет равняться (вписанный угол, опирающийся на ту же дугу). Треугольник ТО 1 М 1 , очевидно, равнобедренный. Поэтому не только угол О 1 ТМ 1 , но и угол ТМ 1 О 1 будут каждый равняться. Таким образом, на долю угла ТО 1 М 1 в треугольнике ТО 1 М 1 остается ровно р — ц радианов (вспомним, что угол 180? равен р радианов). Заметим еще, что отрезок НК равен, очевидно, б (р — ц).

Рассмотрим теперь окружности с центром О 2 , изображенную на рис.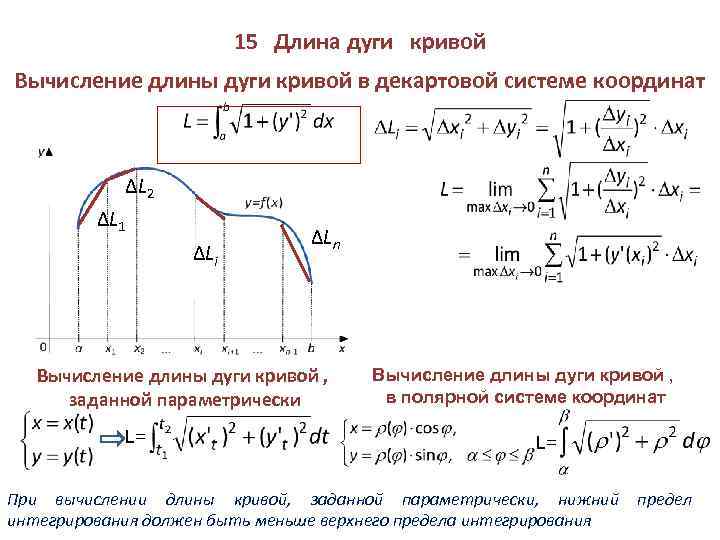 4.3 штриховой линией. Из чертежа ясно, чтом это за окружность. Если катить ее без скольжения по прямой СВ, то её точка В опишет циклоиду ВВ. Когда штриховой круг повернется на угол р — ц, центр О 2 придет в точку О 1 , а радиус О 2 В займет положение О 1 М 1 . Таким образом, построенная нами точка М 1 оказывается точкою циклоиды ВВ.

Описанное построение ставит в соответствие каждой точке М циклоиды АМВ точку М 1 циклоиды ВМ 1 В. На рис. 4.4 это соответствие показано более наглядно. Полученная таким путем циклоида называется сопровождающей. На рис. 4.3 и 4.4 циклоиды, изображенные жирными штриховыми линиями, являются сопровождающими по отношению к циклоидам, изображенными жирными сплошными линиями.

Из рис. 4.3 видно, что прямая ММ 1 является нормалью в точке М 1 к сопровождающей циклоиде. Действительно, эта прямая проходит через точку М 1 циклоиды и через точку Т касания производящего круга и направляющей прямой («наинизшую» точку производящего круга, как мы говорили когда-то; теперь она оказалась «наивысшей», потому что чертеж повернут).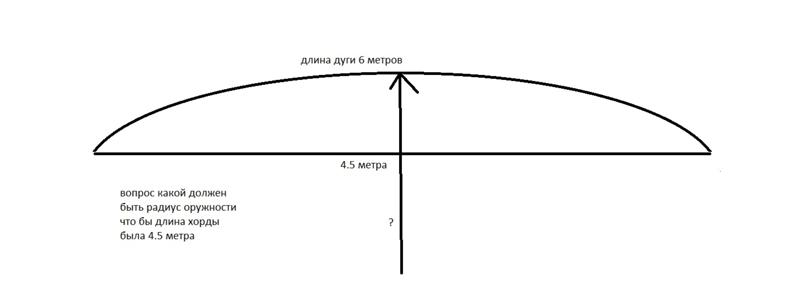 Но эта же прямая, по построению, является касательной к «основанию» циклоиде АМВ. Таким образом, исходная циклоида касается каждой нормали сопровождающей циклоиды. Она является огибающей для нормалей сопровождающей циклоиды, т.е. ее эволютой. А «сопровождающая» циклоида оказывается просто-напросто эвольвентой исходной циклоиды!

Занимаясь этим громоздким, но в сущности простым построением, мы доказали замечательную теорему, открытую голландским ученым Гюйгенсом. Вот эта теорема: эволютой циклоиды служит точно такая же циклоида, только сдвинутая .

Построив эволюту не к одной арке, а ко всей циклоиде (что можно, разумеется, сделать только мысленно), затем эволюту к этой эволюте и т.д., получим рис. 4.5, напоминающий черепицу.

Обратим внимание на то, что при доказательстве теоремы Гюйгенса мы не пользовались ни бесконечно малыми, ни неделимыми, ни приблизительными оценками. Даже механикой мы не пользовались, хотя употребляли иногда заимствованные из механики выражения. Доказательство это совершенно в духе тех рассуждений, которыми пользовались ученые XVII века, когда хотели строго обосновать результаты, полученные с помощью различных наводящих соображений.

Из теоремы Гюйгенса получается сразу важное следствие. Рассмотрим отрезок АВ на рис. 4.4. Длина этого отрезка равна, очевидно, 4a . Представим себе теперь, что на дугу АМВ циклоиды намотана нить, закрепленная в точке А и снабженная карандашом в точке В. Если мы будем «сматывать» нить, то карандаш будет двигаться по развертке циклоиды АМВ, т.е. по циклоиде ВМ 1 В. Длина нити, равная длине полуарки циклоиды, будет, очевидно, равна отрезку АВ, т.е., как мы видели, 4a . Следовательно, длина L всей арки циклоиды будет равна 8a , и формулу L=8a можно считать теперь достаточно строго доказанной.

Вычислим длину дуги при помощи дифференциальной геометрии. Решение, полученное таким способом получится куда короче и легче:

где t?

| r(t)| ===2sin

5. Параметрическое уравнение циклоиды и уравнение в декартовых координатах

Допустим, что у нас дана циклоида, образованная окружностью радиуса а с центром в точке А.

Если выбрать в качестве параметра, определяющего положение точки, угол t=∟NDM на который успел повернуться радиус, имевший в начале качения вертикально е положение АО, то координаты х и у точки М выразятся следующим образом:

х= OF = ON — NF = NM — MG = at-a sin t,

y= FM = NG = ND – GD = a – a cos t

Итак параметрические уравнения циклоиды имеют вид:

При изменении t от -∞ до +∞ получится кривая, состоящая из бесчисленного множества таких ветвей, какая изображена на данном рисунке.

Так же, помимо параметрического уравнения циклоиды, существует и ее уравнение в декартовых координатах:

Где r – радиус окружности, образующей циклоиду.

6. Задачи на нахождение частей циклоиды и фигур, образованных циклоидой

Задача №1. Найти площадь фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрически

и осью Ох.

Решение. Для решения данной задачи, воспользуемся известными нам фактами из теории интегралов, а именно:

Площадь криволинейного сектора.

Рассмотрим некоторую функцию r = r(ϕ), определенную на [α, β].

ϕ 0 ∈ [α, β] соответствует r 0 = r(ϕ 0) и, значит, точка M 0 (ϕ 0 , r 0), где ϕ 0 ,

r 0 — полярные координаты точки. Если ϕ будет меняться, «пробегая» весь[α, β], то переменная точка M опишет некоторую кривую AB, заданную

уравнением r = r(ϕ).

Определение 7.4. Криволинейным сектором называется фигура, ограниченная двумя лучами ϕ = α, ϕ = β и кривой AB, заданной в полярных

координатах уравнением r = r(ϕ), α ≤ ϕ ≤ β.

Справедлива следующая

Теорема. Если функция r(ϕ) > 0 и непрерывна на [α, β], то площадь

криволинейного сектора вычисляется по формуле:

Эта теорема была доказана ранее в теме определенного интеграла.

Исходя из приведенной выше теоремы, наша задача о нахождении площади фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрические x= a (t – sin t) , y= a (1 – cos t) , и осью Ох, сводится к следующему решению.

Решение. Из уравнения кривой dx = a(1−cos t) dt. Первая арка циклоиды соответствует изменению параметра t от 0 до 2π. Следовательно,

Задача №2. Найти длину одной арки циклоиды

Так же в интегральном исчислении изучалась следующая теорема и следствие из нее.

Теорема. Если кривая AB задана уравнением y = f(x), где f(x) и f ’ (x) непрерывны на , то AB является спрямляемой и

Следствие. Пусть AB задана параметрически

L AB = (1)

Пусть функции x(t), y(t) непрерывно-дифференцируемые на [α, β]. Тогда

формулу (1) можно записать так

Сделаем замену переменных в этом интеграле x = x(t), тогда y’(x)= ;

dx= x’(t)dt и, следовательно:

А теперь вернемся к решении нашей задачи.

Решение. Имеем , а поэтому

Задача №3. Надо найти площадь поверхности S, образованной от вращения одной арки циклоиды

L={(x,y): x=a(t – sin t), y=a(1 – cost), 0≤ t ≤ 2π}

В интегральном исчислении существует следующая формула для нахождения площади поверхности тела вращения вокруг оси х кривой, заданной на отрезке параметрически: x=φ(t), y=ψ(t) (t 0 ≤t ≤t 1)

Применяя эту формулу для нашего уравнения циклоиды получаем:

Задача №4. Найти объем тела, полученного при вращении арки циклоиды

Вдоль оси Ох.

В интегральном исчислении при изучении объемов есть следующее замечание:

Если кривая, ограничивающая криволинейную трапецию задана параметрическими уравнениями и функции в этих уравнениях удовлетворяют условиям теоремы о замене переменной в определенном интеграле, то объем тела вращения трапеции вокруг оси Ох, будет вычисляться по формуле

Воспользуемся этой формулой для нахождения нужного нам объема.

Задача решена.

Заключение

Итак, в ходе выполнения данной работы были выяснены основные свойства циклоиды. Так же научились строить циклоиду, выяснила геометрический смысл циклоиды. Как оказалось циклоида имеет огромное практическое применение не только в математике, но и в технологических расчетах, в физике. Но у циклоиды есть и другие заслуги. Ею пользовались ученые XVII века при разработке приемов исследования кривых линий, — тех приемов, которые привели в конце концов к изобретению дифференциального и интегрального исчислений. Она же была одним из «пробных камней», на которых Ньютон, Лейбниц и их первые исследователи испытывали силу новых мощных математических методов. Наконец, задача о брахистохроне привела к изобретению вариационного исчисления, столь нужного физикам сегодняшнего дня. Таким образом, циклоида оказалась неразрывно связанной с одним из самых интересных периодов в истории математики.

Литература

1. Берман Г.Н. Циклоида. – М., 1980

2. Веров С.Г. Брахистохрона, или еще одна тайна циклоиды // Квант. – 1975. — №5

3. Веров С.Г. Тайны циклоиды// Квант. – 1975. — №8.

4. Гаврилова Р.М., Говорухина А.А., Карташева Л.В., Костецкая Г.С.,Радченко Т.Н. Приложения определенного интеграла. Методические указания и индивидуальные задания для студентов 1 курса физического факультета. — Ростов н/Д: УПЛ РГУ, 1994.

5. Гиндикин С.Г. Звездный век циклоиды // Квант. – 1985. — №6.

6. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1. – М.,1969

Такая линия и называется «огибающей».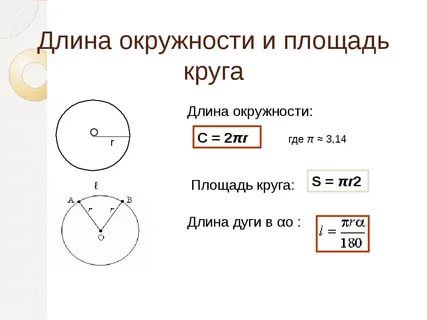 Всякая кривая линия есть огибающая своих касательных.

Материя и движение, и тот метод, который они составляют, дают возможность каждому реализовать свои потенциальные возможности в познании истины. Разработка методики развития диалектико-материалистической формы мышления и овладение аналогичным ему методом познания является вторым шагом на пути решения проблемы развития и реализации возможностей Человека. Фрагмент XX Возможности…

Обстановке могут заболеть неврастенией – неврозом, основу клинической картины которого составляет астеническое состояние. И в случае неврастении, и в случае декомпенсации неврастенической психопатии существо душевной (психологической) защиты сказывается уходом от трудностей в раздражительную слабость с вегетативными дисфункциями: либо от нападения человек бессознательно «отбивается»больше…

Различных видах деятельности; развитии пространственного воображения и пространственных представлений, образного, пространственного, логического, абстрактного мышления школьников; формировании умений применять геометро-графические знания и умения для решения различных прикладных задач; ознакомлении с содержанием и последовательностью этапов проектной деятельности в области технического и. ..

Дуги. Спиралями являются также эвольвенты замкнутых кривых, например эвольвента окружности. Названия некоторым спиралям даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например: · параболическая спираль (а — r)2 = bj, · гиперболическая спираль: r = а/j. · Жезл: r2 = a/j · si-ci-cпираль, параметрические уравнения которой имеют вид: , }

Калькулятор длины дуги

Калькулятор длины дуги находит общее расстояние дуги для любого круга. С помощью этого калькулятора вы можете найти длину дуги как в радианах, так и в градусах.

Этот калькулятор может найти четыре геометрических измерения в двух разных единицах измерения.

1. Площадь сектора
2. Длина дуги
3. Хорда
4. Диаметр

Какова длина дуги?

Длина дуги — это расстояние между конечными точками дуги по окружности. Дуга всегда изогнута, и это отличает ее от хорды, которая представляет собой прямую линию, соединяющую концы дуги.

Изображение выше представляет собой сектор круга. Дуга не указывается только для окружности. Но для того, чтобы рассчитать ее длину, нужно знать радиус окружности, которую можно было бы нарисовать, продолжая дугу.

Формула длины дуги

Длина дуги рассчитывается по следующей формуле:

Дуга (L) = θr

Где тета θ — центральный угол в радианах, а r — радиус. Если у вас центральный угол в градусах, то:

Дуга (L) = (θ/180) x πr

Эта формула получена из того факта, что пропорция между углом и длиной дуги остается неизменной. Имея в виду полный круг, мы можем написать:

L / θ = C / 2π

Где C — длина окружности (длина дуги), а 2 π — центральный угол полного круга. Мы можем заменить C на 2πr , то есть значение длины окружности в радианах.

L / θ = 2πr / 2π

L / θ = r

L = r * θ

Как найти длину дуги окружности?

Длина дуги может быть рассчитана с использованием ряда методов в зависимости от заданных данных, но наиболее подходящим является использование инструмента, описанного выше. Потому что он предоставляет вам другие измерения, связанные с кругом, без особых усилий.

Чтобы вычислить длину дуги, следуйте этим инструкциям.

1. Измерить или рассчитать центральный угол.
2. Найдите радиус по формуле: r = диаметр/2
3. Подставьте оба значения в формулу длины дуги и решите.

Некоторые решенные примеры приведены ниже, чтобы устранить дальнейшую путаницу.

Пример 1 (с использованием радиуса и центрального угла):

Предположим, круг радиусом 10 м . Сектор круга составляет угол 40 градуса. Найдите длину дуги этого сектора.

Решение: 

Шаг 1: Определите значения:

Радиус = 10 

Центральный угол = 40.

Шаг 2: Преобразование градусов в радианы.

1 градус = 0,0175 радиан

40 градусов = 40 x 0,0175 радиан

= 0,6981 радиан

Шаг 3: Используйте значения в формуле.

L = r * θ

L = (10)(0,6981)

L = 6,981 м

радиус, который имеет сектор площадью 40 м ² тогда найдите его длину дуги?

Решение:

Шаг 1: Определите значения.

Радиус = 6 м

Площадь сектора = 40 м ²

Шаг 2: Найдите центральный угол через площадь сектора.

Используйте сектор формулы площади и перестройте его таким образом, чтобы получить значение центрального угла. Формула: 

Площадь сектора (A) = ½ θr ²

Rearranging:

θ = (A* 2) / r ²

θ = (40* 2) / 6 ²  

θ = (80) / 36 

θ = 2,22 

Шаг 3: Используйте значения в формуле.

L = r * θ

L = 2,22 * 6

L = 13,333

Это окончательный ответ. Точно так же, если вам дана площадь сектора и центральный угол, вы можете использовать формулу площади сектора, чтобы найти радиус. Затем вы можете следовать тому же методу, что и в приведенных примерах.

Калькулятор длины дуги

Введите информацию

Заполните форму калькулятора и нажмите кнопку «Рассчитать», чтобы получить результат здесь

РЕЗУЛЬТАТЫ

Площадь сектора

Длина дуги

Аккорд д

Диаметр

Показать шаги

Оставьте свой отзыв!

Худший Бедный Средний Хороший Супер

Содержание:

1	Калькулятор длины дуги
2	Формула длины дуги
3	Ключевые причины использования этого дугового калькулятора
4	. Короткие ступени этой дуги. без всяких офлайн заморочек

Калькулятор длины дуги

Если говорить об определении длины дуги простыми словами, то это длина части окружности. Радиус окружности и угол, под которым построена дуга, являются важными параметрами для вычета этой величины. Помимо этого, они также являются важными частями формул.

 

Формула длины дуги

Длина дуги = радиус * центральный угол (здесь угол берется в радианах)

Предположим, что у вас есть круг с радиусом 6 метров и центральным углом 0,4 радиана . Таким образом, длина дуги будет равна

Длина дуги = 6*0,4
Длина дуги = 2,4

Ключевые причины использования этого калькулятора дуги она выбирает калькулятор длины дуги. Вот некоторые основные плюсы, которые этот конкретный инструмент предлагает пользователям.

1.    Быстрый расчет длины дуги без проблем

Нет ничего лучше, чем быстро и без ошибок выполнить расчет длины дуги. Люди думают, что знания формулы длины дуги достаточно, чтобы получить точные результаты. Факты очень разные, и мы можем получить представление, проверив набор значений, приведенный ниже.

• Длина дуги = 25,77 метра
• Угол = 3,66 радиана

Использование этих значений в формуле длины дуги не является простым орешком. Эти входные данные представлены десятичными числами, поэтому для умножения потребуется большой кусок времени. Работать с десятичными дробями нелегко, и каждый шаг процесса умножения должен выполняться с осторожностью. При ручном расчете велик риск ошибиться. В отличие от целых чисел, при работе с десятичными дробями требуется гораздо большая концентрация.

Этот калькулятор помогает пользователю рассчитать длину дуги, даже если вводятся сложные значения. Когда вы введете значение радиуса и значение угла, этапы расчета будут выполняться автоматически с помощью инструмента.

2.    Бесспорная альтернатива для получения точных значений

Математические расчеты — это не что иное, как получение правильных ответов. Если вы тратите 2 часа на написание шагов решения, а вывод неверен, нет смысла тратить время на эти шаги. Использование этого стандартного калькулятора длины дуги намного лучше, чем изнурять себя умственными вычислениями вручную. Время, которое вы потратите на подсчет результатов вручную, можно использовать для какой-то другой положительной цели. Даже когда вы утомляете себя, выполняя так много шагов расчета, шансы на ошибку все равно остаются. Таким образом, не принимайте такие риски. Использование этого инструмента поможет вам несколькими способами, включая получение точных результатов. Этот качественный онлайн-инструмент не допускает ошибок, связанных с человеческим фактором, поэтому дает ответы. Нет необходимости каким-либо образом подтверждать полученные ответы.

 

Короткие шаги этого калькулятора длины дуги

Некоторые инструменты очень просты в использовании, но шаги, которые приходится выполнять пользователям, занимают много времени. Этот калькулятор длины дуги имеет короткие и простые шаги использования. Вот шаги, которые необходимо выполнить для использования этого калькулятора.

1.    Введите значение радиуса и угла (в радианах)

Для расчета значения длины дуги необходимы два важных ввода. Один из них — радиус окружности, а другой — центральный угол в радианах. Если у вас есть значение диаметра, разделите его на два, чтобы получить значение радиуса. Точно так же, если значение центрального угла выражено в градусах, преобразуйте его в радианы, используя соответствующий метод преобразования. После того, как вы ввели эти входные данные, вы можете перейти к расчету результатов, нажав кнопку «Рассчитать». Время получения значения длины дуги мало.

2.    Проверка значения длины дуги

Некоторым онлайн-калькуляторам требуется много времени для вычисления значения длины дуги. Это может быть проблемой для пользователей, когда им нужно выполнить множество вычислений, а доступное время меньше. Это когда пользователи предпочитают быстрые инструменты, чтобы они могли выполнять расчеты длины дуги в соответствии со своими сроками. Этот инструмент работает довольно быстро, поэтому выполнить несколько расчетов длины дуги за небольшой промежуток времени очень просто. Мы можем взять пример с учителей, которые отвечают за проверку нескольких расчетов одновременно. Они не могут справиться с ручными вычислениями, так как требуемые время и усилия огромны.

3.    Как на самом деле работает этот инструмент (пример)?

Лучший способ увидеть, как работает инструмент, — посмотреть на реальный пример. Чтобы увидеть, как этот калькулятор длины дуги дает результаты, давайте рассмотрим следующий набор значений.

• Длина дуги = 3,2 метра
• Центральный угол в радианах = 0,55

Просто введите эти значения в соответствующие поля. После этого вам будут показаны следующие результаты. Если вы введете значения, указанные выше, сгенерированная длина дуги составит 1,76 метра.

 

Используйте этот калькулятор длины дуги без каких-либо проблем в автономном режиме

Использовать автономный инструмент не так просто, поскольку пользователю необходимо пройти различные этапы настройки среды, процедуры установки и другие шаги.