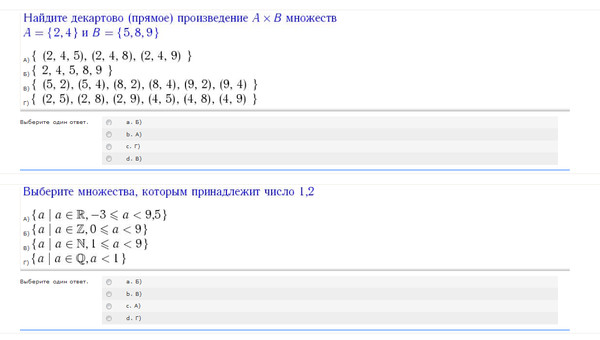
Тесты по дискретной математике doc: Тесты по дискретной математике.

Содержание

Савченко Н.В., Нефидова Е.В. Сборник тестов к курсу Основы дискретной математики

формат pdf
размер 2.84 МБ
добавлен 30 ноября 2011 г.

Учебное пособие. Харьков: НТУ «ХПИ», 2007. — 88 с.
Сборник содержит набор тестов для проверки усвоения учебного материала, предусмотренного программой по дисциплине Основы дискретной математики с вариантами ответов на предложенные тесты.
Предназначено для самостоятельной работы студентов компьютерных специальностей втузов.

Похожие разделы

Академическая и специальная литература
Математика
Математическая логика

Академическая и специальная литература
Математика
Математическая логика
Теория множеств

Смотрите также

формат djvu
размер 7. 17 МБ
добавлен 27 сентября 2010 г.

Сборник возник как пособие для практических занятий но курсу дискретной математики. Он содержит как упражнения, предназначенные для первоначального ознакомления с основными понятиями и фактами дискретной математики, так и задачи повышенной трудности, рассчитанные на такого читателя, который обладает достаточной математической культурой и специальной подготовкой. Книга будет полезна студентам университетов и других вузов, в которых изучаются дискр…

формат djvu
размер 4.23 МБ
добавлен 30 декабря 2008 г.

2000 год. В учебнике излагаются основы многосортных множеств, математической логики, теории графов и мографов, теории формальных грамматик и автоматов, прикладной теории алгоритмов и характеризационного анализа, которые в совокупности образуют основы дискретной математики, представляющие собой методически взаимосвязанный курс «Компьютерно-информационная математика». Для студентов технических университетов, академий и институтов, обучающихся по с…

формат pdf
размер 13.59 МБ
добавлен 09 октября 2011 г.

Москва: Наука. Физмалит. 2000г. В учебнике излагаются основы многосортных множеств, математической логики, теории графов и мографов, теории формальных грамматик и автоматов, прикладной теории алгоритмов и характеризационного анализа, которые в совокупности образуют основы дискретной математики, представляющие собой методически взаимосвязанный курс «Компьютерно-информационная математика». Для студентов технических университетов, академий и инстит…

Статья

формат doc, rtf
размер 230.78 КБ
добавлен 05 января 2009 г.

Предмет дискретной математики, ее структура и содержание. Связь дискретной математики с другими дисциплинами. Дискретные структуры. Подмножества. Алгебра множеств. Декартово произведение множеств. Соответствия. Отношения. Отношения эквивалентности и порядка. Замыкание отношений. Функции. Алгебры и их морфизмы. Основы теории графов. Начальные понятия. Части графа и операции с ними. Деревья. Циклы в графах. Планарность и раскраски графов. Переключа…

Статья

формат gif, htm, jpg, html
размер 375.48 КБ
добавлен 07 сентября 2010 г.

Лекции по основам дискретной математики. Скомп. справка в html, 176 Кб. Основы дискретной математики. Содержание. Теория множеств. Изоморфизм, автоморфизм, гомоморфизм. Бинарные операции. Теория групп. Теория групп (продолжение). Кольца, тела, поля. Теория алгебр. Тождества, бинарные операции. Исчисление высказываний. Теория кодирования. Теория графов. Эйлеровы пути, гамильтоновы пути. Кратчайшие пути в графе. Виды графов. Применение графов. Тео…

формат djvu
размер 833.62 КБ
добавлен 18 февраля 2010 г.

Учебное пособие. Излагаются основы современной дискретной математики. Приводятся практические задачи и даются алгоритмы их решения. 160с.

формат doc
размер 2.54 МБ
добавлен 20 сентября 2011 г.

— Белгород. Изд-во БГТУ, 2008. — 116с. Учебное пособие является некоторым введением в мир дискретной математики. В нём изложены основные разделы дискретной матема-тики: множества, комбинаторика, основы математической логики, гра-фы.

Приведены определения основных понятий, рассмотрены и проиллюстрированы примерами. Основное внимание уделено рассмотрению прикладных оптимизационных задач и алгоритмам их решений.rn

формат pdf
размер 982.38 КБ
добавлен 29 января 2009 г.

Челябинск, ЮУрГУ, 1998 г. Задачник соответствует курсу дискретной математики для студентов специальности «Прикладная математика» (на сайте выложен соответствующий учебник Эвнина «Дискретная математика»)

формат pdf
размер 5.71 МБ
добавлен 04 января 2012 г.

Челябинск: Изд-во ЮУрГУ, 2002. 164 с. Издание второе. Задачник соответствует курсу дискретной математики для студентов специальности «Прикладная математика» «Прикладная математика и информатика» и «Программное обеспечение вычислительное техники и автоматизированных систем».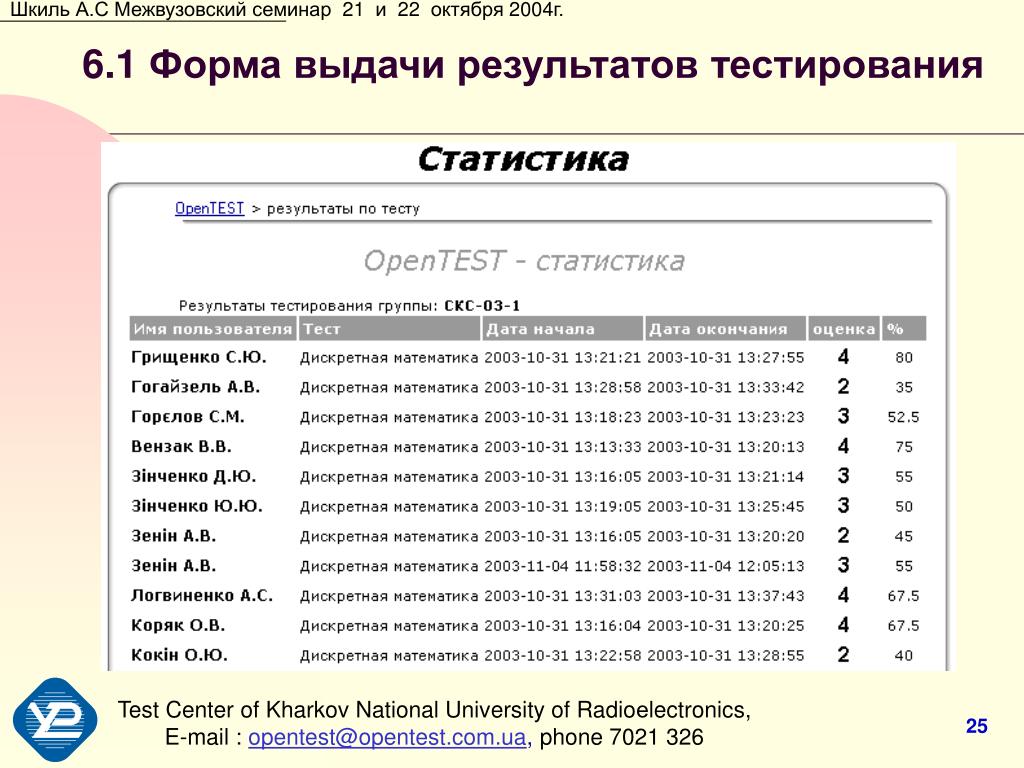

Задачник может быть использован также для проведения практикумов по решению олимпиадных задач.

формат djvu
размер 994.9 КБ
добавлен 04 октября 2010 г.

Издание 2-ое переработанное и дополненное Задачник соответствует курсу дискретной математики для студентов специальности «Прикладная математика» «Прикладная математика и информатика» и «Программное обеспечение вычислительное техники и автоматизированных систем». Задачник может быть использован также для проведения практикумов по решению олимпиадных задач. Челябинск, ЮУрГУ, 2002.

Дискретная математика — бесплатные ответы на тест Синергия ☛ Helpstudent24.ru

Если на множестве всех треугольников на плоскости рассматривается отношение
подобия, то данное отношение является отношением …

толерантности
порядка
эквивалентности+

Матрица смежности для графа

1
2
3+

Полный неориентированный граф с числом вершин n=4 …
обладает эйлеровым циклом
не обладает эйлеровым циклом+
может обладать эйлеровым циклом — это зависит от числа дуг

Полный неориентированный граф с числом вершин, равным n, имеет …ребер

1
2+
3
4

Если на множестве М задано отношение А «х знаком с у», тогда на основе данного соотношения нельзя разбить множество М на непересекающиеся классы, потому что
отношение А …
нерефлексивно
несимметрично
нетранзитивно+
не антирефлексивно

Пустое множество θ … подмножеством некоторого множества
будет собственным
будет несобственным+
не будет никаким
не всегда является

Количество «нулевых» значений таблицы истинности формулы XYZvXYZvXYZ составляет…

0
5+
3

Отношение «х — победитель у» является …
антирефлексивным
симметричным
транзитивным
антисимметричным+

Бинарное отношение, заданное на множестве натуральных чисел соотношением X =
Y(mod3) (остатки отделения на 3 равны), является отношением …
толерантности
порядка
эквивалентности+

Значение X, определяемое уравнением

1+
2
3

Высказывание «Если а — четное число, b — нечетное число, то их произведение делится на 2» в символической… форме имеет вид «…»

1
2
3+
4

Если выразите конъюнкцию АvВ через импликацию и отрицание, получим:

1+
2
3

Если заданы два нечетких отношения R1 и R2 :

, то результат операции пересечения равен

1
2
3
4+

Конечное множество, состоящее из n элементов, имеет …
1 несобственное подмножество+
2 несобственных подмножества
n несобственных подмножеств
n2 несобственных подмножеств

Граф … обладает эйлеровым циклом

G1
G2
G3+
G4

Отношение |x-y|<1 , заданное на множестве действительных чисел, является отношением . толерантности порядка эквивалентности

отношением
толерантности
порядка
эквивалентности+

Решите уравнение

1
2
3
4+

Хроматическое число графа равно

6
3+
2
1

Если из высказывания S1 следует S2 и, наоборот, из S2 следует S1 , то высказывания
S1 и S2 … эквивалентными
являются+
не являются
могут являться, а могут и не являться

Дистрибутивные законы булевой алгебры и алгебры действительных чисел …
совпадают+
не совпадают
совпадают в частном случае

Если даны два высказывания — S1 («Если треугольники равны, то равны их
стороны») и S2 («Стороны треугольников равны тогда и только тогда, когда равны
треугольники»), — то можно утверждать, что …
из S1 следует S2
из S2 следует S1+
ни одно из высказываний не следует из другого

Если заданы два нечетких множества – А=1 |x1 +0,3 |x2 +0,1|хз И В = 0,7 |x1 +0 |x2 +0,5 |хз , то результат операции пересечения равен
1 AnB = l|x1 + 0. 3|x2+0.1|х3
2 AnB =l|x1+0,3|х2+0,5|х3
3 AnB = 057|X1 + 0|х2 + 0.1|х3
4 AnB =0,7|x1 + 0|х2 + 0.5|х3
1
2
3+
4

Решите уравнение

1
2
3
4+

Решите уравнение

1
2+
3
4

Решите уравнение

1
2
3+
4

Логической функции f (0,0,0) = f(0,0,l) = f (1,0,0) = 1
соответствует формула алгебры высказываний

1
2
3+

Отношение ««быть старше»: «х старше у»» является …

рефлексивным
симметричным
транзитивным+
антисимметричным

Пусть А=1.В = 1. С = 1. К = (А —>В)лС л(А <->С) тогда

К=-1
К=1+
К=0

Пусть … тогда …

Выражение S=(A→B)Λ(B→С)->(A→C)… высказыванием

является тождественно истинным+
является тождественно ложным
является переменным
не является

Если А — множество всех книг во всех библиотеках России, а В — множество всех книг в библиотеке МГУ по различным отделам науки и искусства, тогда А\В есть множество …

всех книг в библиотеках России без книг по различным отделам науки и искусства в МГУ+
книг по искусству в библиотеке МГУ
всех книг в российских библиотеках
книг в библиотеке МГУ по искусству и науке, кроме математических

Выражение S = (ABvB)<->B . .. высказыванием

является тождественно истинным
является тождественно ложным+
является переменным
не является

Если отношение А на множестве М рефлексивно, симметрично и транзитивно, то разбить множество М на непересекающиеся классы …

можно+
нельзя
можно, но не всегда
можно только в том случае, если А — отношение порядка

Количество «единичных» значений таблицы истинности формулы (Xv YvZXXv YvZXXv Y vZ)

0
5+
3

Граф … содержит эйлерову цепь, соединяющую две различные вершины

G1
G2
G3
G4+

Преобразовывая формулу S-AnBuCnBuA
1 (An(BuC)nB)uA
2 (AnB)u(Cn(BuA))
3 AH(BU(COB)UA)
4 (AnB)u(CnBM
, нужно производить операции в следующем порядке:

1
2
3
4+

Если заданы два нечетких отношения R1 и R2 :

то результат операции, дополнения R1 равен

1
2+
3

Если заданы два нечетких множества — A = 1| Xl +0,3 |x2+0,l|x3 и B = 0,7|Xl +0|х2
+0,5|x3 , то результат операции

1
2
3+
4

Высказывание «Произведение целых чисел а и b не делится на 2 в том и только в том случае, если а или b

1 С<->АлВ 2 C<->AvB 3 А АВ —> С 4 А лВ vC нечетное» в символической форме имеет вид

1
2+
3
4

Высказывание «Неверно, что первым пришел Петр или Павел» может быть интерпретировано как сложное
1 AvBl
2 AvB
3 АлВ
4 АлВ
высказывание и записано формулой «…»

1
2+
3
4

Полный неориентированный граф с числом вершин п = 5 …
обладает эйлеровым циклом+
не обладает эйлеровым циклом
может обладать эйлеровым циклом — это зависит от числа дуг
может обладать эйлеровым циклом — это зависит от количества вершин с нулевыми
степенями

Если отношение А на множестве M рефлексивно, симметрично и транзитивно, то
разбить множество M на непересекающиеся классы…
можно+
нельзя
можно, но не всегда
можно только в том случае, если А — отношение порядка

Можем решить этот и любой другой тест Синергия. Для заказ необходимо обратиться к менеджеру. Все контакты указаны на сайте, можете выбрать любой удобный.

Другие тесты Синергии:

Макроэкономическое планирование и прогнозирование
Маркетинг
Маркетинговые исследования
Методы и средства проектирования информационных систем и технологий
Муниципальное управление и местное самоуправление
Муниципальное право

EECS 203: Дискретная математика — весна 2016 г.

EECS 203: Дискретная математика — весна 2016 г.

Весна 2016 г.
Главная / объявления | Обзор курса | Штат и часы
Ссылки / Примечания / раздаточные материалы | Домашнее задание | Расписание
Конспект лекций
Лекция 1: Введение в класс; Пропозициональная логика и ее приложения (pdf, docx)
Лекция 2: Завершить логику высказываний и начать с первого порядка Логика. (pdf)
Лекция 3: Квантификаторы, начало с выводов и доказательств (pdf, pptx) — Примечание: pdf – это раздаточный материал, который дается в классе. pptx содержит полные примечания (с ответами и т. д., где они были даны в классе).
Лекция 4: Правила вывода и доказательства. (pdf, docx)

Лекция 5: Наборы и запуск функций (pdf, docx)
Лекция 6: Функции, запуск последовательностей (pdf, docx)
Лекция 7: Последовательности, мощность инф. наборы (pdf, docx)
Лекция 8: Алгоритмы и рост функций (pdf, docx)
Лекция 9: Начало теории чисел (pdf, docx)
Лекция 10: Подробнее Теория чисел (pdf, docx)
Лекция 11: Введение (pdf, pptx)
Лекция 12: Заканчиваем теорию чисел. Шифрование (pdf, docx)
Лекция 13: Начало счета (pdf, docx)
Лекция 14: Перестановки и комбинации (pdf, pptx)
Лекция 15: Завершить подсчет, начать с вероятности (pdf, docx). Также рассмотрена сильная индукция (pdf, pptx)
Лекция 16:
Вероятность окончания, (возможно) начало рекурсии (pdf, docx)
Лекция 17: Повторить байесовский метод и начать рекурсию (pdf, docx)
Лекция 18: Решение рекуррентных соотношений, начало на графиках (pdf, docx)
Лекция 19: Кратчайший путь, путь Дейкстры и некоторые основные определения. (pdf, pptx)
Лекция 20: Финишные графики (pdf, pptx)
Заметки для обсуждения
В настоящее время нет
Викторины
Викторина 1: викторина, викторина с ответами
Викторина 2: викторина, викторина с ответами
Викторина 3: викторина, викторина с ответами
Промежуточный семестр: промежуточный семестр с ответами
Викторина 4: викторина, викторина с ответами
Викторина 5: викторина, викторина с ответами
Финал: Финал, Финал с ответами
Старые викторины и экзамены

Викторина 1: викторина, викторина с ответами
Викторина 2: контрольный опрос, викторина с ответами
Тест 3: контрольный опрос, викторина с ответами
Экзамен 1: экзамен, Экзамен с ответами Очень похожий, но другой практический экзамен,
Тест 4: контрольный опрос, викторина с ответами
Тест 5: контрольный опрос, викторина с ответами
Окончательный: экзамен, Экзамен с ответами Очень похожая, но другая практика экзамен,
Главная / объявления | Обзор курса | Штат и часы
Ссылки / Примечания / раздаточные материалы | Домашнее задание | Расписание
Подготовка к дискретной математике – информатика
Дискретная математика
Дискретная математика является базовым материалом для компьютерных наук. Многие области информатики требуют умения работать с понятиями из дискретной математики, особенно с материалами из таких областей, как теория множеств, логика, теория графов, комбинаторика и вероятность. теория.
Материал по дискретной математике широко распространен в областях структур данных и алгоритмов, но встречается и в других областях информатики. Например, способность создавать и понимать доказательства важна практически во всех областях информатики, включая (и это лишь некоторые из них) формальную спецификацию, проверку, базы данных и криптографию. Концепции теории графов используются в сетях, операционных системах и компиляторах. Концепции теории множеств используются в разработке программного обеспечения и в базах данных. Теория вероятностей используется в искусственном интеллекте, машинном обучении, сетях и ряде вычислительных приложений.
Этот документ отражает точку зрения Департамента компьютерных наук Williams на основной материал по дискретной математике, который студенты должны знать для дальнейшего изучения по специальности CS. Он в значительной степени заимствован из отчета ACM / IEEE-CS Computer Science Curricula 2013, а также из программы Math 200 — Discrete Mathematics, которую преподает в Williams профессор Михая Стойку.
Обратите внимание, что этот документ представляет собой руководство высокого уровня по типам понятий и уровню понимания, ожидаемому для сдачи квалификационного экзамена по дискретной математике. Его не следует воспринимать как исчерпывающий список материалов, которые могут появиться на экзамене. Учащимся должно быть комфортно решать задачи в областях, описанных в этом документе. Эти темы примерно соответствуют следующим разделам текста Discrete Mathematics with Graph Theory , Third Edition, Goodaire and Parmenter, копии которого можно найти в резерве в библиотеке Schow.
Главы 0–3: все разделы
Глава 4: Разделы 4.3, 4.4
Главы 5–7: все разделы
Глава 8: Разделы 8.1, 8.2
Главы 9–10: все разделы
Глава 12: разделы 12. 1–12.3

Множества, отношения и функции
Темы:
Наборы
Методы описания набора, например, перечисление элементов, нотация построителя набора
Диаграммы Венна
Соединение, пересечение, установленная разность, дополнение
Декартово произведение
Блоки питания
Мощность конечных множеств
Отношения
Рефлексивность, симметрия, антисимметрия, транзитивность
Отношения эквивалентности, частичные порядки
Функции
Домен, цель и диапазон/образ функции
Сюръекции, инъекции, биекции
Инверсия
Состав

Результаты обучения:
Дайте определение и объясните на примерах основную терминологию функций, отношений и множеств.
Выполнение операций, связанных с множествами, функциями и отношениями.
Свяжите практические примеры с соответствующим набором, функцией или моделью отношений и интерпретируйте связанные операции и терминологию в контексте.

Базовая логика
Темы:
Логика высказываний
Логические связки
Таблицы истинности
Дизъюнктивная нормальная форма
Действительность правильно построенной формулы
Правила пропозиционального вывода (например, modus ponens, modus tollens)
Универсальные и экзистенциальные кванторы и их отрицания

Результаты обучения:
Преобразование логических утверждений из неформального языка в пропозициональные (и количественные) логические выражения.
Применять формальные методы символической логики высказываний, такие как вычисление достоверности формул и вычисление нормальных форм.
Используйте правила вывода для построения доказательств в логике высказываний.

Методы доказательства
Темы:
Понятия импликации, двойной импликации, эквивалентности, обратного, обратного, противоположного, противоречия, отрицания
Структура математических доказательств
Прямые пробы
Опровержение контрпримером
Доказательство контрапозитивом
Доказательство от противного
Индукция по натуральным числам
Слабая и сильная индукция (т. е. первый и второй принцип индукции)
Рекурсивные математические определения
Заказ скважин

Результаты обучения:
Определите метод доказательства, использованный в данном доказательстве.
Опишите базовую структуру каждого метода доказательства, описанного в этом разделе.
Правильно применяйте каждый из методов доказательства при построении надежного аргумента.
Определите, какой тип доказательства лучше всего подходит для данной проблемы.
Объясните параллель между идеями математической индукции рекурсии и рекурсивно определенными последовательностями.
Объясните взаимосвязь между слабой и сильной индукцией и приведите примеры надлежащего использования каждой из них.
Укажите принцип правильного порядка и его связь с математической индукцией.

Основы счета
Темы:
Подсчет аргументов
Установить кардинальность и подсчет
Правила суммы и произведения
Принцип включения-исключения
Арифметические и геометрические прогрессии
Принцип классификации
Перестановки и комбинации
Основные определения
Биномиальная теорема
Решение рекуррентных соотношений
Пример простого рекуррентного соотношения, такого как числа Фибоначчи
Другие примеры, демонстрирующие различные решения
Базовая модульная арифметика

Результаты обучения:
Применение счетных аргументов, включая правила суммы и произведения, принцип включения-исключения и арифметические/геометрические прогрессии.
Применить принцип сортировки в контексте формального доказательства.
Вычислять перестановки и комбинации набора и интерпретировать значение в контексте конкретного приложения.
Сопоставьте реальные приложения с соответствующими формализмами подсчета, такими как определение количества способов рассадить людей вокруг стола с учетом ограничений на рассадку или количество способов определить определенные руки в картах (например, фулл-хаус). ).
Решить множество основных рекуррентных соотношений.
Проанализируйте проблему, чтобы определить основные рекуррентные отношения.
Выполнение вычислений с использованием модульной арифметики.

Дискретная вероятность
Темы:
Конечное вероятностное пространство, события
Свойства событий
Условная вероятность, теорема Байеса
Независимость

Результаты обучения:
Расчет вероятностей событий для элементарных задач, таких как азартные игры.
Различать зависимые и независимые события.
Сделайте вероятностный вывод в реальной задаче, используя теорему Байеса, чтобы определить вероятность гипотезы при наличии доказательств.

Измерение сложности алгоритма
Темы:
Асимптотический рост функций, включая нотацию Big-Oh и ее значение

Результаты обучения:
Уметь осмысленно сравнивать асимптотические роста пар функций.

Графики и деревья
Темы:
Деревья
Свойства
Стратегии обхода
Неориентированные графы
Ориентированные графы
Взвешенные графики
Стыковые деревья/леса
Изоморфизм графов

Результаты обучения:
Проиллюстрируйте на примере основную терминологию теории графов, а также некоторые свойства и особые случаи каждого типа графа/дерева.
No related posts.