Парабола
График квадратного уравнения называется параболой.
Если a > 0 тогда ветви параболы направлены вниз:
Середина любой параболы есть точкой $x = — \frac{b}{2a}$.
Задачи с квадратными уравнениями
1) x2 — 4 = 0; x = ?
Решение: x2 — 4 = (x — 2)(x + 2)
x = 2 or x = -2
2) 3x2 + 4x + 5 = 0; x = ?
Решение: Дискриминант это уравнения равен 42 — 4⋅3⋅5 = 16 — 60 = -44
3) x2 + 4x — 5 = 0; x = ?
Решение: Дискриминант это уравнения равен 42 — (-4⋅1⋅5) = 16 + 20 = 36 > 0
Поэтому, здесь есть два решения: $\frac{-4 \pm \sqrt{36}}{2}$
x = 1 или x = -5
4) x2 + 4x + 4 = 0; x = ?
Решение: Дискриминант это уравнения равен 42 — (4⋅1⋅4) = 16 — 16 = 0
Поэтому, здесь есть одно решение: $x = \frac{-4}{2}$
5) x2 — 13x + 12 = 0
Решение: 1; 12
Построить график функции: f(x) = x2 — 13x + 12
6) 8x2 — 30x + 7 = 0
Решение: 3,5; 0,25
Построить график функции: f(x) = 8x2 — 30x + 7
Квадратные уравнения на страницах математического форума
Форум о квадратных уравнениях
Страница не найдена | Академия МУБиНТ
Страница не найдена | Академия МУБиНТРазмер:
A
A
A
Цвет: CCC
Изображения
Вкл. Выкл.
Выкл.
Обычная версия сайта
Кажется, вы попали на страницу, которой нет.
Чтобы помочь найти нужную информацию, мы подготовили карту сайта:
|
|
|
полиномиальных графиков: конечное поведение | Purplemath
Множественности «Изгибы» «Выбросы» Графики
Purplemath
Когда вы рисуете (или смотрите на график) многочлены, полезно уже иметь представление о том, как выглядят основные полиномиальные формы. Одним из аспектов этого является «конечное поведение», и это довольно просто. Мы посмотрим на некоторые графики, чтобы найти сходства и различия.
Одним из аспектов этого является «конечное поведение», и это довольно просто. Мы посмотрим на некоторые графики, чтобы найти сходства и различия.
Сначала рассмотрим некоторые многочлены четной степени (в частности, квадратичные числа в первой строке рисунков и квартики во второй строке) с положительными и отрицательными старшими коэффициентами:
Содержание продолжается ниже
MathHelp.com
На всех четырех приведенных выше графиках концы линий входили и выходили из одной и той же стороны изображения. Когда графики представляли собой функции с положительными старшими коэффициентами, концы появлялись, а не в верхней части изображения, как в любом положительном квадратичном выражении, которое вы когда-либо рисовали. Когда графики представляли собой функции с отрицательными старшими коэффициентами, концы появлялись и опускались в нижней части изображения, как и любой отрицательный квадратичный показатель, который вы когда-либо рисовали.
Эти черты будут верны для каждого полинома четной степени. Если вы можете вспомнить поведение для квадратичных уравнений (то есть для парабол), то вы будете знать конечное поведение для каждого многочлена четной степени.
Если вы можете вспомнить поведение для квадратичных уравнений (то есть для парабол), то вы будете знать конечное поведение для каждого многочлена четной степени.
Теперь давайте посмотрим на некоторые полиномы нечетной степени (кубики в первой строке рисунков и квинтики во второй строке):
Как вы можете видеть выше, у полиномов нечетной степени есть концы, расходящиеся в противоположные стороны. Если они начинаются «вниз» (входя в графическую «коробку» через «низ») и идут «вверх» (выходя из графической «коробки» через «верх»), они являются положительными полиномами, точно так же, как любая положительная кубика, которую вы когда-либо рисовал. Но если они начинаются «вверх» и идут «вниз», это отрицательные полиномы.
Это поведение верно для всех полиномов нечетной степени. Если вы можете вспомнить поведение кубиков (или, технически, прямых линий с положительным или отрицательным наклоном), то вы будете знать, что будут делать концы любого полинома нечетной степени.
Все многочлены четной степени ведут себя на концах как квадратичные; все многочлены нечетной степени ведут себя на своих концах как кубики.
Чтобы ответить на этот вопрос, мне важно рассмотреть знак и степень ведущего члена.
Показатель степени говорит, что это полином степени 4; 4 четно, поэтому график будет вести себя примерно как квадратичный; а именно, его график будет либо вверх на обоих концах, либо вниз на обоих концах. Поскольку знак перед старшим коэффициентом отрицательный, график будет направлен вниз на обоих концах.
(Фактическое значение отрицательного коэффициента, −3 в данном случае, на самом деле не имеет значения для этой задачи. Все, что мне нужно, это «минусовая» часть старшего коэффициента.)
Очевидно, что графики A и C представляют нечетную степень многочлены, так как их два конца расходятся в противоположные стороны. График D показывает, что оба конца проходят через верхнюю часть графического прямоугольника, точно так же, как положительный квадратичный бы.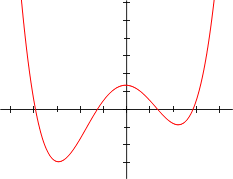 Единственный график с обоими концами вниз:
Единственный график с обоими концами вниз:
График B
Этот многочлен слишком велик, чтобы я мог его просмотреть на стандартном экране графического калькулятора, так что либо я могу потратить много времени на возню с параметрами WINDOW, либо Я могу быстро использовать свои знания о конечном поведении.
Эта функция является многочленом нечетной степени, так что концы расходятся в противоположных направлениях, как и у любого кубика, который я когда-либо рисовал. Положительный кубик входит в график внизу, вниз слева, и выходит из графика вверху, вверх справа. Поскольку старший коэффициент этого многочлена нечетной степени положителен, его конечное поведение будет имитировать положительное кубическое. Следовательно, конечное поведение для этого многочлена будет:
«Вниз» слева и «вверх» справа.
URL: https://www.purplemath.com/modules/polyends.htm
Страница 2Страница 3Страница 4Страница 5
3.4: Графики полиномиальных функций
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 34892
Цели обучения
- Определение нулей и их кратностей.

- Используйте факторинг для нахождения нулей полиномиальных функций.
- Поймите взаимосвязь между степенью и точками поворота.
- Граф полиномиальных функций.
Мы уже исследовали локальное поведение (расположение \(x\)- и \(y\)-перехватов) для квадратичных уравнений, частного случая многочленов. В этом разделе мы исследуем локальное поведение многочленов в целом. 93 \nonumber\]
Примечание на рисунке справа показывает, что поведение этой функции на каждом из \(x\)-отрезков отличается.
Пересечение \(x\) −3 является решением уравнения \((x+3)=0\). Граф проходит непосредственно через точку пересечения \(x\) в точке \(x=−3\). Фактор является линейным (имеет степень 1), поэтому поведение вблизи точки пересечения похоже на поведение прямой — она проходит непосредственно через точку пересечения. Мы называем это одиночным нулем, потому что ноль соответствует одному фактору функции. 9p\), поведение вблизи \(x\)-перехвата определяется степенью \(p\).
- График полиномиальной функции будет касаться оси \(x\) нулями с четными кратностями.
- График пересечет ось \(x\) в нулях с нечетной кратностью.
- Чем выше кратность, тем более пологая кривая у нуля.
- Сумма кратностей есть степень полиномиальной функции.
Для нулей с четной кратностью графики касаются или касаются оси \(x\). Для нулей с нечетной кратностью графики пересекают или пересекают ось \(x\). На рисунке ниже приведены примеры графиков полиномиальных функций с кратностью нуля 1, 2 и 3. Графики ясно показывают, что чем выше кратность, тем более плоский график у нуля.
Для более высоких четных степеней, таких как 4, 6 и 8, график по-прежнему будет касаться и отскакивать от горизонтальной оси, но для каждого увеличения четной степени график будет казаться более плоским по мере приближения и выхода из \ (х\)-ось.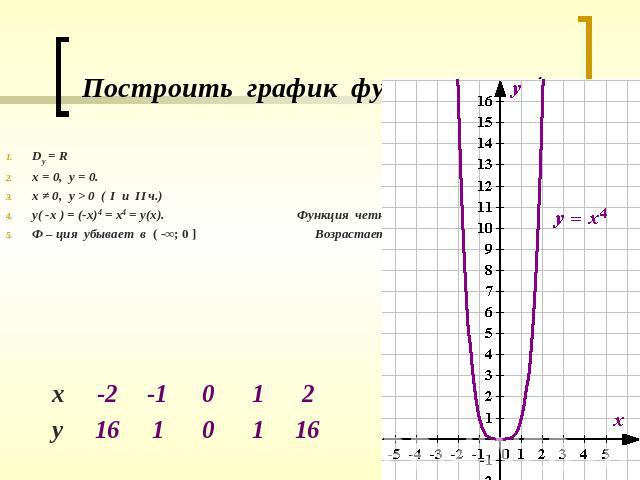 Для более высоких нечетных степеней, таких как 5, 7 и 9, график по-прежнему будет пересекать горизонтальную ось, но с каждым увеличением нечетной степени график будет казаться более плоским по мере приближения и удаления от оси \(x\).
Для более высоких нечетных степеней, таких как 5, 7 и 9, график по-прежнему будет пересекать горизонтальную ось, но с каждым увеличением нечетной степени график будет казаться более плоским по мере приближения и удаления от оси \(x\).
Как: Имея график полиномиальной функции, определить нули и их кратности
- Если график пересекает ось \(x\) в нуле, это ноль с нечетной кратностью.
- Если график касается и отскакивает от оси \(x\), это нуль с четной кратностью.
- Чем выше кратность нуля, тем более плоским становится график у нуля.
Пример \(\PageIndex{1}\): поиск нулей и их кратностей по графику
Используйте график функции степени 6 на рисунке ниже , чтобы определить нули функции и их возможные кратности.
| График полиномиальной функции степени 6. | Раствор Начиная слева, первый нуль находится в точке \(x=−3\).
Следующий ноль находится в точке \(x=−1\). В этот момент график выглядит почти линейным. Это один ноль кратности 1.
Последний нуль находится в точке \(x=4\). График пересекает ось \(x\), поэтому кратность нуля должна быть нечетной. Поскольку вокруг этого нуля график плоский, кратность, скорее всего, равна 3 (а не 1).
Полиномиальная функция имеет степень \(6\), поэтому сумма кратностей должна быть не меньше \(2+1+3\) или \(6\). |
Попробуйте \(\PageIndex{2}\)
Используйте график функции на рисунке ниже , чтобы определить нули функции и их возможные кратности.
График полиномиальной функции.
- Ответить
Ноль в -5 нечетный.
 Поскольку кривая в точке -5 несколько плоская, кратность нуля, скорее всего, равна 3, а не 1.
Поскольку кривая в точке -5 несколько плоская, кратность нуля, скорее всего, равна 3, а не 1.
Ноль в точке -1 имеет четную кратность 2.
Ноль в точке 3 имеет четную кратность. Поскольку кривая более пологая при 3, чем при -1, ноль, скорее всего, имеет кратность 4, а не 2.
Нахождение нулей и их кратностей из полиномиального уравнения
Напомним, что если \(f\) является полиномиальной функцией, значения \(x\), для которых \(f(x)=0\), называются 92+bx+c).\) Когда неприводимые квадратичные множители обнуляются и решаются относительно \(x\), получаются мнимые решения. Запишите каждый повторяющийся множитель в экспоненциальной форме.
 92-7)\) при установке в ноль дает два иррациональных решения, \(x= \pm \sqrt{7}\)
92-7)\) при установке в ноль дает два иррациональных решения, \(x= \pm \sqrt{7}\)Теперь нам нужно подсчитать количество вхождений каждого нуля, тем самым определив кратность каждого действительного числа ноль.
- Решение \(x= 0\) встречается \(3\) раз, поэтому ноль \(0\) имеет кратность \(3\) или нечетную кратность.
- Решение \(x= 3\) встречается \(2\) раз, поэтому ноль \(3\) имеет кратность \(2\) или даже кратность.
- Решения действительных чисел \(x= -2\), \(x= \sqrt{7}\) и \(x= -\sqrt{7}\) встречаются \(1\) раз, поэтому эти нули имеют кратность \(1\) или нечетная кратность. 92+х\).
- Ответить
Нули \(-1\) и \(0\) имеют нечетную кратность \(1\). Ноль \(1\) имеет четную кратность \(2\)
График полиномиальных функций
Мы можем использовать то, что мы узнали о кратностях, поведении концов и точках пересечения, для построения графиков полиномиальных функций.
 Давайте соберем все это вместе и посмотрим на шаги, необходимые для построения графика полиномиальных функций.
Давайте соберем все это вместе и посмотрим на шаги, необходимые для построения графика полиномиальных функций.Как: по заданной полиномиальной функции нарисовать график
- Определите конечное поведение, изучив ведущий член.
- Найдите точки пересечения и используйте кратность нулей, чтобы определить поведение многочлена на точках пересечения \(x\).
- Используйте конечное поведение и поведение на точках пересечения, чтобы нарисовать график.
- Опционально…
- Проверка на симметричность. Если функция четная, ее график симметричен относительно оси \(y\), то есть \(f(−x)=f(x)\). Если функция является нечетной функцией, ее график симметричен относительно начала координат, то есть \(f(-x)=-f(x)\). 93\), так что конечным результатом является поведение вертикально отраженного кубика, при этом график падает вправо и движется в противоположном направлении (вверх) влево: \(\nwarrow \dots \searrow \) См. рисунок \ (\PageIndex{5a}\).

Рисунок \(\PageIndex{5a}\): Иллюстрация конечного поведения многочлена.
Шаг 2.
Этот граф имеет два \(x\)-перехвата. В точке \(x=−3\) множитель возводится в квадрат, что указывает на кратность 2. График будет отскакивать от точки пересечения \(x\). В точке \(x=5\) функция имеет кратность, равную единице, что указывает на то, что график пересечет ось на этом пересечении.
Перехват \(y\) находится путем вычисления \(f(0)\).
Рисунок \(\PageIndex{5b}\): график пересекается в точке пересечения \(x\) \((5, 0)\) и отскакивает в точке \((-3, 0)\). \(y\)-перехват равен \((0, 90)\).
Шаг 3. Соедините конечные линии поведения с точками пересечения.

92&=2 \\ x&=0, \:x=0 &&& x&={\pm}1 &&& x&={\pm}\sqrt{2} \end{align*}\] .
Это дает нам пять \(x\)-отрезков: \( (0,0)\), \((1,0)\), \((−1,0)\), \((\sqrt {2},0)\) и \((−\sqrt{2},0)\).
\(x\)-отрезки \((1,0)\), \((−1,0)\), \((\sqrt{2},0)\) и \((−\ sqrt{2},0)\) имеют нечетную кратность 1, поэтому график будет пересекать ось \(x\) в этих точках пересечения.
Пересечение \(x\) \((0,0)\) имеет четную кратность 2, поэтому график останется на той же стороне оси \(x\) в точке 2. (Говорят, что график касаться оси x в точке 2 или «отскакивать» от оси \(x\) в точке 2). 92+5=0 \\
x=3 & \text{or} & x=−3 &\text{or} &\text{(нет действительного решения)}
\end{массив} \)(x\)-отрезки \((3,0)\) и \((–3,0)\) имеют нечетную кратность 1, поэтому график будет пересекать ось \(x\) в этих точках пересечения.
Шаг 3. Многочлен является четной функцией, поскольку \(f(-x)=f(x)\), поэтому график симметричен относительно оси y. График появится ниже.
 Мнимые нули не являются \(x\)-отрезками, но приведенный ниже график показывает, что они вносят свой вклад в «покачивания» (точки усечения) на графике функции. 93(х+3)(х+2)\)
Мнимые нули не являются \(x\)-отрезками, но приведенный ниже график показывает, что они вносят свой вклад в «покачивания» (точки усечения) на графике функции. 93(х+3)(х+2)\)Поворотные точки
Определение: Поворотные точки
Поворотная точка — это точка графика, в которой график меняется от возрастания к убывающему (от подъема к падению) или от убывания к возрастанию (от падения к росту).
Многочлен степени \(n\) будет иметь не более \(n\) \(x\)-пересечений и \(n−1\) точек поворота.
Степень полиномиальной функции помогает нам определить количество \(x\)-перехватов и количество точек поворота. Полиномиальная функция от \(n\) 93\)
- Ответ
Имеется не более 12 \(x\)-перехватов и не более 11 поворотных точек.
Пример \(\PageIndex{12}\): получение выводов о полиномиальной функции на основе факторов
Учитывая функцию \(f(x)=−4x(x+3)(x−4)\), определить \(y\)-перехват и количество, расположение и кратность \(x\)-перехватов, и максимальное количество точек поворота.

Раствор
Перехват \(y\) находится путем вычисления \(f(0)\).
\[\begin{align*} f(0)&=−4(0)(0+3)(0−4)=0 \end{align*}\]
\(y\)- перехват равен \((0,0)\).
\(x\)-перехваты находятся путем нахождения нулей функции.
\( \begin{array}{ccc}
&0=-4x(x+3)(x-4) \\
x=0 & \text{или} \quad x+3=0 \quad\text {or} & x-4=0 \\
x=0 & \text{or} \quad x=−3 \quad\text{or} & x=4
\end{массив} \)Три \(x\)-перехваты \((0,0)\),\((–3,0)\) и \((4,0)\) имеют нечетную кратность 1,
Степень равна 3, поэтому граф имеет не более 2 поворотных точек.
Попробуйте \(\PageIndex{13}\)
Учитывая функцию \(f(x)=0,2(x−2)(x+1)(x−5)\), определите локальное поведение.
- Ответить
Функция представляет собой многочлен 3-й степени с тремя точками пересечения \(x\) \((2,0)\), \((−1,0)\) и \((5,0)\), все из которых имеют кратность 1, \(y\)-отрезок равен \((0,2)\), а граф имеет не более 2 точек поворота.

Пример \(\PageIndex{14}\): вывод полиномиальной функции из графика
Какой вывод мы можем сделать о степени полинома и старшем коэффициенте, представленном на графике, показанном ниже, на основе его пересечений и точек поворота?
График многочлена.Раствор
- Поведение графика в конце говорит нам, что это график полинома четной степени (концы идут в одном направлении) с положительным старшим коэффициентом (растет вправо).
- Граф имеет 2 \(x\)-отрезка, каждый с нечетной кратностью, что предполагает степень 2 или выше.
- На графике есть 3 поворотные точки, что предполагает степень 4 или выше.
Вывод: степень многочлена четная и не меньше 4.
Попробуйте \(\PageIndex{15}\)
Какой вывод мы можем сделать о многочлене, представленном на графике, показанном ниже, на основе его точек пересечения и точек поворота?
Полиномиальная функция
- Ответ
Поведение в конце указывает на полиномиальную функцию нечетной степени (заканчивается в противоположном направлении) с отрицательным старшим коэффициентом (падает вправо).
 Имеется 3 \(x\)-перехвата с нечетной кратностью и 2 точки поворота, поэтому степень нечетна и не меньше 3.
Имеется 3 \(x\)-перехвата с нечетной кратностью и 2 точки поворота, поэтому степень нечетна и не меньше 3.
Напишите формулу для многочлена, учитывая его график
Теперь, когда мы знаем, как находить нули полиномиальных функций, мы можем использовать их для написания формул на основе графиков. Поскольку полиномиальная функция , записанная в факторизованной форме, будет иметь \(х\)-перехват, где каждый множитель равен нулю, мы можем сформировать функцию, которая будет проходить через набор \(х\)-перехватов, введя соответствующий набор факторов.
Примечание: факторизованная форма полиномов 9{p_n}\), где степени \(p_i\) каждого фактора могут быть определены поведением графика на соответствующем пересечении, а коэффициент растяжения \(a\) может быть определен при заданном значении функции, отличном от \(x\)-перехват.
Как: Имея график полиномиальной функции, напишите формулу для этой функции.
- Определите точки пересечения \(x\) на графике, чтобы найти множители многочлена.

- Изучите поведение графика на пересечениях \(x\), чтобы определить кратность каждого фактора.
- Найдите полином наименьшей степени, содержащий все множители, найденные на предыдущем шаге.
- Используйте любую другую точку на графике (может быть, проще всего пересечь \(y\)), чтобы определить коэффициент растяжения.
Пример \(\PageIndex{16}\): Написание формулы для полиномиальной функции на основе графика
Постройте факторизованную форму возможного уравнения для каждого приведенного ниже графика.
(а) Рисунок \(\PageIndex{16a}\): График \(h(x)\). Раствор
Глядя на график этой функции, как показано на рисунке \(\PageIndex{16}\), видно, что есть \(x\)-перехваты в точках \(x=−3,−2, \text{ и }1\).
Каждый отрезок \(x\) соответствует нулю полиномиальной функции, а каждый нуль дает множитель, так что теперь мы можем записать полином в факторизованной форме.

\(ч(х)=а(х+3)(х+2)(х-1) \)
Коэффициент растяжения \(a\) можно найти, используя другую точку на графике, например точку пересечения \(y\), \((0,-6)\).
\[\begin{align*} f(0)&=a(0+3)(0+2)(0−1) \\ −6&=a(-6) \\ a&=1 \end{align *}\]
Таким образом \( h(x)=(x+3)(x+2)(x−1). \)
(б)
Рисунок \(\PageIndex{16b}\).Решение 92 (х + 3)\)
Ключевые понятия
- Полиномиальные функции степени 2 и выше являются гладкими, непрерывными функциями.
- Чтобы найти нули полиномиальной функции, если ее можно разложить на множители, разложите функцию на множители и приравняйте каждый множитель к нулю.
- Другой способ найти точки пересечения \(x\) полиномиальной функции состоит в том, чтобы построить график функции и определить точки, в которых график пересекает ось \(x\).

- Проверка на симметричность. Если функция четная, ее график симметричен относительно оси \(y\), то есть \(f(−x)=f(x)\). Если функция является нечетной функцией, ее график симметричен относительно начала координат, то есть \(f(-x)=-f(x)\). 93\), так что конечным результатом является поведение вертикально отраженного кубика, при этом график падает вправо и движется в противоположном направлении (вверх) влево: \(\nwarrow \dots \searrow \) См. рисунок \ (\PageIndex{5a}\).

 График касается оси \(x\), поэтому кратность нуля должна быть четной. Ноль числа −3 имеет кратность 2.
График касается оси \(x\), поэтому кратность нуля должна быть четной. Ноль числа −3 имеет кратность 2. Поскольку кривая в точке -5 несколько плоская, кратность нуля, скорее всего, равна 3, а не 1.
Поскольку кривая в точке -5 несколько плоская, кратность нуля, скорее всего, равна 3, а не 1.  Давайте соберем все это вместе и посмотрим на шаги, необходимые для построения графика полиномиальных функций.
Давайте соберем все это вместе и посмотрим на шаги, необходимые для построения графика полиномиальных функций.

 Мнимые нули не являются \(x\)-отрезками, но приведенный ниже график показывает, что они вносят свой вклад в «покачивания» (точки усечения) на графике функции. 93(х+3)(х+2)\)
Мнимые нули не являются \(x\)-отрезками, но приведенный ниже график показывает, что они вносят свой вклад в «покачивания» (точки усечения) на графике функции. 93(х+3)(х+2)\)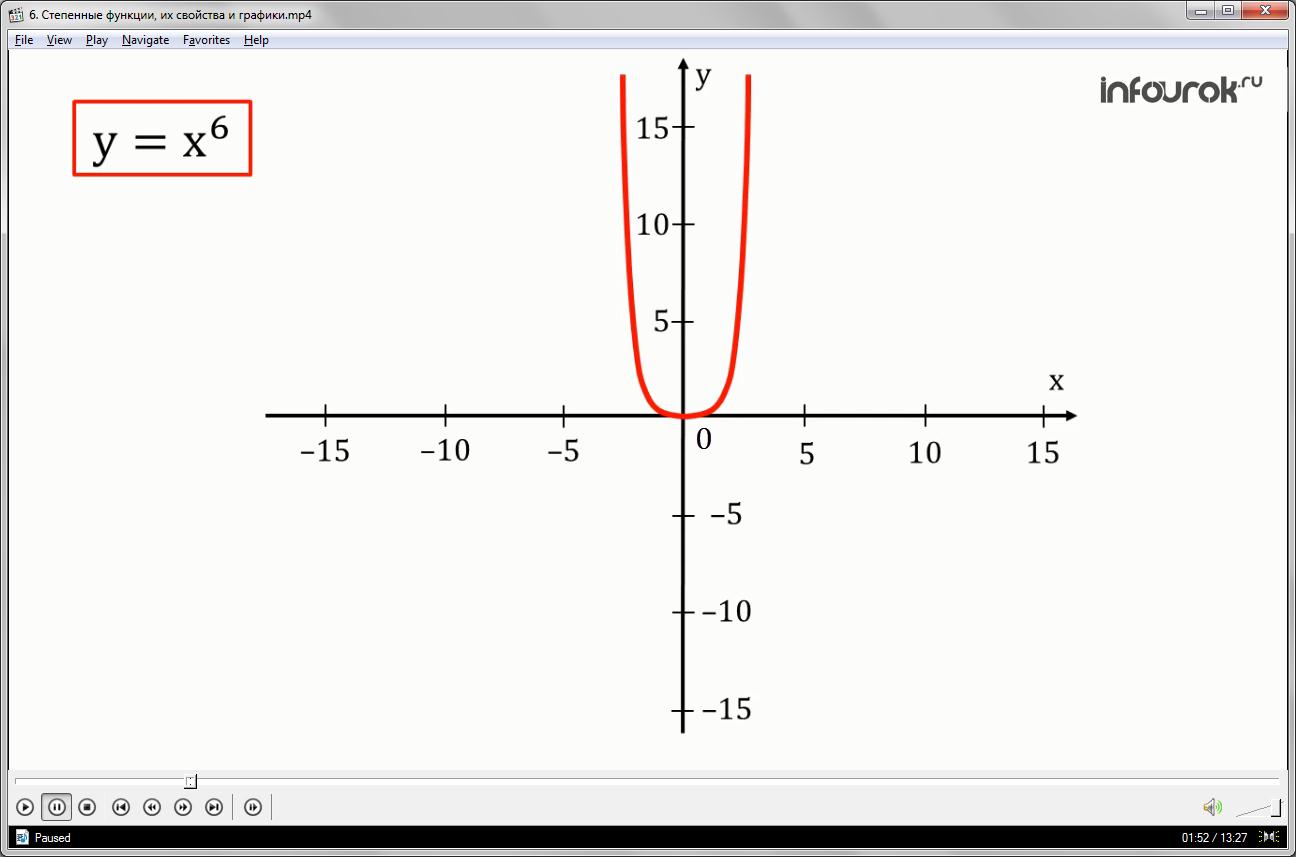

 Имеется 3 \(x\)-перехвата с нечетной кратностью и 2 точки поворота, поэтому степень нечетна и не меньше 3.
Имеется 3 \(x\)-перехвата с нечетной кратностью и 2 точки поворота, поэтому степень нечетна и не меньше 3.

