Множества состоящего из 10 элементов примеры: Приведите примеры пустого множества — Информатика

Приведите примеры: а) пустого множества; б) множества, состоящего из одного элемента; в) множества, состоящего из 10 элементов; г) бесконечного множества. 

Ответы 2

а) Пустое множество — люди в возрасте от 300 до 500 лет.
б) Торт в коробке
с) 10 монет в кошельке
д) Все натуральные числа.

спасибо)

• Автор:

  asarc7u

• Оценить ответ:

  0

Знаешь ответ? Добавь его сюда!

Последние вопросы

• Французский язык

  11 часов назад

  Помогите пожалуйста с французским упр 4🙏🙏🙏

• Математика

  14 часов назад

  24. 02.2022?

  Ділянку прямокутної форми що має розміри 250м на 80м, засіяли кукурудзою. Скільки зерна було використано для цього, якщо на 10000м потрібно 18 кг?

• Математика

  16 часов назад

  32) найдите область определение функции z = (1/x) + (1/y)

• Математика

  16 часов назад

  33) найдите область определение функции z = (y — 1) / (x² + y²)

• Математика

  16 часов назад

  31) найдите область определение функции z = 1 / (x-y)

• Геометрия

  18 часов назад

  100 баллов таму кто поможет

• Английский язык

  18 часов назад

  Subjunctive Mood

  Test

  I. Choose the right form:

  1. Jack doesn’t speak English. If he (spoke/ had spoken) English, he would (get/ have got) a good job at a travel agency. 2. I was in Rome on business. If I (had/ had had) more free time, I would (go/ have gone) sightseeing. 3. It is unlikely that he will repair his car soon. He would (give/ have given) us a ride to the train station if he (repaired/ had repaired) his car soon enough. 4. Bob failed at his exams. If he (

  worked/ had worked) harder he wouldn’t (fail/ have failed) at his exams. 5. The weather is too cold today. If it (were/ had been) a little warmer, we would (go/ have gone) for a walk. 6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.

  II. Describe these situations in a different way. Use the Subjunctive Mood.

  1. The problems of the company were very serious. As a result Tom worked hard all the weekends.
  2. The alarm clock was broken. And John was late for his first lesson.
  3. My mother was in Italy. I had to cook everything on my own.
  4. She lost her mobile phone. That’s why I gave her mine.
  5. She was late for their wedding. Her fiancé got angry.

  III. Translation.

  1. Если бы Майк сдал отчет вовремя, его бы не уволили. 
  2. Жаль, что арбуз оказался гнилой. 
  3. Если бы она не вмешивалась в его дела, он бы не дерзил ей.
  4. Если бы не твоя помощь, я бы не смог закрепить эти шторы.
  5. Если бы Джонни был хорошим студентом, он бы не использовал так много шпаргалок на экзамене.
  6. Мне бы хотелось, чтобы ты заботился о своем здоровье!
  7. Если бы тебе было все равно, ты бы не ревновал ее к другим мужчинам.

• Английский язык

  18 часов назад

  Subjunctive Mood

  Test

  I. Choose the right form:

  1. Jack doesn’t speak English. If he (spoke/ had spoken) English, he would (get/ have got) a good job at a travel agency. 2. I was in Rome on business. If I (had/ had had) more free time, I would (go/ have gone) sightseeing. 3. It is unlikely that he will repair his car soon. He would (give/ have given) us a ride to the train station if he (repaired/ had repaired) his car soon enough. 4. Bob failed at his exams. If he (worked/ had worked) harder he wouldn’t (fail/ have failed) at his exams. 5. The weather is too cold today. If it (were/ had been) a little warmer, we would (go/ have gone) for a walk.

  6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.

  II. Describe these situations in a different way. Use the Subjunctive Mood.

  1. The problems of the company were very serious. As a result Tom worked hard all the weekends.
  2. The alarm clock was broken. And John was late for his first lesson.
  3. My mother was in Italy. I had to cook everything on my own.
  4. She lost her mobile phone. That’s why I gave her mine.
  5. She was late for their wedding. Her fiancé got angry.

  III. Translation.

  1. Если бы Майк сдал отчет вовремя, его бы не уволили. 
  2. Жаль, что арбуз оказался гнилой. 
  3. Если бы она не вмешивалась в его дела
     , он бы не дерзил ей.
  4. Если бы не твоя помощь, я бы не смог закрепить эти шторы.
  5. Если бы Джонни был хорошим студентом, он бы не использовал так много шпаргалок на экзамене.
  6. Мне бы хотелось, чтобы ты заботился о своем здоровье!
  7. Если бы тебе было все равно, ты бы не ревновал ее к другим мужчинам.

• Литература

  1 день назад

  А где почему это напряжоный момент

• Биология

  1 день назад

  У голонасінних рослин уперше з’являєтся:

• Математика

  1 день назад

  Математика третий класс запиши все возможные значения длины и ширины по известному периметру прямоугольника периметр 98 м 120 м 140

• Алгебра

  1 день назад

  Решите графически системы уравнений (выражая у через х) 1 система {х+2у=6 х-4у=0} 2 система{3у-х=3 х-4у=1}

• Физика

  1 день назад

   Електричний нагрівник за 7 хв доводить до кипіння 10 кг води, початкова температура  якої дорівнює 20 °С. Якою є сила струму в його нагрівальному елементі, якщо напруга в  мережі становить 220 В? ККД нагрівника 90 %.

• Физика

  2 дня назад

  Тело движется вдоль оси Ох. График зависимости проекции его скорости Vх от времени t изображён на рисунке. Найди путь S, пройденный телом за рассмотренный промежуток времени. Результат вырази в метрах, округлив до целого числа.

• Українська мова

  2 дня назад

  Допоможіть будь ласка! Написати твір — роздум за алгоритмом.​

Персональный сайт учителя информатики — ответы на «Вопросы и задания»

Объекты окружающего мира Вопросы и задания, Информатика 6 класс Босова Вопросы и задания, Информатика 6 класс Босова ответы на вопросы, Информатика 6 класс Босова ГДЗ, Информатика 6 класс Босова ответы Задание 1 Дайте имена объектам: а) выросшим на грядке; б) проживающим в Москве; в) управляющим трактором; г) посещающим детский сад; д) находящимся в школе. Решение а) овощ; б) москвич; в)тракторист; г) дошкольник; д) школьник, преподаватель, мебель. Задание 2 Приведите примеры: а) пустого множества; б) множества, состоящего из одного элемента; в) множества, состоящего из 10 элементов; г) бесконечного множества. Решение а) числа, которые делятся на 0; б) Солнце; в) цифры; г) натуральные числа. Задание 3 Дайте несколько возможных общих имён каждой группе объектов. Выберите из них самое подходящее. Ответ обоснуйте: а) Буратино, Мальвина, Пьеро, Артемон; б) «12 месяцев», «Морозно», «Золушка», «Синяя борода»; в) Москва, Санкт-Петербург, Новосибирск; г) Енисей, Волга, Лена, Москва; д) Москва, Санкт-Петербург, Тула. Решение а) герои сказок б) сказки в) столицы г) реки д) города науки Задание 4 Вспомните по одному объекту каждого из приведённых множеств и обозначьте его единичным именем в этом множестве: а) мореплаватель; б) орфограмма; в) формула; г) былина. Решение а) Христофор Колумб; б) безударная гласная в корне слова; в) S прямоугольника = a * b; г) Илья Муромец и Соловей разбойник. Задание 5 Назовите общие имена объектов, о которых сообщается в путеводителях. Назовите единичные имена объектов, о которых может рассказать человек после туристической поездки по России. Решение а) общие имена: Кремль, Эрмитаж; б) единичные имена: собор, крепость. Задание 6 Каким образом можно узнать признаки интересующих вас объектов? Решение а) наблюдение за объектом; б) потрогать; в) понюхать; г) механические испытания; д) химические анализ. Задание 7 Какие свойства можно привести при описании множества объектов? Можно ли для множества объектов привести значения величин? Приведите примеры. Решение При описании множества объектов можно привести свойства — цвет, размер, положение и др. Например, множество животных в зоопарке. Задание 8 Для каждого примера укажите объект, его свойство, определяющую свойство величину и её значение: а) рыжеволосый человек; б) семикилограммовый арбуз; в) фарфоровая чашка; г) семнадцатидюймовый монитор. Решение а) Объект — человек; Свойство — рыжий цвет волос. б) Объект — арбуз; Свойство — вес 7 кг. в) Объект — чашка; Свойство — материал фарфор. г) Объект — монитор; Свойство — диагональ 17 дюймов. Задание 9 Назовите для каждого из приведённых действий два предмета, с которыми указанное действие человек выполняет по-разному: собрать; заполнить; открыть; связать; включить; сложить; измерить; поймать. Решение а) друзей, грибы б) анкету, ведро в) магазин, книгу г) факты, верёвки д) логику, свет е) числа, рубашку ж) горе, объём з) удачу, зайца Задание 10 Приведите примеры возможных активных и пассивных действий для объектов «птица», «мяч», «велосипед». Решение Активные действия: птица — летит, мяч — прыгает, велосипед — едет. Пассивные действия: птица — сидит, мяч — лежит, велосипед — стоит. Задание 11 Приведите примеры пошаговых описаний действий человека. Как их называют? Решение Пошаговые действия — это алгоритм. Например: завариваем чай. 1) Вскипятить чайник; 2) Взять кружку; 3) Налить в кружку воду; 4) Добавить заварку; 5) Добавить сахар. Задание 12 Ответьте на следующие вопросы. а) Значением какой величины определяется переход чайника в состояние «кипит»? б) В каком состоянии находится вода, если её нельзя вылить из чашки? в) В каком состоянии находится карандаш, когда с его помощью нельзя ничего написать или нарисовать? г) В каком состоянии находится долька яблока, если её можно согнуть, и она при этом не ломается? Решение а) значением температуры равной 100 градусов Цельсия; б) вода находится в состоянии льда, т. е. температура меньше 0 градусов; в) карандаш не заточен; г) долька яблока запечена в духовке.

Теория наборов | Введение в математику колледжа |

Модуль 1: Базовый набор

Для нас естественно классифицировать предметы по группам или наборам и рассматривать, как эти наборы пересекаются друг с другом. Мы можем использовать эти наборы для понимания отношений между группами и для анализа данных опроса.

Основы

У коллекционера произведений искусства может быть коллекция картин, а у любителя музыки — коллекция компакт-дисков. Любая коллекция предметов может составить набор .

Комплект

Набор представляет собой набор различных объектов, называемых элементами набора

Набор может быть определен путем описания содержимого или путем перечисления элементов набора, заключенных в фигурные скобки.

Пример 1

Некоторые примеры наборов, определяемых описанием содержимого:

1. Набор всех четных чисел
2. Набор всех книг, написанных о путешествии в Чили

Ответы

Некоторые примеры наборов, определяемых перечислением элементов набора:

1. {1, 3, 9, 12}
2. {красный, оранжевый, желтый, зеленый, синий, индиго, фиолетовый}

Набор просто определяет содержимое; порядок не важен. Набор, представленный {1, 2, 3}, эквивалентен набору {3, 1, 2}.

Обозначение

Обычно мы будем использовать переменную для представления набора, чтобы упростить обращение к этому набору позже.

Символ ∈ означает «является элементом».

Набор, который не содержит элементов { }, называется пустым набором и обозначается ∅

Пример 2

Пусть A = {1, 2, 3, 4}

Чтобы отметить, что 2 является элементом множества, мы должны написать 2 ∈ A

. Иногда коллекция может содержать не все элементы набора. Например, у Криса есть три альбома Мадонны. Хотя коллекция Криса представляет собой набор, мы также можем сказать, что это подмножество большего набора всех альбомов Мадонны.

Подмножество

Подмножество множества A — это другое множество, которое содержит только элементы из множества A , но может не содержать все элементы множества A .

Если B является подмножеством A , мы пишем B ⊆ A

Правильное подмножество — это подмножество, которое не идентично исходному набору — оно содержит несколько элементы.

Если B является подмножеством A , пишем B ⊂ A

Пример 3

Рассмотрим эти три набора:

A = набор всех ровных чисел

B = {2, 4, 6}

C = {2, 3, 4, 6}

Здесь B ⊂ A , поскольку каждый элемент B также является четным числом, поэтому элемент A .

Более формально мы могли бы сказать B ⊂ A , так как если x ∈ B , затем x ∈ A .

Также верно, что B ⊂ C .

C не является подмножеством A , так как C содержит элемент 3, который не содержится в A

Пример 4

Предположим, набор содержит пьесы «Много шума из ничего», «Макбет» и «Сон в летнюю ночь». Подмножеством какого большого множества может быть это?

Здесь может быть много возможных ответов. Одним из них будет набор пьес Шекспира. Это также подмножество всех когда-либо написанных пьес. Это также подмножество всей британской литературы.

Попробуйте сейчас

Набор A = {1, 3, 5}. Подмножеством какого большого множества может быть это?

Объединение, пересечение и дополнение

Обычно наборы взаимодействуют. Например, вы с новым соседом по комнате решаете устроить домашнюю вечеринку и приглашаете друзей. На этой вечеринке объединяются два набора, хотя может оказаться, что есть друзья, которые были в обоих наборах.

Объединение, пересечение и дополнение

объединение двух наборов содержит все элементы, содержащиеся в любом наборе (или в обоих наборах). Объединение обозначается как A ⋃ B. Более формально, x ∊ A ⋃ B , если x ∈ A или 9005 9 x ∈ B (или оба)

пересечение двух множеств содержит только те элементы, которые есть в обоих множествах. Пересечение обозначено как A ⋂ B. Более формально, x ∈ A ⋂ B , если x ∈ A и x ∈ B.

Дополнение набора A содержит все, что является , а не в наборе A .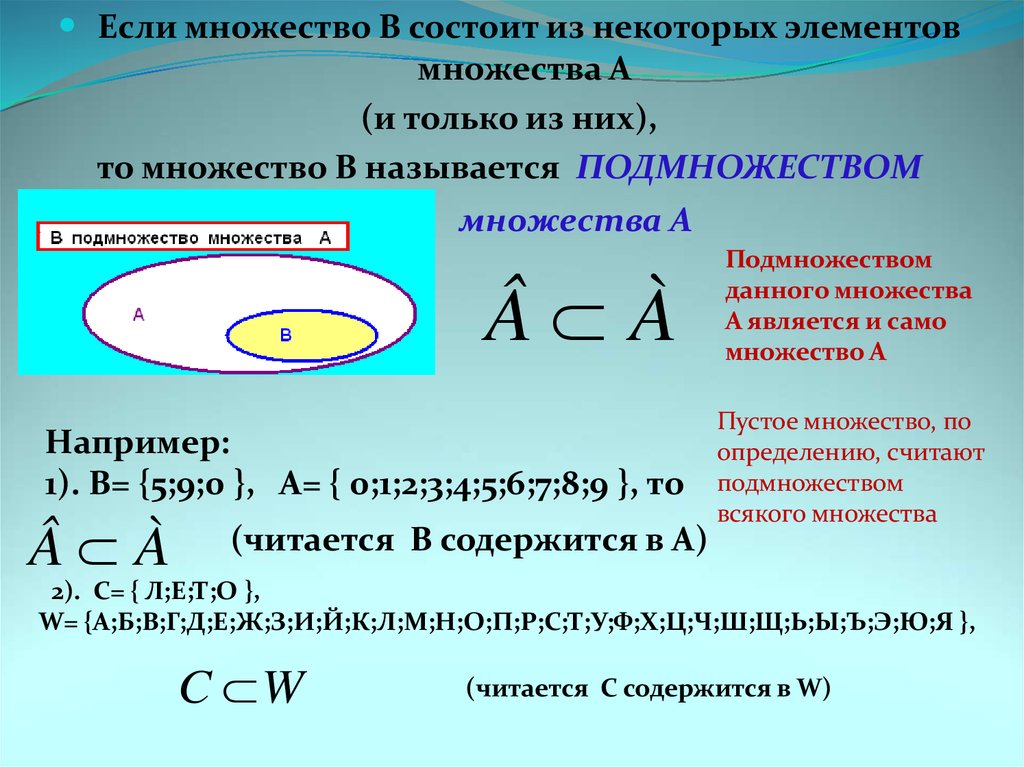 Дополнение обозначается как A’ , или A ^c , или иногда ~ A .

Пример 5

Рассмотрим наборы:

A = {красный, зеленый, синий}

B = {красный, желтый, оранжевый}

C = {красный, оранжевый, желтый, зеленый, синий, фиолетовый}

Найдите следующее:

1. Найдите A ⋃ B
2. Найти А ⋂ В
3. Найти A ^c ⋂ C

Ответы

1. Объединение содержит все элементы любого набора: A ⋃ B = {красный, зеленый, синий, желтый, оранжевый} Обратите внимание, что мы указываем красный только один раз.
2. Пересечение содержит все элементы обоих наборов: A ⋂ B = {red}
3. Здесь мы ищем все элементы, которые , а не , в наборе A , а также в C . A ^c ⋂ C = {оранжевый, желтый, фиолетовый}

Попробуйте сейчас

Используя наборы из предыдущего примера, найдите A ⋃ C и B ^c   ⋂ А

Обратите внимание, что в приведенном выше примере было бы сложно просто попросить A ^c , поскольку в комплект входит все, от цвета фуксии до щенков и арахисового масла. По этой причине дополнения обычно используются только с пересечениями или когда у нас есть универсальный набор.

Универсальный набор

Универсальный набор — это набор, содержащий все интересующие нас элементы. Это должно определяться контекстом.

Дополнение относится к универсальному набору, поэтому A ^c   содержит все элементы универсального набора, которых нет в A .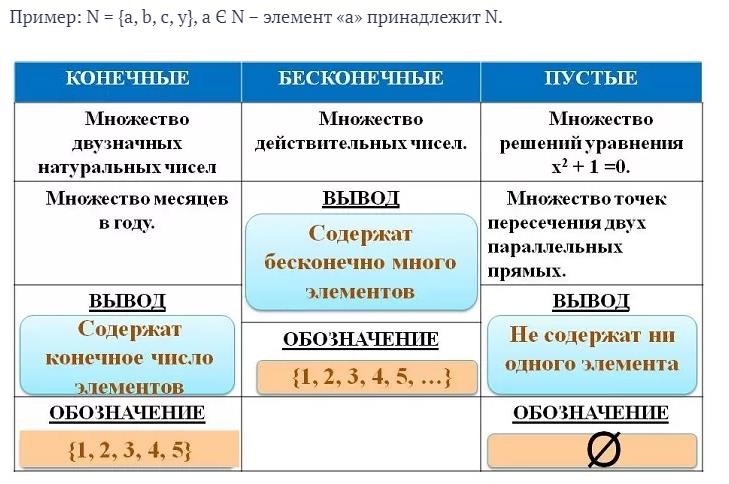

Пример 6

1. Если бы мы обсуждали поиск книг, универсальный набор мог бы включать все книги в библиотеке.
2. Если бы мы группировали ваших друзей на Facebook, универсальным набором были бы все ваши друзья на Facebook.
3. Если вы работали с наборами чисел, универсальный набор мог бы состоять из всех целых чисел, всех целых чисел или всех действительных чисел

Пример 7

Предположим, что универсальный набор равен U = все целые числа от 1 до 9. Если A = {1, 2, 4}, то A ^c = {3, 5, 6, 7, 8 , 9}.

Как мы видели ранее с выражением A ^c   ⋂ C , операции над множествами можно группировать вместе. Символы группировки можно использовать так же, как и с арифметикой — для принудительного порядка операций.

Пример 8

Предположим, H = {кошка, собака, кролик, мышь}, F = {собака, корова, утка, свинья, кролик} и W = {утка, кролик, олень, лягушка, мышь}

1. Найти ( H ⋂ F ) ⋃ W
2. Найти В ⋂ ( Ж ⋃ В )
3. найти ( H ⋂ F ) ^c ⋂ W

Решения

1. Начнем с пересечения: H ⋂ F = {собака, кролик}. Теперь объединяем этот результат с W : ( H ⋂ F ) ⋃ W = {собака, утка, кролик, олень, лягушка, мышь}
2. Начнем с союза: Ж ⋃ Ж = {собака, корова, кролик, утка, свинья, олень, лягушка, мышь}. Теперь мы пересекаем этот результат с H : H ⋂ ( F ⋃ W ) = {собака, кролик, мышь}
3. Начинаем с перекрестка: H ⋂ F = {собака, кролик}. Теперь мы хотим найти элементы W , которые являются , а не в H ⋂ F. ( H ⋂ F) ^c 9 0060  ⋂ W = {утка, олень , лягушка, мышь}

Диаграммы Венна

Чтобы визуализировать взаимодействие множеств, Джон Венн в 1880 году решил использовать перекрывающиеся круги, опираясь на аналогичную идею, использованную Леонардом Эйлером в восемнадцатом веке. Эти иллюстрации теперь называются Диаграммы Венна .

Диаграмма Венна

Диаграмма Венна представляет каждый набор в виде окружности, обычно нарисованной внутри прямоугольника, представляющего универсальный набор. Перекрывающиеся области обозначают элементы, общие для обоих наборов.

Базовые диаграммы Венна могут иллюстрировать взаимодействие двух или трех множеств.

Пример 9

Создайте диаграммы Венна для иллюстрации A ⋃ B , A ⋂ B и A ^c ⋂ B

A ⋃ B содержит все элементы набора или .

A ⋂ B содержит только те элементы в обоих наборах — в перекрытии кружков.

A ^c будет содержать все элементы кроме в наборе A . A ^c   ⋂ B будет содержать элементы набора B , которых нет в наборе A .

Пример 10

Для иллюстрации используйте диаграмму Венна ( H ⋂ F ) ^c ⋂ W

Начнем с определения всего в наборе H ⋂ Ф

Теперь ( H ⋂ F ) ^c ⋂ W будет содержать все , а не в указанном выше наборе, который также находится в наборе 9.0059 Вт .

Пример 11

Создайте выражение для представления выделенной части показанной диаграммы Венна.

Элементы в выделенном наборе есть в наборах H и F , но отсутствуют в наборе W . Таким образом, мы могли бы представить этот набор как H ⋂ F ⋂ W ^c

Попробуйте сейчас

Создайте выражение для представления выделенной части диаграммы Венна, показанной на рисунке 9.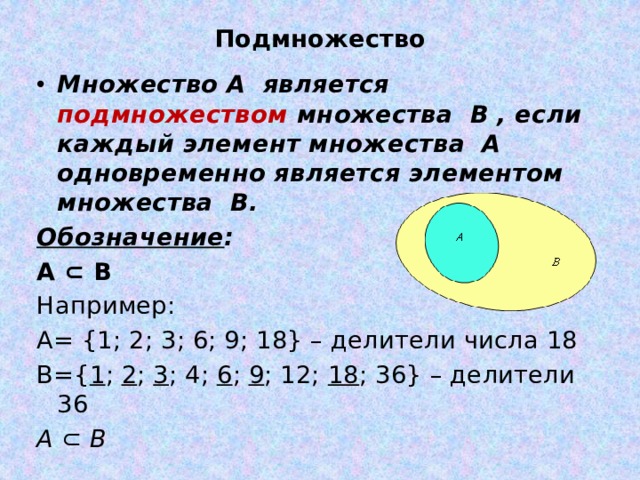 0005

Мощность

Часто нас интересует количество элементов в наборе или подмножестве. Это называется мощностью множества.

Мощность

Количество элементов в наборе является мощностью этого набора.

Мощность множества A часто обозначается как | А | или n( A )

Пример 12

Пусть А = {1, 2, 3, 4, 5, 6} и В = {2, 4, 6, 8}.

Какова мощность B ? А ⋃ Б , А ⋂ Б ?

Ответы

Мощность B равна 4, так как в наборе 4 элемента.

Количество элементов A ⋃ B равно 7, так как A ⋃ B = {1, 2, 3, 4, 5, 6, 8}, которое содержит 7 элементов.

Мощность A ⋂ B равна 3, так как A ⋂ B = {2, 4, 6}, который содержит 3 элемента.

Пример 13

Какова мощность P = множества английских названий месяцев года?

Ответы

Мощность этого множества равна 12, так как в году 12 месяцев.

Иногда нас может интересовать мощность объединения или пересечения множеств, но мы не знаем фактических элементов каждого множества. Это обычное дело в геодезии.

Пример 14

В опросе 200 человек спрашивали: «Какой напиток вы пьете по утрам» и предлагали варианты:

• Только чай
• Только кофе
• Кофе и чай

Допустим, 20 сообщают только о чае, 80 сообщают только о кофе, 40 сообщают и то, и другое. Сколько людей пьют чай по утрам? Сколько людей не пьют ни чай, ни кофе?

Ответы

На этот вопрос проще всего ответить, создав диаграмму Венна. Мы видим, что мы можем найти людей, которые пьют чай, добавляя тех, кто пьет только чай, к тем, кто пьет и то, и другое: 60 человек.

Мы также можем видеть, что те, кто пьет, не входят ни в одну из трех других групп, поэтому мы можем посчитать их, вычитая из мощности универсального множества 200.

200 – 20 – 80 – 40 = 60 человек, которые не пьют.

Пример 15

В опросе спрашивается: «Какими онлайн-сервисами вы пользовались в прошлом месяце?»

• Твиттер
• Фейсбук
• Пользовались обоими

Результаты показывают, что 40% опрошенных использовали Twitter, 70% использовали Facebook, а 20% использовали и то, и другое. Сколько людей не пользовались ни Twitter, ни Facebook?

Ответы

Пусть T будет множеством всех людей, которые использовали Twitter, а F будет множеством всех людей, которые использовали Facebook. Обратите внимание, что в то время как мощность F составляет 70%, а мощность T равна 40%, мощность F ⋃ T не просто 70% + 40%, так как это будет учитывать тех, кто использует оба услуги дважды. Чтобы найти мощность F ⋃ T , мы можем добавить мощность F и мощность T , затем вычтите те пересечения, которые мы посчитали дважды. В символах

n( F ⋃ T ) = n( F ) + n( T ) – n( F ⋂ T )

н( Ж ⋃ Т ) = 70% + 40% – 20% = 90%

Теперь, чтобы узнать, сколько людей не пользовались какой-либо услугой, мы ищем количество элементов ( F ⋃ T ) c . Так как универсальное множество содержит 100% людей и мощность F ⋃ T = 90%, количество элементов ( F ⋃ T ) c должно составлять остальные 10%.

Предыдущий пример иллюстрировал два важных свойства

Кардинальные свойства

n( A ⋃ B ) = n( A ) + n( B ) – n( A ⋂ B )

n(Ac ) = n(U ) – п( А )

Обратите внимание, что первое свойство также можно записать в эквивалентной форме, найдя мощность пересечения:

n( A ⋂ B ) = n( A ) + n( B ) – n( A ⋃ B ) 9 0005

Пример 16

Были опрошены 50 студентов, и их спросили, изучают ли они курс социальных наук (SS), гуманитарных наук (HM) или естественных наук (NS) в следующем квартале.

21 проходил курс SS	26 человек проходили курс HM
19 проходили курс НС	9 брали SS и HM
7 принимали SS и NS	10 принимали HM и NS
3 брали всех троих	7 ничего не брали

Сколько студентов посещают только курс SS?

Ответы

Может быть полезно взглянуть на диаграмму Венна. Из предоставленных данных мы знаем, что в регионе e есть 3 ученика и 7 учеников в регионе h .

Так как 7 студентов изучали курс SS и NS, мы знаем, что n( d ) + n( e ) = 7. Поскольку мы знаем, что в регионе 3 учатся 3 ученика, в регионе d должно быть 7 – 3 = 4 ученика.

Аналогичным образом, поскольку 10 студентов изучают HM и NS, включая регионы e и f , должно быть 10 – 3 = 7 студентов в регионе f .

Поскольку SS и HM сдавали 9 студентов, в регионе b должно быть 9 – 3 = 6 студентов.

Итак, мы знаем, что 21 студент проходил курс СС. В том числе студенты из регионов а, б, г, и е . Поскольку мы знаем количество студентов во всех регионах, кроме и , мы можем определить, что 21 – 6 – 4 – 3 = 8 студентов находятся в регионе и .

8 студентов проходят только курс SS.

Попробуйте сейчас

Было опрошено 150 человек, и их спросили, верят ли они в НЛО, призраков и снежного человека.

43 верили в НЛО	44 верили в призраков
25 верили в снежного человека	10 верили в НЛО и призраков
8 верил в призраков и йети	5 верили в НЛО и снежного человека
2 верил во всех троих

Сколько опрошенных верили хотя бы в одну из этих вещей?

Лицензии и атрибуты

Контент с лицензией CC, совместно используемый ранее

• Наборы. Автор : Дэвид Липпман. Расположен по адресу : http://www.opentextbookstore.com/mathinsociety/. Проект : Математика в обществе. Лицензия : CC BY-SA: Attribution-ShareAlike

Предыдущая

Следующая

Комбинаторика — Сколько подмножеств с нечетным числом элементов имеет набор из 10 элементов?

спросил 3 года, 4 месяца назад

Изменено 2 года, 1 месяц назад

Просмотрено 8к раз 99 = 512 $, чего я не понимаю. Разве вы не считаете количество подмножеств, например, с элементами $2$? (Я знаю, что это одно и то же решение, просто для меня это не имеет смысла).

Может ли кто-нибудь объяснить мне, почему это правильно и что за этим стоит?

• комбинаторика
• дискретная математика

$\endgroup$

$\begingroup$

Один из способов увидеть это комбинаторно — рассмотреть $10$ элементов в некотором порядке. С каждым из первых $9{n-1}$.

$\endgroup$

$\begingroup$

Начните с набора из десяти элементов и удалите один элемент, назвав его $x$. Теперь у нас есть набор из девяти элементов. Для каждого подмножества $S$ из набора из девяти элементов либо

, либо

, либо
• $S$ содержат нечетное количество элементов, поэтому их следует считать подмножеством набора из десяти элементов, содержащего нечетное количество элементов.
• $\{x\} \cup S$ содержит нечетное количество элементов, поэтому его следует считать подмножеством набора из десяти элементов, содержащего нечетное количество элементов. 99$ подмножество набора из девяти элементов. Мы показали, что каждое из них можно превратить в подмножество набора из десяти элементов с нечетным числом элементов.

  Что мы не показали, так это то, что каждое подмножество набора из десяти элементов, имеющего нечетное число элементов, было создано таким образом.

  No related posts.