Краткая запись задачи и её схематический чертёж
- Охо-хо-хо-хо… И куда этот Плюс подевался? Я один с этим заданием не справлюсь. Ну, царица! Каждый раз какое-нибудь новенькое задание подкинет.
- Добрый день, Минус! Прости, я задержался — на природу загляделся. Уж такой сегодня день красивый! Я набрал целую охапку листьев — здесь листья клёна и каштана.
- А что ты с ними делать собираешься?
- Как что — составлю осенний букет. А еще, они помогут нам разобраться в том задании, которое дала нам царица-Математика — научиться выполнять краткую запись задачи и её схематический чертёж.
- Давай скорее начнём, а то ты и так опоздал.
- Ну что же, приступим. Вот смотри — у меня несколько листьев клёна. 5 из них я поставлю в вазу и осталось ещё 4 листа.
- Да-да, я знаю. Если задать вопрос, то получится вот такая задача:
Плюс
собрал несколько листьев клёна.
Ну, и что дальше?
- А дальше составляем краткую запись.
- И как мы это сделаем?
- Выбираем главные, опорные слова. Что происходило в задаче?
- Сначала ты собрал листья, а потом 5 из них поставил в вазу. И у тебя остались 4 листа.
- Вот именно — собрал, поставил, осталось. Вот они, опорные слова. Запишем их:
- Да, но, сколько собрал, в задаче неизвестно. В ней сказано, что собрал несколько листьев.
-
Ну, раз неизвестно, мы поставили вопросительный знак. Ведь именно это и надо
узнать в задаче. Её вопрос звучит так: «Сколько всего листьев собрал Плюс?» А,
чтобы не писать полностью слово листьев, мы поставим только первую букву л.
Ведь, если вместо слова ставится одна или, допустим, две буквы, то говорят, что
слово сократили, и подсказывает нам это маленькая точка.
Ну, вот. У нас получилась краткая запись задачи. Глядя на неё мы можем вспомнить всё условие задачи.
- Но ведь нам еще надо сделать и схематический чертёж!
- Ну что же. В этом нам помогут отрезки. Мы ведь их уже отлично рисовать научились. Итак, вот первый отрезок.
Он показывает, сколько листьев я поставил в вазу. Второй отрезок мы начнем рисовать от той точки, которая является концом первого отрезка.
Этот отрезок показывает, сколько листьев у меня осталось. То есть, нам известна та часть листьев, которую я поставил в вазу и та часть листьев, которая осталась. А вот, если объединить все листья вместе, то получится уже не часть, а все листья, то есть
Когда мы объединяем, то есть собираем что-то вместе, находим целое, то, конечно, используем действие сложения. И без меня, Плюса, здесь не обойтись!
Записываю
ответ задачи: Плюс собрал 9 листьев клёна.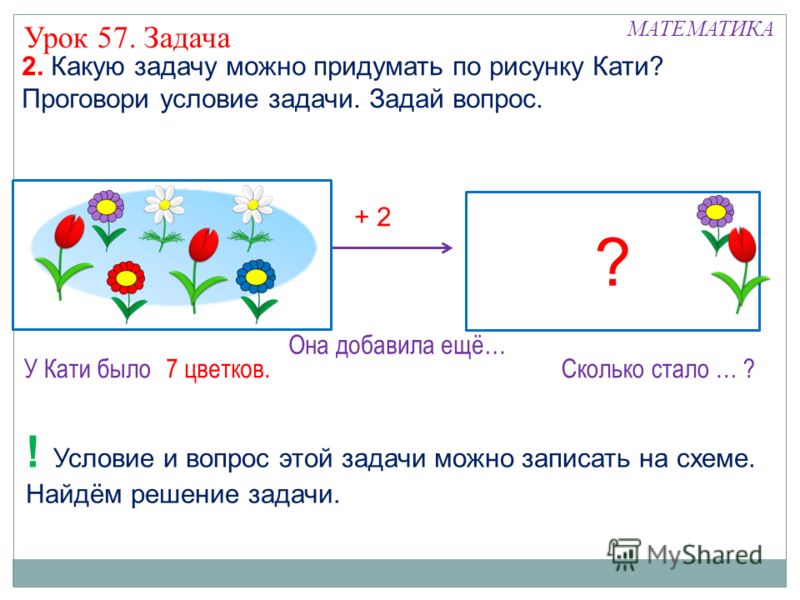
- Так, отлично, с этой задачей мы справились. Но ведь есть и ещё одна задача.
- Что еще за задача?
- А вот она: На лесной поляне росло 7 мухоморов. Несколько мухоморов съел лось. После этого на поляне осталось 2 мухомора. Сколько мухоморов съел лось?
Теперь моя очередь составлять краткое условие и схематический чертёж. Итак, выделяю числа и опорные слова. Что в задаче происходило? Росло 7 мухоморов. Несколько мухоморов съел лось. Раз несколько, значит, мы не знаем сколько. Дальше написано, что осталось 2 мухомора.
Ну вот, с кратким условием я справился. Так ведь, Плюсик?
- Да, молодец!
- Теперь надо выполнить схематический чертёж.
Росло 7 мухоморов. Рисуем отрезок:
Лось съел, это неизвестно. Пока рисовать не буду, осталось 2 мухомора. Как мне их нарисовать? Откуда начинать? С конца первого отрезка?
Не-е-ет.
Ведь семь — это все мухоморы, то есть целое, а два — это часть этих
семи. Поэтому откладываем отрезок, обозначающий эти два мухомора от начала
первого отрезка. Мы как бы отделим оставшиеся мухоморы от съеденных. А вот тот
отрезок, который является второй частью целого отрезка и будет съеденными
мухоморами.
Поэтому откладываем отрезок, обозначающий эти два мухомора от начала
первого отрезка. Мы как бы отделим оставшиеся мухоморы от съеденных. А вот тот
отрезок, который является второй частью целого отрезка и будет съеденными
мухоморами.
Как известно, часть чего-то целого находим действием вычитания. Так что, теперь моя очередь встать в действие:
Ответ: 5 мухоморов съел лось.
- Это у тебя отлично получилось, Минус. Лихо ты справился с такой трудной задачей.
- И ничего трудного тут нет. Чтобы решить любую задачу, надо сначала представить себе все, что в ней происходит. Затем составить краткое условие, выделив опорные слова, которые нам подскажут, что именно происходит в задаче. А потом нарисовать схематический чертёж. Только надо очень внимательно разобраться, что в задаче целое, а что части.
-
Если мы находим наибольшее число, то есть целое, из известных частей, то
отрезки рисуем так: сначала первый отрезок, затем второй.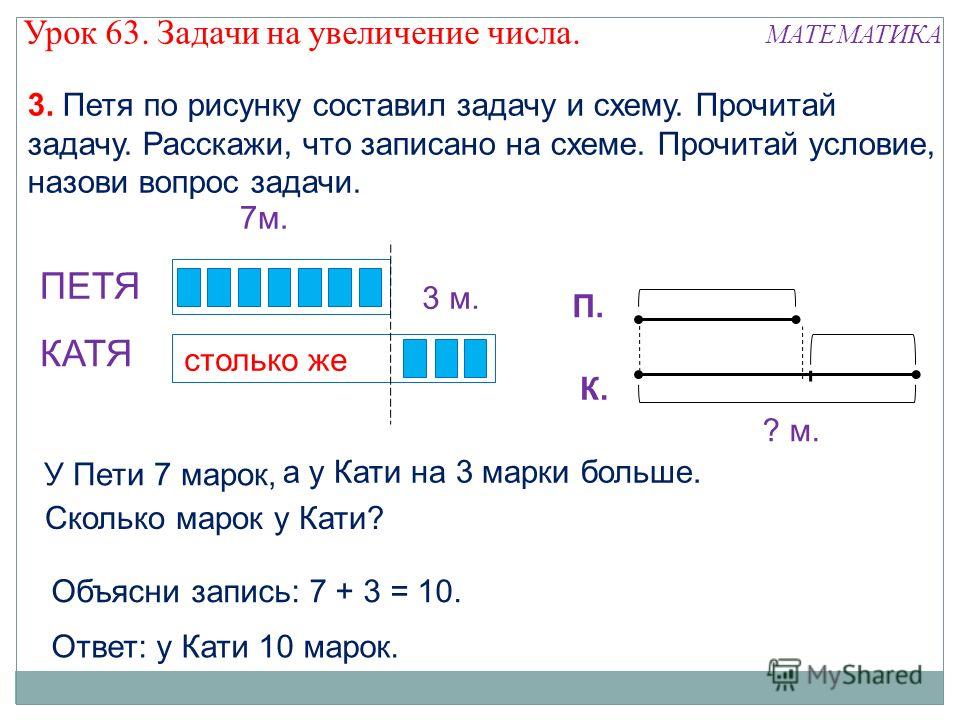 При этом, конец
первого отрезка одновременно является началом второго отрезка. И такую задачу
решаем действием сложения. То есть используем знак плюс.
При этом, конец
первого отрезка одновременно является началом второго отрезка. И такую задачу
решаем действием сложения. То есть используем знак плюс.
- А если в задаче надо узнать часть чего либо, то сначала рисуем отрезок, обозначающий самое большое число, то есть целое. Затем от начала первого отрезка рисуем второй отрезок, обозначающий меньшее известное число. Мы как бы разрезаем больший отрезок на части, одна из которых известна, а вторую нужно узнать. И, конечно, если надо узнать часть, то задачу решаем действием вычитания. То есть используем знак минус.
- Ну что, пойдем к царице сдавать задание?
- Ну да! Побежали! Урра!
Составление косвенных задач | Статья в сборнике международной научной конференции
Библиографическое описание:Жуйкова, Т. П. Составление косвенных задач / Т. П. Жуйкова. — Текст : непосредственный // Педагогика: традиции и инновации : материалы III Междунар. науч. конф. (г. Челябинск, апрель 2013 г.). — Т. 0. — Челябинск : Два комсомольца, 2013. — С. 46-48. — URL: https://moluch.ru/conf/ped/archive/69/3676/ (дата обращения: 05.10.2022).
науч. конф. (г. Челябинск, апрель 2013 г.). — Т. 0. — Челябинск : Два комсомольца, 2013. — С. 46-48. — URL: https://moluch.ru/conf/ped/archive/69/3676/ (дата обращения: 05.10.2022).
В обучении решению арифметических задач условно можно выделить два взаимосвязанных этапа: ознакомление со структурой задачи, способами решения ее, и обучение приемам вычислений [1, с. 201].
Решая задачи, ребенок усваивает: смысл арифметических действий и понятия: прибавить, получится, вычесть, остаток, равно и т. д. Развивается логическое мышление, смекалка, сообразительность, совершенствуются умения проводить анализ и синтез, обобщать, выделять главное в задачи. В дошкольном образовательном учреждении дети решают как простые, так и косвенные задачи.
Исследования
и практика показывают, что детям старшего дошкольного возраста
доступно решение некоторых видов косвенных задач. Их можно предлагать
детям, будучи уверенными, что обязательный программный материал
усвоен ими хорошо. И лишь при необходимости усложнить работу
можно ввести такие задачи. Поскольку в косвенных задачах логика
арифметического действия противоречит действию по содержанию задачи,
они дают большой простор для рассуждений, доказательств, приучают
детей логически мыслить.
И лишь при необходимости усложнить работу
можно ввести такие задачи. Поскольку в косвенных задачах логика
арифметического действия противоречит действию по содержанию задачи,
они дают большой простор для рассуждений, доказательств, приучают
детей логически мыслить.
Исходя из этого, для детей высокого уровня
интеллектуального развития можно предлагать проблемные (косвенные)
задачи. Ознакомление детей седьмого года жизни с задачами такого
типа возможно и имеет большое значение для их умственного
развития. На этой основе в дальнейшем будут формироваться умения
осуществлять анализ более сложных арифметических задач, объяснять ход
решения, выбор арифметического действия. Косвенные задачи отличаются
тем, что в них оба числа характеризуют один и тот же
объект, а вопрос направлен на определение количества другого
объекта. Трудности в решении таких задач определяются самой
структурой и содержанием задачи. Как правило, в этих
задачах есть слова, которые дезорганизуют ребенка при выборе
арифметического действия.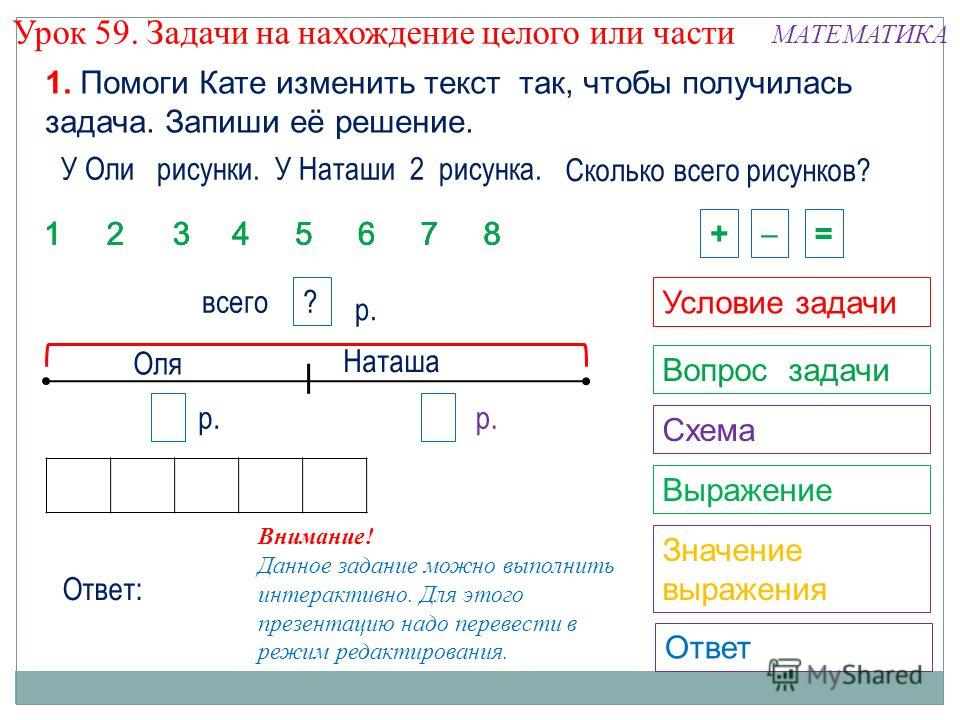
Воспитатель подчеркивает особенности таких задач,
предлагая совместное рассуждение так: в условии задачи оба числа
характеризуют один объект — количество грибов в корзине:
в ней пять грибочков и в ней же на два больше, чем на
столе.
При составлении задач воспитатель должен помнить о том, что важно разнообразить формулировки в условии и вопросе задачи: насколько выше, тяжелее, дороже и т. д.
Приведем примеры косвенных задач:
В большую лодку сели 7 детей, в маленькую 3 ребёнка. Сколько детей разместилось в двух лодках?
а) 10 детей разместились в двух лодках: в большую лодку село 7 детей, а остальные в маленькую. Сколько детей село в маленькую лодку?
б) 10 детей разместилось в двух лодках: несколько детей село в большую лодку, а 3 ребёнка село в маленькую. Сколько детей село в большую лодку?
В одной коробке было 5 карандашей, а во второй 3 карандаша. Сколько карандашей было в двух коробках?
а) В
двух коробках было 8карандашей: 3 в одной, а остальные во
второй коробке. Сколько карандашей было во второй коробке?
Сколько карандашей было во второй коробке?
б) В двух коробках было 8 карандашей. Во второй коробке было 5 карандашей. Сколько карандашей было в первой коробке?
в) В двух коробках было 8 карандашей. Сколько карандашей было в первой коробке? в одной коробке, если в другой лежало пять карандашей?
Школьники сделали 7 флажков. Один флажок был синий, а остальные зелёными. Сколько было зелёных флажков?
Мама и дочка собрали 10 стаканов малины. 5 стаканов мама помыла к ужину. Из остальных ягод она сварила варенье. Сколько стаканов малины пошло на варенье?
Колхозница купила 10 цыплят. Осенью 8 цыплят превратились в курочек, остальные стали петушками. Сколько было петушков?
В 2 солонках было 5 ложек соли. В одной из них было 3 ложки соли. Сколько ложек соли было в другой солонке? [2. с. 195]
Важно,
чтобы задачи, которые мы даём ребёнку, были разнообразными, потому
что если дошкольник, получат однотипные задачи, начинает решать их по
аналогии, не вдумываясь в содержание и не анализируя задачу
при решении. Дети очень скоро усваивает, что если что-то дали, кто-то
приехал, прилетел и т. д. — надо прибавлять,
а если наоборот — отнимать.
Дети очень скоро усваивает, что если что-то дали, кто-то
приехал, прилетел и т. д. — надо прибавлять,
а если наоборот — отнимать.
Не научившись объяснять, как получен ответ задачи, дошкольник привыкает механически ориентироваться только на слово, побуждающее к действию сложения или вычитания.
Однако очень скоро ребёнок сталкивается с такими задачами, где слово, обозначающее, что надо что-то складывать, не совпадает с тем арифметическим действием, которое надо произвести, чтобы решить задачу. Приведём пример такой задачи.
«На дереве сидели птички. После того, как пролетела ещё одна птичка, их стало шесть. Сколько птичек сидело на дереве»
Нередко такого рода задачи могут поставить дошкольников неподготовленных к решению задач, в тупик. Они дают ответ: «Семь птичек, ориентируясь на слово «прилетела» и прибавляя к шести птичкам ещё одну птичку».
По тому, как
умеет ребёнок решать такого рода задачи, можно судить об уровне
умственного развития ребёнка: умеет ли логически мыслить, рассуждать,
доказывать правильность ответа. Именно при решении таких задач
выявляется то, что мы называем нормальным усвоением знаний. Если
дети, услышав знакомые слова «прилетели, прибежали, приехали»,
не давая себе труда вдуматься в смысл задачи, начинают
складывать те числовые данные, которые имеются в задачи —
значит, они не научены рассуждать при решении задачи, рассказывать,
каким образом получился именно такой ответ.
Именно при решении таких задач
выявляется то, что мы называем нормальным усвоением знаний. Если
дети, услышав знакомые слова «прилетели, прибежали, приехали»,
не давая себе труда вдуматься в смысл задачи, начинают
складывать те числовые данные, которые имеются в задачи —
значит, они не научены рассуждать при решении задачи, рассказывать,
каким образом получился именно такой ответ.
Задачи, о которых идёт речь, нельзя решить без рассуждений. Именно важно предлагать детям подобные задачи уже в дошкольном возрасте.
Предлагая
ребёнку задачу, аналогичную, следует его предупредить, что это
особенная задача, не такая, как всегда, труднее. Например, «Собираясь
идти в школу, девочка купила карандашей, но, выйдя из магазина,
она увидела, что их мало. Пошла и купила ещё один карандаш,
после чего карандашей стало пять. Сколько карандашей купила девочка
в начале?» Задачу надо повторить несколько раз, чтобы
ребёнок запомнил её. Потом предложить ему самому пересказать задание.
Потом предложить ему самому пересказать задание.
Теперь давай вместе рассуждать, — предлагает ребёнку взрослый. В задаче сказано, сколько карандашей купила девочка?
Нет, — отвечает ребёнок.
Правильно, это надо узнать, это нам не известно, когда девочка вернулась в магазин и купила ещё один карандаш, карандашей у неё стало больше или меньше?
Очевидно, ребёнок правильно ответит, что карандашей стало больше.
Совершенно верно, после покупки одного карандаша их стало больше: пять. Значит, до покупки этого карандаша их было меньше?
Меньше, — соглашается ребёнок.
На сколько меньше?
На один. Это нам известно из условия задачи.
Значит, чтобы узнать, сколько карандашей купила девочка в начале, то есть, сколько карандашей было у неё до покупки ещё одного, надо от пяти карандашей отнять один карандаш.

Теперь, предложив ребёнку самому узнать, сколько же карандашей купила девочка вначале, можно узнать, понял ли ребёнок задачу. Если он знает правильный ответ: «4 карандаша», можно ещё раз уточнить, как получен такой ответ. Ребёнок должен сказать, что он от 5 карандашей отнял 1 карандаш, получилось 4 карандаша [3].
Если ребёнок не может сразу усвоить логику рассуждений, можно прибегнуть к знакомому способу — предметной иллюстрации задачи и повторить приведённое выше рассуждение, держа в руке, пять карандашей. Ребёнок пересчитывает карандаши и убеждается, что их пять: «Сколько карандашей стало у девочки, когда она вернулась и купила ещё один карандаш.
Теперь давай посмотрим, сколько было карандашей до покупки вот этого карандаша» (При этом убираем один карандаш). Пересчитав карандаши, ребёнок убеждается, что карандашей было четыре.
Кроме того,
путём соответствующего действия с предметами мы иллюстрируем
задачу и помогаем представить ту жизненную ситуацию, которая
описывается в ней. И хотя в задаче говорится, что
девочка купила ещё один карандаш (со словом «купила»
связывается действие сложение), ребёнок наглядно видит, что для
получения правильного ответа необходимо произвести действие
вычитание.
И хотя в задаче говорится, что
девочка купила ещё один карандаш (со словом «купила»
связывается действие сложение), ребёнок наглядно видит, что для
получения правильного ответа необходимо произвести действие
вычитание.
Обучая ребёнка решению обратных арифметических задач, взрослые рассуждают вместе с ребёнком, затем необходимо предложить ребёнку самому попробовать порассуждать. Можно и поиграть с ребёнком, предложив ему самому придумать трудную задачу, для того чтобы её решил взрослый. Ребёнок с удовольствием включается в такую игру, когда он выступает в роли учителя. При этом можно лишний раз убедиться, как ориентируется ребёнок при решении такого рода задачах, и поддержать интерес, необходимый при обучении вычислительной деятельности.
Решите задачи с условием в косвенной форме.
Девочки шили куклам платья. Когда они одели их на кукол, то увидели, что одного платья не хватило.
 Они сшили его. Теперь платьев стало пять.
Сколько платьев они сшили в начале?
Они сшили его. Теперь платьев стало пять.
Сколько платьев они сшили в начале?Девочка собирала грибы. В её корзине лежали только белые. Вдруг под ёлкой она увидела три подосиновика. Срезав их, девочка пересчитала все собранные грибы. Их стало 10. Сколько белых грибов было?
Кате 5 лет. Она моложе своего брата на 1 год. Сколько лет брату?
Юре 9 лет. Он старше своего товарища на 2 года. Сколько лет товарищу?
Красных тюльпанов 8, их на 1 больше чем жёлтых. Сколько жёлтых тюльпанов?
В парке 9 голубых скамеек. Их на 1 меньше, чем белых. Сколько белых скамеек в парке?
Белая курица снесла 2 яйца, это на одно яйцо меньше, чем снесла чёрная курица. Сколько яиц снесла чёрная курица?
Бригада строителей строила 9 этажный дом. Через месяц осталось построить три этажа. Сколько этажей построено?
На блюде лежали яблоки.
 3 из них взяли и съели. Осталось на блюде
4 яблока. Сколько яблок было? [4. с. 196]
3 из них взяли и съели. Осталось на блюде
4 яблока. Сколько яблок было? [4. с. 196]
Подытоживая анализ проблемного поля, обучение детей старшего дошкольного возраста косвенным задачам, рекомендуем предлагать подобные задачи лучше всего в виде сюрприза: «Кто сообразит, как решать задачу, которую я вам сейчас задам?» Надо отметить, что эти задачи вызывают большой интерес у детей.
Итак, работа над задачами не только обогащает детей новыми знаниями, но и дает богатый материал для умственного развития.
Литература:
Щербакова Е. И. Методика обучения математике в детском саду: Учеб пособие для студ. дош. отд-ний и фак. сред. пед. учеб. заведений. — 2-е изд., стереотип. _ М.: Издательский центр «Академия», 2000. — 201 с. 2. Столяр А. А. Формирование элементарных математических представлений у дошкольников: Учеб. пособие для студентов пед. институтов. М.: Просвещение, 1988.
 —
195 с.
—
195 с.Белошистая В. А. Формирование и развитие математических способностей дошкольников: Вопросы теории и практики: Курс лекций для студ. дошк. Факультетов высш. учеб. заведений. — М.: Гуманит, изд. Центр ВЛАДОС, 2003. — 400 с.
Столяр А. А. Формирование элементарных математических представлений у дошкольников: Учеб. пособие для студентов пед. институтов. М.: Просвещение, 1988. — 196 с.
Как научить ребенка решать математические задачи и показать, что это это интересно
- Почему дети не понимают математику
- Пошаговое руководство по решению задач
- Убедитесь, что ваш ребенок понял условие задачи
- Задавайте вопросы
- Возвращайтесь к вопросу задачи
- Закрепите алгоритм на будущее
- Поддерживайте ребенка
Почему дети не понимают математику
“Я ничего не понимаю!” Как часто вы слышите эту полную отчаяния фразу от своего ребенка? “Математика — это сложно”, — повторяют те, кто сами не смогли полюбить считать и рассуждать логически. И вот уже не только ваш сын или дочь неохотно садится делать “домашку”, но и вы сами начинаете сомневаться в его или ее способностях. Не торопитесь с выводами. Возможно, вы просто не знаете, как интересно и по-разному можно научить решать даже самые заковыристые задачи.
И вот уже не только ваш сын или дочь неохотно садится делать “домашку”, но и вы сами начинаете сомневаться в его или ее способностях. Не торопитесь с выводами. Возможно, вы просто не знаете, как интересно и по-разному можно научить решать даже самые заковыристые задачи.
На самом деле чаще всего нелюбовь к математическим дисциплинам начинается с уроков в школе, где материал подается таким образом, что не каждый взрослый с первого раза может уловить суть, не говоря уже о совсем юных учениках. Дети не только с трудом представляют, какими способами можно решить задачу, но и порой просто не понимают, что спрашивается в условии.
Пошаговое руководство по решению задач
Следующие правила помогут научиться анализировать не только задания по алгебре или геометрии, но и по другим предметам, где требуется использовать логическое мышление.
1. Убедитесь, что ваш ребенок понял условие задачи
Самая распространенная проблема в решении задач по математике — непонятное условие.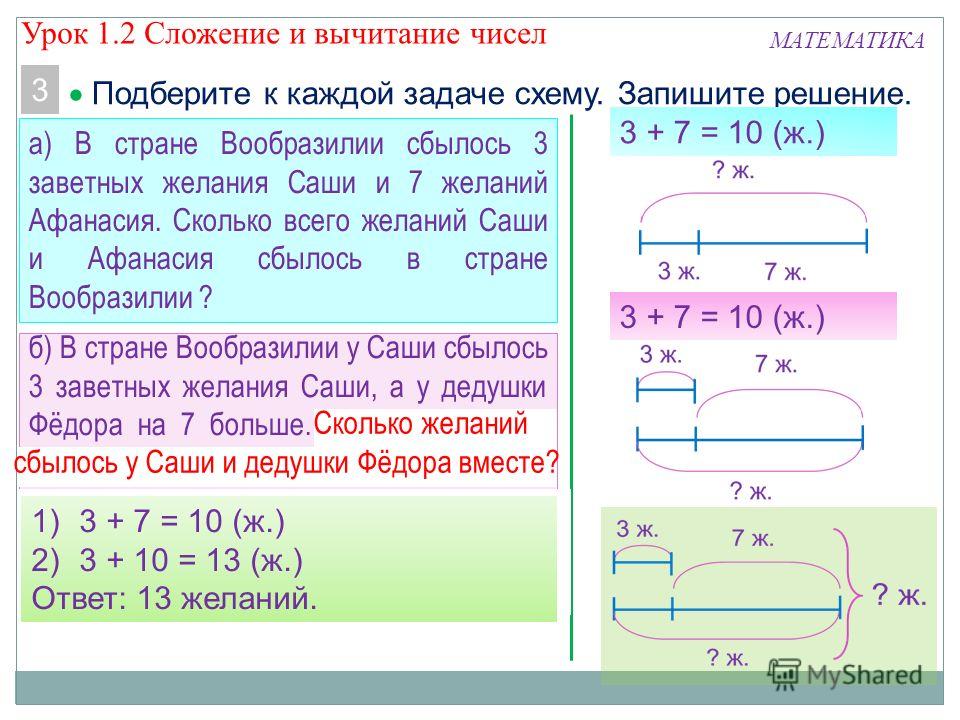 Зачастую школьные учебники и сборники заданий составлены таким образом, что вопрос, на который и нужно дать ответ, сформулирован слишком сложно. Поэтому, чтобы убедиться, что ребенок правильно понял суть, попросите его проговорить условие своими словами. Часто уже на этом этапе все становится очевидно.
Зачастую школьные учебники и сборники заданий составлены таким образом, что вопрос, на который и нужно дать ответ, сформулирован слишком сложно. Поэтому, чтобы убедиться, что ребенок правильно понял суть, попросите его проговорить условие своими словами. Часто уже на этом этапе все становится очевидно.
Если же условие задачи так и осталось чем-то не до конца ясным, попробуйте объяснить его, используя пример из обычной повседневной жизни. Попросите ребенка представить себе то, о чем говорится в задаче, и порассуждать, как обычно выглядит или происходит то, что там описано. Часто детям просто не приходит в голову, что с ситуацией из учебника они хорошо знакомы.
Также отлично работает наглядное изображение. Например, в задаче про футбольные поля их можно нарисовать как прямоугольники, а отрезки пути очень похожи на деления линейки. Использование разных цветов для обозначения отдельных элементов рисунка тоже способствует развитию навыка связывать картинку со смыслом.
2.
 Задавайте вопросы
Задавайте вопросыЧтобы удержать или вернуть внимание ребенка к задаче или показать, на что конкретно нужно сместить фокус, задавайте ему наводящие вопросы. Фразы типа:
“Как ты думаешь, для чего дано …?”
“Какое действие мы можем выполнить с …?”
“На что это похоже?”
“Какой вывод мы можем сделать из…?” и другие помогут включиться в ситуацию и посмотреть на нее под другим углом.
Если вы сможете сюжет задачи переложить на что-то, чем ребенок интересуется в жизни, ему будет проще понять связь между условием и результатом. Плюс ко всему вы сможете показать, что математика есть даже там, где, казалось бы, ее трудно представить. Например, если ваш сын или дочь увлекаются рисованием, а с геометрией все сложно, расскажите, а лучше нарисуйте, из каких геометрических фигур состоят предметы в натюрморте или туловище животного. Кстати, в Матклассе есть целая каникулярная программа для юных художников!
3. Возвращайтесь к вопросу задачи
Часто, окунувшись в процесс поиска решения и перебора в голове имеющихся формул и правил, ребенок забывает, что именно он должен получить в итоге.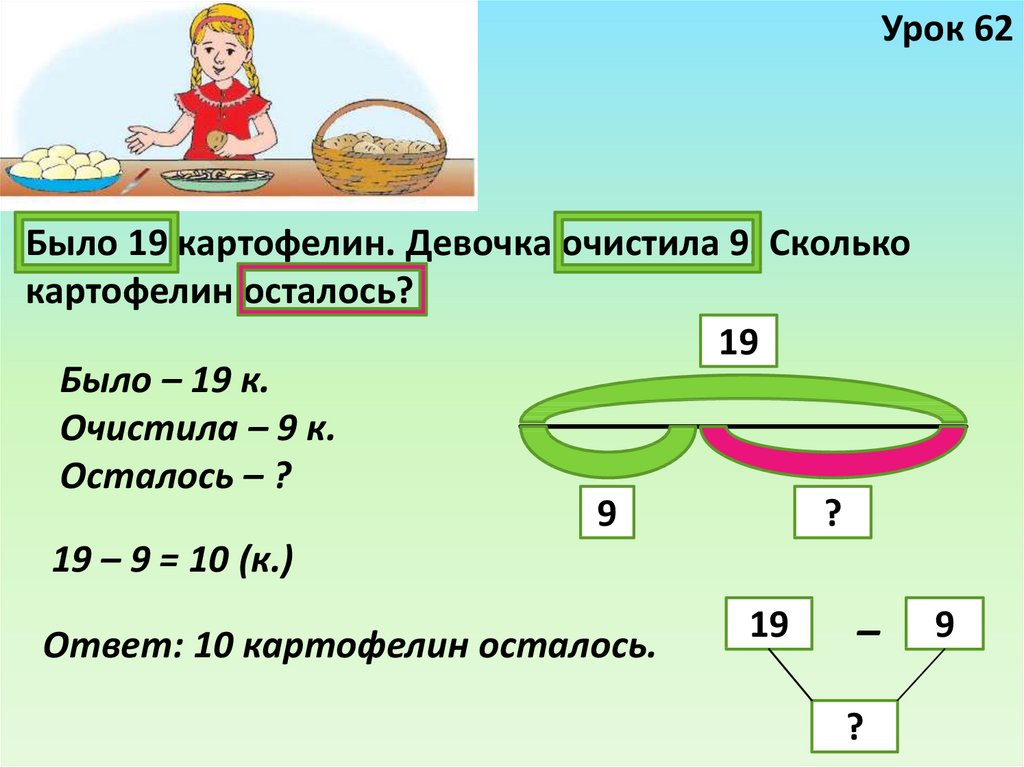 Хорошо, если с самого начала вы вместе определите, что результатом должна быть, например, длина пути в километрах или количество конфет у Васи в штуках, и по ходу будете напоминать, что будет ответом к задаче.
Хорошо, если с самого начала вы вместе определите, что результатом должна быть, например, длина пути в километрах или количество конфет у Васи в штуках, и по ходу будете напоминать, что будет ответом к задаче.
4. Закрепите алгоритм на будущее
Когда задачу удалось решить, попросите ребенка повторить всю последовательность шагов, которые он делал. Спросите его, какие выводы он сделал в процессе поиска ответа, какие ошибки заметил за собой и как ему удалось с ними справиться. Так вы поспособствуете развитию полезной привычки анализировать свои действия и запоминать, что сработало, а от чего лучше отказаться.
5. Поддерживайте ребенка
И последний (но не по важности) совет — старайтесь хвалить ребенка в процессе работы над заданием, по возможности выражая позитивные эмоции. Поддерживайте его не только, когда он все правильно сделал, но и на каждом этапе, например, когда он вспомнил нужную формулу или сделал правильный вывод. Человеческой психике особенно в раннем возрасте необходимо позитивное подкрепление, тогда в следующий раз ребенок не только вспомнит то, что ему удалось, но и почувствует удовольствие от обучения, зная, что это весело и приятно.
Впоследствии, когда ребенку снова потребуется ваша помощь с математикой, вы сможете напомнить ему, как здорово у него получилось в прошлый раз. Это придаст ему сил и веры в себя.
Не стоит злиться или ругать ребенка, если у него не получается быстро сообразить, что к чему, даже если вам все кажется очевидным, и вы с подобными задачами справлялись без помощи родителей. Во-первых, мы все разные, и вполне возможно, что вашему сыну или дочери нужно немного больше времени, чтобы все расставить по своим местам у себя в голове, увидеть взаимосвязи и сделать правильные выводы. Во-вторых, и без того не самый любимый предмет теперь будет прочно связан с ощущением беспомощности и тяжести, а кто же хочет возвращаться к занятию, от которого уверенность в своих силах сходит на нет?
Есть еще немало способов развить у ребенка логическое мышление, научить его видеть причинно-следственные связи.
О том, как изучать математикe легко и весело через занятия, на первый взгляд с ней никак не связанные, а также о том, как полюбить считать и справляться с задачами в процессе увлекательной игры читайте в нашем блоге!
Или присоединяйтесь к занятиям Маткласса.
Мы знаем, как влюбить в математику любого ребенка!
Записаться
на занятия в МатклассУзнать больше
о лагерях МатклассаПрименение стратегии решения проблем к основным задачам со словами
Результаты обучения
- Практикуйте осознанность в своем отношении к задачам со словами
- Применение общей стратегии решения задач для решения текстовых задач
Подойдите к задачам со словами с позитивным настроем
В мире полно задач со словами. Сколько денег мне нужно, чтобы заправить машину бензином? Сколько дать чаевых официанту в ресторане? Сколько носков взять с собой в отпуск? Насколько большую индейку мне нужно купить на ужин в честь Дня Благодарения и во сколько мне нужно поставить ее в духовку? Если мы с сестрой купим маме подарок, сколько каждый из нас заплатит?
Теперь, когда мы можем решать уравнения, мы готовы применить наши новые навыки к решению текстовых задач. Знаете ли вы кого-нибудь, у кого в прошлом был негативный опыт решения проблем со словами? Были ли у вас когда-нибудь мысли, как у студента в карикатуре ниже?
Знаете ли вы кого-нибудь, у кого в прошлом был негативный опыт решения проблем со словами? Были ли у вас когда-нибудь мысли, как у студента в карикатуре ниже?
Негативные мысли о задачах со словами могут стать препятствием на пути к успеху.
Когда мы чувствуем, что не можем себя контролировать, и продолжаем повторять негативные мысли, мы возводим барьеры на пути к успеху. Нам нужно успокоить наши страхи и изменить наши негативные чувства.
Начните с чистого листа и начните мыслить позитивно, как студент из мультфильма ниже. Прочитайте положительные мысли и произнесите их вслух.
Когда дело доходит до текстовых задач, позитивный настрой — это большой шаг к успеху.
Если мы возьмем на себя управление и поверим, что можем добиться успеха, мы сможем решать текстовые задачи.
Подумайте о том, что вы можете сделать сейчас, но не могли сделать три года назад. Будь то вождение автомобиля, катание на сноуборде, приготовление изысканной еды или говорение на новом языке, вы смогли изучить и освоить новый навык. Проблемы со словами ничем не отличаются. Даже если в прошлом вы боролись с текстовыми задачами, вы приобрели много новых математических навыков, которые помогут вам добиться успеха сейчас!
Проблемы со словами ничем не отличаются. Даже если в прошлом вы боролись с текстовыми задачами, вы приобрели много новых математических навыков, которые помогут вам добиться успеха сейчас!
Используйте стратегию решения задач для словесных задач
В предыдущих главах вы переводили словосочетания в алгебраические выражения, используя базовый математический словарь и символы. С тех пор вы увеличили свой математический словарный запас, поскольку узнали больше об алгебраических процедурах, и у вас было больше практики перевода слов в алгебру.
Вы также перевели словесные предложения в алгебраические уравнения и решили некоторые текстовые задачи. Словесные задачи применяли математику к повседневным ситуациям. Вы должны были переформулировать ситуацию в одном предложении, назначить переменную, а затем написать уравнение, которое нужно решить. Этот метод работает до тех пор, пока ситуация вам знакома и математика не слишком сложна.
Теперь мы разработаем стратегию, которую вы сможете использовать для решения любой текстовой задачи. Эта стратегия поможет вам добиться успеха в решении текстовых задач. Мы продемонстрируем стратегию при решении следующей задачи.
Эта стратегия поможет вам добиться успеха в решении текстовых задач. Мы продемонстрируем стратегию при решении следующей задачи.
Пример
Пит купил рубашку на распродаже за [латекс]18[/латекс], что составляет половину первоначальной цены. Какова была первоначальная цена рубашки?
Решение:
Шаг 1. Прочтите проблему. Убедитесь, что вы понимаете все слова и идеи. Возможно, вам придется прочитать задачу два или более раз. Если есть слова, которые вы не понимаете, поищите их в словаре или в Интернете.
- В этой задаче вы понимаете, о чем идет речь? Вы понимаете каждое слово?
Шаг 2. Определите , что вы ищете. Трудно найти что-то, если вы не уверены, что это такое! Прочитайте задачу еще раз и найдите слова, которые говорят вам, что вы ищете!
- В этой задаче слова «какова была первоначальная цена рубашки» говорят вам, что вы ищете: первоначальную цену рубашки.
Шаг 3.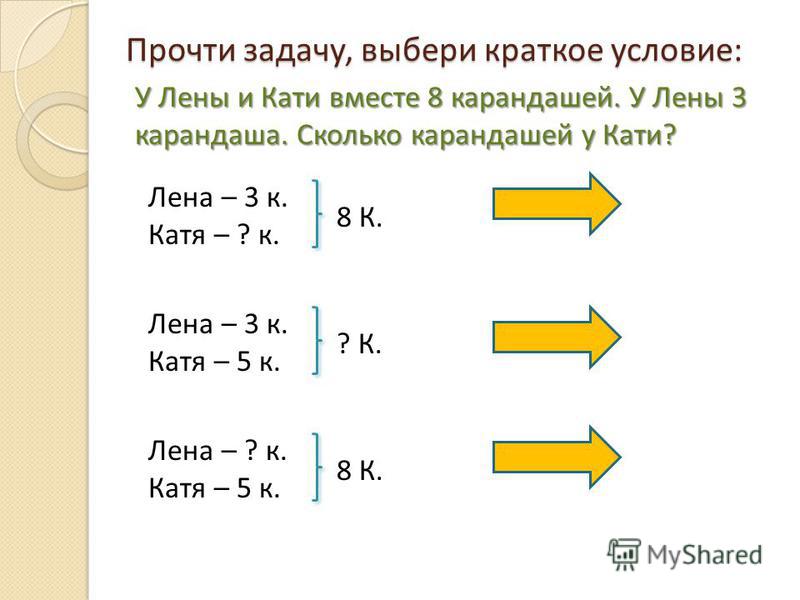 Назовите то, что вы ищете. Выберите переменную для представления этого количества. Вы можете использовать любую букву для переменной, но может помочь выбрать ту, которая поможет вам запомнить, что она представляет.
Назовите то, что вы ищете. Выберите переменную для представления этого количества. Вы можете использовать любую букву для переменной, но может помочь выбрать ту, которая поможет вам запомнить, что она представляет.
- Пусть [латекс]р=[/латекс] первоначальная цена рубашки
Шаг 4. Преобразуйте в уравнение. Может помочь сначала переформулировать проблему в одном предложении со всей важной информацией. Затем переведите предложение в уравнение.
Шаг 5. Решите уравнение, используя хорошие методы алгебры. Даже если вы сразу знаете ответ, использование алгебры лучше подготовит вас к решению задач, на которые нет очевидных ответов.
| Напишите уравнение. | [латекс]18=\большой\фрак{1}{2}п[/латекс] |
| Умножьте обе части на 2. | [латекс]\color{red}{2}\cdot18=\color{red}{2}\cdot\Large\frac{1}{2}\normalsize p[/latex] |
Упростить. | [латекс]36=п[/латекс] |
Шаг 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл.
- Мы обнаружили, что [латекс]p=36[/латекс], означает, что первоначальная цена была [латекс]\text{\$36}[/латекс]. Имеет ли смысл [латекс]\текст{\$36}[/латекс] в задаче? Да, потому что [латекс]18[/латекс] — это половина [латекс]36[/латекс], , а рубашка продавалась за половину первоначальной цены.
Шаг 7. Ответьте на вопрос полным предложением.
- Задача задавалась вопросом: «Какова была первоначальная цена рубашки?» Ответ на вопрос: «Первоначальная цена рубашки была [латекс]\текст{\$36}[/латекс]».
Если бы это было домашним заданием, наша работа могла бы выглядеть так:
Попробуйте
Перечислим шаги, которые мы предприняли для решения предыдущего примера.
Стратегия решения проблем
- Прочитать слово задача.
 Убедитесь, что вы понимаете все слова и идеи. Возможно, вам придется прочитать задачу два или более раз. Если есть слова, которые вы не понимаете, поищите их в словаре или в Интернете.
Убедитесь, что вы понимаете все слова и идеи. Возможно, вам придется прочитать задачу два или более раз. Если есть слова, которые вы не понимаете, поищите их в словаре или в Интернете. - Определите , что вы ищете.
- Имя то, что вы ищете. Выберите переменную для представления этого количества.
- Преобразуйте в уравнение. Может быть полезно сначала переформулировать проблему в одном предложении, прежде чем переводить.
- Решите уравнение, используя хорошие методы алгебры.
- Проверьте ответ в задаче. Убедитесь, что это имеет смысл.
- Ответьте на вопрос полным предложением.
Чтобы узнать, как переводить алгебраические выражения в слова, посмотрите следующий видеоролик.
Давайте применим этот подход к другому примеру.
Пример
Яш принес на пикник яблоки и бананы. Количество яблок было на три больше, чем вдвое больше, чем количество бананов. Яш принес на пикник [латекс]11[/латекс] яблок. Сколько бананов он принес?
Показать решение
Попробуйте
В следующем примере мы применим нашу Стратегию решения проблем к применению процентов.
пример
Страховая премия Нга увеличилась на [латекс]\текст{\$60}[/латекс], что составило [латекс]\текст{8%}[/латекс] от первоначальной стоимости. Какова была первоначальная стоимость премии?
Показать раствор
Попробуйте
Стратегии решения проблем | NZ Maths
Что такое стратегии решения проблем? Стратегии — это вещи, которые Полиа предлагает нам выбрать на втором этапе решения проблем и использовать на третьем этапе (Что такое решение проблем?). На самом деле он назвал их эвристиками . Они представляют собой набор общих подходов, которые могут работать для ряда проблем.
Существует ряд общих стратегий, которые учащиеся младшего возраста могут использовать для решения проблем. Ниже мы обсудим некоторые из них, которые будут полезны для задач на этом веб-сайте и в книгах по решению проблем.
Общие стратегии решения проблем
- Предположение (включая предположение и проверку, предположение и улучшение)
- Act It Out (разыграйте и используйте оборудование)
- Рисование (в том числе рисование рисунков и диаграмм)
- Составление списка (включает составление таблицы)
- Думать (включает в себя использование уже известных вам навыков)
Мы предоставили копирайтера для этих стратегий, чтобы вы могли делать плакаты и демонстрировать их в своем классе. Он состоит из страницы для каждой стратегии 9.0042 с отведенным местом для вставки названия любой проблемы, с которой вы сталкиваетесь и которая использует эту конкретную стратегию (Разыграйте, Нарисуйте, Угадайте, Составьте список). Этот тип плаката обеспечивает хорошее повторение для студентов.
Этот тип плаката обеспечивает хорошее повторение для студентов.
Теперь мы рассмотрим каждую из следующих стратегий и подробно обсудим их. Вы увидите, что каждая стратегия в нашем списке включает две или более подкатегории.
- Угадай
Это означает две стратегии: угадай и проверь и угадай и улучши.- Угадай и проверь — одна из самых простых стратегий. Любой может угадать ответ. Если они также могут проверить, соответствует ли догадка условиям задачи, значит, они справились с догадкой и проверкой. Это стратегия, которая, безусловно, сработает в описанной ниже задаче Фермерского двора, но может потребовать много времени и больших вычислений.
Поскольку это так просто, вам может быть трудно отучить некоторых учеников от угадывания и проверки. По мере усложнения задач другие стратегии становятся более важными и эффективными. Однако иногда, когда учащиеся полностью застряли, предположения и проверки обеспечат полезный способ начать изучение проблемы. Будем надеяться, что это исследование приведет к более эффективной стратегии, а затем к решению.
Будем надеяться, что это исследование приведет к более эффективной стратегии, а затем к решению. - Угадай и улучши немного сложнее, чем угадай и проверь. Идея состоит в том, что вы используете свою первую неверную догадку, чтобы сделать улучшенную следующую догадку. Вы можете увидеть это в действии в задаче «Скотный двор». В относительно простых задачах, подобных этой, часто довольно легко увидеть, как можно улучшить последнее предположение. Однако в некоторых задачах, где имеется больше переменных, поначалу может быть неясно, в какую сторону изменить угадывание.
- Угадай и проверь — одна из самых простых стратегий. Любой может угадать ответ. Если они также могут проверить, соответствует ли догадка условиям задачи, значит, они справились с догадкой и проверкой. Это стратегия, которая, безусловно, сработает в описанной ниже задаче Фермерского двора, но может потребовать много времени и больших вычислений.
- Act It Out
Здесь мы объединили две стратегии, поскольку они тесно связаны между собой. Это «Разыграй это» и «Используй оборудование».- Особенно юным студентам нравится использовать Act it Out . Сами учащиеся берут на себя роль вещей в задаче. В задаче «Скотный двор» ученики могут взять на себя роль животных, хотя маловероятно, что в вашем классе будет 87 учеников! Но если учеников недостаточно, вы можете добавить одного-двух мишек.

Это эффективная стратегия для демонстрации перед всем классом. С другой стороны, это также может быть громоздко при использовании группами, особенно если задействовано большое количество студентов.
Иногда учащиеся, разыгрывающие задачу, могут получить меньше пользы от упражнения, чем учащиеся, наблюдающие за ним. Это происходит потому, что участники настолько поглощены механикой того, что они делают, что не видят лежащей в их основе математики. - Использовать оборудование — это стратегия, связанная с Act it Out. Вообще говоря, любой объект, который можно каким-либо образом использовать для представления ситуации, которую студенты пытаются решить, является оборудованием. Одной из сложностей при использовании оборудования является отслеживание решения. Студентов нужно поощрять следить за своей работой, когда они манипулируют оборудованием.
Некоторые учащиеся нуждаются в поддержке и помощи в использовании оборудования. Многие студенты предпочитают рисовать. Это может быть потому, что это дает им лучшее представление о проблеме. Так как есть проблемы при использовании оборудования — это лучшая стратегия, чем рисование, вы должны поощрять использование учащимися оборудования, время от времени самостоятельно моделируя его использование.
Это может быть потому, что это дает им лучшее представление о проблеме. Так как есть проблемы при использовании оборудования — это лучшая стратегия, чем рисование, вы должны поощрять использование учащимися оборудования, время от времени самостоятельно моделируя его использование.
- Особенно юным студентам нравится использовать Act it Out . Сами учащиеся берут на себя роль вещей в задаче. В задаче «Скотный двор» ученики могут взять на себя роль животных, хотя маловероятно, что в вашем классе будет 87 учеников! Но если учеников недостаточно, вы можете добавить одного-двух мишек.
- Draw
Здесь мы обсуждаем как рисование изображения, так и рисование диаграммы.- Совершенно очевидно, что в стратегии Нарисовать картинку должна использоваться картинка. Но картина не должна быть слишком сложной. Он должен содержать достаточно деталей, чтобы помочь решить проблему. Таким образом, грубый круг с двумя отметками вполне достаточен для цыплят, а капля плюс четыре отметки — для свиньи. Следует поощрять всех студентов к использованию этой стратегии в какой-то момент, потому что она помогает им «увидеть» проблему, а позже может развиться в довольно сложную стратегию.
- Трудно понять, где заканчивается Рисование диаграммы и начинается Рисование диаграммы.
 Вы можете думать о диаграмме как о чем-либо, что вы можете нарисовать, но это не изображение. Но где вы проводите грань между картинкой и диаграммой? Как вы можете видеть на примере цыплят и свиней, о которых говорилось выше, обычное рисование картинок перерастает в рисование диаграмм.
Вы можете думать о диаграмме как о чем-либо, что вы можете нарисовать, но это не изображение. Но где вы проводите грань между картинкой и диаграммой? Как вы можете видеть на примере цыплят и свиней, о которых говорилось выше, обычное рисование картинок перерастает в рисование диаграмм.
Диаграммы Венна и древовидные диаграммы — это особые типы диаграмм, которые мы используем так часто, что им дали собственные имена.
- 4 Составление списка
Составление организованных списков и таблиц — это два аспекта систематической работы. Большинство учащихся начинают очень бессистемно записывать свои усилия по решению проблем. Часто в этом углу есть небольшой расчет или что-то в этом роде, и еще один там, и еще один прямо здесь. Это помогает учащимся привнести логическое и систематическое развитие в свою математику, если они начинают систематизировать вещи по ходу дела. Это относится даже к их исследованиям.- Существует несколько способов использования «Сделай стол» .
 Они варьируются от таблиц чисел, помогающих решать такие задачи, как ферма, до таблиц с галочками и крестиками, которые часто используются в логических задачах. Таблицы также могут быть эффективным способом поиска числовых шаблонов.
Они варьируются от таблиц чисел, помогающих решать такие задачи, как ферма, до таблиц с галочками и крестиками, которые часто используются в логических задачах. Таблицы также могут быть эффективным способом поиска числовых шаблонов. - Когда используется организованный список , он должен быть организован таким образом, чтобы в его построении присутствовал некоторый естественный порядок. Например, списки покупок, как правило, не систематизированы. Обычно они беспорядочно растут по мере того, как вы думаете о каждом элементе. Небольшая мысль может сделать их организованными. Соединив все мясо, все овощи вместе и все напитки вместе, вы можете сделать это за вас. Можно добиться еще большей организации, расставив все мясные продукты в алфавитном порядке и так далее. Кто-то, кого мы знаем, перечисляет продукты в ее списке в том порядке, в котором они появляются на ее маршруте по супермаркету.
- Существует несколько способов использования «Сделай стол» .
- Think
Во многих отношениях мы используем эту категорию стратегий как всеобъемлющую. Отчасти это связано с тем, что эти стратегии обычно используются не сами по себе, а в сочетании с другими стратегиями.
Отчасти это связано с тем, что эти стратегии обычно используются не сами по себе, а в сочетании с другими стратегиями.
Стратегии, которые мы хотим здесь упомянуть, это систематичность, отслеживание, поиск шаблонов, использование симметрии и работа в обратном направлении, а также использование известных навыков.
Систематичность, отслеживание, поиск закономерностей и использование симметрии отличаются от стратегий, о которых мы говорили выше, тем, что они являются всеобъемлющими стратегиями. При решении всех задач и вообще во всей математике вам необходимо помнить об этих стратегиях.- Систематичность может означать составление таблицы или систематизированного списка, но это также может означать соблюдение определенного порядка работы, чтобы было легко следовать, когда вам нужно вернуться к ней. Это означает, что вы должны действовать логически по мере продвижения вперед и следить за тем, чтобы не пропустить ни одного шага в споре. И это также означает какое-то время следовать за идеей, чтобы увидеть, к чему она ведет, вместо того, чтобы прыгать повсюду в погоне за множеством возможных идей.

- Очень важно отслеживать вашей работы. Мы видели, как несколько групп студентов разыгрывали задачу и в конце у них возникали проблемы просто потому, что они не следили за тем, что делали. Поэтому отслеживание особенно важно в режимах «Разыгрывай» и «Используя оборудование». Но это важно и во многих других ситуациях. Студенты должны знать, где они были и куда идут, иначе они безнадежно запутаются. Это становится более важным по мере того, как задачи становятся более сложными и включают в себя все больше и больше шагов.
- Во многих отношениях поиск закономерностей это то, чем занимается математика. Мы хотим знать, как вещи связаны и как они работают, и это станет проще, если мы сможем найти закономерности. Паттерны упрощают работу, потому что они сообщают нам, как группа объектов ведет себя одинаково. Как только мы видим шаблон, у нас появляется гораздо больше контроля над тем, что мы делаем.
- Использование симметрии помогает снизить уровень сложности задачи.
 Например, играя в крестики-нолики, вы поймете, что есть три, а не девять способов положить первый символ. Это сразу уменьшает количество возможностей для игры и упрощает ее анализ. Такого рода аргументы возникают постоянно, и их следует с радостью воспринимать, когда вы их видите.
Например, играя в крестики-нолики, вы поймете, что есть три, а не девять способов положить первый символ. Это сразу уменьшает количество возможностей для игры и упрощает ее анализ. Такого рода аргументы возникают постоянно, и их следует с радостью воспринимать, когда вы их видите. - Наконец, работает в обратном направлении — это стандартная стратегия, которая, похоже, имеет ограниченное применение. Тем не менее, это мощный инструмент, когда его можно использовать. В тех задачах, которые мы будем использовать на этом веб-сайте, чаще всего это будет полезно, когда мы будем рассматривать игры. Часто оказывается, что стоит посмотреть, что происходит в конце игры, а затем вернуться к началу, чтобы увидеть, какие ходы лучше всего.
- Затем мы приходим к использовать известные навыки . Это обычно не упоминается в большинстве списков стратегий решения проблем, но, когда мы рассмотрели проблемы на этом веб-сайте, мы обнаружили, что это довольно распространено.
 Хитрость здесь заключается в том, чтобы увидеть, какие навыки, которые вы знаете, могут быть применены к решению проблемы.
Хитрость здесь заключается в том, чтобы увидеть, какие навыки, которые вы знаете, могут быть применены к решению проблемы.
Одним из примеров этого типа является Удобрение (Измерение, уровень 4). В этой задаче решатель должен знать формулу площади прямоугольника, чтобы иметь возможность использовать данные задачи.
Эта стратегия относится к первому шагу решения проблемы, когда решатель думает: «Сталкивался ли я с такой проблемой раньше?» Уметь связать словесную задачу с каким-то ранее приобретенным навыком непросто, но чрезвычайно важно.
- Систематичность может означать составление таблицы или систематизированного списка, но это также может означать соблюдение определенного порядка работы, чтобы было легко следовать, когда вам нужно вернуться к ней. Это означает, что вы должны действовать логически по мере продвижения вперед и следить за тем, чтобы не пропустить ни одного шага в споре. И это также означает какое-то время следовать за идеей, чтобы увидеть, к чему она ведет, вместо того, чтобы прыгать повсюду в погоне за множеством возможных идей.
Различные стратегии имеют разное применение. Проиллюстрируем это с помощью задачи.
Проблема на ферме : На ферме есть несколько свиней и несколько кур. На самом деле есть 87 животных и 266 ног. Сколько свиней во дворе?
Некоторые стратегии помогают понять проблему. Давайте начнем с одного из них. Угадай и проверь . Предположим, что есть 80 свиней. Если они есть, то их будет 320 ног. Очевидно, мы переоценили количество свиней. Так что, может быть, есть только 60 свиней. Теперь у 60 свиней будет 240 ног. Это оставило бы нас с 16 ногами, которые можно было бы найти у цыплят. Чтобы произвести 16 ножек, нужно 8 цыплят. Но 60 свиней плюс 8 цыплят — это всего 68 животных, поэтому нам не хватило почти 20 животных.
Предположим, что есть 80 свиней. Если они есть, то их будет 320 ног. Очевидно, мы переоценили количество свиней. Так что, может быть, есть только 60 свиней. Теперь у 60 свиней будет 240 ног. Это оставило бы нас с 16 ногами, которые можно было бы найти у цыплят. Чтобы произвести 16 ножек, нужно 8 цыплят. Но 60 свиней плюс 8 цыплят — это всего 68 животных, поэтому нам не хватило почти 20 животных.
Очевидно, что мы еще не решили проблему, но теперь мы подошли к некоторым важным аспектам проблемы. Мы знаем, что есть 87 животных, поэтому количество свиней плюс количество цыплят должно составить 87. Мы также знаем, что мы должны использовать тот факт, что у свиней четыре ноги, а у кур две, и что их должно быть 266. ноги вообще.
Некоторые стратегии сами по себе являются методами решения. Например, возьмем Угадай и улучши . Предположим, мы угадали 60 свиней, всего 240 ног. Теперь 60 свиней подразумевают 27 цыплят, а это дает еще 54 ноги. В общей сложности у нас было бы 294 ноги на данный момент.
К сожалению, мы знаем, что ножек всего 266. Таким образом, мы угадали слишком высоко. Поскольку у свиней больше ног, чем у кур, нам нужно уменьшить догадку в 60 свиней. Как насчет сокращения количества свиней до 50? Это означает, что 37 цыплят и, следовательно, 200 + 74 = 274 ноги.
Мы все еще слишком высоко. Теперь 40 свиней и 47 кур дают 160 + 94 = 254 ноги. Теперь у нас слишком мало ног, поэтому нам нужно угадать больше свиней.
Теперь вы должны видеть, как раскачиваться вперед и назад, пока не наберете нужное количество свиней. Итак, «угадай и улучши» — это метод решения, который можно использовать для решения ряда задач.
Некоторые стратегии могут дать вам представление о том, как можно решить проблему. Создание стола иллюстрирует этот момент. Мы введем несколько значений и посмотрим, что произойдет.
| свиньи | куры | свиные ножки | куриные ножки | всего | разница |
| 60 | 27 | 240 | 54 | 294 | 28 |
| 50 | 37 | 200 | 74 | 274 | 8 |
| 40 | 47 | 160 | 94 | 254 | -12 |
| 41 | 46 | 164 | 92 | 256 | -10 |
Из таблицы видно, что каждый раз, когда мы меняем количество свиней на одну, мы меняем количество ног на две. Это означает, что в нашем последнем предположении в таблице мы в пяти поросятах от правильного ответа. Тогда должно быть 46 свиней.
Это означает, что в нашем последнем предположении в таблице мы в пяти поросятах от правильного ответа. Тогда должно быть 46 свиней.
Некоторые стратегии помогают нам увидеть общие закономерности, чтобы мы могли делать предположения. Некоторые стратегии помогают нам увидеть, как можно обосновать предположения. А некоторые стратегии выполняют другую работу. Мы будем развивать эти идеи по использованию стратегий по мере роста этого веб-сайта.
Какие стратегии можно использовать на каких уровнях
В работе, которую мы проделали за последние несколько лет, кажется, что учащиеся могут решать и использовать больше стратегий по мере того, как они продолжают решать проблемы. Они также могут использовать их на более глубоком уровне. Мы наблюдали, как на указанных уровнях используются следующие стратегии.
Уровни 1 и 2
- Нарисуй картинку
- Разыграй это
- Использовать оборудование
- Угадай и проверь
Уровни 3 и 4
- Нарисуйте диаграмму
- Разыграй это
- Использовать оборудование
- Угадай и улучши
- Сделать стол
- Составьте организованный список
Здесь важно сказать, что исследование не было исчерпывающим. Возможно, младшие школьники могут эффективно использовать и другие стратегии. Тем не менее, мы уверены, что большинство учащихся на данном уровне учебной программы могут использовать стратегии, перечисленные выше для этого уровня. Поскольку решение проблем становится все более распространенным в начальных школах, мы ожидаем, что некоторые из более сложных стратегий станут использоваться на более низких уровнях.
Возможно, младшие школьники могут эффективно использовать и другие стратегии. Тем не менее, мы уверены, что большинство учащихся на данном уровне учебной программы могут использовать стратегии, перечисленные выше для этого уровня. Поскольку решение проблем становится все более распространенным в начальных школах, мы ожидаем, что некоторые из более сложных стратегий станут использоваться на более низких уровнях.
Стратегии могут развиваться как минимум двумя способами. Способность первых студентов использовать стратегии развивается с опытом и практикой. Мы упоминали об этом выше. Во-вторых, сами стратегии могут стать более абстрактными и сложными. Именно это развитие мы и хотим обсудить здесь на нескольких примерах.
Не все учащиеся могут точно следовать этому развитию. Некоторые учащиеся могут пропускать различные этапы. Кроме того, когда возникает совершенно новая проблема, учащиеся могут вернуться к более раннему этапу стратегии во время решения проблемы.
Рисовать: Ранее мы говорили о рисовании картинок и диаграмм. Студенты часто начинают с очень точного представления проблемы. Поскольку они видят, что нет необходимости добавлять все детали или цвет, их изображения становятся более символичными и сохраняются только основные черты. Таким образом, мы получаем пятно для тела свиньи и четыре короткие линии для ее ног. Затем учащиеся, кажется, понимают, что отношения между объектами можно продемонстрировать с помощью линейных рисунков. Объекты могут быть уменьшены до точек или букв. В геометрических задачах могут потребоваться более точные диаграммы, но диаграммы полезны в очень многих задачах, не имеющих геометрического содержания.
Студенты часто начинают с очень точного представления проблемы. Поскольку они видят, что нет необходимости добавлять все детали или цвет, их изображения становятся более символичными и сохраняются только основные черты. Таким образом, мы получаем пятно для тела свиньи и четыре короткие линии для ее ног. Затем учащиеся, кажется, понимают, что отношения между объектами можно продемонстрировать с помощью линейных рисунков. Объекты могут быть уменьшены до точек или букв. В геометрических задачах могут потребоваться более точные диаграммы, но диаграммы полезны в очень многих задачах, не имеющих геометрического содержания.
Простое «нарисуй картинку» со временем превращается в большое разнообразие рисунков, позволяющих учащимся и взрослым решать множество задач.
Угадай: переход от угадывания и проверки к угадыванию и улучшению является очевидным развитием простой стратегии. Угадай и проверь может хорошо работать в некоторых задачах, но угадай и улучши это простое развитие угадывания и проверки.
Но угадывание и проверка могут превратиться в сложную процедуру, которую 5-летние ученики не смогут понять. На более высоком уровне, но все еще в начальной школе, учащиеся могут угадывать закономерности на основе данных, которые им дали или которые они произвели сами. Если они хотят быть уверены, что их догадка верна, они должны каким-то образом обосновать закономерность. Это просто еще один способ проверки.
Все математики-исследователи используют догадки и проверки. Их догадки называются «гипотезами». Их проверки являются «доказательствами». Проверенное предположение становится «теоремой». Решение задач очень близко к математическому исследованию. То, как работают математики-исследователи, точно соответствует четырехэтапному методу Полиа (Что такое решение проблем?). Единственная разница между решением проблем и исследованием заключается в том, что в школе кто-то (учитель) знает решение проблемы. В исследованиях никто не знает решения, поэтому проверка решений становится более важной.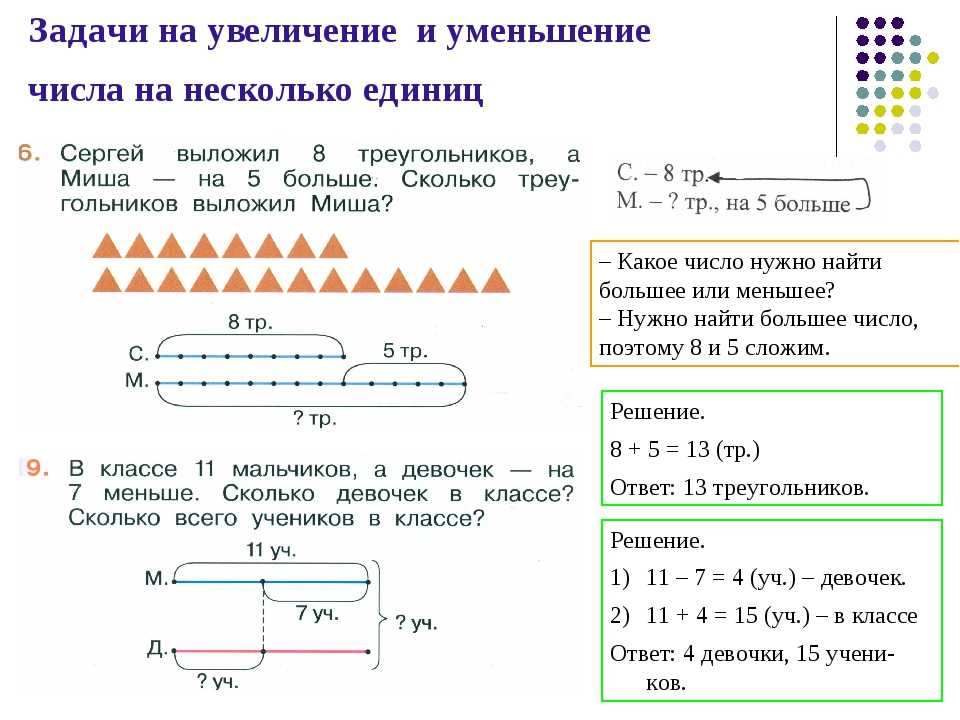
Итак, вы видите, что такая простая стратегия, как «угадай и проверь», может развиться до очень глубокого уровня.
Что такое дискалькулия | Понятно
Дискалькулия — это нарушение обучаемости по математике. Люди с проблемами с математикой на многих уровнях. Они часто борются с ключевыми понятиями, такими как больше или меньше. И им может быть трудно решать базовые математические задачи и более абстрактную математику.
Снимок: что такое дискалькулия
Дискалькулия — это состояние, которое затрудняет выполнение математических и математических задач. Это не так хорошо известно и не так понятно, как . Но некоторые эксперты считают, что это так же распространено. Это означает, что примерно от 5 до 10 процентов людей могут страдать дискалькулией.
Неясно, встречается ли дискалькулия у девочек так же часто, как у мальчиков. Большинство экспертов считают, что разницы нет. (Это также миф, что мальчики лучше разбираются в математике, чем девочки . )
)
Получите информационный бюллетень на одну страницу о дискалькулии.
открывается в новой вкладкеСуществуют разные термины для обозначения дискалькулии. Неспособность к обучению математике является одним из них. Нарушение обучения математике — еще одно. Некоторые люди называют это математической дислексией или числовой дислексией. Это может ввести в заблуждение. Дислексия — это проблемы с чтением. Дискалькулия — это проблемы с математикой.
Люди не перерастают дискалькулию. Дети, которым трудно с математикой, могут продолжать бороться с ней во взрослом возрасте. Но есть стратегии, которые могут помочь им улучшить математические навыки и справиться с трудностями.
Трудности с математикой бывают на всех уровнях. Выучить сложение может быть так же сложно, как и выучить алгебру. Основные понятия, такие как количество, также могут быть проблемой.
Вот почему дискалькулия может затруднить выполнение повседневных задач. Приготовление пищи, покупка продуктов и своевременное посещение места — все это требует базовых математических навыков, известных как чувство числа.
Приготовление пищи, покупка продуктов и своевременное посещение места — все это требует базовых математических навыков, известных как чувство числа.
Погрузитесь глубже
- Узнайте больше о термине числовая дислексия.
- Попробуйте симуляцию, чтобы увидеть дискалькулию глазами ребенка.
- Узнайте истории о дискалькулии — от суперзвезды Шер до студентки колледжа, страдающей дискалькулией.
У людей с дискалькулией могут возникнуть проблемы с математикой по разным причинам. Признаки могут варьироваться от человека к человеку. И в разном возрасте они могут выглядеть по-разному.
У некоторых людей проблемы с восприятием чисел могут проявиться еще в дошкольном возрасте. У других проблемы становятся очевидными по мере усложнения математики в школе.
Общие признаки дискалькулии включают проблемы:
- Понимание значения величин или понятий, таких как наибольшая и наименьшая
- Понимание того, что цифра 5 совпадает со словом пять , и что они оба означают пять предметов
- Запоминание математических фактов в школе, таких как таблица умножения
- Подсчет денег или выдача сдачи
- Оценка времени
- Оценка скорости или расстояния
- Понимание логики математики
- Удержание чисел в голове при решении задач
Познакомьтесь с Хеди, которая вырастила внука с дискалькулией
открывается в новой вкладке Некоторые люди считают дискалькулию просто «плохими математическими способностями». Но это настоящая проблема, основанная на биологии, как и дислексия.
Но это настоящая проблема, основанная на биологии, как и дислексия.
Погрузитесь глубже
- Узнайте больше о признаках дискалькулии у детей и о том, как она может повлиять на взрослых.
- Для семей: получите советы о том, как помочь ребенку с математикой.
- Для преподавателей: узнайте об обучении математике на основе фактических данных для учащихся, испытывающих затруднения.
Возможные причины дискалькулии
Исследователи точно не знают, что вызывает дискалькулию. Но они считают, что это, по крайней мере частично, связано с различиями в том, как устроен мозг и как он функционирует.
Вот две возможные причины дискалькулии:
Гены и наследственность: Дискалькулия обычно передается по наследству. Исследования показывают, что генетика также может играть роль в проблемах с математикой.
Развитие мозга: Исследования визуализации мозга показали некоторые различия между людьми с дискалькулией и без нее. Различия связаны со структурой мозга и тем, как он функционирует в областях, связанных с навыками обучения.
Различия связаны со структурой мозга и тем, как он функционирует в областях, связанных с навыками обучения.
Исследователи не просто изучают причины дискалькулии. Они также пытаются узнать, существуют ли стратегии, которые могут помочь «перепрограммировать» мозг, чтобы упростить математику.
Нырнуть глубже
- Узнайте о пересечении дискалькулии, дислексии и генетики.
- Для семей: изучите термины, чтобы узнать, испытывает ли ваш ребенок трудности с математикой.
- Для педагогов: узнайте о рядах дробей и других стратегиях, которые помогут детям, у которых проблемы с математикой.
Как диагностируется дискалькулия
Единственный способ поставить диагноз — пройти обследование. Это может случиться в любом возрасте. Оценщики используют разные тесты для взрослых и для детей.
Дети могут бесплатно пройти тестирование в школе. Есть также специалисты, которые проводят частные оценки детей и взрослых. Частные оценки могут быть дорогостоящими. Но есть местные ресурсы, которые предлагают бесплатные или недорогие оценки.
Но есть местные ресурсы, которые предлагают бесплатные или недорогие оценки.
Послушайте Марио, страдающего дискалькулией и дислексией
открывается в новой вкладкеОценщики используют набор тестов только на дискалькулию. Но оценки также включают тестирование на другие проблемы. Отчасти это связано с тем, что люди с дискалькулией часто испытывают трудности и в других областях, таких как чтение или рабочая память. Но оценки не просто указывают на проблемы. Они также показывают сильные стороны.
Диагноз (в школах используется слово , идентификатор ) позволяет детям получать поддержку и услуги в школе. Например, дети могут получать специальные инструкции по математике. Школа также может предоставить специальные приспособления, чтобы облегчить изучение математики.
Взрослые с дискалькулией могут получить приспособления на работе. Закон требует от работодателей оказывать поддержку людям с ограниченными возможностями.

 Они сшили его. Теперь платьев стало пять.
Сколько платьев они сшили в начале?
Они сшили его. Теперь платьев стало пять.
Сколько платьев они сшили в начале? 3 из них взяли и съели. Осталось на блюде
4 яблока. Сколько яблок было? [4. с. 196]
3 из них взяли и съели. Осталось на блюде
4 яблока. Сколько яблок было? [4. с. 196] —
195 с.
—
195 с. Убедитесь, что вы понимаете все слова и идеи. Возможно, вам придется прочитать задачу два или более раз. Если есть слова, которые вы не понимаете, поищите их в словаре или в Интернете.
Убедитесь, что вы понимаете все слова и идеи. Возможно, вам придется прочитать задачу два или более раз. Если есть слова, которые вы не понимаете, поищите их в словаре или в Интернете. Будем надеяться, что это исследование приведет к более эффективной стратегии, а затем к решению.
Будем надеяться, что это исследование приведет к более эффективной стратегии, а затем к решению.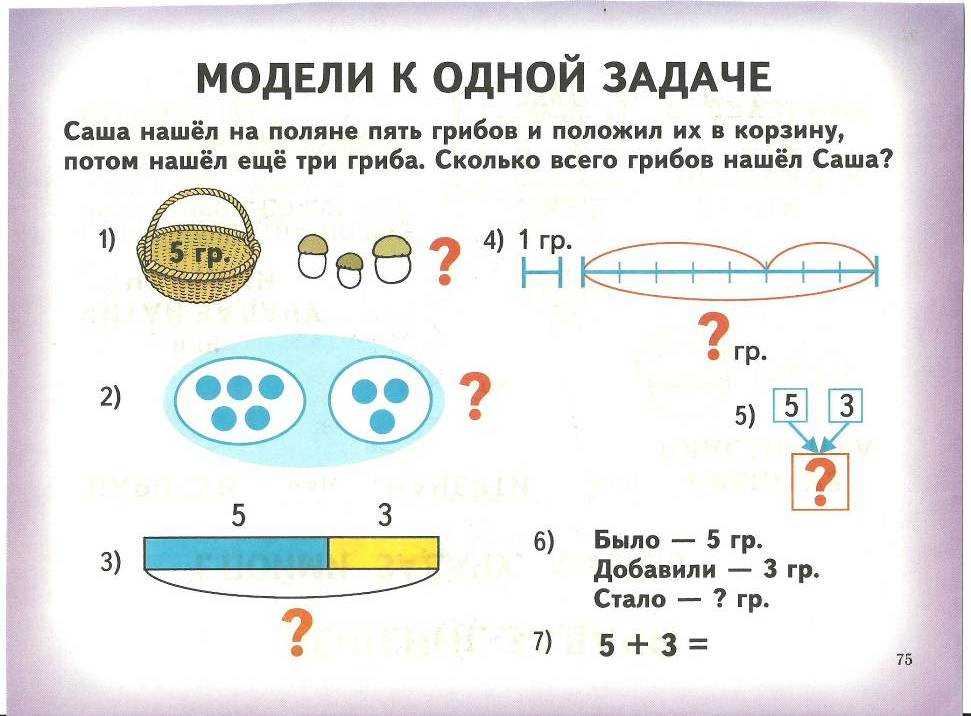
 Это может быть потому, что это дает им лучшее представление о проблеме. Так как есть проблемы при использовании оборудования — это лучшая стратегия, чем рисование, вы должны поощрять использование учащимися оборудования, время от времени самостоятельно моделируя его использование.
Это может быть потому, что это дает им лучшее представление о проблеме. Так как есть проблемы при использовании оборудования — это лучшая стратегия, чем рисование, вы должны поощрять использование учащимися оборудования, время от времени самостоятельно моделируя его использование.  Вы можете думать о диаграмме как о чем-либо, что вы можете нарисовать, но это не изображение. Но где вы проводите грань между картинкой и диаграммой? Как вы можете видеть на примере цыплят и свиней, о которых говорилось выше, обычное рисование картинок перерастает в рисование диаграмм.
Вы можете думать о диаграмме как о чем-либо, что вы можете нарисовать, но это не изображение. Но где вы проводите грань между картинкой и диаграммой? Как вы можете видеть на примере цыплят и свиней, о которых говорилось выше, обычное рисование картинок перерастает в рисование диаграмм. 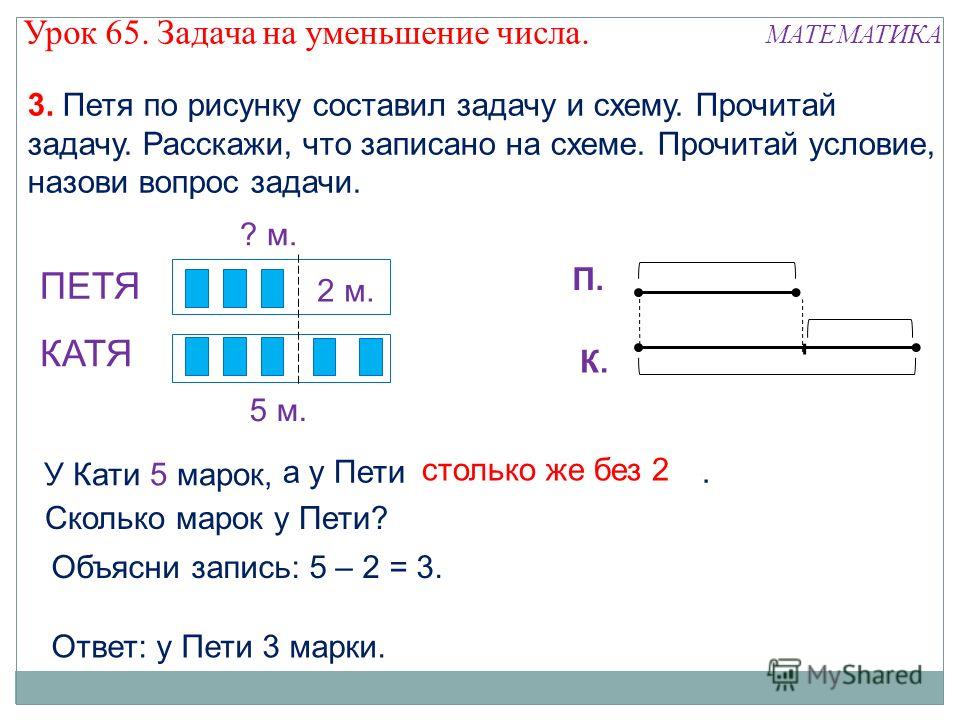 Они варьируются от таблиц чисел, помогающих решать такие задачи, как ферма, до таблиц с галочками и крестиками, которые часто используются в логических задачах. Таблицы также могут быть эффективным способом поиска числовых шаблонов.
Они варьируются от таблиц чисел, помогающих решать такие задачи, как ферма, до таблиц с галочками и крестиками, которые часто используются в логических задачах. Таблицы также могут быть эффективным способом поиска числовых шаблонов. Отчасти это связано с тем, что эти стратегии обычно используются не сами по себе, а в сочетании с другими стратегиями.
Отчасти это связано с тем, что эти стратегии обычно используются не сами по себе, а в сочетании с другими стратегиями. 
 Например, играя в крестики-нолики, вы поймете, что есть три, а не девять способов положить первый символ. Это сразу уменьшает количество возможностей для игры и упрощает ее анализ. Такого рода аргументы возникают постоянно, и их следует с радостью воспринимать, когда вы их видите.
Например, играя в крестики-нолики, вы поймете, что есть три, а не девять способов положить первый символ. Это сразу уменьшает количество возможностей для игры и упрощает ее анализ. Такого рода аргументы возникают постоянно, и их следует с радостью воспринимать, когда вы их видите. Хитрость здесь заключается в том, чтобы увидеть, какие навыки, которые вы знаете, могут быть применены к решению проблемы.
Хитрость здесь заключается в том, чтобы увидеть, какие навыки, которые вы знаете, могут быть применены к решению проблемы.