Решить матричным методом уравнение: Онлайн калькулятор. Решение систем линейных уравнений. Матричный метод. Метод обратной матрицы.

Решение систем линейных уравнений матричным методом

Содержание статьи

1. Матричный способ решения систем линейных уравнений

2. Примеры решения системы с помощью обратной матрицы

Матричный способ решения систем линейных уравнений

Рассмотрим систему линейных уравнений следующего вида:

$\left\{\begin{array}{c} {a_{11} x_{1} +a_{12} x_{2} +…+a_{1n} x_{n} =b_{1} } \\ {a_{21} x_{1} +a_{22} x_{2} +…+a_{2n} x_{n} =b_{2} } \\ {…} \\ {a_{n1} x_{1} +a_{n2} x_{2} +…+a_{nn} x_{n} =b_{n} } \end{array}\right. .$

Числа $a_{ij} (i=1..n,j=1..n)$ — коэффициенты системы, числа $b_{i} (i=1..n)$ — свободные члены.

Определение 1

В случае, когда все свободные члены равны нулю, система называется однородной, в противном случае — неоднородной.

Каждой СЛАУ можно поставить в соответствие несколько матриц и записать систему в так называемом матричном виде.

Определение 2

Матрица коэффициентов системы называется матрицей системы и обозначается, как правило, буквой $A$.

Столбец свободных членов образует вектор-столбец, который, как правило, обозначается буквой $B$ и называется матрицей свободных членов.

Неизвестные переменные образуют вектор-столбец, который, как правило, обозначается буквой $X$ и называется матрицей неизвестных.

Описанные выше матрицы имеют вид:

$A=\left(\begin{array}{cccc} {a_{11} } & {a_{12} } & {…} & {a_{1n} } \\ {a_{21} } & {a_{22} } & {…} & {a_{2n} } \\ {…} & {…} & {…} & {…} \\ {a_{n1} } & {a_{n2} } & {…} & {a_{nn} } \end{array}\right),B=\left(\begin{array}{c} {b_{1} } \\ {b_{2} } \\ {…} \\ {b_{n} } \end{array}\right),X=\left(\begin{array}{c} {x_{1} } \\ {x_{2} } \\ {…} \\ {x_{n} } \end{array}\right).$

Используя матрицы, СЛАУ можно переписать в виде $A\cdot X=B$. Такую запись часто называют матричным уравнением.

Вообще говоря, в матричном виде записать можно любую СЛАУ.

Примеры решения системы с помощью обратной матрицы

Пример 1

Дана СЛАУ: $\left\{\begin{array}{c} {3x_{1} -2x_{2} +x_{3} -x_{4} =3} \\ {x_{1} -12x_{2} -x_{3} -x_{4} =7} \\ {2x_{1} -3x_{2} +x_{3} -3x_{4} =5} \end{array}\right. {-1} \cdot B$.

Если матрица системы имеет определитель, не равный нулю, то данная система имеет единственное решение, которое можно найти матричным способом.

Если матрица системы имеет определитель, равный нулю, то данную систему нельзя решить матричным способом.

Пример 2

Дана СЛАУ: $\left\{\begin{array}{c} {x_{1} +3x_{3} =26} \\ {-x_{1} +2x_{2} +x_{3} =52} \\ {3x_{1} +2x_{2} =52} \end{array}\right. $. Решить СЛАУ методом обратной матрицы, если это возможно.

Решение:

$A=\left(\begin{array}{ccc} {1} & {0} & {3} \\ {-1} & {2} & {1} \\ {3} & {2} & {0} \end{array}\right),B=\left(\begin{array}{c} {26} \\ {52} \\ {52} \end{array}\right),X=\left(\begin{array}{c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \end{array}\right). $

Нахождение определителя матрицы системы:

$\begin{array}{l} {\det A=\left|\begin{array}{ccc} {1} & {0} & {3} \\ {-1} & {2} & {1} \\ {3} & {2} & {0} \end{array}\right|=1\cdot 2\cdot 0+0\cdot 1\cdot 3+2\cdot (-1)\cdot 3-3\cdot 2\cdot 3-2\cdot 1\cdot 1-0\cdot (-1)\cdot 0=0+0-6-18-2-0=-26\ne 0} \end{array}$ Так как определитель не равен нулю, то матрица системы имеет обратную матрицу и, следовательно, система уравнений может быть решена методом обратной матрицы. {-1} =\frac{1}{-26} \cdot \left(\begin{array}{ccc} {-2} & {6} & {-6} \\ {3} & {-9} & {-4} \\ {-8} & {-2} & {2} \end{array}\right)=\frac{1}{26} \cdot \left(\begin{array}{ccc} {2} & {-6} & {6} \\ {-3} & {9} & {4} \\ {8} & {2} & {-2} \end{array}\right)=\left(\begin{array}{ccc} {\frac{2}{26} } & {\frac{-6}{26} } & {\frac{6}{26} } \\ {\frac{-3}{26} } & {\frac{9}{26} } & {\frac{4}{26} } \\ {\frac{8}{26} } & {\frac{2}{26} } & {\frac{-2}{26} } \end{array}\right)=\left(\begin{array}{ccc} {\frac{1}{13} } & {-\frac{3}{13} } & {\frac{3}{13} } \\ {-\frac{3}{26} } & {\frac{9}{26} } & {\frac{2}{13} } \\ {\frac{4}{13} } & {\frac{1}{13} } & {-\frac{1}{13} } \end{array}\right).$

Найдем решение системы:

$X=\left(\begin{array}{ccc} {\frac{1}{13} } & {-\frac{3}{13} } & {\frac{3}{13} } \\ {-\frac{3}{26} } & {\frac{9}{26} } & {\frac{2}{13} } \\ {\frac{4}{13} } & {\frac{1}{13} } & {-\frac{1}{13} } \end{array}\right)\cdot \left(\begin{array}{c} {26} \\ {52} \\ {52} \end{array}\right)=\left(\begin{array}{c} {\frac{1}{13} \cdot 26-\frac{3}{13} \cdot 52+\frac{3}{13} \cdot 52} \\ {-\frac{3}{26} \cdot 26+\frac{9}{26} \cdot 52+\frac{2}{13} \cdot 52} \\ {\frac{4}{13} \cdot 26+\frac{1}{13} \cdot 52-\frac{1}{13} \cdot 52} \end{array}\right)=\left(\begin{array}{c} {2-12+12} \\ {-3+18+8} \\ {8+4-4} \end{array}\right)=\left(\begin{array}{c} {2} \\ {23} \\ {8} \end{array}\right)$

$X=\left(\begin{array}{c} {2} \\ {23} \\ {8} \end{array}\right)$ — искомое решение системы уравнений.

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 18.11.2021

Выполнение любых типов работ по математике

Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами

Подбор готовых материалов по теме

Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы

Решение системы уравнений с помощью excel — Dudom

Решим Систему Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL. В этой статье нет теории, объяснено только как выполнить расчеты, используя MS EXCEL.

Решим систему из 3-х линейных алгебраических уравнений с помощью обратной матрицы (матричным методом).

Запишем в ячейки основную матрицу системы и столбец свободных членов.

Систему n линейных алгебраических уравнений с n неизвестными можно решать матричным методом только тогда, когда определитель основной матрицы системы отличен от нуля (в противном случае мы имеем линейно зависимые уравнения и соответственно решение систем не единственное). В нашем случае определитель =12.

Для этого выделите ячейки A18:C20, а в Строке формул введите =МОБР(A11:C13) , затем нажмите CTRL+SHIFT+ENTER

.

Решение системы уравнений получим умножением обратной матрицы и столбца свободных членов. Перемножить матрицы можно с помощью формулы массива =МУМНОЖ() .

Для этого выделите ячейки F18:F20, а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13) , затем нажмите CTRL+SHIFT+ENTER.

В файле примера также приведено решение системы 4-х и 5-и уравнений.

обучающие:

• повторение и закрепление знаний учащихся правил записи арифметических выражений и формул в электронных таблицах;
• повторение алгоритма решения систем уравнений;
• формирование знаний и умений в решении систем уравнений, используя возможности электронных таблиц;

развивающие:

• формирование умений анализировать, выделять главное, сравнивать, строить аналогии;

воспитывающие:

• осуществление эстетического воспитания;
• воспитание аккуратности, добросовестности.

Тип урока: урок закрепления изученного материала и объяснения нового.

ХОД УРОКА

I. Организационная часть.

Здравствуйте! Все мы знаем, что одну и ту же информацию можно закодировать любым способом. Перед вами набор чисел. Известно, что каждому числу ставится в соответствие буква в русском алфавите. Расшифруйте эту информацию, кто быстрее!

Ответ: “Знание – сила!”

Молодцы! А знаете, кому принадлежит это выражение? (Если нет, то один ученик ищет ответ в Интернете.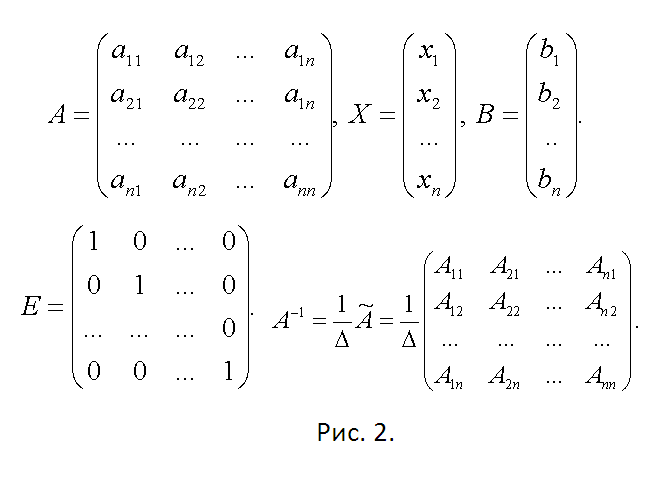 Остальные отвечают на вопросы: Для чего предназначена программа Excel? (Программа Excel предназначена для хранения и обработки данных, представленных в табличном виде) Что собой представляет документ в Excel? (Каждый документ в Excel представляет собой набор таблиц – рабочую книгу, которая состоит из одного или многих рабочих листов) Какая функция используется для подсчета суммы чисел? (Функция СУММ). Как определить адрес ячейки? (Excel вводит номера ячеек автоматически. Адрес ячейки составляется как объединение номеров столбца и строки без пробела между ними)

Выражение английского философа Френсиса Бэкона “Знание – сила!” и будет эпиграфом к нашему уроку. («Нравственные и политические очерки», 1597).

II. Повторение пройденного материала.

Мы уже знакомы с программой Microsoft Excel, умеем записывать арифметические выражения и различные формулы, находить значения арифметических выражений и построить графики функций. Чтобы проверить выполнение домашнего задания, предлагаю каждому пройти тестирование. (Приложение 1)

Хорошо, все справились и каждому поставим соответствующие оценки в журнал. А давайте устроим путешествие в математику и вспомним, что мы понимаем под понятием: “Решить систему уравнений”? (Найти такие значения х и у, которые будут удовлетворять и первое уравнение и второе). Какие способы существуют для решения систем уравнений (метод подстановки, метод сложения и графический способ). Сегодня мы с вами научимся решать системы уравнений, используя возможности электронных таблиц.

III. Объяснение нового.

А. Решим систему

графическим способом. Преобразуем данную систему . Для решения воспользуемся диаграммой, на которой отобразим графики обеих функций. Заполняем столбец А: заполняем ячейки А2:А22 числами от -5 до 5 с шагом 0,5. (в ячейку А2 заносим число -5, в ячейку А3 – число -4,5, выделяем ячейки А2 и А3, установим курсор мыши на правый нижний угол рамки (указатель примет форму черного крестика) и растягиваем рамку вниз, пока последнее значение не станет равным 5). При заполнении столбца В в ячейку В2 заносим формулу =А2*А2, которую затем копируем до ячейки В22. (протянем формулу за правый нижний угол). При заполнении столбца С в ячейку С2 заносим формулу

=1-2*А2, копируем ее до ячейки С22. Выделим блок с данными, с помощью Мастера диаграмм выберем тип диаграммы Точечная и построим графики функций. Координаты точек пересечения графиков – решения системы.

Получены приближенные значения решений. Чем меньше шаг, тем точнее значение координат точек пересечения.

Запишем алгоритм решения систем уравнений графическим способом:

1. Преобразовать систему уравнений, если это необходимо.

2. Задать начальные значения для Х.

3. Найти значение первой функции при заданных Х.

4. Найти значение второй функции при тех же Х.

5. Выделить блок с данными и построить графики функций, используя точечный тип диаграммы.

6. Решение системы — точка пересечения графиков функций.

7. Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.

Б. Решить систему уравнений

. Занесем в электронную таблицу исходные данные и расчетные формулы следующим образом:.

Для решения системы уравнений воспользуемся надстройкой Поиск решения, которая запускается через Сервис (-Надстройки) и заполним диалоговое окно следующим образом:

При нажатии на кнопку Выполнить происходит решение системы уравнений и в ячейках B3 и B4 высвечивается результат.

Запишем примерный алгоритм решения системы уравнений, используя Поиск решения

1. Преобразовать систему уравнений, если это необходимо

2. Записать исходные данные (в ячейку А1 ввести текст “Решите уравнение”, в ячейку В1 записать первое уравнение, в ячейку В2 второе уравнение, в ячейку А3 ввести текст “Х=”, в ячейку А4 “Y=”, в ячейку А5 “уравнение 1”, в ячейку А6 “уравнение 2”. В ячейке B3 хотим получить значение Х, в ячейке В4 – значение Y, их оставляем пустыми.

3. В ячейку В5 переписать уравнение 1, используя правило записи арифметических выражений, следующим образом: в левой части вместо Х указывать ячейку В3, вместо Y ячейку В4, правую часть отбросить. Таким же образом переписать левую часть второго уравнения в ячейку В6.

4. Выбрать команду Сервис – Поиск решения.

5. Установить целевую ячейку — ту ячейку, в которой содержится формула, например, В5 и задать значение, равное значению правой части первого уравнения

6. В поле “изменяя ячейки” указать ячейки, в которых хотим увидеть ответ (В3 и В4)

7. Вести ограничение $B$6 = -3. Для этого щелкнуть на кнопке Добавить и в полученном окне установить реквизиты следующим образом: в поле Ссылка на ячейку указать ячейку, в которой записана левая часть другого уравнения, в другом поле выбрать знак “=”, в третьем ввести число, равное значению правой части. Закрыть окно Добавить ограничение, щелкнув кнопкой ОК

8. Решить систему уравнений, щелкнув кнопкой Выполнить

IV. Практическая работа на компьютере.

А. Решите систему уравнений графическим способом

Б. Решите систему уравнения, воспользовавшись командой Поиск решения:

А. Решите систему уравнений графическим способом

Б. Решите систему уравнения, воспользовавшись командой Поиск решения:

V. Подведение итогов.

Повторить алгоритмы решения систем уравнений

Выставить оценки за тестирование в журнал

VI. Домашнее задание.

Решить рациональным способом системы уравнений:

;

Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.

Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.

Способ 1: матричный метод

Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:

Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.

Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.

Аргумент «Массив» — это, собственно, адрес исходной таблицы.

Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.

Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».

Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.

Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:

Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».

В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».

Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.

После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.

Способ 2: подбор параметров

Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение

Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:

Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.

Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».

Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».

После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».

Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.

Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.

Способ 3: метод Крамера

Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:

Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».

Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.

Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:

Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.

Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».

Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».

Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.

Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.

Аналогичным образом производим подсчет определителей для остальных трех таблиц.

На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.

Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.

Способ 4: метод Гаусса

Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:

Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.

Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:

Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.

После этого копируем полученную строку и вставляем её в строчку ниже.

Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».

Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».

В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:

После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.

Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:

Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.

Поднимаемся на строку вверх и вводим в неё следующую формулу массива:

Жмем привычное уже нам сочетание клавиш для применения формулы массива.

Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:

Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.

Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.

Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. {-1} B$$

Поэтому, чтобы найти неизвестную матрицу $$X$$ надо найти обратную матрицу к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.

Замечание

Данный метод удобно применять тогда, когда нужно решить много одинаковых систем с разными правыми частями.

Примеры решения систем уравнений

Пример

Задание. Найти решение СЛАУ $\left\{\begin{array}{l} 5 x_{1}+2 x_{2}=7 \\ 2 x_{1}+x_{2}=9 \end{array}\right.$ матричным методом.

Решение. Выпишем матрицу системы $A=\left(\begin{array}{ll} 5 & 2 \\ 2 & 1 \end{array}\right)$ и матрицу правых частей $B=\left(\begin{array}{l} 7 \\ 9 \end{array}\right)$ . Найдем обратную матрицу для матрицы системы. Для матрицы второго порядка обратную можно находить по следующему алгоритму: 1) матрица должна быть невырождена, то есть ее определитель не должен равняться нулю: $|A|=1$; 2) элементы, стоящие на главной диагонали меняем местами, а у элементов побочной диагонали меняем знак на противоположный и делим полученные элементы на определитель матрицы. {-1} B=\left(\begin{array}{rr} 1 & -2 \\ -2 & 5 \end{array}\right) \cdot\left(\begin{array}{l} 7 \\ 9 \end{array}\right)=$$ $$=\left(\begin{array}{r} -11 \\ 31 \end{array}\right) \Rightarrow\left(\begin{array}{r} x_{1} \\ x_{2} \end{array}\right)=\left(\begin{array}{r} -11 \\ 31 \end{array}\right)$$

Две матрицы одного размера равны, если равны их соответствующие элементы, то есть в итоге имеем, что $x_{1}=-11, x_{2}=31$

Ответ. $x_{1}=-11, x_{2}=31$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Решить с помощью обратной матрицы систему $\left\{\begin{array}{l} 2 x_{1}+x_{2}+x_{3}=2 \\ x_{1}-x_{2}=-2 \\ 3 x_{1}-x_{2}+2 x_{3}=2 \end{array}\right.$

Решение. Запишем данную систему в матричной форме:

$AX=B$

где $A=\left(\begin{array}{rrr} 2 & 1 & 1 \\ 1 & -1 & 0 \\ 3 & -1 & 2 \end{array}\right)$ — матрица системы, $X=\left(\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right)$ — столбец неизвестных, $X=\left(\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}\right)$ — столбец правых частей. {3+3}\left|\begin{array}{rr} 2 & 1 \\ 1 & -1 \end{array}\right|=-3$$

Таким образом,

$$\tilde{A}=\left(\begin{array}{rrr} -2 & -2 & 2 \\ -3 & 1 & 5 \\ 1 & 1 & -3 \end{array}\right)$$

Определитель матрицы $A$

$$\Delta=\left|\begin{array}{rrr} 2 & 1 & 1 \\ 1 & -1 & 0 \\ 3 & -1 & 2 \end{array}\right|=2 \cdot(-1) \cdot 2+1 \cdot(-1) \cdot 1+1 \cdot 0 \cdot 3-$$ $$-3 \cdot(-1) \cdot 1-(-1) \cdot 0 \cdot 2-1 \cdot 1 \cdot 2=-4 \neq 0$$

А тогда

$$\tilde{A}=-\frac{1}{4}\left(\begin{array}{rrr} -2 & -3 & 1 \\ -2 & 1 & 1 \\ 2 & 5 & -3 \end{array}\right)$$

Отсюда искомая матрица

$$X=\left(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}\right)=-\frac{1}{4}\left(\begin{array}{rrr} -2 & -3 & 1 \\ -2 & 1 & 1 \\ 2 & 5 & -3 \end{array}\right)\left(\begin{array}{r} 2 \\ -2 \\ 2 \end{array}\right)=$$ $$=\left(\begin{array}{r} -1 \\ 1 \\ 3 \end{array}\right) \Rightarrow\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right. $$ $$\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right.$$

Читать дальше: метод Крамера.

{-1}}=\dfrac{AdjA}{\left| \right|}$ и тогда мы решим вопрос.

Полный пошаговый ответ:
В вопросе указано, что мы должны решить систему уравнений, 4x + 3y + z = 16, 2x + y + 3z = 19, x + 2y + 4z = 25 с использованием матричного метода.
Итак, сначала нам нужно преобразовать данные уравнения в матричную форму. Итак, мы можем написать это следующим образом.
\[\left[ \begin{matrix}
   5 & 3 & 1 \\
   2 & 1 & 3 \\
   1 & 2 & 4 \\
\end{matrix} \right]\left[ \begin{matrix}
   x \\
   y \\
   z \\
\end{matrix} \right]=\left[ \begin{matrix}
   16 \ \
   19 \\
   25 \\
\end{matrix} \right]\]
Здесь \[A=\left[ \begin{matrix}
   5 & 3 & 1 \\
   2 & 1 & 3 \ \
   1 & 2 & 4 \\
\end{matrix} \right],X=\left[ \begin{matrix}
   x \\
   y \\
   z \\
\end{matrix} \right] \] и $B=\left[ \begin{matrix}
   16 \\
   19 \\
   25 \\
\end{matrix} \right]$.
Теперь найдем определитель матрицы A, то есть $\left| \право|$. Итак, мы получаем
$A=\left| \begin{matrix}
   5 & 3 & 1 \\
   2 & 1 & 3 \\
   1 & 2 & 4 \\
\end{matrix} \right|$
= 5 (4 — 6) – 3 ( 8 — 3) + 1 (4 — 1)
= 5 (-2) — 3 (5) + (3)
= -10 — 15 + 3
= -22
Теперь найдем сопряжение матрицы A , то есть Adj A. Итак, пусть ${{c}_{ij}}$ являются кофакторами элементов ${{a}_{ij}}$ в $A\left[ {{a}_ {ij}} \right]$. Итак, получаем 9{3+3}}\влево| \begin{matrix}
   5 & 3 \\
   2 & 1 \\
\end{matrix} \right|=1\left( 5-6 \right)=-1 \\
\end{align}\]
Следовательно, мы получаем матрицу кофакторов в виде $\left[ \begin{matrix}
   -2 & -5 & 3 \\
   -10 & 19 & -7 \\
   8 & -13 & -1 \\
\end{matrix} \right]$
Теперь, при транспонировании приведенной выше матрицы, мы получим $AdjA$ as,
$\begin{align}
  & AdjA={{\left[ \begin{matrix}
   -2 & -5 & 3 \\ 9{-1}}=\dfrac{1}{-22}\left[ \begin{matrix}
   -2 & -10 & 8 \\
   -5 & 19 & -3 \\
   3 & -7 & — 1 \\
\end{matrix} \right]$ и $B=\left[ \begin{matrix}
   16 \\
   19 \\
   25 \\
\end{matrix} \right]$.
Следовательно, мы можем написать
$\left[ \begin{matrix}
   x \\
   y \\
   z \\
\end{matrix} \right]=\dfrac{1}{-22}\left [ \begin{matrix}
   -2 & -10 & 8 \\
   -5 & 19 & -3 \\
   3 & -7 & -1 \\
\end{matrix} \right]\left[ \begin{matrix}
   16 \\
   19 \\
   25 \\
\end{matrix} \right]$
Теперь мы выполним умножение двух матриц на правой стороне. Итак, мы можем написать
\[\begin{align}
  & \left[ \begin{matrix}
   x \\
   y \\
   z \\
\end{matrix} \right]=\dfrac{1 }{-22}\left[ \begin{matrix}
   -32-190+200 \\
   -80+361-325 \\
   48-133-25 \\
\end{matrix} \right] \\
 & \left[ \begin{matrix}
   x \\
   y \\
   z \\
\end{matrix} \right]=\dfrac{1}{-22}\left[ \begin{matrix}
-22 \\
   -44 \\
   -110 \\
\end{matrix} \right] \\
\end{align}\]
Теперь возьмем $\dfrac{1}{-22}$ и умножьте его на члены внутри матрицы, так как это константа, а мы знаем, что константы можно умножать на члены внутри матрицы. Итак, мы получим
$\begin{align}
  & \left[ \begin{matrix}
   x \\
   y \\
   z \\
\end{matrix} \right]=\left[ \begin{matrix}
   -22\times \dfrac{1}{-22} \\
   -44\ раз \dfrac{1}{-22} \\
   -110\times \dfrac{1}{-22} \\
\end{matrix} \right] \\
 & \left[ \begin{matrix}
x \\
   y \\
   z \\
\end{matrix} \right]=\left[ \begin{matrix}
   1 \\
   2 \\
   5 \\
\end{matrix} \right] \\
\end{align}$
Следовательно, мы получаем значения x = 1, y = 2 и z = 5.

Примечание. Наиболее распространенная ошибка, которую допускают учащиеся в этом вопросе, заключается в том, что они не транспонируют матрицу, полученную после нахождения сомножителей матрицы A. Это приведет к получению неправильных ответов. Также при нахождении определителя матрицы А некоторые учащиеся могут ошибаться, меняя знаки. И учащиеся также должны знать, как выполнять умножение матриц, так как есть вероятность ошибок в вычислениях. На последнем шаге мы также можем взять -22 из матрицы, как показано ниже.
\[\left[ \begin{matrix}
   x \\
   y \\
   z \\
\end{matrix} \right]=\dfrac{1}{-22}\left[ \begin{matrix}
   -22 \\
   -44 \\
   -110 \\
\end{matrix} \right]\]
\[\left[ \begin{matrix}
   x \\
   y \\
   z \\
\end{matrix} \right]=\dfrac{1}{-22}\times -22\left[ \begin{matrix}
   1 \\
   2 \\
   5 \\
\end{matrix} \right ]\]
\[\left[ \begin{matrix}
   x \\
   y \\
   z \\
\end{matrix} \right]=\left[ \begin{matrix}
   1 \\
   2 \\
   5 \\
\end{matrix} \right]\]
Следовательно, получаем значения x = 1, y = 2 и z = 5.

Объяснение урока: Решение системы из трех уравнений с использованием обратной матрицы

В этом пояснении мы научимся решать систему из трех линейных уравнений используя обратную матрицу коэффициентов.

Мы можем решить систему линейных уравнений, которые также называются одновременными уравнения, используя методы замены или исключения, но эти методы становятся запутанными, когда количество уравнений больше двух. Даже с система из трех уравнений, этот процесс занимает много времени, чтобы решить вручную. Но если мы хотим запрограммировать компьютер для выполнения этой задачи за нас, нам нужен более системный подход к этой задаче.

Здесь на помощь приходит матричный метод. Один из наиболее широко используемых приложений матричных операций состоит в том, чтобы формализовать этот процесс с помощью обратная матрица, так что мы можем легко запрограммировать компьютер для выполнения этого задача. Далее в этом объяснении мы увидим, как писать эти системы 𝑛 линейные уравнения как одно матричное уравнение вида 𝐴𝑋=𝐵, где 𝐴 — квадратная матрица порядка 𝑛×𝑛 и 𝑋 и 𝐵 матрицы порядка 𝑛×1. 𝑋 — неизвестная матрица (т. е. ее 𝑛 элементы неизвестны). Начнем сначала с обсуждения как решить матричное уравнение вида 𝐴𝑋=𝐵 с помощью обратная матрица.

Мы знаем, что 𝐴 — квадратная матрица. Напомним, что обратное квадратной матрицы существует, если ее определитель не равен нулю. Учитывая Матрица 3 × 3 𝐴 с det𝐴≠0, обратная матрица 𝐴 равна матрица 3×3, удовлетворяющая 𝐴𝐴=𝐴𝐴=𝐼, где 𝐼 — единичная матрица 3 × 3.

Теперь, чтобы решить матричное уравнение 𝐴𝑋=𝐵, где 𝐴 и 𝐵 известны матрицы 3×3 и 3×1, соответственно, нам нужно умножить слева на 𝐴 на обе части уравнения, чтобы получить 𝐴𝐴𝑋=𝐴𝐵.

Поскольку 𝐴𝐴=𝐼, это уравнение упрощается до 𝑋=𝐴𝐵.

Обе матрицы 𝐴 и 𝐵 известны; следовательно, это дает решение матричного уравнения 𝐴𝑋=𝐵.

Практическое руководство. Решение матричных уравнений

Пусть 𝐴 — обратимая матрица, а 𝐵 — матрица такое, что умножение 𝐴𝐵 определено. Матрица 𝑋, удовлетворяющая уравнению 𝐴𝑋=𝐵 дан кем-то 𝑋=𝐴𝐵.

Этот метод позволяет решить любое матричное уравнение вида 𝐴𝑋=𝐵, если матрица 𝐴 обратима. Однако этот метод нельзя использовать, если 𝐴 необратима. Это может произойти, если 𝐴 не является квадратной матрицей или если 𝐴 является квадратным и det𝐴=0. В таких случаях, матричное уравнение либо имеет бесконечное число решений, либо не имеет решения. Мы не будем заострять внимание на этих сценариях в этом объяснении, и мы проверим, что матрица коэффициентов обратима перед продолжением.

В нашем первом примере мы будем решать матричное уравнение, когда обратное Предоставляется матрица 3×3.

Пример 1. Решение матричного уравнения с матрицей 3 × 3

Учитывая, что 113025301=−211−15856−3−2, решить следующее матричное уравнение относительно 𝑋: 12370−102−2−113025301𝑋=−1226−112−20.

Ответ

В этом примере нам нужно решить матричное уравнение, чтобы найти неизвестное матрица 𝑋. Чтобы решить это уравнение, мы хотим переставить уравнение так, что 𝑋 является предметом. Мы можем начать с вычитание обеих частей уравнения из крайней левой матрицы в уравнение: −113025301𝑋=−1226−112−20−12370−102−2=−20−1−1−122−42.

Теперь мы можем умножить обе части уравнения на −1, чтобы записать 113025301𝑋=20111−2−24−2.

Наконец, мы можем умножить слева на предоставленную обратную матрицу на обе части уравнения написать −211−15856−3−2113025301𝑋=−211−15856−3−220111−2−24−2.

Мы знаем, что для любой обратимой квадратной матрицы 𝐴 𝐴𝐴=𝐼, где 𝐼 — единичная матрица того же порядка. Следовательно, произведение двух матриц в левой части уравнение приведет к единичной матрице, которая упрощает уравнение к 𝑋=−211−15856−3−220111−2−24−2.

Следовательно, мы можем закончить, вычислив умножение матриц: 𝑋=−2×2+1×1+1×(−2)−2×0+1×1+1×4−2×1+1×(−2)+1×(−2)−15 ×2+8×1+5×(−2)−15×0+8×1+5×4−15×1+8×(−2)+5×(−2)6×2+(−3 )×1+(−2)×(−2)6×0+(−3)×1+(−2)×46×1+(−3)×(−2)+(−2)×(− 2)=−55−6−3228−4113−1116.

В предыдущем примере мы решили матричное уравнение, используя обратную матрицу. Однако нам дали обратную матрицу 3 × 3, что обычно является самой сложной частью. Если нам не задано обратное матрицы, нам нужно сначала найти обратную матрицу. Давайте вспомним сопряженный метод нахождения обратной матрицы 3 × 3.

Как найти обратную матрицу 3 × 3 с помощью Сопряженный метод

Для матрицы 3×3 𝐴 с det𝐴≠0, мы можем найти обратную матрицу 𝐴, выполнив следующие шаги:

1. Найдите определитель 𝐴 и убедитесь, что он ненулевой.
2. Для каждого 𝑖,𝑗∈{1,2,3} найдите определители матричный минор 𝐴, то есть 2×2 матрица, полученная удалением 𝑖-й строки и 𝑗й столбец 𝐴.
3. Запишите матрицу кофакторов, которая представляет собой матрицу 3×3. матрица 𝑐, с 𝑐=(−1)|𝐴|.
4. Найдите сопряженную матрицу, транспонируя матрицу кофакторов: adj𝐴=𝐶.
5. Умножить сопряженную матрицу adj𝐴 на обратную определителя 𝐴 для получения обратной матрицы: 𝐴=1𝐴𝐴.detadj

Как мы видим выше, нахождение обратного числа 3×3 Матрица — утомительный процесс. Тот же метод можно использовать для квадратных матриц высшего порядка; было бы слишком долго даже вычислять определитель матрица вручную, не говоря уже об обратной. По этой причине многие научные калькуляторы или математические программы имеют встроенные функции для вычисления обратная матрица.

Для матрицы 3×3 мы можем вычислить обратную матрицу по формуле рукой, используя метод сопряжения. В следующем примере мы найдем обратное матрицы 3 × 3 с помощью метода сопряжения и использовать его для решить заданное матричное уравнение.

Пример 2. Решение матричного уравнения путем нахождения обратной матрицы

Решите 1−1−111−1110𝑥𝑦𝑧=9−116, используя обратную матрицу.

Ответ

В этом примере нам нужно решить матричное уравнение. Чтобы решить эту уравнение, нам нужно слева умножить на обратную заданную Матрица 3×3 с обеих сторон уравнения. Позволь нам начнем с поиска обратной матрицы 3×3: 𝐴=1−1−111−1110.

Напомним, что квадратная матрица обратима, если ее определитель отличен от нуля. Начнем с вычисления определителя этой матрицы и убедимся, что что оно отлично от нуля.

Напомним, что для матрицы 3×3 𝐴=𝑎, его определитель можно вычислить по формуле det𝐴=𝑎|𝐴|−𝑎|𝐴|+𝑎|𝐴|, где 𝐴 — матричные миноры, полученные 𝑖-я строка и 𝑗-й столбец матрицы 𝐴. Мы можем применить эту формулу к нашей матрице коэффициентов 𝐴 чтобы получить det𝐴=1×||1−110||−(−1)×||1−110||+(−1)||1111||=1(1×0−(−1)×1)−( −1)(1×0−(−1)×1)+(−1)(1×1−1×1)=1+1+0=2.

Поскольку det𝐴≠0, мы знаем, что обратная матрица 𝐴 существует. Мы можем найти обратную матрицу, используя сопряженный метод следующим образом:

1. Найти матрицу кофакторов 𝐶=𝑐× где 𝑐=(−1)|𝐴|.
2. Найдите сопряженную матрицу, транспонируя матрицу кофакторов: adj𝐴=𝐶. 
3. Умножить сопряженную матрицу на обратную величину определителя 𝐴 для получения обратной матрицы: 𝐴=1𝐴𝐴.detadj

Сначала найдем матрицу кофакторов. Записи матрицы кофакторов определители соответствующих миноров матриц, умноженные на знакопеременные знак (−1). Нам нужно вычислить определители 9 матрицы несовершеннолетние с соответствующим знаком для этой цели: +|𝐴|=+||1−110||=1,−|𝐴|=−||1−110||=−1,+|𝐴|=+||1111||=0,−|𝐴 |=−||−1−110||=−1,+|𝐴|=+||1−110||=1,−|𝐴|=−||1−111||=−2,+| 𝐴|=+||−1−11−1||=2,−|𝐴|=−||1−11−1||=0,+|𝐴|=+||1−111||=2 .

Это приводит к матрице кофакторов 1−10−11−2202.

Мы можем найти сопряженную матрицу, выполнив транспонирование: прил𝐴=1−12−1100−22.

Наконец, умножая на обратную величину определителя, который мы вычисленное ранее равным 2, мы получаем 𝐴=121−12−1100−22.

Теперь, когда мы нашли обратную матрицу, мы можем умножить эту матрицу слева в обе части данного уравнения написать 121−12−1100−221−1−111−1110𝑥𝑦𝑧=121−12−1100−229−116.

Мы знаем, что для любой обратимой квадратной матрицы 𝐴 𝐴𝐴=𝐼, где 𝐼 — единичная матрица того же порядка. Следовательно, произведение двух матриц и скаляра слева сторона уравнения приведет к единичной матрице, которая упрощает уравнение к 𝑥𝑦𝑧=121−12−1100−229−116.

Следовательно, мы можем закончить, вычислив матричное и скалярное умножение на правая часть этого уравнения: 𝑥𝑦𝑧=121×9+(−1)×(−11)+2×6−1×9+1×(−11)+0×60×9+(−2)×(−11)+2×6=1232 −2034=16−1017.

Это приводит к 𝑥𝑦𝑧=16−1017.

Приравнивая соответствующие элементы матриц выше, получаем 𝑥=16,𝑦=−10,𝑧=17.

В предыдущем примере мы решили заданное матричное уравнение, сначала найдя обратная матрица 3×3. Матричное уравнение, которое которую мы решили в этом примере, эквивалентна системе из 3 уравнений с 3 неизвестные. Как только мы запишем систему уравнений в матричной форме, мы можно следовать этому методу, чтобы решить систему уравнений. Давайте вспомним как написать матричное уравнение, эквивалентное заданной системе линейных уравнения.

Определение: матричная форма системы линейных уравнений

Рассмотрим общую систему линейных уравнений с неизвестными переменными 𝑥,𝑥,…,𝑥: 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏, 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏, ⋮⋮⋮ ⋮⋮⋮ 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏. 

Матрица коэффициентов 𝐴 определяется как 𝐴 = ⎛⎜⎜⎝𝑎𝑎 ⋯ 𝑎𝑎𝑎 ⋯ 𝑎 ⋮⋮ ⋱ ⋮ 𝑎𝑎 ⋯ 𝑎⎞⎟⎟⎠.

Также переменные и постоянные матрицы 𝑋 и 𝐵 соответственно определяются выражением 𝑋=⎛⎜⎜⎝𝑥𝑥⋮𝑥⎞⎟⎟⎠,𝐵=⎛⎜⎜⎜⎝𝑏𝑏⋮𝑏⎞⎟⎟⎟⎠,0012 Данная система линейных уравнений эквивалентна матричному уравнению 𝐴𝑋=𝐵.

Мы видим, что количество строк в матрице коэффициентов 𝐴 равно количеству уравнений, а количество его столбцов равно количеству неизвестных переменных. Следовательно, если мы начнем с система из трех уравнений, содержащая три неизвестных, порядок матрица коэффициентов 𝐴 будет 3×3. Это означает, что нам нужно найти обратное число 3×3. матрица, чтобы решить это матричное уравнение.

В следующем примере мы напишем матричное уравнение, эквивалентное задана система из 3-х линейных уравнений и 3-х неизвестных. Затем мы решим матричное уравнение с использованием обратной матрицы.

Пример 3. Решение системы одновременных уравнений с использованием матриц

Рассмотрим систему уравнений 2𝑝+2𝑞+4𝑟=4,−𝑝−𝑞−𝑟=14,2𝑝+5𝑞+6𝑟=10.

1. Выразите систему в виде одного матричного уравнения.
2. Вычислите обратную матрицу коэффициентов.
3. Умножить на обратное в левой части, чтобы решить матричное уравнение.

Ответ

Часть 1

В этой части нам нужно написать матричное уравнение, эквивалентное Дана система из 3-х уравнений. Напомним, что система линейных уравнений 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏, 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏, ⋮⋮⋮ ⋮⋮⋮ 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏.  эквивалентно матричному уравнению ⎛⎜⎜⎝𝑎𝑎 ⋯ ⋯ 𝑎 ⋮⋮ ⋱ ⋮ 𝑎𝑎 ⋯ 𝑎⎞⎟⎟⎠⎛⎜⎜⎝𝑥𝑥 ⋮ 𝑥⎞⎟⎟⎠ = ⎛⎜⎜⎜⎝𝑏𝑏 𝑏⎞⎟⎟⎟⎠.  

Матрицы в приведенном выше уравнении называются коэффициентом, переменной, и постоянные матрицы соответственно. Из заданной системы уравнений наши переменные имеют имена 𝑝, 𝑞 и 𝑟, которые формируют записи переменная матрица. Константы 4, 14 и 10 в правых частях данные уравнения образуют элементы постоянной матрицы. Следовательно переменная и постоянная матрицы, соответственно, 𝑝𝑞𝑟,41410.

Чтобы найти матрицу коэффициентов, нам нужно записать коэффициенты каждой переменной в правильном порядке (то есть порядок 𝑝, 𝑞 и 𝑟) для каждого уравнение. Коэффициенты явно не видны во втором уравнения, так как перед переменными стоят только отрицательные знаки. Это указывает на то, что коэффициенты 𝑝, 𝑞 и 𝑟 во втором уравнении равны −1. Мы можем записать это в уравнения: 2𝑝+2𝑞+4𝑟=4,−1𝑝−1𝑞−1𝑟=14,2𝑝+5𝑞+6𝑟=10.

Это приводит к матрице коэффициентов 224−1−1−1256.

Следовательно, матричное уравнение имеет вид 224−1−1−1256𝑝𝑞𝑟=41410.

Часть 2

В этой части нам нужно найти обратную матрицу коэффициентов. Мы получено в предыдущей части, что матрица коэффициентов 𝐴=224−1−1−1256.

Напомним, что квадратная матрица обратима, если ее определитель отличен от нуля. Начнем с вычисления определителя этой матрицы и убедимся, что что оно отлично от нуля.

Напомним, что для матрицы 3×3 𝐴=𝑎, его определитель может быть вычислено det𝐴=𝑎|𝐴|−𝑎|𝐴|+𝑎|𝐴| где 𝐴 — матричные миноры, полученные 𝑖-я строка и 𝑗-й столбец матрицы 𝐴. Мы можем применить эту формулу к нашей матрице коэффициентов 𝐴 чтобы получить det𝐴=2||−1−156||−2||−1−126||+4||−1−125||=2((−1)×6−(−1)×5)−2 ((−1)×6−(−1)×2)+4((−1)×5−(−1)×2)=2×(−1)−2×(−4)+4×( −3)=−6.

Поскольку det𝐴≠0, мы знаем, что обратная матрица 𝐴 существует. Найдем обратное. Напомним, что мы можно найти обратную матрицу с помощью сопряженного метода следующим образом:

1. Найдите матрицу кофакторов 𝐶=𝑐×, где 𝑐=(−1)|𝐴|.
2. Найдите сопряженную матрицу, транспонируя матрицу кофакторов: adj𝐴=𝐶.
3. Умножить сопряженную матрицу на обратную величину определителя 𝐴 для получения обратной матрицы: 𝐴=1𝐴𝐴.detadj

Сначала найдем матрицу кофакторов. Записи матрицы кофакторов – определители соответствующих миноров матриц, умноженные на чередующийся знак (−1). Нам надо вычислить определители числа 9матричные миноры с соответствующим знаком для этой цели: +|𝐴|=+||−1−156||=−1,−|𝐴|=−||−1−126||=4,+|𝐴|=+||−1−125||= −3,−|𝐴|=−||2456||=8,+|𝐴|=+||2426||=4,−|𝐴|=−||2225||=−6,+|𝐴| =+||24−1−1||=2,−|𝐴|=−||24−1−1||=−2,+|𝐴|=+||22−1−1||=0 .

Это приводит к матрице кофакторов −14−384−62−20.

Мы можем найти сопряженную матрицу, выполнив транспонирование: прил𝐴=−18244−2−3−60.

Наконец, умножая на обратную величину определителя, который мы вычисленное ранее равное −6, мы получаем 𝐴=−16−18244−2−3−60.

Часть 3

В этой части нам нужно решить матричное уравнение путем умножения на обратным в левой части. Напомним матричное уравнение, которое мы получено в части 1: 224−1−1−1256𝑝𝑞𝑟=41410.

Если мы умножим слева на обратную матрицу с обеих сторон уравнение, получаем −16−18244−2−3−60224−1−1−1256𝑝𝑞𝑟=−16−18244−2−3−6041410.

Мы знаем, что две матрицы в левой части уравнения равны обратны друг другу, а это означает, что их произведение будет единичная матрица. Это упрощает это уравнение до 𝑝𝑞𝑟=−16−18244−2−3−6041410.

Мы можем закончить вычислением матричного умножения справа сторону уравнения. Это дает нам 𝑝𝑞𝑟=−16−1×4+8×14+2×104×4+4×14+(−2)×10−3×4+(−6)×14+0×10=− 1612852−96.

Вычисляя скалярное умножение и упрощая, получаем −1612852−96=⎛⎜⎜⎜⎝−643−26316⎞⎟⎟⎟⎠=13−64−2648.

Следовательно, 𝑝𝑞𝑟=13−64−2648.

В предыдущем примере мы написали матричное уравнение, эквивалентное заданную систему трех линейных уравнений и решил матричное уравнение с помощью обратная матрица. Если приравнять соответствующие элементы решения задачи матричное уравнение, мы можем найти решение системы уравнений.

В следующем примере мы решим заданное матричное уравнение и найдем неизвестные константы переменной матрицы.

Пример 4. Решение системы из трех уравнений с использованием обратной матрицы

Использование обратной матрицы для решения системы линейных уравнений −4𝑥−2𝑦−9𝑧=−8,−3𝑥−2𝑦−6𝑧=−3,−𝑥+𝑦−6𝑧=7.

Ответ

В этом примере нам нужно решить систему из 3 уравнений с 3 неизвестными с помощью матриц. Мы можем начать с написания матричного уравнения, которое эквивалентна заданной системе уравнений. Напомним, что система линейные уравнения 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏, 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏, ⋮⋮⋮ ⋮⋮⋮ 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏.  эквивалентно матричному уравнению ⎛⎜⎜⎝𝑎𝑎 ⋯ ⋯ 𝑎 ⋮⋮ ⋱ ⋮ 𝑎𝑎 ⋯ 𝑎⎞⎟⎟⎠⎛⎜⎜⎝𝑥𝑥 ⋮ 𝑥⎞⎟⎟⎠ = ⎛⎜⎜⎜⎝𝑏𝑏 𝑏⎞⎟⎟⎟⎠. 

Матрицы в приведенном выше уравнении называются коэффициентом, переменной, и постоянные матрицы соответственно. Из заданной системы уравнений наши переменные имеют имена 𝑥, 𝑦 и 𝑧, которые образуют элементы переменной матрицы. Константы −8, −3 и 7 в правых частях данных уравнений образуют элементы постоянной матрицы. Следовательно, переменная и постоянная матрицы, соответственно, 𝑥𝑦𝑧,−8−37.

Чтобы найти матрицу коэффициентов, нам нужно записать коэффициенты каждой переменной в правильном порядке (то есть порядок 𝑥, 𝑦 и 𝑧) для каждое уравнение. В окончательном уравнении коэффициенты 𝑥 и 𝑦 не видны, что означает, что они равны -1 и 1 соответственно. Мы можем добавить их к уравнению, чтобы написать −4𝑥−2𝑦−9𝑧=−8,−3𝑥−2𝑦−6𝑧=−3,−1𝑥+1𝑦−6𝑧=7.

Это приводит к матрице коэффициентов −4−2−9−3−2−6−11−6.

Следовательно, матричное уравнение имеет вид

−4−2−9−3−2−6−11−6𝑥𝑦𝑧=−8−37.

(1)

Мы можем решить это уравнение, умножив слева обратное матрицы коэффициентов в обеих частях уравнения (1). Найдем обратную матрицу коэффициентов 𝐴=−4−2−9−3−2−6−11−6.

Мы можем использовать сопряженный метод, чтобы получить обратную эту матрицу, если он существует. Напомним, что квадратная матрица обратима, если ее определитель отличен от нуля. Начнем с вычисления определителя эту матрицу и убедившись, что она отлична от нуля.

Напомним, что для матрицы 3×3 𝐴=𝑎, его определитель можно вычислить по формуле det𝐴=𝑎|𝐴|−𝑎|𝐴|+𝑎|𝐴| где 𝐴 — матричные миноры, полученные 𝑖-й ряд и 𝑗-й столбец из матрица 𝐴. Мы можем применить эту формулу к нашему матрица коэффициентов 𝐴 для получения det𝐴=(−4)||−2−61−6||−(−2)||−3−6−1−6||+(−9)||−3−2−11||=( −4)×18−(−2)×12+(−9)×(−5)=−3.

Поскольку det𝐴≠0, мы знаем, что обратное матрица 𝐴 существует. Найдем обратное. Напомним, что мы можем найти обратную матрицу, используя сопряженную следующим образом:

1. Найдите матрицу кофакторов 𝐶=𝑐×, где 𝑐=(−1)|𝐴|.
2. Найдите сопряженную матрицу, транспонируя матрицу кофакторов: adj𝐴=𝐶.
3. Умножить сопряженную матрицу на обратную величину определителя 𝐴 для получения обратной матрицы: 𝐴=1𝐴𝐴. detadj

Сначала найдем матрицу кофакторов. Записи кофактора матрицы являются определителями соответствующих матричных миноров умножить на знак перемены (−1). Нам нужно вычислить определители числа 9матричные миноры с соответствующим для этого знаком цель: +|𝐴|=+||−2−61−6||=18,−|𝐴|=−||−3−6−1−6||=−12,+|𝐴|=+||− 3−2−11||=−5,−|𝐴|=−||−2−91−6||=−21,+|𝐴|=+||−4−9−1−6||= 15,−|𝐴|=−||−4−2−11||=6,+|𝐴|=+||−2−9−2−6||=−6,−|𝐴|=−| |−4−9−3−6||=3,+|𝐴|=+||−4−2−3−2||=2. 

Это приводит к матрице кофакторов 18−12−5−21156−632.

Мы можем найти сопряженную матрицу, выполнив транспонирование: прил𝐴=18−21−6−12153−562.

Наконец, умножая на обратную величину определителя, который мы вычисленное ранее равное −3, мы получаем 𝐴=−1318−21−6−12153−562.

Теперь, когда мы нашли обратную матрицу, умножим уравнение (1) через обратное в левой части: −1318−21−6−12153−562−18−34−386−1219𝑥𝑦𝑧=−1318−21−6−12153−562−8−37.

Поскольку любая матрица, умноженная на обратную, дает тождество матрица, две матрицы и скаляр в левой части этого уравнение сократится. Это упрощает уравнение до 𝑥𝑦𝑧=−1318−21−6−12153−562−8−37.

Следовательно, мы можем закончить вычислением матричного умножения на правая часть уравнения выше: 𝑥𝑦𝑧=−1318×(−8)−21×(−3)−6×7−12×(−8)+15×(−3)+3×7−5×(−8)+ 6×(−3)+2×7=−13−1237236=41−24−12.

Следовательно, 𝑥𝑦𝑧=41−24−12.

Приравнивая соответствующие элементы в приведенных выше матрицах, получаем 𝑥=41,𝑦=−24,𝑧=−12.

В нашем последнем примере мы решим реальную задачу, используя обратную матрица 3×3.

Пример 5. Решение реальной задачи с использованием обратной матрицы

В приведенной ниже таблице показано количество различных типов номеров в трех принадлежащих отелях. компанией.

Hotel	Single Room	Double Room	Suite
First Hotel	45	74	15
Second Hotel	48	74	19
Третья гостиница	49	94	10

Все три отеля берут одинаковую сумму за номер одинакового размера. Когда все номера забронированы, ежедневный доход компании с первого раза, второй и третий отели 50‎ ‎120 LE, 53‎ ‎560 LE и 55‎ 660 LE соответственно. Найдите ежедневный доход от люкса.

Ответ

В этом примере у нас есть три неизвестных величины: стоимость одного номер, двухместный номер и люкс. Обозначим эти неизвестные константами 𝑥, 𝑦 и 𝑧 соответственно. Мы можем найти стоимость люкса в LE, найдя значение из 𝑧.

Нам известно, что ежедневный доход от первой гостиницы составляет 50‎ ‎120 LE, если все номера забронированы. Это может быть записывается в виде следующего уравнения: 45𝑥+74𝑦+15𝑧=50120.

Точно так же мы можем получить еще два уравнения из дневного дохода второй и третий отели соответственно: 48𝑥+74𝑦+19𝑧=53560,49𝑥+94𝑦+10𝑧=55660.

Это дает нам систему из трех уравнений с тремя неизвестными. Давайте решим эту систему с помощью матриц. Мы можем начать с написания матричного уравнения что эквивалентно заданной системе уравнений. Напомним, что система линейных уравнений 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏, 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏, ⋮⋮⋮ ⋮⋮⋮ 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏.  эквивалентно матричному уравнению ⎛⎜⎜⎝𝑎𝑎 ⋯ ⋯ 𝑎 ⋮⋮ ⋱ ⋮ 𝑎𝑎 ⋯ 𝑎⎞⎟⎟⎠⎛⎜⎜⎝𝑥𝑥 ⋮ 𝑥⎞⎟⎟⎠ = ⎛⎜⎜⎜⎝𝑏𝑏 𝑏⎞⎟⎟⎟⎠. 

Матрицы в приведенном выше уравнении называются коэффициентом, переменной, и постоянные матрицы соответственно. Из заданной системы уравнений, наши переменные имеют имена 𝑥, 𝑦 и 𝑧, которые образуют записи переменная матрица. Константы 50‎ ‎120, 53‎ ‎560 и 55‎ ‎660 в правых частях данных уравнений образуют элементы постоянной матрицы. Следовательно, переменная и постоянные матрицы, соответственно, 𝑥𝑦𝑧,501205356055660.

Чтобы найти матрицу коэффициентов, нам нужно записать коэффициенты каждой переменной в правильном порядке (то есть порядок 𝑥, 𝑦 и 𝑧) для каждого уравнения. Это приводит к матрице коэффициентов 457415487419499410.

Следовательно, матричное уравнение имеет вид 457415487419499410𝑥𝑦𝑧=501205356055660.

Мы можем решить это уравнение, умножив слева обратное матрица коэффициентов в обеих частях уравнения выше. Давайте найдем обратная матрица коэффициентов 𝐴=457415487419499410.

Мы можем использовать сопряженный метод, чтобы получить обратную эту матрицу, если это существует. Напомним, что квадратная матрица обратима, если ее определитель отличен от нуля. Начнем с вычисления определителя эту матрицу и убедившись, что она отлична от нуля.

Напомним, что для матрицы 3×3 𝐴=𝑎, его определитель может быть вычислено det𝐴=𝑎|𝐴|−𝑎|𝐴|+𝑎|𝐴| где 𝐴 — матричные миноры, полученные 𝑖-я строка и 𝑗-й столбец матрицы 𝐴. Мы можем применить эту формулу к нашей матрице коэффициентов 𝐴 чтобы получить дет𝐴=45||74199410||−74||48194910||+45||48744994||=45×(−1046)−74×(−451)+45×886=−406.

Поскольку det𝐴≠0, мы знаем, что обратная матрица 𝐴 существует. Найдем обратное. Напомним, что мы можно найти обратную матрицу с помощью сопряженного метода следующим образом:

1. Найти матрицу кофакторов 𝑐=(−1)|𝐴|.
2. Найдите сопряженную матрицу, транспонируя матрицу кофакторов: adj𝐴=𝐶.
3. Умножить сопряженную матрицу на обратную величину определителя 𝐴 для получения обратной матрицы: 𝐴=1𝐴𝐴.detadj

Сначала найдем матрицу кофакторов. Записи матрицы кофакторов – определители соответствующих миноров матриц, умноженные на знак чередования (−1). Нам надо вычислить определители 9 миноров матриц с соответствующим знаком для этой цели: +|𝐴|=+||74199410||=−1046,−|𝐴|=−||48194910||=451,+|𝐴|=+||48744994||=886,−|𝐴|=−| |74159410||=670,+|𝐴|=+||45154910||=−285,−|𝐴|=−||45744994||=−604,+|𝐴|=+||74157419||=296 ,−|𝐴|=−||45154819||=−135,+|𝐴|=+||45744874||=−222. 

Это приводит к матрице кофакторов −1046451886670−285−604296−135−222.

Мы можем найти сопряженную матрицу, выполнив транспонирование: прил𝐴=−1046670296451−285−135886−604−222.

Наконец, умножая на обратную величину определителя, который мы вычисленное ранее равное −406, мы получаем 𝐴=−1406−1046670296451−285−135886−604−222.

Напомним, что мы можем решить матричное уравнение 𝐴𝑋=𝐵, записав 𝑋=𝐴𝐵. Это ведет к 𝑥𝑦𝑧=−1406−1046670296451-285-135886-604-222501205356055660.

Следовательно, мы можем закончить вычислением матричного умножения на правая часть уравнения выше: 𝑥𝑦𝑧=−1406−1046×50120+670×53560+296×55660451×50120−285×5356−135×55660886×50120−604×53560−222×55660−3046=−16406 =160430740.

Это приводит к 𝑥=160, 𝑦=430, 𝑧=740.

Следовательно, стоимость люкса составляет 740 LE.

Давайте закончим повторением нескольких важных понятий из этого объяснения.

Ключевые моменты

• Чтобы решить систему уравнений, используя обратную матрицу, когда матрица коэффициентов обратима, мы можем выполнить следующие шаги:
  • Напишите эквивалентное матричное уравнение в форме 𝐴𝑋=𝐵.
  • Найдите обратную матрицу коэффициентов 𝐴.
  • Умножить слева на обратную матрицу, чтобы записать 𝑋=𝐴𝐵.
  • Приравнять соответствующие элементы матрицы переменных и матрица 𝐴𝐵, чтобы найти решение.
• Дана матрица 3×3 𝐴 с det𝐴≠0, мы можем найти обратную матрицу 𝐴, выполнив следующие шаги:
  • Найдите определитель 𝐴 и убедитесь, что он ненулевой.
  • Для каждого 𝑖,𝑗∈{1,2,3} найдите определители матричный минор 𝐴, то есть 2×2 матрица, полученная удалением 𝑖-й строки и 𝑗й столбец 𝐴.
  • Запишите матрицу кофакторов, которая представляет собой матрицу 3×3. 𝑐, с 𝑐=(−1)|𝐴|. 
  • Найдите сопряженную матрицу, транспонируя матрицу кофакторов: adj𝐴=𝐶.
  • Умножить сопряженную матрицу adj𝐴 на обратную определителя 𝐴 для получения обратной матрицы: 𝐴=1𝐴𝐴.detadj
• Если обратной матрицы коэффициентов не существует, то соответствующая система уравнений либо не имеет решения, либо имеет бесконечное число решений.

Как решить систему уравнений, используя обратную матрицу?

В математике матрица представляет собой массив чисел, расположенных в виде прямоугольника и разделенных на строки и столбцы. Обычно их изображают, заключая все целые числа в квадратные скобки.

Определитель

Определитель матрицы — это скалярное значение, полученное для данной квадратной матрицы. Определитель рассматривается в линейной алгебре и вычисляется с использованием элементов квадратной матрицы. Определитель — это скалярное значение или число, вычисленное с использованием квадратной матрицы. Квадратная матрица может быть 2 × 2, 3 × 3, 4 × 4 или любой другой формы, в которой число столбцов и строк равно, например, n × n. Если S — множество квадратных матриц, R — множество целых чисел (действительных или комплексных) и f: S → R определяется равенством f (A) = k, где A ∈ S и k ∈ R, то f (A ) называется определителем А. Определитель изображается двумя вертикальными линиями, т. е. |A|.

Определитель матрицы 2×2 –     

Определитель матрицы 3×3 –  

Миноры и кофакторы 

Матрица, созданная после исключения строки и столбца матрицы, в которой находится этот конкретный элемент, определяется как минор матрицы.

Минор элемента a ₁₂ равен M ₁₂ –

Кофактор элемента в матрице A получается путем умножения минора элемента _{M ij на (-1) ^i+j . C ij — это символ кофактора элемента. Если минор матрицы M ij , то кофактор элемента будет: C ij = (-1) ^i+j M ij . Матрица кофакторов — это матрица, созданная кофакторами компонентов матрицы.}

Матрица кофакторов:

Сопряженная матрица

Пусть A=[aij] — n-мерная квадратная матрица. Матрица, сопряженная с A, представляет собой транспонированную матрицу кофакторов A. Обозначается буквой adj A. Сопряженные матрицы иногда называют сопряженными матрицами. Сопряженная квадратная матрица A = [aij]n x n определяется как транспонированная матрица [Aij]n x n, где Aij — сомножитель элемента aij.

 

Сопряженное с A = Транспонирование   = 

Обратная матрица

Квадратная матрица A обратима тогда и только тогда, когда A является невырожденной матрицей. Обратную матрицу можно получить, разделив сопряженную матрицу на определитель матрицы. Обратную матрицу можно вычислить, выполнив следующие шаги:

• Шаг 1: Определите минор предоставленной матрицы.
• Шаг 2: Преобразуйте полученную матрицу в матрицу кофакторов.
• Шаг 3: Наконец, вспомогательное и
• Шаг 4: Умножьте его на обратный определитель.

Пусть A =

Сопряженное с A = Транспонирование =

Обратное к матрице A = A ^{-1} =

Применение матриц и определителей может использоваться для решения систем линейных уравнений с двумя или тремя переменными и для оценки непротиворечивости системы.

• Непротиворечивая система : Система уравнений считается непротиворечивой, если она имеет (одно или несколько) решений.
• Несовместимая система :  Если решение системы уравнений не существует, говорят, что система несовместима.

Представление линейных систем с помощью матричных уравнений

Для представления системы уравнений можно использовать расширенную матрицу. Каждая строка в расширенной матрице представляет одно из уравнений системы, а каждый столбец представляет собой переменную или постоянные члены. Мы видим, что расширенные матрицы — это кратчайший путь для формулирования систем уравнений таким образом.

Пример: Запишите следующую систему уравнений в виде расширенной матрицы.

x – 2y = 5

4x – 3y – z = 3

5y – 7z = 9

Представим следующую форму матрицы. Если переменный член не указан в матрице, считается, что коэффициент этого члена равен «0».

(1)х + (-2)у + (0)z = 5

(4)х + (-3)у + (-1)z = 3

(0)х + (5)у + (-7) г = 9

Следующая расширенная матрица:  

Решение линейных систем с помощью матричных уравнений

Решение линейных уравнений с использованием матрицы выполняется матричным методом. В этой статье мы рассмотрим решение линейных уравнений на матричных примерах.

Решение уравнений с обратными матрицами

Предположим, уравнение имеет вид:   

Матричный метод используется для нахождения решения системы уравнений. В уравнениях все переменные должны быть записаны в правильном порядке. На соответствующих сторонах напишите переменные, их коэффициенты и константы.

Метод определения обратного используется для решения системы линейных уравнений и требует двух дополнительных матриц. Переменные представлены матрицей X. Константы представлены матрицей B. Используя матричное умножение, система уравнений с тем же количеством уравнений, что и переменная, определяется как

AX=B

Пусть A будет матрица коэффициентов, X — переменная матрица, а B — постоянная матрица для решения системы линейных уравнений с обратной матрицей. В результате мы хотели бы решить систему AX = B. Взгляните на приведенные ниже уравнения в качестве примера.

AX = B

где:  

Случай 1: Если A невырожденная матрица, она имеет обратную.

Пусть A — матрица коэффициентов, X — матрица переменных, а B — постоянная матрица для решения системы линейных уравнений с обратной матрицей. В результате мы хотим решить систему AX=B. Чтобы получить ответ, умножьте обе части на величину, обратную A.

Поскольку обратная матрица уникальна, это матричное уравнение предлагает единственное решение данной системы уравнений. Матричный метод — это метод решения систем уравнений.

Случай 2: Если A — сингулярная матрица, то | А| = 0. В этом случае вычислить (adj A) B.

Если (adj A) B ≠ O, (O — нулевые матрицы), то решения не существует и система уравнений называется несовместной.

Если (прил. A) B = O, то система может быть либо состоятельной, либо несовместной соответственно, поскольку система либо имеет бесконечно много решений, либо не имеет решений.

Примеры задач

Вопрос 1: Найдите следующее из заданной матрицы  

• determinant of matrix A
• cofactor matrix A 
• adjoint of matrix A
• inverse of matrix A

Solution:

The given matrix is 

• Определитель A =

= 3(0+8)+5(-2+4)+3(-4)

= 3 × 8 + 5 × 2 + 3 × (-4)

= 24 + 10 – 12 единиц

• Кофактор матрицы A =

C ₁₁ ​ = 0 × (-1) -4 × (-2) = 0 + 8 = 8

C ₁₂ ​= -((-5) × (-1) -3 × ( -2)) = -(5 + 6) = -11

C _{13 ​} = (-5) × 4 -3 × 0 = -20

C ₂₁ = −(2 × (-1) -4 × (-1)) = -(-2 + 4) = -2

C ₂₂ ​= 3 × (-1) -3 × (-1) = -3 + 3 = 0  

C _{23 ​} = -(3 × 4 – 3 × 2) = -(12 – 6) = -6

C ₃₁ ​ = 2 × (-2) – 0 × (-1) = -4             

С ₃₂ ​= -(3 × (-2) – (-5) × (-1)) = -(-6 – 5) = 11   

C _33​ = 3 × 0 – (-5) × 2 = 10

Cofactor matrix of A = 

• AdjoinT of matrix A = transpose of cofactor matrix C = 

• Inverse of matrix A = 

= 

= 

Question 2: Ram is нанимается на работу с ежемесячной оплатой определенной суммы и ежегодным повышением на заранее определенную сумму. Найдите его начальную зарплату и ежегодную прибавку, если его зарплата составляла 300 долларов в месяц в конце первого месяца после 1 года службы и 600 долларов в месяц в конце первого месяца после 3 лет службы.

Решение:

Пусть «x» и «y» обозначают месячную зарплату и годовое увеличение на определенную сумму соответственно.

По вопросу;

x + y = 300 ⇢ (i)

x + 3y = 600 ⇢ (ii)

Это можно записать как AX = B, где

Определитель A = 1 × 3 – 1 × 1 = 3 – 1 = 2

Присоединение A =

Таким образом,

Используя обратную матрицу,

X = A ^-1 B

Поэтому; x = 150 долларов, y = 150 долларов

Итак, месячная зарплата равна 150 долларам, а годовой прирост равен 150 долларам.

Вопрос 3: Сумма трех чисел равна 3. Если мы умножим второе число на 2 и прибавим к нему первое число, мы получим 6. Если мы умножим третье число на 4 и прибавим к нему второе число , получаем 10. Представим его алгебраически и найдем числа матричным методом.

Решение:

Пусть x, y и z представляют первое, второе и третье числа соответственно. Тогда согласно вопросу имеем

x + y + z = 3

x + 2y = 6

y + 4z = 10

Это можно записать как AX = B, где

Здесь |A |= 1(8 – 0) – 1(4 – 0) + 1(1 – 0) = 8 – 4 + 1 = 5 ≠ 0. Теперь найдем прил A.

A ₁₁ = 8 – 0 = 8, А ₁₂ = -(4 – 0) = -4, А ₁₃ = 1 – 0 = 1

А ₂₁ = -(4 – 1) = -3, А ₂₂ = 4 – 0 = 4, А ₂₃ = -(1 – 0) = -1

А ₃₁ = 0 – 2 = -2, A ₃₂ = -(0 – 1) = 1, A ₃₃ = 2 – 1 = 1

Прил. A =

Таким образом,

X = A ^-1 B

Следовательно;

Вопрос 4. Предположим, Джо, Макс и Полли пошли за покупками в торговый центр. Джо платит 45/- за 4 кг яблок, 7 кг бананов и 6 кг гуавы, Макс платит 30/- за 2 кг яблок и 5 кг гуавы, а Полли платит 35/- за 3 кг яблок, 1 кг бананов и 4 кг гуавы. Сколько стоят яблоки, бананы и гуава за килограмм?

Решение:

Пусть x, y и z обозначают количество яблок, бананов и гуавы соответственно.

В соответствии с вопросом:

4x + 7y + 6z = 45

2 x + 5 z = 30

3x + y + 4z = 35

Матрица A содержит килограмм купленных яблок, бананов и гуавы Джо, Макс и Полли. Матрица B содержит цены, которые платят все трое, а матрица X содержит переменные.

Решением данной системы уравнений будет X = A ^-1 B.

Чтобы найти обратную величину A, мы сначала найдем определитель A.

Определитель A = |A| = 4(0 х 4 – 1 х 5) – 7(2 х 4 – 5 х 3) + 6(2 х 1 – 3 х 0)

= 4(0 – 5) – 7(8 – 15) + 6(2 – 0)

= -20 – 7(-7) + 12

= -20 + 49 + 12 = 41

Прил. of A =

Стоимость яблок за кг = 8,3/-

Стоимость бананов за кг = 1,1/-

Стоимость гуавы за кг = 2,7/-

Вопрос 5: Стоимость 2 кг картофеля, 3 кг помидоров и 2 кг муки составляет 50. Стоимость 5 кг картофеля, 1 кг помидоров и 6 кг муки — 40. Стоимость 4 кг картофеля, 6 кг помидоров и 3 кг муки — 60. Найдите стоимость каждого продукта за кг с помощью обратной матрицы.

Решение:

Пусть x, y и z обозначают кг картофеля, помидоров и муки соответственно.

В соответствии с вопросом:

2x + 3y + 2z = 50

5x + 1y + 6z = 40

4x + 6y + 3z = 60

Матрица A содержит кг картофеля, помидоров и муки. Матрица B содержит уплаченные цены, а матрица X содержит переменные. Это можно записать как AX = B, где

Решение данной системы уравнений X = A ^-1 B. Чтобы найти обратную величину A, мы сначала найдем определитель A.

No related posts.