Вектора в математике: Недопустимое название | Математика | Fandom

Что такое вектор — Журнал «Код»

Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное. 

Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно. 

⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях. 

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.  

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если a + b = c, то a = c − b. Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой. 

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра. 

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения. 

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать. 

Что такое вектор

Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи.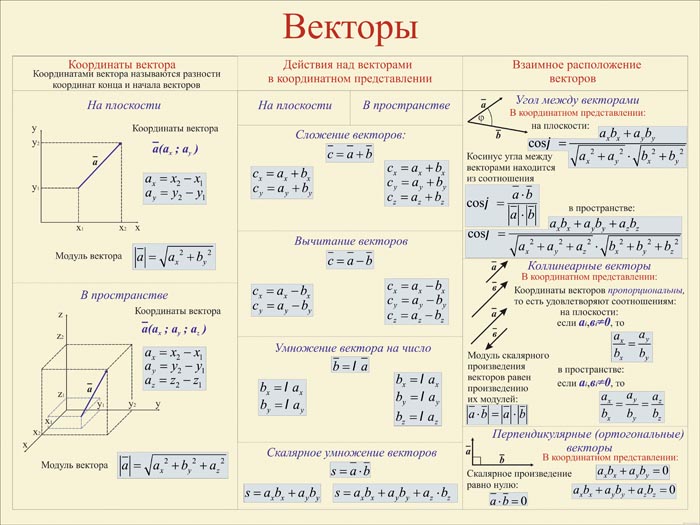 В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

Математическое представление вектора: данные можно перевести в числа или график

В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами. 

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.  

Как записывать

Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант. 

Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.

Способы записи вектора

Скаляр

Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.

Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.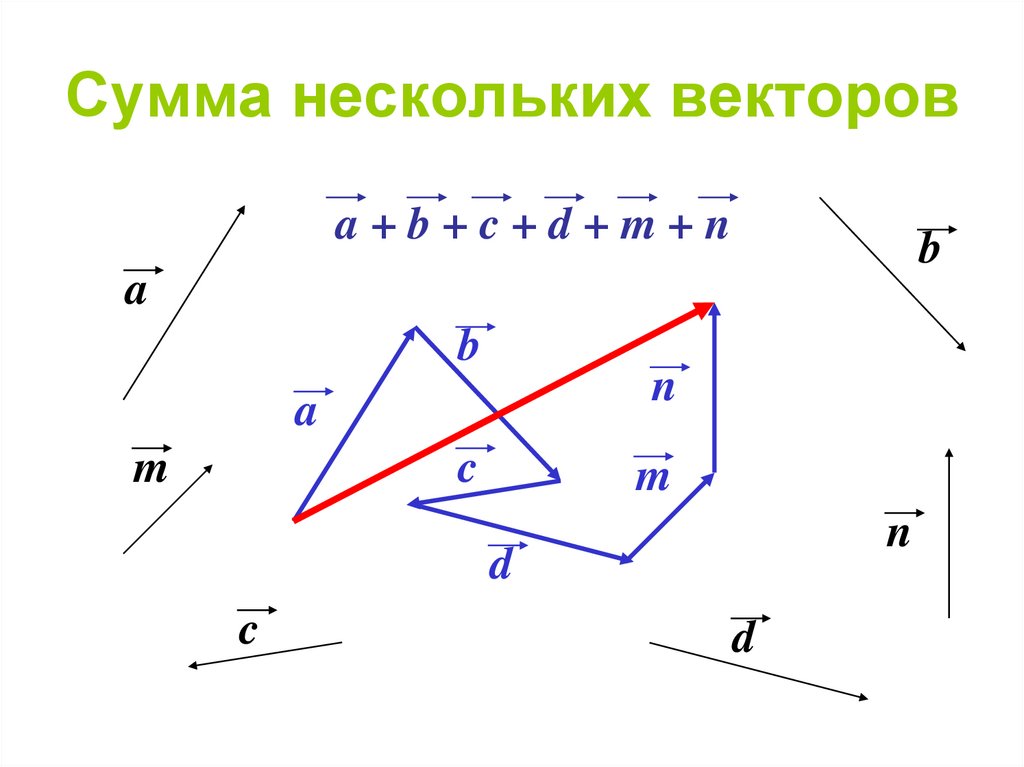

Как изображать 

Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

Графическое представление скаляра. Записывается в круглых скобках

Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз. 

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

Графическое представление числового вектора в двух измерениях

Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.  

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например: 

• На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица. 
• Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом. 

Что такое искусственный интеллект

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте. 

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Что дальше

В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.

Текст

Александр Бабаскин

Редактор

Максим Ильяхов

Художник

Даня Берковский

Корректор

Ирина Михеева

Вёрстка

Мария Дронова

Соцсети

Олег Вешкурцев

Векторы в физике и математике

Слайд 1

в физике Векторы и математике у х А О В n

Слайд 2

Объектом исследования являются Векторы и его свойства

Слайд 3

Предмет исследования Применение вектора и его свойств при решении задач школьного курса физики

Слайд 4

Цель работы -определить сущность, функции межпредметных связей и их классификацию, а так же повысить собственный уровень знаний и умений в применении свойств вектора при решении физических задач; -показать применение вектора и его свойств при решении физических задач школьного курса физики 7-11 классов, олимпиадных задач, а так же задач ЕГЭ;

Слайд 5

Задачи 3. Решить задачи разного уровня сложности, содержащиеся в учебниках физики, сборниках задач, олимпиадных задач и задач ЕГЭ по выбранным темам. 1. Сопоставить понятие вектор, которое дается в учебниках школьного курса физики и геометрии; 2. Проанализировать содержание курса физики 7-11 классов и отобрать темы, в которых при решении задач используется свойства вектора;

Слайд 6

Актуальность Необходимость формирования целостного представления о применении векторов в физике и математике и подготовки к ЕГЭ по этим предметам.

Слайд 7

Практическая значимость работы Заключается в том, что предложенные в работе задачи могут быть использованы на уроках математики, быть полезными учащимся при изучении курса физики и подготовке к ЕГЭ, решении практических задач. Данная работа может представлять интерес для учителей физики и математики при подготовке к урокам и организации повторения.

Слайд 8

Векторы в математике Впервые, понятие вектора дается на уроке геометрии в 8 классе учебника А. В. Погорелова. Вектором называют направленный отрезок, направление которого определяется указанием его начала и конца.

Слайд 9

Векторы в математике Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающая вектор. Если начало вектора совпадает с его концом, такой вектор называется нулевым вектором. Нулевой вектор обозначается .

Слайд 10

Векторы в математике Два вектора называются равными , если они совмещаются параллельным переносом. Равные векторы одинаково направлены и равны по абсолютной величине. Равные векторы имеют равные соответствующие координаты. m n

Слайд 11

Действия над векторами сложение векторов умножение вектора на число скалярное произведение векторов разложение вектора по координатным осям

Слайд 12

Сложение векторов Правило треугольника Правило параллелограмма

Слайд 13

Умножение вектора на число ( λ =

Слайд 14

Скалярное произведение векторов ( . ( = + Если скалярные векторы перпендикулярны, то их произведение равно нулю.

Слайд 15

Разложение вектора по координатным осям Вектор называется единичным, если его абсолютная величина равна единице. Единичные векторы, имеющие направления координатных полуосей, называются координатными векторами. (1;0) (0;1) и ( λ + μ λ . μ

Слайд 16

Векторы в физике В школьном курсе физики учебника А.В. Пёрышкина 7 класса, впервые понятие векторной величины вводится на примере таких физических величин, как Сила и Скорость . Так же вводится понятие Вес тела , которое тоже является векторной величиной. Болеет углубленно понятие вектора и его свойств затрагивается при изучении физики 9 класса учебника А. В. Пёрышкина и Е. М. Гутник .

Слайд 17

Проекция вектора на ось Проекцией точки А на ось l называется число, соответствующее основанию перпендикуляра АВ, опущенного на ось l из точки А. Проекцией вектора на ось l называется разность проекций конца вектора и его начала.

Слайд 18

Решение физических задач векторным методом Задача . С какого расстояния S от центра полусферы радиуса R =1,35 м, с какой скоростью и под каким углом β нужно бросить маленькую шайбу (из положения 1), чтобы она, попав на полусферу, остановилась на её вершине (положение 2) рисунок (а)? Трением шайбы о полусферу и сопротивлением воздуха пренебречь. Ускорение свободного падения считать равным 10 м/с 2 . Сформулируем обратную задачу : На каком расстоянии S от центра полусферы, с какой скоростью U и под каким углом β упадёт шайба, скатывающаяся с вершины полусферы радиуса R рисунок (б)? Трением шайбы о поверхность полусферы и сопротивлением воздуха пренебречь.

Слайд 19

Решение физических задач векторным методом V 0 = . (1.1 ) Решение. mg cos α = m V 0 2 /R, откуда V 0 = . (1.2) h = R(1 – cos α) V 0 = . (1.3) cos α = 2/3 (1.4) V 0 = = = 3 м/с (1.5) Х = V ox t = ( V o cos α)t ( 1.6) Y = V oy t + gt 2 /2 = (V o sin α)t +gt 2 /2 ( 1.7) При t = t п – времени полёта шайбы до точки падения, X = X max , a Y = R cos α = 1,35 . 2/3 = 0,9 м sin α = = = = /3. ………………

Слайд 20

Решение физических задач векторным методом 0,9 = t п + 5t п 2 , (1.8) t п = ( + )/ 10 = 0,7 с. X max = ( V o cos α)t п = 3 . 2/3 . 0,7 = 1,4 м. S = X max + R sin α = 1,4 + 1,35 . /3 = 2,41 м. V = ( 1.9). V ox = V o cos α = 3 . 2/3 = 2 м; V y = V o sin α + gt п = 3 . /3 + 10 . 0,7 = 9,24 м/с , V = = 9,45 м/с. tg β = V y / V ox = 9,24/ 2 = 4,62 β = 77,8 o .

Слайд 21

Решение физических задач векторным метом Задача . Частица массы 2m налетает на неподвижную частицу массы m. После столкновения частицы разлетаются симметрично под углом 45 о к направлению начальной скорости, рисунок (а). Во сколько раз возросла суммарная кинетическая энергия после столкновения?

Слайд 22

Решение. = .(1.1 ) p = (1.2) Е к = р 2 /4m = 2р 1 2 / 4m = р 1 2 / 2m . (1.3 ) Е к1 + Е к2 = (р 1 2 / 2m) + (p 2 2 / 4m) = 3p 1 2 /4m. (1.4) (Е к1 + Е к2 )/ Е к = 3p 1 2 2m / p 1 2 4m = 3/2 = 1,5. (1.7 ) Решение физических задач векторным метом

Слайд 23

Решение физических задач векторным метом По двум длинным параллельным проводникам, расположенным на расстоянии r, текут токи I 1 и I 2 в направлениях, указанных на рисунке (а), на котором изображены сечения проводников плоскостью, перпендикулярной им. Определить индукцию магнитного поля в точке, находящейся на расстоянии r 1 от первого проводника и на расстоянии r 2 от второго. Задача . (а) (б)

Слайд 24

Решение физических задач векторным метом Решение. В= (1.1 ) а cos α по той же теореме, но только для треугольника rr 1 r 2 : cos α = (r 1 2 + r 2 2 – r)/ 2r 1 r 2 . (1.2 ) В = (1.3) (а) (б)

Слайд 25

Задачи из ЕГЭ по физике Через неподвижный блок переброшена нерастяжимая нить. На концах этой нити подвешены грузы равных масс М. На один из грузов поставили груз массой m . Определите ускорение движения грузов, силу натяжения нити, силу давления груза m на M , а также силу давления на ось блока. Массой блока и нити можно пренебречь. Задача .

Слайд 26

Задачи из ЕГЭ по физике Решение. для тела 1 для тела 2 для тела m Найдем mg = a ( 2 M + m ) a = g . Из уравнения (1) T = Mg + Ma = . Из уравнения (3) сила давления P = mg — ma = mg — m = .

Слайд 27

Задачи из ЕГЭ по физике = -2 T = 0 = 2 T

Слайд 28

Задачи из ЕГЭ по физике При скоростном спуске лыжник скользил вниз по склону с углом наклона , не отталкиваясь палками.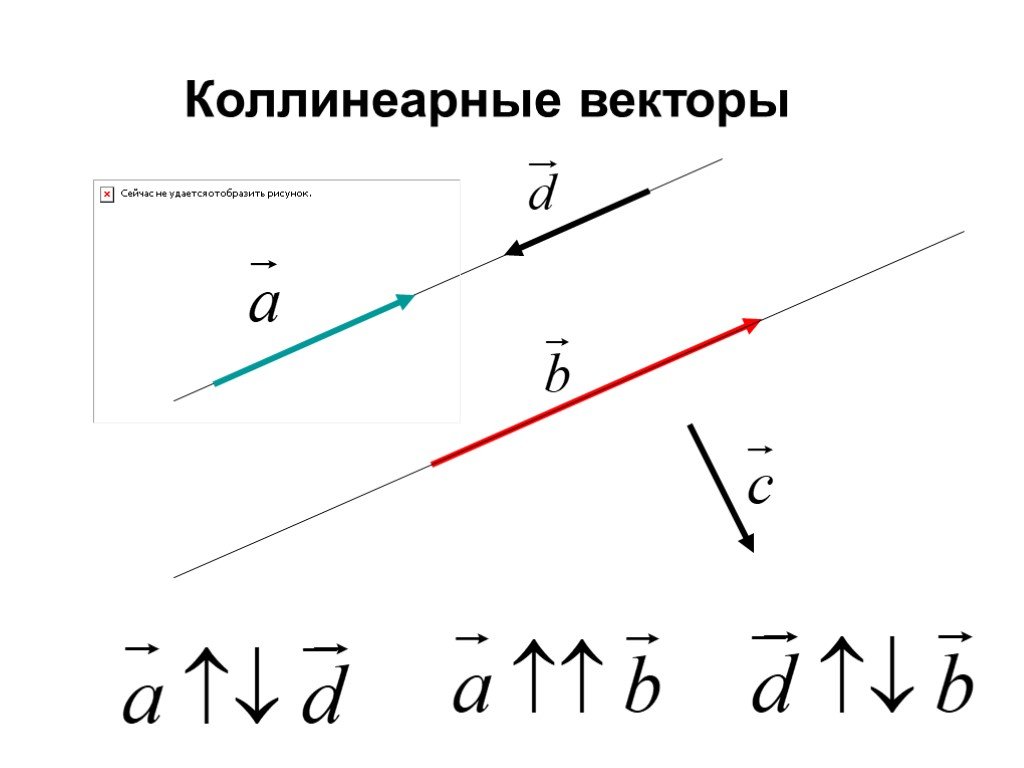 Коэффициент трения лыж о снег 0.1. Сила сопротивления воздуха пропорциональна квадрату скорости: F = k , где k =0.7 кг/м. Какова максимальная скорость лыжника, если его масса 100 кг? Задача.

Слайд 29

Задачи из ЕГЭ по физике Решение. = k a = a ( t ) а= u ’( t )=0 =29,8 м/с

Слайд 30

Задачи из ЕГЭ по физике Два небольших упругих шарика подвешены на нити =10 см и =5 см так, что они соприкасаются, линия их центров горизонтальна, а нити вертикальны. Масса шариков Шарик массой отклоняют на угол от вертикали отпускают. На какие углы отклонятся нити после абсолютно упругого соударения шариков? Задача.

Слайд 31

Задачи из ЕГЭ по физике Решение. Из ∆ AOB OB = BD=OD-OB= cos α= (1) ; = / 2; ⟹ h = m /2⟹ = Рассмотрим систему, состоящую из двух шариков. = /2 = /2 + /2

Слайд 32

Задачи из ЕГЭ по физике = ⟹ = и = = /(2 g ) cos = 1- =1- =1-( ) =1- = = 1- (1- cos α )= =38, cos =1- =1 — = 1- =1- 2gh = = 1- 4(1- cos α) ( = ⟹ = arccos =8,

Слайд 33

в физике Векторы и математике у х А О В n

Вектор | Определение и факты

векторный параллелограмм для сложения и вычитания

Просмотреть все материалы

Похожие темы:

векторные операции величина направление составная часть касательный вектор

Просмотреть весь связанный контент →

вектор , в математике величина, которая имеет как величину, так и направление, но не положение. Примерами таких величин являются скорость и ускорение. В современном виде векторы появились в конце 19 века.век, когда Джозайя Уиллард Гиббс и Оливер Хевисайд (соответственно из США и Великобритании) независимо друг от друга разработали векторный анализ, чтобы выразить новые законы электромагнетизма, открытые шотландским физиком Джеймсом Клерком Максвеллом. С тех пор векторы стали необходимы в физике, механике, электротехнике и других науках для математического описания сил.

Векторы можно представить в виде направленных отрезков, длина которых равна их величине. Поскольку имеют значение только величина и направление вектора, любой направленный отрезок может быть заменен отрезком той же длины и направления, но начинающимся в другой точке, например, в начале системы координат. Векторы обычно обозначаются жирным шрифтом, например v. Величина или длина вектора обозначается |v| или v , представляющее одномерную величину (например, обычное число), известную как скаляр. Умножение вектора на скаляр изменяет длину вектора, но не его направление, за исключением того, что умножение на отрицательное число изменяет направление стрелки вектора.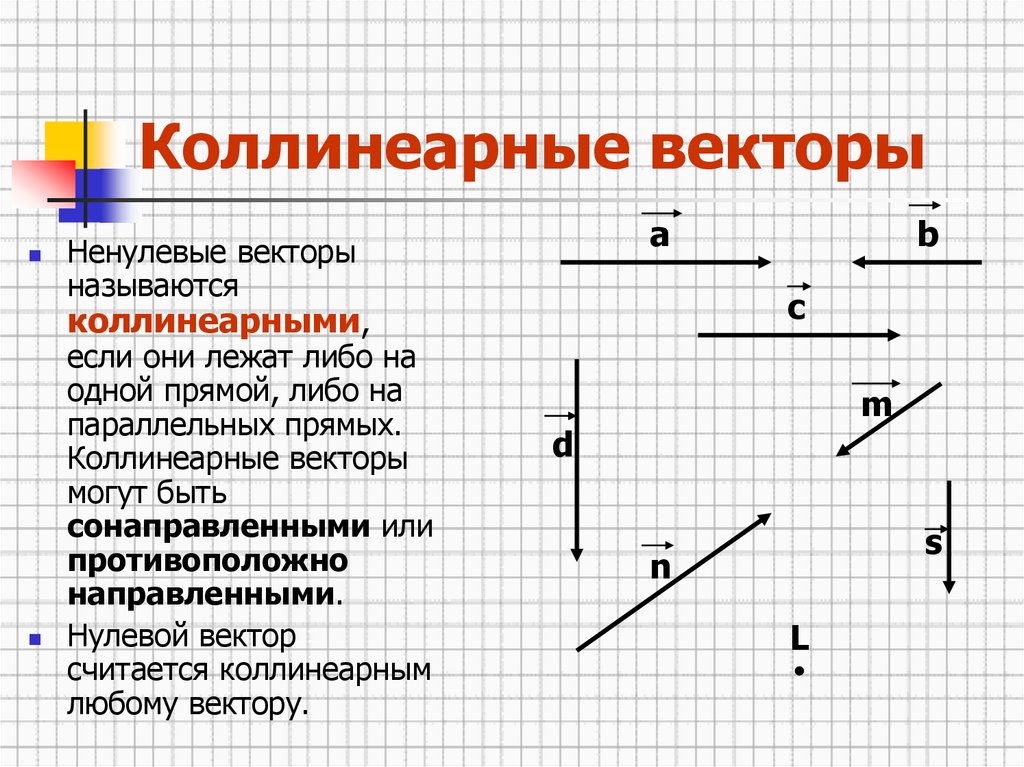 Например, умножение вектора на 1/2 приведет к тому, что вектор будет вдвое короче в том же направлении, а умножение вектора на -2 приведет к тому, что вектор будет вдвое длиннее, но направлен в противоположном направлении.

Britannica Quiz

Числа и математика

A-B-C, 1-2-3… Если вы считаете, что считать числа — это то же самое, что читать алфавит, проверьте, насколько свободно вы владеете языком математики в этом тесте.

Можно сложить или вычесть два вектора. Например, чтобы сложить или вычесть векторы v и w графически ( см. диаграмму), переместите каждый из них в начало координат и завершите параллелограмм, образованный двумя векторами; тогда v + w — один диагональный вектор параллелограмма, а v — w — другой диагональный вектор.

Существует два разных способа умножения двух векторов. Перекрестное или векторное произведение приводит к другому вектору, который обозначается v × w. Величина перекрестного произведения определяется выражением |v × w| = v w sin θ , где θ — меньший угол между векторами (со сложенными вместе их «хвостами»).

Направление v × w перпендикулярно как v, так и w, и его направление можно визуализировать с помощью правила правой руки, как показано на рисунке. Перекрестное произведение часто используется для получения «нормальи» (линии, перпендикулярной) к поверхности в некоторой точке, и это происходит при расчете крутящего момента и магнитной силы, действующей на движущуюся заряженную частицу.

Другой способ умножения двух векторов называется скалярным произведением, а иногда и скалярным произведением, поскольку в результате получается скаляр. Скалярное произведение определяется как v ∙ w = v w cos θ , где θ — меньший угол между векторами. Скалярное произведение используется для нахождения угла между двумя векторами. (Обратите внимание, что скалярное произведение равно нулю, когда векторы перпендикулярны.) Типичное физическое приложение состоит в том, чтобы найти работу W

, выполненную постоянной силой F воздействие на движущийся объект d ; работа определяется выражением W = F d cos θ .

Редакторы Британской энциклопедии Эта статья была недавно отредактирована и обновлена ​​Эриком Грегерсеном.

Векторы и матрицы — Математика

Векторы Введение

Векторы

Что такое вектор?

Это 10-минутное видео на YouTube от 3Blue1Brown охватывает:

• что такое вектор
• векторное сложение
• векторное масштабирование

Обозначение вектора

Векторы в пространстве можно описать с помощью двумерных и трехмерных векторов-столбцов.

Вектор a является трехмерным вектором. Он представляет собой вектор, который проходит 4 единицы в положительном направлении x, 3 единицы в положительном направлении y и 2 единицы в отрицательном направлении z.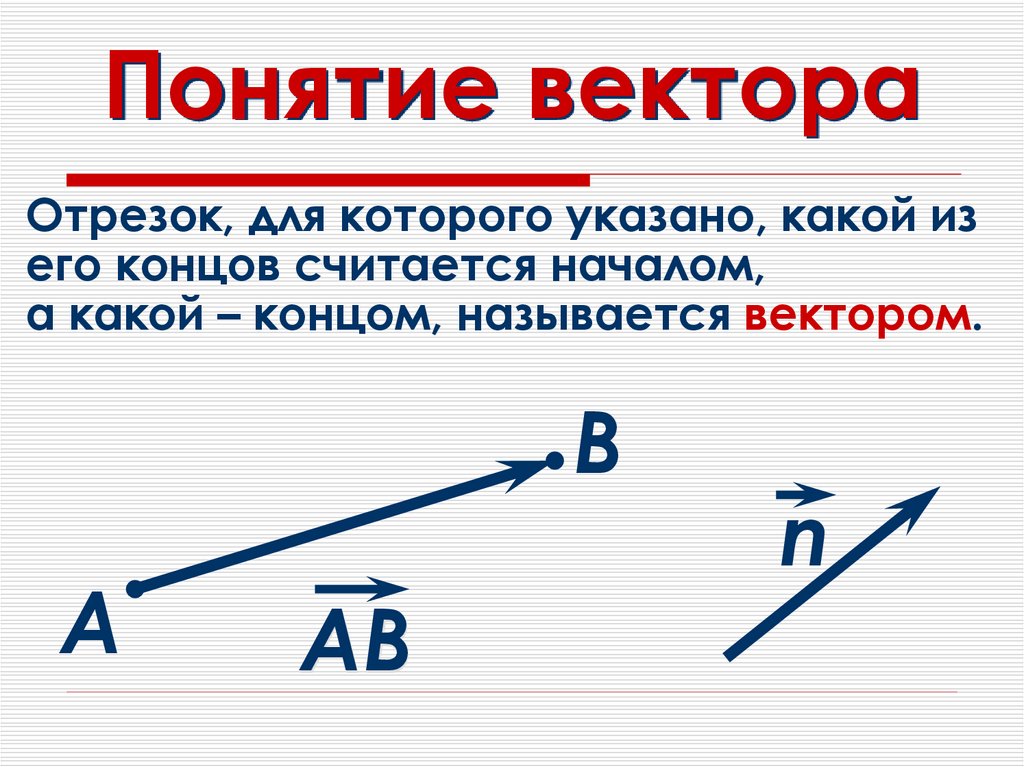

Единичные векторы могут быть определены в направлениях x, y и z. Вектор i  – это вектор, равный 1 единице только в положительном направлении x. Мы можем описать векторы в терминах единичных векторов. Вектор a выше также может быть записан как a = 4 i + 3 j — 2 z .

Величина вектора

Величина вектора — это длина вектора. Его можно найти, воспользовавшись теоремой Пифагора. Пифагор в 3-м очень похож на Пифагор в 2-м (что вы бы сделали в школе). В следующем 10-минутном видео на YouTube от ExamSolutions рассказывается, как вычислить величину вектора в трехмерном пространстве.

Угол между векторами

Угол между векторами

11-минутное видео на YouTube от ExamSolutions рассказывает, как найти угол между двумя векторами. Он охватывает

• О каком угле идет речь?
• Формула нахождения косинуса угла
• Скалярное (или точечное) произведение
• Примеры нахождения углов

Векторное уравнение прямой

Векторное уравнение прямой

Возможно, мы знакомы с декартовым уравнением прямой из школы — y = mx + c. Прямые линии также могут быть определены векторным уравнением

. Для векторного уравнения линии нам нужен вектор положения на линии (вектор, который ведет нас от начала координат к точке на линии) и вектор направления для линии (вектор, который идет параллельно прямой линии).

Два видео на YouTube от ExamSolutions покажут вам, как векторные уравнения определяют линию (первое видео 9минут) и пример нахождения векторного уравнения прямой по двум точкам на прямой (второе видео 8 минут).

Матрицы Введение

Матрицы

Матрица показывает массив значений, представленных в строках и столбцах.

Это 6-минутное видео на YouTube от Mathsispower4u демонстрирует, как найти размерность матрицы.

 

В следующем 4-минутном видео на YouTube от Khan Academy рассматривается транспонирование матриц. Это простая операция, при которой строки и столбцы матрицы меняются местами.

Матричная арифметика

Арифметика матриц

Над матрицами можно выполнять операции сложения, вычитания и умножения.

6-минутное видео на YouTube от Академии Хана демонстрирует, как решать задачи на сложение и вычитание с помощью матриц.

 

Умножение матриц — более сложный процесс. Чтобы выполнить умножение матриц, размеры каждой матрицы должны совпадать определенным образом. Если матрица A имеет размеры p x q (p строк, q столбцов), то матрица B должна иметь размеры q x r (q строк, r столбцов), если мы хотим разработать матрицу AB. Результирующая матрица будет иметь размеры p x r. Порядок умножения важен, AB не обязательно равно BA.

Следующие два видеоролика Академии Хана на YouTube (12 минут) демонстрируют процедуру умножения двух матриц.

Обратные матрицы

Обратная матрица

Определители

Для квадратной матрицы (количество строк = количеству столбцов) числовое значение называется определителем.