Калькулятор для цилиндра — intmag24.ru
Опубликовано от Admin — Оставить комментарийОнлайн калькулятор для цилиндра позволяет по известным данным вычислить:
- объем цилиндра,
- площадь основания, площадь боковой поверхности и площадь полной поверхности цилиндра,
- элементы: радиус, диаметр и высоту.
Калькулятор для цилиндра: комментарий
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра).
Обозначения для цилиндра:
R – радиус, D – диаметр,
V – объем,
Sо – площадь основания, Sб – площадь боковой поверхности, S – площадь полной поверхности,
h – высота прямого кругового цилиндра (h2 и h3 — минимальная и максимальная высота)
π – число Пи которое всегда примерно равно 3,14.
Круговым называется цилиндр, если его направляющая является окружностью. Прямым называется цилиндр, если его образующая перпендикулярна основаниям.
Формулы для прямого кругового цилиндра:Найти объем цилиндра, если известны:
- радиус и высота цилиндра: V=πR2h
- диаметр и высота цилиндра: V=πD2/4h
- площадь и высота цилиндра: V=Sоh
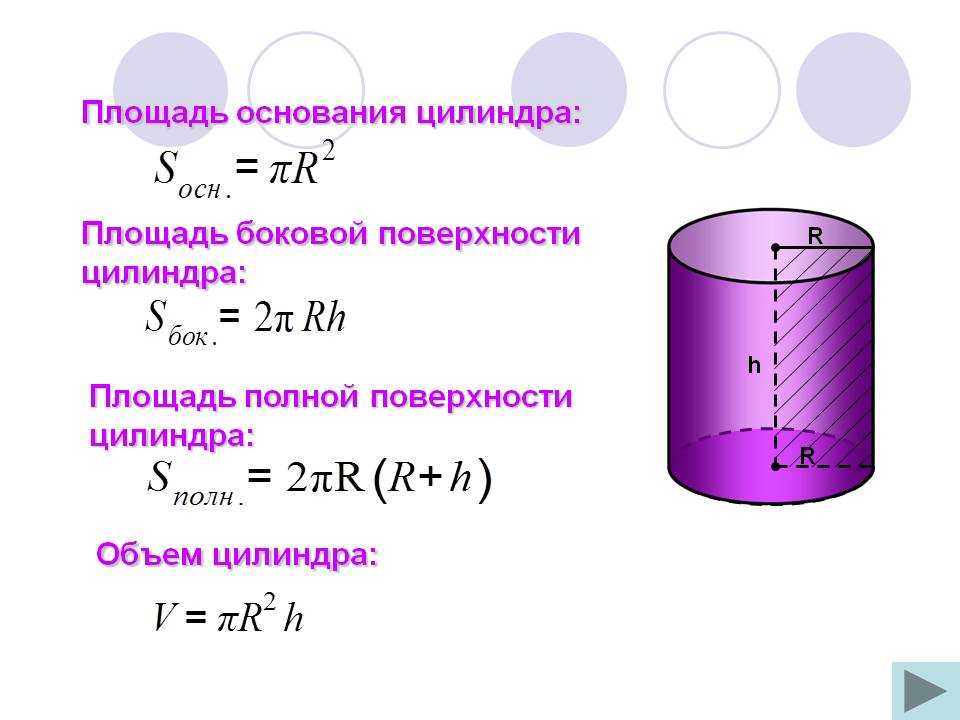
Площадь(Sб) боковой поверхности прямого кругового цилиндра
Так как боковая поверхность представляет собой прямоугольник, то площадь боковой поверхности цилиндра определяется по формуле: Sб=2πR⋅h
Площадь(Sо) основания цилиндра
Основание цилиндра —круг, поэтому площадь одного основания находится по формуле площади круга: Sо=πR2.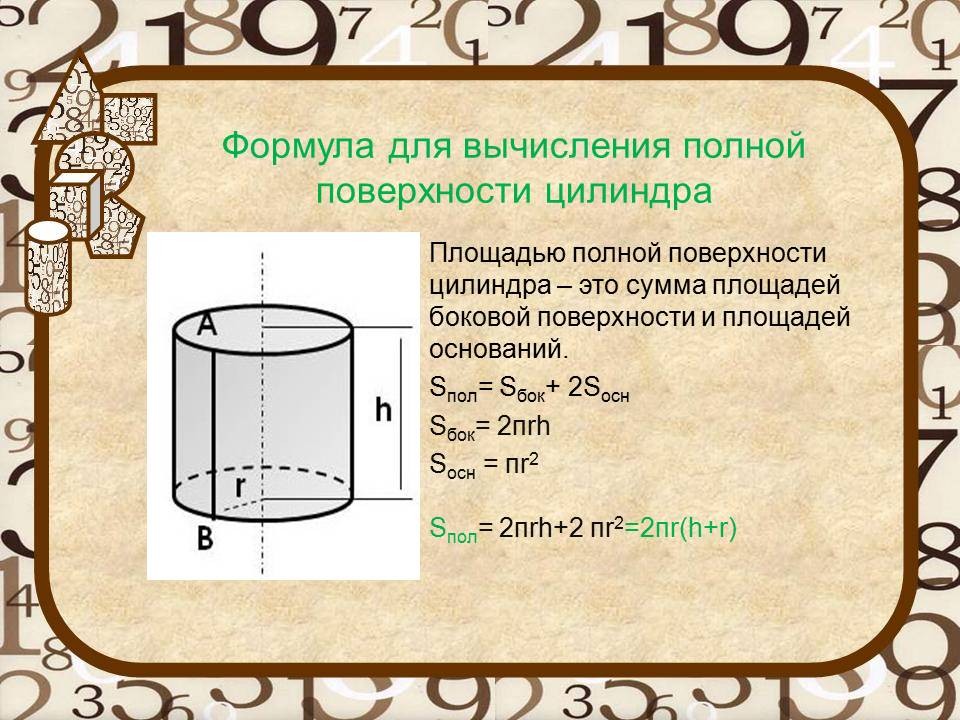
Площадь(S) полной поверхности прямого кругового цилиндра
Площадь полной поверхности цилиндра определяется по формуле: S=2πRh+2πR2=2πR(h+R)
Формулы нахождения радиуса и диаметра по:
- высоте и объему: R=√(V/πh), D=2*√(V/πh)
- площади боковой поверхности и высоте: R=Sб/2πh, D=2*Sб/2πh
- площади основания и высоте: R=√(Sо/π), R=2*√(Sо/π)
Формулы нахождения высоты по:
- радиусу и объему: h=V/πR 2
- площади боковой поверхности и радиусу: h=Sб/2πR
- площади полной поверхности и радиусу: h=S/2πR-R
Прямой круговой цилиндр со скошенным основанием (скошенный цилиндр) определяется радиусом основания R, минимальной высотой h2 и максимальной высотой h3.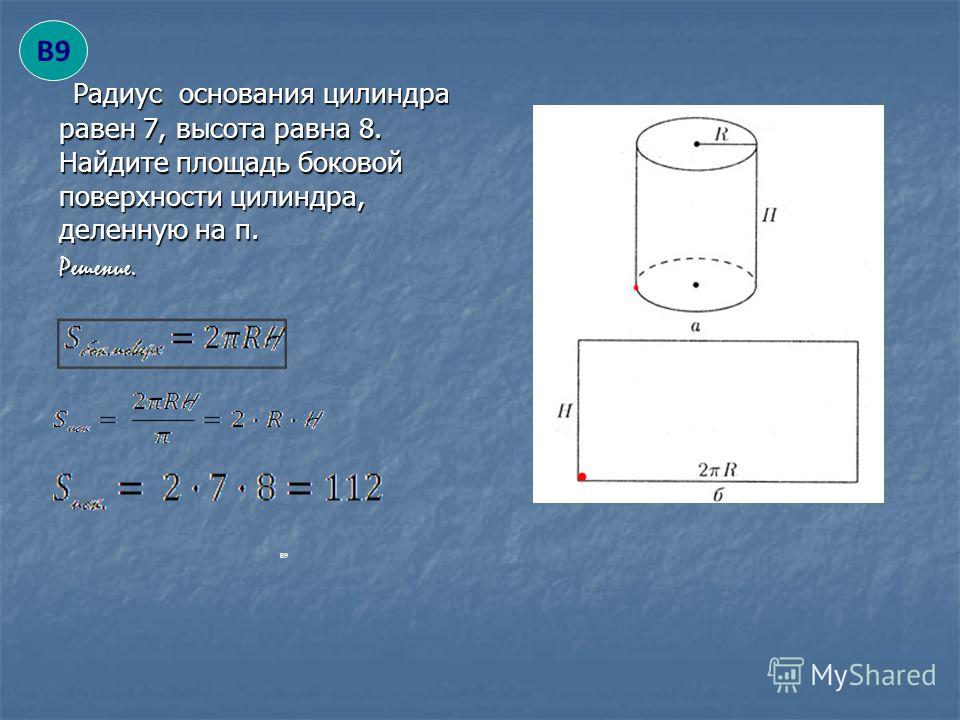
- Объем скошенного цилиндра: V=πR2(h2+h3)2
- Площадь(Sб) боковой поверхности скошенного цилиндра: Sб=πR(h2+h3)
- Площадь(Sо) оснований скошенного цилиндра: Sо=πR2+πR √(R2+((h2−h3)/2)2)
- Площадь(S) полной поверхности скошенного цилиндра
S=Sб+Sо= πR(h2+h3)+ πR2+πR √ (R2+((h2−h3)/2)2) = πR[(h2+h3)+ R+√ (R2+((h2−h3)/2)2) ]
Список всех онлайн-конвертеров на странице «Калькуляторы«.
Рубрика: Калькуляторы
Метки Математика, Геометрия
Площадь боковой поверхности цилиндра 100п. Радиус цилиндра, онлайн расчет
Цилиндр (происходит из греческого языка, от слов «каток», «валик») — это геометрическое тело, которое ограничено снаружи поверхностью, называющейся цилиндрической, и двумя плоскостями. Данные плоскости пересекают поверхность фигуры и являются параллельными друг другу.
Данные плоскости пересекают поверхность фигуры и являются параллельными друг другу.
Цилиндрическая поверхность — это поверхность, которая получена прямой линии в пространстве. Эти движения таковы, что выделенная точка этой прямой линии совершает движение вдоль кривой плоского типа. Такая прямая линия называется образующей, а кривая линия — направляющей.
Цилиндр состоит из пары оснований и боковой цилиндрической поверхности. Цилиндры бывают нескольких видов:
1. Круговой, прямой цилиндр. У такого цилиндра основания и направляющая перпендикулярны образующей линии, и имеется
2. Наклонный цилиндр. У него угол между образующей линией и основанием не является прямым.
3. Цилиндр иной формы. Гиперболический, эллиптический, параболический и другие.
Площадь цилиндра, а также площадь полной поверхности любого цилиндра находится с помощью сложения площадей оснований этой фигуры и площади боковой поверхности.
Формула, по которой вычисляется полная площадь цилиндра для кругового, прямого цилиндра:
Sp = 2п Rh + 2п R2 = 2п R (h+R).
Площадь боковой поверхности ищется чуть сложнее, чем площадь цилиндра целиком, она вычисляется путем умножения длины образующей линии на периметр сечения, образованного плоскостью, которая перпендикулярна образующей линии.
Данная цилиндра для кругового, прямого цилиндра узнается по развертке этого объекта.
Развертка — это прямоугольник, который имеет высоту h и длину P, которая приравнивается периметру основания.
Отсюда следует, что боковая площадь цилиндра является равной площади развертки и может быть вычислена по данной формуле:
Если взять круговой, прямой цилиндр, то для него:
P = 2п R, а Sb = 2п Rh.
Если цилиндр наклонный, то площадь боковой поверхности должна быть равна произведению длины его образующей линии и периметра сечения, которое перпендикулярно данной образующей линии.
К сожалению, не существует простой формулы для выражения площади боковой поверхности наклонного цилиндра через его высоту и параметры его основания.
Чтобы вычислить цилиндра, необходимо знать несколько фактов. Если сечение своей плоскостью пересекает основания, то такое сечение всегда является прямоугольником. Но эти прямоугольники будут разными, в зависимости от положения сечения. Одна из сторон осевого сечения фигуры, которое перпендикулярно основаниям, равна высоте, а другая — диаметру основания цилиндра. А площадь такого сечения, соответственно, приравнивается произведению одной стороны прямоугольника на другую, перпендикулярную первой, или произведению высоты данной фигуры на диаметр его основания.
Если сечение своей плоскостью пересекает основания, то такое сечение всегда является прямоугольником. Но эти прямоугольники будут разными, в зависимости от положения сечения. Одна из сторон осевого сечения фигуры, которое перпендикулярно основаниям, равна высоте, а другая — диаметру основания цилиндра. А площадь такого сечения, соответственно, приравнивается произведению одной стороны прямоугольника на другую, перпендикулярную первой, или произведению высоты данной фигуры на диаметр его основания.
Если сечение будет перпендикулярно основаниям фигуры, но не будет проходить через ось вращения, то площадь этого сечения будет равна произведению высоты этого цилиндра и определенной хорды. Чтобы получить хорду, нужно построить окружность у основания цилиндра, провести радиус и отложить на нем расстояние, на котором находится сечение. А от этой точки нужно провести перпендикуляры к радиусу от пересечения с окружностью. Точки пересечения соединяются с центром. А основание треугольника — это искомая которой ищется по звучит так: «Сумма квадратов двух катетов равна гипотенузе, возведенной в квадрат»:
С2 = А2 + В2.
Если сечение не затрагивает основания цилиндра, а сам цилиндр круговой и прямой, то площадь этого сечения находится как площадь окружности.
Площадь окружности равна:
S окр. = 2п R2.
Чтобы найти R, нужно ее длину C разделить на 2п:
R = C \ 2п, где п — число пи, математическая постоянная, вычисленная для работы с данными окружности и равная 3,14.
Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.
Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.
Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.
Площадь поверхности цилиндра — онлайн калькулятор
Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры. Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.
Площадь боковой поверхности цилиндра
Сначала нужно представить, как выглядит развертка в двухмерном пространстве.
Это не что иное, как прямоугольник, одна сторона которого равна длине окружности. Формула ее известна с незапамятных времен —
S бок = 2π * r * h ,
где число π = 3.14.
Площадь полной поверхности цилиндра
Для нахождения полной площади цилиндра нужно к полученной S бок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле S о = 2π * r 2 .
Конечная формула выглядит следующим образом:
S пол = 2π * r 2 + 2π * r * h.
Площадь цилиндра — формула через диаметр
Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.
Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.
S пол = 2 π * r 2 + 2 π * r * h = 2 π * d 2 /4 + 2 π * h * d /2 = π * d 2 /2 + π * d * h ,
Вместо r в полную формулу нужно вставить значение r = d/2 .
Примеры расчета площади цилиндра
Вооружившись знаниями, приступаем к практике.
Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.
Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:
S пол = 2 * 3. 14 * 24 2 + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм 2).
14 * 24 2 + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм 2).
Переводим в привычные м 2 и получаем 0,01868928, приблизительно 0.02 м 2 .
Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.
Данные следующие: диаметр 0,2 м; высота 2 м. Используем формулу через диаметр:
S пол = 3.14 * 0.2 2 /2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м 2 .
Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.
Один момент, есть формула:
S бок = 2 * 3.14 * 1 * 1 = 6.28 м 2 .
Заключение
В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.
Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.
Точность – вежливость королей.
Название науки «геометрия» переводится как «измерение земли». Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди. Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.
Планиметрия — раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье — цилиндр.
Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже — коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец — знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.
Цилиндрическую (гораздо реже — коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец — знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.
Определение цилиндра как геометрической фигуры
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».
Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами — усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны.
Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра — один из элементов данной геометрической фигуры. Другая её важная составляющая — рассмотренные выше круги. Называются они основаниями.
Виды цилиндров
Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.
Что такое поверхность вращения
Прямой круговой цилиндр, без сомнения — самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.
Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.
Допустим, имеется некая прямая a , расположенная вертикально. ABCD — прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a . Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения — прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.
В данном случае, в результате вращения фигуры — прямоугольника — получается цилиндр. Вращая треугольник, можно получить конус, вращая полукруг — шар и т.д.
Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.
Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П на радиус окружности.
Площадь круга, как известно, равняется произведению П на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.
Определение объёма фигуры
Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.
Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.
Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.
Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.
Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N . Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.
Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.
Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.
Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями — перпендикулярный отрезок, построенный между ними.
Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.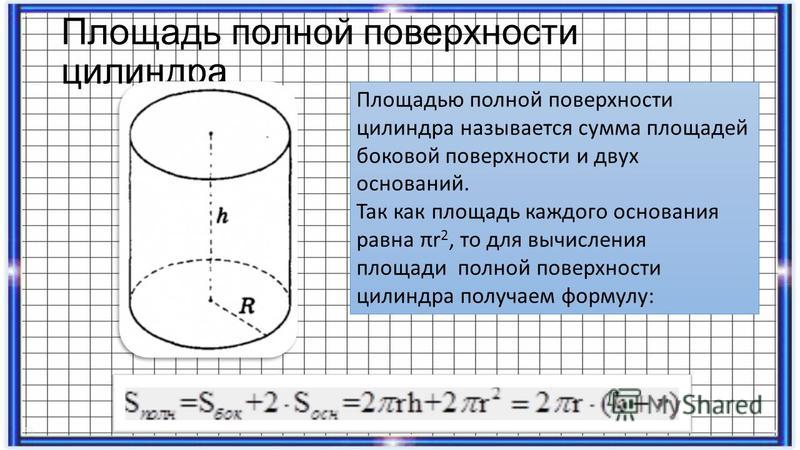
Как построить развёртку цилиндра
В некоторых случаях требуется выкроить развёртку цилиндра. На приведённом рисунке показаны правила, по которым строится заготовка для изготовления цилиндра с заданными высотой и диаметром.
Следует учитывать, что рисунок приведен без учёта швов.
Отличия скошенного цилиндра
Представим себе некий прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. А вот плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.
На рисунке представлен скошенный цилиндр. Плоскость а под неким углом, отличным от 90° к образующим, пересекает фигуру.
Такая геометрическая форма чаще встречается на практике в виде соединений трубопроводов (колена). Но бывают даже здания, построенные в виде скошенного цилиндра.
Геометрические характеристики скошенного цилиндра
Наклон одной из плоскостей скошенного цилиндра слегка изменяет порядок расчёта как площади поверхности такой фигуры, так и ее объёма.
Формула радиуса цилиндра:
где V — объем цилиндра, h — высота
Цилиндр — геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
где Sb — площадь боковой поверхности, h — высота
Цилиндр — геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая).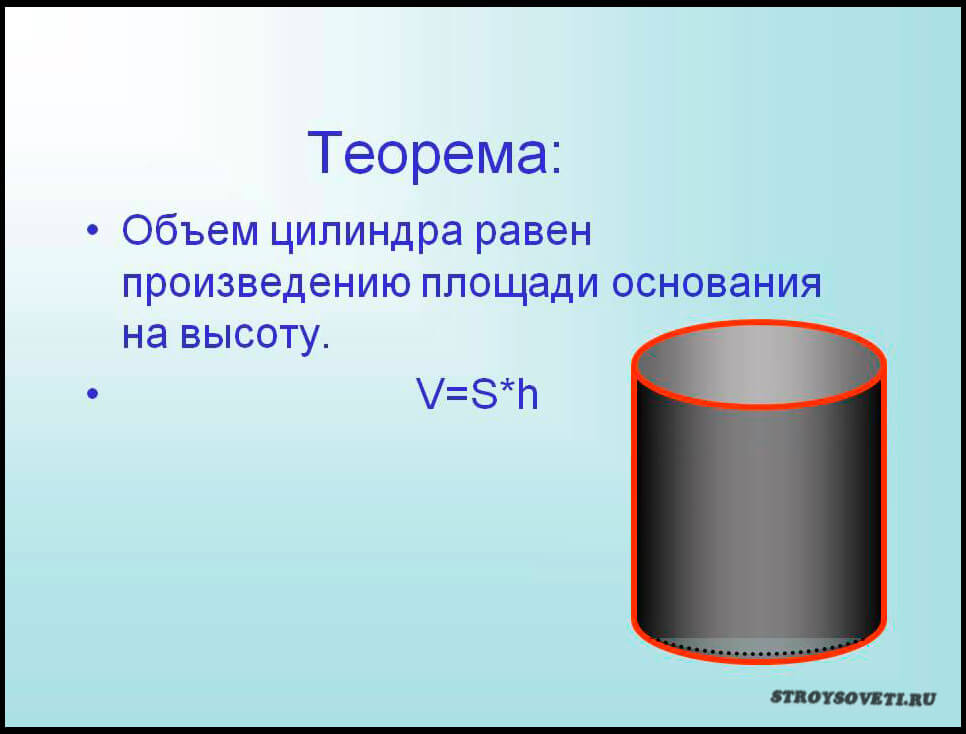
Формула радиуса цилиндра:
где S — площадь полной поверхности, h — высота
При изучении стереометрии одной из главных тем становится «Цилиндр». Площадь боковой поверхности считается если не главной, то немаловажной формулой при решении геометрических задач. Однако важно помнить и определения, которые помогут сориентироваться в примерах и при доказательстве различных теорем.
Понятие цилиндра
Вначале нужно рассмотреть несколько определений. Только после их изучения можно приступать к рассмотрению вопроса о формуле площади боковой поверхности цилиндра. На основе этой записи можно вычислить и иные выражения.
- Под цилиндрической поверхностью понимают плоскость, описываемую образующей, движущейся и остающейся параллельной заданному направлению, скользящей по имеющейся кривой.
- Имеется и второе определение: цилиндрическую поверхность образуют множество параллельных прямых, пересекающих заданную кривую.

- Образующей называют условно высоту цилиндра. При ее перемещении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело.
- Под осью подразумевают прямую, проходящую через оба основания фигуры.
- Цилиндром называется стереометрическое тело, ограниченное пересекающимися боковой поверхностью и 2 параллельными плоскостями.
Существуют разновидности данной объемной фигуры:
- Под круговым подразумевают цилиндр, направляющая которого — это окружность. Его главными составляющими считаются радиус основания и образующая. Последняя равна высоте фигуры.
- Существует прямой цилиндр. Свое название он получил благодаря перпендикулярности образующей к основаниям фигуры.
- Третий вид — скошенный цилиндр. В учебниках можно встретить и другое его название «круговой цилиндр со скошенным основанием». Данную фигуру определяет радиус основания, минимальная и максимальная высоты.
- Под равносторонним цилиндром понимают тело, имеющее равные между собой высоту и диаметр круглой плоскости.

Условные обозначения
Традиционно основные «компоненты» цилиндра принято называть следующим образом:
- Радиус основания — R (он же заменяет аналогичную величину стереометрической фигуры).
- Образующая — L.
- Высота — H.
- Площадь основания — S осн (иначе говоря, необходимо найти указанный параметр круга).
- Высоты скошенного цилиндра — h 1 ,h 2 (минимальная и максимальная).
- Площадь боковой поверхности — S бок (если ее развернуть, то получится своего рода прямоугольник).
- Объем стереометрической фигуры — V.
- Площадь полной поверхности — S.
«Компоненты» стереометрической фигуры
Когда изучается цилиндр, площадь боковой поверхности играет немаловажную роль. Связано это с тем, что данная формула входит в несколько других, более сложных. Поэтому необходимо быть хорошо подкованным в теории.
Основными составляющими фигуры являются:
- Боковая поверхность. Как известно, она получается благодаря движению образующей по заданной кривой.

- Полная поверхность включает в себя имеющиеся основания и боковую плоскость.
- Сечением цилиндра, как правило, выступает прямоугольник, расположенный параллельно оси фигуры. Иначе его называют плоскостью. Оказывается, длина и ширина по совместительству являются составляющими других фигур. Так, условно длинами сечения являются образующие. Ширина — параллельные хорды стереометрической фигуры.
- Под осевым сечением подразумевают расположение плоскости через центр тела.
- И наконец, завершающее определение. Касательной называют плоскость, проходящую через образующую цилиндра и находящуюся под прямым углом к осевому сечению. При этом должно выполниться одно условие. Указанная образующая должна входить в плоскость осевого сечения.
Основные формулы для работы с цилиндром
Для того чтобы ответить на вопрос, как найти площадь поверхности цилиндра, необходимо изучить основные «компоненты» стереометрической фигуры и формулы их нахождения.
Данные формулы отличаются тем, что вначале даются выражения для скошенного цилиндра, а затем — для прямого.
Примеры с разобранным решением
Необходимо узнать площадь боковой поверхности цилиндра. Дана диагональ сечения AC = 8 см (причем оно является осевым). При соприкосновении с образующей получается
Решение. Поскольку известны величины диагонали и угла, то в таком случае:
- CD = AC*cos 30°.
Комментарий. Треугольник ACD, в конкретном примере, прямоугольный. Это означает, что частное от деления CD и AC = косинусу имеющегося угла. Значение тригонометрических функций можно найти в специальной таблице.
Аналогично, можно найти и значение AD:
- AD = AC*sin 30°
Теперь необходимо вычислить по следующей формулировке нужный результат: площадь боковой поверхности цилиндра равна удвоенному результату перемножения «пи», радиуса фигуры и ее высоты. Следует воспользоваться и другой формулой: площадью основания цилиндра. Она равняется результату перемножения «пи» на квадрат радиуса. И наконец, последняя формула: общая площадь поверхности. Она равна сумме предыдущих двух площадей.
Она равна сумме предыдущих двух площадей.
Даны цилиндры. Их объем = 128*п см³. У какого из цилиндров наименьшая полная поверхность?
Решение. Для начала нужно воспользоваться формулами нахождения объема фигуры и ее высоты.
Поскольку площадь полной поверхности цилиндра известна из теории, необходимо применить ее формулу.
Если рассматривать полученную формулу в качестве функции площади цилиндра, то минимальный «показатель» будет достигнут в точке экстремума. Для получения последнего значения необходимо воспользоваться дифференцированием.
Формулы можно посмотреть в специальной таблице по нахождению производных. В дальнейшем найденный результат приравнивается к нулю и находится решение уравнения.
Ответ: S min будет достигнута при h = 1/32 см, R = 64 см.
Дана стереометрическая фигура — цилиндр и сечение. Последнее проведено таким образом, что располагается параллельно оси стереометрического тела. У цилиндра следующие параметры: ВК = 17 см, h = 15 см, R = 5 см.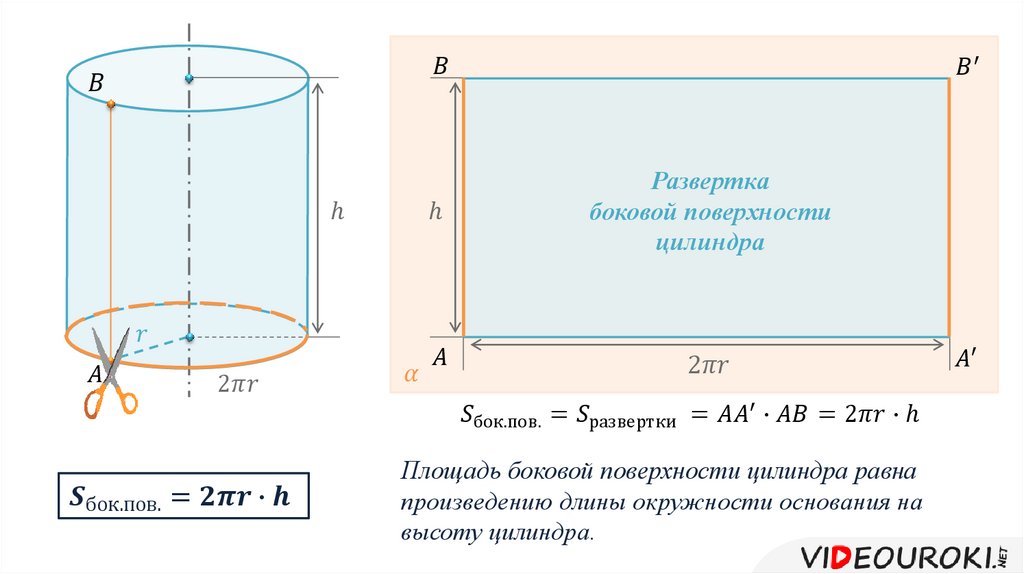 Необходимо найти расстояние между сечением и осью.
Необходимо найти расстояние между сечением и осью.
Поскольку под сечением цилиндра понимается ВСКМ, т. е. прямоугольник, то его сторона ВМ = h. Необходимо рассмотреть ВМК. Треугольник является прямоугольным. Исходя из этого утверждения, можно вывести верное предположение, что МК = ВС.
ВК² = ВМ² + МК²
МК² = ВК² — ВМ²
МК² = 17² — 15²
Отсюда можно сделать вывод, что МК = ВС = 8 см.
Следующий шаг — проведение сечения через основание фигуры. Необходимо рассмотреть получившуюся плоскость.
AD — диаметр стереометрической фигуры. Он параллелен сечению, упомянутому в условии задачи.
BC — прямая, расположенная на плоскости имеющегося прямоугольника.
ABCD — трапеция. В конкретном случае она считается равнобедренной, поскольку вокруг нее описана окружность.
Если найти высоту полученной трапеции, то можно получить ответ, поставленный в начале задачи. А именно: нахождение расстояния между осью и проведенным сечением.
Для этого необходимо найти величины AD и ОС.
Ответ: сечение располагается 3 см от оси.
Задачи на закрепление материала
Дан цилиндр. Площадь боковой поверхности используется в дальнейшем решении. Известны другие параметры. Площадь основания — Q, площадь осевого сечения — М. Необходимо найти S. Иными словами, полную площадь цилиндра.
Дан цилиндр. Площадь боковой поверхности необходимо найти в одном из шагов решения задачи. Известно, что высота = 4 см, радиус = 2 см. Необходимо найти полную площадь стереометрической фигуры.
| Геометрия | Формы | Контакты и конфиденциальность | Геометрические калькуляторы | Немецкий: Geometriechner, Formen |
| 1DЛиния, дуга окружности, парабола, спираль, кривая Коха
2D Правильные многоугольники: Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, многоугольник, десятиугольник, десятиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольника Другие многоугольники: Круглые формы: Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron Archimedean Solids: Catalan Solids: Johnson Solid: Круглые формы: | Anzeige Расчеты на прямом круговом цилиндре. Формулы: пи: Радиус, высота и диагональ имеют одну и ту же единицу измерения (например, метр), площадь имеет эту единицу в квадрате (например, квадратный метр), объем имеет эту единицу в степени 3 (например, кубический метр). У аудио/видео есть этот блок -1 . Боковая поверхность представляет собой криволинейную часть площади поверхности. © Jumk.de Веб-проекты | Онлайн калькуляторы Anzeige |
Калькулятор площади цилиндра онлайн. Как найти площадь цилиндра
Рассмотрим цилиндр вращения радиусом R и высотой h (рис. 383). В основание этого цилиндра впишем правильный многоугольник (на рис.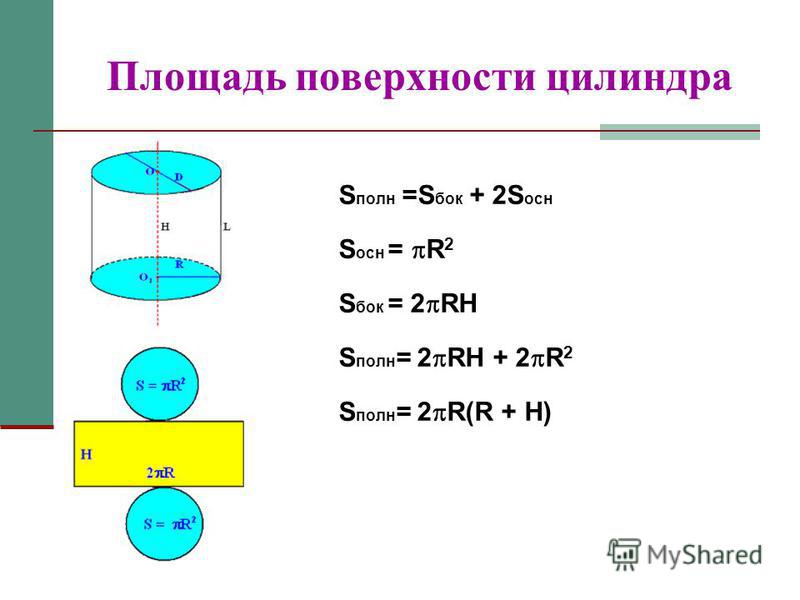 383 — шестиугольник) и с его помощью построим вписанную в цилиндр правильную призму. Точно так же вокруг цилиндра можно описать правильные призмы со сколь угодно большим числом боковых граней.
383 — шестиугольник) и с его помощью построим вписанную в цилиндр правильную призму. Точно так же вокруг цилиндра можно описать правильные призмы со сколь угодно большим числом боковых граней.
По определению площадь боковой поверхности цилиндра принимается за предел, к которому площади боковых поверхностей вписанных и описанных вокруг него правильных призм стремятся удвоить (или даже увеличить) число их боковых граней неограниченно.
То, что такой предел существует, мы сейчас и докажем. Если взять вписанную правильную призму, построенную на правильном -угольнике как на основании, то для ее боковой поверхности будем иметь выражение , где — периметр правильного -угольника, вписанного в окружность основания цилиндра. В . Точно такой же расчет для описываемой призмы дает тот же результат. Итак, площадь боковой поверхности цилиндра вращения выражается формулой
Боковая поверхность цилиндра равна произведению длины образующей на периметр (т.е. длину окружности) основания.
Задача 1. Отрезок, соединяющий диаметрально противоположные точки А и В верхнего и нижнего оснований цилиндра (рис. 384), равен 10 см и наклонен к плоскости основания под углом 60°. Найдите площадь боковой поверхности цилиндра.
Раствор. Проведем Вхождение через отрезок А плоскостью, перпендикулярной основанию цилиндра. Из треугольника имеем
откуда находим для боковой поверхности цилиндра
Задача 2. Треугольник ABC, вершины A и B которого являются концами диаметра нижнего основания цилиндра, а вершина C является концом диаметра перпендикулярное ему верхнее основание, равностороннее со стороной а,
Найти площадь боковой и полной поверхностей цилиндра. Решение. Радиус основания цилиндра равен Высота треугольника ABC (рис. 385) равна и образующая цилиндра вычисляется как
Значит, боковая поверхность цилиндра равна
и полной поверхности (равной сумме площади боковой поверхности и площади двух оснований цилиндра) равно
Упражнения
1. Диагонали боковых граней прямоугольного параллелепипеда наклонены к плоскости основания под углами соответственно равными . Найдите угол наклона к этой же плоскости диагонали параллелепипеда.
Диагонали боковых граней прямоугольного параллелепипеда наклонены к плоскости основания под углами соответственно равными . Найдите угол наклона к этой же плоскости диагонали параллелепипеда.
2. У прямого параллелепипеда острый угол основания равен а, а одна из сторон основания равна а. Сечение, проведенное через эту сторону и противоположный край верхнего основания, имеет площадь Q, а его плоскость наклонена к плоскости основания под углом. Найдите объем и полную площадь параллелепипеда.
3. Основанием наклонной треугольной призмы является равнобедренный прямоугольный треугольник, причем проекция одного из боковых ребер на плоскость основания совпадает с медианой m одного из катетов треугольника. Найти угол наклона боковых ребер к плоскости основания, если объем призмы V.
4. В правильной шестиугольной призме через сторону основания проведены два отрезка: 1) содержащий противоположную сторону верхнего основания, 2) содержащий центр верхнего основания. При какой высоте призмы угол между плоскостями сечений имеет наибольшее значение и чему он равен в этом случае?
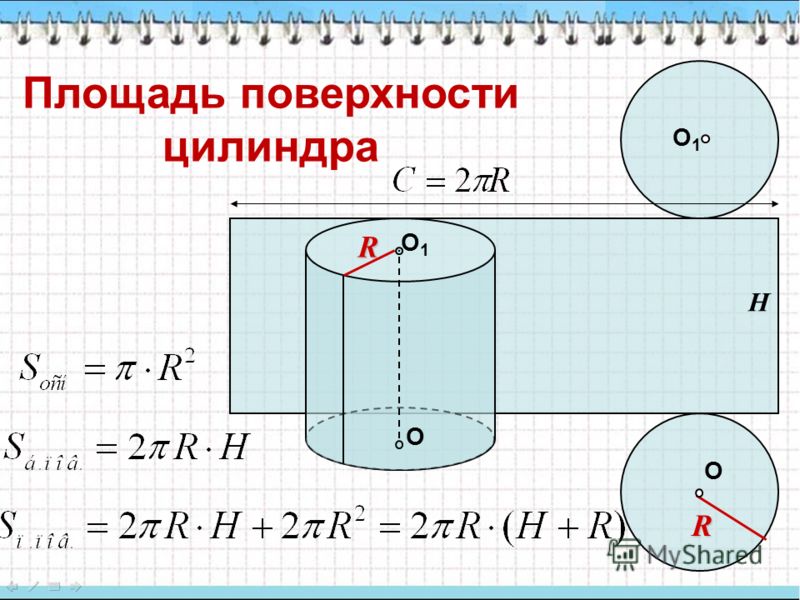
Площадь каждого основания цилиндра π r 2 , площадь обоих оснований будет 2π r 2 (рис. ).
).
Площадь боковой поверхности цилиндра равна площади прямоугольника, основание которого равно 2π r , а высота равна высоте цилиндра h , т.е. 2π rh .
Общая поверхность цилиндра будет: 2π r 2+2π rh = 2π r ( r + h ).
Площадь боковой поверхности цилиндра принимается Площадь развертки его боковой поверхности.
Следовательно, площадь боковой поверхности прямого кругового цилиндра равна площади соответствующего прямоугольника (рис.) и вычисляется по формуле
S до н.э. = 2πRH, (1)
Если к площади боковой поверхности цилиндра прибавить площадь двух оснований цилиндра, то получим полную площадь поверхности цилиндра
S полной = 2πRH + 2πR 2 = 2πR(H + R).
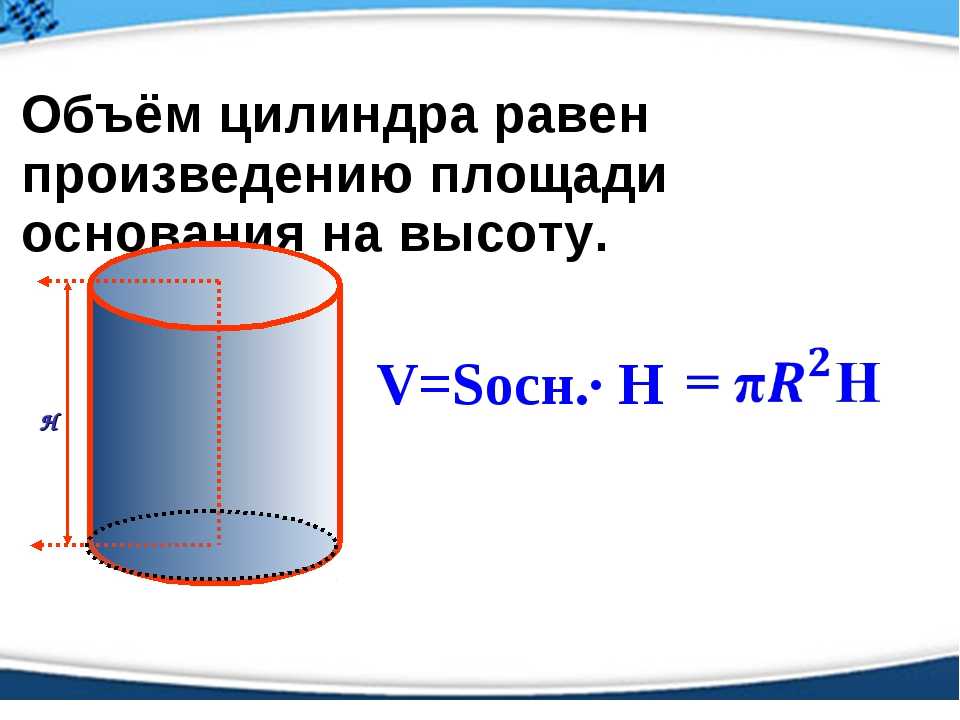
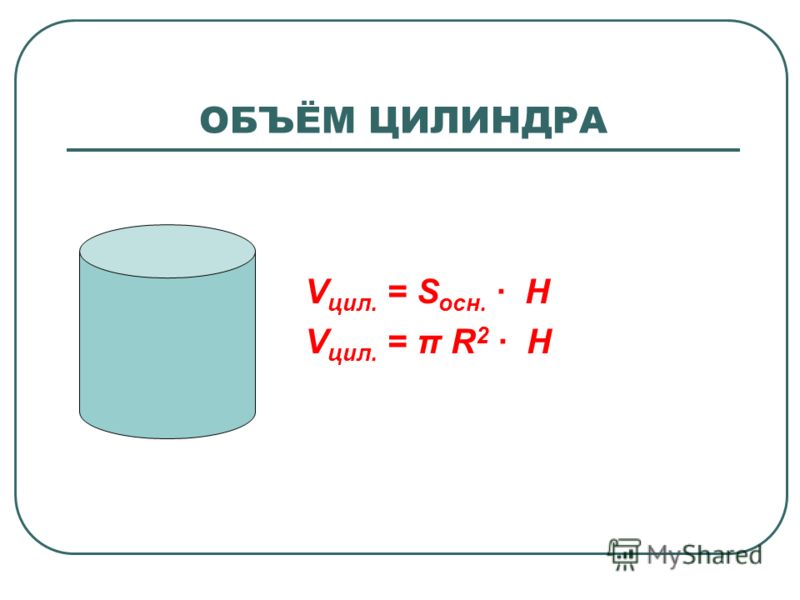
Объем прямого цилиндра
Теорема. Объем правильного цилиндра равен произведению площади его основания на высоту , т. е.
, где Q — площадь основания, а H — высота цилиндра.
Поскольку площадь основания цилиндра равна Q, существуют последовательности описанных и вписанных многоугольников с площадями Q n и Q’ n такие, что
\(\lim_(n \rightarrow \infty )\) Q n = \(\lim_(n \rightarrow \infty)\) Q’ n = Q.
Построим последовательности призм, основаниями которых являются рассмотренные выше описанные и вписанные многоугольники, а боковые ребра параллельны образующей данного цилиндра и имеют длину H. Эти призмы описаны и вписаны для данного цилиндра. Их объемы находятся по формулам
V n = Q n H и V’ n = Q’ n H.
Следовательно,
V= \(\lim_(n \rightarrow \infty)1) 4 Q n 9 H = \(\lim_(n \rightarrow \infty)\) Q’ n H = QH.
Последствия.
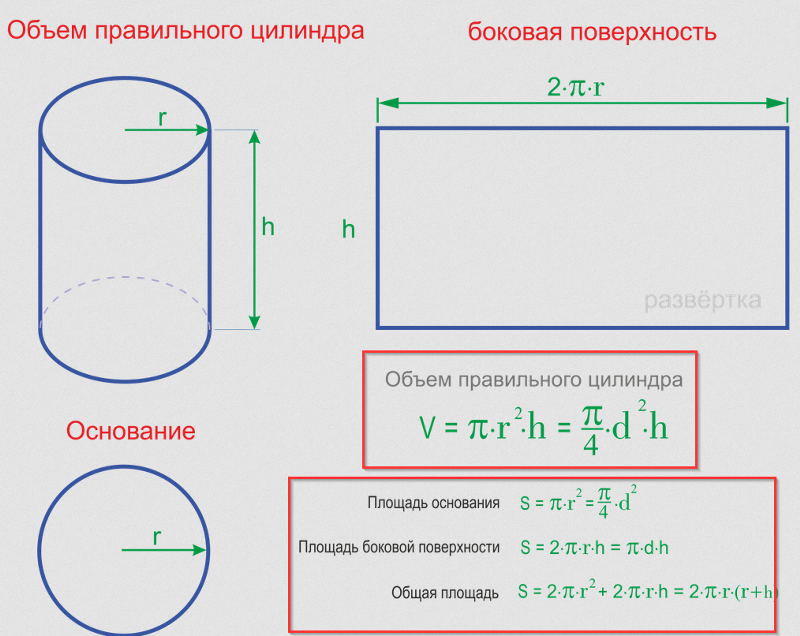
Объем прямого кругового цилиндра рассчитывается по формуле
V = π R 2 H
, где R — радиус основания, а H — высота цилиндра.
Так как основанием круглого цилиндра является окружность радиуса R, то Q = π R 2, а значит
При изучении стереометрии одной из основных тем является «Цилиндр». Площадь боковой поверхности считается если не основной, то важной формулой при решении геометрических задач. Однако важно помнить определения, которые помогут вам ориентироваться в примерах и при доказательстве различных теорем.
Площадь боковой поверхности считается если не основной, то важной формулой при решении геометрических задач. Однако важно помнить определения, которые помогут вам ориентироваться в примерах и при доказательстве различных теорем.
Понятие о цилиндре
Сначала необходимо рассмотреть несколько определений. Только после их изучения можно приступить к рассмотрению вопроса о формуле площади боковой поверхности цилиндра. На основе этой записи можно вычислить другие выражения.
- Под цилиндрической поверхностью понимается плоскость, описываемая образующей, движущаяся и оставаясь параллельной заданному направлению, скользящая по существующей кривой.
- Существует также второе определение: цилиндрическая поверхность образована набором параллельных линий, пересекающих заданную кривую.
- Образующая условно называется высотой цилиндра. При его движении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело.
- Ось — это прямая линия, проходящая через оба основания фигуры.

- Цилиндр – стереометрическое тело, ограниченное пересекающейся боковой поверхностью и двумя параллельными плоскостями.
Существуют разновидности этой объемной фигуры:
- Под круговым понимается цилиндр, направляющей которого является окружность. Его основными составляющими являются радиус основания и образующая. Последняя равна высоте фигуры.
- Имеется прямой цилиндр. Свое название она получила из-за перпендикулярности образующей к основаниям фигуры.
- Третий тип – цилиндр со скошенной кромкой. В учебниках можно встретить и другое его название – «круглый цилиндр со скошенным основанием». Эта цифра определяет радиус основания, минимальную и максимальную высоты.
- Под равносторонним цилиндром понимается тело, имеющее равные высоту и диаметр плоскости окружности.
Условные обозначения
Традиционно основные «компоненты» цилиндра называются так:
- Радиус основания равен R (он также заменяет аналогичное значение стереометрической фигуры).

- Генерация — L.
- Высота — H.
- Базовая площадь S main (иными словами, нужно найти заданный параметр окружности).
- Высота цилиндра со скошенной кромкой — h 1, h 2 (минимальная и максимальная).
- Площадь боковой поверхности S-сторона (если развернуть, получится некий прямоугольник).
- Объем стереометрической фигуры V.
- Общая площадь поверхности — S.
«Компоненты» стереометрической фигуры
При исследовании цилиндра большую роль играет площадь боковой поверхности. Это связано с тем, что эта формула входит в несколько других, более сложных. Поэтому необходимо хорошо разбираться в теории.
Основными составляющими фигуры являются:
- Боковая поверхность. Как известно, она получается за счет движения образующей по заданной кривой.
- Полная поверхность включает существующие основания и боковую плоскость.
- Сечение цилиндра, как правило, представляет собой прямоугольник, расположенный параллельно оси фигуры.
 Иначе его называют самолетом. Получается, что длина и ширина являются неполными составляющими других фигур. Итак, условно длины сечения являются образующими. Ширина — параллельные хорды стереометрической фигуры.
Иначе его называют самолетом. Получается, что длина и ширина являются неполными составляющими других фигур. Итак, условно длины сечения являются образующими. Ширина — параллельные хорды стереометрической фигуры. - Под осевым сечением понимается расположение плоскости, проходящей через центр корпуса.
- И, наконец, окончательное определение. Касательная — это плоскость, проходящая через образующую цилиндра под прямым углом к осевому сечению. При этом должно выполняться одно условие. Указанная образующая должна лежать в плоскости осевого сечения.
Основные формулы работы с цилиндром
Для того чтобы ответить на вопрос, как найти площадь поверхности цилиндра, необходимо изучить основные «составляющие» стереометрической фигуры и формулы их нахождения .
Эти формулы отличаются тем, что сначала даются выражения для скошенного цилиндра, а затем для прямого.
Сломанные примеры решения
Нужно найти площадь боковой поверхности цилиндра.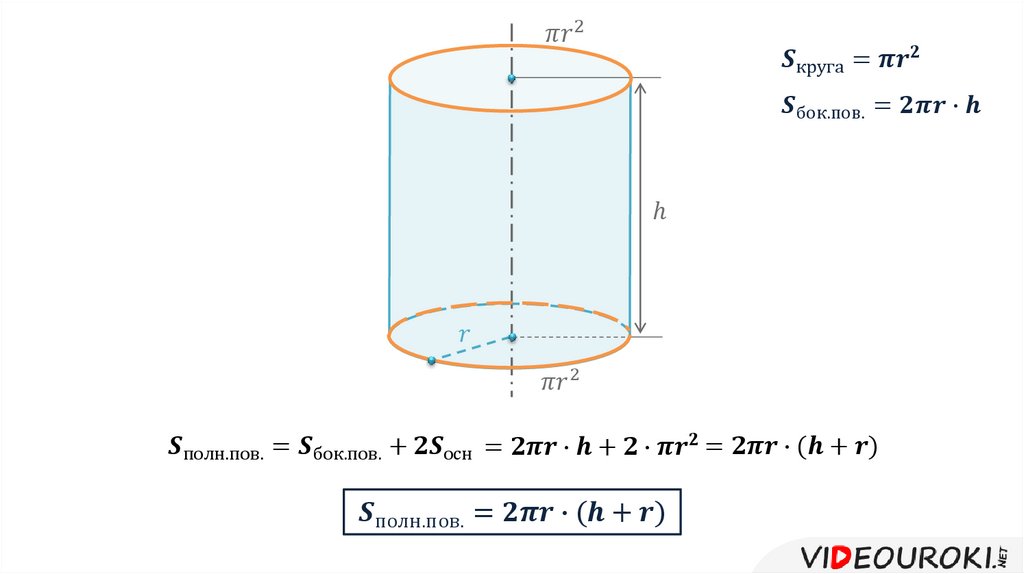 Дана диагональ сечения АС = 8 см (причем она осевая). При контакте с образующей получается
Дана диагональ сечения АС = 8 см (причем она осевая). При контакте с образующей получается
Решение. Так как значения диагонали и угла известны, то в этом случае:
- CD = AC*cos 30°.
Комментарий. Треугольник ACD в данном конкретном примере прямоугольный. Это означает, что частное деления CD и AC = косинусу данного угла. Значение тригонометрических функций можно посмотреть в специальной таблице.
Точно так же можно найти значение AD:
- AD = AC*sin 30°
Теперь необходимо вычислить искомый результат по следующей формулировке: площадь боковой поверхности цилиндра равна удвоенному результату умножения «пи», радиуса фигуры и его высота. Следует использовать и другую формулу: площадь основания цилиндра. Он равен результату умножения «пи» на квадрат радиуса. И, наконец, последняя формула: общая площадь поверхности. Она равна сумме двух предыдущих площадей.
данные цилиндры. Их объем = 128*н см³. Какой цилиндр имеет наименьшую полную площадь?
Какой цилиндр имеет наименьшую полную площадь?
Раствор. Для начала нужно воспользоваться формулами нахождения объема фигуры и ее высоты.
Поскольку общая площадь поверхности цилиндра известна из теории, необходимо применить ее формулу.
Если рассматривать полученную формулу как функцию площади цилиндра, то в точке экстремума будет достигаться минимум «показателя». Чтобы получить последнее значение, нужно использовать дифференцирование.
Формулы можно посмотреть в специальной таблице для нахождения производных. В дальнейшем найденный результат приравнивается к нулю и находится решение уравнения.
Ответ: S min достигается при h = 1/32 см, R = 64 см.
Дана стереометрическая фигура — цилиндр и сечение. Последнюю выполняют таким образом, чтобы она располагалась параллельно оси стереометрического корпуса. Цилиндр имеет следующие параметры: Вк = 17 см, h = 15 см, R = 5 см. Необходимо найти расстояние между сечением и осью.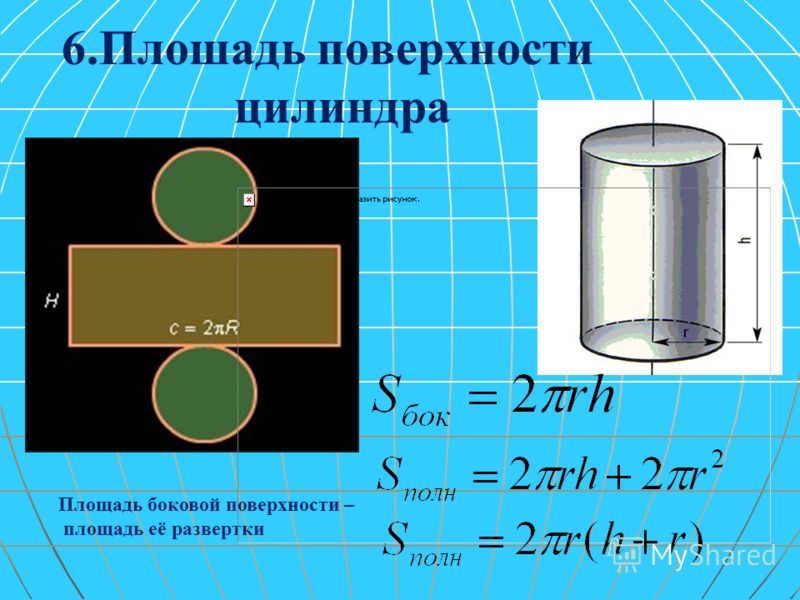
Так как под поперечным сечением цилиндра понимается ВСКМ, т. е. прямоугольник, то его сторона ВМ = h. ВМС нужно учитывать. Треугольник прямоугольный. На основании этого утверждения мы можем сделать правильный вывод о том, что MK = BC.
ВК² = ВМ² + МК²
МК² = ВК² — ВМ²
МК² = 17² — 15²
Отсюда можно сделать вывод, что МК = ВС = 8 см.
Следующим шагом будет создание разреза через основание фигуры. Необходимо рассмотреть получившуюся плоскость.
AD — диаметр стереометрической фигуры. Он параллелен разделу, указанному в условии задачи.
ВС — прямая, расположенная на плоскости существующего прямоугольника.
ABCD — трапеция. В частном случае она считается равнобедренной, так как вокруг нее описана окружность.
Если найти высоту получившейся трапеции, то можно получить ответ, данный в начале задачи. А именно: нахождение расстояния между осью и нарисованным сечением.
Для этого нужно найти значения AD и OS.
Ответ: сечение расположено в 3 см от оси.
Задания по фиксации материала
Дан цилиндр. Площадь боковой поверхности используется в дальнейшем решении. Известны и другие варианты. Площадь основания равна Q, площадь осевого сечения равна M. Необходимо найти S. Другими словами, общая площадь цилиндра.
Дан цилиндр. Площадь боковой поверхности необходимо найти на одном из шагов решения задачи. Известно, что высота = 4 см, радиус = 2 см. Необходимо найти общую площадь стереометрической фигуры.
Название науки «геометрия» переводится как «измерение земли». Он родился стараниями самых первых древних землеустроителей. А происходило это так: во время разливов священного Нила потоки воды иногда размывали границы участков земледельцев, и новые границы могли не совпадать со старыми. Налоги платили крестьяне в казну фараона пропорционально размеру земельного надела. После разлива специальные люди занимались замером площадей пашни в новых границах. Именно в результате их деятельности возникла новая наука, получившая развитие в Древней Греции. Там она и получила свое название, и приобрела почти современный вид. В дальнейшем термин стал международным названием науки о плоских и объемных фигурах.
Там она и получила свое название, и приобрела почти современный вид. В дальнейшем термин стал международным названием науки о плоских и объемных фигурах.
Планиметрия — раздел геометрии, изучающий плоские фигуры. Еще одной отраслью науки является стереометрия, рассматривающая свойства пространственных (объемных) фигур. Цилиндр, описываемый в этой статье, тоже относится к таким фигурам.
Примеров присутствия цилиндрических предметов в быту предостаточно. Почти все детали вращения — валы, втулки, шейки, оси и т. д. имеют цилиндрическую (значительно реже — коническую) форму. Цилиндр широко используется в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы разного диаметра. И, наконец, знаменитые шляпки, давно ставшие символом мужской элегантности. Список бесконечен.
Определение цилиндра как геометрической фигуры
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух окружностей, которые при желании соединяются с помощью параллельного переноса. Именно эти окружности являются основаниями цилиндра. А вот линии (прямые отрезки), соединяющие соответствующие точки, называются «образующими».
Именно эти окружности являются основаниями цилиндра. А вот линии (прямые отрезки), соединяющие соответствующие точки, называются «образующими».
Важно, чтобы основания цилиндра всегда были равны (если это условие не соблюдается, то перед нами усеченный конус, что-то другое, но не цилиндр) и находились в параллельных плоскостях. Отрезки, соединяющие соответствующие точки окружностей, параллельны и равны.
Совокупность бесконечного множества образующих есть не что иное, как боковая поверхность цилиндра — одного из элементов данной геометрической фигуры. Другая его важная составляющая — круги, о которых говорилось выше. Они называются базами.
Типы цилиндров
Самый простой и распространенный тип цилиндра — круглый. Он образован двумя правильными кругами, выступающими в качестве оснований. Но вместо них могут быть другие фигуры.
Основания цилиндров могут образовывать (кроме окружностей) эллипсы и другие замкнутые фигуры. Но цилиндр не обязательно может иметь замкнутую форму.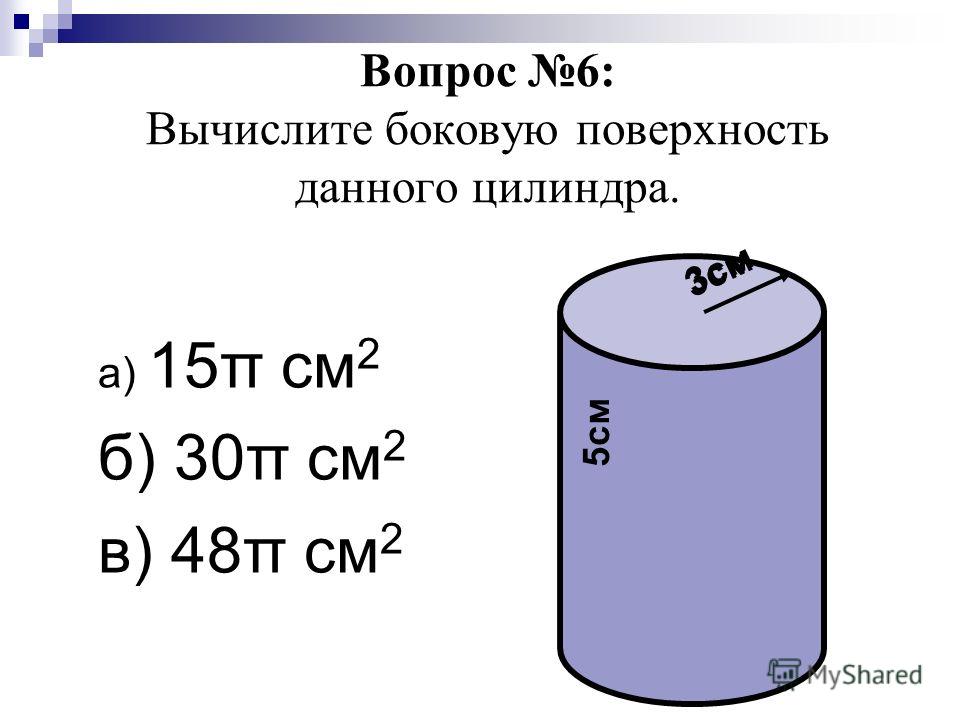 Например, основанием цилиндра может служить парабола, гипербола или другая открытая функция. Такой цилиндр будет открытым или развернутым.
Например, основанием цилиндра может служить парабола, гипербола или другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. Для прямого цилиндра образующие строго перпендикулярны плоскости основания. Если этот угол отличен от 90°, то цилиндр наклонен.
Что такое поверхность вращения
Прямой круговой цилиндр, без сомнения, является наиболее распространенной поверхностью вращения, используемой в технике. Иногда по техническим указаниям применяют конические, сферические и некоторые другие виды поверхностей, но 99% всех вращающихся валов, осей и т.п. выполнены в виде цилиндров. Чтобы лучше понять, что такое поверхность вращения, рассмотрим, как формируется сам цилиндр.
Допустим, есть линия a , расположенная вертикально. ABCD — прямоугольник, одна из сторон которого (отрезок AB) лежит на прямой a . Если мы будем вращать прямоугольник вокруг прямой, как показано на рисунке, то объем, который он будет занимать при вращении, и будет нашим телом вращения — прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.
В этом случае в результате вращения фигуры — прямоугольника — получается цилиндр. Вращая треугольник, можно получить конус, вращая полукруг – шар и т. д.
Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обыкновенного прямого круглого цилиндра, необходимо вычислить площади основания и боковые поверхности.
Во-первых, давайте посмотрим, как рассчитывается площадь боковой поверхности. Это произведение длины окружности и высоты цилиндра. Длина окружности, в свою очередь, равна удвоенному произведению универсального числа 9.0007 P на радиус окружности.
Площадь круга, как известно, равна произведению Р на квадрат радиуса. Итак, сложив формулы для определения площади боковой поверхности с удвоенным выражением для площади основания (их два) и проделав несложные алгебраические преобразования, получим окончательное выражение для определения площади поверхности цилиндр.
Определение объема фигуры
Объем цилиндра определяют по стандартной схеме: площадь поверхности основания умножают на высоту.
Таким образом, окончательная формула выглядит так: желаемое определяется как произведение высоты тела на универсальное число P и квадрат радиуса основания.
Полученная формула, надо сказать, применима для решения самых неожиданных задач. Так же, как объем цилиндра, например, определяется объем электропроводки. Это может понадобиться для расчета массы проводов.
Единственная разница в формуле в том, что вместо радиуса одного цилиндра там диаметр жилы проводки деленный на два и количество жил в проводе фигурирует в выражении Н . Кроме того, вместо высоты используется длина провода. Таким образом, объем «цилиндра» рассчитывается не по одной, а по количеству проволок в оплетке.
Такие расчеты часто требуются на практике. Ведь значительная часть емкостей для воды выполнена в виде трубы. А рассчитать объем баллона часто приходится даже в домашнем хозяйстве.
Однако, как уже было сказано, форма цилиндра может быть разной. А в некоторых случаях требуется вычислить, чему равен объем наклонного цилиндра.
А в некоторых случаях требуется вычислить, чему равен объем наклонного цилиндра.
Отличие в том, что площадь поверхности основания умножается не на длину образующей, как в случае прямого цилиндра, а на расстояние между плоскостями — построенный между ними перпендикулярный отрезок.
Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.
Как построить развертку цилиндра
В некоторых случаях требуется вырезать развертку цилиндра. На рисунке ниже показаны правила, по которым строится заготовка для изготовления цилиндра заданной высоты и диаметра.
Обратите внимание, что рисунок показан без швов.
Различия со скошенным цилиндром
Представим прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. Но плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.
На рисунке показан цилиндр со скошенной кромкой. Плоскость a под некоторым углом, отличным от 90°, к образующим пересекает фигуру.
Эта геометрическая форма чаще встречается на практике в виде соединений трубопроводов (отводов). Но есть даже здания, построенные в виде скошенного цилиндра.
Геометрические характеристики скошенного цилиндра
Наклон одной из плоскостей скошенного цилиндра несколько меняет порядок расчета как площади поверхности такой фигуры, так и ее объема.
Это геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.
Цилиндр состоит из боковой поверхности и двух оснований. Формула площади поверхности цилиндра включает в себя отдельный расчет площади оснований и боковой поверхности. Так как основания в цилиндре равны, то его общая площадь будет рассчитываться по формуле:
Пример вычисления площади цилиндра мы рассмотрим после того, как будем знать все необходимые формулы.


 Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник
Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник 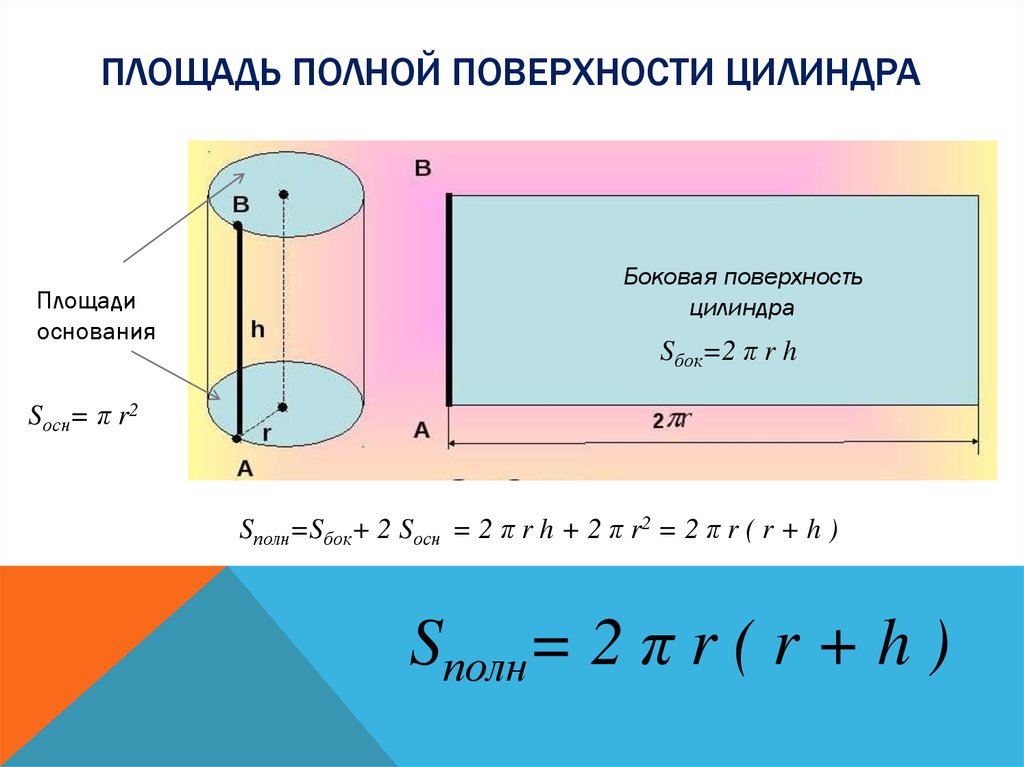 Столб, Треугольная Пирамида, Квадратная Пирамида, Правильная Пирамида, Пирамида, Квадратная Усеченная, Правильная Усеченная, Усеченная, Изогнутая Пирамида, Правильная Бипирамида, Бипирамида, Двуусеченная, Усеченная-Пирамида, Пандус, Прямой Клин, Клин, Половина Тетраэдра, Ромбоэдр, Параллелепипед, Правильный Призма, призма, косая призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клиновидный куб, полукубовид, косой кубоид, слиток, наклонная трехгранная призма, кубовид с вырезом, усеченный кубоид, кубовид с тупыми краями, Удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый куб, полый куб, полая пирамида, полая усеченная пирамида, звездчатая пирамида, звездчатый октаэдр, Sma ll Звёздчатый додекаэдр, Большой звёздчатый додекаэдр, Большой додекаэдр, Большой икосаэдр
Столб, Треугольная Пирамида, Квадратная Пирамида, Правильная Пирамида, Пирамида, Квадратная Усеченная, Правильная Усеченная, Усеченная, Изогнутая Пирамида, Правильная Бипирамида, Бипирамида, Двуусеченная, Усеченная-Пирамида, Пандус, Прямой Клин, Клин, Половина Тетраэдра, Ромбоэдр, Параллелепипед, Правильный Призма, призма, косая призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клиновидный куб, полукубовид, косой кубоид, слиток, наклонная трехгранная призма, кубовид с вырезом, усеченный кубоид, кубовид с тупыми краями, Удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый куб, полый куб, полая пирамида, полая усеченная пирамида, звездчатая пирамида, звездчатый октаэдр, Sma ll Звёздчатый додекаэдр, Большой звёздчатый додекаэдр, Большой додекаэдр, Большой икосаэдр Это окружность, вытянутая перпендикулярно на высоту h. Круг – это основа. Введите радиус и высоту и выберите количество знаков после запятой. Затем нажмите Рассчитать.
Это окружность, вытянутая перпендикулярно на высоту h. Круг – это основа. Введите радиус и высоту и выберите количество знаков после запятой. Затем нажмите Рассчитать.

 Иначе его называют самолетом. Получается, что длина и ширина являются неполными составляющими других фигур. Итак, условно длины сечения являются образующими. Ширина — параллельные хорды стереометрической фигуры.
Иначе его называют самолетом. Получается, что длина и ширина являются неполными составляющими других фигур. Итак, условно длины сечения являются образующими. Ширина — параллельные хорды стереометрической фигуры.