Векторы в высшей математике: Векторы, основные темы

alexxlab / / Математике

ВЕКТОРЫ В ЛИНЕЙНОМ ПРОСТРАНСТВЕ — Лекции по высшей математике

Лекции по высшей математике

Скачать все файлы (2163.9 kb.)

Доступные файлы (30):

n1.doc327kb.21.12.2005 16:14скачать
n2.doc266kb.21.12.2005 16:14скачать
n3.doc249kb.21.12.2005 16:14скачать
n4.doc448kb.21.12.2005 16:15скачать
n5.doc224kb.21.12.2005 16:13скачать
n6.doc164kb.21.12.2005 16:17скачать
n7.doc259kb.21.12.2005 16:19скачать
n8.doc274kb.21.12.2005 16:20скачать
n9.doc336kb.21.12.2005 16:24скачать
n10.doc322kb.21.12.2005 16:31скачать
n11.doc311kb.21.12.2005 16:38скачать
n12.doc504kb.21.12.2005 16:54скачать
n13.doc118kb.21.12.2005 16:58скачать
n14.doc86kb.21.12.2005 17:01скачать
n15.doc225kb.21.12.2005 17:05скачать
n16.doc126kb.21.12.2005 17:15скачать
n17.doc156kb.21.12.2005 17:22скачать
n18.doc150kb.21.12.2005 17:33скачать
n19.doc174kb.21.12.2005 17:45скачать
n20.doc227kb.21.12.2005 17:53скачать
n21.doc86kb.21.12.2005 17:58скачать
n22.doc105kb.21.12.2005 18:02скачать
n23. doc125kb.21.12.2005 18:07скачать
n24.doc260kb.21.12.2005 18:14скачать
n25.doc289kb.21.12.2005 18:29скачать
n26.doc108kb.12.07.2007 11:36скачать
n27.doc221kb.22.12.2005 19:03скачать
n28.doc402kb.22.12.2005 19:06скачать
n29.doc199kb.22.12.2005 19:11скачать
n30.doc295kb.22.12.2005 19:22скачать

n1.doc

ВЕКТОРЫ В ЛИНЕЙНОМ ПРОСТРАНСТВЕ
Аналитическая геометрия изучает геометрические образы (точки, прямые, плоскости, поверхности и т.д.) при помощи аналитического метода. В основе этого метода лежит метод координат Рене Декарта (французский математик 1596-1650), позволяющий ввести соответствия между основными понятиями геометрии (точки, прямые, плоскости) и упорядоченными тройками вещественных чисел.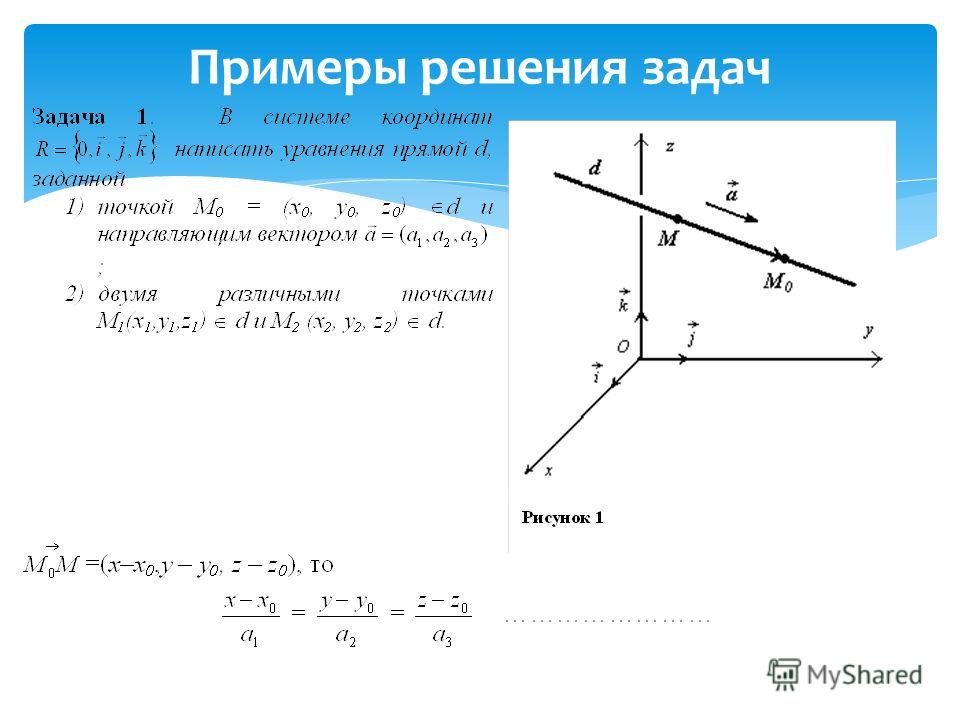 Изучение свойств и взаимного расположения геометрических образов в аналитической геометрии сводится к изучению описывающих эти образы уравнений с привлечением методов алгебры и математического анализа.

I. Вектор, геометрическое определение вектора. Равные векторы.

Пусть на некоторой прямой заданы две точки A и B . Тем самым выделен отрезок AB этой прямой с концами в точках A и B.

Можно считать, что точка A — начало отрезка, B — конец. Тогда мы зададим так называемый направленный отрезок, определяемый упорядоченной парой точек.

Определение . Направленный отрезок (упорядоченную пару точек) называют  вектором. Вектор обозначается или . Если точки A и B совпадают, то говорят, что вектор нулевой или нуль-вектор .

Расстояние между началом и концом вектора называется его  длиной или модулем и обозначается .

В
екторы называются  коллинеарными, если они имеют общую параллельную прямую. При совмещении начал коллинеарных векторов они оказываются лежащими на одной прямой.

В


екторы называются  компланарными, если они параллельны одной и той же плоскости. При совмещении начал компланарных векторов они оказываются лежащими в одной плоскости.

Теперь можно ввести следующее 

определение

: два вектора называются равными, если они коллинеарны, одинаково направлены и равны по длине.


, если

, хотя но

Из определения равенства векторов следует, что каждый вектор можно перенести в любое место параллельно самому себе и не изменить его. Тем самым мы ввели так называемый свободный вектор, задать который — значит задать его модуль и направление. Многие физические величины характеризуются не только числовым значением, но и направлением, и, следовательно, являются векторными (сила, скорость, перемещение, магнитная индукция…).

II. Линейные операции над векторами, их свойства.

Понятие о линейном пространстве.

К линейным операциям над векторами относятся сложение векторов и умножение вектора на скаляр.

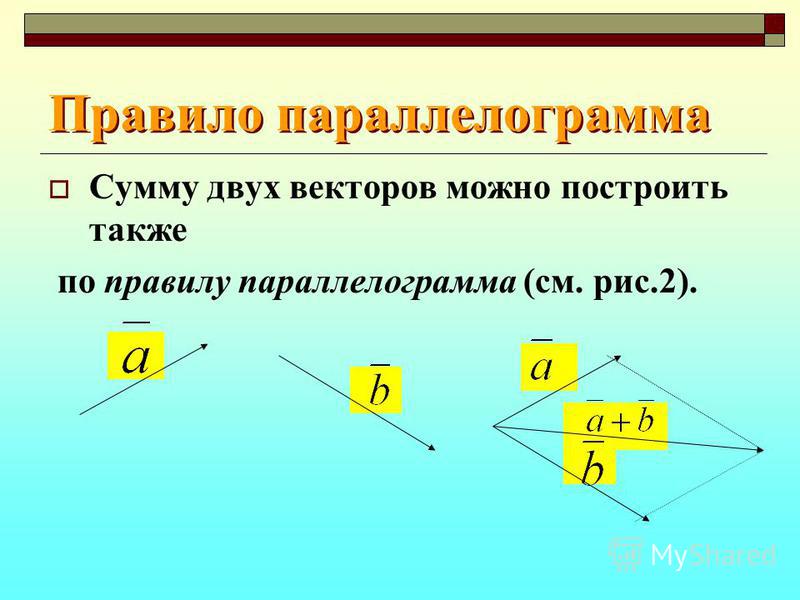
Сложение двух векторов выполняется по правилу параллелограмма:  сумма  двух векторов представляет собой диагональ параллелограмма, построенного на равных им векторах.

Сумма нескольких векторов определяется как вектор, замыкающий ломаную линию, звеньями которой служат векторы-слагаемые, и направленный из начала первого вектора в конец последнего.
Определение: произведением вектора на вещественное число называется

такой вектор , что 1)

2) вектор коллинеарен ,

3) векторы и направлены одинаково,

если ,

и противоположно, если :

,если , ,если .

Вектор называется противоположным вектору . Сумма двух противоположных векторов равна нулевому вектору: .

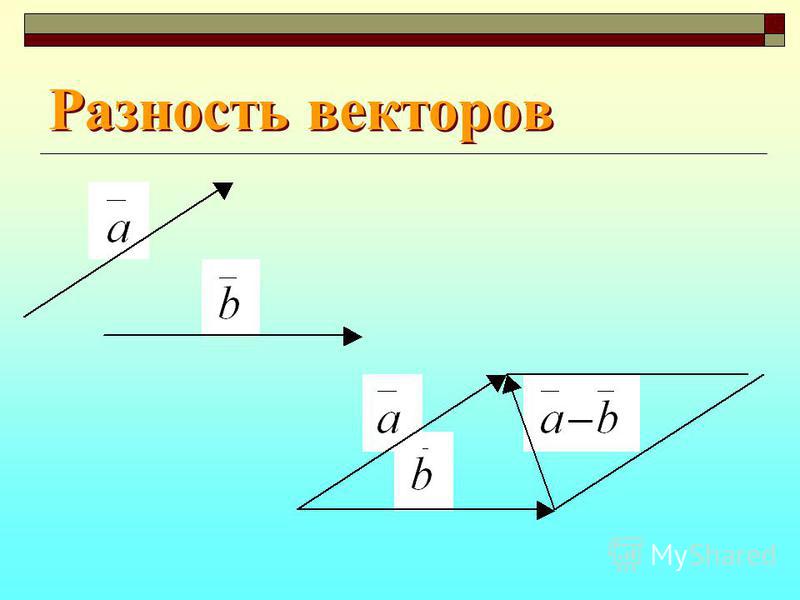
Вычитание векторов — операция, обратная сложению:

Перечислим свойства введенных нами линейных операций:

1
) коммутативность сложения: ;

2) ассоциативность сложения: ;

3) существование нуль-вектора: ;

4) существование противоположного вектора: ;

5) дистрибутивность сложения по отношению к умножению на число:


6) дистрибутивность сложения:

A B C D E

7) ассоциативность умножения:  т. к.

8) существование единицы:  это следует из определения

операции умножения.

Пространство, для элементов которого вводятся операции сложения и умножения на число, обладающие свойствами (1)-(8), называют линейным (векторным) пространством. Элементы линейного пространства обычно называют векторами.
III. Разложение вектора по базису. Координаты вектора.

Пусть заданы векторы и числа  Составим комбинацию из этих векторов, используя только введенные линейные комбинации сложения и умножения вектора на число. В самом общем случае она имеет вид: . Такие комбинации называются линейными комбинациями векторов , а числа — коэффициентами линейной комбинации.

Если вектор представлен как линейная комбинация некоторых векторов, то говорят, что он разложен по этим векторам.

Пусть дан ненулевой вектор . Покажем, что любой коллинеарный ему вектор может быть представлен в виде единственным образом.

По определению операции умножения вектора на число векторы и коллинеарны, следовательно, коллинеарны и векторы и . Одинаковое направление векторов и обеспечивается выбором знака числа . Наконец, из равенства модулей равных векторов следует, что . Единственность представления следует из того, что при умножении вектора на другое число получается новый вектор: при .

Теорема 1. Любой вектор на плоскости может быть разложен по двум неколлинеарным векторам и единственным образом.

Доказательство: В общем случае отложим все три вектора из общей точки О. Из конца вектора (точки А) проведем прямые АР и AQ, параллельные векторам и . Тогда по правилу параллелограмма

.

Вектор коллениарен вектору и, следовательно, единственным образом может быть представлен в виде . Вектор коллинеарен вектору , поэтому . Тогда — единственное разложение вектора по векторам и .

Неколлинеарные векторы и , взятые в определенном порядке, называются базисом на плоскости, а коэффициенты линейной комбинации 1 и 2 — координатами вектора в базисе и .

Т
.
еорема2: любой вектор единственным образом раскладывается по трем фиксированным некомпланарным векторам:
Некомпланарные векторы образуют базис пространства. Коэффициенты разложения называют координатами вектора в базисе .

Таким образом, в пространстве с выбранным базисом нам удалось каждому вектору поставить в соответствие тройку чисел — его координат. Теперь при выполнении введенных линейных операций над векторами можно заменить геометрические построения аналитическими выражениями.

Пусть

тогда

и

Таким образом, при умножении вектора на число все его координаты умножаются на это число, а при сложении векторов складываются их соответствующие координаты, если они определены относительно одного и того же базиса.
IV. Линейная зависимость векторов. Размерность линейного пространства.

Запишем линейную комбинацию векторов Она называется тривиальной, если все ее коэффициенты одновременно равны нулю, то есть , и нетривиальной, если хотя бы один из коэффициентов отличен от нуля.

Определение: векторы называют линейно зависимыми, если можно найти их нетривиальную комбинацию, равную нулю:

при .

Определение: если для векторов обращается в нуль только их тривиальная комбинация, то такие векторы называют линейно независимыми:

при .

Векторы линейно зависимы, если хотя бы один из них можно представить как линейную комбинацию остальных. Пусть , тогда

Тогда на основании доказанных выше теорем оказывается, что линейно зависимыми являются любые два коллинеарных вектора (), любые три компланарных вектора () и любые четыре вектора в пространстве (). В свою очередь линейно независимыми всегда являются базисные векторы, т.е. два неколлинеарных вектора на плоскости и три некомпланарных вектора в пространстве.

Определение: количество векторов, образующих базис линейного пространства, называют размерностью этого пространства.

Размерность определяется наибольшим числом линейно независимых векторов пространства. Линейное пространство, имеющее размерность n, принято обозначать .
V. Системы координат.

Определение: декартовой системой координат называются совокупность точки и базиса.

Точка О называется началом координат,

Ox,Oy,Oz — координатными осями,

Oxy,Oyz,Oxz — координатными плоскостями.

Декартова система координат, базисные векторы которой взаимно перпендикулярны и имеют единичные длины, называется декартовой прямоугольной системой, а ее базис – ортонормированным.

Координатами точки А в выбранной cистеме координат называются координаты радиус-вектора этой точки в этой системе координат.

Если заданы координаты точек и , то можно найти выражение для координат вектора .

Из рисунка 6 следует, что , тогда . Если , то — координаты вектора .

На практике пользуются и другими системами координат, например, косоугольной декартовой, полярной, цилиндрической, сферической и др.

Угол между векторами. Проекция вектора на ось | Математика

Пусть заданы векторы и . Выберем в пространстве произвольную точку и отложим от этой точки векторы и .

Углом между векторами и называется наименьший угол , на который нужно повернуть один из заданных векторов до его совпадения со вторым (рис. 1.1.9).

Рисунок 1.1.9

Помощь с решением задач

Пусть в пространстве заданы вектор и ось (рис. 1.1.10).

Рисунок 1.1.10

Обозначим через и проекции на ось точек и соответственно. Построим вектор и назовем его компонентом вектора по оси .

Проекцией вектора на ось называется длина его компоненты по этой оси, если компонента направлена в ту же сторону, что и ось ; противоположное число, если компонента и ось имеют разные направления, нуль,

если компонента есть нулевой вектор. Проекция вектора на ось обозначается в виде или .

Выберем на оси единичный вектор имеющий то же направление, что и ось . Углом между векторами и называется угол между вектором и осью .

ТЕОРЕМА 1.4 Проекция вектора на ось равна модулю вектора , умноженному на косинус угла между вектором и осью:

(1.34)

Доказательство: Пусть и является компонентой вектора на ось (рис. 1.1.11).

Рисунок 1.1.11

Если угол между и осью острый, то компонента направлена в ту же сторону, что и ось . Тогда . Из треугольника следует, что . Тогда .

Если же , то компонента направлена в противоположную по отношению к оси сторону. Следовательно, . Из треугольника следует, что

. Тогда

.

Если , то компонента есть нулевой вектор. Тогда и .

Итак, для любых углов . Опираясь на ранее рассмотренные линейные операции над векторами, можно убедиться, что для проекций векторов на ось справедливы следующие теоремы (без доказательств).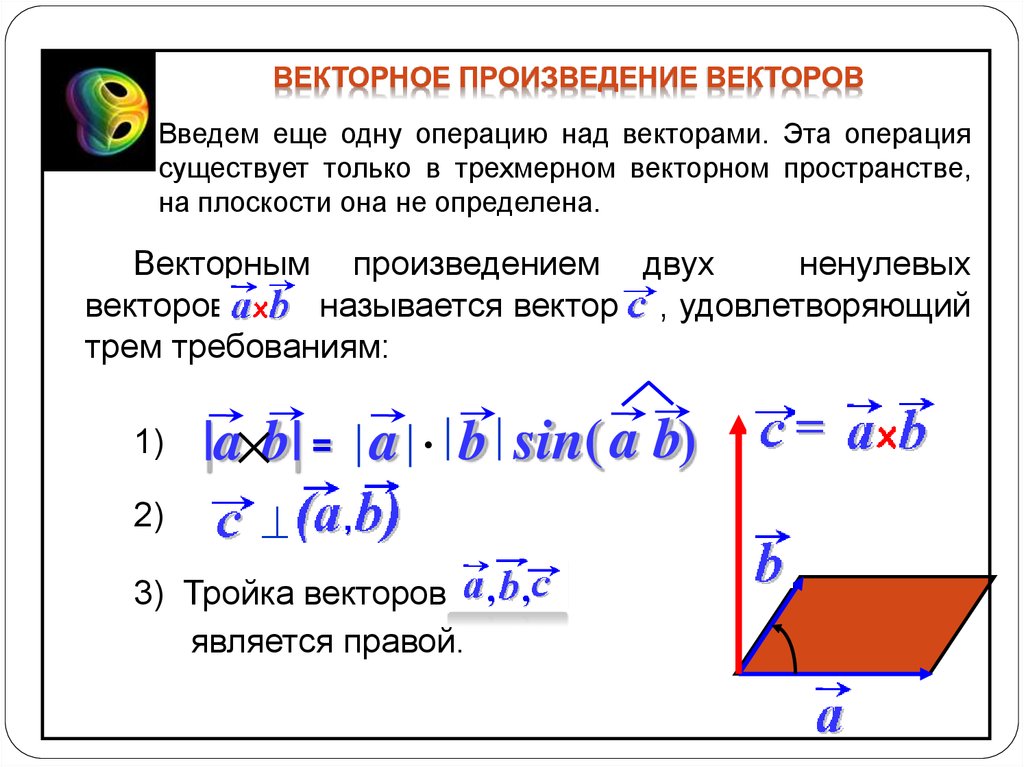

ТЕОРЕМА 1.5

Проекция суммы векторов на ось равна сумме проекции слагаемых векторов на ту же ось:

(1.35)

ТЕОРЕМА>

Если вектор умножить на число , то его проекция на ось умножится на это число:

(1.36)
  • Линейная комбинация векторов. Базис
  • Курс математики

Сохранить или поделиться с друзьями


Вы находитесь тут:


Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Подробнее


Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Сохранить или поделиться с друзьями

  • Решение задач и контрольных
  • Написание учебных работ
  • Онлайн помощь на экзамене

Подробнее


Помощь с решением

Поиск математических формул

Vectors — Высшая математика

Добро пожаловать на сайт highmathematics.co.uk

Хорошее понимание Vectors необходимо для успешной сдачи экзамена.

Прохождение ускоренного курса высшей математики значительно расширит ваши карьерные возможности, помогая вам поступить в колледж/университет, пройти стажировку или даже устроиться на работу. «Хороший» результат по высшей математике подготовит вас к курсу математики AH в следующем году, если вы заинтересованы. Пожалуйста, сделайте все возможное, чтобы продолжать учебу.

Для студентов, которым нужна дополнительная помощь по курсу высшей математики, вы можете рассмотреть возможность подписки на фантастические дополнительные ресурсы, ориентированные на экзамены, доступные в пакете онлайн-обучения.

Чтобы получить доступ к множеству дополнительных бесплатных ресурсов по теме , воспользуйтесь расположенной выше панелью поиска или нажмите ЗДЕСЬ, выбрав тему, которую хотите изучить.

Мы надеемся, что вы найдете этот веб-сайт полезным, и желаем вам всего наилучшего в изучении курса высшей математики в 2023 году. Ниже вы найдете:

1. О векторах

2. Векторы — рабочие листы

3. Векторы — видео, руководства по теории и интеллект-карты

4. Основные навыки высшей математики

5. Листы экзамена по высшей математике 2. Прошлые и практические статьи по темам 

7. Видео по высшей математике, руководства по теории, интеллект-карты и рабочие листы 

8. Прошлые и практические статьи по высшей математике 

9. 40 вопросов и ответов по высшей математике без калькулятора

10. 200 вопросов и ответов по высшей математике 

11. Практические экзаменационные работы от A до H – ответы включены

12. 264 SQA экзамен с несколькими вариантами ответов

13. Контрольные списки экзамена по высшей математике 1

5 Экзаменационные вопросы по математике по темам

15. Решения для учебников по высшей математике

16. Руководства по теории высшей математики 

17. Интеллект-карты по высшей математике 

18. Практические оценки по высшей математике – решения включены

19. Higher Maths Past Paper Video Solutions

20. Рекомендуемый учебник по высшей математике

21. Пакет онлайн-обучения, ориентированный на экзамен — для студентов, которые ищут «хороший» пропуск

 

Ресурсы по высшей математике

4

4

4 .



1. О векторах 

Чтобы узнать о векторах, нажмите ссылку Теория векторов (HSN). Кроме того, в разделах 2 и 3 ниже вы найдете несколько видеороликов, ментальных карт (см. раздел «Векторы») и рабочие листы по этой теме, которые помогут вам понять. Настоятельно рекомендуется использовать рабочие листы для основных навыков 10, 21 и 30, а также рабочие листы, содержащие фактические вопросы экзамена SQA.

Если вам нужна дополнительная помощь в понимании Vectors  в  обучаемом онлайн-пакете вы найдете четкие, простые для понимания, пошаговые решения десятков экзаменационных вопросов Higher Maths Past & Practice по всем темам. Пожалуйста, предоставьте себе все возможности для достижения успеха, поговорите со своими родителями и подпишитесь на онлайн-учебный пакет      , посвященный экзамену , сегодня.

Векторы

  • Высшая математика расширяет возможности изучения Векторов, полученных в рамках Национального курса 5 математики
  • Формула скалярного произведения приведена в списке формул экзамена по высшей математике SQA
    • .

.

В разделе «Векторы» курса высшей математики рассматривается следующее;

  • Векторы и скаляр
  • Компоненты
  • Величина
  • Равные векторы
  • Сложение и вычитание векторов
  • Умножение на скаляр
  • Векторы положения
  • Коллинеарность
  • Разделительные линии в соотношении
  • Скалярное произведение
  • Угол между векторами
  • Перпендикулярные векторы
  • Свойства скалярного произведения

.

2. Векторы – Рабочие листы

Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом. Четкие, простые в использовании, пошаговые рабочие решения для всех рабочих листов, приведенных ниже, доступны в пакете онлайн-обучения.

Higher Worksheets
__________________________		 Recommended
_____________		 Worksheets
____________________________________		 Without Answers
________________		 Notes/Comments
_____________________		 Courtesy
______________________
Книга Heinemann — круги Ex13A, 13B, 13C, 13D, 13E, 13F, 13G, 13I, 13K, 13L, 13M, 13N, 13O, 13P, 13Q, 13R, 1 13S Ответы по ссылкам
Практика экзамена по основным навыкам 11 Векторы Без ответов Только ответы Предоставлено г-ном Г.
Ренни
Базовые навыки 10 Формула раздела Без ответов Только ответы Предоставлено г-ном Г. Ренни
Основные навыки 21 Скалярное произведение Без ответов Только ответы Предоставлено Mr G Rennie
Основные навыки 30 Угол между векторами Без ответов Только ответы Предоставлено г-ном Г. Ренни
Бумага Grade Booster Paper 7 `Векторы Без ответов Включены рабочие решения
Высшие экзаменационные вопросы Рекомендуемые Векторы 1 (2000–2019 гг.)) Без ответов Предоставлено SQA
Высшие экзаменационные вопросы Векторы 2 Без ответов Предоставлено SQA
Высшие экзаменационные вопросы Векторы 3 (Старое высшее) Без ответов Несколько вариантов ответа включены! Предоставлено SQA
Высшие экзаменационные вопросы Векторы 4 (2000 — 2013) Схемы маркировки SQA Предоставлено SQA
Контрольный список экзамена 14 Векторы

.

3. Векторы – видеоролики, теоретические руководства и ментальные карты

Спасибо авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом.

Ларберт Математика Видео
______________________________		 maths180.com Video
________________________________		 HSN Theory Guide
_________________		 Mind Maps
_________________
Трехмерная коллинеарность Векторы Теория векторов (HSN) Векторы (HSN)
Угол между векторами Векторы 1
Базисные векторы Векторы 2
Разделение прямой в заданном отношении Векторы 3
Перпендикулярные векторы
Векторы положения
Свойства скалярных произведений
Скалярные произведения
Скалярные произведения компонентов
Единичные векторы

.

4. Высшие математические навыки 

Спасибо г-ну Г. Ренни за то, что он предоставил в свободный доступ приведенные ниже отличные ресурсы. Рабочие листы основных навыков можно использовать для общего повторения, выполнения домашних заданий, закрепления темы или подготовки к оцениванию, тестам и экзаменам. Четкие, простые в использовании, пошаговые решения для всех 33 рабочих листов основных навыков, приведенных ниже, доступны в онлайн-учебном пакете.

.

5. Рабочие листы экзамена по высшей математике по темам

Спасибо SQA и авторам за то, что они предоставили в свободный доступ превосходные ресурсы, приведенные ниже. Рабочие листы по темам являются фантастическим учебным ресурсом, поскольку они являются реальными вопросами прошлых бумажных экзаменов. Четкие, простые в использовании, пошаговые решения для всех новых вопросов CfE по высшей математике, приведенных ниже, доступны в онлайн-пакете для изучения.

.

6. Прошлые и практические работы по высшей математике по темам

Спасибо SQA за предоставление бесплатного доступа к превосходным ресурсам, указанным ниже. Вопросы и ответы разделены по темам для удобства поиска. Четкие, простые в использовании, пошаговые решения всех приведенных ниже вопросов доступны в пакете онлайн-обучения.

138 Q10,11B138 Q10,11B1488 Q10,11B140138 Q10,11B138 Q10,11B
.
Бумага
_____________		 .
Маркировка
__________		 .
Круги
______		 Дифференциация
и оптимизация
______ 9.
Интеграция
_________		 полиномии
& Quadratics
____________		 Рецидив
Отношения
__________		 СТРИД
Lines
_________		8.
Векторы
________
Волна
Функция
_________
2019 P1 Marking P1 Q3,16 Q1 Q14 Q10,12 Q6,11,17b Q8 Q2 Q4 Q5,7 Q13, 15,17а Q9
2019 P2 Marking P2 Q15 Q7b,11 Q9,12 Q5,8 Q2,13 Q7,10 Q4 Q1 Q6b Q3,14 Q6a
2018 P1 Marking P1 Q4 Q6,11 Q2,11,15 Q3,14 Q10 Q7 Q1,8 Q13 Q5,9 ,12
2018 P2 Marking P2 Q5c,12 Q3,9 Q11 Q6 Q1 Q4,7a,10 7b,c Q5a,b Q2 Q8
2017 P1 Marking P1 Q2 Q8,15c Q12 Q1,6,15a Q3,13 Q10,15b Q4 Q9 Q7,11 Q5 Q14
2017 P2 Маркировка P2 Q3,10 Q4,7 Q9 Q2

00140		 Q1 Q6,11 Q5
2016 P1 Marking P1 Q4,8 Q2,9 Q14 Q6,10,12 Q5 Q15 Q3 Q1 Q13 Q7,11
2016 P2 Marking P2 Q4 Q7 Q6 Q10,11B 3B, 9 3B, 9 3B, 9 3B, 3B, 3B,. 0140 Q8b,11a Q5 Q8a
2015 P1 Marking P1 Q11,14 Q2,7 Q6 Q4,5,13 Q12,15 Q3,8 Q9 Q10 Q1
2015 P2 Marking P2 Q5 Q8 Q2 Q7a Q4 Q3 Q1 Q7b Q6 Q9
Specimen P1 Marking P1 Q11 Q8 Q10 Q1 Q4,7 Q2,5,9 Q6,12 Q3
Specimen P2 Marking P2 Q5 Q3b,8 Q4,7 Q9 Q3a Q2 Q1,6 Q10
Exemplar P1 Marking P1 Q1 Q8,11 Q10 Q3 Q2,5 Q6 Q4,7 Q9
Exemplar P2 Marking P2 Q2 Q9,10 Q7 Q8 Q4 Q3 Q1 Q5,6

.

7. Видео по высшей математике, руководства по теории, интеллект-карты и рабочие листы

Десятки видеороликов по высшей математике содержат качественные уроки по темам. Также включены отличные руководства по теории, интеллект-карты и рабочие листы с актуальными экзаменационными вопросами по высшей математике. Пожалуйста, нажмите на нашу новую страницу с видео и рабочими таблицами по высшей математике по темам.

.

8. Higher Maths Past & Practice Papers

Спасибо SQA за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Четкие, простые в использовании, пошаговые решения для всех представленных ниже документов CfE Higher Papers доступны в пакете онлайн-обучения.

Обработано
Год
_______________		 Тип бумаги
____________________		 Экзаменационный лист
_________________		 Схема маркировки
__________________ 9 Решений 16 ___________
2022 Высшее (CfE) Бумага 1, Бумага 2 Схема выставления оценок В интерактивном учебном пакете
2022 Адаптированный 2022 Адаптированный Бумага Экзаменационный лист Маркировка 2019, 18, образец В интерактивном учебном пакете
2000–2019 Ultimate Revision Guide Весь буклет Ответы на рабочем листе CfE Papers in Online Study Pack
2019 Высшее (CfE) Бумага 1, Бумага 2 Схема выставления оценок В интерактивном учебном пакете
2018 Высшее (CfE) Бумага 1, Бумага 2 Схема маркировки В интерактивном учебном пакете
2018 Образец (CfE) Бумага 1, Бумага 2 Схема маркировки В интерактивном учебном пакете
2017 Высшее (CfE) Экзаменационный лист Схема выставления оценок В интерактивном учебном пакете
2016 Высшее (CfE) Экзаменационный лист Схема выставления оценок В интерактивном учебном пакете
2015 Высшее (CfE) Экзаменационный лист Схема выставления оценок В интерактивном учебном пакете
2015 Образец (CfE) Образец бумаги Схема маркировки In Online Study Pack
2015 Exemplar (CfE) Exemplar Paper Схема маркировки In Online Study Pack
2015 Высшее (Старое) Экзаменационный лист Схема выставления оценок
2014 Высшее Экзаменационный лист Схема выставления оценок Рабочие решения
2013 Высшее Экзаменационный лист Схема выставления оценок Рабочие решения
2012 Высшее Экзаменационный лист Схема выставления оценок Рабочие решения
2011 Высшее Экзаменационный лист Схема оценивания Рабочие решения
2010 Высшее Экзаменационный лист Схема выставления оценок Рабочие решения
2009 Высшее Экзаменационный лист Схема выставления оценок Рабочие решения
2008 Высшее Экзаменационный лист Схема выставления оценок Рабочие решения
2007 Высшее Экзаменационный лист Схема выставления оценок Рабочие решения
2006 Высшее Экзаменационный лист Схема выставления оценок Рабочие решения
2005 Высшее Экзаменационный лист Схема выставления оценок Рабочие решения
2004 Высшее Экзаменационный лист Схема оценивания Рабочие растворы
2003 Высшее Экзаменационный лист Схема выставления оценок Рабочие решения
2002 Высшее Экзаменационный лист Схема выставления оценок Рабочие решения
2002 Высшее (зимняя диета) Экзаменационный лист
2001 Высшее Экзаменационный лист Рабочие растворы
2000 Высшее Экзаменационный лист Рабочие растворы

.

9. 40 Вопросы и ответы по высшей математике без калькулятора

Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Начните с этих вопросов, чтобы укрепить свою уверенность. После завершения вы можете перейти к 200 экзаменационным вопросам по высшей математике в следующем разделе, проверяя свои ответы по ходу. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее. Четкие, простые для понимания, пошаговые решения всех 40 приведенных ниже вопросов доступны в пакете онлайн-обучения.

.

10. 200 вопросов и ответов по высшей математике

Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Пожалуйста, постарайтесь задать как можно больше вопросов, проверяя ответы по ходу. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее. Четкие, простые в использовании, пошаговые решения всех 200 приведенных ниже вопросов доступны в пакете онлайн-обучения.

.

11. Практические экзаменационные работы от A до H – ответы включены

Спасибо SQA и Larkhall Academy за предоставление нижеприведенных превосходных ресурсов в свободный доступ. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом. Четкие, простые в использовании, пошаговые решения для практических работ от A до E доступны в онлайн-пакете для изучения.

.

12. 264 SQA Exam Multiple Choice Questions & Answers 

Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Множественный выбор — это, прежде всего, вопросы уровня C, и это отличное место для начала проверки. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее.

.


13. Контрольные списки для экзамена по высшей математике

Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Это фантастические контрольные списки для оценки ваших знаний по высшей математике. Пожалуйста, старайтесь регулярно использовать их для повторения перед тестами, предварительными экзаменами и выпускным экзаменом.

.

14. Старые экзаменационные вопросы по высшей математике по темам

Благодарим SQA за предоставленный в свободном доступе превосходный ресурс. Рабочие листы по темам являются фантастическим дополнительным учебным ресурсом.

Тема
________		 Название темы
___________________________		 Ссылка
________		 Примечания
___________________
Тема 1 Круги ЗДЕСЬ Ответы включены
Тема 2 Дифференциация ЗДЕСЬ Ответы включены
Тема 3 Экспоненты и логарифмы ЗДЕСЬ Ответы включены
Тема 4 Функции ЗДЕСЬ Ответы включены
Тема 5 Дальнейшее исчисление ЗДЕСЬ Ответы включены
Тема 6 Графики функций ЗДЕСЬ Ответы включены
Тема 7 Интеграция ЗДЕСЬ Ответы включены
Тема 8 Многочлены ЗДЕСЬ Ответы включены
Тема 9 Квадратика ЗДЕСЬ Ответы включены
Тема 10 Рекуррентные соотношения ЗДЕСЬ Ответы включены
Тема 11 Прямая линия ЗДЕСЬ Ответы включены
Тема 12 Триггерные формулы сложения ЗДЕСЬ Ответы включены
Тема 13 Триггерные графики и уравнения ЗДЕСЬ Ответы включены
Тема 14 Векторы ЗДЕСЬ Ответы включены
Тема 15 Волновая функция ЗДЕСЬ Ответы включены

.

15. Решения для учебников по высшей математике 

Спасибо AHS за предоставленные решения для учебников Heinemann по высшей математике, указанные ниже. Они окажутся чрезвычайно полезными для улучшения ваших знаний по высшей математике. Обратите внимание, что может быть нечетная арифметическая ошибка.

.

16. Руководства по высшей математике 

Благодарим HSN за то, что они сделали превосходные руководства по высшей математике бесплатными для всех. Они окажутся фантастическим ресурсом, который поможет вам закрепить ваше понимание высшей математики.

Теоретические руководства
_________________		 Тема
____________________________________________		 Ссылка
_______
Теоретическое руководство 1 Все темы Раздел 1 Теория (HSN) ЗДЕСЬ
Теоретическое руководство 2 Все темы, раздел 1 — краткое руководство на одной странице (HSN) ЗДЕСЬ
Руководство по теории 3 Все темы Раздел 2 Теория (HSN) ЗДЕСЬ
Теоретическое руководство 4 Все темы, раздел 2 — краткое руководство на одной странице (HSN) ЗДЕСЬ
Руководство по теории 5 Все темы Раздел 3 Теория (HSN) ЗДЕСЬ
Теоретическое руководство 6 Все темы, раздел 3 — краткое руководство на одной странице (HSN) ЗДЕСЬ
Руководство по теории 7 Все темы Разделы 1, 2 и 3 Теория (HSN) ЗДЕСЬ
Руководство по теории 8 Теория кругов (HSN) ЗДЕСЬ
Руководство по теории 9 Теория дифференцировки (HSN) ЗДЕСЬ
Руководство по теории 10 Теория экспонент и логарифмов (HSN) ЗДЕСЬ
Руководство по теории 11 Теория функций и графиков (HSN) ЗДЕСЬ
Руководство по теории 12 Дальнейшая теория исчисления (HSN) ЗДЕСЬ
Руководство по теории 13 Теория трансформации графиков (движение и отражение) ЗДЕСЬ
Теоретическое руководство 14 Сводная таблица преобразований графиков ЗДЕСЬ
Руководство по теории 15 Теория интеграции (HSN) ЗДЕСЬ
Руководство по теории 16 Теория многочленов и квадратичных уравнений (HSN) ЗДЕСЬ
Руководство по теории 17 Теория последовательностей (HSN) ЗДЕСЬ
Руководство по теории 18 Теория прямых линий (HSN) ЗДЕСЬ
Руководство по теории 19 Теория тригонометрии (HSN) ЗДЕСЬ
Руководство по теории 19 Теория векторов (HSN) ЗДЕСЬ
Руководство по теории 20 Теория волновых функций (HSN) ЗДЕСЬ

.

17. Интеллект-карты высшей математики

Спасибо авторам за предоставленные ниже отличные ресурсы. Они окажутся фантастическим ресурсом, помогающим вам подготовиться к оценкам, тестам и выпускному экзамену.

.

18. Оценки модулей по высшей математике – решения включены

Спасибо авторам за то, что они сделали нижеприведенные превосходные ресурсы бесплатными для всех. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом.

.

19. Higher Maths Past Paper Video Solutions

Щелкните DLB Maths, чтобы просмотреть видеорешения Higher Maths Past Paper. Это отличный ресурс, который поможет вам подготовиться к оцениванию, тестам и выпускному экзамену.

.

20. Рекомендуемый учебник по высшей математике

Ниже вы найдете рекомендуемый учебник, который можно заказать, нажав на книгу/ссылку.

.

.

21. Учебный онлайн-пакет по высшей математике 

Благодаря пошаговым решениям экзаменационных вопросов, доступным в онлайн-учебном пакете, мы охватим все, что вам нужно знать о Vectors , чтобы сдать выпускной экзамен.

Для студентов, которые ищут «хороший» проход по высшей математике, вы можете рассмотреть возможность подписки на фантастические дополнительные ресурсы, ориентированные на экзамены, доступные в Online Study Pack. Подписка может стать одной из ваших лучших инвестиций.

Пожалуйста, предоставьте себе все возможности для достижения успеха, поговорите со своими родителями и подпишитесь на  ориентированный на экзамен   Online Study Pack сегодня.

Мы надеемся, что ресурсы на этом веб-сайте окажутся полезными, и желаем вам всего наилучшего в изучении курса высшей математики в 2023 году.

Получите учебный пакет — всего 20 фунтов стерлингов

Нажмите здесь для учителей >

Не только векторы, но и 70 других математических концепций подробно описано

Векторы — Математика A-Level Revision

Векторная величина имеет как величину, так и направление. Ускорение, скорость, сила и перемещение — все это примеры векторных величин. Скалярная величина имеет только величину (поэтому направление не имеет значения). Примеры включают скорость, время и расстояние.

Единичные векторы

Единичный вектор — это вектор, величина которого равна 1. Обычно используются три важных единичных вектора, и это векторы в направлении осей x, y и z. . Единичный вектор в направлении оси x равен i , единичный вектор в направлении оси y равен j и единичный вектор в направлении оси z равен k .

Запись векторов в этой форме может упростить работу с векторами.

Величина вектора

Величина вектора может быть найдена с помощью теоремы Пифагора .

Обозначим величину вектора a через | и |

Векторы положения

Векторы положения — это векторы, определяющие положение точки относительно фиксированной точки (начала).

Например, точки A, B и C являются вершинами треугольника с векторами положения a , b и c соответственно:

Вы можете рисовать в начале координат где угодно.

Обратите внимание, что = — a + b = b — a , потому что вы можете попасть из A в B, пройдя из A в O, а затем из O в B.

Векторное уравнение a Прямая

Векторное уравнение прямой, проходящей через точку a и в направлении d равно:

Это означает, что для любого значения t точка r является точкой на прямой.

Если нам даны векторные уравнения двух разных линий, мы можем выяснить, где пересекаются линии, исходя из их уравнений.

Example

Find where the lines with equations r = i + j + t (3 i — j ) and r = — i + s ( j ) пересекаются.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *