Как делать обратную замену: Как делать обратную замену в уравнении. Интегрирование методом замены переменной

Обратная замена в футболе. Что это значит?

Что понимают в футболе под термином «Обратная замена»?

В каких ситуациях осуществляется замена футболистов?

Какими правилами регулируется замена игроков?

Обратная замена – ситуация во время матча, при которой ранее замененный футболист снова вступает в игру, выходя на поле вместо другого игрока.

В настоящее время обратные замены не предусмотрены правилами футбола в официальных матчах, но возможны в рамках благотворительных встреч, матчей в честь открытия стадиона, праздничных и прощальных игр.

Замены в футболе

В футболе под словом «замена» подразумевается смена одного игрока команды другим во время игры. В течение одного матча правилами ФИФА предусмотрено производить до трех замен на протяжении основного времени, и одну дополнительную в овертайме.

Все замены условно можно разделить на два типа:

Получай новые прогнозы: Вконтакте и Telegram.

1. Вынужденные замены.
2. Тактические замены.

Вынужденные замены происходят тогда, когда игрок основного состава команды получает травму или он показывает плохую игру, достаточно вымотан для продолжения работы в том же ритме. Тактическими заменами называют замены стратегического характера, в этом случае на замену защитнику на поле может выйти нападающий.

Игрок, которого заменили в ходе матча, не имеет права снова выйти на поле в течение текущей встречи по правилам ФИФА. Однако существуют исключения для товарищеских матчей и других игр, не являющихся официальными спортивными соревнованиями.

Запасной игрок

Замены футболистов производятся из числа запасных игроков, предварительно указанных в официальной заявке на игру. В основной состав команды входят 11 игроков, количество игроков в запасе предусматривается правилами каждого отдельного турнира. Во время игры такие футболисты занимают место на скамейке запасных в технической зоне, то есть там же, где и располагается тренерский состав данной команды.

Интересно: запасных, показывающих отличные результаты игры и забивших несколько голов в ходе игры на замене, неофициально называют «суперзапасными».

История появления термина «запасной»

В Англии в 1860-х годах этот термин употреблялся в отчетной документации о футбольных матчах среди школьников. Но его значение было несколько иным: тогда «заменой» называлась замена футболиста, не пришедшего на игру. Использование этого термина в матчах между национальными сборными началось с 15 апреля 1889 года в официальной игре между сборными Уэльса и Шотландии.

До середины XX столетия правилами были запрещены замены футболистов на протяжении всей игры, а при травмировании игрока его удаляли с поля, и команда продолжала игру в неполном составе. С 1958 года были внесены изменения в футбольные правила, и с этого времени была разрешена замена травмированного голкипера, так же, как и одного игрока команды. При этом в менее значимых турнирах такие замены происходили уже с 1954 года.

Спустя 14 лет ФИФА увеличила число разрешенных замен еще на одного игрока, а количество игроков «запаса» было равно пяти. Позднее к двум заменам основных игроков добавили дополнительную – возможную замену вратаря (это произошло в 1994 году). В следующем же году число замен увеличили до трех.

В ходе летних Олимпийских игр 2016 года правилами соревнований была утверждена ещё одна замена в течение дополнительного времени игры. Такую замену ФИФА утвердила лишь к 2018 году, её было разрешено производить на мировых чемпионатах, в Лиге чемпионов, Лиге Европы УЕФА.

Исключительным в отношении правил, регламентирующих игру в футбол, стал 2020 год, период повышенного риска заболеваемости коронавирусом: в этот период количество разрешенных замен увеличили до 5.

Замена переменной в неопределённом интеграле

        Итак, друзья, продолжаем наше знакомство с базовыми методами интегрирования! В прошлых уроках мы порешали простенькие интегралы на прямое применение таблицы, а также познакомились с первым базовым методом интегрирования — подведением функции под знак дифференциала. С этого урока уже начнётся серьёзное интегрирование и не менее серьёзные примеры. Так что, у кого пока проблемы с простыми интегралами — читайте предыдущие темы, пока не поздно. 🙂 Почему? А потому, что в этом уроке мы резко расширяем наши возможности! А именно — знакомимся с одним из самых мощных методов интегрирования — методом замены переменной. 

        И в чём же заключается могущество сего метода? А в том, что в подавляющем большинстве случаев именно он позволяет превращать многие ужасные, на первый взгляд, примеры в белые и пушистые.) Например, интеграл с каким-нибудь страшным корнем или арксинусом после удачной замены может свестись к безобидному многочлену. Или к рациональной функции, которая всяко проще для интегрирования. Имеет смысл разобраться!

        Итак, начнём.)

 

Суть замены переменной. Простейшие примеры.

        Процедура замены переменной знакома всем вам ещё со школы. Например, решая жуткое тригонометрическое уравнение

        sin²x — 2sin x — 3 = 0,

что вы обычно делаете? Правильно! Вы заменяете выражение sin x новой буквой — y, z, t — какой хотите. И дальше работаете уже с более простым квадратным уравнением — дискриминант считаете, тыры-пыры…

        Всё то же самое и с интегралами.) Принцип тот же. Основная идея любой замены состоит в том, чтобы выражение, которое нам не нравится, заменить новой буквой. И все остальные части примера также выразить через эту самую новую букву. Тогда, если после всех преобразований пример упрощается, то, значит, основная цель данной замены выполнена. 🙂

        На прошлом уроке я уже говорил, что метод подведения функции под знак дифференциала — это простейший частный случай более общего метода замены переменной. Теперь настал черёд посмотреть, почему же это именно так и как работает сама процедура замены. Примеров в данном уроке будет не так много, но все они будут разобраны максимально подробно. Чтобы суть уловить.) Рассмотрим все проблемные места, исследуем каждую тонкость.

        Начнём сразу с примера. Чтобы далеко не ходить, давайте вернёмся к нашему самому первому примеру из прошлого урока.

        Пример 1

        Что мы делали в прошлый раз, когда решали этот пример? Сначала мы добивались равенства выражений в показателе экспоненты и под дифференциалом. Для этого мы сначала выражали новый дифференциал d(3x) через старый dx, а уже в самом конце вводили новую переменную 3х = t и сводили наш интеграл к табличному.

        Всё решение примера выглядело вот так:

        d(3x) = (3x)’dx = 3dx  

        dx = d(3x)/3

Вспомнили? Отлично!

        А теперь подойдём к данному примеру немного с другой стороны. Для начала вопрос: что вам больше всего не нравится в данном примере? 99 человек из 100 скажут: три икс! И будут правы. ) Вот и будем от этого самого 3х избавляться. Безопасно для самого примера.)

        Для этого поступаем просто и элегантно. Нам ведь в примере не нравится 3х, верно? Вот и заменяем это самое 3х новой буквой! Да-да! Прямо сразу! Безо всяких дифференциалов. Дифференциалы будут потом.)

        Так прямо и пишем:

        3x = t

        В результате данной замены наша подынтегральная функция превращается в простенькую табличную функцию e^t. И наш пример становится уже вот таким:

        Но для применения табличной формулы этого пока мало. Почему? А потому, что, раз уж мы ввели новую переменную t, то, ясное дело, и весь пример целиком также должен быть выражен через t! А у нас в примере пока что торчит старый дифференциал dx. Надо бы его тоже как-то превратить в dt. Как? Очень просто!

        Чтобы понять, во что же у нас превратится дифференциал dx, самым логичным было бы сначала выразить сам икс через новую переменную t. Здесь это проще простого. Для этого берём наше равенство 3x = t и выражаем из него икс через t. Вот так:

        Отлично. Полдела сделано.) И теперь, чтобы выразить интересующий нас дифференциал dx через букву t, просто берём дифференциалы от обеих частей нашего равенства. Думаю, для этой процедуры комментарии уже излишни:

        dx = d(t/3)

        Вот и всё. Вставляем теперь в наш пример вместо dx выражение dt/3, выносим дробь 1/3 за знак интеграла и дорешиваем по таблице. Чистовое оформление примера теперь выглядит немного по-другому. Вот так:

Как видите, ответ получился тем же самым. Что вполне логично.)

        Разберём ещё один пример с непосредственной заменой линейной конструкции. На закрепление.)

 

        Пример 2

        Напрашивается табличная формула с синусом:

        

        Только э-э-э… в формуле стоит просто икс, а в нашем примере под синусом стоит сложный аргумент 11х+5. Неувязочка… А что, если заменить этот сложный аргумент 11х+5 новой буквой? Ведь именно это выражение нам и не нравится! Посмотрим…

        На черновике так прямо и пишем вот такую заготовку:

           

        Отлично! sin(11x+5) превращается в sin t, а dx превращается в dt/11. Жизнь налаживается.) Не пример, а сплошное удовольствие)

 

        А теперь посмотрим на решение того же примера методом подведения выражения 11х+5 под дифференциал:

           

        Получили тот же самый ответ, но оформление всё же немного другое. Почувствовали разницу?

        В чём сходство этих двух способов? В том, что и там и тут мы заменяем новой буквой одно и то же выражение (в наших примерах это 3х и 11х+5). А отличие этих двух способов состоит лишь в том, на каком этапе решения вводится сама замена. Здесь мы сразу заменяем новой буквой то, что нам не нравится, потом связываем переменные старую с новой, а уж потом, в самом конце, находим связь и между их дифференциалами. А в методе подведения мы сначала связываем сами дифференциалы, а уже потом вводим замену. Или даже вообще не вводим, если уже «руку набили».:)

        Как видите, и так и сяк решать можно. Тем, кто крепко дружит с дифференциалами, рекомендую сразу решать подобные интегралы методом подведения. Ибо такое решение гораздо короче. А этот способ, с изначальной заменой, хорош для тех студентов, кто с дифференциалами пока того… не очень…) Или если пример достаточно накрученный. Но зато этот способ более понятен, универсален и надёжен! Спасает в любой ситуации. Если, конечно, удачно выбрана сама замена.)

        Это были самые простые примеры, где заменялась линейная конструкция — так, для разминки. Суть ясна, я думаю.)

        А теперь разберём примеры посерьёзнее. Такие, где надо заменять не линейные, а более сложные выражения и подвести функцию под дифференциал уже не так-то просто, хоть и возможно. Как и в прошлом уроке, суть этой группы примеров будет заключаться в выделении из подынтегральной функции f(x) какой-то вспомогательной функции g(x) и её производной g’(x). И последующей замене g(x) = t. Здесь уже надо уметь чувствовать и узнавать в функциях производные других функций. В лицо! Зачем? А чтобы удачно подобрать замену! Ведь можно и неудачно подобрать, да. Особенно если плохо знать таблицу производных. Об этом мы уже подробно поговорили на прошлом уроке.)

 

        Пример 3

        Внимательно осматриваем пример и ищем в подынтегральной функции конструкцию, которая нам больше всего не нравится. Вот тут, в отличие от предыдущих примеров, уже возможны варианты. Кому-то не понравится корень, кому-то сам по себе корень будет по душе, но не понравится выражение 5х²+1, стоящее под корнем. Отдельным индивидуумам может не понравиться множитель x… Что именно заменять — пока не знаем. Всматриваемся дальше. У нас есть подкоренная конструкция 5х²+1 и есть множитель х, отдалённо похожий на её производную, так как 

        (5х²+1)’ = 10х

        Именно это равенство и должно служить ключевой зацепкой!

        А не попробовать ли заменить наше сложное подкоренное выражение 5х²+1 новой буквой? Что ж, попробуем и посмотрим, к чему это приведёт. Итак, делаем замену:

5х²+1 = t

        Тогда наш корень после такой замены превратится в безобидную степенную конструкцию:

        

        Так, с корнем расправились. Но, помимо корня, под интегралом у нас ещё осталось произведение xdx, которое тоже надо выразить через новую букву t, да.

        Для этого немного схитрим. Не будем выражать «в лоб» икс через t, а затем искать dx. Это можно, но не нужно. Почему — объясню позже. Давайте сразу продифференцируем наше равенство для замены! Да-да! Целиком! Обе части. Вот так:

        5х²+1 = t           (это равенство — наша замена)

d(5х²+1) = dt     (дифференцируем обе части)

(5х²+1)’dx = dt   (раскрываем дифференциалы)

10xdx = dt

        И что нам даёт эта запись? А то, что из неё теперь легко выражается нужная нам конструкция xdx:

        Всё. Начинка интеграла теперь полностью выражена через t. Продолжаем наши игры.)

        Подставляем теперь все данные в наш пример и получаем простенький табличный интеграл от степенной функции (n = 1/3, n+1 = 4/3):

            

        Вот и все дела.) Пример разложили по полочкам. А можно ли решить данный интеграл через подведение под значок d? Можно! В одну строчку!

        Другое дело, что догадаться, какую именно конструкцию надо подводить под дифференциал, уже гораздо сложнее: легко запутаться в коэффициентах. И под силу не каждому студенту. Поэтому те, кто пока не наловчился в подведении функции под дифференциал — решаем подобные примеры сразу через замену. Аккуратно. Чуть длиннее, зато надёжнее.)

        А теперь ответ на вопрос, почему я не стал в явном виде выражать икс через t и затем находить dx. Не стал я этого делать по той причине, что наличие х² в подкоренном выражении резко усложняет эту процедуру из-за того, что возникают корни.

        Смотрите сами:

        Тогда для дифференциала этого самого икса мы получим:

        И, если теперь подставить в наш пример отдельные выражения для x и dx, то наши нехорошие корни благополучно сократятся и мы придём к тому же самому интегралу:

        Как видите, получили всё то же самое, только выкладки более громоздкие. Поэтому, по возможности, сокращаем объём работы: ошибок меньше будет. 🙂

        Иногда встречаются и сюрпризы, когда замену переменной приходится проделывать более одного раза. Ничего страшного! Просто аккуратно заменяем неудобную конструкцию и последовательно упрощаем пример, шаг за шагом добираясь до табличного интеграла. И, конечно, после получения результата корректно осуществляем обратную замену. От новой переменной к предыдущей.)

       

        Пример 4

        Что, внушает? Минутку смотрим на пример, ужасаемся, после чего берём себя в руки и вспоминаем золотое правило всей математики:

        Не знаешь, что нужно — делай, что можно!

        И размышляем. Примерно так:

        «Под интегралом нехорошая дробь. Сплошные синусы, аргументы разные — x и 2x. Да ещё и число «пи» затесалось… Кошмар! Но, очевидно, что чем больше одинаковых значков в примере и меньше разных, тем лучше. Поэтому первым делом упрощу-ка я синус двойного угла. По школьной формуле sin 2x = 2sin x·cos x. Поможет ли нам такое преобразование или нет — неясно. Но начинаем-то с самого простого! А там — видно будет.»

        Если вы мыслите примерно так, то вы движетесь правильным курсом. Да! Сводим всё подынтегральное выражение к одному аргументу — к иксу. Два икс тут явно ни к чему.

        Ну вот, уже лучше. В аргументах остались только иксы. А теперь снова пытаемся выявить родственные функции, опираясь на таблицу производных. Сразу же видно, что в получившейся дроби везде тусуются синусы, а в числителе в качестве множителя затесался косинус. Но косинус — ближайший родственник синуса! Родственник по производной. Ибо таблица производных гласит, что: 

        cos x = (sin x)’ .

        Поэтому вводим напрашивающуюся замену sin x = t и продолжаем упрощать наш злой пример:

        Отлично. Все синусы пропали напрочь, при этом суть примера не изменилась.

        А дальше что делать с этой дробью? Таблица-то не катит! Нету пока подходящей формулы… Тупик? Вовсе нет! Опять внимательно осматриваем нашу дробь, выявляя родню по производной/дифференциалу, и… радостно замечаем, что в числителе стоит дифференциал знаменателя!

        Вот так:

        Мы же понимаем, что под дифференциал мы имеем право спрятать любую константу! В том числе и «пи».)

        А вот теперь снова вводим замену! Да-да!

         

        Тогда вообще красота получится!

        Вот и всё. И нету больше никакого «пи»! Спряталось оно под дифференциал. Как и любая константа, да… А ведь как испугало в самом начале! 🙂 Пример становится всё лучше и лучше:

        Вот мы и свели ужасную дробь к безобидному табличному интегралу. По шагам, через две замены.) Но радоваться ещё рано, так как это ещё не ответ: нам икс нужен, а не z или t. Поэтому теперь последовательно проводим обратную замену. Тоже по шагам:

        z = t²+π, где t = sin x

        Итого z = sin²x + π.

        Всё. Теперь со спокойной душой записываем окончательный ответ нашего злого примера:

        Готово!

        С опытом необходимость так подробно всё расписывать отпадёт сама собой. За ненадобностью. И особо продвинутые студенты этот интеграл легко вычислят в одну строчку вообще без замены! С помощью подведения под дифференциал, ага:

        Быстро, правда? И вы тоже так сможете! Причём опыт нарабатывается достаточно скоро. Тренировка — залог успеха.)

        Ну как, прониклись? Замена переменной (вкупе с подведением под дифференциал) — оч-чень мощный инструмент для интегрирования! И золотой ключик к успешному решению самых разнообразных примеров. 🙂 Это было начальное знакомство с самой сутью замены, чтобы прочувствовать, как именно она работает.

        А со следующего урока мы уже начнём копать глубже и познакомимся с отдельными специфическими видами замен — степенной заменой и тригонометрической заменой. И типовые примеры тоже обязательно порешаем. Посерьёзнее.)

        А теперь несколько несложных примеров для тренировки.

 

        Найти неопределённые интегралы

        а) методом подведения функции под знак дифференциала,

        б) непосредственной заменой переменной,

        в) сравнить результаты и проверить ответ дифференцированием.

           

        Ответов здесь тоже не дам. Не вижу смысла. Примеры довольно простые, и материала сегодняшнего и прошлого уроков вполне достаточно для успешной расправы с ними. ) Проверяйте окончательный ответ обратным дифференцированием, не ленитесь! 🙂 Выучите таблицу производных! Узнавайте в лицо производные популярных функций. Да-да! Обратное дифференцирование — самый надёжный помощник в интегрировании.

        И тогда удача обязательно улыбнётся, поверьте! А у меня пока всё, продолжение следует!

Интеграция путем замены

«Интегрирование путем подстановки» (также называемое «u-подстановкой» или «правилом обратной цепочки») — это метод нахождения интеграла, но только тогда, когда его можно настроить особым образом.

Первый и самый важный шаг — записать наш интеграл в такой форме:

Обратите внимание, что у нас есть g(x) и его производная g'(x)

Как в этом примере:

Здесь f=cos , и у нас есть g=x ² и его производная 2x
Этот интеграл готов!

Когда наш интеграл настроен таким образом, мы можем сделать эту замену :

Затем мы можем проинтегрировать f(u) и закончить на , вернув g(x) обратно как u .

Вот так:

Пример: ∫cos(x

² ) 2x dx

Мы знаем (сверху), что это правильная форма для выполнения замены:

Теперь проинтегрируем:

∫cos(u) du = sin(u) + C

И, наконец, положим u=x ² обратно:

sin(x 9 0 2

Итак, ∫ cos(x ² ) 2x dx = sin(x

2 ) + C

Отлично получилось! (Ну, я так и знал.)

Но этот метод работает только с некоторыми интегралами , конечно, и может потребоваться перестановка:

Пример: ∫cos(x

² ) 6x dx

О нет! Это 6x , а не 2x , как раньше. Наша идеальная установка исчезла.

Никогда не бойся! Просто переставьте интеграл следующим образом:

∫cos(x ² ) 6x dx = 3∫cos(x ² ) 2x dx

(Мы можем вывести постоянные множители вне интегрирования, см. Правила интегрирования.)

Тогда действуйте как раньше:

3∫cos(u) du = 3 sin(u) + C

Теперь поставьте u=x ² обратно:

3 sin(x ² ) + C

Готово!

Теперь давайте попробуем более сложный пример:

Пример: ∫x/(x

² +1) dx

Позвольте мне посмотреть. .. производная от x ² +1 равна 2x… как насчет того, чтобы переставить ее следующим образом:

∫x /(x ² +1) dx = ½∫2x/(x ² +1) dx

Тогда имеем:

Затем проинтегрируем:

½∫1/u du 9 = 008 ln | и | + C

Теперь поставьте u=x ² +1 обратно:

½ ln(x ² +1) + C

А как насчет этого:

Пример: ∫(x+1)

³ dx

Позвольте мне посмотреть… производная от x+1 равна… ну, это просто 1.

Итак, мы можем получить это:

∫(x +1) ³ DX = ∫ (x+1) ³ · 1 DX

, затем мы имеем:

Затем интегрируйте:

∫U ³ DU = U ⁴ 4 4. + C

Теперь поместите u=x+1 обратно:

(x+1) ⁴ 4 + C

Мы можем развить эту идею следующим образом:

Пример: ∫(5x+2)

⁷ dx

Если бы это было в ЭТОЙ форме, мы могли бы это сделать:

∫(5x+2) ⁷

5 dx

Итак, давайте сделаем так, сделав это это:

1 5 ∫(5x+2) ⁷ 5 dx

1 5 и 5 сокращаются, так что все в порядке.

And now we can have u=5x+2

And then integrate:

1 5 ∫u ⁷ du = 1 5 u ⁸ 8 + C

Теперь снова поместите u=5x+2 и упростите:

(5x+2) ⁸ 40 + C

А теперь потренируйся, хорошо?

Когда мы можем представить интеграл в такой форме:

Тогда мы можем положить u=g(x) и проинтегрировать ∫f(u) du

И закончите повторной вставкой

g(x) , где u .

 

 

линейная алгебра — Объяснение обратной замены в исключении Гаусса

спросил 6 лет, 7 месяцев назад

Изменено 6 лет, 7 месяцев назад

Просмотрено 2к раз

$\begingroup$

Я не уверен, что обратная подстановка делает с исключением Гаусса. ..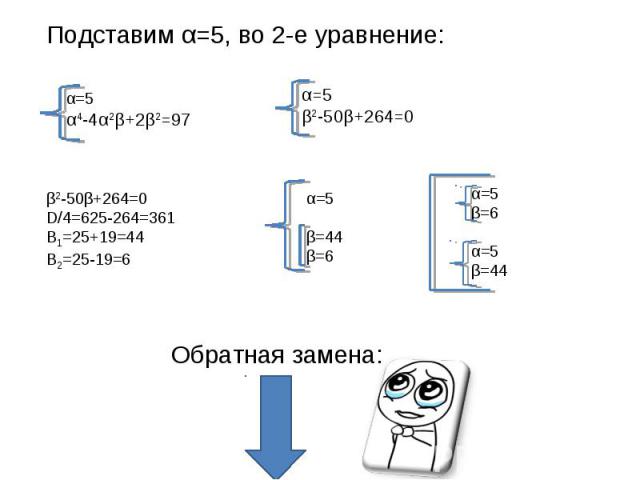

Я понимаю, как она пытается получить верхнюю треугольную матрицу с нулями под диагональю, и поэтому я понимаю, почему мы’ re делает row2 — 4/2 row1 и т. д.

Я просто не понимаю обратную подстановку, например, зачем делать (-2)/2, чтобы получить x3, зачем делать (3-(-3)x3/3, чтобы получить x2 и т. д., например, откуда берутся эти цифры и почему.0003

Мне просто хотелось бы знать, почему книга делает то, что она делает, но на самом деле она не объясняла, что она делала, чтобы получить x3, x2, x1.

• линейная алгебра
• алгоритмы
• исключение Гаусса

$\endgroup$

$\begingroup$

Последняя матрица представляет следующую систему (которая эквивалентна исходной системе): $$\begin{выравнивание} 2x_1 -x_2 +x_3 &= 1 \\ 3x_2 — 3x_3 &=3\ 2x_3 &= -2 \end{выравнивание}$$

Теперь логика обратной замены должна быть понятна. Мы неоднократно подставляем найденные значения (или выражения) для $x_{i+1}, x_{i+2} \ldots x_{n}$ обратно в уравнение, содержащее $x_i$, пока не будут решены все переменные для: $$\begin{выравнивание} x_3 &= \frac{-2}{2} = -1 \\ x_2 &= \frac{3+3x_3}{3} = \frac{3+3(-1)}{3} = 0\\ x_1 &= \frac{1+x_2-x_3}{2} = \frac{1 + 0 -(-1)}{2} = 1 \end{align}$$

$\endgroup$

$\begingroup$

Термин «обратная подстановка» означает именно это: подставьте $x_3 = -1$ обратно в два других исходных уравнения (или эквивалентную систему, заданную последней матрицей после сокращения строк), чтобы найти другие переменные.