Олимпиада по математике 10 класс
Олимпиада по математике 10 класс с решением и ответами
- Вар-т 1
Вар-т 2
Задача 1 :
Докажите, что уравнение x4– 4x3 + 12x2 – 24 x + 24 = 0 не имеет решений.
Задача 2 :
Докажите, что в ходе любого сыгранного футбольного матча был момент, когда одна из команд забила голов столько же, сколько другой осталось забить.
Задача 3 :
Хорда удалена от центра окружности на расстояние h. В каждый из двух сегментов круга, стягиваемый этой хордой, вписан квадрат так, что пара его соседних вершин лежит на хорде, а другая пара соседних вершин – на соответствующей дуге окружности.
Найдите разность длин сторон квадратов.Задача 4 :
Найдите многочлен с целочисленными коэффициентами, корнем которого является число √2 + √3.
Решение олимпиадных заданий по математике для 10 класса
Задача 1 :Уравнение x4 – 4x3 + 12x2 – 24x + 24 = 0 преобразовать к виду (x2 – 2x)2 + 8(x – 1,5)2 + 6 = 0, которое не имеет решений.

Задача 2 :
Пусть первая из команд забила за весь матч m голов, вторая n голов. Сумма числа голов в ходе матча изменяется с шагом 1 от 0 до m + n , значит, в какой-то момент она будет равна m. Данный момент и будет искомым в задаче, потому что при этом число голов, уже забитых второй командой, равно разности m и числа голов, уже забитой первой командой, т. е. числу голов, которое еще предстоит забить первой команде. Аналогично можно рассуждать и с первой командой.
Задача 3 :
Обозначим длины сторон большого и малого квадратов через 2х и 2у соответственно, радиус окружности – через R. Тогда расстояния от центра окружности до вершин вписанных квадратов, лежащих на окружности дают выражения (2 – h)2 + x2 = R2, (2y + h)2 + y2 = R2. Отсюда получим x — y = (4/5)h. Тогда, разность длин сторон квадратов будет равна (8/5)h.
Задача 4 :
Обозначим √2 + √3 =a.
Тогда a2 = 5 + 2 √6, а a2 – 52 = 2 √. 62 или a 4 – 10a2 + 25 = 24, которое равносильно a4 – 10a2 + 1 = 0.
62 или a 4 – 10a2 + 25 = 24, которое равносильно a4 – 10a2 + 1 = 0.
А это и означает, что а является корнем многочлена
x4 – 10x2 + 1.
Задача № 1 :Решите уравнение:
(x — 2)(x — 3)(x + 4)(x + 5) = 1320.
Задача № 2 :
На плоскости дан отрезок АВ.
Где может быть расположена точка С, чтобы угол АВС был остроугольным?
Задача № 3 :
Найти все натуральные числа, оканчивающиеся на 2006,
которые после зачеркивания последних четырех цифр уменьшаются в целое число раз.
Задача № 4 :
Вычислить сумму a2006 + 1/a2006, если a2– a + 1 = 0.
Задача № 5:
Лист бумаги разрезали на 5 частей, некоторые из этих частей разрезали на 5 частей, и т. д.
Может ли за некоторое число разрезаний получиться 2006 листка бумаги?
Решение задач :
Задача № 1 :
Ответ: -8; 6.
Задача № 2 :
Построим на АВ как на диаметр окружность и проведем через А и В две прямые, перпендикулярные отрезку АВ.
Точка С может находится между этими прямыми вне круга.
Задача № 3 :
Пусть натуральные числа имеют вид x•10000 + 2006, где x € N. После вычеркивания последних цифр получим число x.
По условию, где n € N. Отсюда имеем, что должно быть натуральным числом, т. е. x — делитель числа 2006.
Число 2006 имеет делители: 1; 2; 17; 34; 59; 118; 2006.
Следовательно, имеются числа, отвечающие условию задачи: 12006; 22006; 172006; 342006; 592006; 1182006; 20062006.
Задача № 4 :
Так как a<>0, то, разделив обе части исходного уравнения на a, получим a + 1/a = 1.
Заметим, что a3 + 1 = 0, т. к. a3 + 1 = (a + 1)(a2 – a + 1).
Таким образом, a3 = -1. Тогда a2006 + 1/a2006 = (a3)6682 = a2 + 1/a2 = — 1.
Задача № 5 :
Замечаем, что при каждом разрезании из одного листка получаем пять, т. е. число листков увеличивается на 4.
е. число листков увеличивается на 4.
Следовательно, из исходного листа может получиться число листков вида 1 + 4n, где n € N,
т. е. это число при делении на 4 дает остаток 1.
Но 2006 = 4•501 + 2. Следовательно, 2006 листков получиться не может.
Примеры олимпиадных заданий с решением по математике для 10 класса
Задача 1.На базаре продаются рыбки, большие и маленькие. Сегодня три больших и одна маленькая стоят вместе столько же, сколько пять больших вчера. А две большие и одна маленькая сегодня стоят вместе столько же, сколько три больших и одна маленькая вчера.
Можно ли по этим данным выяснить, что дороже: одна большая и две маленьких сегодня, или пять маленьких вчера.
Решение
Обозначим «рыбные цены»: сегодня большая рыба стоит bc, а маленькая mc. Вчера большая стоила bv, а маленькая — mv.
Тогда из условий задачи имеем два уравнения
3bc + mc = 5bv, 2bc + mc = 3bv + mv.
Отсюда получаем:
5mv = (2bc + mc — 3bv)5 = 10bc + 5mc — 3(3bc + mc) = bc + 2mc.
То есть пять маленьких вчера стоили столько же, сколько одна большая и две маленькие сегодня.
Задача 2
Несколько ящиков вместе весят 10 тонн, причем каждый из них весит не более одной тонны.
Сколько трехтонок заведомо достаточно, чтобы увезти этот груз?
Решение
Покажем, что пяти машин заведомо достаточно. Будем грузить машины ящиками в любом порядке до тех пор, пока ящики не кончатся, следя лишь за тем, чтобы не наступила «перегрузка» машины. Это возможно, так как в любой момент погрузки будет хотя бы одна машина, загруженная не более чем двумя тоннами. Действительно, если бы все машины были загружены больше, чем на две тонны, то общий вес груза составлял бы больше, чем 5 2т = 10т, что противоречит условию задачи. Эту машину можно догрузить любым ящиком, поскольку по условию задачи он весит не более тонны. Осталось показать, что четырех машин может не хватить. Например, для вывоза 13 ящиков весом т каждый, четырех машин недостаточно. Действительно, каждая машина может увезти не более трех таких ящиков, так как четыре ящика весят т > 3т. Значит, все машины увезут не больше 12 ящиков.
Осталось показать, что четырех машин может не хватить. Например, для вывоза 13 ящиков весом т каждый, четырех машин недостаточно. Действительно, каждая машина может увезти не более трех таких ящиков, так как четыре ящика весят т > 3т. Значит, все машины увезут не больше 12 ящиков.
Олимпиадные задания по математике для 10 класса
1. Между числами 4/7 и 5/7 найти натуральное число, являющееся квадратом рационального числа.
2. Разложить многочлен x5
3. Вершины D, Е и F треугольника DEF лежат на продолжениях сторон АВ, ВС и СА треугольника ABC за вершины В, С и А соответственно. Известно, чти BD = AC, AF = CE = AB и треугольник DEF — равносторонний. Докажите, что и треугольник ABC — равносторонний.
4. Докажите, что в пятиугольнике, все углы и стороны которого равны, сумма расстояний от произвольной внутренней точки до сторон не зависит от выбора этой точки.
5. Волк и Заяц играют в следующую игру: на доске написано число; ход состоит в том, чтобы вычесть из этого числа какую-либо его ненулевую цифру и записать получившееся число на месте старого.
Ходят по очереди.
Выигрывает тот, кто первым получает ноль.
На доске исходно написано число 1234, первым ходит Волк.
Вар-т 1 Вар-т 2
Олимпиадные задачи по математике. 10 класс. Ответы.
Главная / Математика / Олимпиадные задачи /
1.Графики функций у = х2 + ах + b и у = х2 + сх + d пересекаются в точке с координатами (1; 1). Сравните a5 + d6 и c6— b5.
2.Какое наибольшее число ребер шестиугольной призмы может пересечь плоскость, не проходящая через вершины призмы?
3.Решите уравнение :
4.Докажите, что если стороны треугольника образуют геометрическую прогрессию, то их высоты тоже образуют геометрическую прогрессию.
5.В клетки квадрата 3 ? 3 требуется вписать девять различных натуральных чисел так, чтобы все они не превосходили n, и чтобы произведения чисел в каждой строке и каждом столбце были равны. При каком наименьшем n это возможно?
Ответы.
1.a5 + d6 = c6 – b5.
Так как графики функций проходят через точку (1; 1), то выполняются равенства: 1 = 1 + а + b и 1 = 1 + с + d, то есть, a = -b и с = -d. Следовательно, а5 = -b5 и d6 = c6. Складывая эти неравенства почленно, получим, что а5 + d6 = c6 – b5.
2. Горизонтальной плоскостью можно пересечь все 6 боковых ребер. Наклоним эту плоскость так, чтобы она пересекла верхнее основание около одной из вершин. Ясно, что при этом она станет пересекать два ребра в верхнем основании, но перестанет пересекать одно из боковых ребер. Таким образом, мы увеличим число пересеченных ребер на 1.
Точно также можно увеличить это число еще на 1 за счет ребер нижнего основания. Так мы получили плоскость, пересекающую 8 ребер призмы.
Так мы получили плоскость, пересекающую 8 ребер призмы.
3. Умножим числитель и знаменатель каждой дроби на выражение, сопряженное знаменателю:
4. Пусть стороны треугольника равны b, bq, bq2, площадь треугольника S, тогда высоты треугольника соответственно равны: 2S/b, 2S/bq, 2S/db2, то есть тоже образуют геометрическую прогрессию.
5. Покажем, что n = 14 слишком мало. Среди чисел 1, 2, …, 14 только 2 делятся на 5 (5 и 10), поэтому их нельзя использовать (не во всех строках произведение будет делиться на 5). По тем же соображениям нельзя использовать числа 7 и 14. Тем более, нельзя использовать числа 11 и 13.
| 5 | 12 | 2 |
| 3 | 10 | 4 |
| 8 | 1 | 15 |
Вас может это заинтересовать
Написать комментарий
Обсуждения
Олимпиадные задания по литературе. 9 класс. Ответы…
JRKFHYYYYYCD login2:Олимпиадные задания по литературе. 9 класс. Ответы…
CJGJEYJFKGTB login:Олимпиадные задания по литературе. 9 класс. Ответы…
Martinlix:Тест по теме «Классификация химических реакций»
Олина:Олимпиадные задания по литературе. 9 класс. Ответы…
casino:
10 класс Английский язык: Математика — Электронный класс
- [электронная почта защищена]
- +27 (0)21 785 1214
Ресурсы для рабочих листов $40/год
- Дом
- Оценки
- 10 класс
- Английский
- Математика
Тесты 2 Алгебраические выражения 14 Уравнения и неравенства 6 Экспоненты 2 Факторинг 6
Пробные экзамены 4 Евклидова геометрия 6 Функции 10 Тригонометрия 16
Аналитическая геометрия 10 Финансовая математика 8 Измерение 2 Статистика 8
Экзаменационные работы и исправления 14 Вероятность 6
Dbe Прошлые документы
Прошлые документы и заметки 4Ресурсы Касио 23
Загрузка. ..
..
[PDF] Сравнение решения нестандартных задач учащимися 10–12 классов по математике
- title={Сравнение решения нестандартных задач учащимися 10–12 классов по математике},
автор={Давид Могари и Муньярадзи Чирове},
journal={Евразийский журнал по математике, естественным наукам и технологиям},
год = {2017},
объем = {13},
страницы={4523-4551}
}
- Д. Могари, Муньярадзи Чирове
- Опубликовано 21 июля 2017 г.
- Образование
- Евразийский журнал по математике, естественно-научному и техническому образованию
Исследование, основанное на более крупном исследовании, сравнивает учащихся 2-х и 10-х классов математики. «Решение нестандартных задач. Было проведено предварительное исследование на удобной выборке из трех высокоэффективных средних школ, расположенных в Северном округе Тшване, провинция Гаутенг, Южная Африка. Учащиеся написали нестандартный тест на решение задач.
 Результаты показали, что учащиеся 11-х классов получили самый высокий средний балл, а учащиеся 10-х классов — самый низкий. Средняя школа…
Результаты показали, что учащиеся 11-х классов получили самый высокий средний балл, а учащиеся 10-х классов — самый низкий. Средняя школа… Исследование стратегий учащихся средней школы при решении рутинных и нестандартных задач
Целью данного исследования является определение ситуаций учащихся средней школы при решении рутинных и нестандартных задач и стратегий, которые они используют при решении этих задач . Исследование…
Выявление способностей к решению задач по математике у учащихся младших классов средней школы
- Сяйфул С., Камид Камид, Муслим М., Худа Н.
Образование
- 2020
Цель: Это исследование направлено на выявление способностей решать проблемы, которыми обладают учащиеся младших классов средней школы. Используемый тип исследования является количественным, в котором используется опрос по дизайну исследования. Образец…
Эвристика решения задач и математические способности разнородных учащихся
Описательный дизайн использовался для определения эвристики решения задач и математических способностей учащихся при решении нестандартных задач с точки зрения концептуального понимания, процедурных…
Связь между эвристическим подходом к решению задач активного обучения и отношением учащихся к математике
- Роберт Вахата, Ведасте Мутарутинья, Суди Балимуттайо
Образование, бизнес
Eurasia Journal of Mathematics, Science and Technology Education
- 8
- Талиха Келеш, Елиз Язган
Образование
- 2021
- Nurdan Özreçberoğlu, Çağda Kıvanç Çağanağa
Education
- 2018
- Роуз Р. Андраде, Аллен Э. Пасиа
Образование
- 2020
- Цзинь Сун, Хань Цинь, Керри Ли, Альфредо Баутиста, Цяопин Чжан
Образование
Математика
- 2021
- Роберт Вахата, Суди Балимуттайо, Ведасте Мутарутинья
Образование, бизнес
bioRxiv
- 2022
- Д. Могари, Нхланхла Лупахла
Образование
- 2013
- Чигдем Арслан, Мурат Алтун
Образование
- 2007
- Рина А. Мабиланган, А. Лимджап, Рене Р. Белечина
Образование
- 2011
- Марья ван ден Хойвель-Панхуйзен, Анжелики Колову, А. Робич
Образование
- 2013
- С. Бансилал, Д. Бриджлалл , T. Mkhwanazi
Образование
- 2014
- Кобус Мари, К.
 Олдос, А. Хаттинг, А. Свейнпол, М.В. Восемьсот девяносто девять (431 мальчик, 467 девочек и одно пропущенное значение) 8-х и 9-х классов (n = 184 и 713, соответственно, с двумя пропущенными значениями) учащихся средних школ в Мпумаланге…
Олдос, А. Хаттинг, А. Свейнпол, М.В. Восемьсот девяносто девять (431 мальчик, 467 девочек и одно пропущенное значение) 8-х и 9-х классов (n = 184 и 713, соответственно, с двумя пропущенными значениями) учащихся средних школ в Мпумаланге…Шестиклассники и нерегулярные Проблемы: какие стратегии являются решающими для успеха?.
- Елиз Язган
Образование
- 2015
В этом исследовании изучалась роль каждой стратегии в объяснении успеха шестиклассников (учащихся 12-13 лет) в решении нестандартных задач и в различии между успешным и неудачным …
Изучение использования стратегии и гибкости стратегии при решении нестандартных задач учащимися начальной школы, достигшими высоких результатов по математике
- И. Элиа, Марья ден Хойвель-Панхуизен, Анжелики Коловоу
Образование, бизнес
- 2009
Многие исследователи исследовали гибкость стратегий в различных областях математики.

Eurasia Journal of Mathematics, Science and Technology Education
- 8
В ходе исследования была изучена прямая связь между активным обучением, эвристическим подходом к решению задач и отношением учащихся к математике с использованием словесных задач линейного программирования (ЛП).
 Два…
Два…Стратегическая гибкость одаренных учащихся восьмого, девятого, десятого и одиннадцатого классов при решении нестандартных задач
Резюме успех и стратегическая гибкость в решении нестандартных задач. Учебная группа состояла из 50 одаренных студентов. Тест…
Различия в типах школ между учащимися четвертого класса из сельской местности Успеваемость учащихся четвертого класса из Малайзии в решении математических задач, требующих навыков мышления более высокого порядка
Культурное разнообразие Малайзии уступает место трем типам государственных начальных школ, различающихся культурными особенностями и методами обучения. This study aimed to explore the difference between…
Making it count: Strategies for improving problem-solving skills in mathematics for students and teachers’ classroom management
Понимание проблемы так же важно, как и ее решение, чтобы понять значение математики.
 Широко распространено мнение, что навыки решения проблем помогают людям легко преодолевать проблемы в…
Широко распространено мнение, что навыки решения проблем помогают людям легко преодолевать проблемы в…Математическое творчество будущих учителей при решении нестандартных задач в Государственном университете в Лагуне
9 цели системы математического образования. Математическое творчество рассматривается как продукт и процесс. Точно так же это варьируется среди людей. The…
Раннее изучение и преподавание математики в дошкольных учреждениях Китая: анализ содержания учебных пособий для учителей дошкольных учреждений
С 1980-х годов было обнаружено, что дети из разных стран стабильно хорошо успевают по китайскому языку исследования академических достижений.
 Это исследование является одним из первых, в котором систематически…
Это исследование является одним из первых, в котором систематически…Взаимосвязь между отношением учащихся к математическим задачам и успеваемостью в них
В исследовании изучалась прямая и косвенная связь между отношением учащихся к математическим текстовым задачам (MWT) и их успеваемостью, опосредованная эвристической задачей активного обучения…
ПОКАЗЫВАЕТСЯ 1-10 ИЗ 41 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантность Наиболее влиятельные документыНедавность
Составление карты группы жителей Северной Намибии 12 класс Алгебраические навыки учащихся в решении нестандартных задач
В этой статье исследуются навыки решения алгебраических нестандартных задач учащимися 12-го класса школы в северной Намибии.
 Школа была выбрана на основе ее выдающихся…
Школа была выбрана на основе ее выдающихся…Обучение решению нестандартных математических задач
Обсуждается пробное исследование, предназначенное для поощрения учащихся седьмого и восьмого классов к изучению и использованию стратегий решения проблем, которые состоят из шести эвристических стратегий, известных как «Упростить задачу», «Угадать и проверить», «Найти закономерность», «Создать рисунок», «Сделать систематический анализ». Список и работа в обратном направлении.
Стратегии решения нестандартных задач старшеклассниками
Исследование того, насколько хорошо некоторые учащиеся средней школы университета решают нестандартные задачи, требовало использования их концептуального понимания математики и процедурных знаний алгоритма, задействованного в решении, показало, что каждый учащийся использовал не менее четырех задач.
 -решающие стратегии.
-решающие стратегии.Стратегии учащихся начальных классов в решении задач по начальной алгебре при поддержке онлайн-игры
В этом исследовании мы исследовали роль динамической онлайн-игры в решении задач по начальной алгебре учащихся. В общей сложности 253 ученика 4, 5 и 6 классов (10–12 лет) использовали игру дома, чтобы…
Изучение общего содержания знаний учителей математики средней школы
Многие исследования указывают на проблему плохого знания содержания математики учителями математики в Южной Африке. Целью данного исследования было изучить знания учителей по математике…
Предикторы успеваемости учащихся по математике и естественным наукам в соответствии с крупномасштабным исследованием, проведенным в Мпумаланге


 62 или a 4 – 10a2 + 25 = 24, которое равносильно a4 – 10a2 + 1 = 0.
62 или a 4 – 10a2 + 25 = 24, которое равносильно a4 – 10a2 + 1 = 0.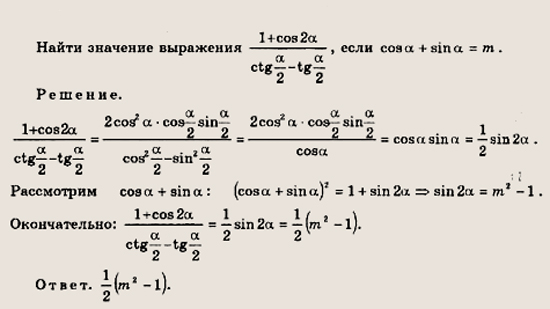 Результаты показали, что учащиеся 11-х классов получили самый высокий средний балл, а учащиеся 10-х классов — самый низкий. Средняя школа…
Результаты показали, что учащиеся 11-х классов получили самый высокий средний балл, а учащиеся 10-х классов — самый низкий. Средняя школа…  Два…
Два… Широко распространено мнение, что навыки решения проблем помогают людям легко преодолевать проблемы в…
Широко распространено мнение, что навыки решения проблем помогают людям легко преодолевать проблемы в… Это исследование является одним из первых, в котором систематически…
Это исследование является одним из первых, в котором систематически… Школа была выбрана на основе ее выдающихся…
Школа была выбрана на основе ее выдающихся… -решающие стратегии.
-решающие стратегии. Олдос, А. Хаттинг, А. Свейнпол, М.В. Восемьсот девяносто девять (431 мальчик, 467 девочек и одно пропущенное значение) 8-х и 9-х классов (n = 184 и 713, соответственно, с двумя пропущенными значениями) учащихся средних школ в Мпумаланге…
Олдос, А. Хаттинг, А. Свейнпол, М.В. Восемьсот девяносто девять (431 мальчик, 467 девочек и одно пропущенное значение) 8-х и 9-х классов (n = 184 и 713, соответственно, с двумя пропущенными значениями) учащихся средних школ в Мпумаланге…