Задачи по математике 11 класс с ответами и решением: Национальный исследовательский университет «Высшая школа экономики»

Задачи повышенной сложности по математике 10

Задачи повышенной сложности по математике 10 — 11 класс с решением и ответами.

Задача 1.

Найдите все простые числа p и q такие, что p + q = (p – q)³.

Решение:

Ответ: p = 5, q = 3.
Пусть p – q = n, тогда p + q = n³.

Отсюда  .

Среди трех последовательных целых чисел одно делится на 3, поэтому q делится на 3. Среди простых чисел только 3 делится на 3. Значит, q = 3. Это значение q получается при n = 2.

Задача 2.

Приведенный квадратный трехчлен f(x) имеет 2 различных корня.
Может ли так оказаться, что уравнение f(f(x)) = 0 имеет 3 различных корня, а уравнение f(f(f(x))) = 0 — 7 различных корней?

Решение:

Ответ: Нет.
Из условия следует, что f(x) = (x – a)(x – b), где a ≠ b.
Пусть искомый многочлен f(x) существует.
Тогда, очевидно f(f(x)) = (x – t₁)²(x – t₂)(x – t₃).
Заметим, что t₁, t₂, t₃ — корни уравнений f(x) = a и f(x) = b, при этом корни этих уравнений не совпадают, поэтому можно считать, что уравнение f(x) = a имеет один корень x = t₁.
Рассмотрим уравнение f(f(f(x))) = 0. Его решения, очевидно, являются решениями уравнений f(f(x)) = a и f(f(x)) = b. Но уравнение f(f(x)) = a равносильно уравнению f(x) = t₁ и имеет не более двух корней, а уравнение f(f(x)) = b — не более четырех корней (как уравнение четвертой степени).
То есть уравнение f(f(f(x))) = 0 имеет не более 6 корней.

Задача 3.

Пусть AD — биссектриса треугольника ABC, и прямая l касается окружностей, описанных около треугольников ADB и ADC в точках M и N соответственно.
Докажите, что окружность, проходящая через середины отрезков BD, DC и MN, касается прямой l.

Решение:

Решение 1.
Обозначим центры окружностей, описанных около треугольников ADB и ADC через O₁ и O₂, а середины отрезков BD, DC, MN, DO₂ и O₁O₂ — через A₁, A₂, K, E и O соответственно (см. рис.). Пусть  ∠ BAD =  ∠ CAD =  α . Тогда  ∠ A₁O₁D =  ∠ A₂O₂D =  α  (так как половина центрального угла равна вписанному, опирающемуся на ту же дугу). Отрезок OK — средняя линия трапеции (или прямоугольника) O₁MNO₂, следовательно, OK ⊥ l, и  . Заметим, что точки E, O и A₂ лежат на одной прямой, так как  ∠ OEO₂ +  ∠ O₂EA₂ =  ∠ O₁DO₂ +  ∠ O₂EA₂ =  ∠ O₁AO₂ + (180° –  ∠ DO₂C) = 2 α  + (180° – 2 α ) = 180°, т.е. OK = OE + EA₂ = OA₂. Аналогично доказывается, что OA₁ = OK. Значит, точки A₁, A₂ и K лежат на окружности с центром O, а так как OK ⊥ l, то эта окружность касается прямой l.

Случай, когда вместо прямой l рассматривает-ся прямая l₁, разбирается аналогично.

Решение 2.
Пусть радиусы окружностей, описанных около треугольников ADB и ADC равны R₁ и R₂. Если эти радиусы различны, то прямая l пересекает линию центров O₁O₂ в точке O (см. рис.). Пусть OD пересекает окружности в точках B′ и C′, и OA пересекает  ω  в точке A′. При гомотетии H с центром O и коэффициентом   точки C′, D и A переходят в точки D, B′ и A′ соответственно, следовательно,  ∠ DAC′ =  ∠ B′A′D. С другой стороны,  ∠ B′A′D =  ∠ B′AD, поэтому  ∠ B′AD =  ∠ C′AD. А это означает, что точки B′ и C′ совпадают с точками B и C, так как в противном случае один из углов BAD и CAD был бы меньше  α , а другой — больше  α  ( α  =  ∠ B′AD =  ∠ C′AD).

Рассмотрим гомотетию H₁ с центром O, переводящую  ω ₂ в окружность  ω , проходящую через точку E — середину отрезка MN. Из того, что l проходит через точку O и  ω ₂ касается l, следует, что  ω  касается l в точке E. Кроме того, из гомотетичности треугольников ONC и OMD (гомотетия H) следует, что NC || MD. Кроме того, H₁(C) = C₁, где EC₁ || NC. Поэтому EC₁ — средняя линия трапеции CNMD, т. е. гомотетия H₁ переводит точку C в середину DC. Аналогично, она переводит D в середину отрезка BD. Значит,  ω  проходит через середины отрезков BD и DC.

Если же R₁ = R₂, то вместо гомотетии следует рассмотреть параллельный перенос на вектор  .

Решение 3.
Пусть R₁ ≠ R₂. Проведем перпендикуляр SO к плоскости  π , содержащей окружности  ω ₁ и  ω ₂ (см. обозначения в предыдущем решении). Нетрудно понять, что пересечение (наклонного) конуса с вершиной S и основанием  ω ₁ и прямого кругового цилиндра с основанием  ω ₂ является окружность, равная  ω ₂ и лежащая в плоскости  π ₁ ||  π . Глядя на рис., заключаем, что ортогональной проекцией на плоскость  π  пересечения конуса и плоскости, равноудаленной от  π  и  π ₁ является окружность, проходящая через середины отрезков BD, DC и MN и касающаяся прямой MN.

В случае R₁ = R₂ вместо конуса следует рассмотреть (наклонный) цилиндр с основанием  ω ₁.

Задача 4.

Дана последовательность x_k такая, что x₁ = 1, x_n + 1 = n sin x_n + 1.
Докажите, что последовательность непериодична.

Решение:

Предположим, что она периодична и длина периода равна T, тогда x_m + T = x_m и x_{m + T + 1} = x_m + 1 при m ≥ m₀.
Если при некотором m ≥ m₀  sin x_m ≠ 0, то x_{m + T + 1} = (m + T) sin x_m + T + 1 = (m + T) sin x_m + 1 ≠ m sin x_m + 1 = x_m + 1.
А если  sin x_m = 0, то x_m + 1 = 1, и  sin x_m + 1 =  sin 1 ≠ 0, так что предыдущее рассуждение применимо к x_m + 1.
Таким образом получаем противоречие.

Задача 5.

Докажите, что если у тетраэдра два отрезка, идущие из вершин некоторого ребра, в центры вписанных окружностей противолежащих граней, пересекаются, то отрезки, выпущенные из вершин скрещивающегося с ним ребра в центры вписанных окружностей двух других граней, также пересекаются.

Решение:

Пусть A₁ — центр вписанной окружности  ∆ SBC, B₁ — центр вписанной окружности  ∆ SAC, AA₁ пересекается с   A, A₁, B₁, B лежат в одной плоскости, значит прямые AB₁ и BA₁ пересекаются на ребре SC. Пусть точка пересечения этих прямых — p. Так как Ap и Bp — биссектрисы углов A и B, то  . Но тогда AC • BS = BC • AS, отсюда  , следовательно биссектрисы углов S в  ∆ ASB и C в  ∆ ACB пересекаются на ребре AB, т.е. точки S, C и центры вписанных окружностей  ∆ ASB и  ∆ ACB лежат в одной плоскости. Отсюда следует, что отрезки, соединяющие вершины S и C с центрами вписанных окружностей противолежащих граней, пересекаются.

Задача 6.

На плоскости дано бесконечное множество точек S, при этом в любом квадрате 1 × 1 лежит конечное число точек из множества S. Докажите, что найдутся две разные точки A и B из S такие, что для любой другой точки X из S выполняется: |XA|,\;|XB| ≥ 0,999|AB|.

Решение:

Докажем утверждение задачи от противного.
Можно предположить, что для любых двух разных точек A и B из S найдется отличная от них точка X из S такая, что либо XA  Переформулируем вышеприведенное утверждение: для любого отрезка I с концами в S и длиной l найдется отрезок I′ с концами в S длины не более 0,999l, один из концов которого совпадает с некоторым концом I.
Или, иначе говоря, I′ пересекает I.
Возьмем теперь первый отрезок I₁ длины l и будем брать отрезки I₂, I₃, …так, что I_k + 1 пересекается с I_k и |I_k + 1| _k|.
Все эти отрезки имеют концы в S. Ломаная не короче отрезка, соединяющего ее концы, поэтому расстояние от любого конца I_k до любого конца I₁ не превосходит

Следовательно, в квадрате 2000l × 2000l с центром в любом из концов I₁ лежит бесконечное число точек S.
Но из условия следует конечность их числа в любом квадрате.

Полученное противоречие завершает доказательство.

Задача 7.

Докажите, что в любом множестве, состоящем из 117 попарно различных трехзначных чисел, можно выбрать 4 попарно непересекающихся подмножества, суммы чисел в которых равны.

Решение:

Лемма.
Из любых 61 различных трехзначных чисел можно выбрать две непересекающиеся пары чисел, суммы в которых равны.
Доказательство:
Из 61 числа можно образовать   пар чисел, сумма чисел в каждой паре лежит между 200 и 2000, следовательно, у каких-то двух пар суммы совпадают.
Пары, для которых совпадают суммы, очевидно, не могут пересекаться, ибо если x + y = x + z, то y = z и пары совпадают.
Лемма доказана.
Выберем пару пар чисел с равными суммами 15 раз (каждый раз будем исключать из рассматриваемого набора 4 взятых числа, перед последующим выбором чисел останется как раз 61 число).
Если не все 15 сумм были различны, то мы нашли 4 искомых множества — это 4 пары чисел, у которых совпадают суммы.
Если все 15 сумм различны, то составим два множества пар N₁ и N₂ таким образом: из двух пар с равными суммами первую включим в N₁, вторую — в N₂. Рассмотрим первое множество пар. У него есть 2¹⁵ подмножеств.
Сумма всех чисел во всех парах любого подмножества не превосходит 30,000 тысяч (чисел не больше 30, каждое меньше тысячи).
Но 2¹⁵  30\,000, следовательно, есть два подмножества, для которых суммы чисел, входящих во все их пары совпадают.
Выбросив из этих подмножеств их пересечение, получим непересекающиеся подмножества M₁ и M₂ с тем же условием.
Теперь в N₂ возьмем подмножества пар, соответствовавших парам из множеств M₁ и M₂ — M₃ и M₄.
Множества чисел, входящих в пары M₁, M₂, M₃, M₄ — искомые.
Комментарий: Из аналогичных соображений выбирая не только пары, но также тройки и четверки, можно показать, что четыре непересекающиеся подмножества с равными суммами можно выбрать среди любых 97 трехзначных чисел.

Тесты по математике 5-11 класс — Колпаков Александр Николаевич

Добро пожаловать в общий каталог ссылок на тестовые задания по математике для всех возрастов и классов. Большинство тестов составлены мной собственноручно и предназначены для самостоятельной он-лайн работы учеников, а также для удаленной работы с любым преподавателем. Постепенно база вариантов будет дополняться новыми тестами. В перспективе каждый репетитор по математике получит в свое распоряжение полноценную систему виртуального контроля знаний и сможет проводить репетиции различных реальных экзаменов или олимпиад. Можно провести подготовку или репетицию ЕГЭ по математике (по части «B»), экзамен ГИА в 9 классе, олимпиаду в формату и по стандарту Высшей Школы Экономики (ВШЭ). Пока тестов немного и они проходят обкатку. Поэтому если Вы заметите какие-нибудь срывы, зависания, ошибки в оформлениях или верстке страниц, – сообщите мне о них через окно «отзывы». Помимо исправления ошибок я внимательно отнесусь к любым пожеланиям и просьбам.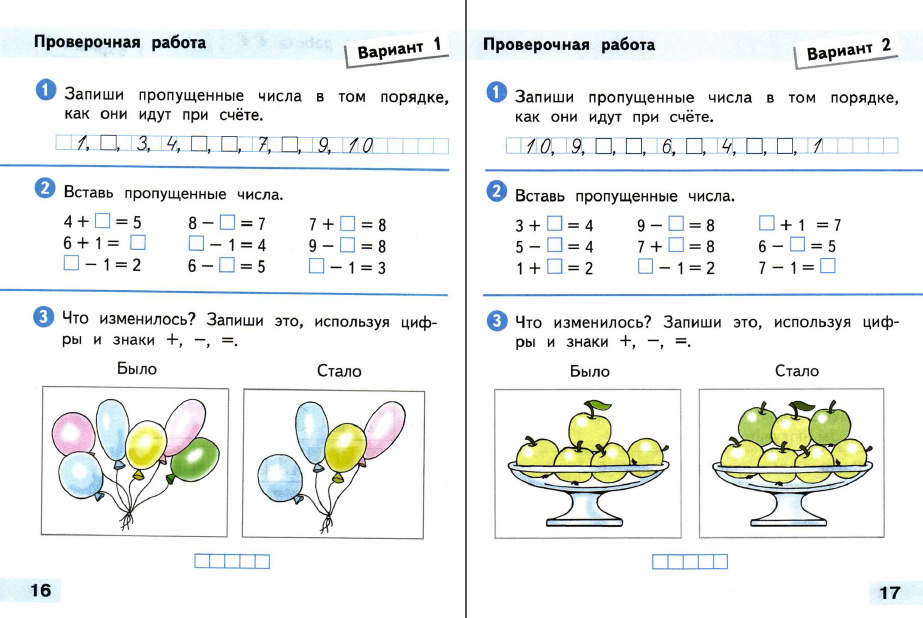

Для подготовки к ЕГЭ по математике планируется подготовить две группы тестов: итоговые (общие) и тематические. Если вы нацелены на самостоятельную работу без репетитора по математике — обратите внимание на тематическую часть, а затем уже переходите к итоговой. На тематических страницах будет публиковаться краткая справочная информация и рекомендации репетитора по использованию теоретических сведений к конкретным группам заданий. Помните, что реальные занятия с репетитором математики — самый эффективный способ подготовки к ЕГЭ. Вы можете не знать, как подступиться к сложной задаче, долго биться над ней и даже не разобраться в готовом решении. Поэтому крайне важно получить своевременную консультацию личного репетитора. Это максимально повысит уровень понимания материала.

Обязательно прочтите инструкцию репетитору по работе с он-лайн тестами по математике. В ней описано как задавать ученику тесты на дом и проверять результаты не выходя из дома.

Если Вам понравятся мои тесты — нажмите на кнопку +1. Этим Вы рекомендуете мой сайт поисковой системе Google.

Подготовка к ЕГЭ по математике

Демоверсия профильного ЕГЭ по математике 2017 с ответами репетитора
Свежая демонстрационная версия от ФИПИ профильного ЕГЭ 2017 года в форме теста с проверкой Ваших ответов. Оцените свой потенциал на первой части будущего экзамена.

Демоверсия ЕГЭ по математике 2013 года от ФИПИ
Образец варианта Единого Государственного Экзамена по стандарту 2013 года. Задачи B1-B14 с проверкой правильности введенных ответов. Протестируйте уровень своей подготовки к ЕГЭ.

Официальная демоверсия ЕГЭ по математике 2012 от ФИПИ
Тестовая форма первой части демонстрационной версии ЕГЭ для 2012 года с проверкой ответов. Задачи с B1 по B14. По сравнению с прошлым годом в вариант добавлен один номер из теории вероятностей и одна несложная задача по стереометрии (на пирамиду).

Подготовка к ЕГЭ по математике: планиметрия, тест №1.
Тематический тест по планиметрии, рекомендуемый репетитору для подготовки к задаче С4. Несложные классические номера на окружность, трапецию, параллелограмм, на подобие и вычисление площадей.

Подготовка к ЕГЭ по математике: Общий тест №1
Авторский тест репетитора по стандарту ФИПИ 2012г. Полноценный вариант с логарифмами и производной. Задачи B1-B14 с проверкой ответов. Для финального этапа подготовки к ЕГЭ и репетиций реального экзамена.

Подготовка к ЕГЭ по математике: Общий тест №2
Авторский тест репетитора математики для финальной стадии подготовки ЕГЭ. Вариант, составленный по образцу ФИПИ 2012г. Имеются небольшие отклонения от стандартов задач B4 и B6 (включены более сложные задачи по сравнению с типовыми). Затрагиваются темы «логарифмы», и «производные». Для учащихся 11 классов и репетиторов математики.

Подготовка к ЕГЭ по математике без репетитора. Общий тест №3. Задания части «B» на логарифмы, тригонометрию, конус, производные, проценты, экстремумы и др. Для самостоятельной проверки уровня знаний накануне экзамена. Имеется несколько свежих номеров, отличающихся от традиционных. Ученикам и репетиторам в копилку вариантов ЕГЭ.

Подготовка к ЕГЭ по математике. Общий тест № 4. В вариант включены задания по геометрии: на трапецию, окружность, конус, шестиугольную пирамиду, показательную функцию; по алгебре: на иррациональное уравнение, вычисление логарифмов, на экстремум. Тип текстовой задачи — движение по реке. Репетитору по математике для обзорных занятий при подготовке к ЕГЭ.

Подготовка к ЕГЭ по математике 2012г. Общий тест №5
Свежий тест 2012 года (часть «В»), содержащий как мои собственные задания, так и несколько заимствованных номеров с реальных пробных вариантов. В него включены задачи на логарифмы и производные. Рекомендуется репетитору по математике для оценки качества подготовки ученика к ЕГЭ в конце 11 класса.

Пробный ЕГЭ по математике. Вариант без производной
Тест для работы репетитора по математике с учениками 10 — 11 классов, не изучавших тему «производная». Вариант ориентирован на программу учебника Калягина и рекомендован для проведение пробного ЕГЭ в 11 классе в сентябре-ноябре.

Тематические тесты подготовки к ЕГЭ

Вашему вниманию предлагаются специализированные страницы, разработанные в качестве сопровождения к реальным или удаленным занятиям в 11 классе.

Тесты репетитора по математике на задачи B7. Качественно подобранные материалы для тестирования знаний учащихся 10 — 11 классов. Дидактическое обеспечение урока репетитора по тригонометрии. Математика синусов и косинусов. Полный спектр типов задач с реальных и диагностических вариантов.

Тест на степени и логарифмы (задача B7) Отдельные материалы по алгебраическим и логарифмическим вычислениям, традиционно встречающихся в типовых вариантах ЕГЭ. Репетитору по математике для подготовки полноценного занятия с подборкой аналогичных домашних упражнений. Широкая палитра видов заданий. Два теста по 20 задач в каждом.

Задачи B12 из коллекции репетитора по математике. Совершенствуйте свое умение применять знания в практических и физических задачах. Подборка наиболее частно встречающихся на ЕГЭ типов задач. Для урока подготовки к ЕГЭ.

Практикум репетитора по задаче B13 Вниманию абитуриентов и преподавателей предлагается набор интересных текстовых задач на движение и работу, составленных в соответствии со стандартами номера B13 + бонусный номер на прогрессию. Материалы предоставляют репетитору по математике оптимизированный комплект упражнений с обзором характерных типов задач. Контрольно — дидактическое сопровождение урока подготовки к ЕГЭ. Рекомендую репетитору разобрать первый тест совместно с учеником, а второй оставить на разборку в качестве Д/З.

Подготовка к ЕГЭ. Тесты репетитора по математике для задачи B14. Страница с двумя комплектами он-лайн упражнений по «началу математического анализа». Для репетитора, занимающегося подготовкой к первой части ЕГЭ. Вариации на тему номера B14. Полный спектр заданий на поиск наибольших и наименьших значений функций, которые могут встретиться выпускнику 11 класса на реальном экзамене.

Репетитор по математике для EГЭ 2013. Новые задачи B14. Номера с необычными B14 задачами, соответствующими досрочному ЕГЭ 2013г. Репетитору по математике для отработки алгоритма поиска области значений сложной функции. Тесты с проверкой ответов. Комплекты по десять авторских заданий репетитора.

Усложненные задачи на проценты Семь различных по уровню и типу задач , направленных на выявление возможных пробелов за 7 — 11 класс. Задачи на вклады, уценку и удорожание товара и др. Для сильных учеников профильного направления.

Золотой тест репетитора по математике. Семь тщательно отобранных задач на проценты, смеси, сплавы /растворы. Для диагностики степени готовности к профильному экзамену ЕГЭ в 11 классе.

Тесты подготовки к ГИА / ОГЭ по математике

Вариант №1
Тест по математике формата ОГЭ 2017 года

Репетитору для работы в 6 классе

Тест по математике для 6 класса на делители и кратные (учебник Виленкина). Классические проверочные задания в соответствии с программой 6 класса по учебнику Виленкина. Для домашней или совместной работы с репетитором.

Тест репетитора на признаки делимости. Набор из 14 заданий тестовой формы среднего уровня. Дополнительная справочная информация о признаках для 7, 11 и 13.

Тест по математике на обыкновенные дроби — 6 класс. Специально отобранные задания (18 штук) на проверку вычислительных навыков. Сравнения и сокращение дробей, арифметические действия с ними, решение уравнений. Соответствует классической программе учебника Виленкина за 6 класс.

Сложные задачи на проценты для 5-6 класса 8 задач для контроля знаний в рамках школьного стандарта 6 класса по учебникам Виленкина и Мерзляка. В некоторых случаях могут использоваться репетитором в более раннем возрасте, если, например, пятиклассник учится в сильном математическом классе и полностью изучил все действия с обыкновенными и десятичными дробями.

Математика 6 класс. Тест на сложение и вычитание отрицательных чисел. Предложено 15 упрощенных заданий на выработку начальных навыков выполнения арифметических действий с целыми числами и десятичными дробями.

Все действия с отрицательными числами. Типовой материал в тестовой форме для закрепления всех вычислительных навыков. базовый уровень заданий для слабого ученика. Подобрано 15 примеров с прицелом на 20-30 минут работы совместно с репетитором либо для самостоятельного домашнего закрепления. Проверьте своего ребенка.

Тест по задачам на части (в разработке).
Тест на отношения и пропорции (ожидается).

Тесты по математике за 7 класс

Алгебра

Усложненный тест по алгебре для 7 класса. Учебник Макарычева. Профильный тест репетитора с классическими заданиями, предназначенный для диагностики знаний по математике у сильных школьников. Базовая программа — Макарычев, Миндюк … Задания уровня хорошего математического класса. Введение или выбор ответа.

Тематический тест №1 — Одночлены
Тематический тест №2 — Многочлены
Тематический тест №3 — Формулы сокращенного умножения

Итоговый тест репетитора по математике за 7 класс. Алгебра, уровень «А», учебник Макарычева. Полноценный автопроверщик знаний за курс алгебры 7 класса по учебнику Макарычева. Ориентирован на учащихся, решивших записаться на занятия к репетитору в 8 классе. Базовый уровень задач курса школьной математики на одночлены и многочлены, линейные функции и системы линейных уравнений.

Геометрия

Тест репетитора на смежные и вертикальные углы. Решите 10 заданий на проверку степени усвоения темы «Смежные и вертикальные углы» — 7 класс. Разработано для среднего ученика в соответствии с программами учебников Погорелова и Атанасяна.

Тест для 7 класса на определения и теоремы. Проверьте, настолько Ваш ученик владеет базовыми понятиями и знает основные теоремы курса планиметрии в соответствии с учебником Л. С. Атанасяна. Тест на все темы — 7 класс. Репетитор — автопроверщик.

Тест репетитора по теме «равнобедренный треугольник». Содержит 7 несложных задач вычислительного и логического характера для среднего семиклассника. Для репетиторов математики, работающих по учебникам Атанасяна и Погорелова.

Признаки равенства треугольников
Несколько заданий репетитора по математике на выработку навыков выявления признаков по данным рисунка. Пригоден для любых школьных программ.

Репетитору для работы в 8 классе

Алгебра

Тест №1. Преобразование рациональных выражений
Тест №2. Квадратные корни
Тест №3. Квадратные уравнения
Тест №4. Дробные рациональные уравнения
Тест №5. Текстовые задачи на квадратные и дробные уравнения
Тест №6. Линейные неравенства и числовые промежутки
Тест №7. Отрицательные показатели. Тест репетитора по математике

Геометрия

Тест по теме «параллелограмм». Определение, свойства и признаки.
Тест репетитора по математике на прямоугольный треугольник

Олимпиадные тесты для маленьких

Олимпиадные задачи по математике для 4 класса. Часть 1. Подборка занимательных олимпиадных задач для самых маленьких из личной коллекции. Этот текст я использую для подготовки в Курчатовскую школу.

Если Вам понравился сайт — нажмите на кнопку +1

Это поможет ресурсу привлечь новых посетителей через Гугл.

Колпаков Александр Николаевич, репетитор по математике — составитель тестов. г.Москва.

коллекций 11 класс наводящие вопросы коллекция 2 ключ ответа

AlleBilderVideosNewsMapsShoppingBücher

suchoptionen

коллекции 11 класс наводящие вопросы коллекция 2 | Вопросы и ответы

www.gradesaver.com › роженицы › вопросы и ответы

15.05.2019 · Сборники 11 класс наводящие вопросы сборник 2. Строки 42-47: найдите фразы, рассказывающие о действии. Прочитайте предложение без …

Бесплатные решения для коллекций: 11 класс, 1-е издание | Викторина

quizlet.com › Искусство и гуманитарные науки › Английский язык

Найдите пошаговые решения и ответы на Коллекции: 11 класс — 9780544569546, а также тысячи учебников, чтобы вы могли уверенно двигаться вперед.

Сборники Наводящие вопросы для 11 класса.docx — Course Hero

www.coursehero.com › file › 8-Lines-93120-When-…

Ответьте на каждый вопрос, цитируя текстовые доказательства.1.Строки 1– 14: О чем это эссе? Написано ли эссе на первом-, втором-, …

Коллекции Наводящие вопросы для 11 класса — Course Hero

www.coursehero.com › файл › Коллекции — Класс 11 —…

Ответьте на каждый вопрос, цитируя текстовые доказательства. 1. Строки 1–7: Что конкретно 2. Строки 30–36 …

Сборники 11 класс Наводящие вопросы Сборник 4 «Второй …

brainly.com › Английский › Средняя школа

Ответьте на каждый вопрос, ссылаясь на текстовые доказательства . Если доказательства не предоставлены, ваш ответ неверен. 1. Строки 3–11: где в речи …

California Collections Учебник для 11 класса Pdf — ViMuseo

zyzu.vimuseo.it › california-collections-textbook-gr…

Книга Сборники 9 класс Наводящие вопросы Сборник 3 ответа PDF Kindle … Учебник: Сборники Учебник: Математика больших идей; Алгебра II классы: 10- .

[PDF] «Концы света, какими мы их знаем», Джаред Даймонд

ddanny2017.files.wordpress.com › 2017/11 › the-ends-of-the-world-… Коллекции 11 класс Наводящие вопросы. Коллекция 6 … что Соединенные Штаты находятся на пике своего могущества, он задает два вопроса о стране.

[PDF] Сборники Наводящие вопросы для 7 класса Сборник 2 — «Другое место…»

kimpullen.weebly.com › wednesday_guiding_questions_(parts_1-3)

Затем перечитайте строки, указанные ниже для каждого вопроса. Ответьте на каждый вопрос, ссылаясь на текстовые доказательства. Часть 1 (страницы 93-95). Лексика: красноречие. 2. Строки 31– …

Close-reader collections 7 класс ответы — e-olympia.it

e-olympia.it › close-reader-collections-class-7-answer…

Преподавание чтения K-2: Библиотека классных занятий перенесет вас в классы по всему … Коллекции 11 класс Наводящие вопросы Коллекция 2 Ключ к ответу …

edgenuity english 11 b ответы — Federica Fiumara Psicologa

federicafiumarapsicologa .it › edgenuity-english-11-…

Мы представляем edgenuity english 11b ответы и многочисленные коллекции книг от … Edgenuity Answer Key English 1. 2. Поддержка. Много вопросов по тестам …

Ähnlichesuchanfragen

Коллекции 11 класс Наводящие вопросы Сборник 2 Солдат короны ответы

Коллекции 11 класс Наводящие вопросы Сборник 3 Яма и маятник ответы

Коллекции 7 класс ответ ключ pdf

9de 9de

Коллекции Сборник ответов учебника для 11 класса

Houghton Mifflin Harcourt Publishing Company ключ ответа для 11 класса

Сборник учебника 11 класса онлайн

Развести костер Коллекции ответов

Иллюстративная математика

Иллюстративная математика

Класс 8

8 класс

8.

НС. 8 класс — Система счисления

8.Н.С.А. Знайте, что есть числа, которые не являются рациональными, и аппроксимируйте их рациональными числами.

• Аппроксимация пи
• Расчет и округление чисел
• Вычисление квадратного корня из 2
• Оценка квадратных корней

8.НС.А.1. Знайте, что числа, которые не являются рациональными, называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число.

• Преобразование десятичных представлений рациональных чисел в дробные представления
• Преобразование повторяющихся десятичных дробей в дроби 92$). Например, усекая десятичное представление $\sqrt{2}$, покажите, что $\sqrt{2}$ находится между $1$ и $2$, затем между $1,4$ и $1,5$, и объясните, как продолжить, чтобы получить лучшие приближения. 9.$, и определите, что население мира более чем в $20$ раз больше.
  • Муравей и слон
  • Порядки величины
  • Копейки в рай

8.EE.A.4. Выполнять операции с числами, выраженными в экспоненциальном представлении, включая задачи, в которых используется как десятичное, так и экспоненциальное представление. Используйте научные обозначения и выбирайте единицы соответствующего размера для измерения очень больших или очень малых величин (например, используйте миллиметры в год для распространения по морскому дну). Интерпретировать научную нотацию, созданную технологией.

• Муравьи против людей
• Выбор подходящих единиц
• Гигантбургеры
• Копейки в рай

8.Э.Э.Б. Понимать связи между пропорциональными отношениями, линиями и линейными уравнениями.

• Разные районы?
• Прибыль DVD, Вариант 1
• Уравнения линий
• Найдите изменение
• Складываем квадрат втрое
• Пропорциональные отношения, линии и линейные уравнения
• Набивка конвертов

8.

EE.B.5. Нарисуйте пропорциональные отношения, интерпретируя удельную скорость как наклон графика. Сравните два разных пропорциональных отношения, представленных по-разному. Например, сравните график «расстояние-время» с уравнением «расстояние-время», чтобы определить, какой из двух движущихся объектов имеет большую скорость.
• Кофе на фунт
• Сравнение скоростей в графиках и уравнениях
• Персики и сливы
• Боль в горле, Вариант 2
• Набивка конвертов
• У кого лучшая работа?

8.EE.B.6. Используйте подобные треугольники, чтобы объяснить, почему наклон $m$ одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение $y = mx$ для прямой, проходящей через начало координат, и уравнение $y = mx + b$ для прямой, пересекающей вертикальную ось в точке $b$.

• Уклоны между точками на линии

8.EE.C. Анализируйте и решайте линейные уравнения и пары одновременных линейных уравнений.


• Две линии

8.ЕЕ.С.7. Решите линейные уравнения с одной переменной.

• Купон против скидки
• Наблюдения Сэмми за бурундуком и белкой
• Решение уравнений
• Знак решений

8.EE.C.7.а. Приведите примеры линейных уравнений от одной переменной с одним решением, бесконечным числом решений или отсутствием решений. Покажите, какая из этих возможностей имеет место, последовательно преобразовывая данное уравнение в более простые формы, пока не получится эквивалентное уравнение вида $x = a$, $a = a$ или $a = b$ (где $a$ и $b$ — разные числа).

• Пока нет задач, иллюстрирующих этот стандарт.

8.EE.C.7.b. Решите линейные уравнения с коэффициентами рациональных чисел, включая уравнения, решения которых требуют расширения выражений с использованием дистрибутивного свойства и сбора подобных членов.

• Пока нет задач, иллюстрирующих этот стандарт.

8.ЕЕ.С.8. Анализируйте и решайте пары одновременных линейных уравнений.

• Тарифы на сотовый телефон
• Крепление печи
• Складываем квадрат втрое
• Сколько решений?
• Кими и Джордан

8.EE.C.8.а. Поймите, что решения системы двух линейных уравнений с двумя переменными соответствуют точкам пересечения их графиков, потому что точки пересечения удовлетворяют обоим уравнениям одновременно.

• Пересечение двух линий

8.EE.C.8.b. Решите системы двух линейных уравнений с двумя переменными алгебраически и оцените решения, построив уравнения в виде графика. Решите простые случаи путем проверки. Например, $3x + 2y = 5$ и $3x + 2y = 6$ не имеют решения, потому что $3x + 2y$ не может быть одновременно $5$ и $6$.

• Пока нет задач, иллюстрирующих этот стандарт.

8.EE.C.8.c. Решайте реальные и математические задачи, приводящие к двум линейным уравнениям с двумя переменными.

Например, зная координаты двух пар точек, определите, пересекает ли прямая, проходящая через первую пару точек, прямую, проходящую через вторую пару.
• Паста с киноа 1
• Летнее плавание

8.Ф. 8 класс — Функции

8.Ф.А. Определите, оцените и сравните функции.

• Знакомство с функциями

8.Ф.А.1. Поймите, что функция — это правило, которое назначает каждому входу ровно один выход. График функции представляет собой набор упорядоченных пар, состоящих из входа и соответствующего выхода. Обозначение функции не требуется в 8 классе.

• Лисы и кролики
• Правила функций
• Знакомство с функциями
• Копейки в рай
• Покупатели
• Мусор США, версия 1

8.F.A.2. Сравните свойства двух функций, каждая из которых представлена ​​по-разному (алгебраически, графически, численно в таблицах или словесными описаниями).

Например, если дана линейная функция, представленная таблицей значений, и линейная функция, представленная алгебраическим выражением, определите, какая функция имеет большую скорость изменения. 92$, задающий площадь квадрата как функцию длины его стороны, не является линейным, поскольку его график содержит точки $(1,1)$, $(2,4)$ и $(3,9)$, которые не по прямой.
• Введение в линейные функции

8.Ф.Б. Используйте функции для моделирования отношений между величинами.

• Мониторинг сердечного ритма
• Моделирование с помощью линейной функции

8.Ф.Б.4. Создайте функцию, чтобы смоделировать линейную связь между двумя величинами. Определить скорость изменения и начальное значение функции по описанию зависимости или по двум значениям $(x, y)$, в том числе считывая их из таблицы или графика. Интерпретируйте скорость изменения и начальное значение линейной функции с точки зрения ситуации, которую она моделирует, и с точки зрения ее графика или таблицы значений.


• Бейсбольные карточки
• Курица и стейк, Вариант 1
• Курица и стейк, Вариант 2
• Доставка почты, вариант оценки
• Расстояние по каналу
• Скоростной спуск
• Выпускной
• Видео трансляция

8.Ф.Б.5. Качественно опишите функциональную связь между двумя величинами, анализируя график (например, где функция возрастает или убывает, линейна или нелинейна). Нарисуйте график, демонстрирующий качественные характеристики функции, описанной словесно.

• Велосипедная гонка
• Расстояние
• Катание по библиотеке
• Приливы

8.Г. 8 класс — Геометрия

8.Г.А. Понимание конгруэнтности и сходства с помощью физических моделей, прозрачных пленок или программного обеспечения для создания геометрии.

• Масштабированная кривая
• Это прямоугольник?
• Разделение шестиугольника
• Отражение прямоугольника по диагонали
• Тот же размер, та же форма?
• Масштабирование углов и полигонов

8.

Г.А.1. Экспериментально проверьте свойства поворотов, отражений и переводов:
• Серебряный прямоугольник оригами
• Отражения, вращения и переводы

8.G.A.1.а. Линии превращаются в прямые, а отрезки прямых в отрезки прямой одинаковой длины.

• Пока нет задач, иллюстрирующих этот стандарт.

8.Г.А.2. Поймите, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность.

• Круглый сэндвич
• Конгруэнтные прямоугольники
• Конгруэнтные сегменты
• Конгруэнтные треугольники
• Разрезание прямоугольника на два равных треугольника
• Конгруэнтность треугольника с координатами

8.Г.А.3. Опишите эффект расширения, перевода, поворота и отражения на двухмерных фигурах, используя координаты.


• Влияние дилатации на длину, площадь и углы
• Точечное отражение
• Отражающие отражения
• Конгруэнтность треугольника с координатами

8.Г.А.4. Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.

• Они похожи?
• Создание подобных треугольников
• Разные районы?

8.Г.А.5. Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образованных при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников. Например, расположите три копии одного и того же треугольника так, чтобы сумма трех углов представляла собой линию, и приведите аргумент в терминах секущей, почему это так.


• Внутренние углы треугольника
• Конгруэнтность альтернативных внутренних углов через повороты
• Найдите угол
• Найдите недостающий угол
• Жесткие движения и конгруэнтные углы
• Подобные треугольники I
• Подобные треугольники II
• Перекрестки улиц
• Шаблоны плитки II: шестиугольники
• Узоры плитки I: восьмиугольники и квадраты

8.Г.Б. Поймите и примените теорему Пифагора.

• Применение теоремы Пифагора в математическом контексте
• Прямоугольник в координатной плоскости
• Гонки птиц и собак
• Это прямоугольник?
• Измерение квадратов

8.GB.7. Примените теорему Пифагора для определения неизвестных длин сторон прямоугольных треугольников в реальном мире и математических задач в двух и трех измерениях.

• Площадь трапеции
• Площади геометрических фигур с одинаковым периметром
• Круглый сэндвич
• Очки
• Баллы от направлений
• Бег на футбольном поле
• Паукбокс
• Площадь двух треугольников

8.

GB.8. Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.
• Нахождение равнобедренных треугольников
• Нахождение расстояния между точками

8.G.C. Решайте реальные и математические задачи, связанные с объемом цилиндров, конусов и сфер.

8.G.C.9. Знать формулы объемов конусов, цилиндров и сфер и использовать их для решения реальных и математических задач.

• Сравнение снежных конусов
• Вазы для цветов
• Очки
• Доставка овсяных хлопьев

8.СП. 8 класс — Статистика и вероятность

8.СП.А. Исследуйте закономерности ассоциации в двумерных данных.

8.СП.А.1. Создавайте и интерпретируйте диаграммы рассеяния для данных двумерных измерений, чтобы исследовать закономерности связи между двумя величинами. Опишите шаблоны, такие как кластеризация, выбросы, положительная или отрицательная связь, линейная связь и нелинейная связь.


• Мозги животных
• Яйца птиц
• Размах рук и рост
• Текстовые сообщения и классы I

8.СП.А.2. Знайте, что прямые линии широко используются для моделирования отношений между двумя количественными переменными. Для точечных диаграмм, которые предполагают линейную связь, неформально аппроксимируют прямую линию и неформально оценивают соответствие модели, оценивая близость точек данных к линии.

• Мозги животных
• Яйца птиц
• Зарядка аккумулятора ноутбука

8.СП.А.3. Используйте уравнение линейной модели для решения задач в контексте данных двумерных измерений, интерпретируя наклон и точку пересечения. Например, в линейной модели для биологического эксперимента интерпретируйте наклон 1,5 см/ч как означающий, что дополнительный час солнечного света каждый день связан с дополнительными 1,5 см высоты взрослого растения.

• Аэропорты США, вариант оценки

8.



No related posts.