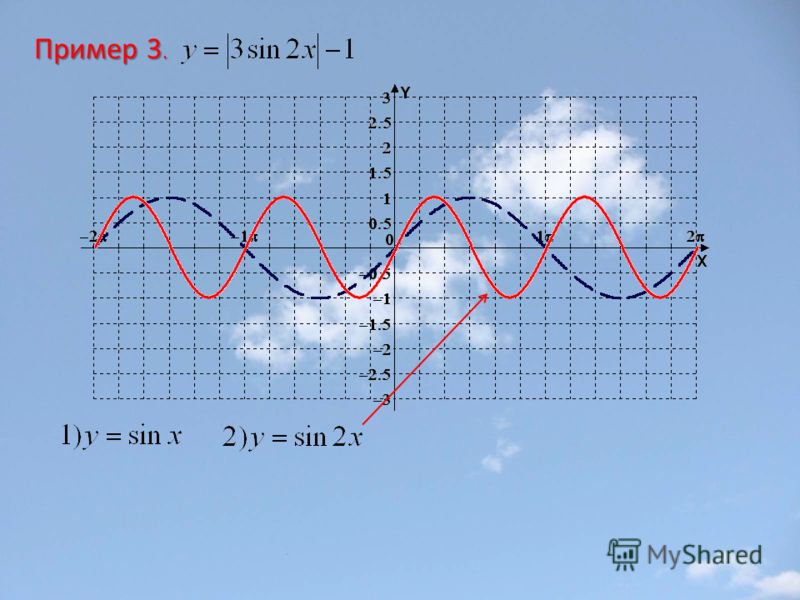
Построить график функции у=sin2x и у=sin. График функции y=sin x График sin 2x
Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .
Единичный отрезок берём длиной 2 клеточки тетради. На оси Oy отмечаем единицу.
Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.
На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.
При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на промежутке :
Полученные точки отметим на координатной плоскости:
Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0). С учётом этого факта продолжим построение графика влево, то точки -π:
Функция y=sin x — периодическая с периодом T=2π.
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
Функция называется нечетной если
выполняется равенство: y(-x)=-y(x). Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π]. Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке .
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x). Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
«Построение графика функции с модулем» — Y = lnx.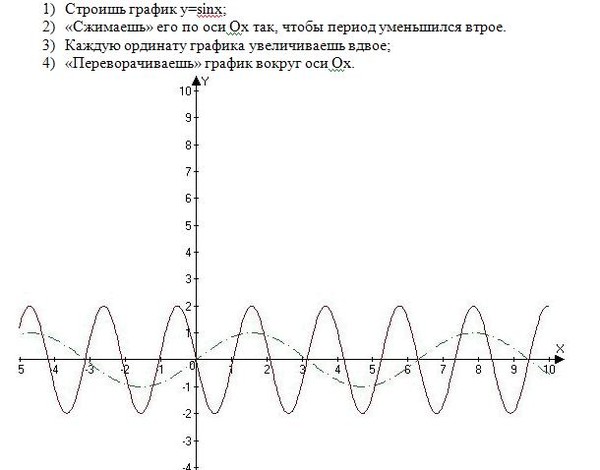
««Графики функций» 9 класс» — Цели урока. Большему значению аргумента соответствует большее значение функции. Нули функции. Определение. Заполните пропуски. Установите соответствие между функцией и вершиной. Тренажер. Выберите уравнение, с помощью которого задана линейная функция. Установите соответствие. Выберите уравнение. Обратная пропорциональность.
«Графики функций с модулями» — Найдём вершину функции. Кубическая функция. Отрицательная сторона. Графики функций. Квадратичная функция. Сложная функция. Функция с модулем. Графики функций надо обязательно уметь строить. Подготовка к ЕГЭ. Графики функций с модулями. Парабола. График функции.
«Уравнение касательной к графику функции» — Производная в точке.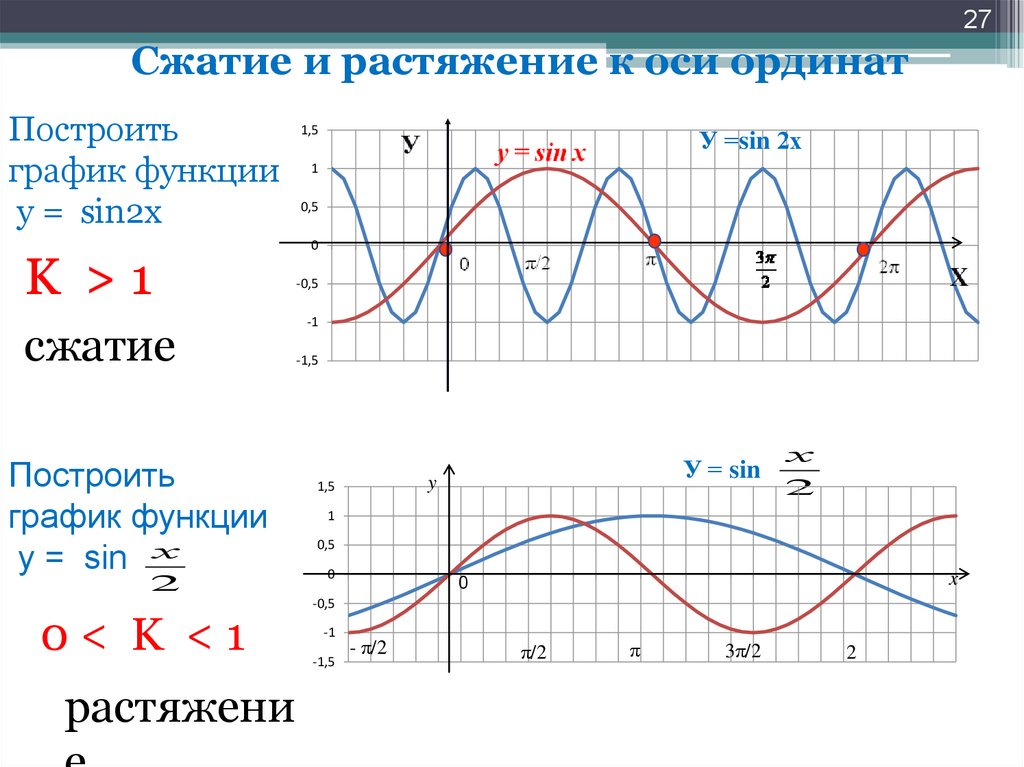
Правила дифференцирования. График функции. Алгоритм нахождения уравнения. Ответьте на вопросы. Геометрический смысл производной. Номера из учебника. Уравнение касательной к графику функции. Определение. Касательная к графику функции. Основные формулы дифференцирования. Провести касательную.
«Построение графиков функций» — Построение графика функции y = sinx. Линия тангенсов. Алгебра. Тема: Построение графиков функций. График функции y = sinx. Выполнила: Филиппова Наталья Васильевна учитель математики Белоярская средняя общеобразовательная школа №1. Построить график функции y=sin(x) +cos(x).
«График обратной пропорциональности» — Применение гиперболы. Гипербола. Монотонность функции. Чётность, нечётность. Функция «Обратная пропорциональность». График. Построение графика обратной пропорциональности. Гипербола и космические спутники. Однополостной гиперболоид. Асимптота. Применение гиперболоидов. Определение обратной пропорциональности.
Всего в теме 25 презентаций
«Функция y=sin(x).
_6.png)
Определения и свойства»«Построение графика функции с модулем» — Y = lnx. Закрепили знания на ранее изученных функциях. Построение графиков функций. Вопрос классу. Y = x2 – 2x – 3. Проектная деятельность. Урок обобщения и систематизации знаний. График функции. Актуализация знаний о графиках функций. Обобщение. Попробуйте самостоятельно построить графики. Y = f(x).
««Графики функций» 9 класс» — Цели урока. Большему значению аргумента соответствует большее значение функции. Нули функции. Определение. Заполните пропуски. Установите соответствие между функцией и вершиной. Тренажер. Выберите уравнение, с помощью которого задана линейная функция. Установите соответствие. Выберите уравнение. Обратная пропорциональность.
«Графики функций с модулями» — Найдём вершину функции. Кубическая функция. Отрицательная сторона. Графики функций. Квадратичная функция. Сложная функция. Функция с модулем. Графики функций надо обязательно уметь строить. Подготовка к ЕГЭ. Графики функций с модулями.
«Уравнение касательной к графику функции» — Производная в точке. Правила дифференцирования. График функции. Алгоритм нахождения уравнения. Ответьте на вопросы. Геометрический смысл производной. Номера из учебника. Уравнение касательной к графику функции. Определение. Касательная к графику функции. Основные формулы дифференцирования. Провести касательную.
«Построение графиков функций» — Построение графика функции y = sinx. Линия тангенсов. Алгебра. Тема: Построение графиков функций. График функции y = sinx. Выполнила: Филиппова Наталья Васильевна учитель математики Белоярская средняя общеобразовательная школа №1. Построить график функции y=sin(x) +cos(x).
«График обратной пропорциональности» — Применение гиперболы. Гипербола. Монотонность функции. Чётность, нечётность. Функция «Обратная пропорциональность». График. Построение графика обратной пропорциональности. Гипербола и космические спутники. Однополостной гиперболоид. Асимптота. Применение гиперболоидов.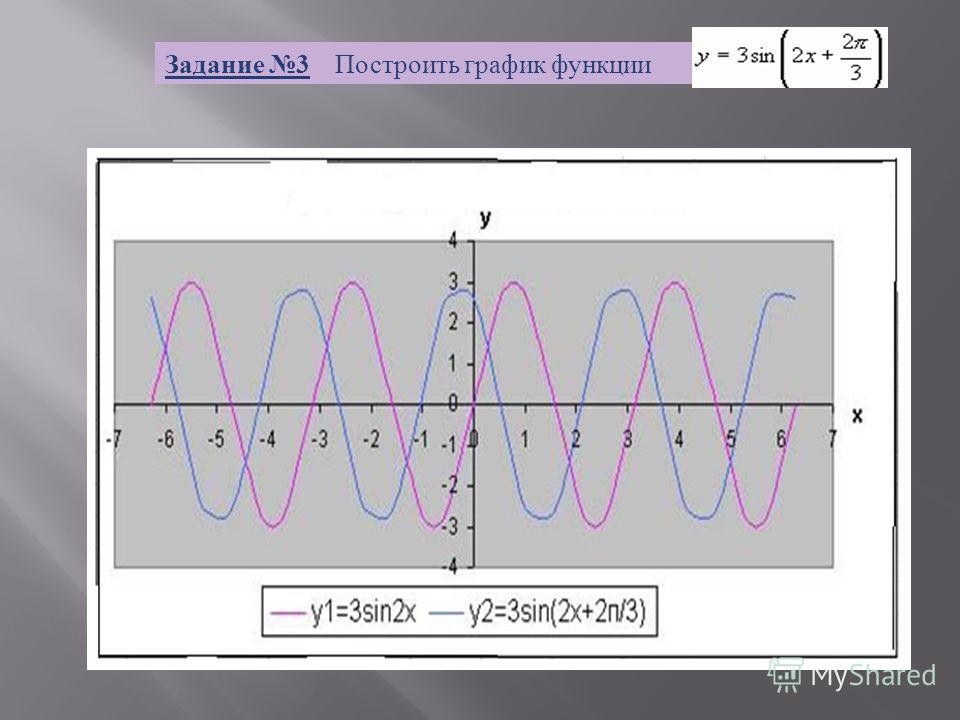
Определение обратной пропорциональности.
Всего в теме 25 презентаций
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
2) Функция нечетная. Давайте вспомним определение нечетной функции.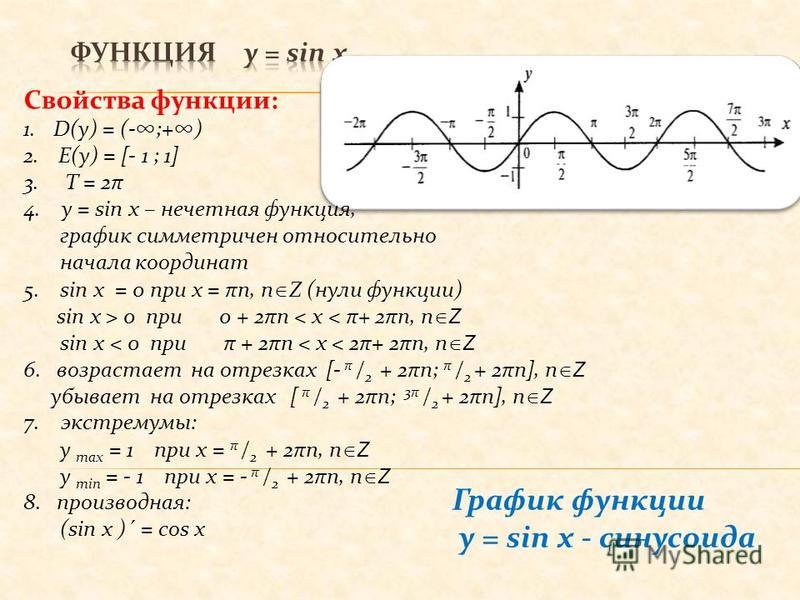
Функция называется нечетной если
выполняется равенство: y(-x)=-y(x). Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.
3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π]. Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке .
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x). Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
7) Функция Y=sin(X) – непрерывная функция. Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
Построить функцию
Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos .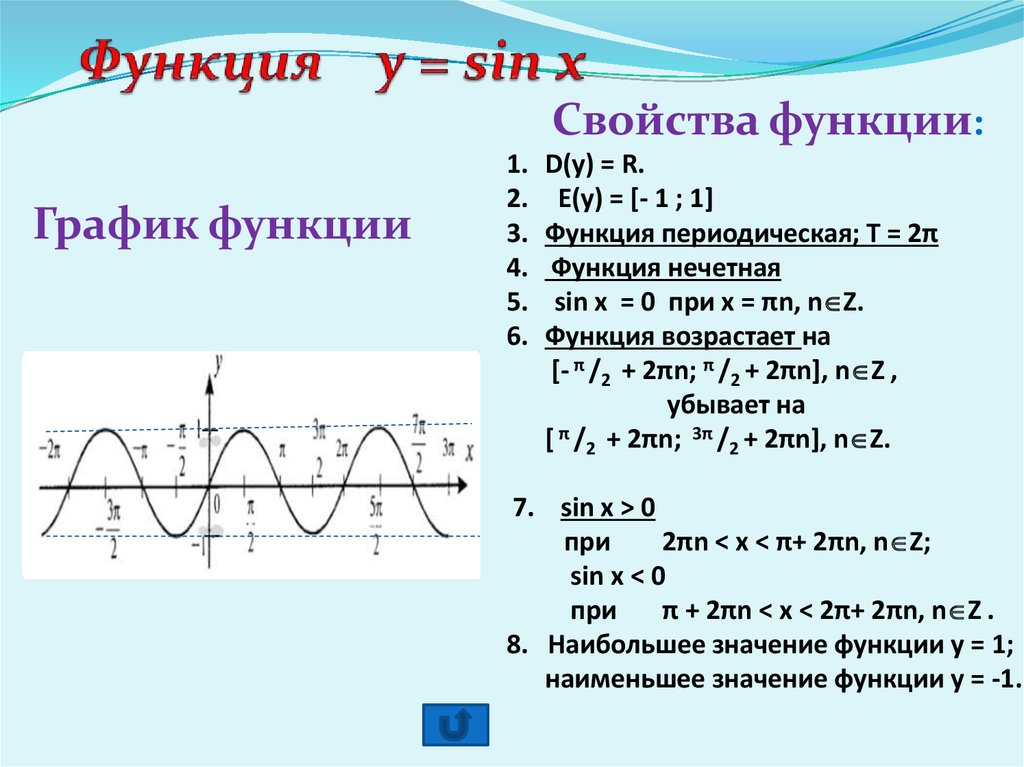
2/16=1)
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .
Единичный отрезок берём длиной 2 клеточки тетради.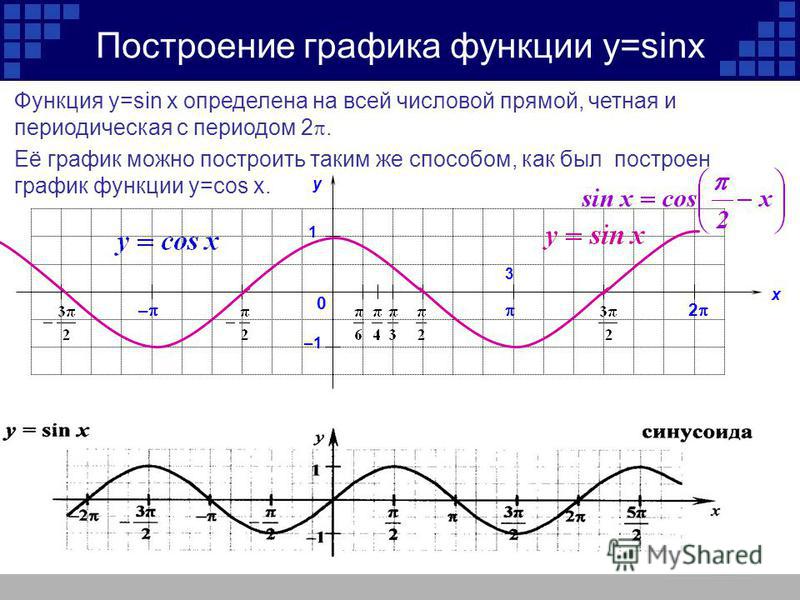
На оси Oy отмечаем единицу.
Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.
На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.
При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на промежутке :
Полученные точки отметим на координатной плоскости:
Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0). С учётом этого факта продолжим построение графика влево, то точки -π:
Функция y=sin x — периодическая с периодом T=2π. Поэтому график функции, взятый на на промежутке [-π;π], повторяется бесконечное число раз вправо и влево.
2) = 1$$ Мне было трудно это вычислить, поэтому я прибегнул к графическому калькулятору Desmos.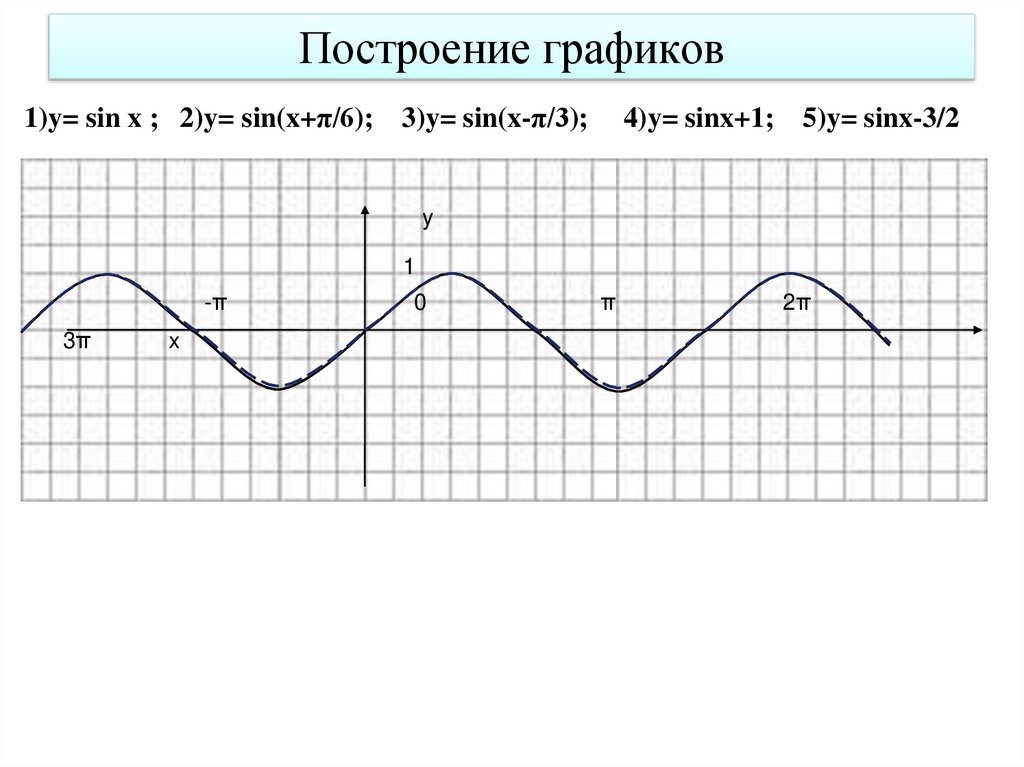
Это выглядит так:
Я могу объяснить некоторые части этой картины, но другие ускользают от меня, и я думаю, что кто-то с большим опытом лучше объяснит, почему эта штука выглядит именно так.
Мне было бы особенно интересно узнать, является ли фигура в середине частным случаем какой-то другой функции, как и завитушки на осях. (У меня есть хорошее представление о том, что такое горошек.) 94}{4} = 1$$
На случай, если это кому-то пригодится, вот изображение (от Desmos) двух упомянутых мною сюжетов.
На приведенном выше рисунке синим цветом обозначен секстик, а красным — квартик.
- алгебра-предварительное исчисление
- тригонометрия
- графические функции
- неявные функции
$\endgroup$
7
$\begingroup$
Поверхность уравнения $$z=\sin x+\sin y$$ имеет форму «лотка для яиц».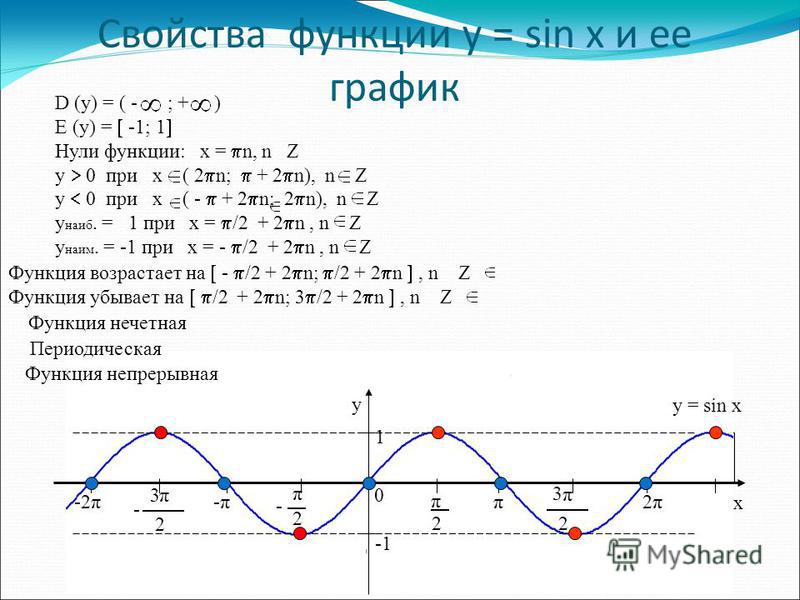
Он имеет максимумы $z=2$ на периодической сетке, поэтому линии уровня $z=1$ представляют собой равномерно расположенные приближенные окружности. 92}2=\pm\cfrac\pi3\end{cases}\;\;\;+2k\pi\;,\;\;\;k\in\Bbb N\cup\{0\}$$
и т. д. Решение приведенных выше бесконечных систем уравнений дает вам странный сюжет.
$\endgroup$
3
График функции y sin x 2. График функции y=sin x
«Йошкар-Олинский колледж сервисных технологий»
Построение и исследование графика тригонометрической функции y=sinx в табл. Построение и исследование графика тригонометрической функции y = синкс в электронной таблице MS Excel
Тип урока – интегрированный (приобретение новых знаний)
Цели:
Дидактическая цель — исследовать поведение графиков тригонометрической функции y = sinx в зависимости от коэффициентов с помощью компьютера
Учебники:
1.
Узнать изменение графика тригонометрической функции y = sin x в зависимости от коэффициентов
2. Показать внедрение компьютерных технологий в преподавание математики, интеграцию двух предметов: алгебры и информатики.
3. Формировать навыки использования компьютерной техники на уроках математики
4. Закреплять навыки исследования функций и построения их графиков
Развивающая:
1. Развивать у студентов познавательный интерес к учебным дисциплинам и умение применять свои знания в практических ситуациях
2. Развивать умение анализировать, сравнивать, выделять главное
3. Способствовать совершенствованию общий уровень развития учащихся
педагоги :
1. Воспитывать самостоятельность, аккуратность, исполнительность
2. Воспитывать культуру общения
Формы работы на уроке — комбинированные
Дидактическая техника и оборудование: 9000 2
9000 ЭВМ Мультимедийный проектор 4.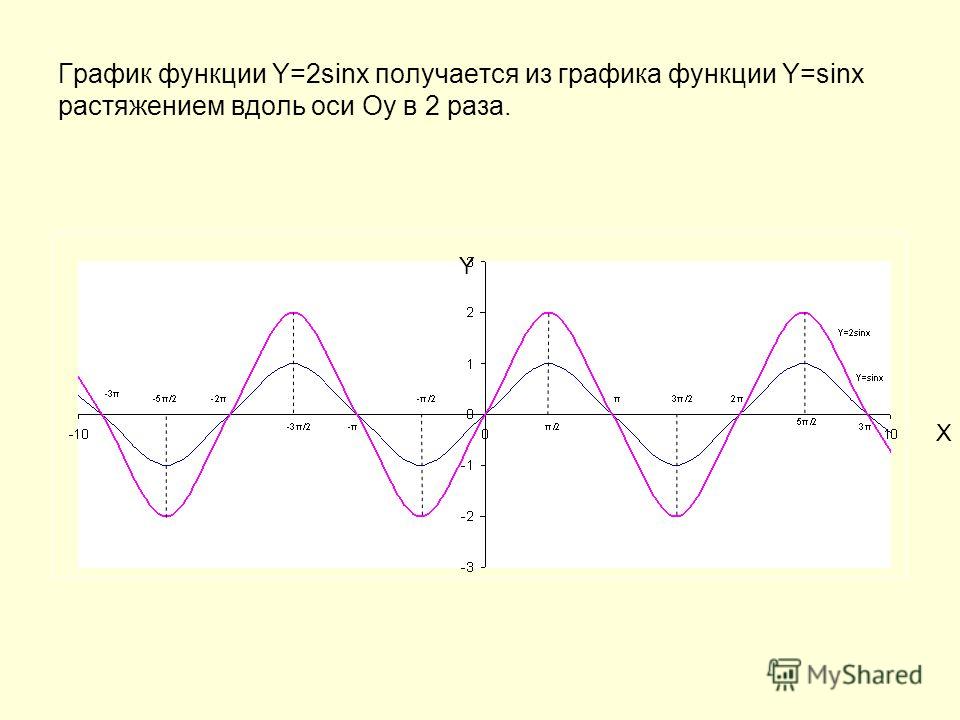
Раздаточный материал
5. Слайды презентации
Во время занятий
I . Организация начала урока
Приветствие учащихся и гостей
· Подготовка к уроку
II . Целеполагание и актуализация темы
На изучение функции и построение ее графика уходит много времени, приходится производить много громоздких вычислений, это не удобно, на помощь приходят компьютерные технологии.
Сегодня мы научимся строить графики тригонометрических функций в среде электронных таблиц MS Excel 2007.
Тема нашего урока «Построение и исследование графика тригонометрической функции y = sinx в электронной таблице»
Из курса алгебры мы знаем схему изучения функции и построения ее графика. Вспомним, как это сделать.
1. Область значений функции (D(f))
2. Область значений функции Е(f)
3. Определение четности
4. Периодичность
5. Нули функции (y=0)
6.
Интервалы знакопостоянства (y>0, y
7. Интервалы монотонности
8. Экстремумы функций
III . Первичная ассимиляция нового образовательного материала
Open MS Excel 2007.
Давайте построить функцию y = sin x
.
График этой функции будет построен на отрезке x Є [-2π; 2π]
Значения аргумента будем брать с шагом , , чтобы сделать график более точным.
Поскольку редактор работает с числами, переведем радианы в числа, зная, что P ≈ 3,14 . (таблица перевода в раздаточном материале).
1. Найти значение функции в точке х = -2Р. В остальном редактор автоматически вычисляет соответствующие значения функции для соответствующих значений аргумента.
2. Теперь у нас есть таблица со значениями аргументов и функций. С этими данными мы должны построить эту функцию с помощью мастера диаграмм.
3. Для построения графика необходимо выделить нужный диапазон данных, строки со значениями аргументов и функциями
4.
.jpg»>
Записываем выводы в тетрадь (Слайд 5)
Заключение. График функции вида y=sinx+k получается из графика функции y=sinx с помощью параллельного переноса по оси y на k единиц
Если k >0, то график сдвигается вверх на k единиц
Если k
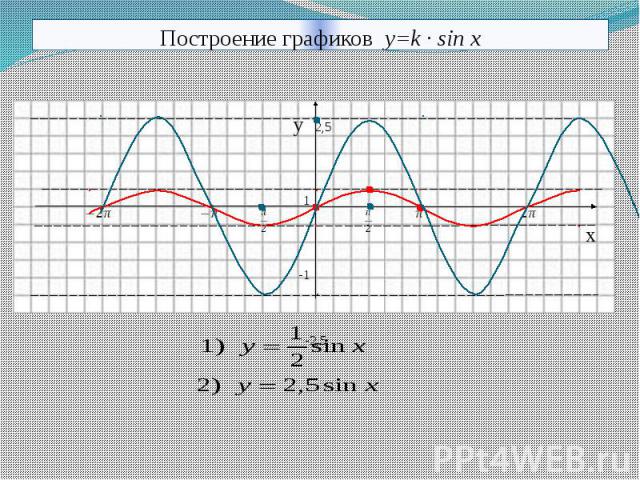
Построение и исследование функции вида y= k *sinx, k — const
Задание 2. В работе Лист2 Построить функции в одной системе координат y = синх у =2* синкс , у = * синкс , на интервале (-2π; 2π) и посмотрите, как изменится график.
(Чтобы не переустанавливать значение аргумента, скопируем существующие значения. Теперь нужно задать формулу, и построить график по полученной таблице.)
Сравниваем полученные графики. Анализируем вместе со студентами поведение графика тригонометрической функции в зависимости от коэффициентов.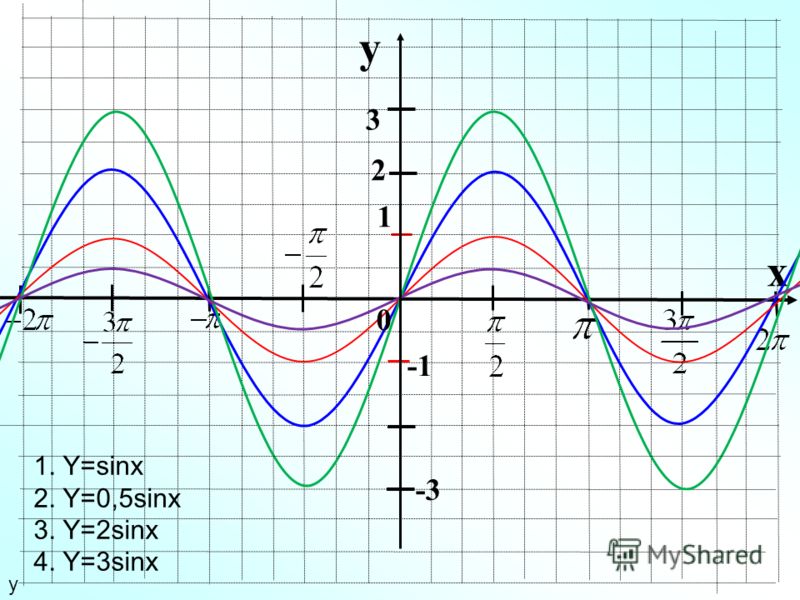
(Слайд 6)
https://pandia.ru/text/78/510/images/image005_66.gif»>x , на интервале (-2π; 2π) и посмотрите, как изменится график.
Сравним полученные графики. Анализируем вместе со студентами поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 8)
https://pandia.ru/text/78/510/images/image008_35.jpg»>
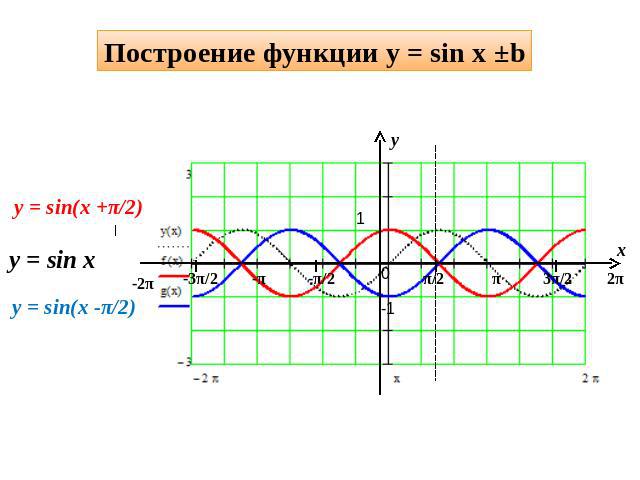
Записываем выводы в тетрадь (Слайд 11)
Заключение. График функции вида y=sin(x+k) получен из графика функции y=sinx с помощью параллельного переноса вдоль оси ОХ на k единиц
Если k >1, то график сдвинут вправо по оси OX
Если 0
IV . Первичное закрепление полученных знаний
Дифференцированные карточки с заданием построить и изучить функцию с помощью графика
Y=6 *sin(x) | Д= 1-2 грех Х | Д= — грех (3x+ ) | |
1. | |||
2. Объем значения | |||
3. Паритет | |||
4. Периодичность | |||
5. Интервалы постоянства | |||
6. зазоры монотонность | |||
Функция повышения | |||
Функция убавки | |||
7. | |||
Минимум | |||
Максимум |
Домен 
Крайние значения функции В . Организация домашних заданий
Постройте график функции y=-2*sinх+1 , исследуйте и проверьте правильность построения в среде электронных таблиц Microsoft Excel. (Слайд 12)
ВИ . Отражение
Теперь рассмотрим вопрос о том, как строить тригонометрические функции кратных углов ωx , где ω — некоторое положительное число.
Построить график функции y = sin ωx Сравним эту функцию с уже изученной нами функцией y = sinx . Предположим, что при x = x 0 функция y = sin x принимает значение равное 0 .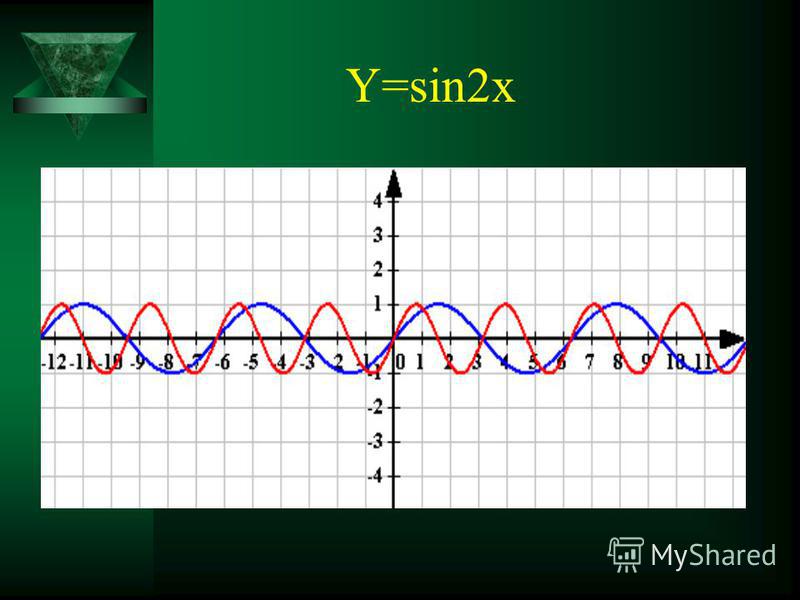
Затем
у 0 = грех х 0 .
Преобразуем это отношение следующим образом:
Следовательно, функция y = sin ωx at X = x 0 / ш принимает то же значение в 0 , что является функцией y = sin x at x = x 0 . А это значит, что функция y = sin ωx повторяет свои значения в ω раз чаще, чем функция y = sinx . Итак, график функции y = sin ωx получено «сжатием» графика функции y = sinx в ω раз по оси X.
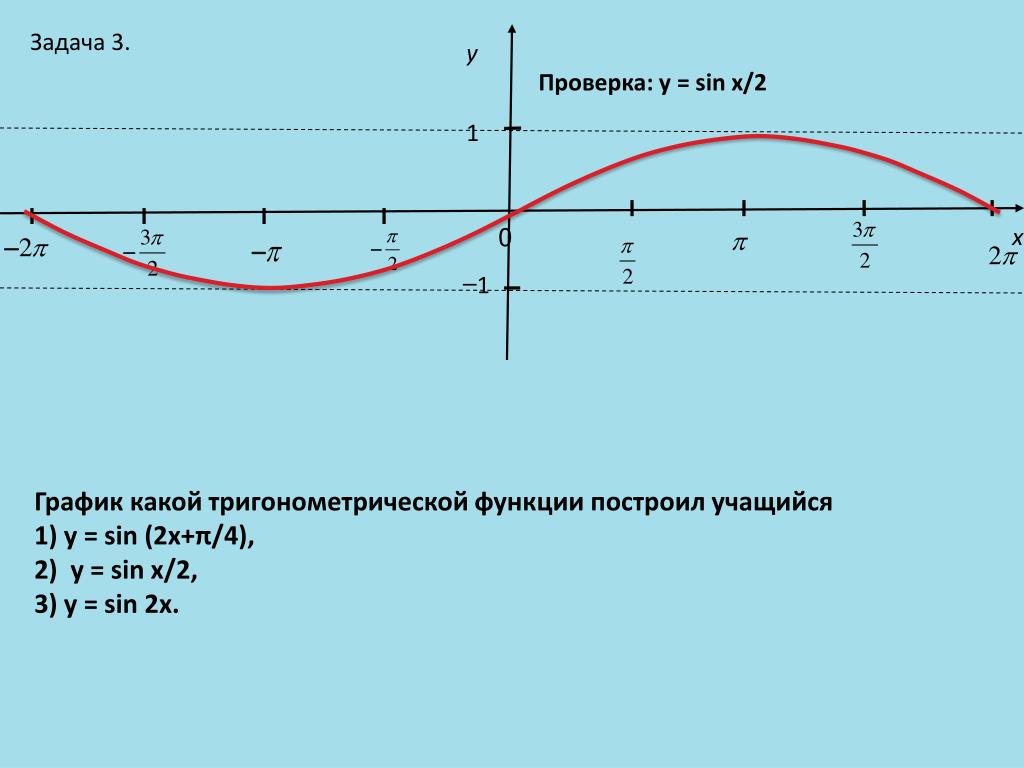
Например, график функции y = sin 2x получен «сжатием» синусоиды y = sinx два раза по оси абсцисс.
График функции у = sin х / 2 получается «растягиванием» синусоиды у = sin х в два раза (или «сжатием» в 1 / 2 раз) по оси x.
Так как функция y = sin ωx повторяет свои значения в ω раз чаще, чем функция
y = sinx , то ее период в ω
В раз меньше периода функции y = sinx .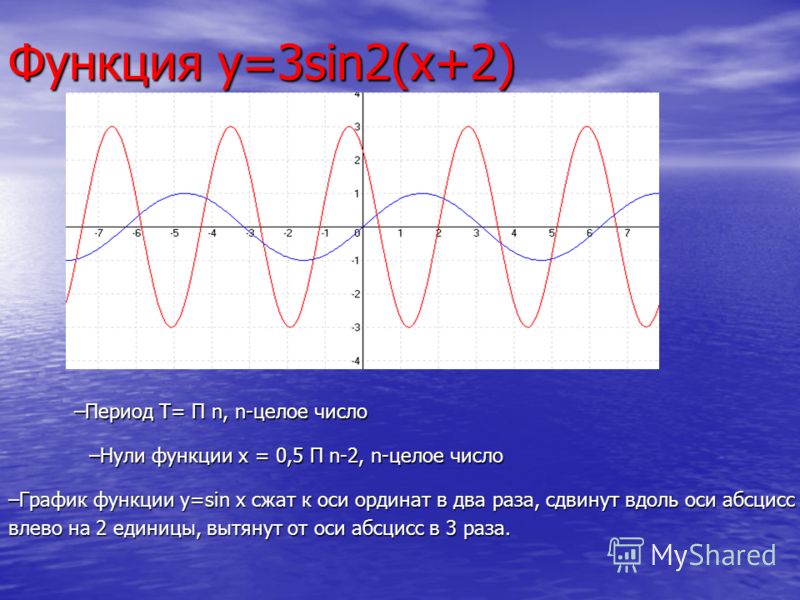
Например, период функции y = sin 2x равен 2π / 2 = π , а период функции у = sin х / 2 равно π
/ х / 2 = 4π .
Интересно изучить поведение функции y = sin ax на примере анимации, которую очень легко можно создать в программе maple :
Аналогично строятся графики и для других тригонометрических функций кратных углов. На рисунке показан график функции y = cos 2x , которая получается «сжатием» косинуса y = cos x дважды по оси x.
График функции y = cos x / 2 получается путем «растягивания» косинуса y = cos x дважды вдоль оси x.
На рисунке вы видите график функции y = tg 2x , полученный «сжатием» тангенсоида y = tgx дважды по оси абсцисс.
График функции y = tg x / 2 , полученный «растягиванием» тангеноида y = tgx дважды вдоль оси x.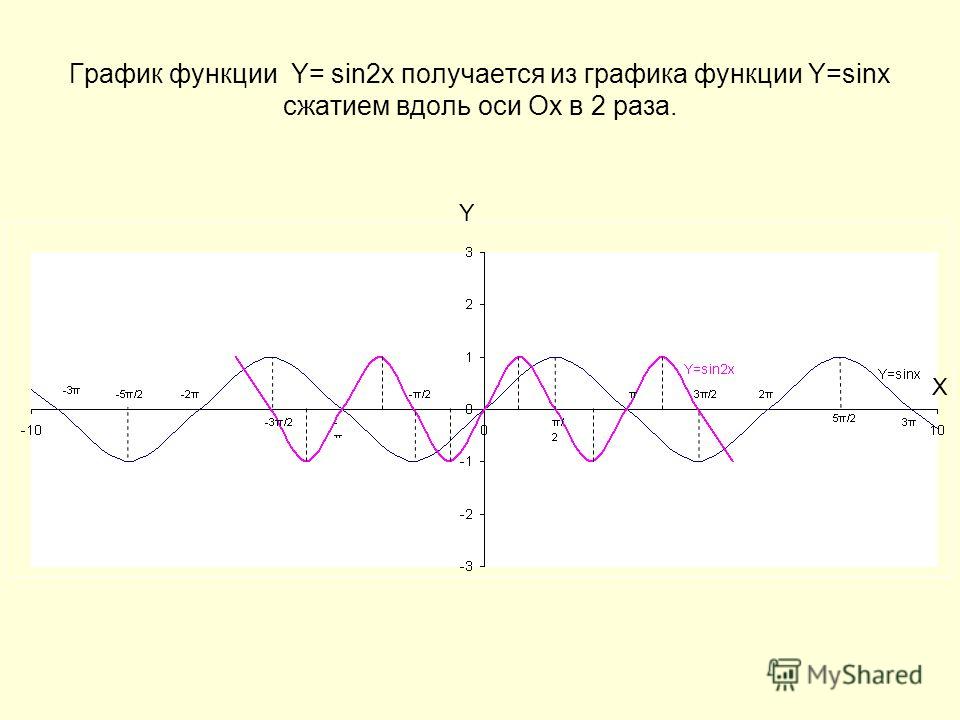
И, наконец, анимация в исполнении программы maple:
Упражнения
1. Постройте графики этих функций и укажите координаты точек пересечения этих графиков с осями координат. Определить периоды этих функций.
а). у = грех 4x / 3 Г). у=тг 5x / 6 и). у = cos 2x / 3
б). у= cos 5x / 3 д). у=ctg 5x / 3 ч). у=ctg х / 3
в). у=тг 4x / 3 д). у = sin 2x / 3
2. Определить периоды функций y = sin (πx) и y = tg ( πх/2 ).
3. Приведите два примера функции, которая принимает все значения от -1 до +1 (включая эти два числа) и периодически изменяется с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и периодически изменяются с периодом π/2 .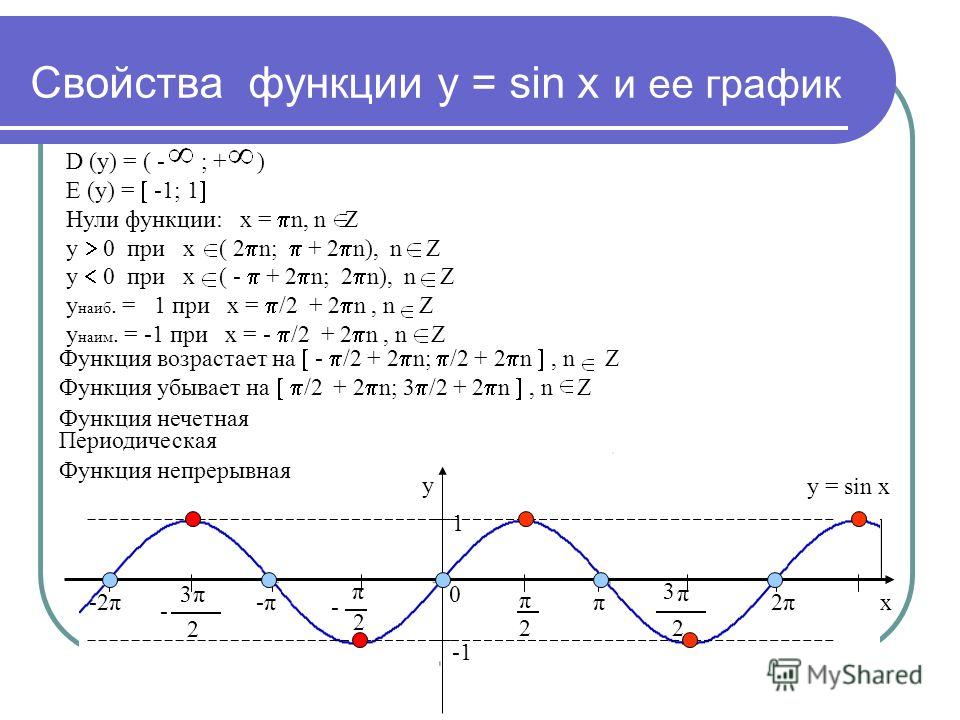
5. Приведите два примера функций, которые принимают все вещественные значения и периодически изменяются с периодом 1.
6 *. Приведите два примера функций, принимающих все отрицательные значения и нуль, но не принимающих положительных значений и периодически изменяющихся с периодом 5.
Как построить график функции y=sin x? Сначала рассмотрим график синуса на отрезке.
Берем один отрезок длиной 2 клетки тетради. Отмечаем единицу на оси Оу.
Для удобства число π/2 округлим до 1,5 (а не до 1,6, как того требуют правила округления). В этом случае отрезок длины π/2 соответствует 3 клеткам.
На оси Ох отмечаем не одиночные отрезки, а отрезки длиной π/2 (каждые 3 клетки). Соответственно отрезок длины π соответствует 6 клеткам, отрезок длины π/6 соответствует 1 клетке.
При таком выборе одного отрезка график, изображенный на листе тетради в рамке, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на интервале:
Полученные точки отмечаются на координатной плоскости:
Поскольку y=sin x является нечетной функцией, график синусов симметричен относительно начала координат — точки O(0;0).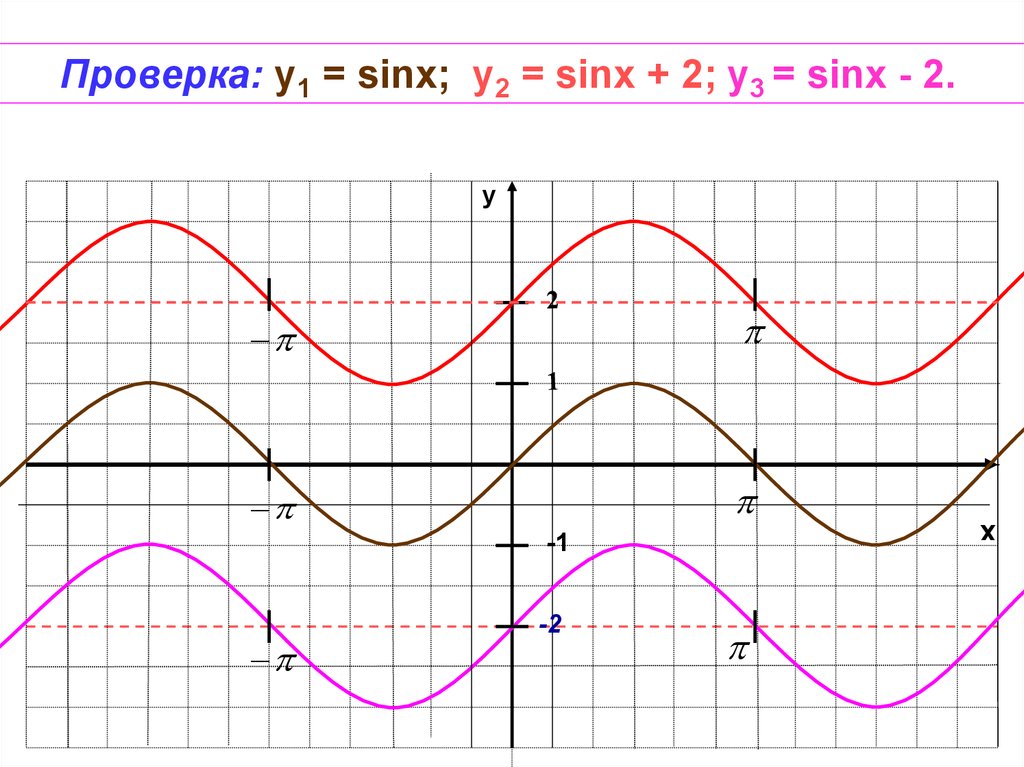
С учетом этого факта продолжаем строить график влево, тогда точек -π:
Функция y=sin x является периодической с периодом T=2π. Поэтому график функции, взятый на отрезке [-π; π], повторяется бесконечное число раз вправо и влево.
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, предложения! Все материалы проверяются антивирусной программой.
Учебники и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные конструкторские задачи для 7-10 классов
Программная среда «1С:Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).
- График функций.
- Как построить график и его масштаб.
- Примеры.
свойств синуса. Y=грех(Х)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы их помните?
Давайте подробнее рассмотрим функцию Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения — множество действительных чисел.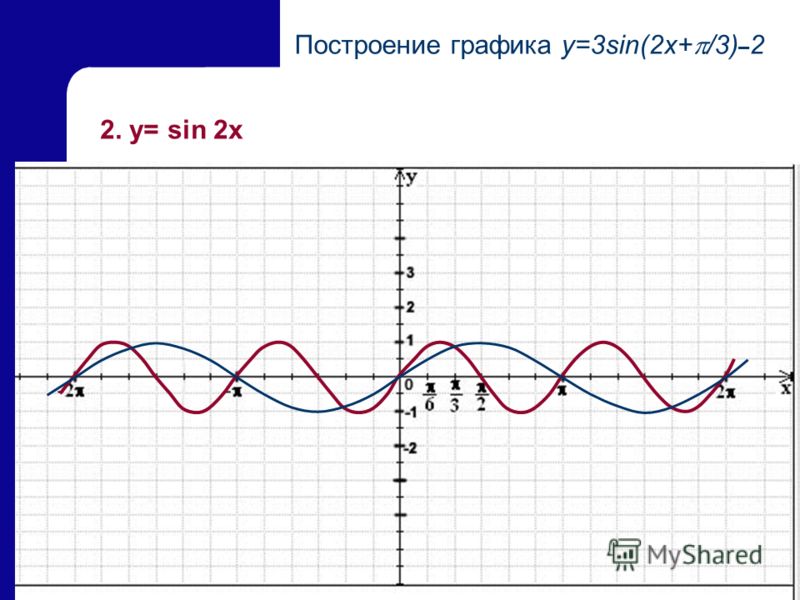
2) Нечетная функция. Напомним определение нечетной функции. Функция называется нечетной, если верно равенство: y(-x)=-y(x). Как мы помним из формул призраков: sin(-x)=-sin(x). Определение выполнено, поэтому Y=sin(X) — нечетная функция.
3) Функция Y=sin(X) возрастает на интервале и убывает на интервале [π/2; π]. При движении по первой четверти (против часовой стрелки) ордината увеличивается, а при движении по второй четверти – уменьшается.
4) Функция Y=sin(X) ограничена снизу и сверху. Это свойство связано с тем, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при x = — π/2+ πk). Наибольшее значение функции равно 1 (при x = π/2+ πk).
Воспользуемся свойствами 1-5 для построения графика функции Y=sin(X). Мы будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке.
Особое внимание следует уделить шкале. По оси ординат удобнее взять один отрезок, равный 2 клеткам, а по оси абсцисс — один отрезок (две клетки) принять равным π/3 (см.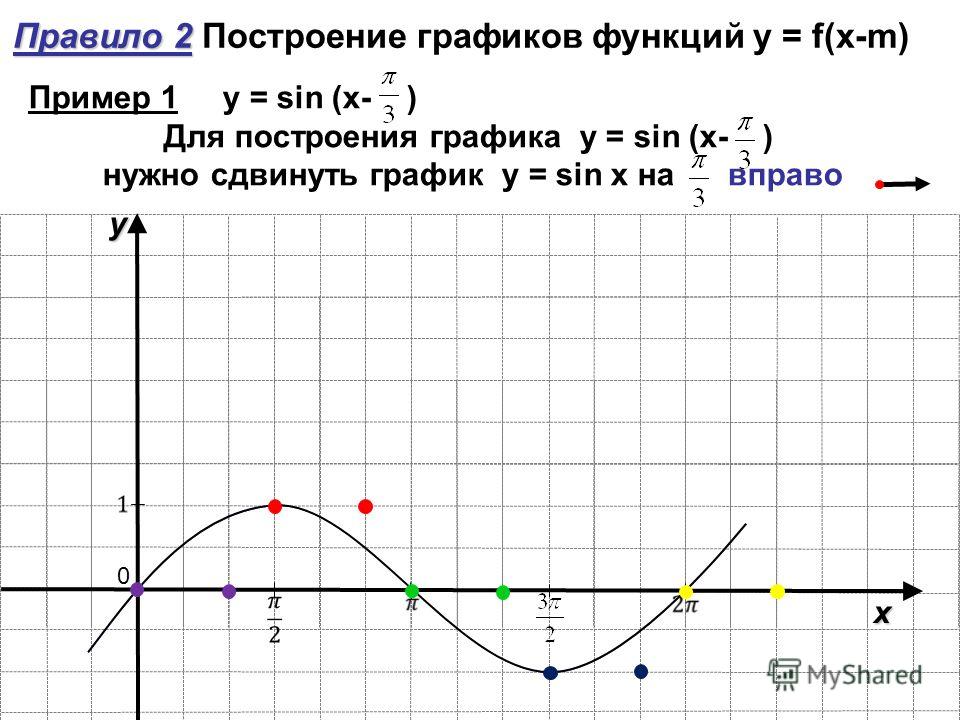
рисунок).
Построение графика функции sine x, y=sin(x)
Вычислим значения функции на нашем отрезке:
Построим график для наших точек с учетом третьего свойства.
Таблица преобразования формул призраков
Воспользуемся вторым свойством, которое говорит о том, что наша функция нечетна, а это означает, что она может быть отражена симметрично относительно начала координат:
Мы знаем, что sin(x+ 2π) = sin( Икс). Это означает, что на интервале [- π; π] график выглядит так же, как и на отрезке [π; 3π] или или [-3π; — пи] и так далее. Нам осталось аккуратно перерисовать график на предыдущем рисунке по всей оси абсцисс.
График функции Y=sin(X) называется синусоидой.
Запишем еще несколько свойств по построенному графу:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k является целым числом и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k — целое число.
7) Функция Y=sin(X) является непрерывной функцией. Посмотрим на график функции и убедимся, что наша функция не имеет разрывов, это означает непрерывность.
8) Диапазон значений: сегмент [- 1; один]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) является периодической функцией. Посмотрим еще раз на график и увидим, что функция принимает одни и те же значения через некоторые промежутки времени.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок) .
Наши графики пересекаются в одной точке A(π; 0), это ответ: x = π
2. Постройте график функции y=sin(π/6+x)-1
Решение: Искомый график получается путем перемещения графика функции y=sin(x) на π/6 единиц в влево и на 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
График функции показывает, что наибольшее и наименьшее значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.