Как решать Задачи по Математике 5 класс (2017) + Примеры, Таблицы
Editor choiceСохранитьSavedRemoved 10

Существует много причин, по которым ребёнок не может решить задачу по математике 5 класс. В большинстве из них он не виноват, поэтому стоит ему помочь разобраться с проблемой. Задачи не такие трудные, но в связи с появлением дробей и уравнений иногда сложно определить способ и верный путь их решения.
Содержание статьи:
Почему инструкция лучше решебника
В этой инструкции вы сможете найти типовые задачи, которые встречаются в курсах математики за 5 класс и разобранное, подробное, пошаговое решение. Это значительно полезнее книг, так как в них собраны далеко не все задачи, а те решения, которые есть, сжаты до минимума. Поэтому пользоваться решебником — порой не самый лучший выход.

Решебник по математике не всегда может дать исчерпывающую информацию
Как правило, при составлении ответов на свои задачи авторы не расписывают подробности и дают решения не ко всем номерам. Возможно, в расчёт идёт тот факт, что ученик способен справиться самостоятельно. Но вдруг ребёнок пропустил тему, что же тогда делать?
Лучший вариант — посмотреть решение типовых задач с пояснениями каждого действия. В этой инструкции собраны самые распространённые примеры, которые вызывают трудности у детей при решении, а также родителей при попытке объяснить задачу.
вернуться к меню ↑ вернуться к меню ↑Почему важно уметь решать задачи по математике
Математика — точная дисциплина, связанная с вычислениями. Но её часто называют царицей всех наук. Это не просто так. Основное, чему учатся дети — решение конкретно поставленных задач. Это самое важное для развития любого человека.
Для построения правильного ответа на задачу нужно выделить:
- главную мысль;
- заданное условие;
- что требуется найти;
- связь между искомым и данным.

Математика — один из самых важных предметов в школьной программе
На основе этого строится логичное решение с использованием условий для получения требуемого результата. Вместе с этим развивается познавательная активность, логические мышление.
вернуться к меню ↑ вернуться к меню ↑Какие бывают задачи по математике в 5-ом классе
В 5-ом классе по математике встречается несколько разновидностей задач. Этот год самый важный для ученика, потому что здесь собраны все базовые условия, которые углублённо решаются в следующие годы обучения. Здесь представлен список самых распространённых задач:
- на базовые арифметические действия;
- на скорость, время и расстояние;
- на движение;
- решаемые алгебраическим способом — проценты, дроби, уравнения;
- решаемые геометрическим способом — площадь, длина.

Существует немало различных задач и путей их решения
Для грамотного решения всех типов задач можно составить единый алгоритм:
- Прочитайте вдумчиво, не торопясь полный текст задачи;
- Определите к какому типу она относится;
- На основе этого составьте краткое условие или таблицу;
- Начните читать каждое предложение отдельно, заполняя таблицу или краткое условие;
- Определите вопросом то, что нужно найти;
- Выберите вариант решения и составьте выражение, в результате которого получится ответ;
- Проверьте правильность и соответствие условию;
- Запишите полученный ответ.
Этот алгоритм можно применять ко всем типам задач. В разных заданиях отличаться будут только числа и способ решения.
Далее представлены все типы задач, которые могут встретить пятиклассники в учебниках и задачниках по математике. Все они будут разобраны на двух примерах с подробным разъяснением.
вернуться к меню ↑ вернуться к меню ↑Задачи на сложение, вычитание, умножение и деление
вернуться к меню ↑Пример 1
На кухне лежит пакет, в котором 3000 грамм муки. Повар для выпечки из него брал 4 раза муку. В первый раз 250 грамм, во второй 320 грамм, в третий 140 грамм, в четвёртый 690 грамм. Найдите сколько муки осталось в пакете.
Решение
Таблица 1 — Краткое условие
| Условие | Количество |
|---|---|
| Было | 3000 |
| Первый раз | 250 |
| Второй раз | 320 |
| Третий раз | 140 |
| Четвёртый раз | 690 |
| Осталось | ? |
- Сделанная таблица наглядно показывает, что для расчёта остатка нужно из 3000 вычесть количество, которое повар забрал всего;
- Для этого сложим количество муки, которое повар израсходовал за четыре раза. Получается такое выражение: 250+320+140+690=1400 грамм;
- Теперь найдём остаток. Для этого из того, что было, вычтем полученное значение — 1400. Получим выражение: 3000-1400=1600 грамм. Это то, что от нас требовалось — найти сколько осталось муки;
- Записываем это в ответ к задаче.
Пример 2
В пассажирском поезде 12 вагонов. В каждом из них по 40 мест. Сколько осталось свободных мест, при условии, что в поездку отправились 352 пассажира?
Решение
Таблица 2 — Условие задачи
| Места в вагоне | Количество |
|---|---|
| Кол-во вагонов | 12 |
| Кол-во мест в вагоне | 40 |
| Кол-во пассажиров | 352 |
| Осталось мест | ? |
- Теперь приступаем к вычислениям. Для начала нам нужно узнать сколько всего свободных мест было в вагонах. Для этого умножим количество вагоном на количество свободных мест в каждом. Получается выражение: 40×12=480;
- Для того, чтобы найти сколько осталось свободных мест нужно, из полученного значения вычесть занятые места. Получим выражение: 480-352=128;
- Полученное число — это ответ на вопрос из условия задачи. Записываем его.
Эти задачи самые простые и встречаются в начале учебного года. Используют их авторы учебников для того, чтобы ученик мог вспомнить алгоритм решения и базовые правила.
вернуться к меню ↑ вернуться к меню ↑Задачи на скорость, время, расстояние
вернуться к меню ↑Пример 1
За 7 часов теплоход проделал путь в 210 км. Поезд за 4 часа преодолел 420 км. Во сколько раз скорость поезда больше скорости теплохода?
Решение
Таблица 3 — Краткое условие
| Скорость | Время | Расстояние | |
|---|---|---|---|
| Теплоход | ? | 7 | 210 |
| Поезд | ? | 3 | 360 |
- Приступим к поиску неизвестных. Нам нужно узнать скорость у теплохода и поезда. Для этого используется формула — скорость равна результату деления расстояния на время. Математически записывается так — V=S:T;
- Подставив числа из условия, получаем выражение для скорости теплохода. 210:7=30 км/ч;
- Также поступаем и для расчёта скорости поезда. 360:3=120 км/ч;
- Мы нашли все неизвестные и теперь возвращаемся к главному вопросу задачи. Нам нужно определить во сколько раз скорость поезда превышает скорость теплохода;
- Для этого делим большее значение на меньшее. Получается: 120:30=4;
- В ответ пишем, что скорость теплохода и поезда отличается в 4 раза.
Пример 2
Автомобилист за 4 часа проехал 320 километров. Какой путь проделает автомобиль за 8 часов с той же скоростью?
Решение
Таблица 4 — краткое условие
| Скорость | Время | Расстояние | |
|---|---|---|---|
| Автомобиль | ? | 4 | 320 |
- Ищем неизвестные. В нашем случае нужно найти скорость. Для этого воспользуемся формулой V=S:T. Подставляем числа и получаем: 320:4=80 км/ч;
- После того, как стали известны все значения, переходим к главному вопросу задачи — сколько проедет автобус за 8 часов с той же скоростью;
- Для расчёта используем формулу S=VT. Подставляем числа и получаем: 80×8=640 км;
- Записываем полученное значение в ответ к задаче.
Решение этих задач требует знать основную формулу S=VT. Расшифровывается она так: расстояние равно произведению скорости на время. Из неё вытекают все решения для нахождения неизвестных. Также для упрощения задачи можно рисовать схему.
вернуться к меню ↑ вернуться к меню ↑Задачи на движение
вернуться к меню ↑Пример 1
Расстояние между двумя городами 125 километров. В одно и то же время выезжают два велосипедиста навстречу. Скорость первого велосипедиста 10 км/ч. Второй едет со скоростью 15 км/ч. Через какое время они встретятся?
Решение
Таблица 5 — краткое условие
| Скорость | Время | Расстояние | |
|---|---|---|---|
| 1 велосипедист | 10 | ? | 125 |
| 2 велосипедист | 15 | ? | 125 |
- Теперь переходим к расчётам. Логично, что для встречи велосипедисты должны проехать в сумме весь путь. Необязательно одинаковое расстояние, так как оно зависит от скорости каждого из них;
- Нам нужно посчитать какое расстояние они преодолевают в час. Для этого сложим скорости первого и второго. Получаем выражение: 10+15=25 км/ч;
- Для расчёта времени через которое они встретятся нужно воспользоваться формулой T=S:V. Подставляем числа и получаем выражение: 125:25=5 ч;
- Соответственно, велосипедисты пересекутся между собой через 5 часов. Записываем это в ответ.
Пример 2
Расстояние, на котором между собой находятся два города — 600 км. Из них одновременно на встречу друг другу выехали два автомобиля. В пути они встретились через 5 часов. Найдите скорость первого автомобиля, если известно, что второй ехал со скоростью 80 км/ч.
Решение
Таблица 6 — краткое условие
| Скорость | Время | Расстояние | |
|---|---|---|---|
| 1 автомобиль | ? | 5 | 600 |
| 2 автомобиль | 80 | 5 | 600 |
- Переходим к расчётам. Для нахождения скорости первого автомобиля нам нужно знать, сколько километров он проехал. Найти это можно, вычтя из общего пути расстояние, которое проехал второй до их встречи;
- Используем формулу S=VT. Подставляем числа из таблицы, получаем выражение: 80×5=400 км. Это расстояние прошёл второй автомобиль до встречи с первым. Значит, первый проехал всего: 600-400=200 км;
- Теперь можно найти скорость первого автомобиля. Используем формулу V=S:T. Подставляем числа: 200:5=40 км/ч;
- Полученное значение — ответ на главный вопрос задачи. Записываем его.
Если вас смущает время, которое написано один раз для всех объектов, то можно поступить следующим образом. Записывайте его отдельно к каждой строке и рядом нарисуйте отрезок, который снизу отмечен расстоянием, а сверху подписан временем.
вернуться к меню ↑ вернуться к меню ↑Задачи, решаемые алгебраическим способом
вернуться к меню ↑Пример 1
Из цистерны отлили 80 литров молока, в нем осталось на 240 литров больше, чем отлили. Сколько литров молока было в цистерне с самого начала?
Решение
Таблица 7 — краткое условие задачи
| Было | Х |
|---|---|
| Отлили | 80 |
| Осталось | 240+80 |
- Приступаем к расчётам. Нам нужно узнать, сколько было молока изначально. Для этого составляем уравнение. От начального количества вычитаем отлитое и получаем остаток;
- Математически получаем такую запись: x-80=240+80;
- Начинаем решение с того, что считаем всё, что можно посчитать. В данном случае складываем правую часть уравнения. 240+80=320. Теперь уравнение имеет вид: x-80=320;
- Теперь находим «x». Используем базовое правило математики и получаем следующее: x=320+80. Считаем правую часть и получаем: x=400;
- Возвращаемся к началу и смотрим, что мы обозначили за «x». В этом примере за икс мы взяли объём молока, который был изначально. То есть, изначально было 400 литров молока;
- Записываем полученное значение в ответ.
Пример 2
Первое слагаемое на 52 больше второго слагаемого, а второе слагаемое на 14 меньше третьего слагаемого. Сумма трех слагаемых равна 327. Найдите каждое слагаемое.
Решение
- Записываем краткое условие в виде таблицы;
- Потребуется четыре строки, так как нам дали три слагаемых и их сумму;
- Заполняем таблицу числами, обозначив за икс последнее слагаемое. Выбираем третье, потому что от него зависят все остальные;
Таблица 8 — краткое условие задачи
| 1 слагаемое | (x-14)+52 |
|---|---|
| 2 слагаемое | x-14 |
| 3 слагаемое | x |
| Сумма | 327 |
- Приступаем к расчётам. Для нахождения слагаемых нужно решить уравнение, после чего число подставить в выражения из таблицы.
- Уравнение составляется исходя из условия – три слагаемых и сумма – складываем значения из второго столбца таблицы и приравниваем это к сумме.
- Получится такое выражение: (x-14)+52+(x-14)+x=327.
- Открываем скобки и упрощаем выражение: 3x+24=327.
- Переносим числа в правую часть: 3x=303
- Считаем икс: 303:3=101.
- Теперь подставляем число 101 в таблицу вместо икса.
- Получается третье слагаемое равно 101; второе: 101-14=87; первое: 87+52=139.
- Эти числа записываем в ответ. Легко проверить правильность решения просто сложив эти значения. Если пример получается правильный, то и решено всё верно.
Для правильного решения этих типовых задач необходимо ничего не напутать с иксом. Лучше потратить больше времени и сразу всё проверить, чем переделывать задание сначала. Неправильное обозначение повлечёт за собой ошибку на протяжении всего решения
вернуться к меню ↑ вернуться к меню ↑Задачи, решаемые геометрическим способом
вернуться к меню ↑Пример 1
В доме 4 двери. Ширина каждой 1 метр, высота — 2 метра. Сколько нужно белил, чтобы покрасить их с обеих сторон, при условии, что на 1 квадратный метр поверхности требуется 100 грамм белил? Ответ дайте в граммах.
Решение
Пример 2
Площадь прямоугольника 192 квадратных сантиметра, длина одной из сторон — 16 см. Найдите периметр прямоугольника.
Решение
Для решения геометрических задач нужно знать наизусть все формулы площадей и периметров. Без этого не получится даже приступить к решению задания.
вернуться к меню ↑ вернуться к меню ↑Нужен ли ребёнку репетитор по математике в пятом классе?
После перехода в средний этап школы у ребёнка может упасть успеваемость по некоторым предметам, в том числе и по математике. Более того математика — самый проблематичный предмет для детей. Некоторые родители сразу бьют тревогу и ищут репетиторов, чтобы исправить эту ситуацию.
На самом деле, не стоит делать поспешных выводов. Для начала нужно определить причину падения успеваемости. Возможно, некоторые из новых учителей просто халатно относятся к преподнесению нового учебного материала. Другие преподаватели не могут найти особый подход к ребёнку в связи с ограничением по времени.

У многих детей в школе возникают сложности с изучением математики
Это не значит, что ваш ребёнок неспособный к определённым дисциплинам. Попробуйте объяснить ему материал самостоятельно, ведь именно вы знаете своё чадо лучше других. Если и это не помогло, то обращайтесь к помощи репетитора.
Главная задача специалиста — найти персональный подход к каждому ученику. Они смогут максимально эффективно и просто объяснить ребёнку тему в зависимости от особенностей его восприятия и склада ума.
Перед обращением убедитесь, что ухудшение оценок произошло только по нескольким взаимосвязанным предметам, а не в целом. Если успеваемость сильно упала в общем плане, то скорее всего ребёнок ленится. Связано это может быть со скукой на уроках и утратой интереса к учёбе. В таком случае, поговорите с ним, объясните, что это очень важно и пригодится в жизни, приводя аргументы и наглядные примеры.
Конечно, если это связано, например, с пропуском занятий по причине болезни, или в школе неправильно преподносится материал, то стоит задуматься о найме репетитора. Он поможет в кратчайшие сроки улучшить результаты ребёнка.
вернуться к меню ↑ вернуться к меню ↑Как решить проблемы с математикой
Как только у ребёнка появляются проблемы с математикой родители почему-то начинают думать, что причина заключается в плохой предрасположенности к точным наукам. Потому что формулы вроде бы знает, простые примеры решить тоже может, но каждая контрольная и самостоятельная работа превращается в целое испытание для всей семьи. Все сидят в ожидании результатов. Никогда нельзя сказать точно какую оценку получит ребёнок — четвёрку или двойку.
Дети часто получают плохие отметки именно по математике
Также много жалоб по типу: занимаемся все выходные напролёт, учим эту математику, учим, а в итоге всё равно результат прежний. На самом деле, причина такого плохого восприятия — отсутствие адекватных причин заниматься всеми этими цифрами. Большинство родителей сходятся во мнении, что ребёнок просто гуманитарий, главное — литература, история, обществознание, а математика неважна.
вернуться к меню ↑Гуманитариям математика не нужна?
Это огромная ошибка, ведь для лучшего восприятия точных наук этому самому «гуманитарию» нужно лишь вдохновение и цель. Отлично будет, если ребёнку объяснить, что математика — это такая же наука, как и любая другая, и она не ограничивается уравнениями и задачами. Это нечто большее. Математика позволяет изменить мышление, воспринимать старые вещи по-новому.
Главная проблема всех гуманитариев, которые имели проблемы с математикой — это логика. Для составления, например, грамотной и структурированной статьи нужно руководствоваться не только правилами русского языка, но и логикой изложения мысли. Все части должны быть связаны между собой, в то же время, должны легко читаться отдельные фрагменты.
Именно логическое мышление в первую очередь развивает математика и воспринимать это нужно, как возможность расширения кругозора и свежего взгляда на старое. Также точные науки помогают дисциплинировать свой ум и комплексно подходить к решению поставленных задач.
вернуться к меню ↑Математика — сложный предмет
Самая популярная отговорка заключается в том, что математика — самый сложный предмет из всех. Нет, на самом деле это одна из самых простых и понятных дисциплин. Для сравнения, возьмите наш богатый русский язык.
Мало того, что в нём существует немало правил орфографии, пунктуации, стилистики, так ещё и исключения есть почти в каждом правиле. Вот уж где нужно запоминать «тонну» информации.
В то же время в математике существуют базовые правила, на которых строятся все остальные. То есть, более сложное всегда можно привести к простому. Всё построено на железной логике, и, следуя этим правилам, вы сможете решить задачи, которые казались на первый взгляд непосильными.
Вспомните, как учат всех детей. Для того, чтобы научить их писать, сначала нужно выводить палочки, точки, изгибы. Потом уже буквы, а из букв — простые слова, из слов — предложения.
Начните изучать математику с самых простых уравнений
В математике с самого начала всё объясняется на пальцах или предметах. При этом, за то же самое время, потраченное на русский язык и на математику, прогресс в изучении второй будет больше. Например, считать учатся дети на яблоках, конфетках.
Используйте это и для решения более сложных задач. В пятом классе аналогии привести не составит труда. Это поможет ребёнку ассоциировать вычисления не с сухими числами, а, например, с мандаринами.
вернуться к меню ↑ вернуться к меню ↑Формула спокойствия
Часто плохие оценки становятся причиной ссор между родителями и детьми. Это категорически неправильно. Вместо того, чтобы высказывать ребёнку, что он «ленится», «не думает о будущем» да и в общем «туго соображает», следует отвести от неудачи или помочь исправиться с ней.
Но под помощью подразумевается не «вдалбливание» и «зубрёжка» неинтересных формул и правил. Следует возбудить интерес к теме, которая была плохо воспринята. Да и к тому же поставить правильную цель ребёнку. Не нужно говорить, что от оценок зависит его будущее. Вообще не зацикливайте внимание на оценках.
По исследованиям российских психологов дети, которые хотели стать врачами, инженерами и просто хорошими людьми, быстро повышали свою успеваемость. А те ученики, которым с первого класса «вдалбливают» в голову знания, думали только о том, как не стать худшим в классе, и уделяли своим отметкам слишком большое внимание.
Лучшим вариантом по-прежнему остаются занятия с репетитором. Он сохранит нервы, и вам, и ребёнку. Обеспечивая нужное количество времени на обучение и выбрав правильный подход, ученик станет показывать результаты лучше прежнего. Но, моментально отличником вашего ребёнка это не сделает.
Надеемся, что вы смогли найти решение задач, которое искали. Также для понимания темы рекомендуем посмотреть видео по этой теме от организаторов специальной математической школы федерального уровня «Аристотель».
8.5 Общий Балл
Некоторые ученики, как пятых, так и других классов, часто сталкиваются с проблемами в изучении математики. В этом случае родителям не стоит впадать в панику. Следует уделить больше внимания детальному разбору примеров и задач. Если это не улучшит успеваемость, есть смысл обратиться за помощью к репетитору.
Плюсы
- Подробные инструкции помогут разобраться в решении задач и примеров
- Для изучения математики можно пользоваться решебниками
Минусы
- Полученных знаний в школе не всегда достаточно для понимания предмета
slovami.net
Тренажеры по математике 2 класс (задачи и примеры)
В математике, конечно же, важно уметь думать и мыслить логически, но не менее важна в ней практика. Половина ошибок на экзаменах по математике делается из-за неправильного вычисления простых действий с числами — сложение, вычитание, умножение, деление. А отработать эти навыки важно еще в начальной школе. Чтобы ничего не упустить, необходимо систематически заниматься с ребенком по специальным тетрадям — тренажерам. Они позволяют отработать математические навыки и умения и довести их до автоматизма. Тренажеры разнообразные, не обязательно скачивать их все, достаточно одного-двух понравившихся. Пособия можно использовать в работе с младшими школьниками не зависимо от программы, по которой ведется обучение.
Один из самых важных моментов математики за 2 класс — отработать до автоматизма таблицу умножения. Отводим этой теме целую страницу. Чтобы перейти на нее и скачать тренажер на таблицу умножения, кликните по картинке:

Далее пособия расположены сверху вниз в порядке увеличения сложности. Чтобы посмотреть и скачать тренажер, кликните по обложке.
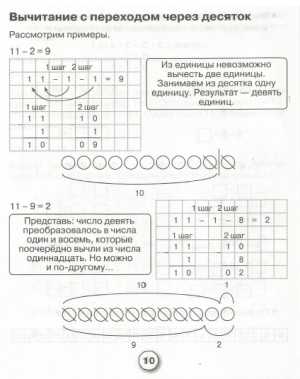
Математика. Решаем примеры с переходом через десяток.
Тетрадь для отработки навыков сложения и вычитания с переходом через десяток. Не просто примеры, а интересные игры и задания.

Карточки-задания. Математика. Сложение и вычитание. 2 класс
Удобные карточки для учителя второклашек. 2 варианта на сложение и вычитание одного вида. Подойдут для организации самостоятельной работы по математике в зависимости от продвижения по программе.


Математика. Сложение и вычитание в пределах 20. 1-2 классы. Е.Э.Кочурова
В разных курсах математике тема сложения и вычитание в пределах 20 изучается или в конце 1 класса, или в начале 2-го. В любом случае пособие поможет закрепить изученные способы манипуляций с числами, в некоторых заданиях эти способы представлены в виде своеобразных подсказок. В ходе самостоятельной работы с тетрадью ребенок ориентируется на образец выполнения и алгоритмические предписания. Умение пользоваться такими подсказками в учебе позволит ученику не только находить и использовать нужную информацию в ходе выполнения задания, но и осуществлять самопроверку.
Начинается тетрадь с отработки навыков сложения и вычитание в пределах 10, эта часть подойдет и для первоклашек.


Математика тренажерная тетрадь для 2 класса
Тетрадь содержит не только примеры на сложение и вычитание, но и перевод единиц друг в друга, и сравнение результатов вычисления (больше-меньше).

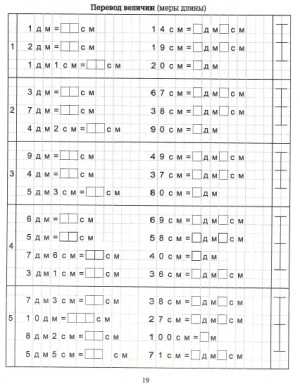
3000 примеров по математике (счет в пределах 100 часть 1)


Счет от 0 до 100
В этой прописи дается много примеров на сложение и вычитание, чтобы закрепить навыки устного счета в пределах 100.


Считаем правильно. Рабочая тетрадь по математике. Г.В.Белых
Тетрадь также выполнена в виде тренажера, сплошные примеры и уравнения. Начинается со счета в пределах десяти, далее — в пределах сотни (сложение, вычитание, умножение и деление), заканчивается сравнением уравнений (примеры со знаками больше, меньше, равно).


Пособия пригодятся и учителям начальных классов в их работе, и родителям для занятий дома с детьми, в частности, в летние каникулы. Задания разных уровней сложности позволят осуществить дифференцированный подход к обучению.
А еще у нас есть отличный онлайн тренажер по математике! Родителям не нужно ничего распечатывать и проверять, все это за вас совершенно бесплатно сделаем мы! Выбирайте режим и вперед >>
7gy.ru
Материал по математике (2 класс) по теме: Задачи по математике для 2 класса
По теме: методические разработки, презентации и конспекты
Сборник задач по математике для 2 классаВ данном сборнике собраны 14 задач на изученные виды для 2 класса по программе «Школа России»….
Задания по математике для 2 класса. (примеры и задачи)Предлагаемые задания предназначены для отработки математических умений (быстро и правильно вычислять, решать текстовые задачи). Материал может быть использован для работы на уроке…
Задачи по математике для 2 класса по теме «Косвенные задачи»Задачи по математике для 2 класса по теме «Косвенные задачи»….
Презентация к уроку по математике для 2 класса. Тема:Чтение и запись трехзначных чисел. Решение задач.Презентация к уроку по математике для 2 класса УМК «Гармония». Тема:Чтение и запись трехзначных чисел. Решение задач.Цель урока: Совершенствовать умения: читать и записывать трёхзначные чи…
Элективный курс по математике для 2 класса «Решение логических задач «В данном курсе рассматривается различные типы задач на развитие логического мышления ….
Карточки для индивидуальной работы по математике для 2 класса по теме «Решение задач в два действия». УМК Школа РоссииКарточки для индивидуальной работы по математике для 2 класса по теме «Решение задач в два действия. Повторение» можно использовать по любому УМК, как на уроке, так и во внеурочное время….
Карточки для индивидуальной работы по математике для 2 класса по теме «Составные задачи на нахождение третьего числа»». УМК Школа РоссииКарточки для индивидуальной работы можно использовать как на уроке, так и дома для закрепления решения задач….
nsportal.ru
Олимпиада по математике 2 класс, уравнения, задачи и загадки с ответами
Проводя в своем образовательном учреждении дистанционную олимпиаду, вы сможете привить ученикам 2-го класса любовь и познавательный интерес к изучению математики. Задания для проведения олимпиады во втором классе должны быть не слишком сложны и вместе с этим достаточно разнообразными и интересными. Именно поэтому в составлении заданий стоит довериться профессионалам, работающим в этом направлении.
На этой странице представлены примеры олимпиадных заданий с готовыми ответами. Этот материал может быть использован учителями в качестве тренажера для подготовки учеников к олимпиаде.
Скачайте задания, заполнив форму!
После того как укажете данные, кнопка скачивания станет активной
Уравнения для 2-го класса
1. Решите уравнения:
45 – х = 25
х + 7 = 17
28 – х = 13
2. Решите уравнения:
22 + x = 28
x – 12 = 13
х – 15 = 15
3. Решите уравнения:
13 + х = 20
x – 16 = 13
x – 6 = 10
4. Определите уравнение, решение которого равно 7
a) 19 — х = 10
b) х + 5 = 12
c) x — 5 = 2
5. Решите уравнения:
x + 37 = 49
x — 35 = 59
6. Найдите решение уравнений:
22 + x = 48
100 — x = 67
7. Решите предложенные уравнения
x + 25 = 49
x — 23 = 45
x + 13 = 37
8. Найдите решения данных уравнений
x — 18 = 34
x + 36 = 65
9. Решите уравнения
12 + x = 25
x – 18 = 30
х – 18 = 18
10. Верно ли решено уравнение
99 — 18 = x + 59
x = 22
Задачи для олимпиад в 2 классе
Задача №1
В бочке 26 ведер воды. Из нее забрали 17 ведер. Сколько необходимо ведер воды долить, чтобы в бочке стало 30 ведер воды?
Задача №2
Начало сказки «Снежная королева» на 20 странице, а конец – на 50. Сколько страниц нужно прочитать?
Задача №3
Катя, Галя и Оля, играя, спрятали по игрушке. Они играли с медвежонком, зайчиком и слоником. Известно, что Катя не прятала зайчика, а Оля не прятала ни зайчика, ни медвежонка. У кого какая игрушка?
Задача №4
В поезде 22 вагона. Класс расположился в 11 вагоне. Сколько вагонов перед ними и сколько за ними?
Задача №5
Написано 99 чисел: 1, 2, 3, …98, 99. Сколько раз в записи чисел встречается цифра 5?
Задача №6
В кастрюле одновременно варились 5 морковок. Сварились они за 20 минут. За сколько минут сварилась одна морковка?
Задача №7
Какое число меньше 29, от которого можно отнять 3 раза по 9?
Задача №8
Рыбаки выловили за один улов 46 кг рыбы. Сколько ещё надо выловить рыбы, если по плану нужно 90 кг?
Задача №9
Механик отремонтировал за месяц 67 мотоциклов. Сколько ему ещё осталось отремонтировать, если всего в мастерской 77 мотоциклов?
Задача №10
В лагерь приехали отдыхать 15 групп детей. Хотя лагерь может принять на отдых ещё 8 групп. Сколько групп всего может принять лагерь на отдых?
Математические загадки
Загадка №1
Мельник пошел на мельницу и увидел в каждом углу по 3 кошки. Сколько ног на мельнице?
Загадка №2
Термометр показывает плюс 15 градусов. Сколько градусов покажут два таких термометра?
Загадка №3
Около столовой, где обедали лыжники, пришедшие из похода, стояли 20 лыж, а в снег было воткнуто 20 палок. Сколько лыжников ходило в поход?
Загадка №4
Дед, баба, внучка, Жучка, кошка и мышка тянули-тянули репку и, наконец, вытянули. Сколько глаз смотрело на репку?
Загадка №5
В 9-этажном доме есть лифт. На первом этаже живет 2 человека, на втором — 4 человека, на третьем — 8 человек, на четвертом — 16, на пятом — 32 и так далее. Какая кнопка в лифте этого дома нажимается чаще других?
Ответы к уравнениям
| Уравнение | № 1 | № 2 | № 3 | № 4 | № 5 |
| Ответ | x=20 x=10 x=15 | x=6 x=25 | x=7 x=29 x=16 | b) c) | x=32 x=12 x=24 |
| Уравнение | № 6 | № 7 | № 8 | № 9 | № 10 |
| Ответ | x=26 x=33 | x=24 x=68 x=24 | x=52 x=29 | x=13 x=48 x=36 | да |
Ответы к задачам
Задача 1
21 ведро
Задача 2
31 страницу
Задача 3
У Оли — слоник, у Кати — медвежонок, у Гали — зайчик
Задача 4
10 и 11 вагонов
Задача 5
20 раз
Задача 6
за 20 минут
Задача 7
27
Задача 8
44 кг
Задача 9
10 мотоциклов
Задача 10
23 группы
Ответы на загадки
Загадка 1
3*4*4+2=50
Загадка 2
15 градусов
Загадка 3
10 лыжников
Загадка 4
12 глаз
Загадка 5
Кнопка первого этажа
Скачайте задания, заполнив форму!
После того как укажете данные, кнопка скачивания станет активнойДругие классы
Обновлено: , автор: Валерия Токареваruolimpiada.ru
Олимпиадные задачи по математике 1 класс
 Школьные программы все разные, а олимпиады для всех равны, и задания в них не из легких. Но все же, при правильном подходе, и олимпиадные задачки ребенка можно научить щелкать, как орешки. Наша подборка задач по математике выросла из задач разных современных международных олимпиад по математике: математические ступеньки, зеленая математика и других. В принципе, задания перекликаются, и поняв саму стратегию и тактику, дети с легкостью смогут решить и другие подобные задачи, поставленные перед ним.
Школьные программы все разные, а олимпиады для всех равны, и задания в них не из легких. Но все же, при правильном подходе, и олимпиадные задачки ребенка можно научить щелкать, как орешки. Наша подборка задач по математике выросла из задач разных современных международных олимпиад по математике: математические ступеньки, зеленая математика и других. В принципе, задания перекликаются, и поняв саму стратегию и тактику, дети с легкостью смогут решить и другие подобные задачи, поставленные перед ним.
Задачи из олимпиад по математике:
1. У Маши 8 книг. Это на две книги меньше, чем у Васи. Сколько книг у Васи?
Ответ:
2. Если размотать паутину, то получится нить длиной 4 дм 1 см. Укажи длину только в сантиметрах.
Ответ:
3. Синичка ест разных насекомых. Определи по схеме, сколько комаров и мошек могла бы съесть синичка?
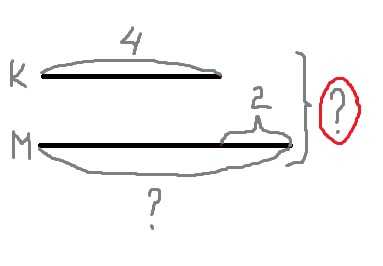
Ответ:
4. На одной дорожке Вася заметил 6 муравьев, это на 3 муравья меньше, чем на второй. Сколько насекомых ползло по второй дорожке?
Ответ:
5. Длина ящерицы 15 сантиметров. Укажи эту величину в дециметрах и сантиметрах.
Ответ: дм см
6. Кошка ест за день 4 раза. Сколько раз она поест за 2 дня?
Ответ:
7. Сколько насекомых съели птенцы за 2 дня, если в первый день им принесли 8 насекомых, во второй – на 5 насекомых больше, чем в первый?
Ответ:
8. Птица делает по 2 взмаха крыльев за секунду. А сколько взмахов крыльями она сделает за 6 секунд?
Ответ:
9. На елке 12 веток. Это на 8 веток больше, чем у березы. Сколько веток у березы?
Ответ:
10. Игуана ростом 3 дм 8 см. Укажи эту величину в сантиметрах.
Ответ: см
11. На полянку, где росло 4 подосиновика и 7 подберезовиков, приползло 13 улиток. Всем ли улиткам хватит грибов, если кроме них на полянке никого нет?
Ответ:
12. Три девочки готовили елочные игрушки к Новому году. Втроем они работали 3 часа. Сколько часов работала каждая из них?
Ответ:
13. В пакет можно положить 2 килограмма продуктов. Сколько пакетов должно быть у мамы, если она хочет купить 4 килограмма картошки и дыню массой 1 килограмм?
Ответ:
14. На аллее между деревьями, растущими друг за другом, стоят скамейки. Деревьев всего 15. А сколько скамеек, если одна скамейка сломалась, и ее унесли?
Ответ:
15. В семье трое детей: два мальчика и девочка. Их зовут Валя, Женя и Саша. Среди имен Валя и Женя есть имя одного мальчика. И среди имен Валя и Саша есть имя одного мальчика. Как зовут девочку?
Ответ:
16. Запиши в пустые клетки каждого квадрата числа от 1 до 9 так, чтобы сумма чисел в каждом столбце и каждой строке была равна числу, записанному в кружке. Числа не должны повторяться.
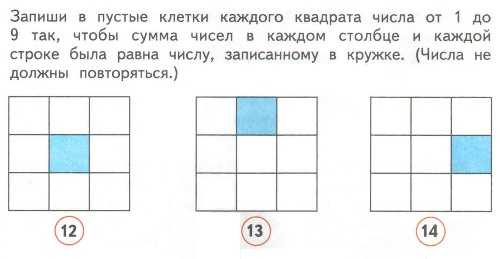
Ответ
Надеемся, задачи помогут и ученикам, и их родителям, и даже учителям первых классов.
Ответы на задания:
- 10
- 41
- 10
- 9
- 1дм 5см
- 8
- 21
- 12
- 4
- 38 см
- нет
- 3 часа
- 3
- 13
- Валя
7gy.ru
Олимпиада по математике 7 класс, задания, уравнения, задачи с ответами
Усвоить школьную программу по математике могут только те, кто проявляет достаточно упорства. На уроках 7 классе учащиеся знакомятся с такими разделами, как степень с натуральным показателем, одночлен и многочлен, линейная функция, системы линейных уравнений с двумя переменными.
Принимая участие в олимпиадах, ученики углубляют свои знания и совершенствуют навыки, приобретенные на уроках. Но, чтобы добиться высокого результата, нужно долго и усердно готовиться.
На нашем сайте вы найдете олимпиадные задания по математике с ответами и решениями. Предложенные задания помогут подготовиться к олимпиаде. Мы советуем вам использовать их в качестве тренажера как на уроках, так и в ходе внеклассной самостоятельной подготовки.
Скачайте задания, заполнив форму!
После того как укажете данные, кнопка скачивания станет активной
Уравнения
1. Оба корня уравнения x2 – ax + 2 являются натуральными числами. Чему равно a?
2. Решите в натуральных числах уравнение:
zx + 1 = (z + 1)2
3. Решите уравнение:
12 – (4х – 18) = (36 + 5х) + (28 – 6х)
4. Найдите решение уравнения:
7x + 3 (x+0,55) = 5,65
5. Решите уравнение:
10у – 13,5 = 2у — 37,5.
6. Преобразуйте в многочлен:
(4х – 5у)2
7. Представьте выражение в виде квадрата двучлена:
4у2 — 12у + 9
8. Решите уравнение:
8у – (3у + 19) = -3(2у — 1)
9. Решите уравнение:
5х2 – 4х = 0
10. Решите систему уравнений:
{ x+2*y = 12
{ 2*x-3*y = -18
Задачи
Задача №1
Из чисел A, B и C одно положительно, одно отрицательно и одно равно 0. Известно, что A = B (B – C). Какое из чисел положительно, какое отрицательно и какое равно 0? Почему?
Задача №2
Последовательность строится по следующему закону. На первом месте стоит число 7, далее за каждым числом стоит сумма цифр его квадрата, увеличенная на 1. Какое число стоит на 2000 месте?
Задача №3
В XIX-XX веках Россией правили 6 царей династии Романовых. Вот их имена и отчества по алфавиту: Александр Александрович, Александр Николаевич, Александр Павлович, Николай Александрович, Николай Павлович, Павел Петрович. Один раз после брата правил брат, во всех остальных случаях после отца — сын. Как известно, последнего русского царя, погибшего в Екатеринбурге в 1918 году, звали Николаем. Найдите порядок правления этих царей.
Задача №4
Сколько чисел от 1 до 90 делятся на 2, но не делятся на 4?
Задача №5
В трех мешках 114 кг сахара. В первом на 16 кг меньше, чем во втором, а в третьем на 2 кг меньше, чем во втором. Сколько килограммов сахара во втором мешке?
Задача №6
Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если цифры в числе не повторяются.
Задача №7
Точка D — середина основания AC равнобедренного треугольника ABC. Точка E — основание перпендикуляра, опущенного из точки D на сторону BC. Отрезки AE и BD пересекаются в точке F. Установите, какой из отрезков BF или BE длиннее.
Задача №8
Пол в гостиной барона Мюнхгаузена вымощен одинаковыми квадратными каменными плитами. Барон утверждает, что его новый ковер (сделанный из одного куска ковролина) закрывает ровно 24 плиты и при этом каждый вертикальный и каждый горизонтальный ряд плит в гостиной содержит ровно 4 плиты, покрытых ковром. Не обманывает ли барон?
Задача №9
Саша выписал первые миллион натуральных чисел, не делящихся на 4. Рома подсчитал сумму 1000 подряд идущих чисел в Сашиной записи. Могло ли у него получиться в результате 20012002?
Задача №10
Автомобиль из A в B ехал со средней скоростью 50 км/ч., а обратно возвращался со скоростью 30 км/ч.. Какова его средняя скорость?
Математические загадки
Загадка №1
Не пользуясь калькулятором и компьютером (в уме) вычислите сумму всех чисел от одного до ста?
Загадка №2
Позавчера Васе было 17 лет. В следующем году ему будет 20 лет. Как такое может быть?
Загадка №3
Два отца и два сына разделили между собой 3 апельсина так, что каждому досталось по одному апельсину. Как это могло получиться?
Загадка №4
На острове живут два племени: молодцы. Которые всегда говорят правду, и лжецы, которые всегда лгут. Путешественник встретил островитянина, спросил его, кто он такой, и когда услышал, что он из племени молодцов, нанял его в проводники. Они пошли и увидели вдали другого островитянина, и путешественник послал своего проводника спросить его, к какому племени он принадлежит. Проводник вернулся и сказал, что тот утверждает, что он из племени молодцов. Спрашивается: был проводник молодцом или лгуном?
Загадка №5
В двух футбольных лигах в сумме 39 команд. Команда играет с каждой командой из своей лиги по одному разу; при этом никаких матчей между лигами не происходит. За победу полагается 3 очка, за ничью — 1 очко, за проигрыш — 0. В прошлом году в одной лиге состоялось на 171 матч больше, чем в другой. Команда «Чемпионы», входящая в одну из лиг, проиграла всего три матча и набрала 32 очка.
Вопрос: со сколькими командами играли «Чемпионы» и сколько раз они сыграли вничью?
Ответы к уравнениям
| Уравнение | № 1 | № 2 | № 3 | № 4 | № 5 |
| Ответ | a = 3 | z = 2 x = 3 | x = — 15¹/₃ | x = 0,4 | y = -3 |
| Уравнение | № 6 | № 7 | № 8 | № 9 | № 10 |
| Ответ | 16х2 — 40ху + 25у2 | (2у — 3)2 | y = 2 | x = 0 x=0,8 | x = 0,6 |
Ответы к задачам
Задача 1
Если A = 0, то либо B = 0, либо B – C = 0. Ни то, ни другое невозможно. Поэтому A не 0. Если B = 0, то и A = 0. Это тоже невозможно. Поэтому B не 0. Следовательно, C = 0, и равенство из условия задачи можно переписать в виде A = B. Отсюда следует, что B > 0. Значит, B положительно, а A – отрицательно.
Задача 2
Так как 2000 = 3 x 666 + 2, то 2000-м месте стоит число 5.
Задача 3
Павел Петрович, Александр Павлович, Николай Павлович, Александр Николаевич, Александр Александрович, Николай Александрович.
Задача 4
23
Задача 5
44 кг
Задача 6
60 чисел
Задача 7
Отрезок BE длиннее
Задача 8
Примером такой клетчатой фигуры может служить квадрат 6 на 6 без двух подходящих обобщенных диагоналей. Конечно, если трактовать это как ковер в гостиной, получится нечто экстравагантное, но ведь барон не зря слыл незаурядным человеком.
Задача 9
Из любых трёх чисел, идущих в Сашиной записи подряд, одно имеет остаток 1 пр делении на 4, другое – остаток 2, а оставшееся – остаток 3. Значит их сумма при делении на 4 даёт остаток 2. Среди первых 999 Роминых чисел есть ровно 333 таких тройки, сумма чисел в них даёт при делении на 4 такой же остаток, как 333 • 2, то есть 2. Оставшееся число на 4 не делится, поэтому вся сумма не может также давать остаток 2. А 20012002 даёт именно этот остаток.
Задача 10
37,5 км/ч
Ответы на загадки
Загадка 1
5050
Загадка 2
Если нынешний день 1 января, а у Васи день Рождения тридцать первого декабря. Позавчера, т.е. тридцатого декабря ему было еще семнадцать лет. Вчера, т.е. тридцать первого декабря исполнилось восемнадцать лет. В этом году исполнится девятнадцать лет, а в следующем году двадцать лет.
Загадка 3
Всего деливших было трое: дед, его сын и внук
Загадка 4
На острове на данный вопрос никто не мог ответить ничего, кроме того, что он молодец. Так как проводник воспроизвел правильно этот единственно возможный ответ, то ясно, что он молодец.
Загадка 5
«Чемпионы» играли с 23 командами (следовательно, в их лиге 24 команды, а в другой — 15) и сыграли вничью 14 матчей из 23.
Скачайте задания, заполнив форму!
После того как укажете данные, кнопка скачивания станет активной
Другие классы
Обновлено: , автор: Валерия Токареваruolimpiada.ru
