Понятие степень в математике – Степень и ее свойства.

Обобщение понятия о показателе степени

Чтобы обобщить понятие о показателе степени, вспомним, что такое степень.

 – степень с натуральным показателем, здесь а – основание степени, n – показатель степени;

                 n штук

Кроме того, напомним, что:

 и ;

Выражение  не существует.

Основные свойства степеней:

1.      ;

Для того чтобы умножить степени с одинаковым основанием, нужно сложить их показатели, основание оставить тем же самым.

2.      ;

Можно разделить степени с одинаковым основанием, для этого их показатели нужно вычесть, а основание оставить тем же самым;

3.      ;

Для того чтобы степень возвести в степень, нужно перемножить показатели степени, основание оставить без изменений.

4.      ;

При умножении степеней с одинаковым показателем, нужно перемножить основания и возвести результат в исходную степень;

5.      ;

Чтобы разделить степени с одинаковыми показателями, нужно разделить основания и возвести результат в исходную степень;

Напомним основные числовые множества:

 – натуральные числа;

 – целые числа;

 – рациональные числа;

Числа, которые не могут быть представлены в виде дроби , назвали иррациональными, например . Если к множеству рациональных чисел прибавить множество иррациональных чисел, получим множество действительных чисел

 – действительные числа;

Напомним связь между множеством действительных чисел и числовой осью. Между множеством действительных чисел и множеством точек числовой оси существует взаимооднозначное соответствие. То есть, если мы говорим, что есть число , то ему на оси соответствует единственная точка. Точно так же каждой точке соответствует единственное действительное число.

Рис. 1. Числовая ось

Определение:

Степенью неотрицательного числа а с рациональным положительным показателем  называется число

Например:

 

Пример 1 – вычислить:

 

Пример 2 – вычислить:

 

Пример 3 – вычислить:

 

Пример 4 – представить в виде степени:

 

Пример 5 – представить в виде степени:

 

Пример 6 – представить в виде степени:

 

Пример 7 – представить в виде степени:

Определение:

Степенью положительного числа а с рациональным отрицательным показателем  называется число .

Например:

Пример 8 – вычислить:

Пример 9 – вычислить:

Пример 10 – вычислить:

Обратим внимание на типовую ошибку. Вычислить:

Ответ: не существует

Пояснение:

 – выражение 1;

Данное равенство неверно, так как наше определение не должно противоречить определениям, данным ранее, например основному свойству дроби:

 – выражение 2;

Из выражений 1 и 2 получили , неверное числовое равенство.

Запомним:

 определено только при .

Пример 11 – построить графики функций:

График первой функции нам известен, он проходит через три фиксированные точки: (0;0), (1;1) и (-1;-1), область определения .

График второй функции по определению соответствует графику функции  при .

Отличие заданных функций наглядно продемонстрировано на графиках 2 и 3.

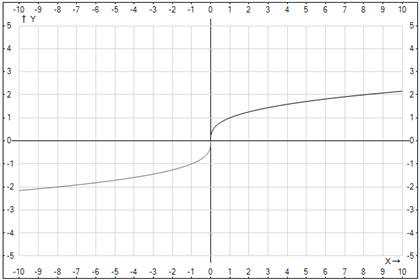
Рис. 2. График функции

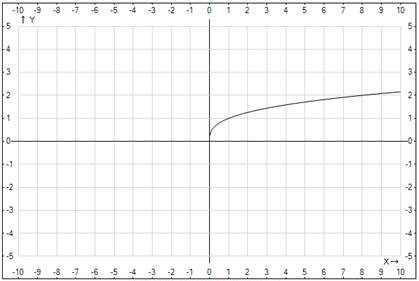
Рис. 3. График функции

Пример 12 – найти область определения выражения:

По определению положительного рационального показателя степени:

По определению отрицательного рационального показателя степени:

По определению положительного рационального показателя степени:

По определению отрицательного рационального показателя степени:

Итак, мы рассмотрели понятие степени с рациональным показателем, дали важные определения. На следующем уроке мы рассмотрим свойства таких степеней.

 

Список литературы

1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Matematika.mpt.ru (Источник).
2. Nado5.ru (Источник).
3. Terver.ru (Источник).

 

Домашнее задание

1. Алгебра и начала анализа, 10–11 класс (А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын) 1990, № 430, 431, 436, 437;

2. Вычислить:

а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з)

3. Вычислить:

а) ; б) ; в) ; г)

 

interneturok.ru

История возникновения степени числа

История возникновения степени числа

Сложение, вычитание, умножение и деление идут первыми в списке арифметических действий. У математиков не сразу сложилось представление о возведении в степень как о самостоятельной операции, хотя в самых древних математических текстах Древнего Египта и Междуречья встречаются задачи на вычисление степеней.

В своей знаменитой «Арифметике» Диофант Александрийский описывает первые натуральные степени чисел так:

«Все числа… состоят из некоторого количества единиц; ясно, что они продолжаются, увеличиваясь до бесконечности. …среди них находятся: квадраты, получающиеся от умножения не­которого числа самого на себя; это же число называется стороной квадрата, затем кубы,  получающиеся от умножения квадратов на их сторону, далее квадрато-квадраты — от умножения квадратов самих на себя, далее квадрато-кубы, получающиеся от умно­жения квадрата на куб его стороны, далее кубо-кубы — от умножения кубов самих на себя».

Немецкие математики Средневековья стремились ввести единое обозначение и сократить число символов. Книга Михеля Штифеля «Полная арифметика» (1544 г.) сыграла в этом значительную роль.

«Сумма знаний…» Луки Пачоли была одним из первых опубликованных  сочинений.  Но математики продолжали искать более простую систему обозначений так как его обозначения были не удобны.

Француз, бакалавр медицины Никола Шюке (? — около 1500 г.) смело ввёл в свою сим­волику не только нулевой, но и отрицательный показатель степени. Он писал его мелким шрифтом сверху и справа от коэффициента.

В XVI в. итальянец Раффаэле Бомбелли в своей «Алгебре» использовал ту же идею. Он обозначал неизве­стное специальным символом 1, а символами 2, 3,… — его степени. Обозначе­ния Бомбелли  также оказали влияние и на символику нидерландского математика Симона Стевина (1548—1620). Он обозначал неиз­вестную величину кружком О,  внутри которого указывал показатели степени. Стевин предложил называть степени по их показателям — четвёртой, пятой и т. Д. и отверг Диофантовы составные выражения «квадрато-квадрат», «квадрато-куб».

У Рене Декарта в его «Геометрии» (1637) мы находим современное обозначение степеней а?, а?,… Любопытно, что Декарт считал, что а*а не занимает больше места, чем а² и не пользовался этим обозначением при записи произведения двух одинаковых множителей. Немецкий ученый Лейбниц считал, что упор должен быть сделан на необходимости применения символики для всех записей произведений одинаковых множителей  и применял знак а

2.

mirurokov.ru

Степень числа. Степень с натуральным показателем

Правило чтения и записи степеней с натуральным показателем

Краткую запись произведения одинаковых сомножителей очень удобно использовать, — длинная строка описания математических действий сокращается до записи нескольких шагов:

17^5=17 \cdot 17 \cdot 17 \cdot 17 \cdot 17=1\,419\,857

17 — основание степени,

5 — показатель степени,

1419857 — значение степени.

Степень с нулевым показателем равна 1, при условии, что a \neq 0:

a^0=1.

Например: 2^0=1

Когда нужно записать большое число обычно используют степень числа 10.

Например, один из самых древних динозавров на Земле жил около 280 млн. лет назад. Его возраст записывается следующим образом: 2,8 \cdot 10^8.

Каждое число большее 10 можно записать в виде a \cdot 10^n, при условии, что 1 < a < 10 и n является положительным целым числом. Такую запись называют стандартным видом числа.

Примеры таких чисел: 6978=6,978 \cdot 10^3, 569000=5,69 \cdot 10^5.

Можно говорить как и «a в n-ой степени», так и «n-ая степень числа a» и «a в степени n».

4^5 — «четыре в степени 5 » или «4 в пятой степени» или также можно сказать «пятая степень числа 4»

В данном примере 4 — основание степени, 5 — показатель степени.

Приведем теперь пример с дробями и отрицательными числами. Для избежания путаницы принято записывать основания, отличные от натуральных чисел, в скобках:

(7,38)^2, \left(\frac 12 \right)^7, (-1)^4 и др.

Заметьте также разницу:

(-5)^6 — означает степень отрицательного числа −5 с натуральным показателем 6.

-5^6 — соответствует числу противоположному 5^6.

Свойства степеней с натуральным показателем

Основное свойство степени

a^n \cdot a^k = a^{n+k}

Основание остается прежним, а складываются показатели степеней.

Например: 2^3 \cdot 2^2 = 2^{3+2}=2^5

Свойство частного степеней с одинаковыми основаниями

a^n : a^k=a^{n-k}, если n > k.

Показатели степени вычитаются, а основание остается прежним.

Данное ограничение n > k вводится для того, чтобы не выходить за рамки натуральных показателей степени. Действительно, при n > k показатель степени a^{n-k} будет являться натуральным числом, иначе он будет либо отрицательным числом (k < n), либо нулем (k-n).

Например: 2^3 : 2^2 = 2^{3-2}=2^1

Свойство возведения степени в степень

(a^n)^k=a^{nk}

Основание остается прежним, перемножаются лишь показатели степеней.

Например: (2^3)^6 = 2^{3 \cdot 6}=2^{18}

Свойство возведения в степень произведения

В степень n возводится каждый множитель.

a^n \cdot b^n = (ab)^n

Например: 2^3 \cdot 3^3 = (2 \cdot 3)^3=6^3

Свойство возведения в степень дроби

\frac{a^n}{b^n}=\left(\frac{a}{b} \right) ^n, b \neq 0

В степень возводится и числитель и знаменатель дроби. \left(\frac{2}{5} \right)^3=\frac{2^3}{5^3}=\frac{8}{125}

academyege.ru

Слово СТЕПЕНЬ — Что такое СТЕПЕНЬ?

Слово степень английскими буквами(транслитом) — stepen

Слово степень состоит из 7 букв: е е н п с т ь

---

Значения слова степень. Что такое степень?

Степень

СТЕПЕНЬ — произведение нескольких равных сомножителей (напр., 24=2.2.2.2=16). число, повторяющееся сомножителем (в примере число 2), называют основанием степени; число, показывающее, сколько раз повторяется сомножитель (в примере число 4)…

Большой энциклопедический словарь

Степень, в первоначальном понимании (целая и положительная С.) есть произведение нескольких равных сомножителей. Обозначение:, где а — основание, n — показатель степени, an — степень.

БСЭ. — 1969—1978

СТЕПЕНЬ — в первоначальном понимании (целая и положительная С.) есть произведение нескольких равных сомножителей. Обозначение: где а — основание, п — показатель, а n — степень. Основные действия над С. даются формулами a n x a m=a n+m, a n…

Математическая энциклопедия. — 1977-1985

Степень, математ., произведение равных множителей, например, а.а.а……а (n раз) есть n-ая степень а и обозначается аn причем а назыв. основанием степени, n- показателем степени, а самое действие возвышением в С.

Брокгауз и Ефрон. — 1907—1909

Степень определяется двумя числами; одно из них назыв. основанием, или корнем, а другое — показателем. Выражение ab обозначает степень, у которой основание а, а показатель b. Если b равно целому положительному числу n…

Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — 1890-1907

Степень сжатия

Степень сжатия — отношение объёма надпоршневого пространства цилиндра двигателя внутреннего сгорания при положении поршня в нижней мёртвой точке (НМТ) (полный объем цилиндра)…

ru.wikipedia.org

Степень сжатия, отношение объёма рабочего тела в начале сжатия к объёму его в конце сжатия в цилиндре двигателя внутреннего сгорания. С увеличением С. с. рабочее тело…

БСЭ. — 1969—1978

СТЕПЕНЬ СЖАТИЯ — отношение полного объёма цилиндра двигателя внутр. сгорания к объёму камеры сжатия. В дизелях С. с. составляет 12 — 22, а в двигателях с принудит. воспламенением — 6 — 11.

Большой энциклопедический политехнический словарь

Учёная степень

Учёная сте́пень — ступень квалификационной системы в науке, позволяющей ранжировать научных деятелей на отдельных этапах академической карьеры. В настоящее время в Российской Федерации присуждают учёные степени кандидата и доктора наук.

ru.wikipedia.org

УЧЁНАЯ СТЕПЕНЬ, научная квалификация в определенной отрасли знания. Как правило, присуждается после соответствующих этапов обучения в вузе или по завершении образования в исследовательском (например, аспирантском)…

Современная энциклопедия. — 2000

УЧЕНАЯ СТЕПЕНЬ — научная квалификация в определенной отрасли знания. Как правило присуждается после соответствующих этапов обучения в вузе или по завершении образования в его исследовательском (напр., аспирантском)…

Большой энциклопедический словарь

Степень двухконтурности

Степень двухконтурности — параметр турбореактивного двигателя, показывающий отношение расхода воздуха через внешний контур двигателя к расходу воздуха через внутренний контур.

ru.wikipedia.org

Степень двухконтурности параметр рабочего процесса турбореактивного двухконтурного двигателя (см. Параметры рабочего процесса двигателя), равный отношению расхода воздуха в наружном контуре к расходу воздуха во внутреннем контуре.

Энциклопедия техники

Степень двухконтурности — параметр рабочего процесса турбореактивного двухконтурного двигателя (см. Параметры рабочего процесса двигателя), равный отношению расхода воздуха в наружном контуре к расходу воздуха во внутреннем контуре.

Энциклопедия техники

Степень риска (фильм, 1968)

СТЕПЕНЬ РИСКА. 1968, 95 мин., ч/б, 1то. жанр: мелодрама. реж. Илья Авербах, сц. Илья Авербах, опер. Владимир Ковзель, худ. Василий Зачиняев, зв. Михаил Лазарев, музыка из произведений Цезаря Франка.

Ленфильм. Аннотированный каталог фильмов (1918-2003)

«СТЕПЕНЬ РИСКА», СССР, Ленфильм, 1968, ч/б, 95 мин. Киноповесть. По мотивам книги известного хирурга Николая Амосова «Мысли и сердце». Обреченный на смерть математик попадает в клинику известного хирурга.

Энциклопедия кино. — 2010

«Степень риска» — художественный фильм, снятый режиссёром Ильёй Авербахом по мотивам повести кардиохирурга Николая Амосова «Мысли и сердце» на киностудии «Ленфильм» в 1968 году. Премьера фильма состоялась 10 февраля 1969 года.

ru.wikipedia.org

Русский язык

Сте́пень/.

Морфемно-орфографический словарь. — 2002

Сте́пень, -и, мн. -и, -е́й.

Орфографический словарь. — 2004

Степени сравнения

Степени сравнения — общее название трёх форм прилагательного или наречия, выражающих различные степени качества, присущего предмету, имя которого определяется этим прилагательным или наречием.

ru.wikipedia.org

СТЕПЕНИ СРАВНЕНИЯ. Формы прилагательных или наречий, или 1. указывающие на то, что признак, обозначенный основой прилагательного или наречия, присущ известному предмету или его признаку (в том числе и действию или состоянию) в большей степени…

Литературная энциклопедия: Словарь литературных терминов

Степени сравнения Грамматическая категория качественных прилагательных и наречий, выражающая относительную разницу или превосходство в качестве, присущем предметам или действиям.

Розенталь Д.Э. Словарь-справочник лингвистических терминов. — 1976

---

Примеры употребления слова степень

Джейд очень ответственный, он понимает, что от этого зависит и степень его свободы.

Когда такой стресс происходит два раза в год, степень адаптации организма нарушается.

И государство востребовало ту степень репрессий и абсурда, которая перешла границы ratio.

Хотя докторскую степень актёру дали за совокупность заслуг перед искусством.

Лин поднял планку качества высоко и степень ответственности данной ленты возросла в разы.

Это серьезная степень наказания для чиновников за смерть ребенка в санатории.

---

1. степенность
2. степенный
3. степенство
4. степень
5. степка
6. степной
7. степняк

wordhelp.ru

Понятие степени с любым рациональным показателем. Алгебра, 11 класс: уроки, тесты, задания.

1.	Выражения, которые имеют смысл Сложность: лёгкое	4
2.	Степень с дробным показателем (обыкновенная дробь) Сложность: лёгкое	1
3.	Степень с дробным показателем (смешанное число) Сложность: лёгкое	2
4.	Степень с дробным показателем (десятичная дробь) Сложность: лёгкое	2
5.	Корень степени n из обыкновенной дроби Сложность: лёгкое	1
6.	Корень степени n из степени Сложность: лёгкое	1
7.	Степень с рациональным показателем Сложность: лёгкое	2
8.	Произведение степеней с рациональными показателями Сложность: лёгкое	2
9.	Частное степеней с рациональными показателями Сложность: лёгкое	1
10.	Возведение степени в степень (рациональные показатели) Сложность: лёгкое	1
11.	Значение степени с рациональным показателем Сложность: среднее	4
12.	Упрощение выражения, содержащего радикалы, замена переменных Сложность: сложное	5
13.	Степень с целым показателем Сложность: среднее	6
14.	Произведение степени и корня Сложность: среднее	2,5
15.	Свойства степеней с рациональными показателями (десятичные и обыкновенные дроби) Сложность: среднее	3
16.	Свойства степеней с рациональными показателями (десятичные дроби) Сложность: среднее	6
17.	Произведение в рациональной степени (степень и дробь) Сложность: среднее	6
18.	Сумма корней и степеней Сложность: среднее	4
19.	Свойства степеней с рациональными показателями (дробь) Сложность: среднее	4
20.	Произведение бинома на одночлен Сложность: среднее	5
21.	Квадрат бинома Сложность: среднее	4
22.	Произведение суммы и разности (степень и число) Сложность: среднее	3
23.	Сокращение дроби Сложность: среднее	4
24.	Упрощение выражения, содержащего радикалы, формула разложения на множители кв. трёхчлена Сложность: среднее	4
25.	Произведение суммы и разности двух степеней Сложность: сложное	4

www.yaklass.ru

Степень (математическая операция) — Викизнание… Это Вам НЕ Википедия!

Степень — математическая операция третьего порядка.

Определяется двумя числами; одно из них назыв. основанием, или корнем, а другое — показателем. Обозначается следующим образом:

где а — основание , а b — показатель.

Если b равно целому положительному числу n, то — произведение n множителей, из которых каждый равен а. Например, . Если b равно целому отрицательному числу (-n), то .

Если b равно рациональному числу , то есть число, удовлетворяющее условию:

Если b число иррациональное, то можно сосоставить множеством способов ряд рациоциональных чисел , безусловно сходящийся к b. В таком случае определяется как предел выражения .

Основные свойства степеней[править]

,

(дистрибутивность степени относительно умножения),

.

Возьмем для примера равенство: . Здесь 32 — степень, имеющая основание, или корень, 2 и показатель 5. Для краткости говорят, что 32 есть пятая степень числа 2 и что 2 корень пятой степени из 32.

Так как и выражают площадь квадрата и объем куба, то вторая и третья С. называются квадратом и кубом. В этом смысле, напр., говорят, что 25 есть квадрат числа 5, 8 есть куб числа 2, 5 — корень квадратный из 25, 2 — корень кубический из 8.

Уравнением n-ой степени называется уравнение вида:

, где не равно нулю.

Шаблон:БЭСБЕ

www.wikiznanie.ru

No related posts.