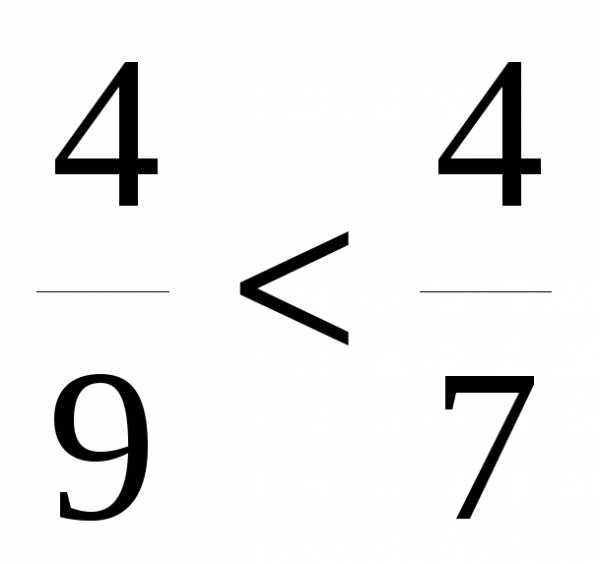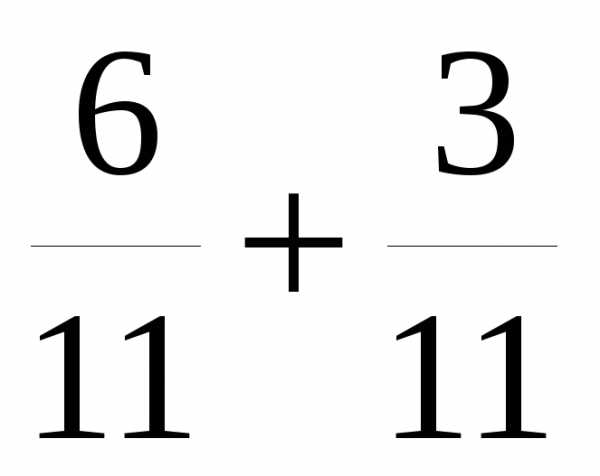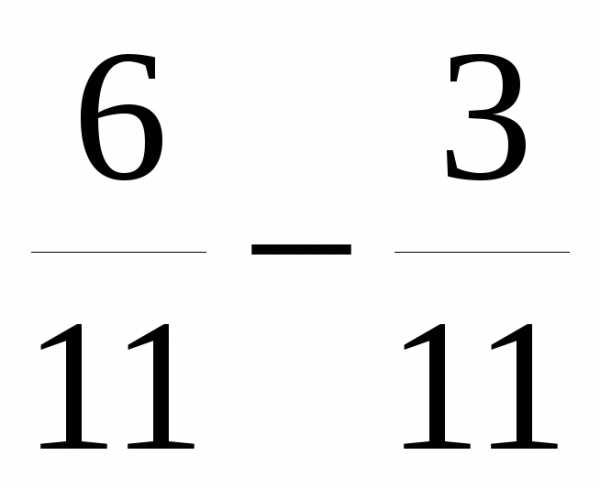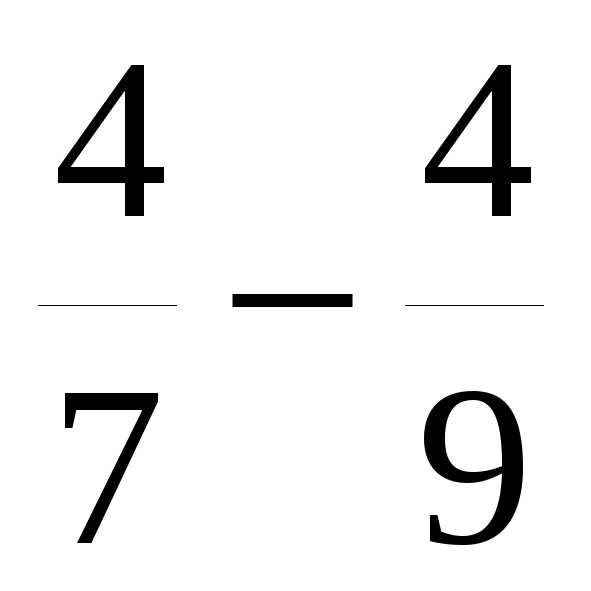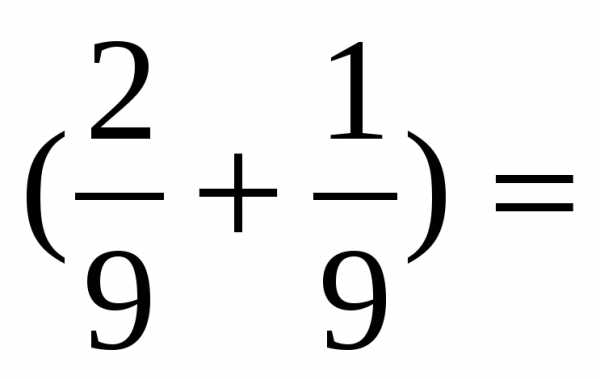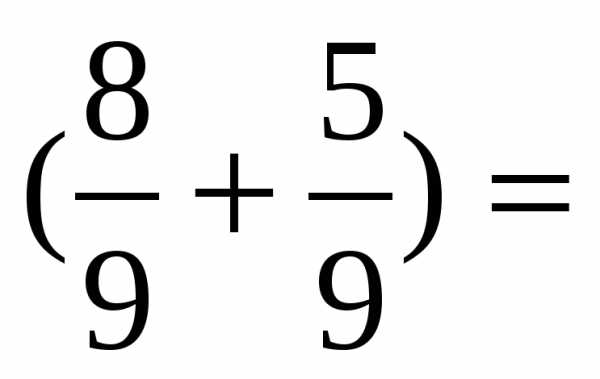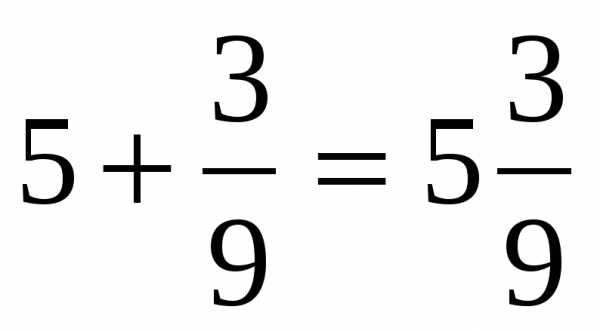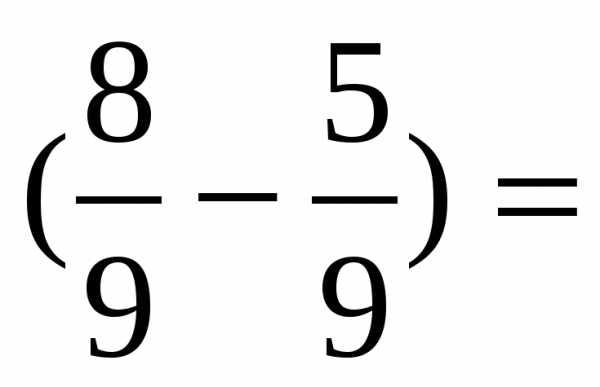Правила по математике дроби 5 класс – Действия с дробями

Содержание

Справочник для учащихся 5 класса по теме «Обыкновенные дроби»

Харцызск 2013

Дробные числа

правильная 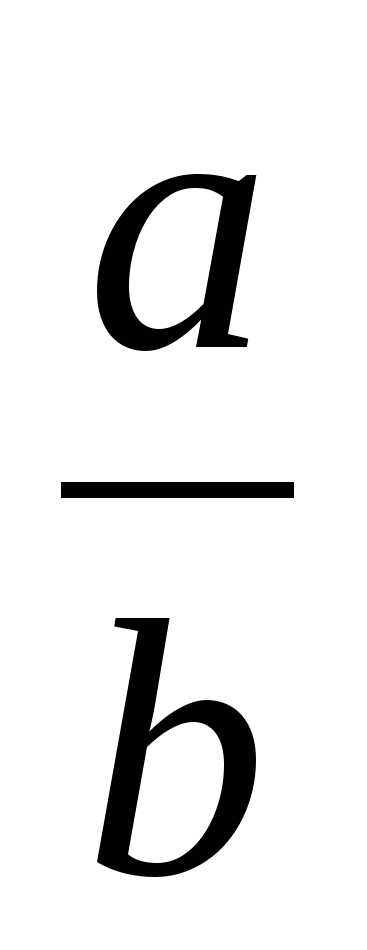неправильная

a b a b

обыкновенная дробь

Дробные числа вида 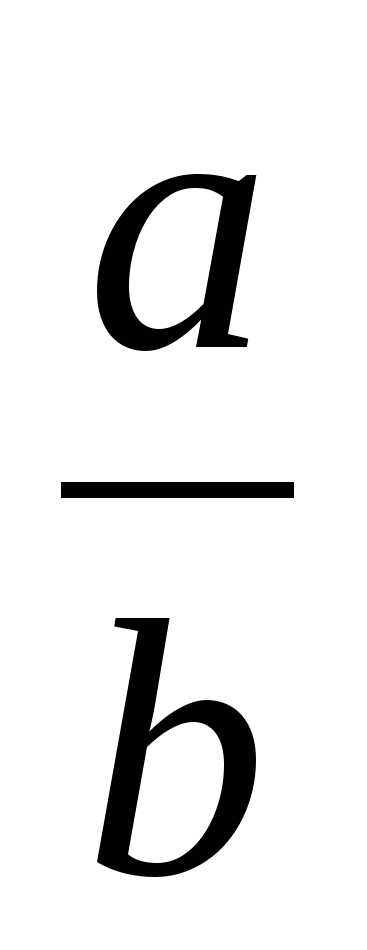называют обыкновенными дробями, или дробями. Изображаются дроби двумя натуральными числами, разделенными горизонтальной чертой, выполняющей роль знака деления.

Число, записанное под чертой, называют знаменателем дроби. Знаменатель указывает на сколько равных частей разделено одно целое. В дроби 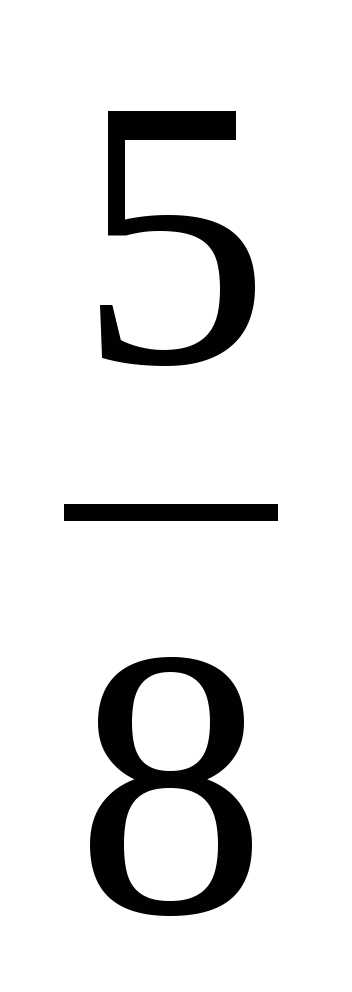это число 8.

Число, записанное над чертой, называется числителем дроби. Числитель показывает сколько взято равных частей целого. В дроби 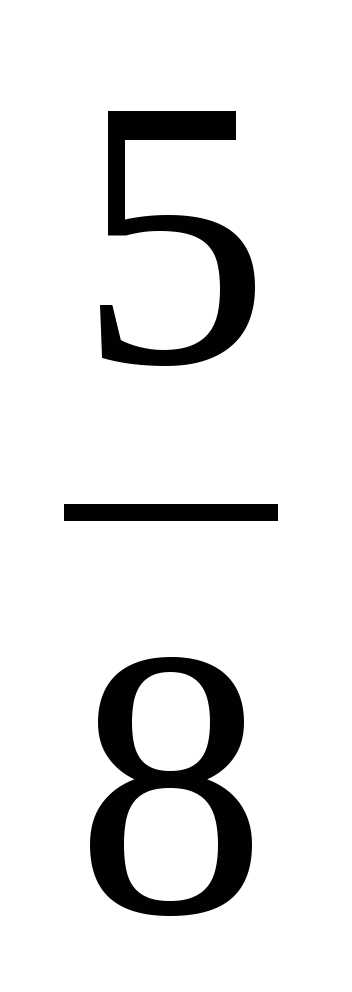это число 5.

Дробь, числитель которого меньше знаменателя, называется правильной. Например, дробь 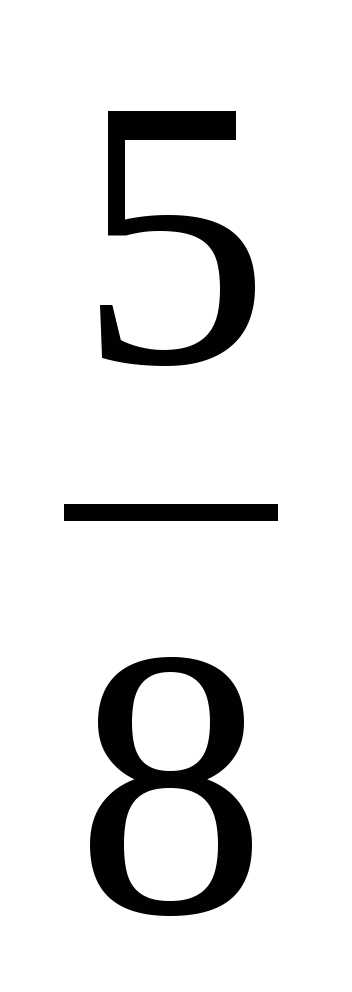правильная, так как 5 неправильной. Например, дроби 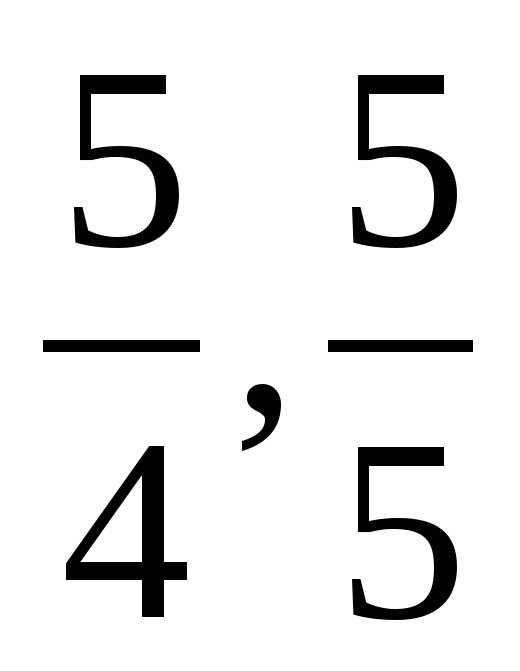— неправильные, так как в первом случае 54, а во втором 5=5.

Любую неправильную дробь можно записать в виде суммы целой и дробной части.

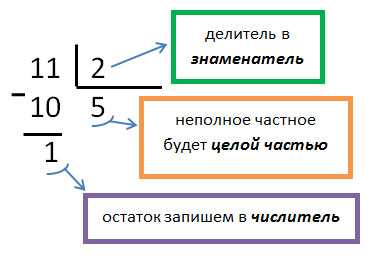
Для этого необходимо выполнить деление с остатком числителя на знаменатель.

Целая часть – это натуральное число, представляющее собой неполное частное, а дробная часть – правильная дробь, числитель которой – остаток, а знаменатель – делимое.
Алгоритм 1.
Запись результата выполнения деления с остатком:

При делении с остатком необходимо записать:
25 : 6 = 4 (ост. 1)
неполное частное как целую часть
остаток – в числитель
делитель – в знаменатель
25 : 6 =
Дробное число, имеющее целую и дробную часть, называют смешанным числом.
Алгоритм 2.
Запись неправильной дроби в виде смешанной дроби
Шаг
Действие
Пример
1
Выполнить деление числителя на знаменатель
25 : 6
2
Выполнить алгоритм 1
Чтобы смешанное число записать в виде неправильной дроби, нужно его целую часть умножить на знаменатель и прибавить числитель, а знаменатель оставить без изменений.
Алгоритм 3.
Запись смешанной дроби в виде неправильной дроби

Шаг
Действие
Пример
Чтобы смешанную дробь представить в виде неправильной дроби, нужно:
1
Целую часть умножить на знаменатель дробной части и прибавить числитель
5  7 + 6 = 41
2
Полученное число записать в числитель дроби
3
Знаменатель оставить тем же
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше, и меньше та дробь, у которой числитель меньше.

Чтобы сравнить две дроби с одинаковыми знаменателями, нужно сравнить их числители. Например, 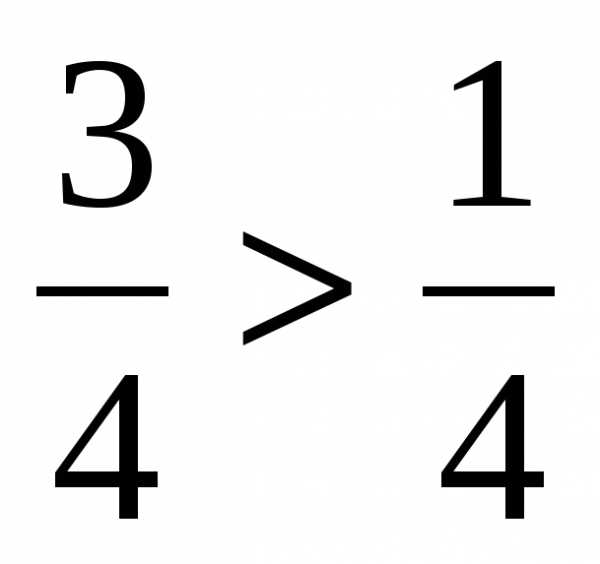, так как 3 1.
Алгоритм 4.
Сравнение дробей с одинаковыми знаменателями
Шаг
Действие
Пример
1
Сравнить знаменатели сравниваемых дробей
Если знаменатели различны, то это правило для сравнения не подходит
а)
11=11 — одинаковы
б)
79, правило не подходит

2
Если числитель первой дроби больше числителя второй дроби, то первая дробь больше второй;
если меньше, то и дробь меньше
6, следовательно,
.
Алгоритм 5
Правила сравнения дробей с единицей
Неправильная дробь, у которой числитель равен знаменателю, равна 1:
Неправильная дробь, у которой числитель и знаменатель различны, больше 1:
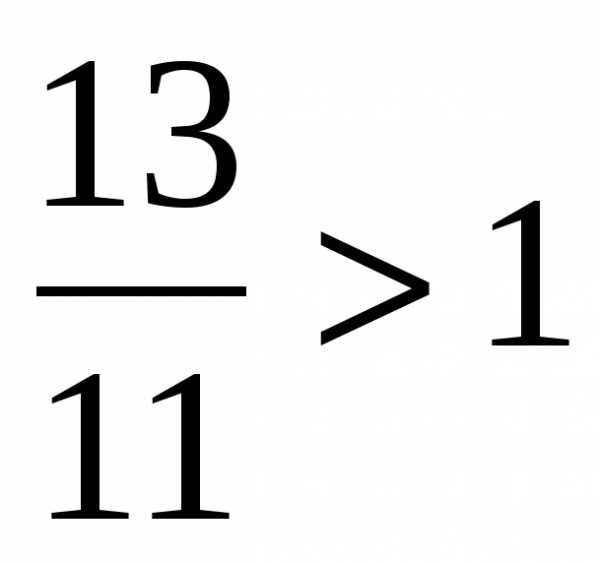, так как 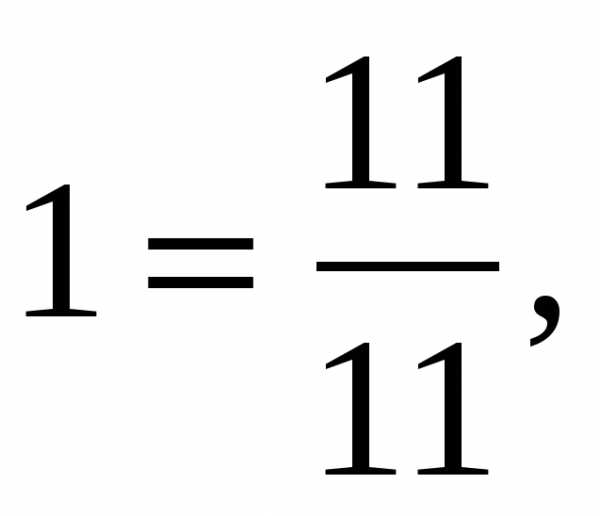а .

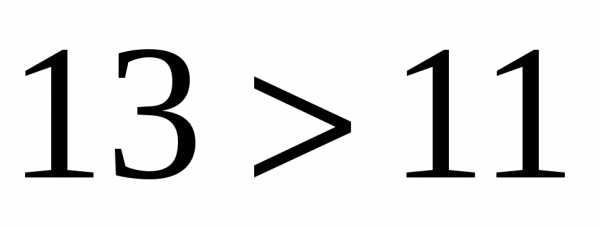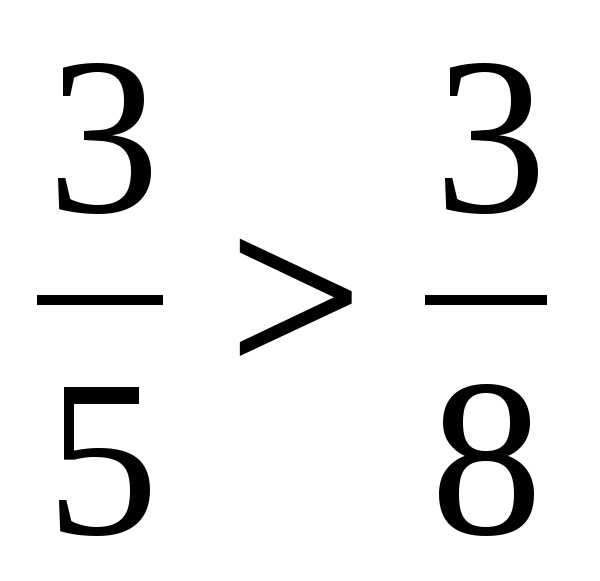Например, , так как 5
Алгоритм 6.
Сравнение дробей с одинаковыми числителями
Шаг
Действие
Пример
1
Проверяем, равны ли числители
Если числители различны, то это правило для сравнения не подходит
а)
69, правило не подходит
б)
4=4, одинаковы
2
Сравниваем знаменатели
Если знаменатель первой дроби меньше знаменателя второй дроби, то первая дробь больше второй;

если больше, то дробь меньше
7, следовательно,
.
Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
Алгоритм 7.
Сложение дробей с одинаковыми знаменателями
Шаг
Действие
Пример
1
Проверяем, равны ли знаменатели
Если знаменатели различны, то это правило для сложения не подходит
а)

11=11 — одинаковы
б)
79, правило не подходит
2
Складываем числители обеих дробей и записываем в числитель результата
.
33
Знаменатель записываем без изменений
Чтобы вычесть две дроби с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого и полученный результат записать в числитель, а знаменатель оставить тот же.
Алгоритм 8.
Вычитание дробей с одинаковыми знаменателями
Шаг
Действие
Пример
1
Проверяем, равны ли знаменатели
Если знаменатели различны, то это правило для вычитания не подходит
а)
11=11 — одинаковы
б)
79, правило не
подходит
2
Из числителя уменьшаемого вычитаем числитель вычитаемого, и результат записываем в числитель дроби
.
3
Знаменатель записываем без изменений
Чтобы найти сумму (разность) двух смешанных чисел, нужно отдельно найти сумму (разность) их целых и дробных частей, а затем записать их рядом, как одно дробное число.

Алгоритм 9.
Сложение смешанных дробей
Шаг
Действие
Пример
1
Складываются целые части
2
Складываются дробные части по алгоритму 7
Если получилась неправильная дробь, то применяем алгоритм 2
+
+
3
Целую и дробную части записываем как одно число
=
=
Алгоритм 10.
Вычитание смешанных дробей
Шаг
Действие
Пример
1
Из целой части уменьшаемого вычитается целая часть вычитаемого
2
Вычитаются дробные части по алгоритму 8
+
3
Целую и дробную части записываем как одно число
=
Частные случаи применения алгоритма 10
1. Из числа, содержащего целую и дробную части, вычитается дробь, равная дроби уменьшаемого:
2. Из числа, содержащего целую и дробную части, вычитается дробь, причем дробь уменьшаемого больше дроби вычитаемого.
3. Из числа, содержащего целую и дробную части, вычитается число, содержащее целую и дробную части, причем дробь уменьшаемого меньше дроби вычитаемого.
Шаг
Действие
Пример
1
У целого числа занимается единица
2
Эта единица вместе с дробью обращается в неправильную дробь
3
Применяется алгоритм 10
Чтобы найти дробь от числа, надо это число разделить на знаменатель дроби и полученный результат умножить на числитель дроби.
Алгоритм 11.
Нахождение дроби от числа
Шаг
Действие
Пример
Найти от 3200
1
Найти сколько приходится на одну часть
Знаменатель дроби показывает, что 3200 состоит из 8 равных частей, значит, на одну часть приходится в 8 раз меньше, т.е.:
3200 : 8 =400
2
Найти сколько приходится на количество частей, указанных в числителе
Число 3 показывает, что из 8 частей взяли 3 равные части. Следовательно, на них приходится в 3 раза больше, чем на одну часть, т.е.: 400  3 = 1200
Чтобы найти число по его части, надо эту часть разделить на числитель дроби и результат умножить на знаменатель дроби.
Алгоритм 12.
Нахождение числа по его дроби
Шаг
Действие
Пример
Найти длину отрезка, если составляют 12 см.
1
Найти сколько приходится на одну часть
Дробь означает, что весь отрезок разделен на 4 равные части, из них на 3 части приходится 12 см, т.е. одна часть составляет 12 : 3 = 4 (см)
2
Найти сколько приходится на количество частей, указанных в знаменателе
Так как отрезок состоит из 4 частей, то на них приходится в 4 раза больше, чем на одну часть, т.е.: 4  4 = 16 (см)

intolimp.org
повторение. 5 класс. Определение обыкновенной дроби.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Закрашенные области всех трех кругов равны между собой, но над кругами записаны различные обыкновенные дроби. Почему? И все ли верно? Да, все верно, ведь можно разделить круг на:
4 части и закрасить 3 такие части;
8 частей и закрасить 6 таких частей;
12 частей и закрасить 9 таких частей.
Следовательно,
Мы убедились в правильности высказывания: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Примеры. Используя основное свойство дроби, замените звездочку таким числом, чтобы равенство было верным.
Рассуждаем так: числитель нужно увеличить во столько же раз, во сколько увеличили знаменатель дроби, т. е. в 4 раза (16:4=4). Вместо звездочки запишем значение 3·4=12.
Еще такие примеры.
Рассуждаем так: знаменатель нужно уменьшить во столько же раз, во сколько уменьшили числитель дроби, т. е. в 7 раз (21:3=7). Вместо звездочки запишем значение 28:7=4.
Еще такие примеры.

Запись имеет метки: обыкновенная дробь
www.mathematics-repetition.com
Правила по математике 5-6 класс
Правила по математике 5-6 класс:
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. ( основное свойство дроби)
Из двух дробей с одинаковыми знаменателями, та дробь больше, числитель которой больше.
Из двух дробей с одинаковыми числителями та дробь больше, знаменатель которой меньше.
Чтобы сравнить две дроби с разными знаменателями, их нужно привести к общему знаменателю, а затем применить правило сравнения дробей с общим знаменателем.
Правильная дробь меньше 1, а неправильная дробь больше или равна 1.
Сумма дробей с общим знаменателем есть дробь, числитель которой равен сумме числителей, а знаменатель равен знаменателю данных дробей.
Чтобы сложить две дроби с разными знаменателями, их надо привести к общему знаменателю, а затем применить правило сложения дробей с общим знаменателем.
Произведение двух дробей есть дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Чтобы умножить натуральное число на дробь, нужно числитель дроби умножить на это натуральное число, а знаменатель оставить тот же.
Произведение взаимно обратных чисел равно 1.
Чтобы разделить дробь на дробь, нужно делимое умножить на дробь, обратную делителю.
Чтобы разделить дробь на натуральное число, нужно её знаменатель умножить на это число.
Сумму натурального числа и правильной дроби называют смешанной дробью.
Чтобы сложить смешанные дроби, надо сложить отдельно их целые и их дробные части и полученные результаты сложить.
Чтобы умножить или разделить смешанные дроби, нужно записать их в виде неправильных дробей и выполнить действия с обыкновенными дробями.
Площадь прямоугольника равна произведению длины на ширину.
Периметр прямоугольника равен сумме длин сторон прямоугольника.
Площадь квадрата равна квадрату его стороны.
Периметр квадрата равен сумме сторон.
Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
Чтобы сложить (вычесть) десятичные дроби, нужно:
уравнять в этих дробях количество знаков после запятой;
записать их друг под другом так, чтобы запятая была записана под запятой;
выполнить сложение (вычитание), не обращая внимания на запятую;
поставить в ответе запятую под запятой в данных дробях.
22.Чтобы умножить десятичную дробь на натуральное число, надо:
умножить её на это число, не обращая внимания на запятую;
в полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби.
Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д., надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.
Чтобы разделить десятичную дробь на натуральное число, надо:
разделить дробь на это число, не обращая внимания на запятую;
поставить в частном запятую, когда кончится деление целой части.
Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит в множителе после единицы.
Чтобы перемножить две десятичные дроби, надо:
выполнить умножение, не обращения внимания на запятые;
отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе.
Умножить число на 0,1; 0,01; 0.001 – то же самое, что разделить его на 10, 100, 1000. Для этого надо перенести запятую влево на столько цифр, сколько нулей стоит перед единицей в множителе.
Чтобы разделить число на десятичную дробь, надо:
в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;
после этого выполнить деление на натуральное число.
28.Чтобы разделить десятичную дробь на 0,1; 0,01; 0,001, надо перенести в ней запятую вправо на столько цифр, сколько в делителе стоит нулей перед единицей (то есть умножить её на 10, 100, 1000).
29.Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
30.Процентом называют одну сотую часть.
31. Средняя скорость — отношение всего пройденного пути на всё время движения.
32. Простым числом называют такое натуральное число, которое больше единицы и делится только на 1 и само на себя.
33. Если число оканчивается одной из цифр 0, 2, 4, 6, 8, то оно делится на 2.
34. Если сумма цифр числа делится на 9, то и само число делится на 9.
35. Если сумма цифр числа делится на 3, то и само число делится на 3.
36.Если две последние цифры числа нули или образуют число, делящиеся на 4, то и само число делится на 4.
37.Если число делится и на 2 и на 3, то число делится на 6.
38. Если три последние цифры числа нули или образуют число, делящееся на 8, то и само число делится на 8.
infourok.ru
Обыкновенные дроби. Видеоурок. Математика 5 Класс
Слово «дробь» означает часть, нецелое количество, нецелое число.
Пол-литра молока. Для обозначения такого количества, для половины, мы используем дробь (рис. 1).
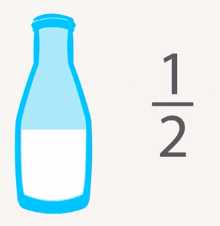
Рис. 1. литра молока
Треть пути. Если мы прошли треть пути, то мы знаем, что путь делится на три части и мы прошли одну такую часть (рис. 2).
Рис. 2. Треть пути
Одну часть мы обозначаем дробью . Оставшийся путь составляет . Если весь путь был 6 км, то треть пути – это 2 км, оставшиеся – это 4 км (рис. 3).
Рис. 3. Путь, разделенный на части
Четверть часа. Один час, то есть 60 минут, удобно делится на 4 части (рис. 4).
Рис. 4. Час, разделенный на четыре части
В каждой части по 15 минут. Одна такая часть называется четвертью. Обозначается как (рис. 5). Оставшаяся часть часа, 45 минут, содержит три таких четверти по 15 минут, обозначается (рис. 6).

Рис. 5. Четверть часа

Рис. 6. Три четверти часа

Во всех этих примерах одинаковым было то, что мы брали объект (литр молока, путь, час) и делили на несколько равных частей. Потом брали одну или несколько таких частей и это количество и называли дробью.
Разделим торт на шесть равных частей. Каждая часть торта – это торта (рис. 7).
Рис. 7. Торт, разделенный на шесть равных частей
Если взять две части торта, то получится (две шестых) торта (рис. 8). А оставшаяся часть будет составлять (четыре шестых) торта (рис. 9).

Рис. 8. Две шестых торта

Рис. 9. Четыре шестых торта

Какую часть торта означает дробь ?
Речь идет о пятых, значит, торт нужно разделить на пять частей (рис. 10) и взять три из них: (рис. 11). Мы получаем чуть больше половины торта.

Рис. 10. Торт, разделенный на пять частей

Рис. 11. Три пятых торта

Не обязательно делить что-то целое, например торт, на части. Можно взять несколько предметов (множество) и разделить его на равные части.
Пусть есть 10 яблок (рис. 12). Разделим их на 5 равных частей, так как речь идет о пятых. Каждая часть будет состоять из двух яблок. Сама доля будет обозначаться , ведь делили мы на 5 частей (рис. 13).

Рис. 12. Множество, состоящее из яблок

Рис. 13. Множество яблок, разделенное на пять частей

множества из 10 яблок будет содержать 2 яблока, а уже будет содержать 3 раза по 2 яблока, то есть 6 яблок.
Не обязательно представлять конкретные объекты, как торт или множество яблок, чтобы работать с дробями. Можно оперировать с дробью как с математическим объектом.
Возьмем дробь . Нижняя часть дроби, 7, называется знаменателем. Она сообщает, на сколько частей мы делили. Делили на 7 равных частей (рис. 14).
Рис. 14. Семь равных частей
Верхняя часть дроби, 3, называется числителем. Она сообщает, сколько таких частей мы взяли. То есть дробь состоит из трех долей (рис. 15), полученных при делении на 7 равных частей.
Рис. 15. Три доли, взятые из семи равных частей
Что означает дробь ? Нужно разделить объект на 873 равные части. Каждая часть – это . Теперь нужно взять 214 таких долей.
Потренируемся находить дроби от разных количеств.
В классе 30 человек. класса пойдет на французский язык, класса – на английский. Сколько человек каким языком будет заниматься?
Чтобы найти от 30, нужно класс разделить на три равные части, то есть 30 разделить на 3. Тот факт, что мы ищем от 30, будем записывать как . Предлог «от» мы заменяем знаком умножения:
Полученное число 10 – это и есть доля от общего количества учеников, от 30. Мы выяснили, что 10 учеников пойдут заниматься французским языком.
Найдем общего количества учеников, то есть от 30. Разделим 30 на 3 и умножим полученный результат на два.
Найдем от общего количества учеников, то есть от 30 или . Делим 30 на 5, получаем от 30, а именно 6. Тогда от 30 будет равна четырем таким долям, то есть 24.
Давайте теперь сформулируем, как мы находили дробь для числа.
Пусть дано число и необходимо найти его часть , то есть дробь от . Знаменатель говорит, на сколько частей надо делить, а числитель – сколько таких долей брать, умножать. То есть необходимо разделить на и умножить на .
Сколько минут составляет часа? часа? часа? от трех часов?
часа – это от 60 минут. Делим 60 на 2. Мы сразу получаем долю , это 30 минут. Или, как чаще говорят, полчаса. Половина часа.
от 60 минут. Делим 60 на 3 и умножаем на 2.
interneturok.ru
Обыкновенные дроби — это ДРОБНЫЕ ЧИСЛА И Действия С НИМИ — Математика 5 класс — А.С. Истер

Глава 2 ДРОБНЫЕ ЧИСЛА И Действия С НИМИ

В этом разделе вы:
вспомните
понятие обыкновенной дроби;
ознакомитесь
с правильными и неправильными дробями, смешанными числами; десятичными дробями, понятиями среднего арифметического, процента;
научитесь сравнивать обыкновенные дроби с одинаковыми знаменателями, складывать и вычитать дроби с одинаковыми знаменателями, выполнять все действия над десятичными дробями; решать простейшие задачи с процентами.

27. Обыкновенные дроби

До сих пор рассматривались в 5-м классе натуральные числа и число 0. Но, как известно с младших классов, в математике существуют другие числа — дробные.
Возьмем полоску бумаги и примем его длину за единицу. Делим полоску на две равные части (рис. 218). Каждая из этих частей будет одной второй, или половиной этой полоски.
На рисунке 219 видим яблоко, разрезанное на три равные части. Каждая часть равна одной третьей яблока, а две части — двум третьим яблоки.
Рис. 219

Рис. 219
Числа — дробные. Дробные числа записываются с помощью двух натуральных чисел и горизонтальной черты в виде
Такие записи называют обыкновенными дробями. Число b, записанное под чертой, называется знаменателем дроби, показывает, на сколько равных частей разделили единицу (целое). Число а, записанное над чертой, называется числителем дроби, показывает, сколько взято равных частей единицы (целого).
Пример 1. Обычный дробь показывает, что целое разделили на 5 равных частей и взяты 3 такие части.
Пример 2. Если отрезок длиной 1 м разделен на 100 равных частей, то длина каждой части составляет 1 см.
Поэтому можно записать:
(одна сотая метра), (две сотых метра), 17 см = (семнадцать сотых метра) и тому подобное.
Пример 3. Так как 1 кг = 1000 г, то 1 г = (одна тысячная килограмма).
Рассмотрим задачу на нахождение дроби от числа.
Задача 1. Сколько градусов составляет раскрою того угла?
Решения. Развернутый угол разделим на 5 равных частей.развернутого угла равна 180° : 5 = 36°, тогда развернутого угла — это 36° ∙ 2 = 72°.
Рассмотрим задачу на нахождение числа по его дроби.
Задача 2. Дорога от А до В равно 120 км, что составляет пути от А до C. Какое расстояние между А и C?
Решение (рис. 220). Поскольку три четверти дороги составляет 120 км, то одна четвертая часть дороги равна 120 : 3 = 40 км. Тогда вся дорога в четыре раза длиннее, чем 40 км, то есть равен 40 ∙ 4 = = 160 км.
Рис. 220
Рис. 221
Дробные числа, как и натуральные, можно изображать на координатном луче. Например, для изображения дроби (рис. 221) разделим единичный отрезок на 8 равных частей. Затем от начала луча отложим последовательно 3 такие части. Получим точку А, которая изображает число
Можно записать:
Длина отрезка OA равна единице.
Начальный уровень
918. Прочитай дроби, названия числитель и знаменатель каждой дроби и объясни, что они означают:
919. Молоко из кувшина разлили в стаканы четырем детям — поровну каждому. Какую часть молока получила каждый ребенок? Как это записать?
920. Участок пути, что ремонтируется, поделили на 5 равных частей. Три части ремонтировала большая бригада, а две части — меньшая бригада. Какую часть участка отремонтировала каждая бригада?
921. Записать в виде дроби число:
1) одна третья;
2) одна двенадцатая;
3) три седьмых;
4) пять двадцатых;
5) тридцать семь сотых;
6) двадцать восемь сто пятнадцатых.
922. Запиши в виде дроби число:
1) одна седьмая; 2) одна тринадцатая;
3) три восьмых; 4) четыре двадцать первых.
923. Запиши дробью, какая часть фигуры заштрихована (рис. 222-227).
Рис. 222
Рис. 223
Рис.224

Рис. 225
Рис. 226
Рис. 227
924. Запиши дробью, какая часть фигуры заштрихована (рис. 228-231).
Рис. 228
Рис. 229
Рис. 230
Рис. 231
925. Единицу разделили на 5, 7, 13, 24, 100, 317 равных частей. Как назвать одну часть в каждом из этих случаев?</span>
Средний уровень
926. Как называется:
1) одна сотая часть метра;
2) одна тысячная часть тонны;
3) одна двадцать четвертая часть суток;
4) одна шестидесятая часть часа?
927. Как называется:
1) одна сотая часть гривны;
2) одна тысячная часть килограмма;
3) одна шестидесятая часть минуты?
928. В саду 30 деревьев, из них 13 вишен. Какую часть всех деревьев составляют вишни?
929. Начерти отрезок длиной 10 см и отрезки, длины которых составляют длины данного отрезка.
930. Начерти отрезок длиной 12 см и отрезки, длины которых составляют длины данного отрезка.
931. Начерти в тетради квадрат со стороной 3 см. Раздели его на 9 равных квадратиков. Заштрихуй большого квадрата в зеленый цвет, а — в красный.
932. Заполни ячейки:
1) 1 мм = □ см; 2) 1 см = □ м;
3) 1 м = □ км; 4) 1 кг = □ ц;
5) 1 ц = □ т; 6) 1 с = □ мин;
7) 1 ч = □ суток; 8) 1 коп. = □ грн.
933. Заполни пропуски:
934. Рабочий выполняет задание за 8 ч. Какую часть задания он выполнит за 1 ч? 2 ч? 5 ч? 7 ч?
935. Автобус преодолевает расстояние от А до В за 6 часов. Какую часть расстояния он проедет за 1 ч? 2 ч? 5 ч?
936. Составь задачу, решением которой является дробь
937. Купили кусок ткани длиной 2 м 40 см и из куска сшили платье для куклы. Сколько сантиметров ткани ушло на платье?
938. В классе 30 учеников, из них — девушки. Сколько девочек в классе?
939. В мотке 60 м. Найди длины таких его частей:
940. Автомобиль должен проехать расстояние между городами А и B, которая равна 360 км. За первый час машина проехала по этому пути. Сколько километров осталось проехать автомобилю?
941. От дыни массой 3 кг 600 г Ивану отрезали часть, а Марии — часть. Найдите массу каждого куска. Какая масса части дыни осталась?
942. Каким числам соответствуют точки А, В, C, D на координатном луче (рис. 232)?
Рис. 232
Достаточный уровень
943. Начерти с помощью транспортира угол, что составляет:
944. Выражения:
1) в метрах: 3 дм, 18 см, 5 дм 2 см, 3 мм, 1 см 5 мм;
2) в часах: 5 мин, 7 мин, 15 с, 3 мин 5 сек.
945. Выражения:
1) в тоннах: 15 кг, 321 кг, 4 ц 7 ц, 3 ц 12 кг;
2) в часах: 7 мин, 5 сек, 5 мин 12 сек.
946. Сергей, Иван и Петр собрали вместе 144 грибы. Сергей собрал всех грибов, а Иван — всех грибов. Сколько грибов собрал Петр?
947. Автобус проехал 180 км за три часа. За первый час он проехал всего расстояния, а за вторую — всей расстоянии. Сколько километров проехал автобус за третий час?
948. Площадь двора составляет 800 м2. Детская площадка занимает двора, а автостоянка — остальной площади. Какова площадь автостоянки?
949. Магазин получил для реализации 240 кг конфет. За первый день он продал полученного, а за второй — остальных. Сколько килограммов конфет продал магазин за два дня?
950. Длина прямоугольного параллелепипеда равна 36 см, ширина составляет длины, а высота — ширины. Найди в объем прямоугольного параллелепипеда.
951. За день ученик прочитал 36 страниц, что составило книги. Сколько страниц в книге?
952. Сколько молока в бидоне, если этого молока составляют 24 л?
953. У Иванки 42 наклейки, что составляет количества наклеек, которые имеет Оля. У кого из девочек наклеек больше? На сколько?
Высокий уровень
954. За первый день турист прошел 24 км, за второй день — того, что прошел за первый, а за третий день — того, что за первые два дня вместе. Сколько километров прошел турист за три дня?
955. Ширина прямоугольника равна 28 см, что составляет его длины. Найди периметр и площадь прямоугольника.
956. Ширина прямоугольного параллелепипеда равна 20 см, что составляет
Найди площадь поверхности этого параллелепипеда.
957. Один из двух слагаемых равна 115 и составляет суммы. Найди второе слагаемое.
958. Найди число, которого равна от числа 270.
959. В Автомобиль за первый час проехал всего пути. Какую часть пути ему осталось проехать?
Решение (рис. 233). Автомобилю осталось проехать пути.
Рис. 233

Упражнения для повторения
960. Обчисли сумму всех:
1) семицифрових чисел, которые меньше числа 1 000 003;
2) шестицифрових чисел, которые больше числа 999 995.
961. Есть квадрат.
1) Периметр квадрата равен 48 дм. Найди площадь квадрата.
2) Периметр квадрата равен 16 см. Сторону квадрата уменьшили на 1 см. Как изменилась площадь квадрата?
3) Периметр квадрата равен 20 м. Сторону квадрата увеличили на 2 м. Как изменилась площадь квадрата?
962. Отец приобрел под застройку прямоугольный участок земли шириной 20 м и длиной b м. Часть земли площадью m м2 он отдал сыну. Какую площадь отец оставил себе? Склады буквенный выражение и обчисли его, если b = 25 м, m = 150 м2.
schooled.ru
Правильные и неправильные дроби. Видеоурок. Математика 5 Класс
На этом уроке мы узнаем, что такое дробь и для чего она нужна. Научимся обозначать половину и представлять по-разному одно и то же количество. Также рассмотрим, всегда ли дробь меньше единицы, и узнаем, что такое правильные и неправильные дроби.
Само слово «дробь» старинное и означает «часть». Сейчас это слово осталось только у охотников (они стреляют дробью) и в математике. И еще нам остались слова «дробный», «дробить».
Потому что часто мы имеем дело с частями, с нецелыми количествами. Например, делим яблоко на три части.
Без дроби не обойтись. Одна часть – это . (Рис. 1.)
Рис. 1. Изображение
Две части – . (Рис. 2.)
Рис. 2. Изображение
Не обязательно что-то резать на части.
Для множества из пяти яблок одно яблоко – это , два яблока – от общего количества. (Рис. 3.)
Рис. 3. Изображение
То есть дробь нужна, чтобы обозначить некое количество, в том числе нецелое.
Одно и то же количество можно обозначить разными дробями.
Разрежем торт на 2 части, возьмем одну часть.
Можно разрезать на 4 части и взять две, будет то же самое количество, половина. (Рис. 4.)
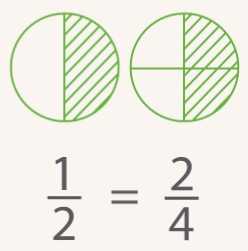
Рис. 4. Изображение половины
Способов бесконечно много. Можно разделить на 10 частей и взять пять, или на миллион частей и взять полмиллиона.
Иногда нам удобно одно представление, иногда другое.
Маша съела торта, потом еще другого. Сколько всего было съедено?
Надо найти сумму . (Рис. 5.)
Разные куски по размеру сложно складывать, поэтому представим первое количество другой дробью. Разделим каждый кусок еще на две части, то есть всего на 6. То есть кусок первого торта можно обозначить не только , но и эквивалентной записью – .
и – это .
А снова можно обозначить эквивалентной записью – . Всего было съедено полторта.
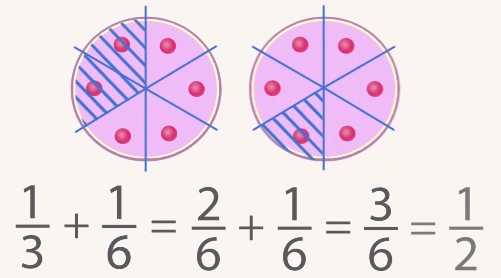
Рис. 5. Сумма дробей
Предположим, что мы читаем рецепт блинов. И прикидываем, хватит ли нам одного литрового пакета молока.
5 стаканов молока – это 1 литр.
Если требуется один стакан – это литра. Это, несомненно, меньше 1 литра.
Два стакана тоже меньше 1. При этом два стакана – это литра.
Если по рецепту требуется 5 стаканов молока, то это уже литра. Но, очевидно, это равно целому литру.
По рецепту может потребоваться, например, 6 стаканов, литра. Но это уже на 1 стакан больше, чем литр.
То есть дробью может быть обозначено количество меньше единицы, равное единице или больше единицы.
Так как слово «дробь» обозначало часть, то есть меньше целого, то те дроби, которые обозначают количество, меньшее единицы, назвали «правильными» дробями, а остальные – «неправильными».
То есть дроби и называются правильными, так как они меньше единицы.
А вот уже и – неправильными.
Если числитель меньше знаменателя, то дробь меньше единицы и мы называем ее правильной.
Если числитель равен знаменателю, то дробь равна единице и уже называется неправильной.
Если числитель больше знаменателя, то дробь больше единицы и тоже неправильная.
Пример
Правильные дроби со знаменателем 259:
Неправильные дроби со знаменателем 259:
Сравним следующие дроби:
– правильная дробь, меньше единицы;
– неправильная, равна единице;
– неправильная, больше единицы.
Таким образом:
Итак,
1. Если дробь меньше единицы, то ее называют правильной. В этом случае числитель всегда меньше знаменателя.
2. Если у дроби числитель и знаменатель равны, то дробь равна единице и называется неправильной.
3. Если числитель больше знаменателя, то дробь больше единицы и тоже называется неправильной.

Список литературы
Виленкин Н.Я., Жохов В.И. Учебник по математике 5 класс (2008), глава II. ДРОБНЫЕ ЧИСЛА, с.151.

Никольский С.М., Потапов М.К. Учебник по математике 5 класс (2012), глава 4.

Дорофеев Г.В., Петерсон Л.Г. Учебник по математике 5 класс. Часть 1 – 2 (2011), часть 2, глава 3.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет
5klass.net (Источник).

Formula-xyz.ru (Источник).

5klass.net (Источник).

Домашнее задание
Что такое дробь? Как обозначить половину?

При каких значениях х дробь будет неправильной: , , ?

Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 5 класса (5-е изд., испр.) с. 97.

interneturok.ru
5 класс Смешанные дроби (памятка ученику)
Смешанные дроби
Смешанная Неправильная
5 =
Сложение и вычитание смешанных дробей
Чтобы сложить смешанные числа, нужно:
1) привести к наименьшему общему знаменателю дробные части;
2) сложить отдельно целые и дробные части;
3) если необходимо, сократить дробную часть;
4) если дробная часть суммы окажется неправильной дробью, выделить из нее целую часть и полученное число прибавить к целой части суммы.
Например:
Чтобы вычесть смешанные числа, нужно:
1) привести к наименьшему общему знаменателю дробные части;
2) если дробные части «не вычитаются» (дробная часть уменьшаемого меньше дробной части вычитаемого),то нужно «занять» единицу из целой части;
3) вычесть отдельно целые и дробные части;
4) если необходимо, сократить дробную часть.
Например:
Например:
Смешанные дроби
Сложение:
1 шаг: к общ. знам. (НОЗ)
2 шаг: + цел1+цел2,
др1+др2 (числ1+числ2)
3 шаг: неправ. смеш.
4 шаг: сократить
Вычитание:
1 шаг: к общ. знам. (НОЗ)
2 шаг: занять ед. (если нужно)
3 шаг: — цел1 — цел2
др1 — др2 (числ1 — числ2)
4 шаг: сократить
Умножение:
1 шаг: смеш. неправ.
2 шаг: числ1 числ2
зн1 зн2 сократить!
3 шаг: вычислить
4 шаг: неправ. смеш.
Деление:
1 шаг: смеш. неправ.
2 шаг: числ1 зн2
зн1 числ2 сократить!
3 шаг: вычислить
4 шаг: неправ. смеш.
infourok.ru
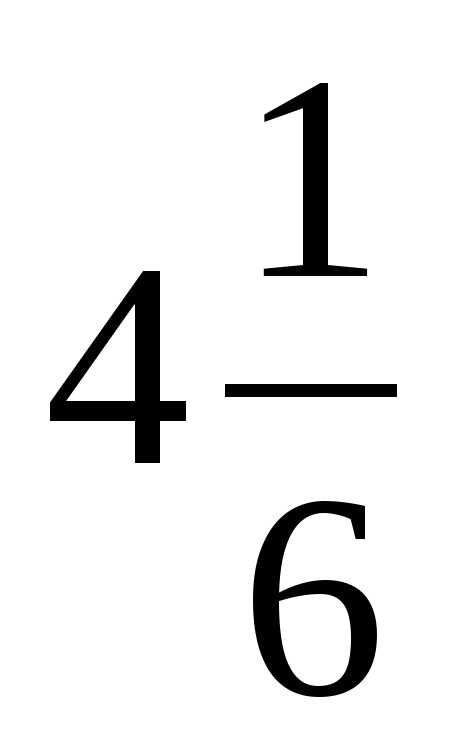
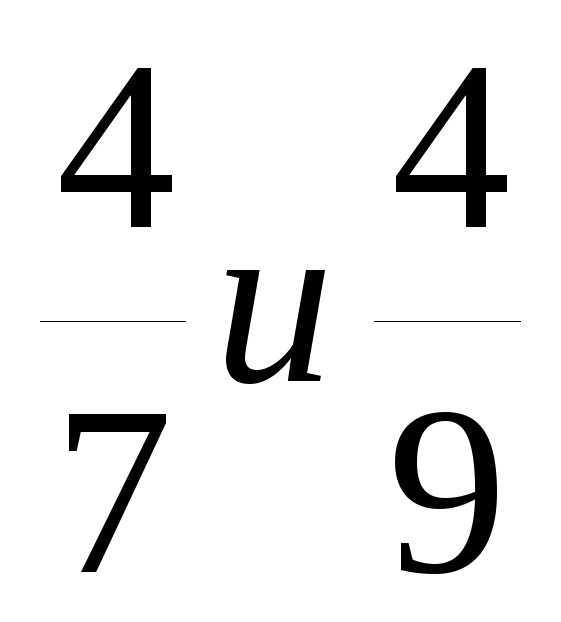
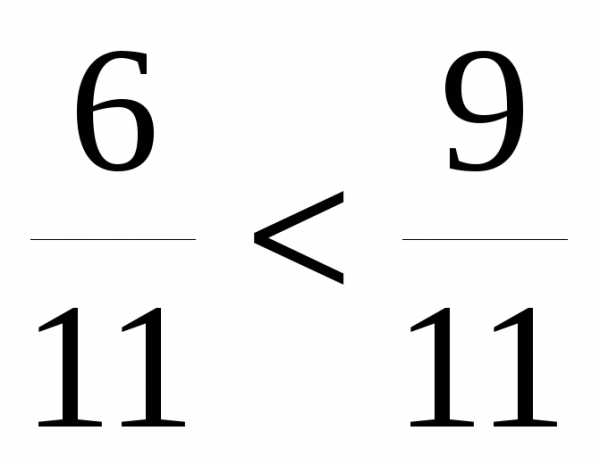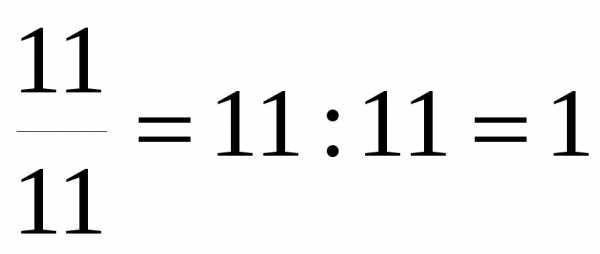
No related posts.