Текстовые задачи егэ по математике как решать – Текстовая задача B13 — задачи на движение и работу

Задача 11 — текстовые задачи

Для текстовых задач не существует единого алгоритма решения — в этом вся их сложность. Фактически, каждую задачу приходится решать «с нуля». Зубрить их тоже бесполезно, потому что текстовых задач слишком много.

Тем не менее, существуют типовые задачи, которые вполне стандартно решаются и постоянно встречаются на ЕГЭ по математике. Ими мы и займемся.

§ 1.

Вебинар по задачам B14: движение, работа, смеси и сплавы

Глава 1.

Классические задачи на движение

§ 1.

Особенности решения текстовых задач

§ 2.

Задача B14: движение навстречу

§ 3.

Движение вдогонку и сравнение времени

§ 4.

Тест по задачам B14: легкий уровень, 1 вариант

§ 5.

Тест по задачам B14: легкий уровень, 2 вариант

§ 6.

B14 и эскалаторы: считаем скорость

§ 7.

Задача B14 про эскалаторы: считаем ступеньки

Глава 2.

Работа и производительность труда

§ 1.

Производительность совместного труда

§ 2.

B14: количество вопросов в тесте

§ 3.

Трубы и резервуары: одинаковый объем

§ 4.

Трубы и резервуары: разный объем

§ 5.

Более сложные задачи на производительность

Глава 3.

Движение по воде

§ 1.

Решение задач на движение по воде

§ 2.

Тест по задачам B14: средний уровень, 1 вариант

§ 3.

Тест по задачам B14: средний уровень, 2 вариант

Глава 4.

Смеси и сплавы

§ 1.

Как решать задачи про смеси и сплавы

§ 2.

Простая задача B14 на смеси и сплавы

§ 3.

Сложная задача B14 на смеси и сплавы

§ 4.

Смеси и сплавы в задаче B14: неизвестна масса

Глава 5.

Проценты и нестандартные задачи

§ 1.

Задача B14: сложные проценты

§ 2.

Семья из трех человек (нестандартная задача)

§ 3.

Сложная задача B14: работа трех исполнителей

§ 4.

Изюм и виноград (смеси и сплавы)

Задачи на проценты, смеси, сплавы

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

Задачи на движение по прямой

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

61

62

63

64

65

66

67

68

69

70

71

72

73

Задачи на движение по окружности

74

75

76

77

78

79

80

Задачи на движение по воде

81

82

83

84

85

86

87

88

89

90

91

92

93

94

95

96

97

98

99

100

101

102

103

104

Задачи на совместную работу

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

Задачи на прогрессии

141

142

143

144

145

146

147

148

149

www.berdov.com

Решение текстовых задач на движение при подготовке к ЕГЭ

Часть B единого государственного экзамена содержит текстовые задачи, в частности, задачи на движение.

В большинстве задач на движение используется формула s = vt, где v – это скорость движения, t – время движения, s – длина пройденного пути. При этом надо учитывать, что указанные величины должны быть в одной системе единиц. Из данной формулы можно получить еще две: v = s/t, t = s/v. Если в задаче говорится о нескольких движущихся объектах, то формулы следует записать для каждого.

Если в явном виде заданы не все величины, часть из них дана в сравнении (меньше – больше, позже – раньше и т.п.), то используя эти сравнения, можно записать соответствующие уравнения. Как правило, число уравнений совпадает с числом сравнений, содержащихся в условии задачи.

Решить задачу можно с помощью системы уравнений, а можно с помощью одного уравнения. Рассмотрим несколько примеров задач на движение по дороге и на движение по воде.

Движение по дороге

Задача 1.

Из города А в город В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 15 км/ч, а вторую половину пути – со скоростью 90 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 54 км/ч. Ответ дайте в км/ч.

Решение.

При решения текстовых задач эффективно построение схем и составление таблиц.

Используя сравнение скоростей, указанное в задаче, и обозначая скорость первого автомобилиста v, запишем скорость второго автомобилиста на протяжении всего пути: первую половину пути он прошел со скоростью (v – 15) км/ч, а вторую половину со скоростью 90 км/ч.

Таблица будет иметь такой вид:

Объект	Путь, км	Скорость, км/ч	Время, ч
Автомобилист 1	S	v	t
Автомобилист 2	S	I половина пути   v – 15 II половина пути  90	t

Условие, что автомобилисты прибыли в пункт назначения одновременно, используем для составления уравнения. Выражаем время первого автомобилиста, которое он затратил на весь путь через S и v: S/v, время второго (учитывая, что первую и вторую половину пути он проезжал с разной скоростью) 1/2S/(v – 15) + 1/2S/90, и приравниваем их. Получаем уравнение относительно скорости первого автомобилиста:

S/v = 1/2S / (v – 15) + 1/2S/90.

Сокращаем его на множитель S ≠ 0 и умножаем обе части уравнения на 2. В результате получаем

2/v = 1/(v – 15) + 1/90.

Для решения последнего уравнения умножаем обе его части на произведение 90v(v – 15) ≠ 0. После всех преобразований получаем квадратное уравнение:

v² – 105v + 2700 = 0.

Откуда v₁ = 60, v₂ = 45. Условию задачи (v > 54 км/ч) удовлетворяет только корень v₁ = 60, следовательно, скорость первого автомобилиста 60 км/ч.

Ответ: 60 км/ч.

Решая задачи на движение, полезно выяснитьсколько раз в условии задачи сравниваются однородные величины. В нашей задаче два сравнения: скоростей автомобилистов и времени их движения на одном и том же пути. Первое сравнение используем для выражения одной скорости через другую. Итоговое уравнение – это сравнение времени движения автомобилистов.

Задача 2.

Велосипедист и пешеход вышли из пунктов А и В, расстояние между которыми 12 км, и встретились через 20 мин. Пешеход прибыл в пункт А на 1ч 36 мин позже, чем велосипедист в пункт В. Найти скорость пешехода. Ответ дайте в км/ч.

Решение.

Из первого условия задачи найдем зависимость между скоростями велосипедиста и пешехода. Пусть v₁ – скорость пешехода, v₂ – скорость велосипедиста. Тогда 20/60(v₁ + v₂) = 12, откуда v₁ + v₂ = 36. Заполним таблицу, принимая за х км/ч скорость пешехода, тогда скорость велосипедиста (36 – х) км/ч.

Объект	Путь, км	Скорость, км/ч	Время, ч
Велосипедист	12	36 – х	12/(36 – х)
Пешеход	12	х	12/х

Сравнение, что пешеход прибыл в пункт А на 1ч 36 мин позже, чем велосипедист в пункт В, используем для составления уравнения

12/x – 12/(36 – x) = 1 – 36/60.

Откуда получаем квадратное уравнения 1,6x² – 81,6x + 432 = 0, корни которого х₁ = 45, х₂ = 6. Так как х – скорость пешехода, следовательно, подходит только х = 6. Скорость пешехода 6 км/ч.

Ответ: 6 км/ч.

Движение по реке

Особенность движения по реке состоит в том, что течение реки увеличивает или уменьшает скорость плывущего объекта. Это изменение равно скорости течения.

Задача 3.

Теплоход проходит по течению реки до пункта назначения 384 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 48 часов после отплытия из него. Ответ дайте в км/ч.

Решение.

Обозначим буквой х – скорость теплохода. Скорость течения (4 км/ч) дает возможность выразить скорость теплохода по течению (х + 4) км/ч и против течения (х – 4) км/ч. Заполним таблицу:

Направление	Путь, км	Скорость, км/ч	Время, ч
По течению	384	х + 4	384/(х + 4)
Против течения	384	х – 4	384/(х – 4)

Общее время, затраченное на путь туда и обратно, составляет 48 – 8 = 40 часов. Это условие и есть ключевым для составления уравнения

384/(x + 4) + 384/(x – 4) = 40.

После сокращения на 8 уравнение принимает вид

48/(x + 4) + 48/(x – 4) = 5.

Откуда получаем квадратное уравнение 5x² – 96x – 80 = 0, положительным корнем которого является х = 20. Значит, скорость теплохода в неподвижной воде составляет 20 км/ч.

Ответ: 20 км/ч.

Таким образом, составление таблицы и анализ условий позволяет упростить решение задачи на движение.

 Остались вопросы? Не знаете, как решать задачи на движение?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Текстовые задачи B13 из ЕГЭ по математике

Текстовая задача B13 из ЕГЭ по математике посвящена решению математических задач или, как их еще называют, задач на составление уравнений. Все эти задачи можно условно разбить на три большие группы: задачи на движение, задачи на работу и задачи на растворы, расплавы, проценты и доли. Как репетитор по математике, занимающийся подготовкой к ЕГЭ и ГИА по математике, могу сказать, что умение решать подобные задачи является ключевым при подготовке к Единому государственного экзамену по математике.

В данной статье мы кратко остановимся на основных проблемах, которые возникают у школьников при решении текстовых задач B13. Как обычно, будем разбирать все на примере конкретных задач B13, взятых из реальных вариантов ЕГЭ по математике прошлых лет. К каждому разобранному примеру в статье будет приведена аналогичная задача для самостоятельного решения для осуществления самоконтроля, без него никак. Тем не менее, если при их решении у вас возникнут какие-то вопросы, вы можете смело задавать их в комментариях. Ни один вопрос без ответа не останется.

Прежде чем мы приступить к разбору конкретных текстовых задач B13, посмотрим, какие вообще существуют подходы к их решению. Наиболее распространенный и, надо сказать, довольно эффективный способ — использование таблиц. В зависимости от типа решаемой задачи (будь то задача на движение, работу, сплавы, растворы и проценты) столбики в этой таблице будут иметь разные названия:

Таблицы для решения текстовых задач B13 (задач на составление уравнений) из ЕГЭ по математике

Почему использование таких таблиц упрощает решение текстовых задач B13 на составление уравнений? Просто потому, что это удобно. Данные таблицы позволяют в наглядном и понятном виде записать условие задачи и провести его анализ для составления уравнения. Разберем это на конкретных примерах.

Текстовые задачи B13 на движение

Пример 1. Из пунктов A и B одновременно выехали навстречу друг другу два автомобиля. Первый автомобиль двигался в 2 раза быстрее второго и приехал в пункт B на 1 час раньше, чем второй приехал в пункт A. На сколько минут раньше встретились бы автомобили, если бы скорость второго автомобиля была равна скорости первого?

Решение. Итак, по шагам рассмотрим как заполняется таблица в данной задаче. Читаем текст задачи еще раз. Первое предложение: «Из пунктов A и B одновременно выехали навстречу друг другу два автомобиля.» Речь идет о двух автомобилях, значит наша таблица будет выглядеть следующим образом:

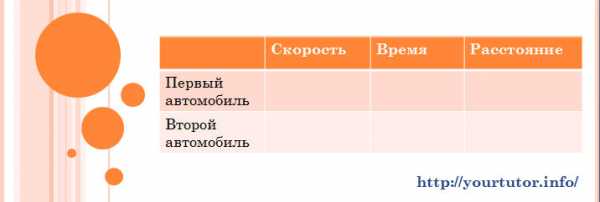
Внешний вид таблицы, используемой для решения текстовой задачи B13 на движение

Читаем дальше. Второе предложение: «Первый автомобиль двигался в 2 раза быстрее второго и приехал в пункт B на 1 час раньше, чем второй приехал в пункт A.» В данном предложении, как видите, содержатся данные, которые нужно занести в соответствующие ячейки нашей таблицы. Фраза «он (первый автомобиль) приехал в пункт B на 1 час раньше, чем второй приехал в пункт A» означает, что время движения первого автомобиля было на 1 час меньше, чем второго. Попутно мы осознаем, что оба автомобиля проехали одинаковое расстояние, которое можно обозначить за 1. Заносим эти данные в таблицу, и она принимает вид:

yourtutor.info

Решение текстовых задач № 11 (профильный уровень)

Презентация содержит различные типы заданий №11 (задачи на движение, на работу, на проценты, на смеси и сплавы) из экзаменационных работ, составленных в соответствии с демонстрационным вариантом и спецификацией 2015 года с учётом проекта изменений на 2016 год (под ред. И.В.Ященко).
Цель: формирование умений выполнять задания №11 (текстовые задачи) из II части заданий, включаемых в итоговую аттестацию за курс средней (полной) общеобразовательной школы профильного уровня.

Задачи:
Образовательные: Повторить понятия: процент, производительность, скорость, средняя скорость, процентное содержание; рассмотреть основные идеи, подходы и методы решения заданий №11; систематизировать знания по данным темам, их значение в математике, связи с другими темами; развить умение проводить анализ полученных результатов.
Воспитательная: формировать представление о математике как части общечеловеческой культуры; формировать осознание значения математики в повседневной жизни человека.
Развивающая: формировать аналитическое мышление, развивать память, кругозор, умение преодолевать трудности при решении более сложных задач; формировать умение точно и грамотно выражать свои мысли с применением математической терминологии и символики.

© Коломина Наталья Николаевна Коломина Наталья Николаевна

Понравилось? Сохраните и поделитесь:

По кнопке ниже вы можете скачать Решение текстовых задач № 11 (профильный уровень) категории ЕГЭ по математике бесплатно. Будем благодарны, если вы оставите отзыв или посмотрите еще другие материалы на нашем сайте. Документ является презентация.

Скачать материал 2.9Mb
Загрузка началась… Понравился сайт? Получайте ссылки
на лучшие материалы еженедельно! Подарок каждому подписчику!

easyen.ru

Особенности решения текстовых задач

28 января 2014

Этим видео я открываю серию уроков, посвященных текстовым задачам B14 из ЕГЭ по математике. Сегодня мы рассмотрим вполне типичную задачу на движение, однако ее условие специально составлено так, что многие ученики «зависают» при решении. Но это нормально: просто некоторые задачи не вписываются в стандартный алгоритм решения.

Задача B14. Два человека отправляются одновременно из одного и того же места на прогулку до опушки леса, находящейся в 4,5 км от места отправления. Один идет со скоростью 2,4 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от места отправления произойдет их встреча? Ответ выразите в километрах.

Итак, существуют два подхода к решению задач на движение:

1. С помощью таблиц — самый распространенный прием, который в большинстве случаев помогает быстро получить уравнение, но именно в сегодняшней задаче этот прием дает осечку.
2. Последовательный анализ условия с привлечением иллюстраций — классический прием из средней школы, о котором к 11-му классу многие забывают. Именно его мы сегодня и применим.

Обратите внимание: на практике любую задачу B14 можно решить каждым из этих способов. И ответ получится одинаковым. Однако некоторые задачи проще решаются таблицами, а другие — иллюстрациями и анализом. Поэтому какой способ выбрать — зависит исключительно от предпочтений ученика.

Смотрите также:

1. Задача B14: движение навстречу
2. Движение вдогонку и сравнение времени
3. Тест к уроку «Сложение и вычитание дробей» (легкий)
4. Пробный ЕГЭ 2012. Вариант 12 (без логарифмов)
5. Задача C2: уравнение плоскости через определитель
6. Тест по задачам B14: легкий уровень, 2 вариант

www.berdov.com

Решение текстовых задач (по материалам ЕГЭ)

МОУ СОШ №36 г. Липецка

Учитель: Куликова Ирина Юрьевна

Предмет: алгебра и начала анализа

Программно-методические обеспечение:

Программа — базовый уровень

Класс: 11 – общеобразовательный

Модуль: «Итоговое повторение. Решение текстовых задач. Подготовка к ЕГЭ»

Использованная литература: 1. Варианты ЕГЭ по математике 2008;

2. Никушкина С.Л., Судавная О.И. Математика ЕГЭ Раздаточный материал тренировочных тестов. Санкт-Петербург, «Тригон»,2009

3.Учебно-тренировочные материалы для подготовки к ЕГЭ. Математика, М:Интеллект-Центр,2004.

Урок. Тема: «Решение текстовых задач».

Цели урока:

ЭУ(этап урока) — 0

1)отработка практических навыков решения задач на совместную работу;

2)закрепить навык решения дробно-рациональных уравнений;

3)отработка практических навыков решения задач на части;

4) повторить понятие процента и отработать навык нахождения процента от числа;

3)отработка практических навыков решения задач на арифметическую прогрессию;

4) вспомнить и закрепить формулы n-го члена арифметической прогрессии и формулу суммы n-первых членов арифметической прогрессии;

5)подготовка выпускников к ЕГЭ.

Оборудование: раздаточный материал, компьютер, экран

Ход урока

ЭУ-1. Цель: мотивация учащихся

Учитель: На сегодняшнем уроке мы с вами рассмотрим текстовые задачи, которые предлагались на ЕГЭ по математике в прошлые годы.

Вместе мы рассмотрим три типа задач: на совместную работу, на части и на арифметическую прогрессию, отработаем решение дробно-рациональных уравнений, вспомним понятие процента и правило нахождения процента от числа. При решении задач на арифметическую прогрессию мы повторим формулу суммы n-первых членов арифметической прогрессии.

Некоторые задачи мы будем решать с вами вместе, решение некоторых будет предложено для самостоятельного выполнения.

Надеюсь, что этот урок поможет вам успешно подготовится к решению задания В9, которое будет вам предложено на ЕГЭ по математике в этом году.

ЭУ-2 I.Решение задачи на совместную работу вместе с учителем.

Задача 1. Два мебельных мастера, работая вместе, могут за 1 неделю собрать 50 столов. Работая отдельно, первый мастер собирает 60 столов на одну неделю дольше, чем такое же число столов собирает второй мастер. За

сколько недель первый мастер соберет 40 столов?

Решение. Пусть первый мастер собирает за неделю x столов, тогда второй- 50-х столов. Тогда 60 столов первый мастер соберет за 60:х недель, а второй за 60:(50-х) недель. Зная, что первый мастер собирает 60 столов на 1 неделю дольше, составим и решим уравнение:

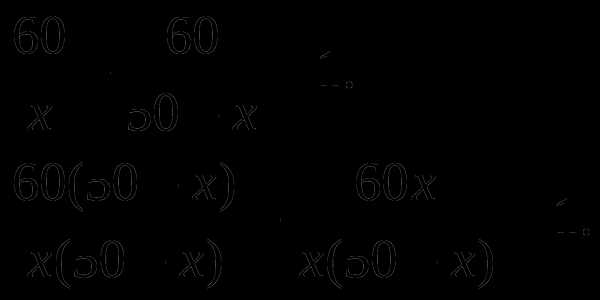ОДЗ уравнения

Получаем квадратное уравнение:

Решая его, находим корни х=20; х=150.

х=150 не удовлетворяет условию задачи, значит для нашей задачи х=20.

Таким образом, первый мастер за неделю собирает 20 столов. Значит 40 столов он соберет за 40:20=2(недели).

ОТВЕТ: первый мастер соберет 40 столов за 2 недели.

II К доске вызываются двое учащихся. Им предлагается самостоятельно решить по одной задаче на совместную работу. Класс в это время работает самостоятельно, потом происходит проверка решения.

Текст задач для учащихся.

Два маляра, работая вместе, могут за 1 ч покрасить стену площадью

40 м2. Первый маляр, работая отдельно, может покрасить 50 м2 стены

на 4 ч быстрее, чем второй покрасит 90 м2 такой же стены. За сколько

часов первый маляр сможет покрасить 100 м2 стены?

Два оператора, работая вместе, могут набрать 40 страниц текста за 1ч.

Работая отдельно, первый оператор на набор 90 страниц этого текста

тратит на 5 ч больше, чем второй оператор на набор 25 страниц. За

сколько часов второй оператор сможет набрать 275 страниц этого текста?

III.Решение задачи на части вместе с учителем.

Задача 2. Объемы ежегодной добычи угля первой, второй и третьей шахтами

относятся как 1: 2: 4. Первая шахта планирует уменьшить годовую

добычу угля на 8%, а вторая – на 2%. На сколько процентов должна

увеличить годовую добычу угля третья шахта, чтобы суммарный объем

добываемого за год угля не изменился?

Решение: Пусть х-объем 1 части добываемого угля, а у- планируемое увеличение годовой добычи угля третьей шахтой.

У нас 2 задачные ситуации: первая — первоначальная добыча, вторая-планируемая добыча. Составим таблицу:

Первоначальная добыча

Планируемая добыча

1 шахта х

0,92х

2 шахта 2х

0,98*2х

3 шахта 4х

4ху

Зная, что суммарный объем добываемого угля не должен измениться, составим и решим уравнение:

Зная, что х не равен нулю, т.к. величина 1 части не может быть нулевой, разделим данное уравнение на х.

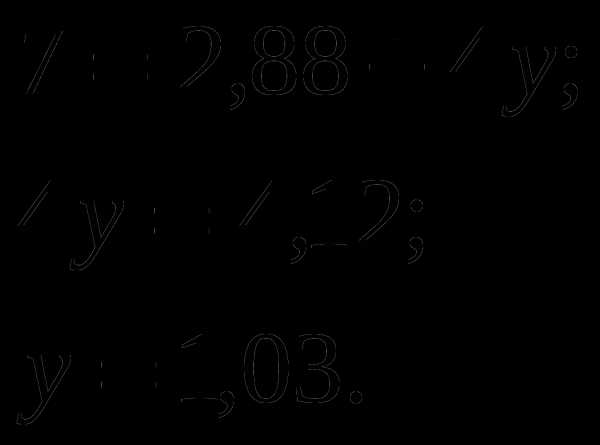
Вывод: добыча угля 3 шахтой должна увеличится на 3 %.

Ответ: третья шахта должна увеличить добычу на 3 процента.

IV.К доске вызываются двое учащихся. Им предлагается самостоятельно решить по одной задаче на совместную работу. Класс в это время работает самостоятельно, потом происходит проверка решения.

Подарочный набор состоит из трех сортов конфет. Массы конфет

первого, второго и третьего сортов в этом наборе относятся как 3:8:17.

Массу конфет первого сорта увеличили на 10%, а второго – на 9%. На

сколько процентов надо уменьшить массу конфет третьего сорта, чтобы

масса всего набора не изменилась?

Набор химических реактивов состоит из трех веществ. Массы первого,

второго и третьего веществ в этом наборе относятся как 5:8:12. Массу

первого вещества увеличили на 8%, а второго – на 4%. На сколько

процентов надо уменьшить массу третьего вещества, чтобы масса всего

набора не изменилась?

V. Решение задачи на арифметическую прогрессию (вместе с учителем).

Задача 3. В первый день подготовки к экзамену школьник повторил 3 вопроса. В каждый следующий день он повторял на 2 вопроса больше, чем в предыдущий, и успел вовремя подготовить все 48 вопросов программы. Сколько дней заняла подготовка?

Решение. Количество вопросов, повторяемых школьником ежедневно составляет арифметическую прогрессию, первый член которой равен трем, а разность равна 2. Пусть n(натуральное число) — число дней, потраченных на подготовку. Тогда количество повторенных вопросов(48 вопросов) равно сумме n членов этой арифметической прогрессии, т.е.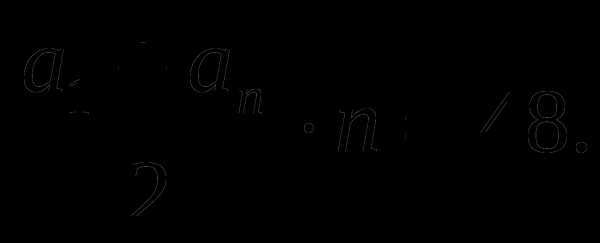

Получаем:

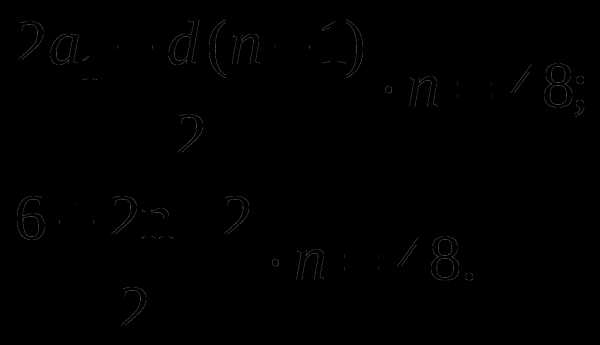
Необходимо решить квадратное уравнение:

Решая, находим корни: n=6, n= — 8. Берём положительный корень. Таким образом, подготовка заняла 6 дней.

Ответ: подготовка заняла 6 дней.

VI. К доске вызывается 1 учащийся для решения аналогичной задачи.

Группа туристов в первый день путешествия прошла 10 км. Далее туристы решили ежедневно преодолевать на 5 км больше, чем в предшествующий день, пользуясь при этом, если потребуется, автостопом. В результате они преодолели расстояние 450 км. Сколько дней туристы были на маршруте, если в течение этого времени 8 дней они отдыхали?

ЭУ-3.: подведение итога урока (желательно, чтобы он был сформулирован учащимися(какие понятия и формулы повторили на уроке(проценты, совместная работа, арифметическая прогрессия)), определение и инструктаж домашнего задания, оценивание учащихся.

Выставление оценок. Отмечаются учащиеся, работавшие у доски.

Домашнее задание: Решить задачи:

1. Один рабочий изготавливает 120 деталей на 1 ч дольше, чем такие же 120

деталей изготавливает второй рабочий. Работая вместе, они за 1 ч

изготавливают 100 таких деталей. За сколько часов второй рабочий

может изготовить 300 деталей?

2. Объемы ежегодной добычи угля первой, второй и третьей шахтами

относятся как 13:14:8. Первая шахта планирует уменьшить годовую

добычу угля на 2%, а вторая – на 1%. На сколько процентов должна

увеличить годовую добычу угля третья шахта, чтобы суммарный объем

добываемого за год угля не изменился?

3.Десятый член арифметической прогрессии равен 19, а сумма первых пятидесяти членов равна 2500.Найти сумму третьего, двенадцатого и двадцатого членов этой прогрессии.

infourok.ru

ТЕКСТОВЫЕ ЗАДАЧИ – Репетитор по математике

ДВИ в МГУ, 14.07.2107.  Вариант 2, задача 6. Текстовая задача.

Анатолий с друзьями решили устроить пикник. Для этого им от пункта нужно добраться вверх по реке до  пункта , причем в их распоряжении есть два катера. Считая себя самым ответственным, Анатолий вызвался самостоятельно доехать до пункта на самом быстроходном катере и начать готовить место для пикника. Оба катера вышли одновременно из пункта . Однако, промчавшись км, Анатолий заметил на берегу машущего ему рукой Бориса, который просил по старой дружбе довезти его до  пункта . И хоть пункт Анатолий уже проехал, он согласился. По пути в пункт Анатолий с Борисом встретили  идущий навстречу второй катер с друзьями Анатолия, откуда те крикнули, что пункт уже совсем близко, и чтобы Анатолий нигде не задерживался. Доставив Бориса в пункт , Анатолий немедленно помчался догонять друзей. Определите, какую долю пути оставалось пройти друзьям Анатолия от момента встречи с ним и Борисом, если известно, что оба катера пришли в пункт одновременно, расстояние между пунктами и равно 2 км, скорости катеров постоянны, а Анатолий действительно нигде не задерживался.

Решение. показать

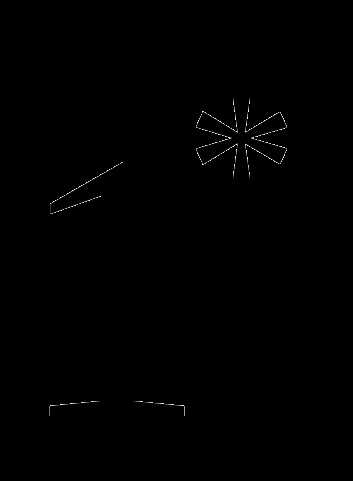
Сделаем рисунок:

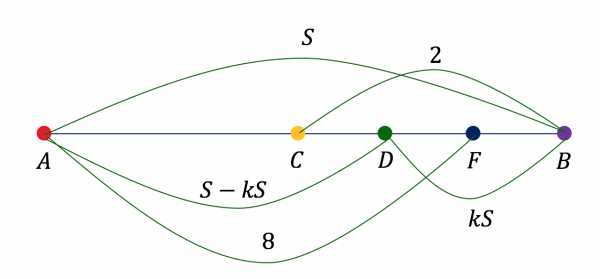
В пункте  встретились Анатолий и Борис, в пункте Анатолий с Борисом встретили друзей Анатолия.

Пусть расстояние между пунктами и равно , и пусть расстояние между пунктами  и  составляет — ю часть всего пути. 

Пусть скорость катера Анатолия по течению равна , скорость катера друзей Анатолия равна , скорость течения равна , тогда скорость катера Анатолия против течения равна .

Составим уравнения для описания встречи в пункте и в пункте .

До встречи Анатолия с Борисом с друзьями Анатолия в пункте Анатолий проплыл путь, равный

; .

Участок  Анатолий проплыл по течению, а участок — против.

За это время друзья Анатолия на втором катере проплыли путь  

Анатолий и друзья Анатолия были в пути одинаковое время. 

Получаем уравнение:

 

До встречи с друзьями в пункте Анатолий проплыл путь, равный по течению и участок   против течения.

Друзья Анатолия за это время пропыли путь .

Получаем второе уравнение:

 

Получили систему уравнений:

Вычтем из второго уравнения первое.

Получим уравнение:

Получим систему:

Приведем правые части уравнений к общему знаменателю:

Разделим первое уравнение на второе:

Умножим обе части на знаменатель,

получим:

Ответ: 

2 способ.

После того, как мы выразили длины отрезков пути через и , задачу можно было решить другим способом.

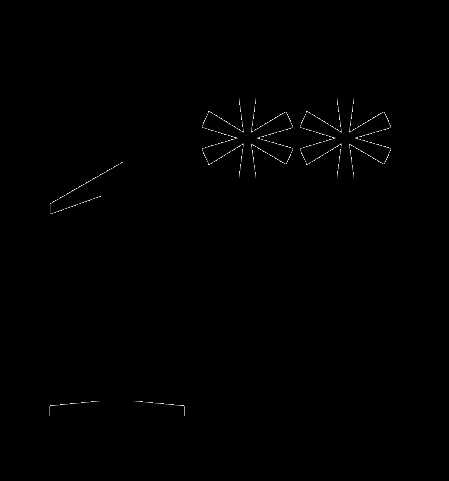
Нарисуем график движения:

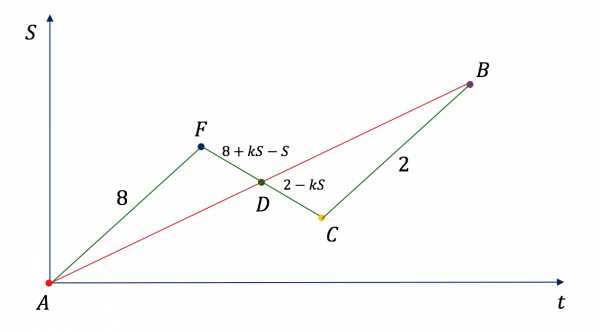
Зеленая ломаная изображает движение катера Анатолия. Участки и — движение по течению с постоянной скоростью. Эти участки изображены параллельными отрезками. Участок — движение против течения.

Красная прямая изображает движение катера друзей Анатолия. Катер двигался с постоянной скоростью в одном направлении.

Точки и — точки встречи катера Анатолия и катера его друзей. Длины участков и мы нашли ранее.

Рассмотрим треугольники и .  Они подобны по двум углам   (  как накрест лежащие, как вертикальные), следовательно,

Подставим длины участков пути:

По свойству пропорции получим:

Разделим обе части равенства на :

Ответ: 

И.В. Фельдман, репетитор по математике

ege-ok.ru