| 1. |
Ягода и сахар
Сложность: лёгкое |
2 |
| 2. |
Пешеход и велосипедист
Сложность: среднее |
2 |
| 3. |
Призовой фонд
Сложность: среднее |
3 |
| 4. |
Сумма на счёте через год
Сложность: среднее |
2 |
| 5. |
Доход с суммы
|
2 |
| 6. |
Проценты по вкладу
Сложность: среднее |
3 |
| 7. |
Расстояние до турбазы
Сложность: среднее |
6 |
| 8. |
Баранина и телятина
|
7 |
| 9. |
Насосы и вода
Сложность: сложное |
4 |
| 10. |
Задача на составление уравнения
Сложность: среднее |
4 |
www.yaklass.ru
решение задач за 5 — 6 класс — Колпаков Александр Николаевич
На этой странице публикуются решения задач по математике для 5 и 6 класса: части, проценты, пропорции, вычисления, простые текстовые задачи на движение, на работу, не требующие применения никаких уравнений кроме линейных. Помните о том, что виртуальный репетитор по математике не знает по какой программе учится Ваш ребенок и поэтому возможны расхождения со школой. Часто одну и ту же задачу на дроби можно решить по разному: средствами 5 класса (при помощи отдельных действий с числителями и знаменателями), а можно, например, средствами 6 класса, выполняя умножение или деление на соответствующие дроби. Для того, чтобы помочь репетитору математики выбрать оптимальный способ оформления номера, указывайте ссылки на авторов школьных учебников и Ваш класс. Пожалуйста, не заваливайте репетитора целыми списками номеров. Ориентировочное ограничение: 1-2 номера для каждого посетителя. Если Вам понравилась эта страница — нажмите на кнопку +1:
Виртуальный репетитор по математике (5-6 класс). Решения ваших задач.
Вопрос от Вовы: Из пункта М в пункт N выехал почтальон со скоростью 23 км/ч, и одновременно с ним из N в M выехал второй почтальон со скоростью 19 км/ч. Когда первый почтальон прибыл N, второму еще оставалось до М проехать 24 км. Каково расстояние между М и N?
Репетитор по математике о задаче про почтальона (А.Н. Колпаков)
Обозначим буквой t время, за которое первый почтальон прибыл в N, тогда 23t — путь, пройденный первым, а 19t — путь, пройденный вторым почтальоном за это же время. Так как второму езе оставалось 24 км, то он прошел за это время расстояние на 24 км меньшее, чем первый, поэтому 23t-19t=24. Решим это простенькое уравнение и получим в ответе t=6 часов. В итоге (км) — пусть первого, равный всему расстоянию от M до N.
Ответ: 138 км.
Вопрос репетитору по математике от Оксаны: Помогите с задачей. Она элементарная, но нам надо ее решить без использования дробей!!! У квадрата одну его сторону увеличили на 9 см, а другую сторону уменьшили в 5 раз. В результате этого получилcя прямоугольник с периметром равным 66 см. У какой фигуры — у прямоугольника или у квадрата — получилась больше площадь и на сколько?
Репетитор по математике о задаче c квадратом:
Если Вы хотите решить эту задачу без применения каких-либо дробей, не выходя за рамка программы 5 класса, то буквой икс необходимо обозначить наименьшую из величин, то есть ширину прямоугольника.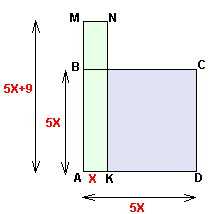 Итак, пусть AK=x, тогда AD=AB=5x. Поскольку сторону AB увеличили на 9 см, то длина полученного прямоугольника выражается как 5x+9. Принимая во внимание условие с периметром, получаем простенькое уравнение без дробей:
Итак, пусть AK=x, тогда AD=AB=5x. Поскольку сторону AB увеличили на 9 см, то длина полученного прямоугольника выражается как 5x+9. Принимая во внимание условие с периметром, получаем простенькое уравнение без дробей:
x+x+5x+9+5x+9=66
Решая его получим, что x=4. Теперь легко найти интересующие нас площади: кв.см., кв.см.
И тогда 400-116=284 кв.см. — разница между ними.
Вопрос от Анны: Помогите решить задачу.
Отец и сын, работая вместе, покрасили забор за 12 ч. Если бы отец красил забор один, он выполнил бы эту работу за 21 ч. За сколько часов покрасил бы этот забор сын?
Репетитор по математике, Тимур Розугнов
Примем весь объем работы (забор) за единицу и воспользуемся тем, что совместная скорость равна сумме отдельных скоростей отца и сына. Следить за решением удобно при помощи табличного метода оформления:
1) (заб/час) — совместная скорость
2) (заб/час) — скорость отца
3) (заб/час) — скорость сына
4) (часов) — время работы сына
Ответ: 28 часов
Вопрос от Марины:
Редактор прочитал две пятых рукописи, что составило 80 страниц. На другой день он прочитал четверть оставшихся страниц. ВОПРОСЫ: 1) Сколько страниц в рукописи? 2) Сколько страниц осталось не прочитано?
Репетитор по математике, Никита Афанасьевич
Для лучшего усвоения решения полезно сделать краткую запись. Выглядеть она будет следующим образом:
Решение:
1) (страниц) в рукописи.
2) (рукописи) — составляет остаток.
3) (страниц) — остаток.
4) (страниц) — прочитано во второй день.
5) (страниц) не прочитано.
Ответ: 90 страниц.
Задача от Наташи:
Мотоциклист в первый час проехал 3/8 всего пути ,во второй час 3/5 остатка,а в третий час остальные 40 км. Найдите весь путь. Помогите решить!
Репетитор по математике, Александр Колпаков
Старайтесь указывать для какого класса и по какой программе репетитору оформлять решение !!! будем считать, что что вы в 6 классе. Оформим краткую запись ровно так, как я это рекомендую делать своим ученикам: (в вертикальную рамку я выделяю доли, связанные законом сложения)
1) (остатка) — проехал мотоциклист за третий час
2) (км) — остаток
3) (всего пути) — остаток после пройденного мотоциклистом пусти за I час.
4) (км) — составляет весь путь
Ответ: 160 км
Вопрос от Оксаны: Объясните, пожалуйста, как правильно решить задачу: поезд проходит расстояние АВ за 10,5 ч. На сколько процентов следует увеличить его скорость, чтобы то же расстояние он преодолел за 8 ч? Решение нужно СРОЧНО к 1 сентября! Пыталась сама решить ее через уравнение, но не знаю правильно ли.
Репетитор по математике, Григорий Александров: Не нужно никаких уравнений. Они только Вас запутают. Вот мое решение: поскольку прирост любой вличины в процентах не зависит от ее единицы измерения, то примем за единицу полное расстояние от А до В. Тогда скорости будут такими: и Тогда прирост по скорости составит
Найдем какую часть эта величина составляет от прежней скорости:
Осталось эту часть перевести в проценты умножением на 100. Получим в итоге %
Задача от Арины:
У Шынар в копилке 80 монет достоинством 20 и 50 тенге Всего 2590 тенге. Сколько монет в копилке у Шынар достоинством 20 тенге? достоинством 50 тенге? Заранее спасибо очень надеюсь на вашу помощь.
Репетитор по математике, Колпаков А.Н.
Если бы все монеты были по 50 тенге, то Шынар имела бы всего 4000 тенге. Замена одной монеты в 50 тенге на одну монету достоинство в 20 тенге приводит к снижению капитала ровно на 30 тенге. На сколько тенге нам необходимо уменьшить общий капитал Шынар с 4000 до 2590? Ровно на 4000—2590=1410 тенге. Тогда сколько раз необходимо произвести замену? 1410:30=47 раз. Поэтому 47 монет нужно поменять на двадцатитенговые. Останется 80-47=33 монеты по 50 тенге.
Ответ: 47 монет по 20 тенге и 33 монеты по 50 тенге.
Вопрос от Татьяны: нужно решить задачу:
В первый день садовод вскопал на 40% своего участка, а во второй — 40% оставшейся части. На третий день он закончил работу, вскопав 180 кв.м. Определить площадь всего участка?
Репетитор по математике и физике, Галкин Р.А.
Можно предложить 3 способа решения. Остановлюсь на том, который ориентирован на 5 класс. В целях лучшего восприятия задачи составим схему (краткую запись) условия:Здесь все проценты переведены в дроби . Найдем какую часть (или сколько процентов) составляет вскопанная часть в 3 день от того, что осталось вскопать после 1-го дня:
1) %(остатка) -вскопали в 3 день.
По известному значению 180кв.м дроби найдем целую величину, то есть остаток:
2) (кв.м) — осталось после 1 дня
Найдем какую часть остаток составляет от всего участка:
3) %(всего участка) — осталось
По известному значению 300 кв.м дроби найдем целую величину, то есть весь участок:
4) (кв.м) — площадь всего участка.
Ответ: 500 кв.м.
Вопрос от Ангелины:
У меня возник вопрос с решением задачи. Помогите пожалуйста. Можно ли из какого угодно кол-ва троек получить в ответе 100, при помощи действий сложение, вычитание и умножение?
Репетитор по математике, Файгойз М.Ю.
Не очень понял вопрос. Что значит из «какого-угодно»? Угодно нам или угодно составителю задачи? Эх … не математик условие писал. Если на нас спускается количество троек как приказ, то не из любого. Ведь из двух троек никак нельзя составить 100. А если мы сами вправе выбирать количество троек, то можно так: . Конечно, условие должно быть переписано: можно ли из какого-нибудь количества троек получить 100?
Pages: 1 2 3
ankolpakov.ru
| Виленкин и др., Математика, 6 класс. Задача из контрольной, 2-я четверть | Просмотров: 4058 |
| Виленкин и др., Математика, 6 класс. Задача из контрольной, 2-я четверть (2) | Просмотров: 4049 |
| Виленкин и др., Математика, 6 класс. Задача №1002, решение | Просмотров: 2527 |
| Виленкин и др., Математика, 6 класс. Задача №1017, решение | Просмотров: 1512 |
| Виленкин и др., Математика, 6 класс. Задача №1018, решение | Просмотров: 1376 |
| Виленкин и др., Математика, 6 класс. Задача №1019, решение | Просмотров: 1217 |
| Виленкин и др., Математика, 6 класс. Задача №1020, решение | Просмотров: 1079 |
| Виленкин и др., Математика, 6 класс. Задача №1024, решение | Просмотров: 1205 |
| Виленкин и др., Математика, 6 класс. Задача №1025, решение | Просмотров: 1334 |
| Виленкин и др., Математика, 6 класс. Задача №1028, решение | Просмотров: 1073 |
| Виленкин и др., Математика, 6 класс. Задача №1042, решение | Просмотров: 1175 |
| Виленкин и др., Математика, 6 класс. Задача №1043, решение | Просмотров: 1240 |
| Виленкин и др., Математика, 6 класс. Задача №1049, решение | Просмотров: 897 |
| Виленкин и др., Математика, 6 класс. Задача №1062, решение | Просмотров: 1449 |
| Виленкин и др., Математика, 6 класс. Задача №1063, решение | Просмотров: 1085 |
| Виленкин и др., Математика, 6 класс. Задача №1068, решение | Просмотров: 845 |
| Виленкин и др., Математика, 6 класс. Задача №1069, решение | Просмотров: 1064 |
| Виленкин и др., Математика, 6 класс. Задача №1072, решение | Просмотров: 937 |
| Виленкин и др., Математика, 6 класс. Задача №1090, решение | Просмотров: 946 |
| Виленкин и др., Математика, 6 класс. Задача №1091, решение | Просмотров: 1374 |
oftob.ru
Олимпиада по математике 6 класс, задания с ответами
На уроках математики в 6 классе ученики знакомятся с множеством новых тем, а также углубляют и расширяют знания, полученные ранее. В частности, на уроках ребята знакомятся с положительными и отрицательными числами, учатся выполнять арифметические действия с ними, а также узнают про отношения и пропорции, координаты на плоскости.
Чтобы определить самых способных учеников, учителя проводят разнообразные тестовые и контрольные работы. Но особое место занимают олимпиады по математике. Мы предлагаем вам задания для 6 класса с ответами, которые могут использовать на уроках или во время самостоятельной подготовки.
Скачайте задания, заполнив форму!
После того как укажете данные, кнопка скачивания станет активной
Уравнения
1. Решить уравнение:
5x + 13 = 3x – 3
2. Найдите решение уравнения:
2x + 5x = –14
3. Найдите решение уравнения:
4x – 5х = 20
4. Найдите решение уравнения:
–5x + 3x = 16
5. Найдите решение уравнения:
х : 2 = –8
6. Найдите решение уравнения:
4х + 3 = 2х + 13
7. Найдите решение уравнения:
((x : 2 − 3) : 2 − 1) : 2 − 4 = 3
8. Найдите решение уравнения:
11 — 5x = 12 — 6x
9. Найдите решение уравнения:
4 • (х + 5) = 12
10. Найдите решение уравнения:
5x = 2x + 6
Задачи
Задача №1
Гравировщик делает таблички с буквами. Одинаковые буквы он гравирует за одинаковое время, разные — возможно, за разное. На две таблички «ДОМ МОДЫ» и «ВХОД» вместе он потратил 50 минут, а одну табличку «В ДЫМОХОД» сделал за 35 минут. За какое время он сделает табличку «ВЫХОД»?
Задача №2
Раньше называли число, равное миллиону миллионов , словом «легион». Если разделить миллион легионов на легион миллионов, то получится:
A) легион
B) миллион
C) миллион миллионов
D) легион легионов
Задача №3
В магазин доставили 6 бочонков с квасом, в них было 15, 16, 18, 19, 20 и 31 литр. В первый же день нашлось два покупателя: один купил два бочонка, другой – три, причем первый купил вдвое меньше кваса, чем второй. Не пришлось даже раскупоривать бочонки. Из шести бочонков на складе остался всего лишь один. Какой?
Задача №4
Молодой человек согласился работать с условием, что в конце года он получит автомобиль «Запорожец» и 2600. Но по истечении 8 месяцев уволился и при расчёте получил «Запорожец» и 1000. Сколько стоил «Запорожец»?
Задача №5
На окраску деревянного кубика затратили 4 г краски. Когда она высохла, кубик распилили на 8 одинаковых кубиков меньшего размера. Сколько краски потребуется для того, чтобы закрасить образовавшиеся при этом неокрашенные поверхности?
Задача №6
Гриша с папой ходил в тир. Уговор был такой: Гриша делает 5 выстрелов и за каждое попадание в цель получает право сделать ещё два выстрела. Всего Гриша сделал 17 выстрелов. Сколько раз Гриша попал в цель?
Задача №7
Ученик Вовочка любит решать математические задачи. Известно, что вчера он решил на 11 задач меньше, чем позавчера и на 32 задачи меньше, чем позавчера и сегодня вместе. Сколько задач решил Вовочка сегодня?
Задача №8
Чтобы сжить с белого света Змея Горыныча, которому исполнилось 40 лет, Кощей Бессмертный придумал приучить его к курению. Кощей Бессмертный подсчитал, что если Змей Горыныч каждый день в течение года будет выкуривать по 17 сигарет, то он умрет через 5 лет, если же он будет выкуривать по 16 сигарет, то умрет через 10 лет. До скольких лет доживет Змей Горыныч, если он не будет курить?
Задача №9
В затруднительном положении оказались однажды трое пеших разведчиков, которым необходимо было перебраться на противоположный берег реки при отсутствии моста. Правда, по реке катались в лодке два мальчика, готовые помочь солдатам, Но лодка была так мала, что могла выдержать вес только одного солдата; даже солдат и один мальчик не могли одновременно сесть в нее без риска ее потопить. Плавать солдаты совсем но умели. Казалось бы, при таких условиях мог переправиться через реку только один солдат. Между тем все три разведчика вскоре благополучно переправились на противоположный берег и возвратили лодку мальчикам. Как это они сделали?
Задача №10
Один из пяти братьев – Андрей, Витя, Дима, Толя или Юра разбил окно. Андрей сказал: “Это сделал или Витя, или Толя”. Витя сказал: “Это сделал не я и не Юра”. Дима сказал: “Нет, один из них сказал правду, а другой – неправду”. Юра сказал: “Нет, Дима, ты не прав”. Их отец, которому, конечно, можно доверять, уверен, что не менее трех братьев сказали правду. Кто же из братьев разбил окно?
Математические загадки
Загадка №1
У 28 человек 5 «Ы» класса на собрание пришли папы и мамы. Мам было — 24, пап — 18. У скольких учеников на собрание пришли одновременно и папа и мама?
Загадка №2
В ящике лежат 100 синих, 100 красных, 100 зелёных и 100 фиолетовых карандашей. Сколько карандашей необходимо достать, не заглядывая в ящик, чтобы среди них обязательно нашлись по крайней мере 1 красный и 1 фиолетовый.
Загадка №3
На сколько нулей оканчивается произведение 1•2•3•4•…•37?
Загадка №4
Два невисокосных года идут подряд. В первом из них больше понедельников, чем сред. Какой из семи дней чаще всего встречается во втором году?
Загадка №5
Разбейте число 186 на три попарно различных натуральных слагаемых, сумма любых двух из которых делится на третье.
Ответы к уравнениям
| Уравнение | № 1 | № 2 | № 3 | № 4 | № 5 |
| Ответ | x = – 8 | x = –2 | х = 4 | x = 8 | х = 16 |
| Уравнение | № 6 | № 7 | № 8 | № 9 | № 10 |
| Ответ | х = –5 | x = 66 | x = 1 | х = -2 | х = 2 |
Ответы к задачам
Задача 1
20 минут
Задача 2
Вариант А
Задача 3
Первый покупатель купил 15-литровый и 18-литровый бочонки. Второй – 16-литровый, 19-литровый и 31-литровый. Остался не проданным 20-литровый бочонок.
Задача 4
2200
Задача 5
4 грамма
Задача 6
6 раз
Задача 7
21 задачу
Задача 8
130 лет
Задача 9
9 цифр
Задача 10
Толя разбил окно
Ответы на загадки
Загадка 1
14 учеников
Загадка 2
301 карандаш
Загадка 3
8 нулей
Загадка 4
Вторник
Загадка 5
31+62+93
Скачайте задания, заполнив форму!
После того как укажете данные, кнопка скачивания станет активной
Другие классы
Обновлено: , автор: Валерия Токареваruolimpiada.ru
Олимпиадные задачи по математике, 6 класс.
Олимпиадные задачи по математике, 6 класс.
1.На некотором острове необычайно регулярный климат: по понедельникам и средам идут дожди, по субботам – туман, зато в остальные дни – солнечно. Утром какого дня недели нужно начать свой отдых группе туристов, если они хотят пробыть там 44 дня и захватить при этом как можно больше солнечных дней? ( 3 балла )
А- в понедельник, В- в среду, С- в четверг, Д- в пятницу, Е – во вторник.
2.Остаток от деления 100 на некоторое число равен 4. При делении 90 на это же число в остатке получается 18. На какое число делили? ( 3 балла )
А – 18, В – 32, С – 24, Д – 36, Е – 48.
3.Если кенгуру научится прыгать в 1,5 раза дальше, чем умеет, ему понадобится ровно 6 прыжков, чтобы добраться до тенистого дерева. За сколько прыжков кенгуру может это сделать сейчас? ( 3 балла )
А – 3, В -4, С – 6, Д – 9, Е – невозможно определить.
4.На каждой кочке в маленьком болотце сидят не меньше, чем по 3 лягушки, а всего лягушек 145. Тогда число кочек в этом болотце не может равняться: ( 3 балла )
А – 1, В – 23, С – 31, Д – 44, Е – 55.
5.Выполните действия рациональным способом
354 * 73 + 23 *25 + 354 * 27 +17 * 25 ; ( 5 баллов )
6.На одной чашке весов лежат шесть одинаковых пачек чая и гиря массой 50 г, а на другой – одна пачка чая и две гири массой 100 г и 200 г. Весы находятся в равновесии. Определите, сколько граммов весит одна пачка чая? ( 6 баллов )
7.Из 40 учащихся 6 класса 32 ходят на кружок «Умелые руки», 21 посещают спортивную секцию, 15 учащихся ходят и на кружок и на секцию. Сколько учащихся не ходят на этот кружок, ни на эту секцию? ( 6 баллов )
Ответы. 1.- С; 2.- С; 3.- Д; 4.- Е; 5.-36400; 6.-50 г; 7.- 2 уч.
Олимпиадные задачи по математике, 6 класс, 2 тур.
1.Гусеница ползёт по стволу яблони. За первый час она поднялась на 10 см, за второй час опустилась на 4 см, за третий час вновь поднялась на 10см, а за четвёртый опустилась на 4 см. Так она продолжала подниматься и опускаться в течение нескольких часов. На сколько сантиметров поднимется гусеница за 11 ч? (5 баллов)
2.Решите уравнение |2x|*|-3,5|=|-28|. (3 балла)
3.В детский летний лагерь приехали три друга: Миша, Володя, Петя. Известно. Что каждый из них имеет одну из фамилий: Иванов, Семёнов, Герасимов. Миша не Герасимов. Отец Володи инженер. Володя учится в 6 классе. Ребёнок с фамилией Герасимов учится в 5 классе. Отец с фамилией Иванов – слесарь. Какая фамилия у каждого из друзей? (4 балла)
4.Запиши число 100 девятью различными цифрами, соединёнными знаками действий. (4 балла)
5.У фермера было несколько одинакового веса поросят и несколько ягнят также одинакового веса. Мальчик спросил фермера, сколько весит один поросёнок и один ягнёнок. Фермер ответил, что 3 поросёнка и 2 ягнёнка весят 22 кг, а 2 поросёнка и 3 ягнёнка весят 23 кг. Как узнать, сколько весит один поросёнок и сколько весит один ягнёнок? (5 баллов)
infourok.ru
Тестовые задания по математике для 6 класса
I вариант
Найдите значение выражения:
 .
.
а)  ;
;
б)  ;
;
в)  ;
;
г) другой ответ.
За 2,5 часа автомобиль прошел 145 км. За какое время автомобиль пройдет 261 км, если будет двигаться с той же средней скоростью?
а) 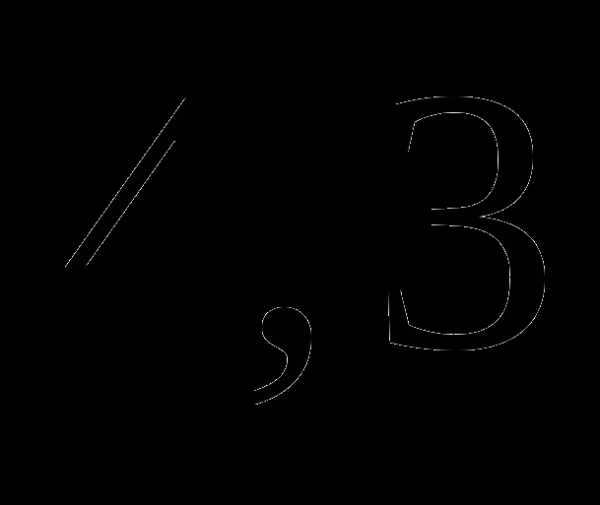 часа;
часа;
б)  часа;
часа;
в) 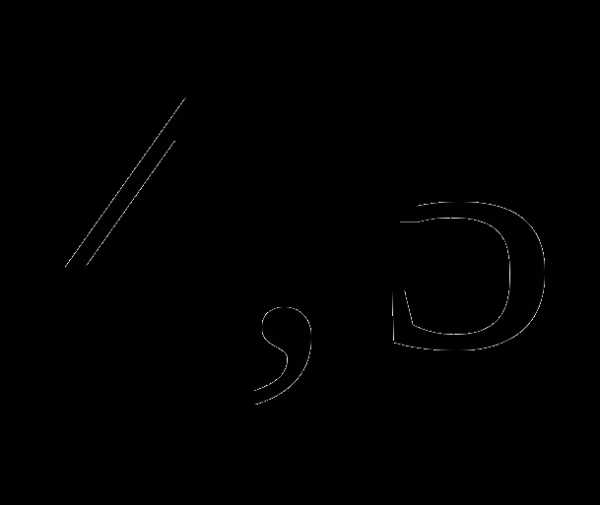 часа;
часа;
г) другой ответ.
Решите уравнение:
 .
.
а) 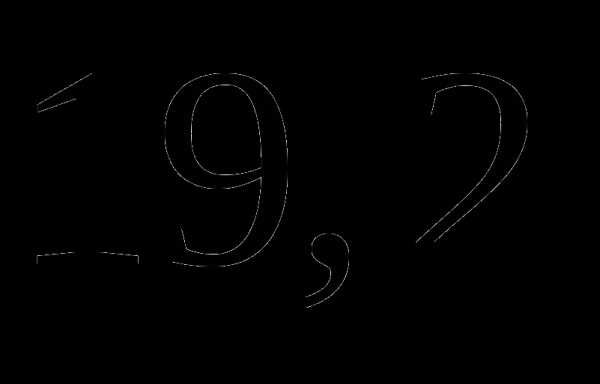 ;
;
б) 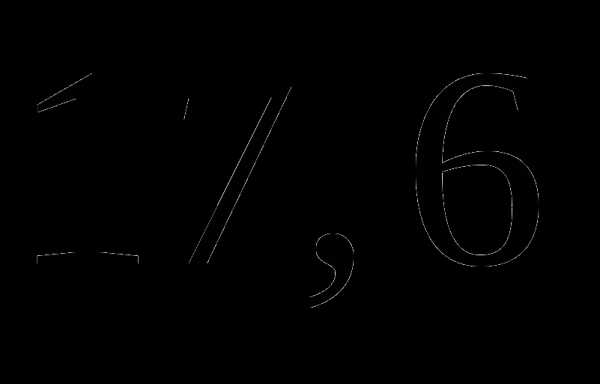 ;
;
в) 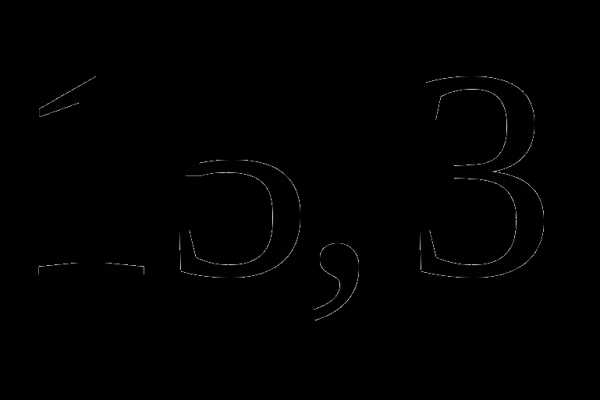 ;
;
г) другой ответ.
Какую цифру следует поставить вместо
 в число
в число  , чтобы полученное число делилось на
, чтобы полученное число делилось на  ?
?
а) 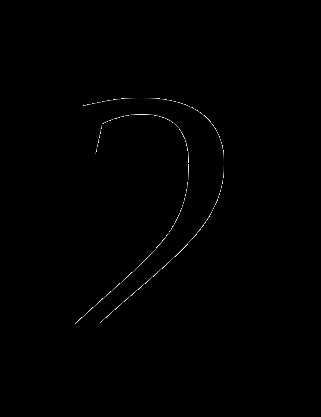 ;
;
б) 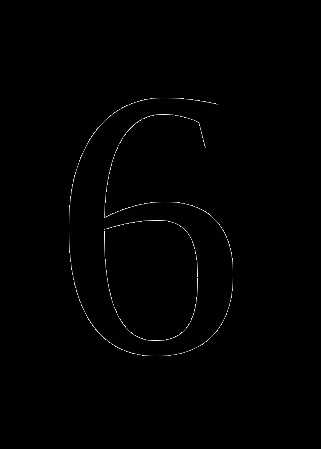 ;
;
в)  ;
;
г) другой ответ.
Теплоход за 3 дня прошел 595 км. В первый день он прошел
 пути, а во второй –
пути, а во второй –  оставшегося пути. Какое расстояние он прошел за третий день?
оставшегося пути. Какое расстояние он прошел за третий день?
а)  км;
км;
б) 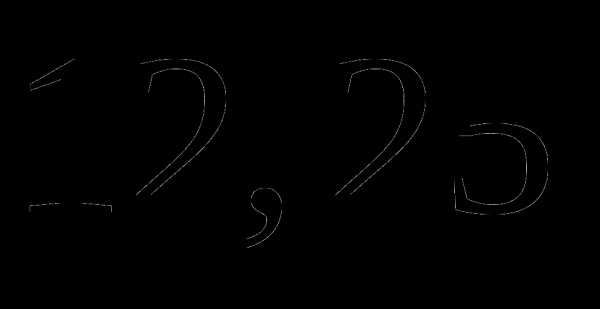 км;
км;
в) 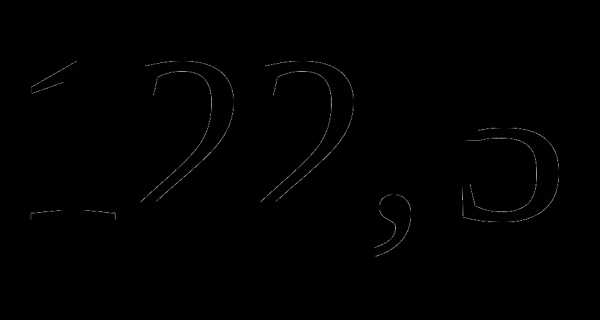 км;
км;
г) другой ответ.
Найдите число,
 которого равны
которого равны  .
.
а) 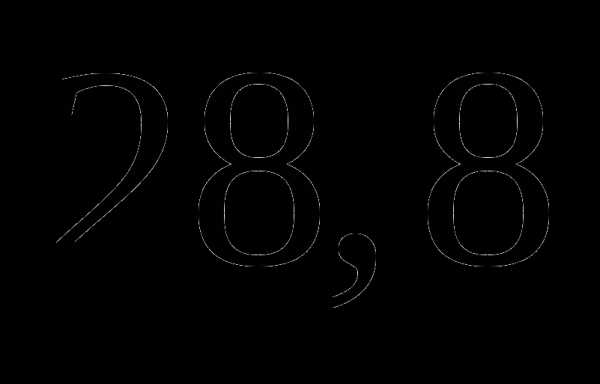 ;
;
б) 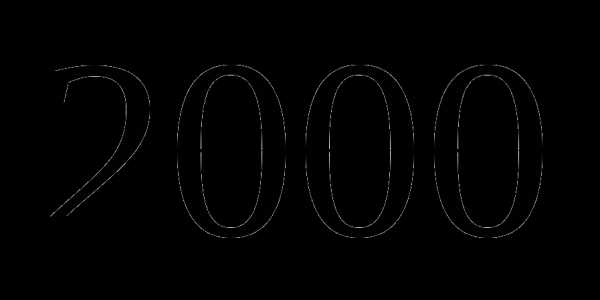 ;
;
в)  ;
;
г) другой ответ.
Упростите выражение: .
а) ;
б) ;
в) ;
г) другой ответ.
Длина окружности равна
 см. Найдите ее диаметр. Ответ округлите до сотых. Число
см. Найдите ее диаметр. Ответ округлите до сотых. Число  .
.
а) 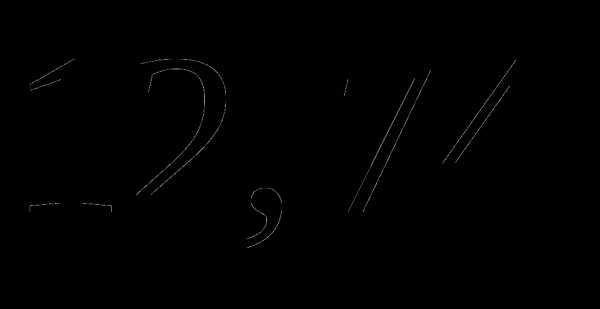 ;
;
б) 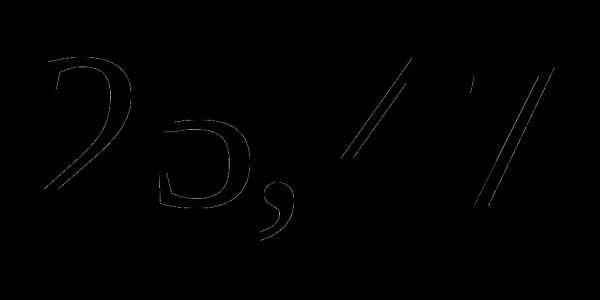 ;
;
в) 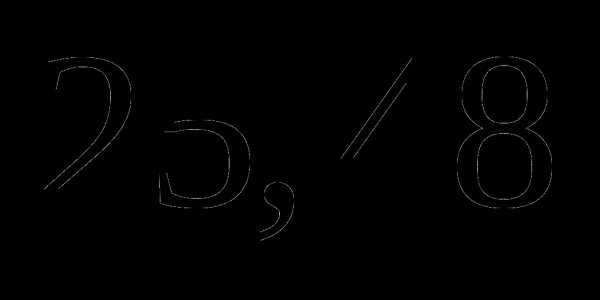 ;
;
г) другой ответ.
Найдите координаты середины отрезка
 , если .
, если .
а) 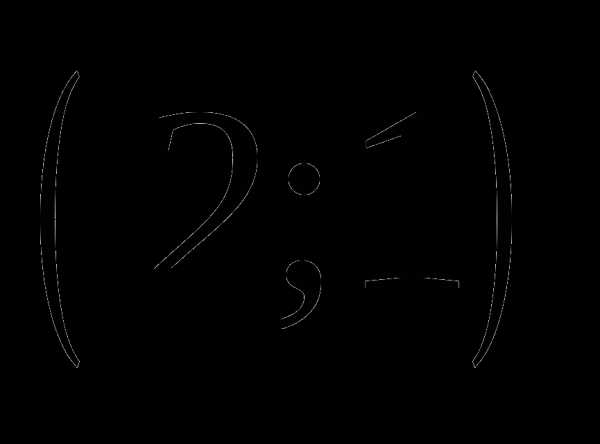 ;
;
б)  ;
;
в) 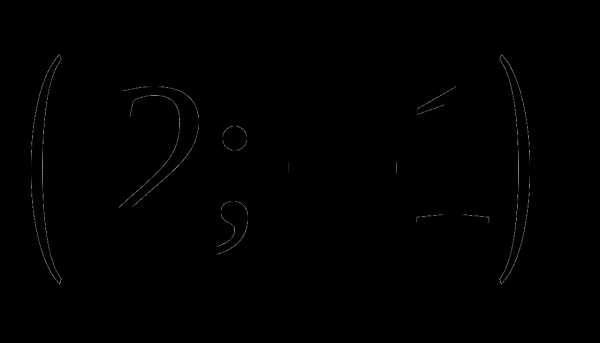 ;
;
г) другой ответ.
Какова последняя цифра числа: ?
а)  ;
;
б) 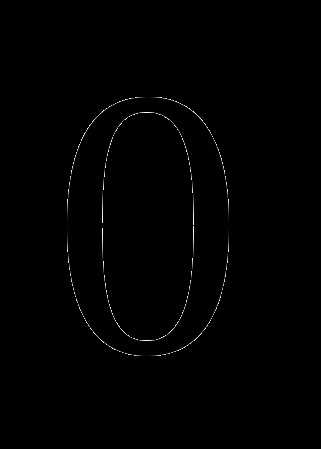 ;
;
в)  ;
;
г) другой ответ.
II вариант
Найдите значение выражения:
 .
.
а)  ;
;
б) 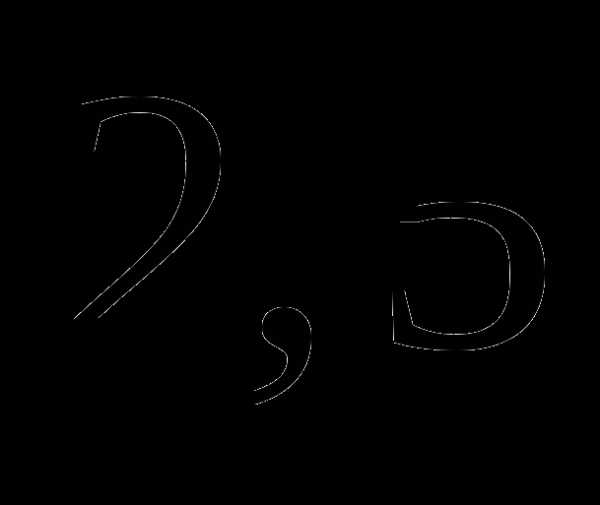 ;
;
в) 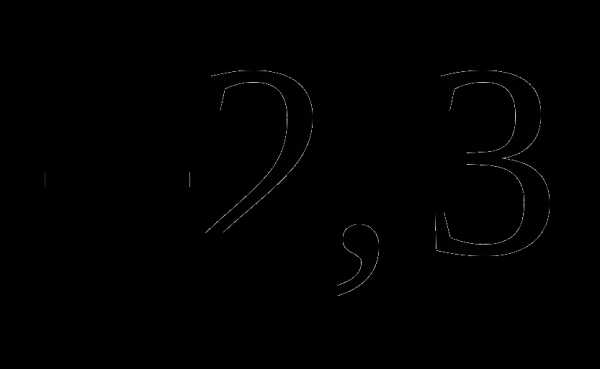 ;
;
г) другой ответ.
За 3,5 часа корабль прошел 238 км. За какое время корабль пройдет 578 км, если будет двигаться с той же средней скоростью?
а) 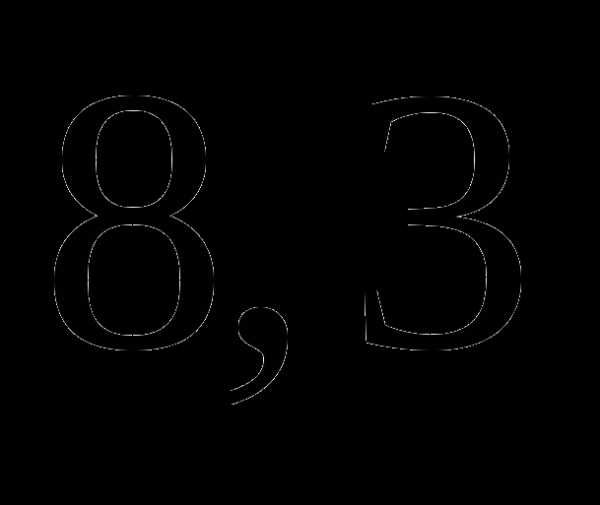 часа;
часа;
б) 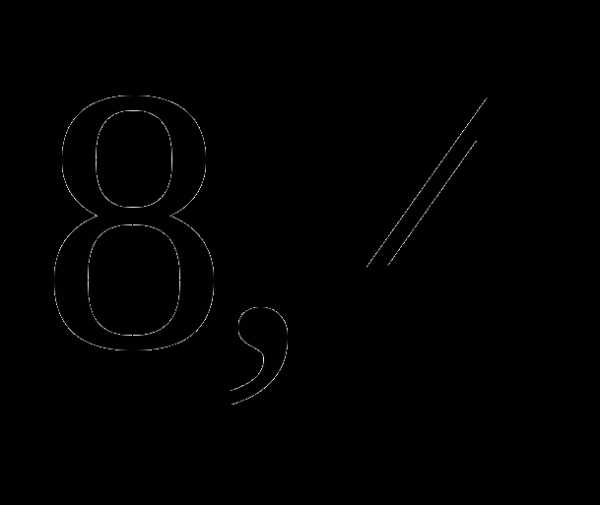 часа;
часа;
в) 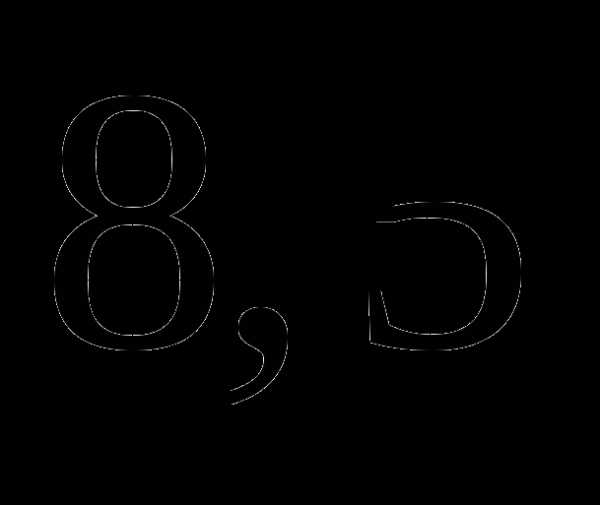 часа;
часа;
г) другой ответ.
Решите уравнение: .
а)  ;
;
б) 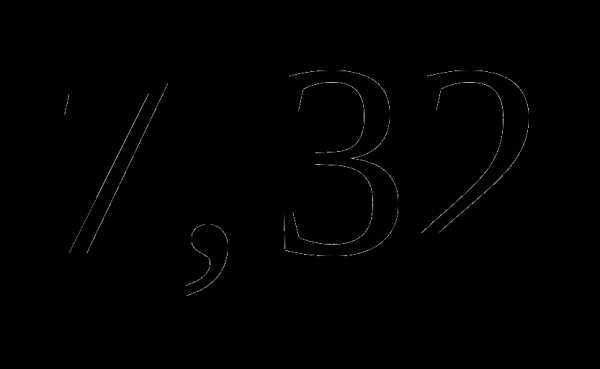 ;
;
в)  ;
;
г) другой ответ.
Какую цифру следует поставить вместо
 в число
в число  , чтобы полученное число делилось на
, чтобы полученное число делилось на  ?
?
а)  ;
;
б) 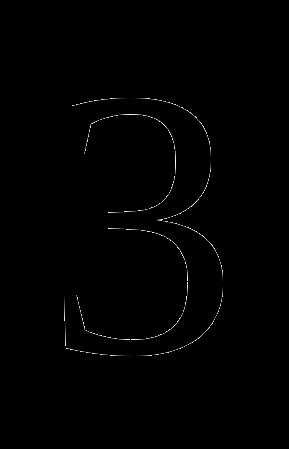 ;
;
в)  ;
;
г) другой ответ.
Теплоход за 3 дня прошел 675 км. В первый день он прошел
 пути, а во второй –
пути, а во второй –  оставшегося пути. Какое расстояние он прошел за третий день?
оставшегося пути. Какое расстояние он прошел за третий день?
а) 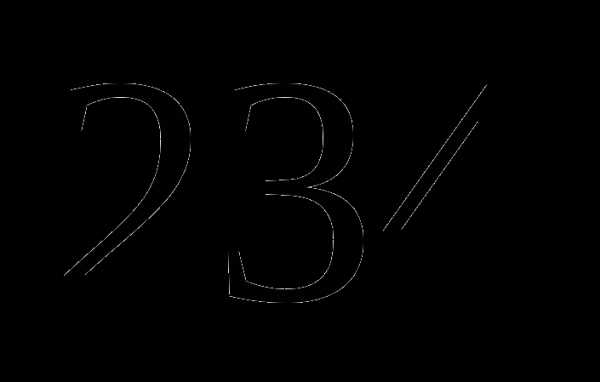 км;
км;
б)  км;
км;
в) 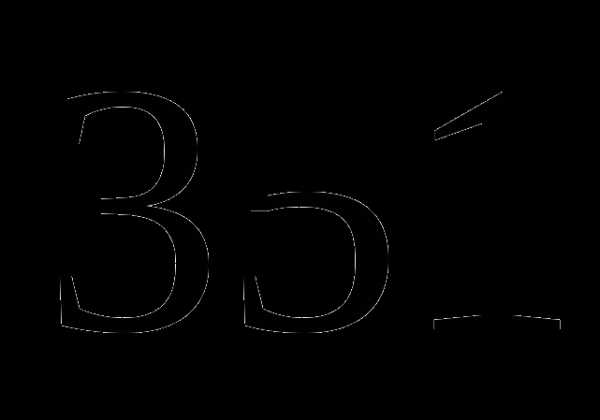 км;
км;
г) другой ответ.
Найдите число,
 которого равны
которого равны  .
.
а) 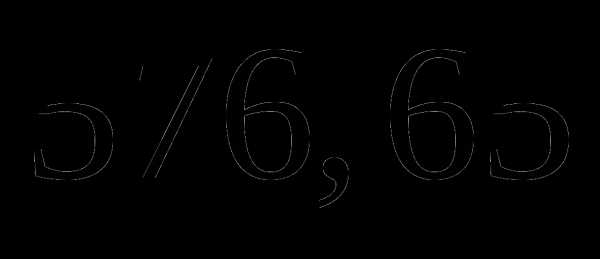 ;
;
б) 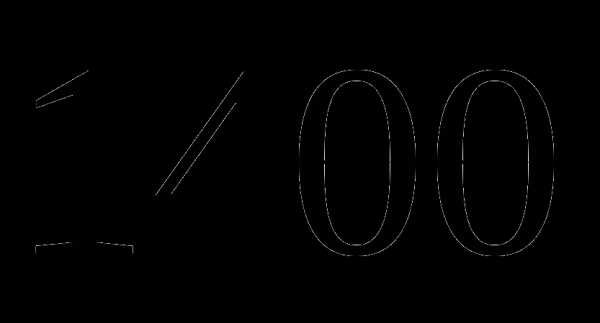 ;
;
в)  ;
;
г) другой ответ.
Упростите выражение: .
а) ;
б) ;
в) ;
г) другой ответ.
Длина окружности равна
 см. Найдите ее радиус. Ответ округлите до сотых. Число
см. Найдите ее радиус. Ответ округлите до сотых. Число  .
.
а)  ;
;
б)  ;
;
в) 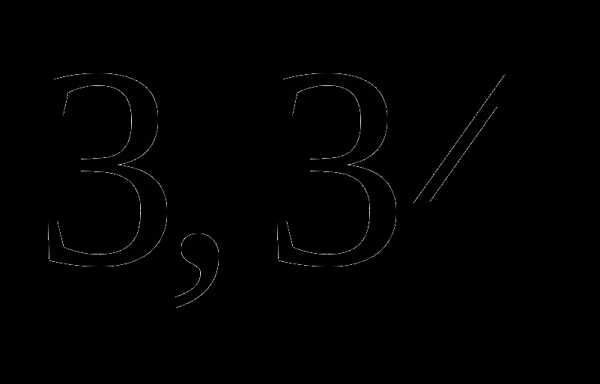 ;
;
г) другой ответ.
Найдите координаты середины отрезка
 , если .
, если .
а) 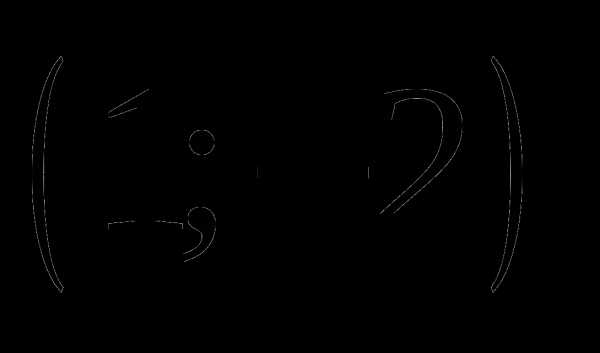 ;
;
б)  ;
;
в) 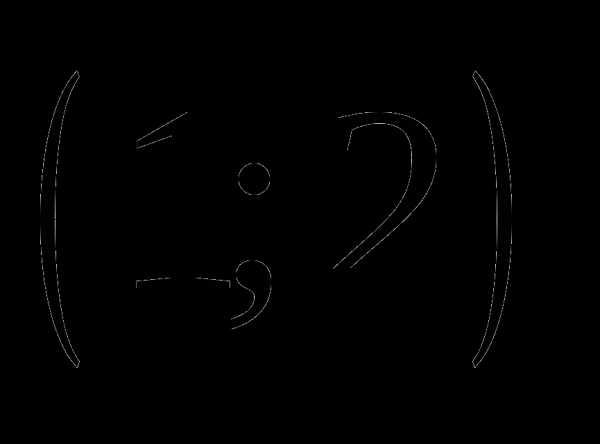 ;
;
г) другой ответ.
Какова последняя цифра числа: ?
а)  ;
;
б) 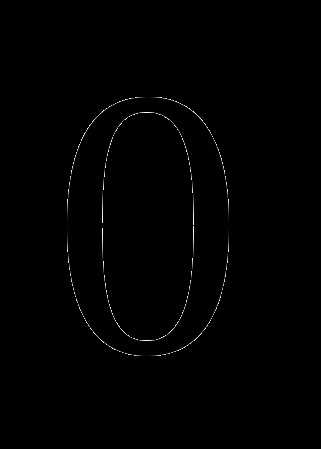 ;
;
в)  ;
;
г) другой ответ.
III вариант
Найдите значение выражения:
 .
.
а)  ;
;
б) 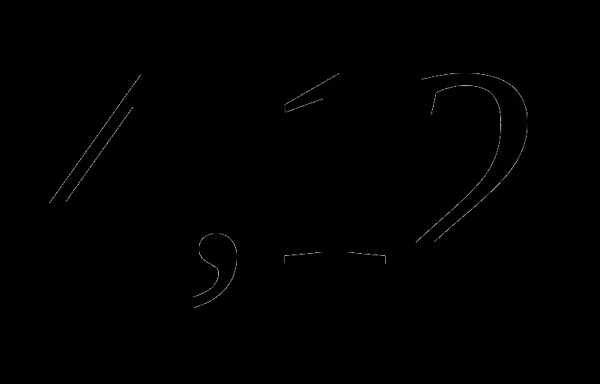 ;
;
в) 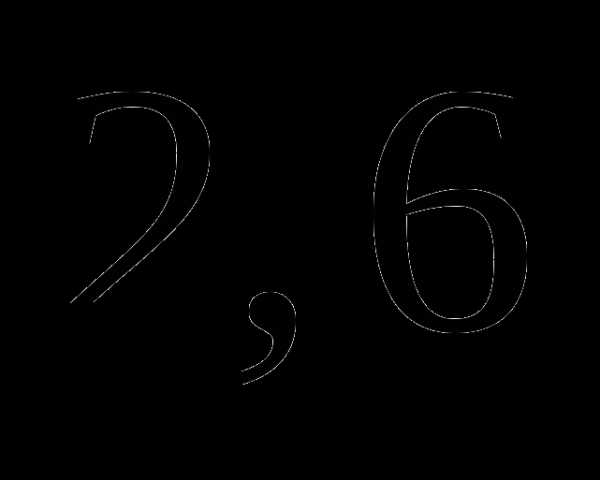 ;
;
г) другой ответ.
За 1,4 часа автомобиль прошел 91 км. За какое время автомобиль пройдет 351 км, если будет двигаться с той же средней скоростью?
а) 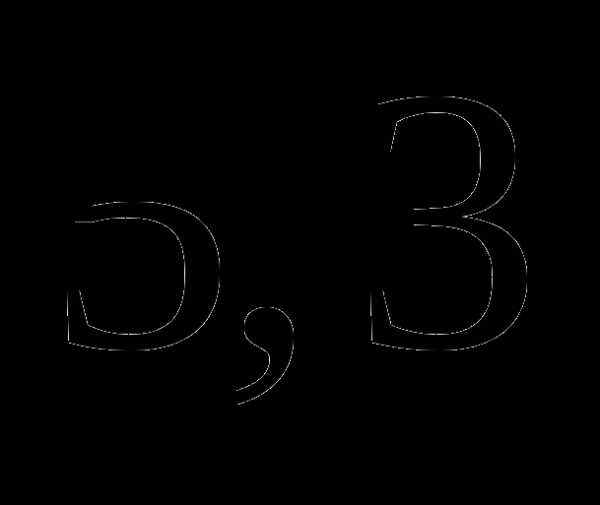 часа;
часа;
б) 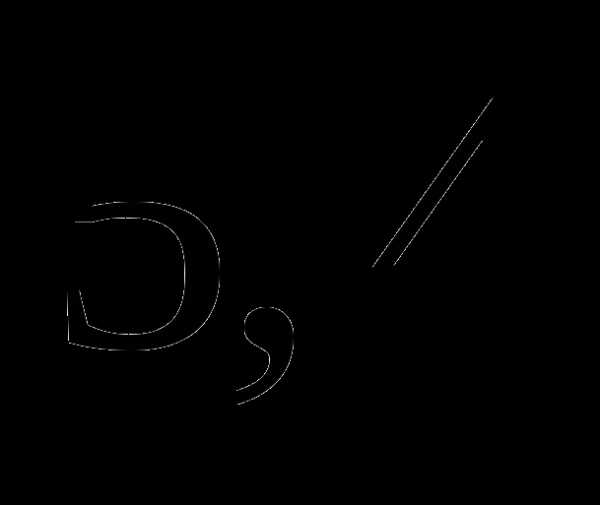 часа;
часа;
в) 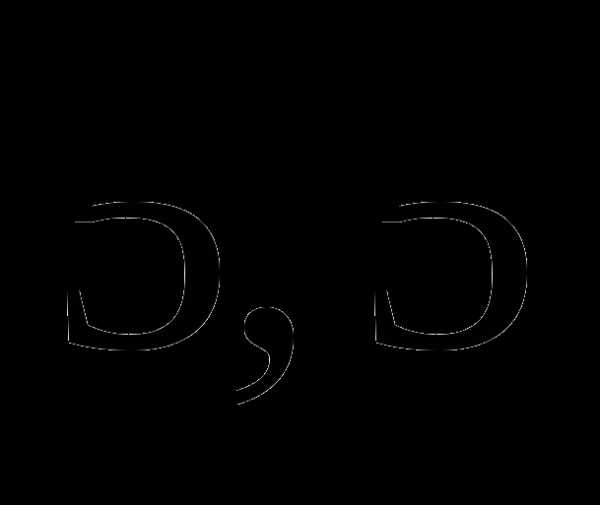 часа;
часа;
г) другой ответ.
Решите уравнение:
 .
.
а) 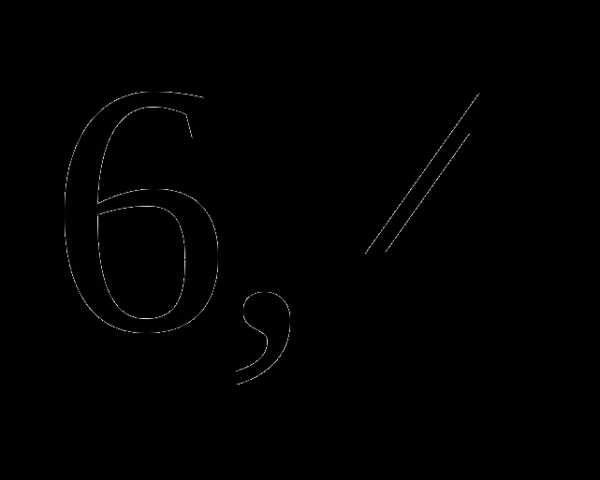 ;
;
б) 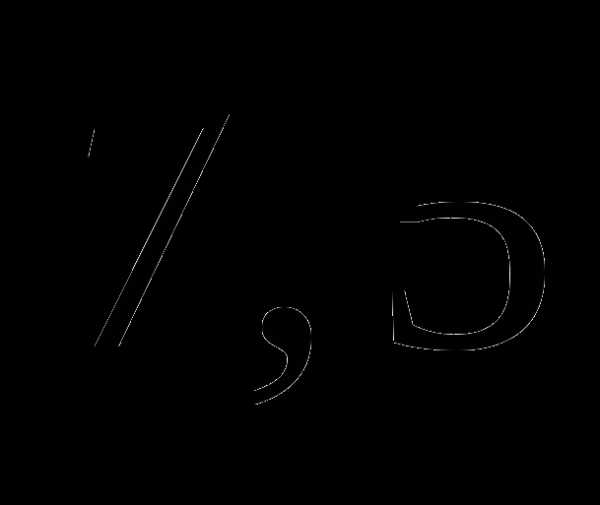 ;
;
в) 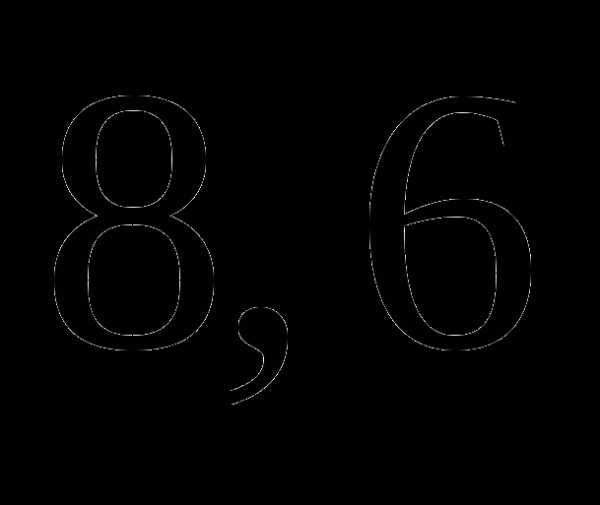 ;
;
г) другой ответ.
Какую цифру следует поставить вместо
 в число
в число  , чтобы полученное число делилось на
, чтобы полученное число делилось на  ?
?
а) 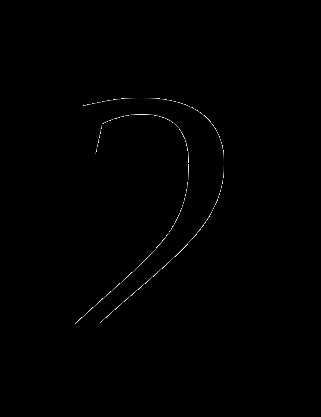 ;
;
б) 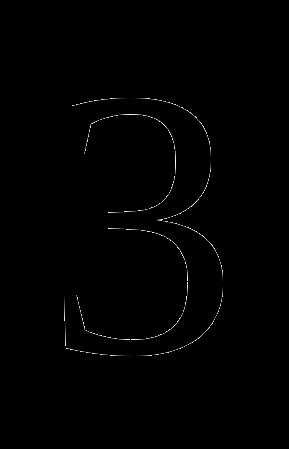 ;
;
в)  ;
;
г) другой ответ.
Теплоход за 3 дня прошел 800 км. В первый день он прошел
 пути, а во второй –
пути, а во второй –  оставшегося пути. Какое расстояние он прошел за третий день?
оставшегося пути. Какое расстояние он прошел за третий день?
а) 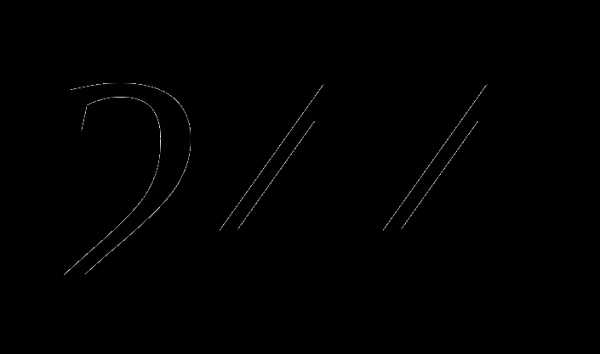 км;
км;
б) 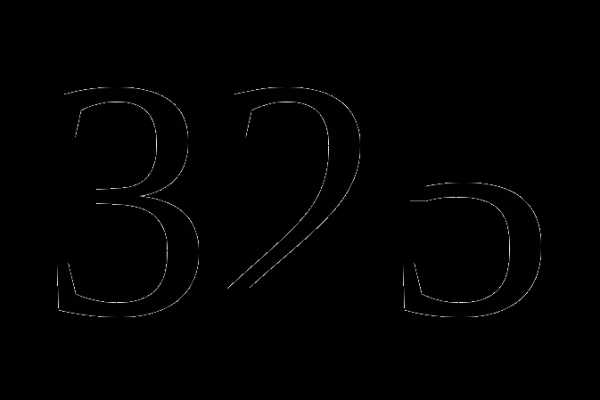 км;
км;
в)  км;
км;
г) другой ответ.
Найдите число,
 которого равны
которого равны  .
.
а)  ;
;
б) 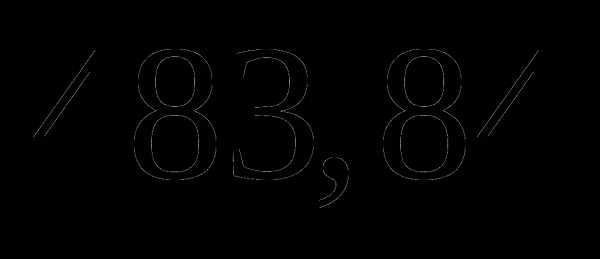 ;
;
в) 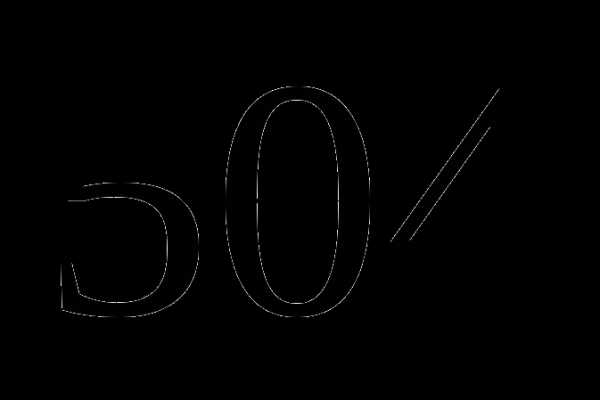 ;
;
г) другой ответ.
Упростите выражение: .
а) 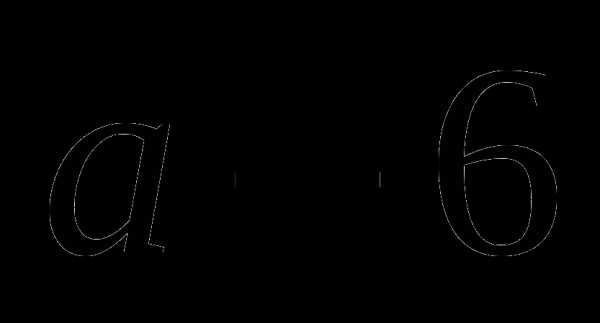 ;
;
б) 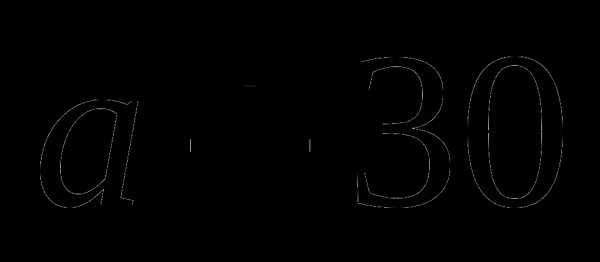 ;
;
в) 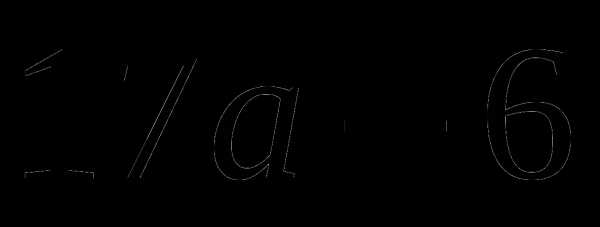 ;
;
г) другой ответ.
Длина окружности равна
 см. Найдите ее диаметр. Ответ округлите до сотых. Число
см. Найдите ее диаметр. Ответ округлите до сотых. Число  .
.
а) 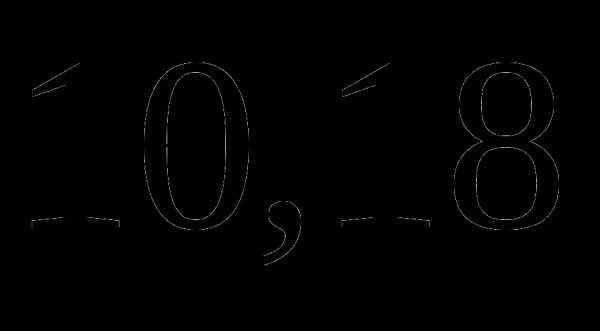 ;
;
б) 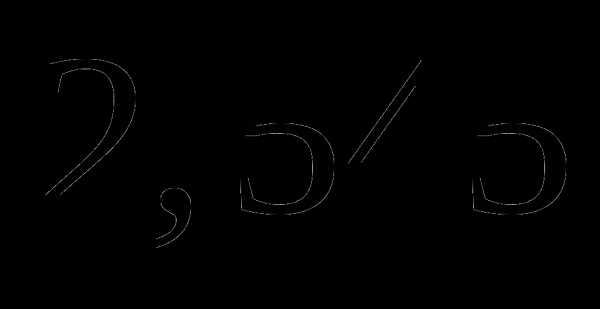 ;
;
в)  ;
;
г) другой ответ.
Найдите координаты середины отрезка
 , если .
, если .
а) 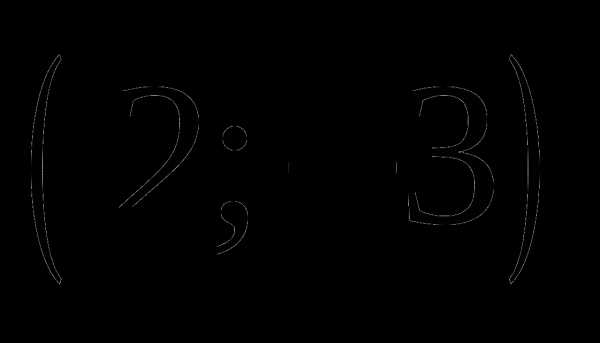 ;
;
б)  ;
;
в) 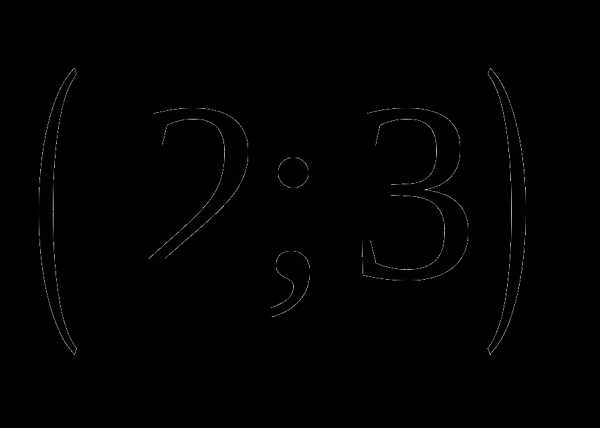 ;
;
г) другой ответ.
Какова последняя цифра числа: ?
а)  ;
;
б) 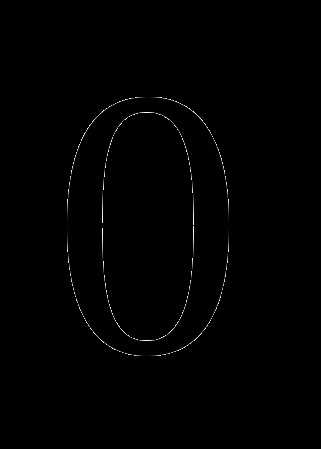 ;
;
в)  ;
;
г) другой ответ.
IV вариант
Найдите значение выражения:
 .
.
а) 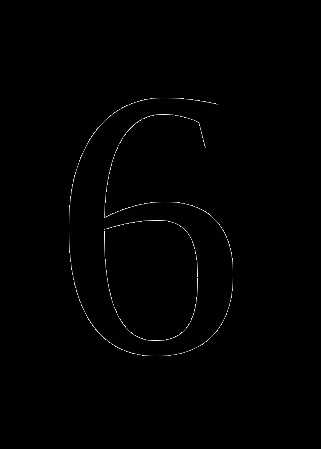 ;
;
б)  ;
;
в)  ;
;
г) другой ответ.
За 4,6 часа автомобиль прошел 253 км. За какое время автомобиль пройдет 341 км, если будет двигаться с той же средней скоростью?
а) 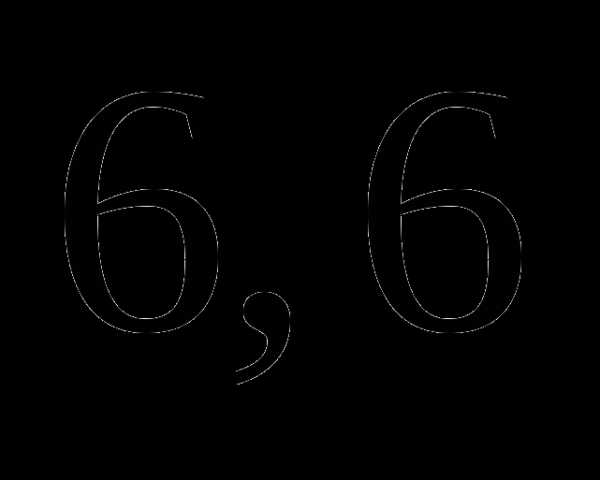 часа;
часа;
б) 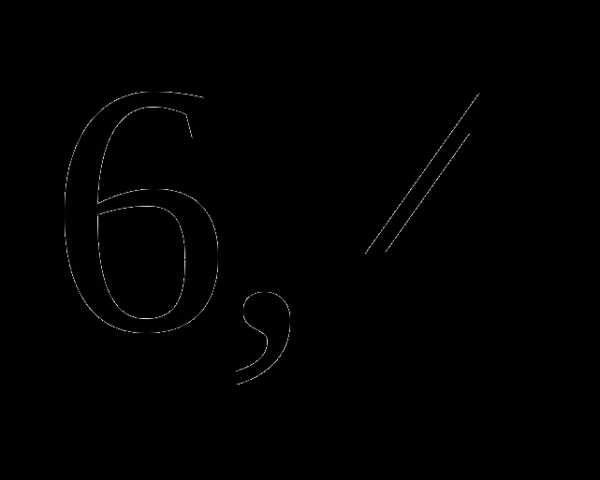 часа;
часа;
в) 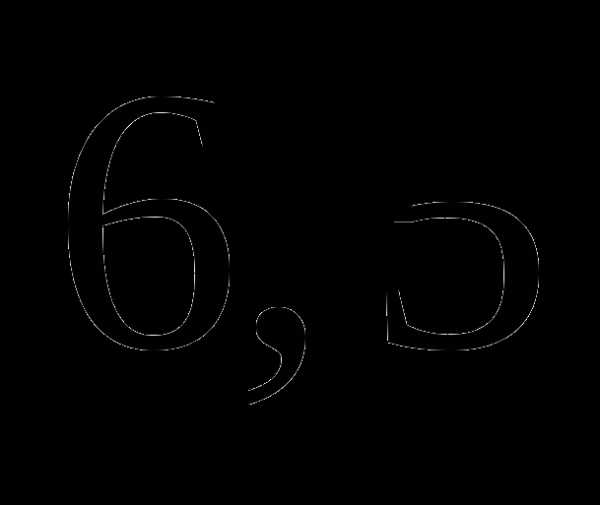 часа;
часа;
г) другой ответ.
Решите уравнение: .
а) 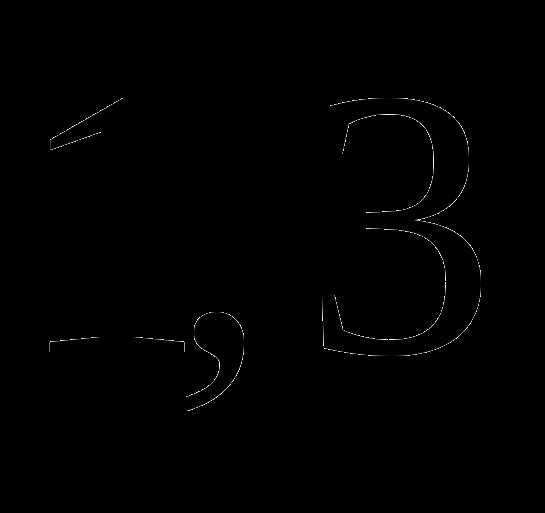 ;
;
б)  ;
;
в) 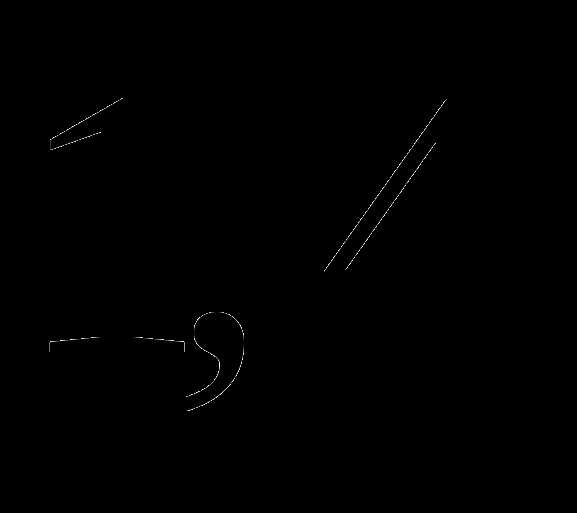 ;
;
г) другой ответ.
Какую цифру следует поставить вместо
 в число
в число  , чтобы полученное число делилось на
, чтобы полученное число делилось на  ?
?
а) 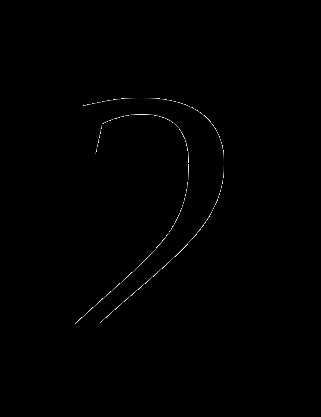 ;
;
б)  ;
;
в) 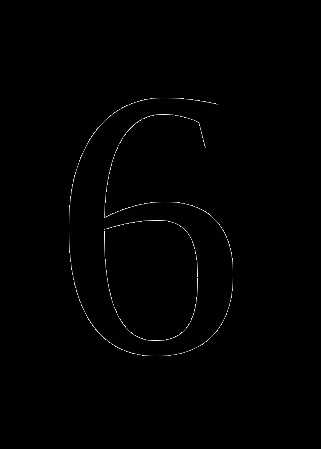 ;
;
г) другой ответ.
Теплоход за 3 дня прошел 1200 км. В первый день он прошел
 пути, а во второй –
пути, а во второй –  оставшегося пути. Какое расстояние он прошел за третий день?
оставшегося пути. Какое расстояние он прошел за третий день?
а) 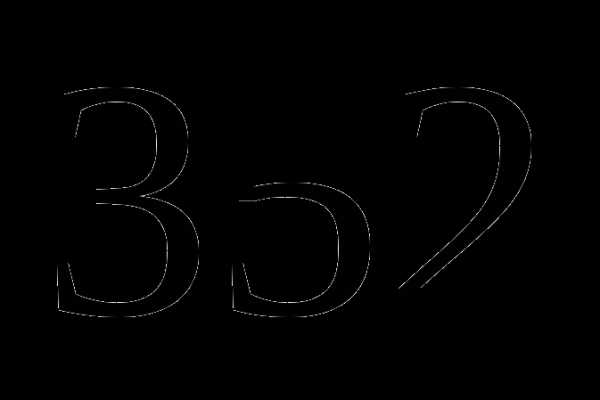 км;
км;
б)  км;
км;
в) 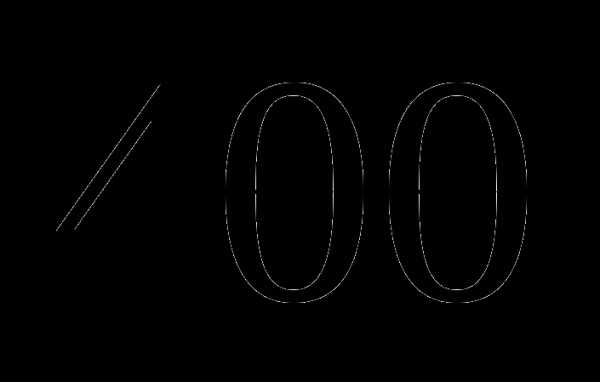 км;
км;
г) другой ответ.
Найдите число,
 которого равны
которого равны  .
.
а) 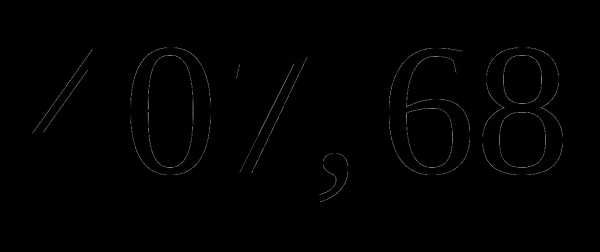 ;
;
б) 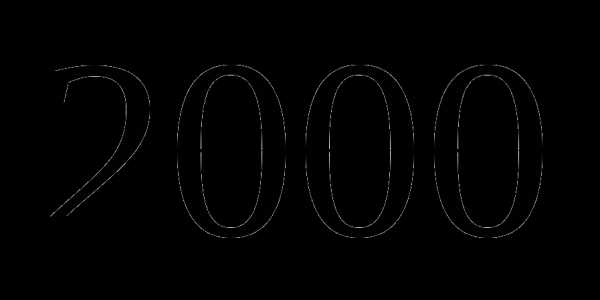 ;
;
в) 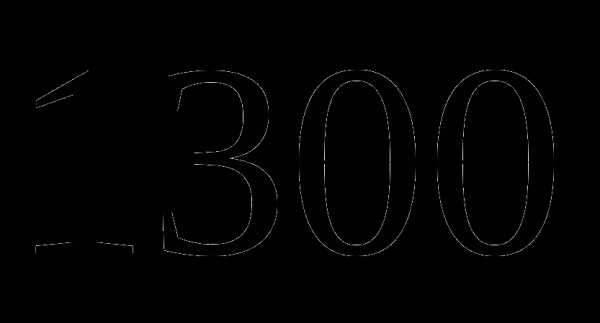 ;
;
г) другой ответ.
Упростите выражение: .
а) 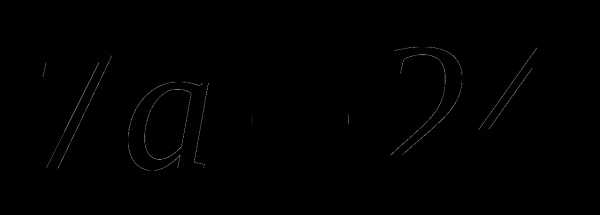 ;
;
б)  ;
;
в)  ;
;
г) другой ответ.
Длина окружности равна
 см. Найдите ее диаметр. Ответ округлите до сотых. Число
см. Найдите ее диаметр. Ответ округлите до сотых. Число  .
.
а) 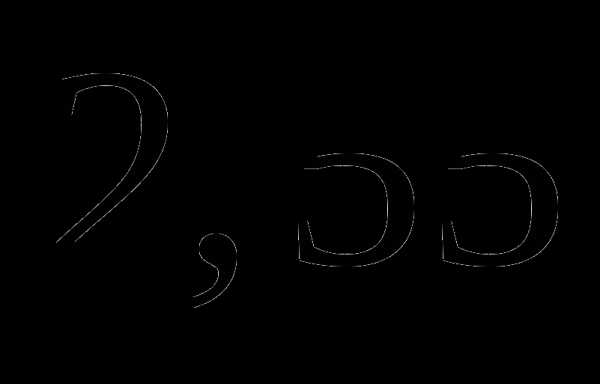 ;
;
б) 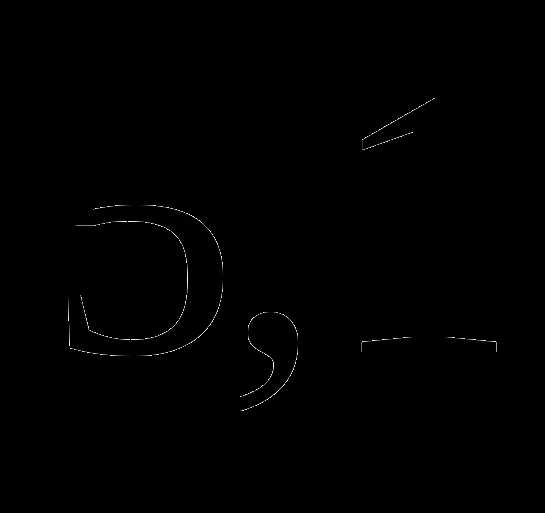 ;
;
в) 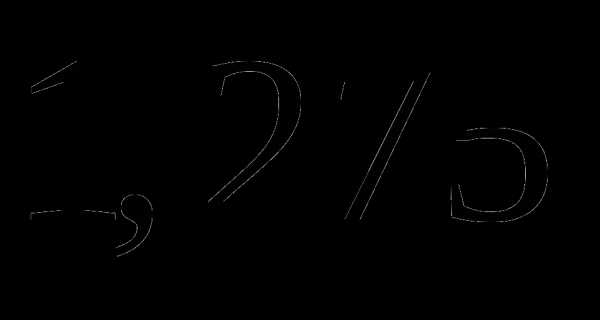 ;
;
г) другой ответ.
Найдите координаты середины отрезка
 , если .
, если .
а) 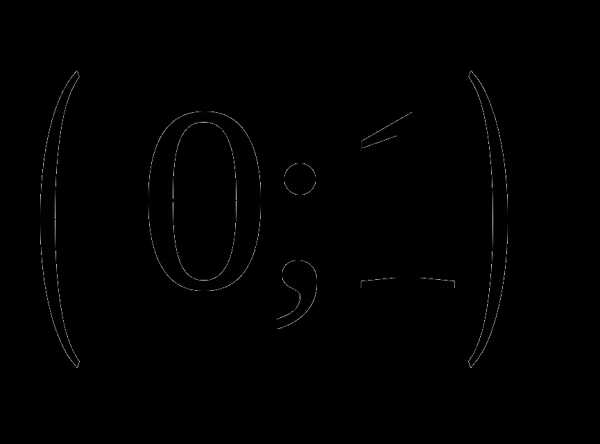 ;
;
б)  ;
;
в)  ;
;
г) другой ответ.
Какова последняя цифра числа: ?
а) 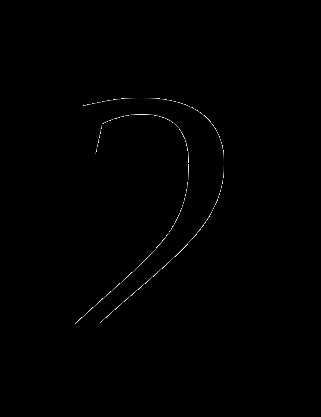 ;
;
б)  ;
;
в) 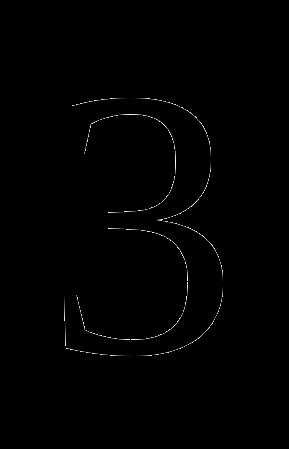 ;
;
г) другой ответ.
Итоговый тест — ключ
№
1
2
3
4
5
6
7
8
9
10
В-1
в
в
а
а
а
б
в
г
а
г
В-2
б
в
г
г
г
б
а
а
в
б
В-3
в
б
а
в
в
а
г
в
а
в
В-4
г
г
а
б
а
в
а
а
г
б
infourok.ru
Сборник нестандартных задач по математике 6 класс
1.Кувшинки на пруду
На поверхности пруда плавает одна кувшинка, которая постоянно делится и разрастается. Таким образом, каждый день площадь, которую занимают кувшинки, увеличивается в два раза. Через месяц покрытой оказывается вся поверхность пруда. За сколько времени покроется кувшинками вся поверхность пруда, если изначально на поверхности будут плавать две кувшинки?
ОТВЕТ: Две кувшинки покроют озеро за месяц минус один день.
2.Сумма чисел
В XIX веке один учитель задал своим ученикам вычислить сумму всех целых чисел от единицы до ста. Компьютеров и калькуляторов тогда еще не было, и ученики принялись добросовестно складывать числа. И только один ученик нашел правильный ответ всего за несколько секунд. Им оказался Карл Фридрих Гаусс — будущий великий математик. Как он это сделал?
ОТВЕТ: Он выделил 49 пар чисел: 99 и 1, 98 и 2, 97 и 3 … 51 и 49. В сумме каждая пара чисел равнялась ста, и оставалось два непарных числа 50 и 100. Следовательно, 49х100+50+100=5050.
Либо 100 и 1, 99 и 2, 98 и 3… В сумме каждая пара дает 101, следовательно 101*50=5050
3.Король и премьер-министр
Один король хотел сместить своего премьер-министра, но при этом не хотел его слишком обидеть. Он позвал премьер-министра к себе, положил при нем два листка бумаги в портфель и сказал: «На одном листке я написал «Уходите», а на втором — «Останьтесь». Листок, который вы вытащите, решит вашу судьбу». Премьер-министр догадался, что на обоих листках было написано «Уходите». Как же, однако, умудрился он при этих условиях сохранить свое место?
ОТВЕТ: Премьер-министр вытащил листок бумаги и, не глядя на него, скатал из него шарик — и проглотил. Поскольку на оставшемся листке стояло «Уходите», то королю пришлось признать, что на проглоченном листке значилось «Останьтесь».
4.Кто изображен на портрете?
Один джентльмен, показывая своему другу портрет, нарисованный по его заказу одним художником, сказал: «У меня нет ни сестер, ни братьев, но отец этого человека был сыном моего отца».
Кто был изображен на портрете?
ОТВЕТ: На портрете изображен сын этого джентльмена.
5.Пожар на острове
Человек находится на острове. Из-за долгой засухи трава и кусты на острове сильно пересохли. Внезапно на одном конце острова возник пожар, и ветер погнал огонь в сторону человека. Спастись в море человек не может, так как в море у самого берега плавает множество акул. Берегов без растительности на острове нет. Как человеку спастись?
ОТВЕТ: Человеку нужно зажечь огонь на подветренной от себя стороне и немного отойти навстречу основному пожару. Ветер погонит огонь, зажженный человеком, к подветренному концу острова. Когда этот участок выгорит, человек сможет вернуться на него и спокойно ждать, пока основной пожар дойдет до этого участка и погаснет, так как гореть уже будет нечему.
6.Переправа через реку
Отец с двумя сыновьями отправился в поход. На их пути встретилась река, у берега которой находился плот. Он выдерживает на воде или отца, или двух сыновей. Как переправиться на другой берег отцу и сыновьям?
ОТВЕТ: Вначале переправляются оба сына. Один из сыновей возвращается обратно к отцу. Отец перебирается на противоположный берег к сыну. Отец остается на берегу, а сын переправляется на исходный берег за братом, после чего они оба переправляются к отцу.
7.Незадачливый рыбак
Один рыбак купил себе новую удочку длиной 5 футов. Домой ему приходиться добираться общественным транспортом, в котором правилами запрещено перевозить предметы длиной более 4-х футов. Как необходимо упаковать удочку, чтобы проехать в общественном транспорте не нарушая правил?
ОТВЕТ: Удочку необходимо упаковать в коробку длиной 4 фута и шириной 3 фута (расположить по диагонали коробки).
8.Приготовление краски
Для того чтобы получить краску оранжевого цвета, необходимо смешать краски желтого цвета (6 частей) и красного цвета (2 части). Сколько грамм краски оранжевого цвета можно получить (максимально), имея в наличии 3 грамма желтой и 3 грамма красной краски?
ОТВЕТ: Из условия задачи видно, что желтой краски требуется в 3 раза больше, чем красной. Следовательно, имея в наличии 3 грамма желтой краски, необходимо взять 1 грамм красной краски. То есть оранжевой краски при смешивании получиться 4 грамма.
9.Сколько страниц в книге?
При издании книги потребовалось 2 775 цифр того, чтобы пронумеровать ее страницы. Сколько страниц в книге?
ОТВЕТ: На первые 9 страниц требуется 9 цифр. С 10-й по 99-ю страницу (90 страниц) требуется 90х2=180 цифр. С 100-й по 999-ю страницу (900 страниц) требуется 900х3=2700 цифр (по 300 цифр на каждую сотню страниц с трехзначной нумерацией). Следовательно, на 999 страниц необходимо 2700+180+9=2889 цифр. Мы перебрали (2889-2775)/3=38 страниц. Итого: 999-38=961 страница была в книге.
infourok.ru

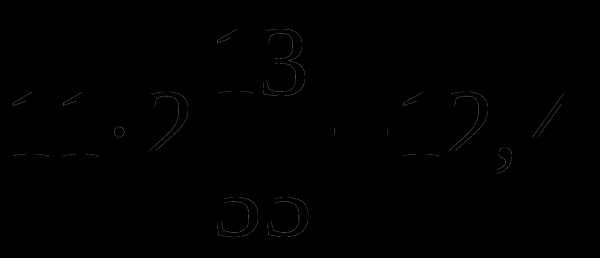 .
.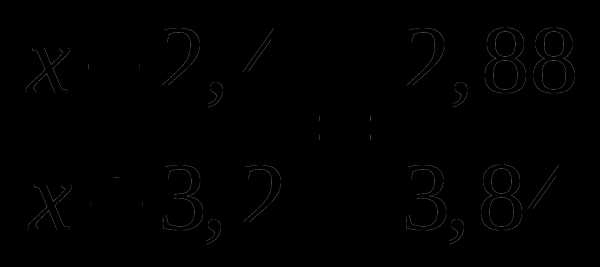 .
. в число
в число 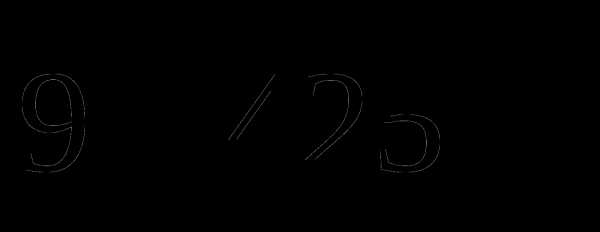 , чтобы полученное число делилось на
, чтобы полученное число делилось на  ?
?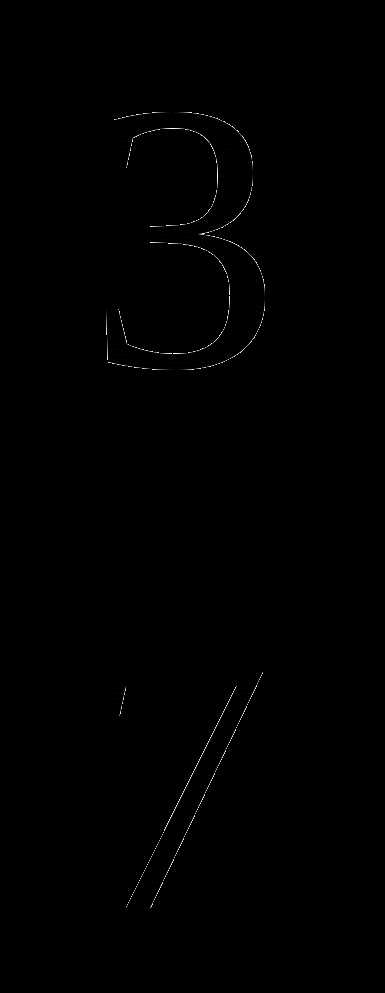 пути, а во второй –
пути, а во второй – 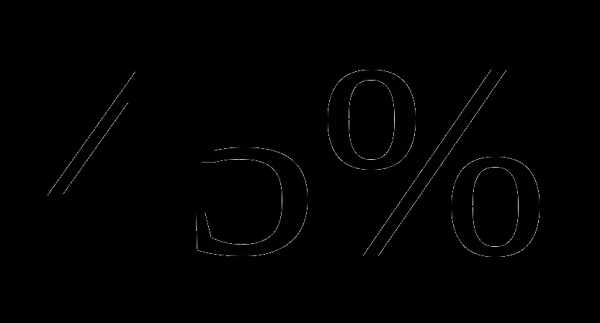 оставшегося пути. Какое расстояние он прошел за третий день?
оставшегося пути. Какое расстояние он прошел за третий день? которого равны
которого равны 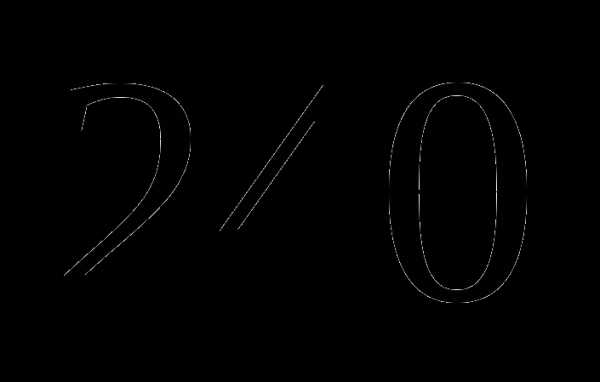 .
.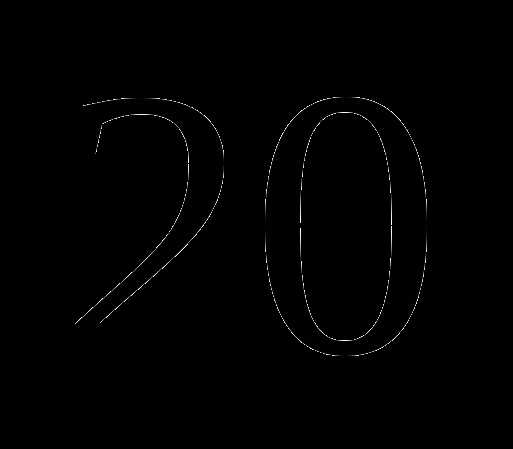 см. Найдите ее диаметр. Ответ округлите до сотых. Число
см. Найдите ее диаметр. Ответ округлите до сотых. Число 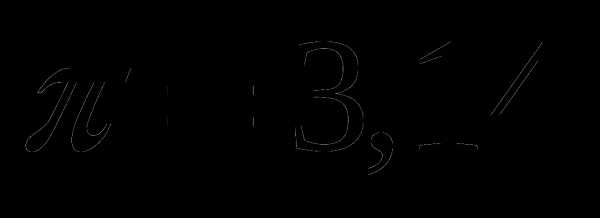 .
. , если .
, если . .
.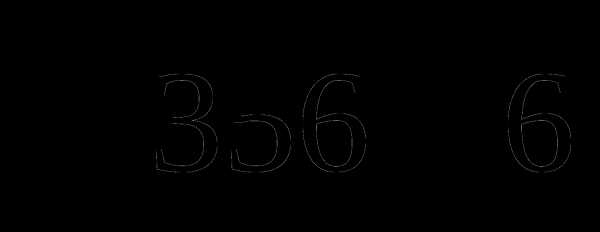 , чтобы полученное число делилось на
, чтобы полученное число делилось на  ?
?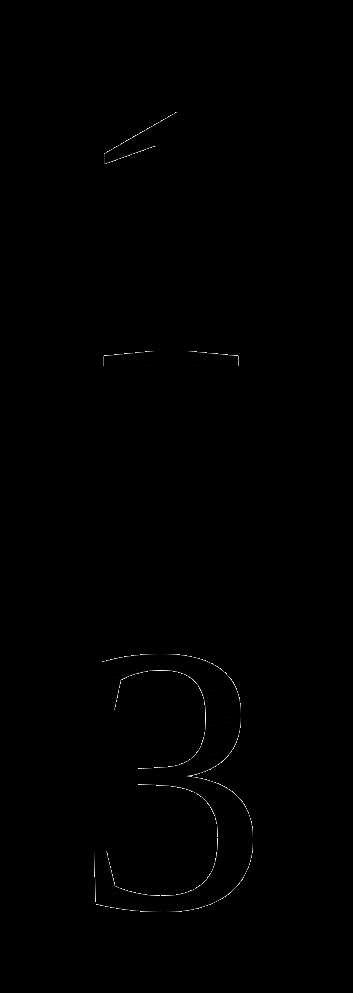 пути, а во второй –
пути, а во второй – 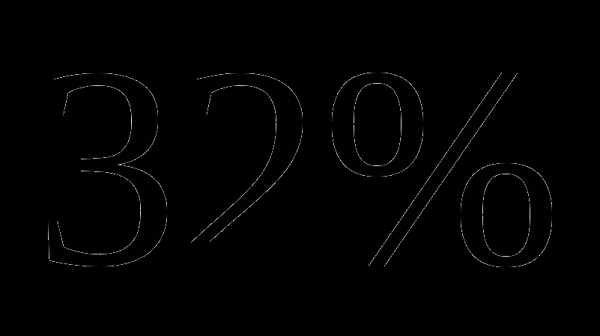 оставшегося пути. Какое расстояние он прошел за третий день?
оставшегося пути. Какое расстояние он прошел за третий день? которого равны
которого равны 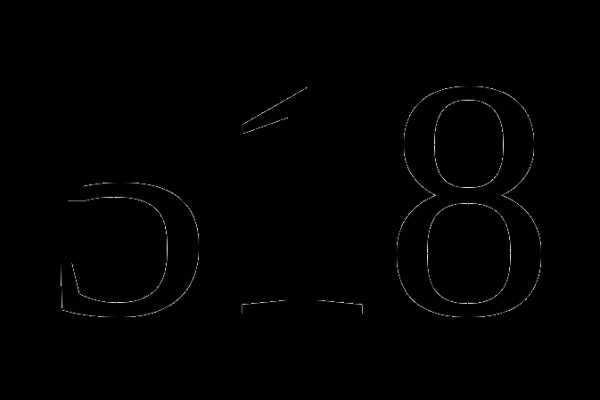 .
.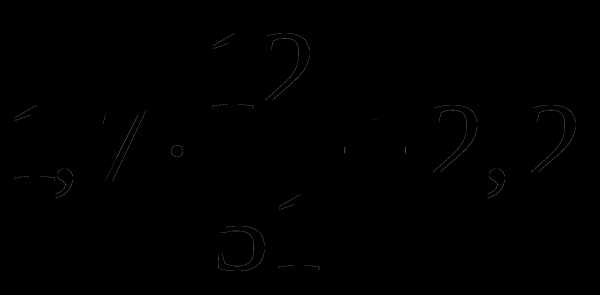 .
. .
. , чтобы полученное число делилось на
, чтобы полученное число делилось на 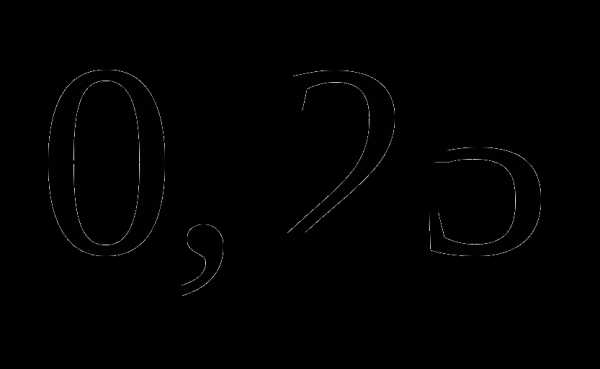 пути, а во второй –
пути, а во второй –  оставшегося пути. Какое расстояние он прошел за третий день?
оставшегося пути. Какое расстояние он прошел за третий день? которого равны
которого равны 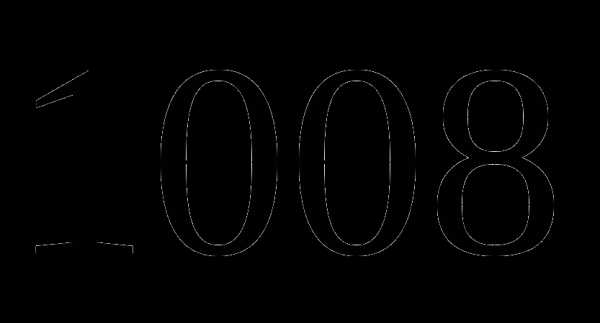 .
.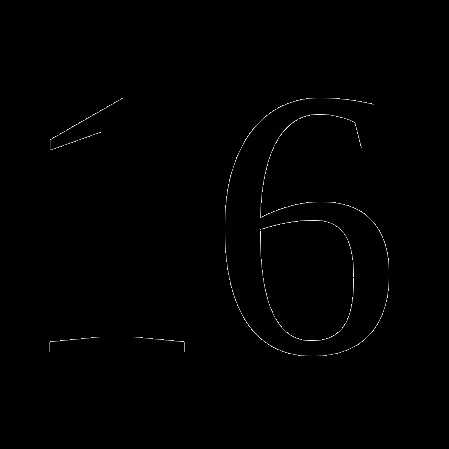 см. Найдите ее диаметр. Ответ округлите до сотых. Число
см. Найдите ее диаметр. Ответ округлите до сотых. Число 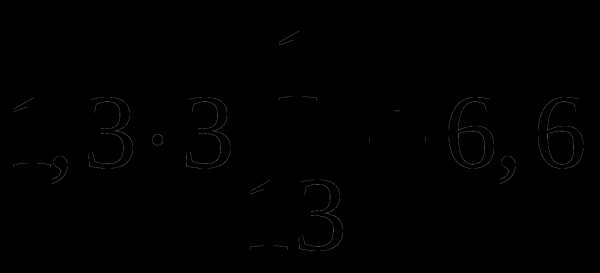 .
.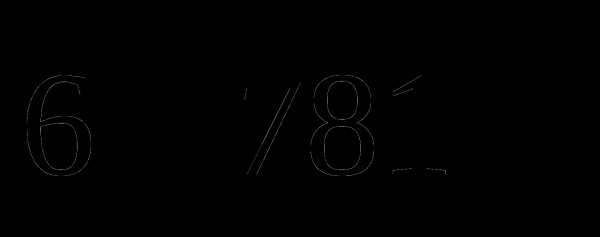 , чтобы полученное число делилось на
, чтобы полученное число делилось на 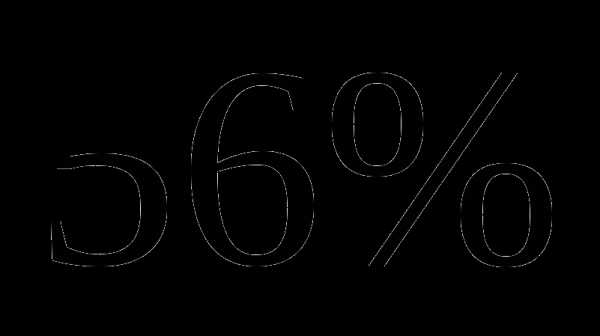 оставшегося пути. Какое расстояние он прошел за третий день?
оставшегося пути. Какое расстояние он прошел за третий день?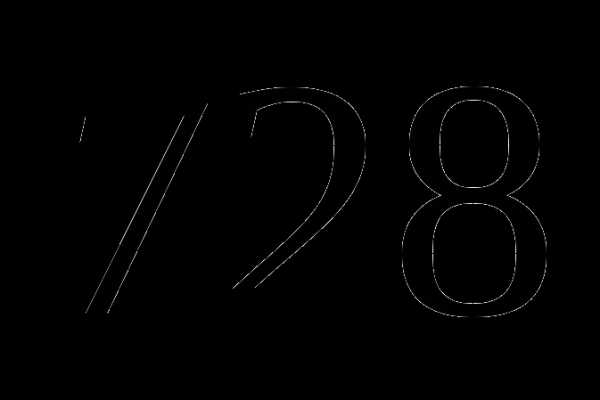 .
.