0.12 в виде обыкновенной дроби
Калькулятор «Конвертер десятичных дробей в обыкновенные»
Десятичная дробь
Как записать 0.12 в виде дроби?
Ответ: Десятичная дробь 0.12 в обыкновенном виде это 3/25
0.12=
Число 0.12 в виде обыкновенной дроби это 3/25
Объяснение конвертации дроби 0.12 в десятичную
Для того, чтобы найти простейшую дробную форму числа 0.12 необходимо сперва записать нашу десятичную дробь 0.12 как обыкновенную. Любое число можно легко записать в виде дроби, для этого нужно всего лишь разделить его на 1 (единицу):
0.12 =
0.12
/
1
Далее, нам необходимо избавиться от дробной части в числителе (0.12), т.е. сделать числитель целым числом. Для этого мы умножим числитель и знаменатель на 100 (т. к. в дробном числе 0.12 после запятой находится 2 знака)
к. в дробном числе 0.12 после запятой находится 2 знака)
0.12 × 100
/
1 × 100
=
12
/
100
Теперь необходимо сократить получившуюся дробь до самой простой формы. Для этого нужно найти Наибольший Общий Делитель (НОД) для чисел 12 и 100. Для того чтобы найти НОД для двух чисел, вы можете воспользоваться нашим Калькулятором НОД . НОД для чисел 12 и 100 равен 4. Следовательно, для того, чтобы упростить нашу дробь, необходимо разделить числитель и знаменатель на 4:
12 ÷ 4
/
100 ÷ 4
=
Вот и все! 0.12 как обыкновенная правильная дробь в самой простой форме это 3/25.
Похожие расчеты
Поделитесь текущим расчетом
Печать
https://calculat.io/ru/number/decimal-as-a-fraction/.12
<a href=»https://calculat. io/ru/number/decimal-as-a-fraction/.12″>0.12 в виде обыкновенной дроби — Calculatio</a>
io/ru/number/decimal-as-a-fraction/.12″>0.12 в виде обыкновенной дроби — Calculatio</a>
О калькуляторе «Конвертер десятичных дробей в обыкновенные»
Данный онлайн-конвертер десятичных дробей в обыкновенные дроби — это инструмент, который поможет вам быстро и легко конвертировать любое десятичное число в обыкновенную дробь. Например, он может помочь узнать как записать 0.12 в виде дроби? Конвертер будет особенно полезен тем, кто ежедневно работает с дробями или использует их в учебных или профессиональных целях.
Чтобы использовать данный конвертер, все, что вам нужно сделать, это ввести десятичное число, которое вы хотите конвертировать, в соответствующее поле, например, ‘0.12’. После того как вы ввели десятичное число, нажмите кнопку ‘Конвертировать’, чтобы начать процесс конвертации.
Конвертер выведет результат и покажет обыкновенную дробь, которая эквивалентна введенному вами десятичному числу, а также предоставит пошаговое объяснение процесса конвертации. Кроме того, конечная дробь будет упрощена до простейшей формы, используя наибольший общий делитель (НОД).
Кроме того, конечная дробь будет упрощена до простейшей формы, используя наибольший общий делитель (НОД).
Например, если вы введете ‘0.12’ в конвертер, он покажет вам, что данное десятичное число эквивалентно дроби ‘3/25’. Он также объяснит, как был получен данный ответ, показав шаги, выполненные в процессе конвертации.
В целом, онлайн-конвертер десятичных дробей в обыкновенные дроби — это необходимый инструмент для всех, кто работает с дробями в повседневной жизни, в учебной или профессиональной сфере. Он быстрый, простой в использовании и предоставляет точные результаты, что делает его ценным инструментом для всех, кто нуждается в конвертации десятичных дробей в обыкновенные.
Калькулятор «Конвертер десятичных дробей в обыкновенные»
Десятичная дробь
Таблица конвертации десятичных дробей в обыкновенные
| Десятичная дробь | Обыкновенная дробь |
|---|---|
| 0.145 | 29/200 |
0. 17 17 | 17/100 |
| 0.195 | 39/200 |
| 0.22 | 11/50 |
| 0.245 | 49/200 |
| 0.27 | 27/100 |
| 0.295 | 59/200 |
| 0.32 | 8/25 |
| 0.345 | 69/200 |
| 0.37 | 37/100 |
| 0.395 | 79/200 |
| 0.42 | 21/50 |
| 0.445 | 89/200 |
| 0.47 | 47/100 |
| 0.495 | 99/200 |
| 0.52 | 13/25 |
| 0.545 | 109/200 |
| 0.57 | 57/100 |
| 0.595 | 119/200 |
| 0.62 | 31/50 |
| 0.645 | 129/200 |
| 0.67 | 67/100 |
| 0.695 | 139/200 |
| 0.72 | 18/25 |
| 0.745 | 149/200 |
| 0.77 | 77/100 |
| 0.795 | 159/200 |
| 0.82 | 41/50 |
0. 845 845 | 169/200 |
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример |
|---|---|---|---|
| + | плюс | 0046 | 1/2 + 1/3 |
| — | знак минус | вычитание | 1 1/2 — 2/3 |
| * | звездочка | умножение | 2/3 * 3/4 9 | знак умножения | умножение | 2 /3 × 5/6 |
| : | знак деления | деление | 1/2 : 3 |
| 4 деления 4 деления 6 | деление | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
другие математические задачи »
Эталонные дроби — определение, диаграммы, примеры, фактыЧто такое эталонные дроби?Эталонные дроби — это дроби, которые легко идентифицировать и визуализировать. Давайте разберемся в этом на реальном примере. Что вы делаете, когда пытаетесь найти новый адрес или исследуете новую улицу? Вы пытаетесь определить точку отсчета рядом с ней или близлежащее место, с которым вы знакомы, а затем вы находите новый адрес, сравнивая его с точкой отсчета. Точно так же, когда сравнение или упорядочивание дробей становится затруднительным, мы можем воспользоваться эталонными дробями. Дробь может быть определена как часть целого. Знаменатель представляет собой общее количество равных частей целого и записывается внизу. Числитель представляет собой количество частей, взятых из целого, и пишется вверху. $\frac{3}{5}$ представляет 3 части из 5 равных частей. 3 — числитель, 5 — знаменатель. Связанные игрыЭталонные дроби ОпределениеВ математике эталонные дроби можно определить как дроби, которые мы можем использовать при измерении, сравнении или упорядочении других дробей. Они используются в качестве «эталона» для других общих факторов. Примеры стандартных эталонных дробей: $0, 1,\frac{1}{4} , \frac{1}{2}$ и т. д. на числовой строке. Вот эталонная таблица дробей, расположенная на числовой прямой, которая поможет вам сравнивать дроби: Давайте разберемся, чем полезна полоса дробей. Давайте легко сравним разные дроби $\frac{3}{5}$ и $\frac{7}{8}$, используя эту диаграмму. Обратите внимание на одну пятую полосу и одну восьмую полосу. 3 части одной пятой полосы представляют 35, а 7 частей одной восьмой полосы $\frac{7}{8}$. Сравнивая область, занятую заштрихованными частями, получаем $\frac{3}{5} \lt \frac{7}{8}$. Связанные рабочие листыКак сравнивать дроби с помощью эталонных дробейЭталонную диаграмму можно использовать для сравнения двух или более дробей с учетом длины соответствующих дробей. Этот процесс сравним с использованием дробных полос для аппроксимации измерений. Наиболее распространенная эталонная дробь — $\frac{1}{2}$. Это ровно посередине нуля и единицы. Его также можно записать в форме эквивалентной дроби как $\frac{2}{4}, \frac{3}{6}, \frac{4}{8}$ и т. д. Если числитель равен половине знаменателя, то дробь эквивалентна $\frac{1}{2}$. Если дробь эквивалентна $\frac{1}{2}$, ее положение на числовой прямой будет таким же, как у $\frac{1}{2}$. Пример 1: Выясним, меньше ли дробь $\frac{5}{12}$ $\frac{1}{2}$ или больше $\frac{1}{2}$ или равно $\frac{1}{2}$. Какая эквивалентная доля $\frac{1}{2}$ ближе к $\frac{5}{12}$? Это $\frac{6}{12}$. Итак, $\frac{6}{12} = \frac{1}{2}$ Ясно, что $\frac{5}{12} \lt \frac{6}{12}$, поскольку знаменатель тот же и $5\lt6$. Итак, что мы знаем? $\frac{5}{12}$ меньше, чем $\frac{6}{12}$, а $\frac{6}{12}$ равно $\frac{1}{2}$. Легко сделать вывод, что $\frac{5}{12}$ меньше, чем $\frac{1}{2}$. Мы знаем, что $\frac{4}{16} = \frac{1}{4}$. Кроме того, $\frac{5}{16}$ больше, чем $\frac{4}{16}$. Итак, мы можем сказать, что $\frac{5}{16}$ больше, чем $\frac{1}{4}$. Использование эталонных дробей для округления дробей1. Если числитель намного меньше знаменателя, мы округляем данную дробь до 0 Пример: $\frac{1}{9}, \frac{1}{5 }$ можно округлить до 0, так как они намного ближе к 0 на числовой прямой. 2. Если числитель почти половина знаменателя, то округляем данную дробь до $\frac{1}{2}$. Пример: $\frac{5}{11}, \frac{2}{6}, \frac{5}{8}$ можно округлить до $\frac{1}{2}$. 3. Если числитель и знаменатель почти равны, то округляем данную дробь до 1. Пример: $\frac{10}{11}, \frac{5}{6}$ можно округлить до 1. Давайте споем!При сравнении или заказе двух разных фракций Ориентируйтесь на эталонные дроби! Просто начните с расстановки дробей на числовой прямой. Затем выберите бенчмарк для сравнения — все будет хорошо! Решенные примеры1. Сравните $\frac{5}{8}$ и $\frac{1}{2}$ . Решение: Мы уже знаем, что $\frac{4}{8}$ является эквивалентной дробью $\frac{1}{2}$. Поскольку 5 больше 4, мы можем сказать, что $\frac{5}{8}$ больше, чем $\frac{4}{8}$. Итак, $\frac{5}{8}$ больше, чем $\frac{1}{2}$. 2. Сравните, является ли $\frac{2}{6}$ меньше или больше $\frac{2}{3}$ . Решение: $\frac{2}{6}$ является эквивалентной дробью $\frac{1}{3}$. Итак, $\frac{2}{6} = \frac{1}{3}$. Поскольку $\frac{1}{3}$ меньше, чем $\frac{2}{3}, \frac{2}{6}$ меньше, чем $\frac{2}{3}$. 3. Что больше: $\frac{4}{8}$ или $\frac{6}{12}$ ? Решение: $\frac{4}{8}$ также можно записать как $\frac{1}{2}$. $\frac{6}{12}$ также можно записать как $\frac{1}{2}$. Значит, обе дроби равны. Практические задачи1 Какая дробь ближе к $0: \frac{1}{2} ,\frac{1}{4}$ или $\frac{3}{4}$ ?$\frac{1}{2}$ $\frac{1}{4}$ $\frac{3}{4}$ Все вышеперечисленное Правильный ответ: $\ frac{1}{4}$ 2 Сравните дроби $\frac{1}{4}$ и $\frac{3}{12}$.$\frac{1}{4} \gt \frac{3}{12}$ $\frac{1}{4} \lt \frac{3}{12}$ Оба равны Ни Правильный ответ: Оба равны 3 Что больше из $\frac{12}{18}, \frac{14}{21}$ и $\frac{18}{27}$?$\frac{12}{18}$ $\frac{14}{21}$ $\frac{18}{27}$ Все равны Правильный ответ: Все равны 4 Сравните $0, \frac{2}{6}$ и $\frac{6}{9}$.$\frac{2}{6} \gt \frac{6}{9} \gt 0$ $\frac{6}{9} \gt \frac{2}{6} \gt 0$ $\frac{2}{6} \gt \frac{6}{9}$ $0 \gt \frac{6}{9} \gt \frac{2}{6}$ Правильный ответ: $\frac{6}{9} \gt \frac{2}{6} \gt 0$ Часто задаваемые вопросыДля чего используются дробные полоски? Полоски дробей — это практический способ для учащихся понять основы дробей. Полоски дробей упрощают изучение деления дробей на половинки, трети, четверти и т. д. Например, эти полоски можно разрезать на разные размеры, поэтому можно работать над несколькими задачами. Они особенно полезны для понимания сложения, вычитания и умножения. Как проще всего сравнивать дроби? Преобразование дробей в десятичные числа значительно упрощает определение того, какая дробь больше. Дробь с большим десятичным значением является большей дробью. Что означает сравнение дробей? Вы сравниваете две дроби, чтобы определить, является ли одна из них меньше, больше или равна другой. |

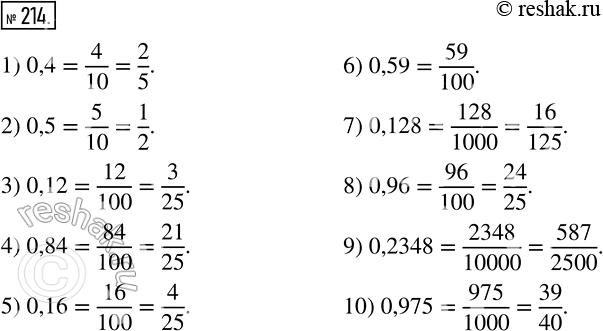 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций: 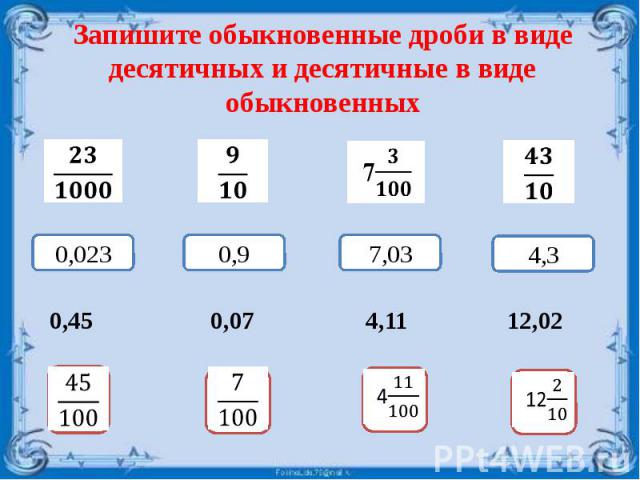
 1/6 рядов — морковь. Остальное петрушка. Сколько рядов засажено петрушкой?
1/6 рядов — морковь. Остальное петрушка. Сколько рядов засажено петрушкой? Давайте сначала освежим некоторые основные понятия!
Давайте сначала освежим некоторые основные понятия!





