0 sinx решить уравнение: Решите уравнение sin(x)=0 (синус от (х) равно 0)

Содержание

3.3: Тригонометрические уравнения — Математика LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 37221

Ричард В. Беверидж
Общественный колледж Клэтсопа

В предыдущем разделе, посвященном тригонометрическим тождествам, мы работали с уравнениями, которые были бы верны для всех значений определенного угла \(\theta .\). (2 x+10=\) \(2(x+1)+8 .\) В этом разделе мы будем решать тригонометрические уравнения, набор решений которых включает только определенные значения рассматриваемого угла. Из-за циклической природы углов, с которыми мы работаем, часто будет бесконечное количество решений, хотя и не «все действительные числа».

9{2} х-\sin х-1=0\)

Эта страница под названием 3.3: Тригонометрические уравнения распространяется по лицензии CC BY-NC-SA, ее автором, ремиксом и/или куратором выступил Ричард В. Беверидж.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Автор
Ричард В. Беверидж
Лицензия
CC BY-NC-SA
Показать страницу TOC
нет
Теги

Калькулятор — уравнение_решателя (ln (sin (x)) = 0; x) — Solumaths

Резюме:

Решатель уравнений позволяет решать уравнения с неизвестным с шагом расчета: линейное уравнение, квадратное уравнение, логарифмическое уравнение, дифференциальное уравнение.

уравнение_решатель онлайн

Описание:

Уравнение — это алгебраическое равенство, включающее одно или несколько неизвестных. Решить уравнение — это то же самое, что определить то неизвестное или неизвестные. Неизвестное также называют переменной. это калькулятор уравнений может решать уравнения с неизвестным, Калькулятор может решить уравнений с переменными с обеих сторон , а также уравнений со скобками :

Решение линейного уравнения

Решение квадратного уравнения
Решение кубического уравнения
Решение уравнения с нулевым произведением
Решение уравнения абсолютного значения (уравнение с функцией абс. )
Решение показательного уравнения
Решение логарифмического уравнения (уравнения с логарифмами)
Решение тригонометрического уравнения (уравнение с косинусом или синусом)
Решить онлайн дифференциальное уравнение первой степени
Решить онлайн дифференциальное уравнение второй степени

Решение линейного уравнения онлайн

Уравнение первой степени представляет собой уравнение вида `ax=b`. Этот тип уравнения также называется линейным уравнением . Для решения этих уравнений мы используем следующую формулу `x=b/a`.

линейное

решение уравнения вида ax=b s делается очень быстро, когда переменная не неоднозначна, просто введите уравнение до решить и затем нажмите решить, затем результат возвращается решателем . Также отображаются детали расчетов, которые привели к решению линейного уравнения.

Чтобы решить линейное уравнение после 3x+5=0, просто введите выражение 3x+5=0 в области расчета, затем нажмите кнопку «решить», результат возвращается `[x=-5/3]`. можно и решить уравнения в форме `(ax+c)/g(x)=0` или уравнения, которые могут быть в этой форме , g(x) представляет собой функцию. Когда вы вводите выражение без знака ‘=’; функция возвращает при возможных значениях, для которых выражение равно нулю. Например, введите x+5, вернитесь к x+5=0 и решите.

Уравнения с переменными с обеих сторон

Калькулятор может решать уравнения с переменными с обеих сторон, например: «3x+5=2x», просто введите 3x+5=2x, чтобы получить результат. 92-4ас`.

Дискриминант — это число, определяющее количество решений уравнения.

При положительном дискриминанте уравнение второй степени допускает два решения, которые даются формулой `(-b-sqrt(Delta))/(2a)` и `(-b+sqrt(Delta))/(2a)`;
Когда дискриминант равен нулю, квадратное уравнение допускает только одно решение, говорят, что оно является двойным корнем, которое дается формулой `(-b)/(2a)`; 92-1)/(x-1)=0` возвращает -1, все определение учитывается при вычислении числителя допускает два корня 1 и -1, но знаменатель равен нулю при x = 1, 1 не может быть решением уравнения. n=0`, если A является меньшей степенью полинома или равен 2. 92-1)(x+2)(x-3)=0` возвращает `[1;-1;-2;3]`.

Решение уравнения абсолютного значения

Решатель позволяет решить уравнение , включающее абсолютное значение . он может решать линейные уравнения с использованием абсолютных значений, квадратные уравнения с абсолютными значениями, а также многие другие типы уравнений с абсолютными значениями.

Вот два примера использования калькулятора уравнений для решения уравнения с абсолютным значением: 92-4)=4`, решатель показывает этапы расчета для решения квадратного уравнения с абсолютным значением.

Решение показательного уравнения

Калькулятор уравнений позволяет решать уравнение , включающее экспоненциальную . он может решать линейные уравнения, используя экспоненциальные, квадратные уравнения, включающие экспоненциальные, а также многие другие типы уравнений с экспоненциальным.

Вот два примера использования калькулятора для решения уравнения с экспонентой: 92-4)=4`, решатель показывает этапы расчета для решения квадратного уравнения с экспонентой.

Решение логарифмического уравнения

Решите логарифмическое уравнение т.е. возможны некоторые уравнения с логарифмами. Помимо предоставления результата, калькулятор предоставляет подробные шаги и расчеты, которые привели к решению логарифмического уравнения. Чтобы решить следующее логарифмическое уравнение ln(x)+ln(2x-1)=0, просто введите выражение в области расчета, затем нажмите кнопку расчета.

Решение тригонометрического уравнения

Калькулятор уравнений позволяет решать круговые уравнения , он способен решить уравнение с косинусом вида cos(x)=a или уравнение с синусом вида sin(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `cos(x)=1/2` или `2*sin(x)=sqrt(2)` с этапами расчета.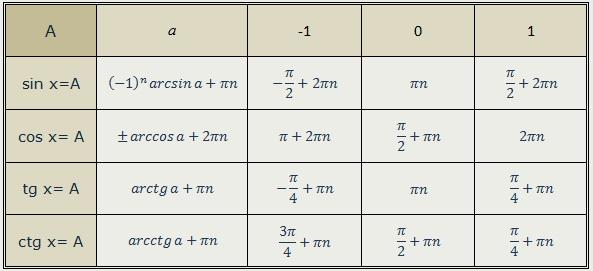

Решение линейного дифференциального уравнения первого порядка

Функция уравнения_решателя может решать линейные дифференциальные уравнения первого порядка онлайн , решить следующее дифференциальное уравнение: y’+y=0, вы должны ввести уравнение_решателя(`y’+y=0;x`).

Решение дифференциального уравнения второго порядка

Функция уравнения_решателя может решать дифференциальное уравнение второго порядка онлайн , решить следующее дифференциальное уравнение: y»-y=0, вы должны ввести уравнение_решателя(`y»-y=0;x`).

Игры и викторины по решению уравнений

Для отработки различных методов расчета предлагается несколько викторин по решению уравнений.

Синтаксис:

уравнение_решатель(уравнение;переменная), переменный параметр может быть опущен, если нет двусмысленности.

Примеры:

Разрешение уравнения первой степени

уравнения_решателя(`3*х-9`) равно записи Equation_solver(`3*x-9=0;x`) возвращенный результат равен 3.
No related posts.