Найти синус угла и косинус угла: Синус, косинус и тангенс угла — урок. Геометрия, 9 класс.

Как найти угол в прямоугольном треугольнике?

Тригонометрия — важный раздел математики, изучающий соотношение между длинами сторон и углами прямоугольного треугольника. Слово тригонометрия происходит от греческих слов, где «три» означает «три», «гон» означает «стороны», а «метрон» означает «мера». Гиппарх известен как «отец тригонометрии». Тригонометрия используется в различных приложениях в нашей повседневной жизни.

Прямоугольный треугольник

Тригонометрические соотношения

Используя тригонометрические соотношения, мы можем найти недостающие углы или стороны прямоугольного треугольника. Синус, косинус, тангенс, косеканс, секанс и котангенс — это шесть тригонометрических соотношений или функций. Где тригонометрическое отношение изображается как отношение между сторонами прямоугольного треугольника.

Сторона, противоположная прямому углу или самая длинная сторона, называется гипотенузой. Сторона, противоположная данному углу, называется противоположной стороной, а сторона, расположенная рядом с данным углом, называется прилежащей стороной. Функция синуса определяется как отношение противолежащего катета к гипотенузе. Функция косинуса определяется как отношение прилежащего катета к гипотенузе. Функция тангенса определяется как отношение противолежащей стороны к прилежащей стороне. Функция косеканса обратна функции синуса. Функция секанса обратна функции косинуса, а функция котангенса обратна функции тангенса. Следовательно, функции синуса, косинуса и тангенса являются тремя основными тригонометрическими функциями.

• sin θ = Противоположная сторона/Гипотенуза
• cos θ = Прилежащая сторона/Гипотенуза
• tang θ = sin θ/cos θ = Противоположная сторона/Прилегающая сторона
• cosec 6p 0 сторона θ = O 1/sinuse 0 сторона
• сек θ = 1/cos θ = гипотенуза/прилежащая сторона
• cot θ = 1/tan θ = прилежащая сторона/противоположная сторона = cos θ/sin θ 

Как найти угол в прямоугольном треугольнике?

Для нахождения неизвестного угла данного треугольника необходимо использовать обратные тригонометрические соотношения. Где обратные тригонометрические функции являются обратными функциями тригонометрических функций. Мы знаем, что sin θ = противолежащая сторона/гипотенуза.

Теперь θ = sin ^-1 (противоположная сторона/гипотенуза)

Аналогично, 

• θ = cos ^-1 (прилежащая сторона/гипотенуза)
5 035 03
• 03 тангенс 1 смежная сторона)
• θ = cosec ^-1 (гипотенуза/противоположная сторона)
• θ = sec ^-1 (гипотенуза/прилегающая сторона)
• θ = cot ^-1 (прилежащая сторона/противоположная сторона)

Мы знаем, что с помощью шести тригонометрических соотношений можно найти недостающие или неизвестные углы и стороны прямоугольного треугольника. Но, используя формулу правила синусов и формулу правила косинуса, мы можем найти стороны и углы любого заданного треугольника.

Правило синусов или закон синусов

Правило синусов или закон синусов — это тригонометрический закон, определяющий соотношение между сторонами и углами треугольника (непрямоугольного треугольника).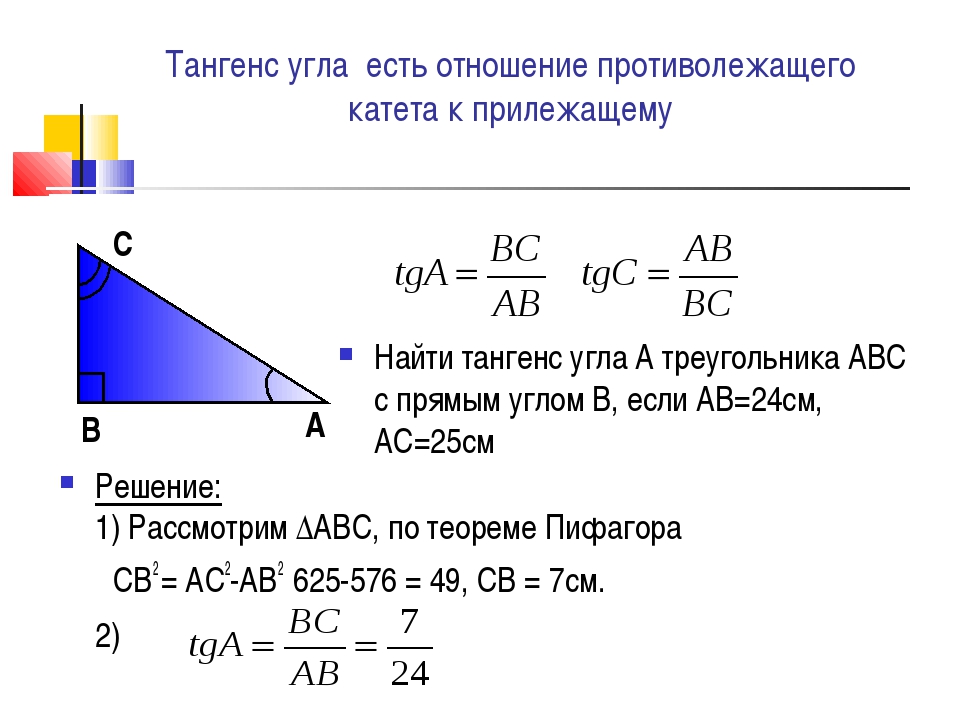 Пусть a, b и c будут длинами трех сторон треугольника ABC и A, B и C относительно их противоположных углов. Теперь выражение для правила синусов дается как:

Треугольник ABC

sin A/a = sin B/b = sin C/c (или) a/sin A = b/sin B = c/ грех С

Правило косинусов или закон косинусов

Правило косинусов или закон косинусов используется для нахождения неизвестной стороны или угла треугольника. Пусть a, b и c — стороны, а A, B и C — углы треугольника ABC. Теперь выражения для правила косинуса задаются следующим образом: а ² )/2bc

B ² = A ² + C ² — 2AC COS B (OR) COS B = (A ² + C ² — B ² )/2AC

C ^2. = A ² + B ² — 2AB COS C (OR) COS C = (A ² + B ² — C ² )/2AB

Проблемы

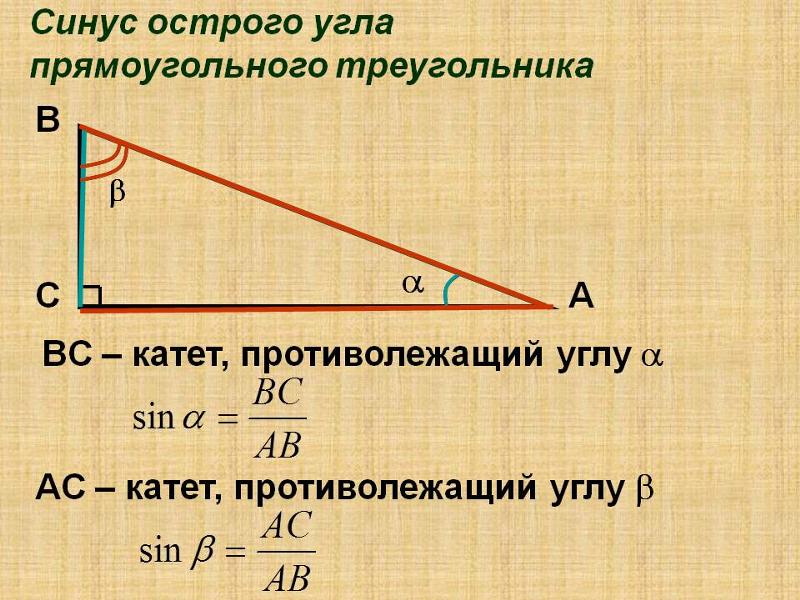. ПРОБЛЕМА 1. : Найдите угол ∠ACB (в градусах) прямоугольного треугольника ABC, если стороны AB = 5 см, а AC = 13 см.

Решение:

Треугольник ABC

Дано, AB = 5 см и AC = 13 см.

Итак, мы знаем длину стороны, противоположной ∠ACB, и длину гипотенузы. Следовательно, мы можем использовать тригонометрическую функцию синуса, чтобы найти ∠ACB.

sin C = противолежащая сторона/ гипотенуза

⇒ sin C = AB/AC

⇒ sin C = 5/13 °

Следовательно, ∠ACB = 22,61°

Задача 2: Найдите ∠Z (в градусах) прямоугольного треугольника XYZ, когда XY = 6 см и YZ = 8 см.

Решение:

Треугольник XYZ

Дано, XY = 6 см и YZ = 8 см.

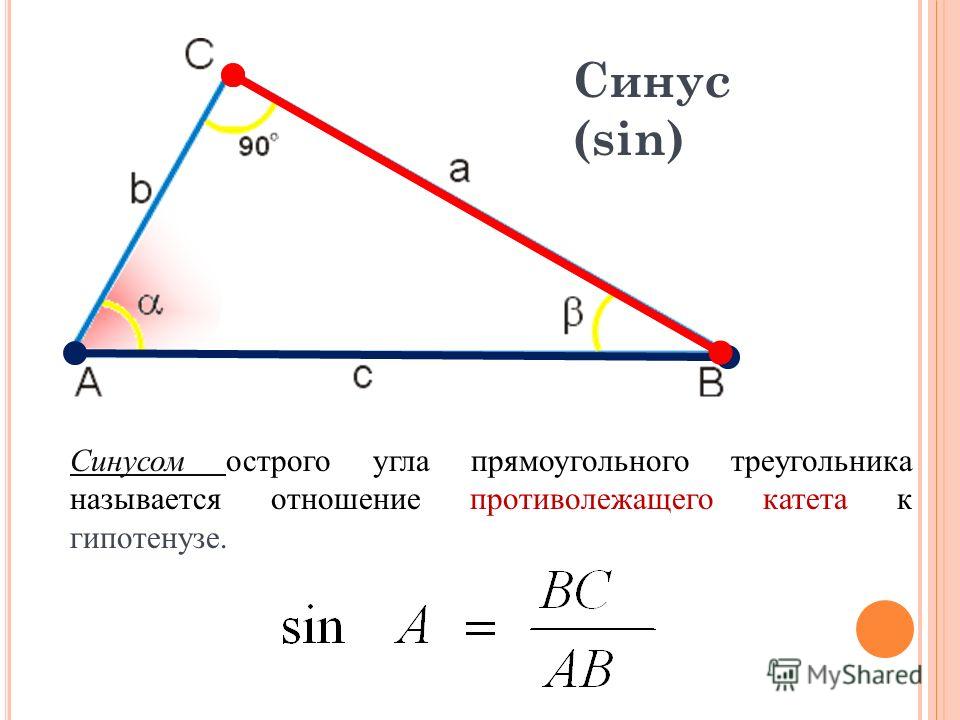
Итак, мы знаем длины противолежащей и прилежащей сторон ∠Z. Следовательно, мы можем использовать функцию касательной, чтобы найти ∠Z

. У нас есть тангенс Z = противоположная сторона/прилегающая сторона

⇒ тангенс Z = XY/YZ

⇒ тангенс Z = 6/8 = 3/4

⇒ ∠Z = tan ^-1 (3/4) ⇒ ∠Z = 36,87°

Следовательно, ∠Z = 36,87°

Задача 3. Найти ∠A (в градусах) прямоугольного треугольника АВС, если АВ = 3 см и АС = 5 см.

Решение:

Треугольник ABC

Дано, AB = 3 см и AC = 5 см

Итак, мы имеем длину прилежащей стороны ∠A и длину гипотенузы. Следовательно, мы можем использовать функцию косинуса, чтобы найти ∠A

cos A = смежная сторона/гипотенуза

⇒ cos A = AB/AC

⇒ cos A = 3/5

⇒ ∠A = cos ^-1 (3/5) ⇒ ∠A = 53,13°

A = 5,13°

A,

Задача 4: Найти ∠P (в градусах) и ∠R (в градусах) и длину гипотенузы прямоугольного треугольника, если PQ = 24 см и QR = 7 см.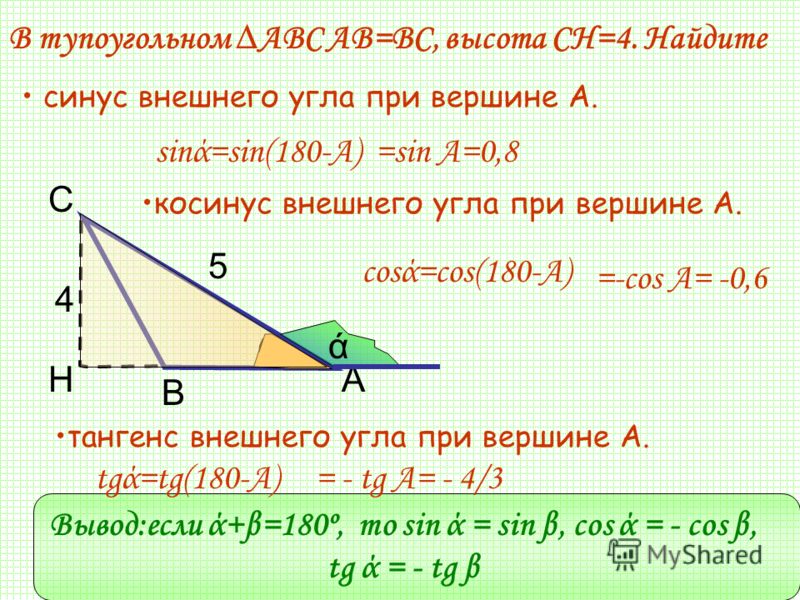

Решение:

 

Данные, PQ = r = 24 см и QR = p = 7 см

По теореме Пифагора имеем, p ² + Q ² = R ²

⇒ 24 ² + 7 ² = R ²

⇒ R ² = 576 + 49 = 625

⇒ R ² = 576 + 49 = 625

⇒ тит. r = 25 см

Имеем, sin P = противолежащая сторона/гипотенуза

⇒ sin P = 7/25

⇒ ∠P = sin ^-1 (7/25) ⇒ ∠P = 190,263

Мы знаем, что сумма углов в треугольнике = 180°

⇒ ∠P + ∠Q + ∠R = 180°

⇒ 16,26° + 90° + ∠R = 180°

⇒ ∠R = 180° – 16,26° – 90° ⇒ ∠R = 73,76°

Следовательно, ∠P = 16,26° & ∠R = 73,76° и PR = q = 25 см

Задача 5. Найдите ∠B (в градусах) и ∠C (в градусах), если ∠A = 30°, AB = 16 дюймов и BC = 12 дюймов.

Решение:

При данных данных ∠A = 30°, AB = c = 16 дюймов и BC = a = 12 дюймов.

Треугольник ABC

Мы можем использовать закон синусов, чтобы найти ∠B и ∠C.

a/sin A = b/sin B = c/sin C

Рассмотрим, a/sin A = c/sin C

⇒ 12/sin 30° = 16/sin C [sin 30° = ½]

⇒ 12/(½) = 16/sin C

⇒ sin C = 16/24 = 2/3

⇒ ∠C = sin ^-1 (2/3) = 41,81° Сумма углов треугольника = 180°

∠A + ∠B + ∠C = 180°

⇒ 30° + ∠B + 41,81° = 180° ⇒ ∠B = 180° – 30° – 41,81°

⇒ ∠B = 101,19°

Следовательно, ∠B = 101,19° и ∠C = 41,81°

Задача 6: Найдите меру ∠Y (в градусах), если площадь треугольника XYZ = 24 см ² и YZ = 12 см и XY = 5 см.

Решение:

Данные, Площадь треугольника XYZ = 24 см ^2, , YZ = x = 12 см и XY = z = 5 см

Треугольник XYZ 900 у нас есть синусы, Площадь треугольника = ½ × (x) × (z) × sin Y

⇒ 24 см ² = ½ × (12) × (5) × sin Y

⇒ sin Y = 48/60 = 4/5

⇒ ∠Y = sin ^-1 (4/5)

⇒ ∠Y = 53,12°

в градусах) треугольника PQR, когда PQ = 14 см, QR = 6 см и PR = 5 см.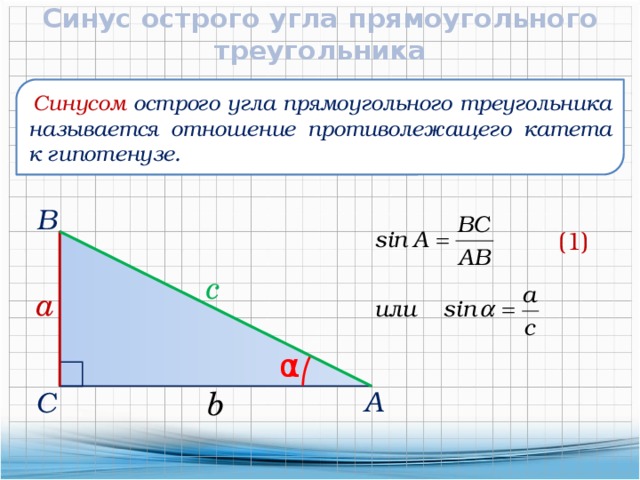

Решение:

Данные, PQ = r = 5 см, QR = p = 7 см и PR = q = 8 см

Треугольник PQR

Здесь мы знаем длины трех сторон треугольника PQR. Итак, мы можем использовать закон косинусов, чтобы найти ∠Q.

Имеем, cos Q = (p ² + r ² – q ² )/2pr

⇒ cos Q = {[(7) ^{20 + (30 3} 0 (8) ² ]/(2 × 7 × 5)}

⇒ cos Q = {[49 + 25 – 64]/70}

⇒ cos Q = 10/70 = 1/7

⇒ ∠ Q = cos ^-1 (1/7) ⇒ ∠Q = 81,79°

Аналогично, cos P = (q ² + r ² – p ² )/2qs P 0 cos

6

6 0 = {[(8) ² + (5) ² – (7) ² ]/(2 × 8 × 5)}

⇒ cos P = {[64 + 25 – 49]/80}

⇒ cos P = 40/80 = ½

⇒ ∠ P = cos ^-1 (½) ⇒ ∠P = 60°

cos R = (p ² + q ² – r ² )/2pq

3 )/2pq

3 7)

² + (8) ² – (5) ² ]/2 × 7 × 8}

⇒ cos R = {[49 + 64 – 25]/112}

⇒ cos R = 88/112 ⇒ cos R = 11/14

⇒ ∠R = cos ^-1 (11/14) ⇒ ∠R = 38,21°

Следовательно, углы треугольника PQR равны ∠P = 60°, ∠Q = 81,79° и ∠R = 38,21°

найти меру указанного угла с точностью до ближайшего градуса

[PDF] Использование тригонометрии для нахождения угловых величин

mrurbanc. weebly.com › загрузки › trigonometry_to_find_angle_meas…

Использование тригонометрии для нахождения угловых мер. Найдите меру каждого угла с точностью до градуса. … Найдите меру указанного угла с точностью до градуса.

Найди меру указанного угла с точностью до… — YouTube

www.youtube.com › смотреть

31.01.2023 · Найди меру указанного угла с точностью до градуса. Решение с использованием обратного триггера. № 9.
Добавлено: 5:25
Прислан: 31.01.2023

Es fehlt: ответ | Muss Folgendes enthalten:ответить

Как найти меру указанного угла — YouTube

www.youtube.com › смотреть

15.11.2020 · Как найти меру указанного угла с точностью до градуса?
Dauer: 11:25
Прислан: 15.11.2020

[PDF] Обратные тригонометрические отношения (Trig) 8-4

tmpsantafe.org › wp-content › uploads › 2018/12 › 04_ans_000T2… Найдите меру каждого угла с точностью до градуса. 1) sin В = 0,4848.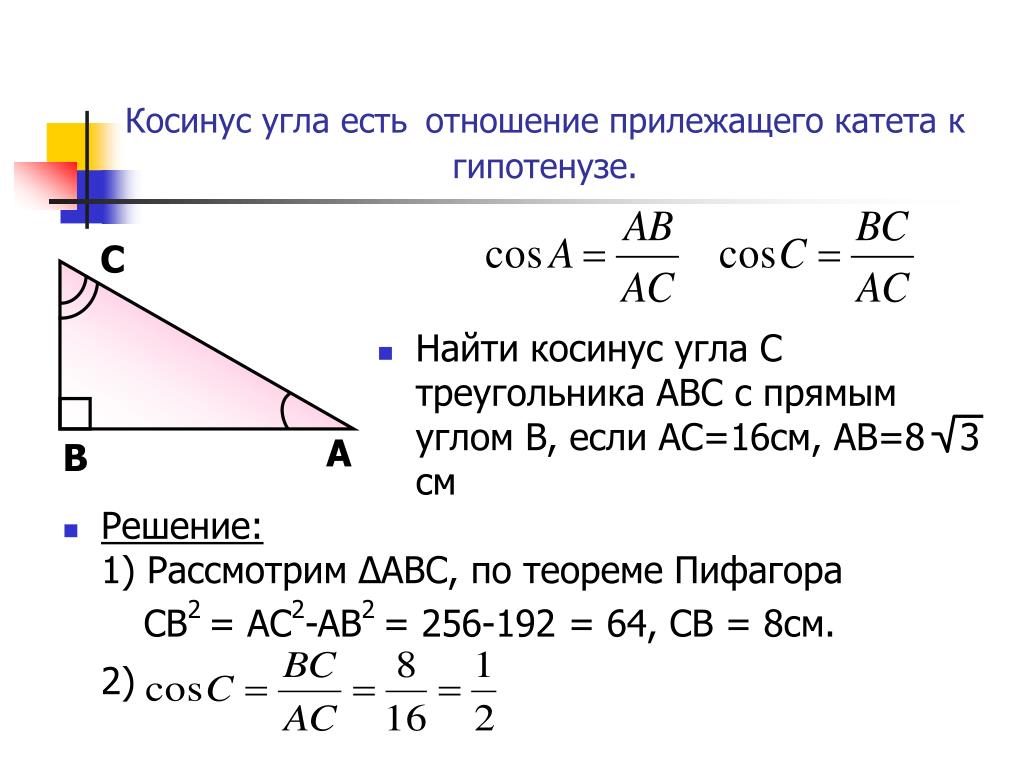 ·B=sin(0,4848)=29°. 3) cos А = 0,7431. Имя cw-Ключ. 2) sin А = 0,5150.

[PDF] Тригонометрия для нахождения угловых мер — Kuta Software

cdn.kutasoftware.com › Рабочие листы › Alg1 › Тригонометрия для нахождения мер угла…

Рабочий лист от Kuta Software LLC … Найдите меру каждого угла с точностью до градуса. … Найдите меру указанного угла с точностью до градуса.

Ähnliche Fragen

Что такое указанный угол?

[PDF] Нахождение недостающих углов в прямоугольном треугольнике-Название заметки — iBlog

iblog.dearbornschools.org › нахождение углов-заметкидомашнее задание-ответы

Найдите x в каждом и округлите до десятых. Tan z=4,705 … Найдите величину указанного угла с точностью до градуса. … Ключ. Период. СОХКА К А.

Найдите градус указанного угла с точностью до … — Brainly.com

brainly.com › Математика › Высшая школа

Ответ: 23°. Пошаговое объяснение: Это прямоугольный треугольник, поэтому мы можем найти угол с помощью тригонометрических соотношений.

No related posts.