Формула синус альфа: Синус, косинус и тангенс угла — урок. Геометрия, 9 класс.

Математика для гуманитариев 11

  вернуться Время чтения: 5 минут   |   Комментариев: 4

Сохранить

Продолжаем уроки математики от профессора Нелли Литвак. В прошлый раз мы говорили о математическом основании вакцинации, математике и численности популяций, и, надеемся, все усвоили, зачем нам нужны степени и логарифмы. Сегодня нам предстоит новое знакомство с синусом и косинусом, а ещё мы узнаем, почему математикам нужно уметь сдаваться.

Популяризация тригонометрии в интернет-сообществах.

(источник: pikabu.ru)

Напомним, в группе «Математика — великая и ужасная!» Нелли вместе с журналистом Аллой Кечеджан помогают взрослым гуманитариям освоить великую и ужасную науку «с нуля». А на сайте Newtonew публикации из группы с обсуждениями собраны в виде уроков, чтобы их не поглотил океан соцсетей. Все предыдущие занятия можно найти здесь.

 Передаём слово профессору.

Тригонометрия начинается с окружности, а точнее, с движения по окружности.

Синусы и косинусы рассказывают нам историю о вращении — и историю вечного бессилия, с которым математики сталкиваются на каждом шагу.

Нелли Литвак, профессор прикладной математики, университет Твенте, Нидерланды

Что же такое эти синусы и косинусы? Что они означают и зачем они нужны?

Представьте себе окружность радиуса 1 с центром в начале координат, как на рисунке 1.  

Рисунок 1.

Теперь давайте возьмём точку (1,0) и повернём эту точку против часовой стрелки на какой-то угол, скажем, 50 градусов, как на рисунке 2.

Рисунок 2.

Почему против часовой стрелки? Потому что мы так договорились: угол вращения увеличивается против часовой стрелки. Точно так же, как координата х увеличивается слева направо, а координата у — снизу вверх. Не обязательно угол 50 градусов, давайте возьмём любой угол, назовём его великой и ужасной греческой

буквой альфа, как на рисунке 3. Альфа у нас будет любым углом от 0 до 360 градусов против часовой стрелки.

Рисунок 3.

Получилась точка, на рисунке 3 я её обвела красным цветом. Мы точно знаем, где она находится и как её найти: надо только повернуться на угол альфа градусов по окружности против часовой стрелки.

И поскольку эта точка на плоскости, то у неё есть координата х и координата у, на рисунке 3 я написала (х,у). И вот математики задаются вопросом: если мы всё знаем про эту точку, то какие у неё координаты х и у? А?

Даже если мы знаем угол альфа, то мы просто не в состоянии подсчитать координаты этой точки! У нас для этого нет формулы! В университете на курсе анализа выясняется, что формула всё-таки есть. Она называется «ряд Тейлора». Но в ней бесконечное число слагаемых. А простой короткой формулы нет.

В подобной ситуации математики используют приём, который Джейсон Вилкес в книге «Сожгите класс математики» называет «Искусство сдаться».  

Я не ослышался: искусство сдаться???

(источник: cdn. pixabay.com)

Если для какого-то объекта нет формулы, то мы просто придумываем название для этого объекта. Желательно, конечно, название великое и ужасное. Чтобы никто не догадался о нашем бессилии.

Вот так. Поскольку мы не можем подсчитать координаты х и у, то мы назовём координату х косинусом угла альфа, а координату у — синусом угла альфа. Как на рисунке 4. Это синус и косинус. И всё. И больше НИЧЕГО!  

Синус и косинус — всего лишь координаты точки на окружности с радиусом 1. 

Рисунок 4. 

Задание №1. Разбираемся со школьной формулой

Может показаться удивительным, но «искусство сдаться» математиков полностью устраивает. Ведь самое главное в математике — выяснять закономерности. Для этого нам нужно только знать, что означают синус и косинус. Мы договорились, что это координаты точки на окружности радиуса 1. И этого достаточно, чтобы выяснить закономерности, связанные с синусом, косинусом, окружностью и вращением.

Именно об этом будет задание. Давайте разберёмся в одной из школьных формул.  

ЗАДАНИЕ. Чтобы получить поворот на угол (90+альфа) градусов, нужно сначала повернуться против часовой стрелки на 90 градусов, а потом ещё на альфа градусов, см. рисунок 5. Объясните, почему:

cos(90+alpha) = — sin(alpha) sin(90+alpha) = cos(alpha).

Формулы написаны на рисунке 5. Удачи!  

Рисунок 5.

Кстати, рекомендую почитать обсуждения этого задания в группе. Я сама узнала много нового. Посмотрите комментарии, там есть великолепная интерпретация с хордами и история происхождения слова «синус»!  

Тригонометрическая церемония в престижном женском колледже Вассара, США, 1889.

(источник: math.vassar.edu)

Задание №2. Торжественное тождество

Как мы поняли, подсчитать синус и косинус по формуле нельзя. Зато между ними можно устанавливать связи. Сегодня мы поговорим об одной такой связи.

На рисунке 6 я нарисовала окружность, угол альфа, синус и косинус. Какая связь между синусом и косинусом? Ну, например, такая (см. внизу рисунка):

[синус альфа в квадрате] +[косинус альфа в квадрате] = 1  

Рисунок 6. Внизу — основное тригонометрическое тождество.

В формуле квадрат (маленькая двойка наверху) ставится после sin, а не после альфа, чтобы было понятно, что мы возводим в квадрат синус, а не угол.

Это равенство в школе называют основное тригонометрическое тождество. Звучит очень торжественно. Но посмотрите внимательно: этот прямоугольный треугольник и эти квадраты ничего вам не напоминают?

ЗАДАНИЕ. Объясните, почему [синус альфа в квадрате] +[косинус альфа в квадрате] = 1. Заметьте, что равенство верно для любых углов. Для примера я нарисовала тупой угол на рисунке 7. 

Рисунок 7.

Получилось? Теперь мы можем подсчитать синус и косинус 45 градусов, см. рисунок 8.

Рисунок 8.

Объяснения к этому заданию можно найти здесь.

А к следующему разу я приготовлю вам ещё кое-что великое и ужасное.   

13 октября 2017, 12:00

Внештатный автор

Нелли Литвак

профессор прикладной математики, университет Твенте, Нидерланды. Автор книг «Кому нужна математика?», «Формула призвания. Семь правил выбора вуза» и «Наши хорошие подростки».

наука лайфхаки

школьник вечный студент

Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.

– Oбразование как Стиль Жизни

Присылайте свои колонки

и предложения

У вас есть интересная новость или материал из сферы образования или популярной науки?
Расскажите нам!

[email protected]

© 2014-2023 Newtonew. 12+

Просветительский медиа-проект об образовании, посвящённый самым актуальным и полезным концепциям, теориям и методикам, технологиям и исследованиям, продуктам и сервисам.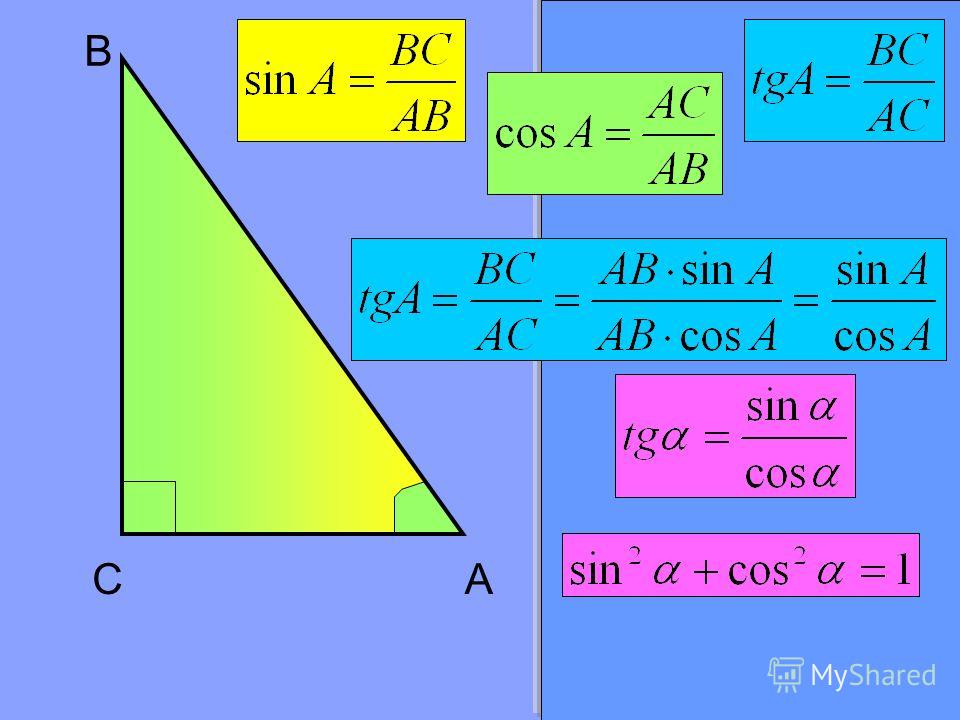 Мы говорим о том, как развиваются и изменяются образование и наука.
Копирование материалов возможно только с разрешения редакции Newtonew.

ЕГЭ спецпроект ProTeachers

MOOC 2016 Большая переменная

Физика: игра света

Маршрут в будущее

Считаные годы

Образование XXI века

Мы используем файлы cookie для улучшения пользовательского опыта. Подробнее вы можете посмотреть в нашем пользовательском соглашении.

App Store Google Play

Подписаться на рассылку

Подписаться на рассылку

Подготовка к ЕГЭ по математике

Меню сайта Наш опрос Статистика Онлайн всего: 1 Гостей: 1 Пользователей: 0

Тригонометрические формулы приведения В таблице приведены формулы приведения для тригонометрических функций (sin, cos, tg, ctg).     Формулы тригонометрических функций суммы углов               Формулы тригонометрических функций разницы углов Тригонометрические формулы преобразования разности аргументов               Формулы тригонометрических функций двойного угла Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)   sin(2α)- через sin и cos:   sin(2α)- через tg и ctg:   cos(2α)- через sin и cos:   cos(2α)- через tg и ctg:     tg(2α) и сtg(2α):     Формулы тригонометрических функций тройного угла Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):             Синус, косинус, тангенс, котангенс половинного угла               Формулы суммы тригонометрических функций               Формулы разницы тригонометрических функций               Формулы произведения тригонометрических функций, (sin cos tg ctg)                   Квадрат синуса, косинуса, тангенса, котангенса (альфа) Уравнения разложения тригонометрических функций: квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.             Синус, косинус в кубе               Значения синуса, косинуса, тангенса, котангенса       sin(α)=OA cos(α)=OC tg(α)=DE ctg(α)=MK R=OB=1             Значения функций для некоторых углов, α

Вход на сайт Друзья сайта Онлайн тесты по математике Официальный блог Сообщество uCoz FAQ по системе Инструкции для uCoz

Неправильные треугольники: закон синусов

Цели обучения

В этом разделе вы будете:

• Использовать закон синусов для решения косоугольных треугольников.
• Найдите площадь косоугольного треугольника с помощью функции синуса.
• Решение прикладных задач по закону синусов.

Предположим, что две радиолокационные станции, расположенные на расстоянии 20 миль друг от друга, обнаруживают самолет между собой. Угол места, измеренный первой станцией, составляет 35 градусов, тогда как угол места, измеренный второй станцией, равен 15 градусам. Как определить высоту самолета? Мы видим на (Рисунок), что треугольник, образованный самолетом и двумя станциями, не является прямоугольным, поэтому мы не можем использовать то, что знаем о прямоугольных треугольниках. В этом разделе мы узнаем, как решать задачи, связанные с неправильными треугольниками.

Рисунок 1.

Использование закона синусов для решения наклонных треугольников

В любом треугольнике мы можем провести высоту, перпендикулярную линию из одной вершины к противоположной стороне, образуя два прямоугольных треугольника. Однако было бы предпочтительнее иметь методы, которые можно было бы применять непосредственно к непрямоугольным треугольникам без предварительного создания прямоугольных треугольников.

Любой треугольник, не являющийся прямоугольным, является косоугольным. Решение косоугольного треугольника означает нахождение измерений всех трех углов и всех трех сторон. Для этого нам нужно начать как минимум с трех из этих значений, включая хотя бы одну из сторон. Мы исследуем три возможные ситуации в задаче о косом треугольнике:

1. ASA (угол-сторона-угол) Нам известны измерения двух углов и прилежащей стороны. См. (Рисунок).

   Рисунок 2.

2. AAS (угол-угол-сторона) Нам известны измерения двух углов и стороны, которая не находится между известными углами. См. (Рисунок).

   Рис. 3.

3. SSA (угол сторона-бок) Нам известны измерения двух сторон и угла, который не лежит между известными сторонами. См. (Рисунок).

   Рисунок 4.

Знание того, как подходить к каждой из этих ситуаций, позволяет нам решать косоугольные треугольники, не опуская перпендикуляр, чтобы образовать два прямоугольных треугольника. Вместо этого мы можем использовать тот факт, что отношение измерения одного из углов к длине его противоположной стороны будет равно двум другим отношениям измерения угла к противоположной стороне. Давайте посмотрим, как это утверждение получается, рассматривая треугольник, показанный на (Рисунок).

Рисунок 5.

Используя соотношения прямоугольного треугольника, мы знаем, что [латекс]\,\mathrm{sin}\,\alpha =\frac{h}{b}\,[/latex]и[латекс]\ ,\mathrm{sin}\,\beta =\frac{h}{a}.\,\,[/latex]Решение обоих уравнений для [latex]\,h\,[/latex] дает два разных выражения для[ латекс]\,h.[/latex]

[латекс]h=b\mathrm{sin}\,\alpha \text{ и }h=a\mathrm{sin}\,\beta [/latex]

Затем мы устанавливаем выражения равными друг другу.

[латекс]\begin{array}{ll}\text{ }b\mathrm{sin}\,\alpha =a\mathrm{sin}\,\beta \hfill & \hfill \\ \text{ }\ влево(\frac{1}{ab}\right)\left(b\mathrm{sin}\,\alpha \right)=\left(a\mathrm{sin}\,\beta\right)\left(\ frac{1}{ab}\right)\begin{array}{cccc}& & & \end{array}\hfill & \text{Умножить обе части на}\,\frac{1}{ab}. \hfill \\ \text{ }\,\frac{\mathrm{sin}\,\alpha }{a}=\frac{\mathrm{sin}\,\beta}{b}\hfill & \hfill \end {массив}[/латекс]

Точно так же мы можем сравнить другие коэффициенты.

[латекс] \ frac {\ mathrm {sin} \, \ alpha {a} = \ frac {\ mathrm {sin} \, \ gamma} {c} \ text {and} \ frac {\ mathrm {sin }\,\beta }{b}=\frac{\mathrm{sin}\,\gamma }{c}[/latex]

В совокупности эти соотношения называются Законом синусов .

[латекс] \ frac {\ mathrm {sin} \, \ alpha {a} = \ frac {\ mathrm {sin} \, \ beta} {b} = \ frac {\ mathrm {sin} \, \ lambda }{c}[/latex]

Обратите внимание на стандартный способ маркировки треугольников: угол[латекс]\,\альфа \,[/латекс](альфа) противоположен стороне[латекс]\,а;\,[/ латекс]угол[латекс]\,\бета \,[/латекс](бета) является противоположной стороной[латекс]\,b;\,[/латекс]и угол[латекс]\,\гамма \,[/латекс] (гамма) находится на противоположной стороне[латекс]\,с. \,[/латекс]См. (рисунок).

При вычислении углов и сторон не забудьте ввести точные значения в окончательный ответ. Как правило, окончательные ответы округляются до десятых, если не указано иное.

Рисунок 6.

Закон синусов

Дан треугольник с углами и противоположными сторонами, обозначенными как на (рисунок), отношение измерения угла к длине его противоположной стороны будет равно другому два отношения меры угла к противоположной стороне. Все пропорции будут равны. Закон синусов основан на пропорциях и символически представлен двумя способами.

[латекс] \ frac {\ mathrm {sin} \, \ alpha {a} = \ frac {\ mathrm {sin} \, \ beta} {b} = \ frac {\ mathrm {sin} \, \ гамма }{c}[/latex]

[латекс]\frac{a}{\mathrm{sin}\,\alpha }=\frac{b}{\mathrm{sin}\,\beta }=\frac {c}{\mathrm{sin}\,\gamma }[/latex]

Чтобы решить косой треугольник, используйте любую пару применимых соотношений.

Решение для двух неизвестных сторон и угла треугольника AAS

Решите треугольник, показанный на (Рисунок), с точностью до десятых.

Рисунок 7.

Показать решение

Попробуйте

Решите треугольник, показанный на (Рисунок), с точностью до десятых.

Рис. 8.

Показать решение

Использование закона синусов для решения треугольников SSA

Мы можем использовать закон синусов для решения любого косоугольного треугольника, но некоторые решения могут быть непростыми. В некоторых случаях заданным критериям может удовлетворять более одного треугольника, что мы описываем как неоднозначный случай. Треугольники, классифицируемые как SSA, те, в которых мы знаем длины двух сторон и измерение угла, противоположного одной из данных сторон, могут иметь одно или два решения или даже не иметь решения.

Возможные исходы для треугольников SSA

Косоугольные треугольники в категории SSA могут иметь четыре различных исхода. (Рисунок) иллюстрирует решения с известными сторонами[латекс]\,а\,[/латекс]и[латекс]\,b\,[/латекс]и известным углом[латекс]\,\альфа . [/латекс]

Рис. 9.

Решение косого треугольника SSA

Решите треугольник на (рис.) для отсутствующей стороны и найдите отсутствующий угол с точностью до десятых.

Рисунок 10.

Показать решение

Попробуйте

Дано[латекс]\,\альфа =80°,а=120,\,[/латекс]и[латекс]\,b=121,\,[/латекс]найдите недостающую сторону и углы . Если существует более одного возможного решения, покажите оба.

Показать раствор

Нахождение неизвестных сторон и углов треугольника SSA

В треугольнике, показанном на (рис.), найдите неизвестные стороны и углы. Округлите свои ответы до десятых.

Рис. 13.

Показать решение

Попробуйте

Дано[латекс]\,\альфа =80°,а=100,\,\,b=10,\,[/латекс]найдите недостающую сторону и углы. Если существует более одного возможного решения, покажите оба.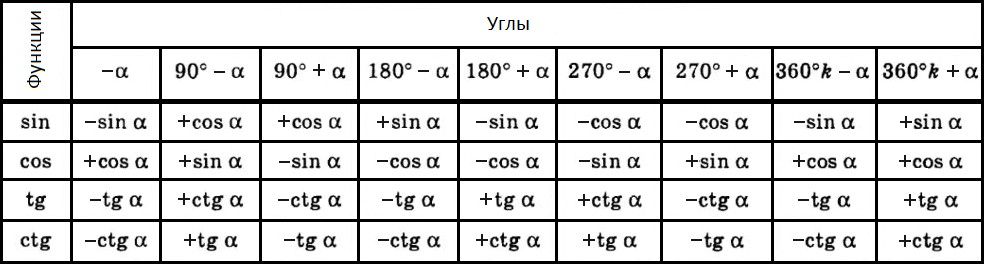 Округлите свои ответы до десятых.

Показать раствор

Нахождение треугольников, удовлетворяющих заданным критериям

Найдите все возможные треугольники, если одна сторона имеет длину 4 напротив угла 50°, а вторая сторона имеет длину 10.

Показать решение

Попробуй

Определить возможное количество треугольников при условии [латекс]\,а=31,\,\,b=26,\,\,\бета =48°.\,\,[/латекс]

Показать решение

Нахождение площади косоугольного треугольника с помощью функции синуса

Теперь, когда мы можем решить треугольник для пропущенных значений, мы можем использовать некоторые из этих значений и функцию синуса, чтобы найти площадь косоугольного треугольника. Напомним, что формула площади треугольника имеет вид[латекс]\,\текст{Площадь}=\фракция{1}{2}bh,\,[/латекс],где[латекс]\,b\,[/латекс ] — основание, а [латекс]\,h\,[/латекс] — высота. {\простое число},\,[/латекс]или[латекс]\,180-\альфа .[/латекс]

Рисунок 15.

Таким образом,

[латекс]\текст{Площадь}=\frac{1}{2}\left(\text{база}\right)\left(\text{height}\ right)=\frac{1}{2}b\left(c\mathrm{sin}\,\alpha \right)[/latex]

Аналогично,

[latex]\text{Area}=\frac{ 1}{2}a\left(b\mathrm{sin}\,\gamma\right)=\frac{1}{2}a\left(c\mathrm{sin}\,\beta \right)[/ латекс]

Площадь косоугольного треугольника

Формула площади косоугольного треугольника:

[латекс]\begin{array}{l}\text{Area}=\frac{1}{2} bc\mathrm{sin}\,\alpha \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,=\frac{1}{2}ac\mathrm {sin}\,\beta \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,=\frac{1}{2}ab\mathrm{sin} \,\gamma \hfill \end{массив}[/latex]

Эквивалентно половине произведения двух сторон и синуса прилежащего к ним угла.

Нахождение площади наклонного треугольника

Нахождение площади треугольника со сторонами[латекс]\,а=90,b=52,\,[/латекс]и углом[латекс]\,\гамма =102° . \,[/latex]Округлите площадь до ближайшего целого числа.

Показать раствор

Попробуйте

Найдите площадь заданного треугольника[латекс]\,\beta =42°,\,\,a=7,2\,\text{ft},\,\,c=3,4\,\text {ft}.\,[/latex]Округлите площадь до десятых.

Показать решение

Решение прикладных задач с использованием закона синусов

Чем больше мы изучаем тригонометрические приложения, тем больше мы обнаруживаем, что их бесчисленное множество. Некоторые из них представляют собой плоские ситуации типа диаграммы, но многие приложения в исчислении, технике и физике включают трехмерное пространство и движение.

Определение высоты

Найдите высоту самолета в задаче, представленной в начале этого раздела, показанной на (рис.). Округлите высоту до ближайшей десятой мили.

Рисунок 16.

Показать решение

Диаграмма, показанная на (Рисунок), представляет высоту дирижабля, летящего над футбольным стадионом. Найдите высоту дирижабля, если угол возвышения в южной оконечности, точка А, равен 70°, а угол возвышения в северной оконечности, точка [латекс]\,В,\,[/латекс] равен 62°. °, а расстояние между точками обзора двух концевых зон составляет 145 ярдов.

Рис. 17.

Показать решение

Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с тригонометрическими приложениями.

• Закон синусов: основы
• Закон синусов: неоднозначный случай

Ключевые уравнения

Закон синусов	[латекс] \ begin {array} {l} \ frac {\ mathrm {sin} \, \ alpha {a} = \ frac {\ mathrm {sin} \, \ beta} {b} = \ frac {\ mathrm{sin}\,\gamma}{c}\,\hfill \\\frac{a}{\mathrm{sin}\,\alpha}=\frac{b}{\mathrm{sin}\,\beta }=\frac{c}{\mathrm{sin}\,\gamma }\hfill \end{массив}[/latex]
Площадка для наклонных треугольников	[латекс]\begin{array}{r}\hfill \text{Area}=\frac{1}{2}bc\mathrm{sin}\,\alpha \\ \hfill \text{ }=\frac{ 1}{2}ac\mathrm{sin}\,\beta \\ \hfill \text{ }=\frac{1}{2}ab\mathrm{sin}\,\gamma \end{array}[/latex ]

Ключевые понятия

• Закон синусов можно использовать для решения косоугольных треугольников, которые не являются прямоугольными треугольниками.
• По закону синусов отношение измерения одного из углов к длине его противоположной стороны равно двум другим отношениям измерения угла к противоположной стороне.
• Возможны три случая: ASA, AAS, SSA. В зависимости от предоставленной информации мы можем выбрать соответствующее уравнение для нахождения требуемого решения. См. (Рисунок).
• Неоднозначный случай возникает, когда косой треугольник может иметь разные исходы.
• Возможны три случая, возникающие из-за схемы SSA: одно решение, два возможных решения и отсутствие решения. См. (Рисунок) и (Рисунок).
• Закон синусов можно использовать для решения треугольников с заданными критериями. См. (Рисунок).
• Общая формула площади для треугольников преобразуется в косые треугольники, если сначала найти соответствующее значение высоты. См. (Рисунок).
• Существует множество тригонометрических приложений. Их часто можно решить, сначала нарисовав диаграмму данной информации, а затем используя соответствующее уравнение. См. (Рисунок).

Раздел Упражнения

Вербальные

Опишите высоту треугольника.

Показать раствор

Сравните прямоугольные и косоугольные треугольники.

Когда можно использовать закон синусов, чтобы найти недостающий угол?

Показать раствор

Каково соотношение между углом в числителе и стороной в знаменателе в законе синусов?

Какой тип треугольника приводит к неоднозначному случаю?

Показать раствор

Алгебраический

Для следующих упражнений предположим, что [латекс]\,\альфа \,[/латекс]противоположная сторона[латекс]\,а,\бета \,[/латекс]противоположная сторона[латекс]\, b,\,[/latex] и [латекс]\,\gamma \,[/latex]противоположная сторона[латекс]\,c.\,[/latex]Решите каждый треугольник, если это возможно. Округлите каждый ответ до десятых.

[латекс]\альфа=43°,\гамма=69°,а=20[/латекс]

[латекс]\альфа=35°,\гамма=73°,с=20[/латекс]

Показать решение

[латекс]\альфа =60°,\,\,\бета =60°,\,\гамма =60°[/латекс]

[латекс]а=4,\,\,\альфа =\, 60°,\,\beta =100°[/latex]

Показать решение

[латекс]b=10,\,\бета =95°,\гамма =\,30°[/латекс]

В следующих упражнениях используйте закон синусов, чтобы найти недостающую сторону для каждого косоугольного треугольника. . Округлите каждый ответ до сотых. Предположим, что угол[латекс]\,А\,[/латекс]противоположная сторона[латекс]\,а,\,[/латекс]угол[латекс]\,В\,[/латекс]противоположная сторона[латекс] \,b,\,[/latex]и угол[latex]\,C\,[/latex]является противоположной стороной[latex]\,c.[/latex]

Найти сторону[латекс]\,b\,[/латекс],когда[латекс]\,А=37°,\,\,В=49°,\,с=5.[/латекс]

Показать решение

Найти сторону[латекс]\,а[/латекс], когда[латекс]\,А=132°,С=23°,b=10.[/латекс]

Найти сторону[латекс]\,с\, [/latex]when[latex]\,B=37°,C=21°,\,b=23.[/latex]

Показать решение

В следующих упражнениях предположим, что [латекс]\,\альфа \,[/латекс]противоположная сторона[латекс]\,а,\бета \,[/латекс]противоположная сторона[латекс]\,b,\ ,[/latex]и[латекс]\,\гамма\,[/латекс]противоположная сторона[латекс]\,c.\,[/латекс]Определить, нет ли треугольника, один треугольник или два треугольника. Затем решите каждый треугольник, если это возможно. Округлите каждый ответ до десятых.

[латекс]\alpha =119°,a=14,b=26[/латекс]

[латекс]\gamma =113°,b=10,c=32[/латекс]

Показать решение

[латекс]b=3,5,\,\,c=5,3,\,\,\gamma =\,80°[/латекс]

[латекс]a=12,\,\,c=17,\ ,\,\alpha =\,35°[/latex]

Показать решение

[латекс]a=20,5,\,\,b=35,0,\,\,\beta=25°[/латекс]

[латекс]a=7,\,c=9,\,\,\ альфа =\,43°[/латекс]

Показать решение

[латекс]a=7,b=3,\beta=24°[/латекс]

[латекс]b=13,c=5,\gamma=\,10°[/латекс]

Показать решение

[латекс]a=2.3,c=1.8,\gamma=28°[/латекс]

[латекс]\beta=119°,b=8.2,a=11.3[/латекс]

Показать решение

В следующих упражнениях используйте закон синусов, чтобы найти недостающую сторону или угол для каждого треугольника или треугольников в неоднозначном случае. Округлите каждый ответ до десятых.

Найти угол[латекс]А[/латекс],когда[латекс]\,а=24,b=5,В=22°.[/латекс]

Найти угол[латекс]А[/латекс],когда[латекс] ]\,a=13,b=6,B=20°.[/латекс]

Показать решение

Найдите угол[латекс]\,В\,[/латекс],когда[латекс]\,А=12°,а=2,b=9.[/латекс]

Для следующих упражнений найдите площадь треугольник с заданными размерами. Округлите каждый ответ до десятых.

[латекс]a=5,c=6,\beta=\,35°[/латекс]

Показать решение

[латекс]b=11,c=8,\alpha=28°[/латекс]

[латекс]a=32,b=24,\gamma=75°[/латекс]

Показать решение

[латекс]a=7,2,b=4,5,\gamma=43°[/латекс]

Графический

Для следующих упражнений найдите длину стороны[латекс]\,х.\,[/латекс]Округлите до десятых.

Показать раствор

Показать раствор

Показать раствор

Для следующих упражнений найдите меру угла[латекс]\,х,\,[/латекс], если возможно. Округлите до десятых.

Показать раствор

Показать раствор

Обратите внимание, что [латекс]\,х\,[/латекс] — тупой угол.

Показать решение

В следующих упражнениях найдите площадь каждого треугольника. Округлите каждый ответ до десятых.

Показать раствор

Показать раствор

Показать раствор

Показать раствор

Расширения

Найдите радиус окружности на (рис.). Округлите до десятых.

Рис. 18.

Найдите диаметр окружности на (рис.). Округлите до десятых.

Рис. 19.

Показать решение

Найдите [латекс]\,m\угол АЦП\,[/латекс]в (Рисунок). Округлите до десятых.

Рисунок 20.

Найдите [латекс]\,AD\,[/латекс]в (рисунок). Округлите до десятых.

Рис. 21.

Показать решение

Решите оба треугольника на (Рисунок). Округлите каждый ответ до десятых.

Рис. 22.

Найдите[латекс]\,АВ\,[/латекс]в параллелограмме, показанном на (рис.).

Рисунок 23.

Показать решение

Решите треугольник на (Рисунок). (Подсказка: проведите перпендикуляр от [латекс]\,H\,[/латекс]к[латекс]\,JK).\,[/латекс]Округлите каждый ответ до десятых.

Рисунок 24.

Решите треугольник на (Рисунок). (Подсказка: проведите перпендикуляр от [латекс]\,N\,[/латекс]к[латекс]\,LM).\,[/латекс]Округлите каждый ответ до десятых.

Рис. 25.

Показать решение

На (Рисунок)[латекс]\,ABCD\,[/латекс]не является параллелограммом. [латекс]\,\угол m\,[/латекс]тупой. Решите оба треугольника. Округлите каждый ответ до десятых.

Рис. 26.

Реальные приложения

Столб отклоняется от солнца под углом [латекс]\,7°\,[/латекс] к вертикали, как показано на (рис.). Когда высота солнца составляет [латекс]\,55°,\,[/латекс] полюс отбрасывает тень длиной 42 фута на ровной поверхности. Какой длины столб? Округлите ответ до десятых.

Рис. 27.

Показать решение

Чтобы определить, насколько далеко лодка находится от берега, две радиолокационные станции, находящиеся на расстоянии 500 футов друг от друга, определяют углы от лодки, как показано на (Рисунок). Определите расстояние лодки от станции[latex]\,A\,[/latex]и расстояние лодки от берега. Округлите свои ответы до ближайшего целого фута.

Рисунок 28.

(Рисунок) показывает спутник, вращающийся вокруг Земли. Спутник проходит прямо над двумя станциями слежения [латекс]\,А\,[/латекс]и[латекс]\,В,\,[/латекс], которые находятся на расстоянии 69 миль друг от друга.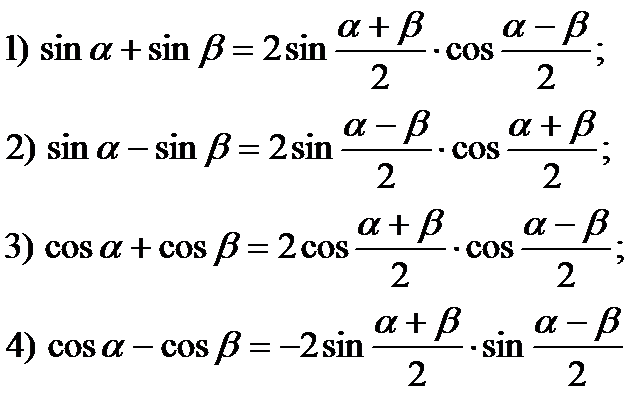 Когда спутник находится по одну сторону от двух станций, углы места в точках [латекс]\,А\,[/латекс] и [латекс]\,В\,[/латекс] измеряются как [латекс]\ ,86,2°\,[/латекс] и [латекс]\,83,9°,\,[/латекс] соответственно. Как далеко находится спутник от станции[latex]\,A\,[/latex]и на какой высоте находится спутник над землей? Округлите ответы с точностью до целой мили.

Рисунок 29.

Показать решение

Башня связи расположена на вершине крутого холма, как показано на (Рисунок). Угол наклона холма составляет[латекс]\,67°.\,[/латекс]К вершине башни и к земле в 165 метрах вниз по склону от основания башни должна быть прикреплена оттяжка. Угол, образованный оттяжкой и холмом, равен[latex]\,16°.\,[/latex]Найдите длину троса, необходимого для оттяжки, с точностью до целого метра.

Рис. 30.

Крыша дома расположена под углом [латекс]\,20°\,[/латекс]. 8-футовая солнечная панель должна быть установлена ​​на крыше и должна быть расположена под углом [латекс]\,38°\,[/латекс] по отношению к горизонтали для достижения оптимальных результатов. (См. (Рисунок)). Какой длины должна быть вертикальная опора, удерживающая заднюю часть панели? Округлите до десятых.

Рис. 31.

Показать решение

Аналогично углу подъема, угол наклона — острый угол, образованный горизонтальной линией и линией визирования наблюдателя на объект ниже горизонтали. Летчик летит по прямой трассе. Он определяет углы наклона к двум верстовым столбам, расположенным на расстоянии 6,6 км друг от друга, как [латекс]\,37°[/латекс] и [латекс]\,44°,[/латекс], как показано на (рис.). Найдите расстояние от точки [латекс]\,А\,[/латекс] до ближайшей десятой доли километра.

Рис. 32.

Пилот летит над прямой трассой. Он определяет углы падения к двум верстовым столбам, отстоящим друг от друга на 4,3 км, равными 32° и 56°, как показано на (рис.). Найдите расстояние от точки [латекс]\,А\,[/латекс] до ближайшей десятой доли километра.

Рисунок 33.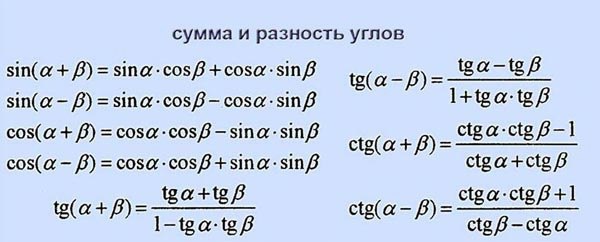

Показать решение

Чтобы оценить высоту здания, два ученика встают на определенном расстоянии от здания на уровне улицы. Отсюда они находят, что угол подъема от улицы до верха здания равен 39°. Затем они приближаются к зданию на 300 футов и обнаруживают, что угол подъема равен 50°. Предполагая, что улица ровная, оцените высоту здания с точностью до фута.

Чтобы оценить высоту здания, два ученика встают на определенном расстоянии от здания на уровне улицы. Отсюда они находят угол подъема от улицы до верха здания равным 35°. Затем они приближаются к зданию на 250 футов и обнаруживают, что угол возвышения составляет 53°. Предполагая, что улица ровная, оцените высоту здания с точностью до фута.

Показать решение

Точки[латекс]\,А\,[/латекс]и[латекс]\,В\,[/латекс]на противоположных сторонах озера. Точка[латекс]\,С\,[/латекс]находится в 97 метрах от[латекс]\,А.\,[/латекс]Мера угла[латекс]\,ВАС\,[/латекс] определяется как 101°, а мера угла [латекс]\,ACB\,[/латекс] определяется как 53°.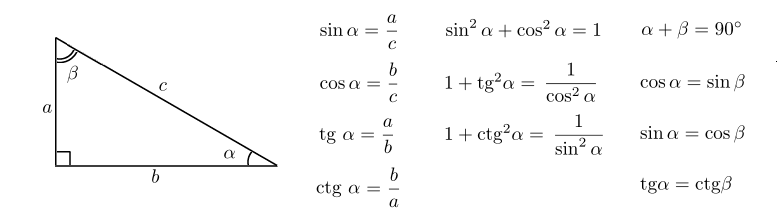 Каково расстояние от [латекс]\,А\,[/латекс]до[латекс]\,В,\,[/латекс], округленное до ближайшего целого метра?

Мужчина и женщина, стоящие[latex]\,3\frac{1}{2}\,[/latex]мили друг от друга, одновременно замечают воздушный шар. Если угол подъема от мужчины до воздушного шара равен 27°, а угол подъема от женщины к воздушному шару равен 41°, найдите высоту воздушного шара с точностью до ближайшего фута.

Показать решение

Две поисковые группы обнаруживают застрявшего в горах альпиниста. Первая поисковая группа находится в 0,5 мили от второй поисковой группы, и обе группы находятся на высоте 1 мили. Угол возвышения от первой поисковой группы до севшего на мель альпиниста составляет 15°. Угол возвышения от второй поисковой группы до альпиниста 22°. На какой высоте находится альпинист? Округлите до ближайшей десятой мили.

Уличный фонарь установлен на столбе. Мужчина ростом 6 футов стоит на улице недалеко от столба, отбрасывая тень. Угол возвышения от кончика тени человека до макушки его головы 28°. Женщина ростом 6 футов стоит на той же улице с противоположной от мужчины стороны столба. Угол возвышения от кончика ее тени до макушки составляет 28°. Если мужчина и женщина находятся на расстоянии 20 футов друг от друга, как далеко уличный фонарь от кончика тени каждого человека? Округлите расстояние до ближайшей десятой доли фута.

Показать решение

Три города,[латекс]\,А,В,[/латекс]и[латекс]\,С,[/латекс]расположены так, что город[латекс]\,А\,[/латекс]находится строго на восток города[латекс]\,В.\,[/латекс]Если город[латекс]\,С\,[/латекс] расположен в 35° к западу от севера от города[латекс]\,В\,[/латекс] и находится в 100 милях от города[латекс]\,А\,[/латекс]и в 70 милях от города[латекс]\,В,[/латекс]как далеко находится город[латекс]\,А\,[/латекс] from city[latex]\,B?\,[/latex]Округлите расстояние до ближайшей десятой мили.

Две улицы пересекаются под углом 80°. На углу строится парк в форме треугольника. Найдите площадь парка, если вдоль одной дороги длина парка составляет 180 футов, а по другой дороге — 215 футов.

Показать решение

Дом Брайана находится на угловом участке. Найдите площадь переднего двора, если стороны имеют размеры 40 и 56 футов, как показано на (рис.).

Рисунок 34.

Бермудский треугольник — это регион Атлантического океана, соединяющий Бермудские острова, Флориду и Пуэрто-Рико. Найдите площадь Бермудского треугольника, если расстояние от Флориды до Бермудских островов составляет 1030 миль, расстояние от Пуэрто-Рико до Бермудских островов составляет 980 миль, а угол между двумя расстояниями равен 62°.

Показать решение

Знак доходности имеет размеры 30 дюймов со всех трех сторон. Какова площадь знака?

Наоми купила современный обеденный стол со столешницей в форме треугольника. Найдите площадь столешницы, если две стороны имеют размеры 4 фута и 4,5 фута, а меньшие углы равны 32° и 42°, как показано на (рис. ).

Рис. 35.

Показать решение

Глоссарий

высота над уровнем моря

перпендикулярная линия из одной вершины треугольника к противоположной стороне или, в случае тупоугольного треугольника, к прямой, содержащей противоположную сторону, образующая два прямоугольных треугольника

неоднозначный случай

сценарий, в котором более чем один треугольник является допустимым решением для данного наклонного треугольника SSA

Закон синусов

утверждает, что отношение измерения одного угла треугольника к длине его противоположной стороны равно двум оставшимся отношениям измерения угла к противоположной стороне; любая пара пропорций может быть использована для определения отсутствующего угла или стороны 90 582

косой треугольник

любой треугольник, не являющийся прямоугольным

Тригонометрический метод R | Brilliant Math & Science Wiki

Адитья Вирани, Александр Кац, и Чимин Хим внес

Содержание

• Формальное заявление и доказательство
• Использование метода R 92=4\) и \(\arctan\frac{1}{\sqrt{3}}=\frac{\pi}{6},\) имеем \[\sin\frac{\pi}{6}+\sqrt{3}\cos\frac{\pi}{6}=2\cos\left(\frac{\pi}{6}-\frac{ \pi}{6}\right)=2\cos0=2. \ _\квадрат\]

  20 25 30 35

  Если \(\sqrt{3}\cos \theta-\sin \theta=\frac{1}{3}\) и \(0 < \theta < \frac{\pi}{2},\ ) значение \(\sqrt{3}\sin\theta+\cos\theta\) может быть выражено как \(\frac{\sqrt{a}}{3}\). Каково значение \(а?\) 92=4\) и \(\arctan\frac{-1}{\sqrt{3}}=-\frac{\pi}{6},\) имеем

  \[\begin{выравнивание} \sqrt{3}\sin x-\cos x=2\sin\left(x-\frac{\pi}{6}\right)&=\sqrt{2}\\ \стрелка вправо \sin\left(x-\frac{\pi}{6}\right)&=\frac{\sqrt{2}}{2}. \конец{выравнивание}\]

  Пусть \(x-\frac{\pi}{6}=\theta.\) Учитывая \(-\pi

  \[\begin{выравнивание} x-\frac{\pi}{6}=\frac{\pi}{4}&\ подразумевает x=\frac{5}{12}\pi\\ x-\frac{\pi}{6}=\frac{3}{4}\pi&\ подразумевает x=\frac{11}{12}\pi. \конец{выравнивание}\]

  Следовательно, ответ равен \(x=\frac{5}{12}\pi, \frac{11}{12}\pi.\) \(_\square\)

  При использовании метода R существует множество возможных значений \(R\) и \(\alpha,\), поскольку синус и косинус являются периодическими функциями. Добавление \(2n\pi\) к \(\alpha\) для любого целого числа \(n\) даст тот же ответ. Кроме того, добавление \((2n-1)\pi\) к \(\alpha\) для любого целого числа \(n\) и изменение знака \(R\) также будет эквивалентно ответу. Однако мы чаще всего используем \(-\frac{\pi}{2}<\alpha<\frac{\pi}{2}\) и \(R>0\) для удобства.

  Метод R часто используется для нахождения максимума или минимума уравнений в форме \(a\sin\theta+b\cos\theta.\) Известно, что \(-1\leq\sin x\ leq1\) и \(-1\leq\cos x\leq1\) для любого действительного числа \(x,\), поэтому максимум и минимум \(a\sin\theta+b\cos\theta\) равны \ (R\) и \(-R,\) соответственно.

  Найдите сумму максимального и минимального значений

  \[3\sin\left(x-\frac{\pi}{3}\right)-4\cos\left(x-\frac{\pi}{3}\right)+2.

  No related posts.