 2}4.
$$
2}4.
$$Заметно сложнее угадать формулу для суммы четвертых степеней. В отличие от предыдущих случаев, у $S_4(n)$ практически не видно общих делителей с $S_1(n)$ (кроме двойки). Зато можно заметить, что 14 и 98 делятся на 7, 55 и 979 на 11… Посмотрим на отношение $S_4/S_2$.
| $n$ | 1 | 2 | 3 | 4 | 5 | 6 |
| $S_2$ | 1 | 5 | 14 | 30 | 55 | 91 |
| $S_4$ | 1 | 17 | 98 | 354 | 979 | 2275 |
| $S_4/S_2$ | 1 | 17/5 | 7 | 59/5 | 89/5 | 25 |
Видно, что после домножения этого отношения на 5 получится последовательность целых чисел: 5, 17, 35, 59, 89, 125… Тут уже нельзя сказать, что разность соседних чисел неизменна… Все же посмотрим на эти разности: 12, 18, 24, 30… — закономерность сразу видна!
Таким образом, гипотеза состоит в том, что
$$
S_4(n)/S_2(n)=
\frac{5+6\cdot2+6\cdot3+\ldots+6n}5=
\frac{6\frac{n(n+1)}2-1}5=
\frac{3n^2+3n-1}5,
$$
и соответственно
$$
S_4(n)=\frac{n(n+1)(2n+1)(3n^2+3n-1)}{30}. 2}6$ (т. е. значений
знаменитой дзета-функции), и в комбинаторике, и в теории
чисел, и в топологии…
2}6$ (т. е. значений
знаменитой дзета-функции), и в комбинаторике, и в теории
чисел, и в топологии…
Литература
- Д. Пойа. Математика и правдоподобные рассуждения (М.: Наука, 1975)
http://ilib.mccme.ru/djvu/polya/rassuzhdenija.htm
Мало где можно прочитать не о конкретной области математики, а о том, как вообще решать новую для себя математическую задачу. Подсказки и решение выше по существу следуют главе 7 этой замечательной книги. - Интервью с академиком И. М. Гельфандом // Квант, 1989, № 1, 3–12
http://kvant.mccme.ru/1989/01/akademik_izrail_moiseevich_gel.htm
В решении выше сделана попытка объяснить, как некоторые формулы для сумм степеней мог бы искать любой человек. Интересующимся математикой может быть интересно прочитать, как такую задачу решал в школьные годы один из выдающихся математиков 20 века (собственно про это — небольшой фразмент на стр. 8–9, но все интервью интересное). - В. С. Абрамович. Суммы одинаковых степеней натуральных чисел // Квант, 1973, № 5, 22–25
http://kvant. n)?
n)?06.02.2018, 13:13
25/11/08
449
Как можно посчитать сумму ряда ? С чего начинать? |
| pogulyat_vyshel |
| |||
27/12/17 |
| |||
| ||||
| B@R5uk |
| ||
26/05/12 |
| ||
| |||
| grizzly |
| |||
09/09/14 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 5 ] |
Модераторы: Модераторы Математики, Супермодераторы
Ряды
Ряды — это просто бесконечные суммы. Мы с ними уже несколько раз сталкивались
— например, когда обсуждали, что некоторые функции оказываются равны своим рядам
Тейлора (см. замечание 2 из
лекции 22). Пришло время поговорить про ряды
подробнее.
Мы с ними уже несколько раз сталкивались
— например, когда обсуждали, что некоторые функции оказываются равны своим рядам
Тейлора (см. замечание 2 из
лекции 22). Пришло время поговорить про ряды
подробнее.
28.1Сходящиеся и расходящие ряды
28.1.1Определения и примеры
Пусть есть какая-то последовательность {ak}.
Определение 1. Бесконечным рядом (или просто рядом) называется такая бесконечная сумма:
∞∑k=1ak=a1+a2+a3+….
Если вместо бесконечности взять первые n слагаемых, получится частичная сумма ряда:
Sn:=n∑k=1ak=a1+a2+…+an.
По определению, суммой ряда называется предел частичных сумм:
∞∑k=1ak:=limn→∞Sn=limn→∞n∑k=1ak.
Конечно, этот предел может существовать, а может не существовать. В первом случае ряд называется сходящимся, во втором — расходящимся.
Пример 1.
∞∑k=112k=12+14+18+…
сходится. Это геометрическая прогрессия со знаменателем, по модулю меньшим 1, но сходимость здесь можно увидеть и непосредственно. Если у вас была одна шоколадка, вы съели от неё половину, потом половину от оставшейся половины (то есть четверть), потом половины от того, что осталось (то есть одну возьмую) и т.д. — в пределе ничего не останется, но и больше, чем целую шоколадку, вы не съедите. Значит, сумма съеденных кусочков стремится к единице.
Рис. 28.1: Сумма бесконечной геометрической прогрессии «на шоколадках»
Пример 2. Ряд
∞∑k=1k2=1+4+9+16+…
расходится: поскольку все слагаемые больше или равны 1, частичные суммы неограничены: Sn≥n, и значит расходятся. Можно сказать, что сумма равна плюс бесконечности:
∞∑k=1k2=+∞.
28.1.2Геометрическая прогрессия
Важным примером рядов являются суммы геометрических прогрессий, то есть
последовательностей вида {b0qk}, где q называется знаменателем прогрессии.
Поскольку я никогда не могу запомнить формулу для суммы членов геометрической прогрессии и каждый раз вывожу её заново, приведу этот вывод и здесь.
Утверждение 1. Для всяких b0∈R, q≠1 и n∈N справедливо утверждение
n∑k=1b0qk=b0q1−qn1−q.
Доказательство. Вынесем b0q за знак суммирования, а потом сделаем замену индекса суммирования m=k−1:
n∑k=1b0qk=b0qn∑k=1qk−1=b0qn−1∑m=0qm.
Остаётся найти, чему равна сумма ∑n−1m=0qm. Обозначим её через S. Тогда
S=1+q+q2+…+qn−1qS=q+q2+…+qn−1+qn
Вычитая из первого равенства второе, получаем:
S−qS=1−qn,
S=1−qn1−q.
∎
Следствие 1. При |q|<1,
∞∑k=1b0qk=b0q1−q
поскольку в этом случае qn стремится к нулю при n стремящемся к
бесконечности. При |q|>1 при b0≠0 ряд расходится, поскольку qn
стремится к бесконечности. При q=1 последовательность является постоянной
и ряд расходится при b0≠0.
При |q|>1 при b0≠0 ряд расходится, поскольку qn
стремится к бесконечности. При q=1 последовательность является постоянной
и ряд расходится при b0≠0.
В примере 1, b0=1 и q=1/2, значит сумма равна
∞∑k=112k=1⋅121−12=1,
как и ожидалось.
28.1.3«Телескопические суммы»
Вообще есть мало сколь-нибудь универсальных способов нахождения бесконечных сумм в явном виде. Но чтобы вам не казалось, что нет никаких поддающихся анализу рядов, кроме геометрической прогрессии, обсудим ещё один тип.
Пример 3. Найдём сумму ряда∞∑k=11k(k+1).(28.1)
Для этого заметим, что
1k(k+1)=1k−1k+1.
Дальше хочется сделать такую штуку:
∞∑k=11k(k+1)=∞∑k=1(1k−1k+1)=(11−12)+(12−13)+(13−14)+…==11+(−12+12)+(−13+13)+…=11+0+0+…=1.
∞∑k=11k(k+1)=∞∑k=1(1k−1k+1)==(11−12)+(12−13)++(13−14)+…==11+(−12+12)++(−13+13)+…==11+0+0+…=1.
Это преобразование выглядит реалистично — в самом деле, нас учили, что при суммировании неважно, как расставлять скобки — однако таит в себе опасность. Рассмотрим, например, такой ряд:
∞∑k=1(−1)k=−1+1−1+…(28.2)
Его частичными суммами Sn будут числа −1 (при нечётных n) и 0 — при чётных. Мы знаем, что предела у такой последовательности нет. Однако, казалось бы, можно записать:
∞∑k=1(−1)k=−1+1−1+1−…=(−1+1)+(−1+1)+…=0+0+…=0.
∞∑k=1(−1)k=−1+1−1+1−…==(−1+1)+(−1+1)+…==0+0+…=0.
Впрочем, с тем же успехом мы могли бы получить и −1, если бы сгруппировали слагаемые иначе (первое оставили отдельно, а второе сгруппировали с третьим, четвертой с пятым и т.д.)
Пример с рядом ∑∞k=1(−1)k показывает, что бесконечные суммы
могут быть коварными — привычные нам операции типа группировки слагаемых
могут менять результат. Как же всё-таки найти сумму ряда (28. 1)?
1)?
Если мы не уверены, что некоторое преобразование сработает с бесконечным рядом, мы можем вернуться в ту область, где всё просто и понятно — в область конечных сумм. Давайте рассмотрим частичные суммы этого ряда:
n∑k=11k(k+1)=11−12+12−13+…+1n−1−1n+1n−1n+1.
n∑k=11k(k+1)=11−12+12−13+…++1n−1−1n+1n−1n+1.
Тут уже скобки не важны, потому что группировка слагаемых в конечных суммах не меняет их значения. Мы видим, что слагаемые (−1/2) и 1/2 сокращаются, и дальше сократятся все пары слагаемых, заканчивая (−1/n) и 1/n. Останется только первое и последнее слагаемое. (Если вы чувствуете малейшие сомнения в этом месте, подставьте какое-нибудь небольшое конкретное n — например, n=3, и проследите, как это работает.) Итак:
n∑k=1=11−1n+1
и значит предел частичных сумм равен 1. То есть наше вычисление дало
правильный результат, и теперь мы это аккуратно обосновали. (Проверьте, что
будет, если попытаться применить то же самое рассуждение к ряду
(28. 2).)
2).)
Суммы такого вида, у которых слагаемые последовательно сокращаются, иногда называют «телескопическими» — в процессе сокращения сумма как бы складывается, как складная подзорная труба или телескоп.
28.1.4Простейшие свойства
Как показвает пример с рядом (28.2), не все привычные нам операции с конечными суммами можно применять к рядам. Однако, некоторые всё-таки можно.
Утверждение 2. Пусть ряды ∑∞k=1ak и ∑∞k=1bk сходятся и c∈R — какая-то константа. Тогда
- ∞∑k=1(ak+bk)=∞∑k=1ak+∞∑k=1bk.
- ∞∑k=1(cak)=c∞∑k=1ak.
Доказательство. Это прямое следствие из аналогичных свойств пределов. Докажем, например, первое свойство. Рассмотрим n-ю частичную сумму:
n∑k=1(ak+bk)=(a1+b1)+(a2+b2)+…+(an+bn)=…
n∑k=1(ak+bk)=(a1+b1)+(a2+b2)+…++(an+bn)=…
Это конечная сумма, в ней можно раскрывать скобки и переставлять слагаемые,
как нас учат в школе. Поэтому можно продолжить равенство:
Поэтому можно продолжить равенство:
…=(a1+a2+…+an)+(b1+b2+…+bn)=n∑k=1ak+n∑k=1bk.
…=(a1+a2+…+an)++(b1+b2+…+bn)==n∑k=1ak+n∑k=1bk.
Значит
∞∑k=1(ak+bk)=limn→∞n∑k=1(ak+bk)=limn→∞(n∑k=1ak+n∑k=1ak)==limn→∞n∑k=1ak+limn→∞n∑k=1bk=∞∑k=1ak+∞∑k=1bk.
∞∑k=1(ak+bk)=limn→∞n∑k=1(ak+bk)==limn→∞(n∑k=1ak+n∑k=1ak)==limn→∞n∑k=1ak+limn→∞n∑k=1bk==∞∑k=1ak+∞∑k=1bk.
В третьем равенства мы использовали теорему о пределе суммы.
Второе свойство доказывается аналогично, запишите доказательство самостоятельно.∎
28.2Признаки сходимости и расходимости
28.2.1Необходимое условие сходимости: члены стремятся к нулю
Утверждение 3. Если ряд ∑∞k=1ak сходится, то
limn→∞an=0.
Доказательство. Обозначим через Sn частичную сумму нашего ряда:
Sn:=n∑k=1ak.
Тогда для всех n>1
an=Sn−Sn−1.
Рассмотрим предел последовательности {an}:
limn→∞an=limn→∞(Sn−Sn−1)=limn→∞Sn−limn→∞Sn−1,
но пределы Sn и Sn−1 — это фактически один и тот же предел (во втором случае последовательность просто сдвинута на один элемент вправо, но предел от этого не изменился). И оба предела существуют, потому что по определению, предел частичных сумм — это сумма ряда, а ряд сходится. Обозначим сумму ряда за S. Тогда
limn→∞an=S−S=0.
∎
28.2.2Гармонический ряд
Условие an→0 является необходимым для сходимости ряда, но является ли оно достаточным? Оказывается, нет. Приведём в качестве примере известный гармонический ряд.
Утверждение 4. Ряд
∞∑k=11k=11+12+13+…(28.3)
расходится.
Доказательство. Заметим, что
12≥1213+14≥2⋅14=1215+16+17+18≥4⋅18=1219+110+111+112+113+114+115+116≥8⋅116=12
12≥1213+14≥2⋅14=1215+16+17+18≥4⋅18=1219+110+111+112+113+114+115+116≥8⋅116=12
Каждая из сумм в левой части не меньше, чем своё последнее слагаемое (самое
маленькое) умножить на число слагаемых. Понятно, что так можно продолжать и
дальше. Для произвольного натурального m возьмём слагаемые с номерами от
2m+1 до 2m+1. Их количество равно разности между этими двумя
числами, плюс один. (Потому что и первое и последнее число включатся в
подсчёт: например, если бы эти числа совпадали, разность равнялась нулю, но
при этом одно слагаемое мы бы взяли.) Значит, общее число слагаемых равно
Понятно, что так можно продолжать и
дальше. Для произвольного натурального m возьмём слагаемые с номерами от
2m+1 до 2m+1. Их количество равно разности между этими двумя
числами, плюс один. (Потому что и первое и последнее число включатся в
подсчёт: например, если бы эти числа совпадали, разность равнялась нулю, но
при этом одно слагаемое мы бы взяли.) Значит, общее число слагаемых равно
2m+1−(2m+1)+1=2m+1−2m=2m(21−1)=2m
2m+1−(2m+1)+1=2m+1−2m==2m(21−1)=2m
и каждое слагаемое не меньше последнего, то есть 1/2m+1. Итак:
2m+1∑k=2m+11k≥2m12m+1=12.(28.4)
Возьмём первые 2N слагаемых ряда (28.3). В них есть первое слагаемое, равное 1/1, и ещё N «блоков» вида (28.4), каждый из которых не меньше 1/2. Значит, их сумма не меньше, чем N12+1 и стремится к бесконечности. Значит, ряд расходится.∎
28.2.3Признак сравнения
Ну хорошо, у нас есть необходимое условие сходимости — может быть, есть и
какие-то достаточные? Да, есть.
Теорема 1. Рассмотрим два ряда:
∞∑k=1ak,∞∑k=1bk.
Если известно, что для всех натуральных k верны неравенства
0≤ak≤bk(28.5)
и ряд
∞∑k=1bk(28.6)
сходится, то ряд
∞∑k=1ak(28.7)
тоже сходится.
Доказательство. Доказательство полностью аналогично доказательству похожей теоремы для несобственных интегралов. Попробуйте написать его самостоятельно.
Узнать ответ
Верный ответ.
Обозначим сумму ряда (28.6) через B, частичные суммы
ряда (28.6) через Bn, а частичные суммы ряда
(28.7) через An. Поскольку все слагаемые
неотрицательны, обе последовательности {An} и {Bn}
неубывают. Также в силу (28.5), для всех n, An≤Bn. С другой стороны, в силу неубывания, все элементы Bn не
превосходят предела B (если бы какой-то элемент перескочил
через предел, все следующие элементы были бы отделены от предела
и не могли бы к нему стремиться). Значит, для всех n, An≤Bn≤B и значит последовательность {An} является
неубывающей и ограниченной. Значит, по теоремe
Вейерштрасса, у неё есть предел.
Значит, для всех n, An≤Bn≤B и значит последовательность {An} является
неубывающей и ограниченной. Значит, по теоремe
Вейерштрасса, у неё есть предел.
∎
Пример 4. Докажем, что ряд
∞∑k=11kk
сходится. Действительно, для всех k≥2, kk≥2k и следовательно 1/kk≤1/2k. Никакое конечное число начальных членов на сходимость ряда не влияет и значит в признаке сравнения достаточно выполнения неравенства для всех k, начиная с некоторого. А ряд
∞∑k=112k
сходится. Значит, и наш ряд сходится.
Пример 5. Докажем, что ряд
∞∑k=1lnkk(28.8)
расходится. Действительно, для всех k≥3, lnk≥1 и следовательно
1k≤lnkk.
Но если бы ряд (28.8) сходился, тогда и ограниченный им ряд
∑∞k=11/k тоже сходился бы. Но мы знаем, что последнее
неверно. Значит, наш ряд расходится.
Значит, наш ряд расходится.
28.2.4Интегральный признак сходимости
Как мы уже отмечали, между несобственными интегралами и рядами много общего. При этом анализировать интегралы часто проще, чем ряды — есть разнообразные способы преобразования интегралов, которые к рядам применяются плохо. К счастью, есть теорема, которая позволяет переносить результаты о сходимости интегралов на ряды и наоборот.
Теорема 2. Пусть функция f:[1,+∞)→R невозрастает, неотрицательна и интегрируема на любом отрезке [a,t], t>a. В этих условиях ряд
n∑k=1f(k)(28.9)
сходится тогда и только тогда, когда сходится несобственный интеграл
∫∞1f(x)dx.(28.10)
Доказательство.
Если интеграл сходится, то и ряд тоже сходится. Построим график
функции y=f(x). Мы хотим представить сумму ряда (28.9) в виде
некоторой площади, чтобы сравнить её с площадью, которая соответствует
интегралу (28.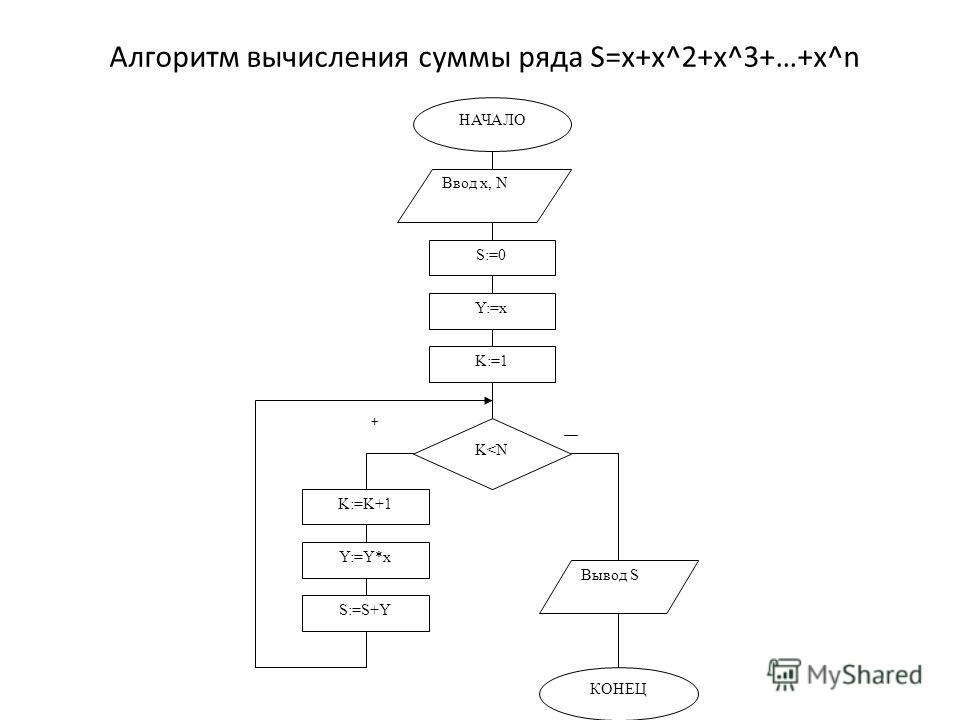 10). Для этого над каждым отрезком [k−1,k]
построим прямоугольник высотой f(k), k=1,2,….
10). Для этого над каждым отрезком [k−1,k]
построим прямоугольник высотой f(k), k=1,2,….
Рис. 28.3: Интеграл оценивает сумму ряда, начиная со второго слагаемого
Площадь k-го прямоугольника равна f(k), сумма всех площадей равна сумме ряда. Все прямогольники, кроме первого, находятся не выше графика функции: в силу неубывания на каждом отрезке [k−1,k] значение функции не меньше f(k). Разобьём наш ряд в сумму первого члена и всех остальных:
∞∑k=1=f(1)+∞∑k=2f(k).
Слагаемое f(1) не меняет сходимости ряда, и значит достаточно изучить сходимость ∑∞k=2f(k). Любая частичная сумма этого ряда не превосходит значение интеграла (28.10) и последовательность частичных сумм неубывает в силу неотрицательности f. Значит, последовательность частичных сумм имеет предел и ряд сходится.
Формально можно записать так. Заметим, что
∞∑k=2f(k)=∫+∞1f(⌈x⌉)dx,(28.11)
где ⌈x⌉ — окугление «вверх» от числа x. Этот интеграл равен
площади суммы всех прямоугольников, которую мы обсуждали выше (на каждом
полуинтервале (k−1,k] мы интегрируем константу f(k)). С другой стороны,
⌈x⌉≥x и значит f(⌈x⌉)≤f(x). По признаку
сравнения для интегралов, если интеграл (28.10)
сходится, то и интеграл (28.11) сходится.
С другой стороны,
⌈x⌉≥x и значит f(⌈x⌉)≤f(x). По признаку
сравнения для интегралов, если интеграл (28.10)
сходится, то и интеграл (28.11) сходится.
Если ряд сходится, то и интеграл сходится. Доказательство полностью аналогично, только всю картинку с прямоугольниками нужно сдвинуть на одну позицию вправо. То есть на отрезке [k,k+1] нужно построить прямоугольник высотой f(k). Теперь верхние стороны наших прямуогльники будут ограничивать график функции y=f(x) сверху, и из сходимости ряда будет следовать сходимость интеграла.
Рис. 28.4: Сумма ряда оценивает интеграл сверху
Формально, можно записать:
∞∑k=1f(k)=∫+∞1f(⌊x⌋)dx,(28.12)
гда ⌊x⌋ — округление вниз числа x, и использовать неравенство f(⌊x⌋)≥f(x). Значит ряд ограничивает интеграл и из сходимости ряда следует сходимость интеграла.∎
Пример 6. Докажем, что ряд
∞∑k=11k2(28.13)
сходится.
Действительно, этот ряд можно представить в виде ряда ∑∞k=1f(k), где f(x)=1/x2 — невозрастающая неотрицательная функция. Значит сходимость этого ряда эквивалентна сходимости интеграла
∫∞11x2dx.
Но мы уже доказывали, что этот интеграл сходится. Значит, ряд тоже сходится.
28.2.5Знакочередующиеся ряды
Признаки сравнения, обсуждающиеся выше, применимы к рядам с неотрицательными членами. Легко придумать их аналоги для рядов, чьи члены всегда неположительны. Если условие знакопостоянства верно для всех членов, начиная с некоторого, эти признаки тоже работают: никакое конечное число первых членов на сходимость ряда не влияют.
Можно ли что-то сказать в том случае, когда среди членов ряда есть бесконечно много положительных и бесконечно много отрицательных членов (такие ряды называют знакопеременными)? В некоторых случаях — можно.
Определение 2. Пусть ak — некоторая последовательность с положительными членами.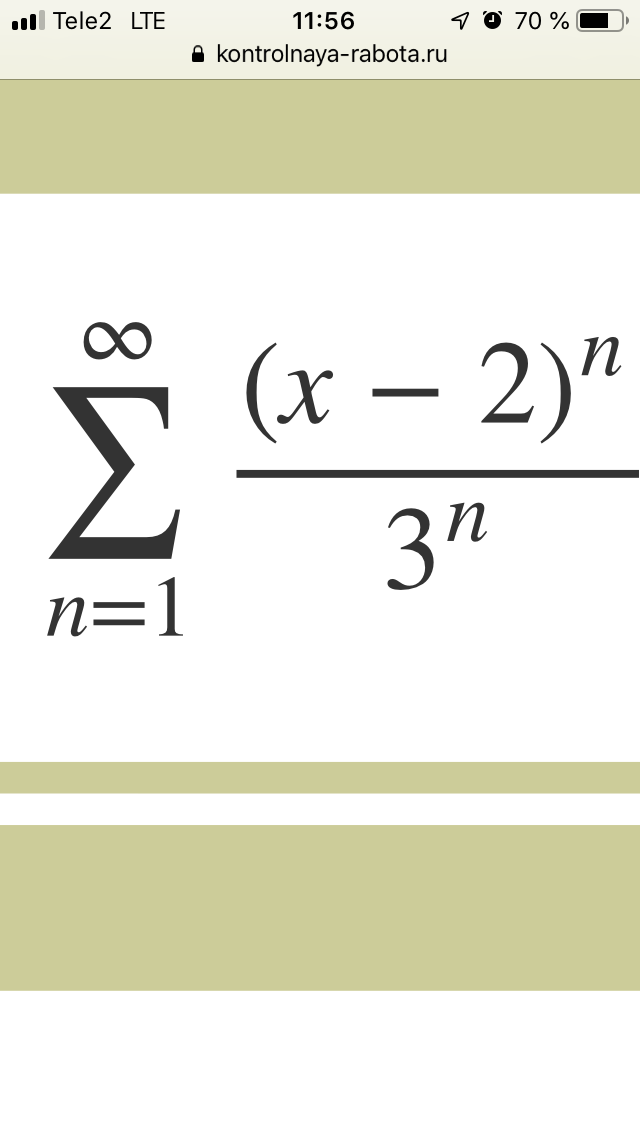 Рассмотрим ряд
Рассмотрим ряд
∞∑k=1(−1)k+1ak.(28.14)
Он называется знакочередующимся. Также можно поставить коэффициент (−1)k, получится тоже знакочередующийся ряд.
Про знакочередующиеся ряды обычно просто сказать, сходятся они или нет: необходимое условие сходимости в этом случае почти совпадает с достаточным (но не совсем совпадает, нужно дополнительное условие).
Теорема 3. (Признак Лейбница.) Пусть для знакочередующегося ряда (28.14) модули членов невозрастают, то есть для всех k, ak+1≤ak. Если при этом
limk→∞ak=0,
то ряд сходится.
Доказательство. Обозначим частичные суммы ряда через Sn. Тогда S1=a1, S2=a1−a2, S3=a1−a2+a3 и т.д. Будем откладывать эти точки на числовой прямой, см. рис. 28.5.
Вот мы отложили точку S1. Затем нужно сдвинуться влево на a2, чтобы
получить S2. Отсюда нужно сдвинуться вправо на a3, чтобы получить
S3. Может ли оказаться, что мы «перескочим» при этом S1? Нет, потому
что последовательность ak невозрастает, и значит a3≤a2, то есть
сдвиг от S2 до S3 не превосходит длину отрезка [S2,S1]. Значит
точка S3 лежит в отрезке [S2,S1].
Может ли оказаться, что мы «перескочим» при этом S1? Нет, потому
что последовательность ak невозрастает, и значит a3≤a2, то есть
сдвиг от S2 до S3 не превосходит длину отрезка [S2,S1]. Значит
точка S3 лежит в отрезке [S2,S1].
Рис. 28.5: Частичные суммы знакочередующегося ряда с убывающими членами
Следующий шаг должен быть влево, и поскольку a4≤a3, точка S4 лежит на отрезке [S2,S3]. И так далее.
Можно построить последовательность вложенных отрезков {Ik}, определяемых следующим образом:
Ik=[min(Sk,Sk+1),max(Sk,Sk+1)],
то есть концы k-го отрезка — это просто частичные суммы
(k-я и k+1-я), записанные в правильном порядке (та, что больше, справа,
а та, что меньше, слева).
Тогда
I1=[S2,S1],I2=[S2,S3],I3=[S4,S3],I4=[S4,S5],
и т.д. По построению, Ik+1⊂Ik и |Ik|=ak+1→0 при
k→0. Значит по лемме о вложенных
отрезках существует единственная точка c,
принадлежащая всем Ik, и концы отрезков стремятся к c. Но концами
являются наши предельные суммы и значит если они стремятся к c, то ряд
сходится к c.∎
Но концами
являются наши предельные суммы и значит если они стремятся к c, то ряд
сходится к c.∎
Пример 7. Ряд
∞∑k=1(−1)k+1k(28.15)
является сходящимся.
28.3Абсолютная и условная сходимость
Определение 3. Рассмотрим ряд
∞∑k=1ak.(28.16)
Если ряд из модулей
∞∑k=1|ak|
сходится, ряд (28.16) называется абсолютно сходящимся.
Утверждение 5. Если ряд сходится абсолютно, то он сходится. (Звучит забавно, но, действительно, в определении абсолютной сходимости ничего не сказано про то, сходится сам ряд, или нет — сказано только про ряд из модулей.)
Доказательство. Докажите самостоятельно. Подсказка: пусть bn=an+|an|. Тогда bn≥0 и bn≤2|an|. Но an=bn−|an|.∎
Определение 4. Если ряд сходится, но не является абсолютно сходящимся, говорят, что он сходится условно.
Пример 8. Ряд (28.15) сходится условно, потому что соответствующий ему ряд из модулей является гармоническим (см. (28.3)) и расходится.
Оказывается, что абсолютно и условно сходящиеся ряды ведут себя существенно по-разному — некоторые естественные операции можно безопасно делать с абсолютно сходящимися рядами, но нельзя с условно сходящимися. В частности, для условно сходящихся рядов не действует принцип «от перемены мест слагаемых сумма не меняется».
Определение 5. Биективное отображение φ:N→N называется перестановкой натурального ряда.
Если задана какая-то перестановка натурального ряда φ, с её помощью можно из ряда
∞∑k=1ak
изготовить ряд
∞∑k=1aφ(k),
то есть ряд, члены которого совпадают с {ak}, но их порядок изменён с помощью перестновки φ.
Теорема 4. В результате перестановок членов абсолютно сходящегося ряда его сумма не меняется.
Набросок доказательства. Если ряд имеет только положительные элементы, легко показать, что частичные
суммы переставленного ряда оцениваются частичными суммами исходного, и
наоборот. Ряд с положительными и отрицательными членами можно представить
как разность двух рядов с положительными членами.∎
Если ряд имеет только положительные элементы, легко показать, что частичные
суммы переставленного ряда оцениваются частичными суммами исходного, и
наоборот. Ряд с положительными и отрицательными членами можно представить
как разность двух рядов с положительными членами.∎
Теорема 5. (Римана) Пусть есть какой-то условно сходящийся ряд ∑∞k=1ak. Тогда выбором подходящей перестановки его членов можно получить ряд с любой заранее заданной суммой. Иными словами, для всякого c найдётся такая перестановка φ, что в результате этой перестановки получается ряд, сумма которого равна c.
Доказательство.
Положительные и отрицательные члены. Будем для простоты считать, что в исходном ряду нет нулевых членов — если они есть, на сумму они никак не влияют, и в силу расходимости ряда из модулей, количество ненулевых членов не может быть конечным.
Ключевой момент доказательства состоит в том, чтобы отдельно рассмотреть
положительные и отрицательные члены ряда. Для этого введём такие
обозначения:
Для этого введём такие
обозначения:
a+k:={ak,ak>0,0,ak<0,,a−k:={0,ak>0,ak,ak<0.
Тогда ряд
∞∑k=1a+k(28.17)
состоит только из его положительных слагаемых исходного ряда, а
∞∑k=1a−k(28.18)
только из отрицательных. Заметим, что
ak:=a+k+a−k,|ak|=a+k−a−k.
Докажем, что оба ряда (28.17) и (28.18) расходятся. Действительно, пусть, например, ряд ∑∞k=1a+k сходится (другой случай рассматривается так же). Тогда
∞∑k=1a−k=∞∑k=1(ak−a+k)=∞∑k=1ak−∞∑k=1a+k
тоже сходится, как разность сходящихся рядов (см. утверждение 2). Но в этом случае и ряд
∞∑k=1|ak|=∞∑k=1(a+k−a−k)=∞∑k=1a+k−∞∑k=1a−k
тоже сходится, а это противоречит предположению, что исходный ряд ∑∞k=1ak сходится лишь условно, а не абсолютно.
Итак, оба ряда (28.18) и (28.17) расходятся. Первый состоит
только из неотрицательных слагаемых. Единственный способ, каким он может
расходиться, то есть не иметь предела — это стремиться к плюс бесконечности.
Действительно, последовательность частичных сумм {S+N} неубывает.
Она не может быть ограниченной сверху, поскольку неубывающая ограниченная
сверху последовательность имеет предел по теореме
Вейерштрасса 2. Значит, она не является ограниченной, то
есть для всякого C найдётся такое N, что S+N>C. Но в силу
неубывания, для всех n>N, S+n≥S+N>C. Значит, S+n→+∞ при n→∞.
Первый состоит
только из неотрицательных слагаемых. Единственный способ, каким он может
расходиться, то есть не иметь предела — это стремиться к плюс бесконечности.
Действительно, последовательность частичных сумм {S+N} неубывает.
Она не может быть ограниченной сверху, поскольку неубывающая ограниченная
сверху последовательность имеет предел по теореме
Вейерштрасса 2. Значит, она не является ограниченной, то
есть для всякого C найдётся такое N, что S+N>C. Но в силу
неубывания, для всех n>N, S+n≥S+N>C. Значит, S+n→+∞ при n→∞.
Аналогично доказывается, что ряд (28.18) стремится к минус бесконечности.
Точная подгонка. Пусть из последовательности {a+k} выкинули все нулевые члены. Подпоследовательность, составленную из оставшихся членов, назовём {b+m}. Порядок следования членов последовательности {b+m} — такой же, как в {a+k}, просто все нулевые пропущены.
Аналогично определим последовательность {b−l} — последовательность
из всех ненулевых членов {a−k}, идущих в том же порядке, в котором они
были.
Иными словами, {b+m} и {b−l} — это последовательности положительных и отрицательных членов исходной последовательности {ak}.
Эта лекция читается в конце декабря, так что можно представить себе, что {b+m} — это мешок с бесконечным количеством подарков, каждый подарок имеет свой размер, влияющий на то, насколько повышается настроение у человека, которому вы его дарите. Про этот мешок вы знаете, что подарки в нём пронумерованы, и что мешок этот бесконечно большой, подарков в нём достаточно, чтобы поднять настроение на любой уровень.
Тогда {b−l} — это мешок антиподарков, которые снижают настроение, а не повышают его. Подарки в нём также пронумерованы и имеют в совокупности неограниченный потенциал для снижения настроения.
Пусть теперь нам задано какое-то число c∈R. Мы будем
выписывать элементы последовательностей b+m и b−l таким образом,
чтобы сумма выписанных элементов стремилась к c. Каждый элемент будет
выписан ровно один раз, и до любого элемента мы рано или поздно доберёмся.
Алгоритм устроен так. Допустим, c≥0, обратный случай рассматривается аналогично. Мы начинаем из точки 0 и будем выписывать элементы из последовательности {b+m} по порядку, до тех пор, пока сумма выписанных элементов не превзойдёт c. Если в какой-то момент эта сумма попала ровно в c, выпишем ещё один элемент. Визуально это соответствует тому, что мы делаем скачки вправо на величину b+1, b+2 и т.д., до тех пор, пока не «перескочим» через c.
Как только это произошло, мы меняем направление. Теперь будем выписывать элементы из последовательности {b−l} по порядку. Они отрицательные, поэтому сумма всех выписанных элементов будет каждый раз сдвигаться влево на модуль очередного выписанного элемента. В какой-то момент мы перескочим через c (теперь в обратном направлении, слева направо). Сразу после этого нужно снова сменить направление движения.
Теперь мы опять должны выписывать элементы из {b+m}, продолжая ровно
с того места, где остановились в прошлый раз. Если последний выписанный нами
на предыдущем этапе элемент был {b+m1}, то начать надо с элемента
{b+m1+1}. И снова мы выписываем элементы из {b+m} до тех
пор, пока сумма всех элементов (включая все выписанные ранее) не превзойдёт
c. В этот момент мы снова переключимся, и будем так продолжать до
бесконечности.
И снова мы выписываем элементы из {b+m} до тех
пор, пока сумма всех элементов (включая все выписанные ранее) не превзойдёт
c. В этот момент мы снова переключимся, и будем так продолжать до
бесконечности.
Почему этот алгоритм работает.
Я утверждаю, что описанный нами алгоритм реализует искомую перестановку — а именно, что получится последовательность, которая является перестановкой исходной последовательности {ak}, и что предел её частичных сумм равен c.
Во-первых, этот алгоритм никогда не остановится, и будет делать бесконечное
количество переключений между движением вправо и движением влево. Почему
так? Потому что сумммы (28.17) и (28.18) расходятся, и
значит в наших «мешках с подарками и антиподарками» подарков достаточно,
чтобы сделать сколь угодно хорошее и сколь угодно плохое настроение. Более
того, поскольку начальные члены ряда не влияют на сумму, эти свойства
сохранятся и после того, как какое-то конечное количество слагаемых из
последовательностей {b+m} и {b−l} было выписано. Значит мы
всегда можем взять достаточно много элементов из «хвостов» этих
последовательностей, чтобы сдвинуться как угодно далеко вправо или как
угодно далеко влево. Значит, нам всегда удастся перескочить через c и
сменить направление движения.
Значит мы
всегда можем взять достаточно много элементов из «хвостов» этих
последовательностей, чтобы сдвинуться как угодно далеко вправо или как
угодно далеко влево. Значит, нам всегда удастся перескочить через c и
сменить направление движения.
В ходе каждого этапа движения вправо или влево из соответстующей последовательности берётся по крайней мере один элемент. По построению, мы не пропускаем никакие элементы и не повторяем одни и тот же элемент дважды. Поскольку этапов бесконечно много, это означает, что любой элемент рано или поздно будет выписан, причём ровно один раз. Это означает, что новая последовательность — перестановка старой.
Наконец, почему предел её частичных сумм стремится к c? Заметим,
что в силу необходимого условия сходимости, ak→0 при k→∞ и значит a+k→0 и a−k→0. Это
означает, что limm→∞b+m=0 и liml→∞b−l=0. То есть скачки, которые мы совершаем каждый раз, стремятся к нулю.
Однако, расстояние от c до очередной частичной суммы не превосходит
модуля длины последнего скачка, после которого мы перескочили через c. Этот скачок равен соответствующему элементу последовательности ak, и его
номер стремится к бесконечности, поскольку при каждом проходе «вправо» мы
берём как минимум один элемент из последовательности положительных членов, а
при проходе «влево» берём как минимум один элемент из последовательности
отрицательных членов. Значит, k как минимум не меньше, чем число проходов
вправо и влево. Поэтому расстояние от c до очередной частичной суммы
стремится к нулю.
Этот скачок равен соответствующему элементу последовательности ak, и его
номер стремится к бесконечности, поскольку при каждом проходе «вправо» мы
берём как минимум один элемент из последовательности положительных членов, а
при проходе «влево» берём как минимум один элемент из последовательности
отрицательных членов. Значит, k как минимум не меньше, чем число проходов
вправо и влево. Поэтому расстояние от c до очередной частичной суммы
стремится к нулю.
Теорема доказана.∎
28.4Заключение
Ряды естественным образом возникают в ситуациях, когда есть какая-то величина,
меняющаяся дискретно (в отдельные моменты времени), и нас интересует, как это
величина накапливается. Сложные проценты в финансах, расчёты платежей в теории
игр, математические ожидания дискретных случайных величин в теории вероятностей
— во всех этих областях появляются ряды. Особенно важно понимать, какие ряды
сходятся, а какие нет — и мы подробно обсудили несколько достаточно
универсальных признаков, применимых в широком спектре ситуаций. К сожалению,
нахождение значений рядов — задача ещё более сложная, чем нахождение сумм
интегралов. Впрочем, если вы хотите углубиться в эту тему, могу рекомендовать
книгу «Конкретная математика. Основание информатики» (Р. Грэхем, Д. Кнут, О.
Поташник). Там эта тема обсуждается подробно.
К сожалению,
нахождение значений рядов — задача ещё более сложная, чем нахождение сумм
интегралов. Впрочем, если вы хотите углубиться в эту тему, могу рекомендовать
книгу «Конкретная математика. Основание информатики» (Р. Грэхем, Д. Кнут, О.
Поташник). Там эта тема обсуждается подробно.
А мы подходим к концу курса. Осталась буквально одна тема. И это будет что-то новое!
← Предыдущая глава Следующая глава →
Сумма ряда на практике
Вычислить сумму ряда можно только в случае, когда ряд сходится. Если ряд расходится то сумма ряда бесконечна и нет смысла что-то вычислять. Ниже приведены примеры из практики нахождения суммы ряда, которые задавали в Львовском национальном университете имени Ивана Франка. Задания на ряды подобраны так, что условие сходимости выполняется всегда, однако проверку на сходимость мы выполнять будем. Эта и следующие за ней статьи составляют решение контрольной работы по анализе рядов.
Пример 1. 4 Вычислить сумму рядов:
4 Вычислить сумму рядов:
а)
Вычисления: Поскольку граница общего члена ряда при номере следующему до бесконечности равна 0
то данный ряд сходится. Вычислим сумму ряда. Для этого преобразуем общий член, разложив его на простейшие дроби I и II типа. Методика разложения на простые дроби здесь приводиться не будет (хорошо расписана при интегрировании дробей), а лишь запишем конечный вид разложения
В соответствии с этим можем сумму расписать через сумму ряда образованного из простейших дробей, а дальше из разницы сумм рядов
Далее расписываем каждый ряд в явную сумму и выделяем слагаемые (подчеркивание), которые превратятся 0 после сложения. Таким образом сумма ряда упростится к сумме 3 слагаемых (обозначены черным), что в результате даст 33/40.
На этом базируется вся практическая часть нахождения суммы для простых рядов.
Примеры на сложные ряды сводятся к сумме бесконечно убывающих прогрессий и рядов, которые находят через соответствующие формулы, но здесь такие примеры рассматривать не будем.
б)
Вычисления: Находим границу n-го члена суммы
Она равна нулю, следовательно заданный ряд сходится и имеет смысл искать его сумму. Если граница отличная от нуля, то сумма ряда равна бесконечности со знаком «плюс» или «минус».
Найдем сумму ряда. Для этого общий член ряда который является дробью превратим методом неопределенных коэффициентов к сумме простых дробей I типа
Далее по инструкции которая приводилась ранее записываем сумму ряда через соответствующие суммы простейших дробей
Расписываем суммы и выделяем слагаемые, которые станут равными 0 при суммировании.
В результате получим сумму нескольких слагаемых (выделенные черным) которая равна 17/6.
Пример 1.9 Найти сумму ряда:
а)
Вычисления: Вычислениям границы
убеждаемся что данный ряд сходится и можно находить сумму. Далее знаменатель функции от номера n раскладываем на простые множители, а весь дробь превращаем к сумме простых дробей I типа
Далее сумму ряда в соответствии с расписанием записываем через два простые
Ряды записываем в явном виде и выделяем слагаемые, которые после добавления дадут в сумме ноль. Остальные слагаемые (выделенные черным) и представляет собой конечную сумму ряда
Остальные слагаемые (выделенные черным) и представляет собой конечную сумму ряда
Таким образом, чтобы найти сумму ряда надо на практике свести под общий знаменатель 3 простых дроби.
б)
Вычисления: Граница члена ряда при больших значениях номера стремится к нулю
Из этого следует что ряд сходится, а его сумма конечна. Найдем сумму ряда, для этого сначала методом неопределенных коэффициентов разложим общий член ряда на три простейшего типа
Соответственно и сумму ряда можно превратить в сумму трех простых рядов
Далее ищем слагаемые во всех трех суммах, которые после суммирования превратятся в ноль. В рядах, содержащих три простых дроби один из них при суммировании становится равным нулю (выделен красным). Это служит своеобразной подсказкой в вычислениях
Сумма ряда равна сумме 3 слагаемых и равна единице.
Пример 1.15 Вычислить сумму ряда:
а)
Вычисления: При общем член ряда стремящемся к нулю
данный ряд сходится. Преобразуем общий член таким образом, чтобы иметь сумму простейших дробей
Преобразуем общий член таким образом, чтобы иметь сумму простейших дробей
Далее заданный ряд, согласно формулам расписания, записываем через сумму двух рядов
После записи в явном виде большинство членов ряда в результате суммирования станут равны нулю. Останется вычислить сумму трех слагаемых.
Сумма числового ряда равна -1/30.
б)
Вычисления: Поскольку граница общего члена ряда равна нулю,
то ряд сходится. Для нахождения суммы ряда разложим общий член на дроби простейшего типа.
При разложении использовали метод неопределенных коэффициентов. Записываем сумму ряда из найденного расписание
Следующим шагом выделяем слагаемые, не вносящие никакого вклада в конечную сумму и остальные оставшиеся
Сумма ряда равна 4,5.
Пример 1.25 Вычислить сумму рядов:
а)
Вычисления: Находим границу общего члена ряда
Поскольку она равна нулю то ряд сходится. Можем найти сумму ряда. Для этого по схеме предыдущих примеров раскладываем общий член ряда через простейшие дроби
Это позволяет записать ряд через сумму простых рядов и, выделив в нем слагаемые, упростив при этом суммирование.
В этом случае останется одно слагаемое которое равен единице.
б)
Вычисления: Находим границу общего члена ряда
и убеждаемся что ряд сходится. Далее общий член числового ряда методом неопределенных коэффициентов раскладываем на дроби простейшего типа.
Через такие же дроби расписываем сумму ряда
Записываем ряды в явном виде и упрощаем к сумме 3 слагаемых
Сумма ряда равна 1/4.
На этом ознакомление со схемами суммирования рядов завершено. Здесь еще не рассмотрены ряды, которые сводятся к сумме бесконечно убывающей геометрической прогрессии, содержащие факториалы, степенные зависимости и подобные. Однако и приведенный материал будет полезен для студентов на контрольных и тестах.
- Назад
- Вперёд
Сумма ряда x в степени n – dj-sensor.ru
Содержание
- Введите данные для подчета суммы ряда
- Сходимость ряда
- Правила ввода выражений и функций
- Лучшие эксперты в этом разделе
Введите данные для подчета суммы ряда
Найдем сумму ряда чисел. Если не получается ее найти, то система вычисляет сумму ряда с определенной точностью.
Если не получается ее найти, то система вычисляет сумму ряда с определенной точностью.
Сходимость ряда
Данный калькулятор умеет определять – сходится ли ряд, также показывает – какие признаки сходимости срабатывают, а какие – нет.
Также умеет определять сходимость степенных рядов.
Также строится график ряда, где можно увидеть скорость сходимости ряда (или расходимости).
Правила ввода выражений и функций
© Контрольная работа РУ – калькуляторы онлайн
Проверить сходимость ряда можно несколькими способами. Во-первых можно просто найти сумму ряда. Если в результате мы получим конечное число, то такой ряд сходится. Например, поскольку
то ряд сходится. Если нам не удалось найти сумму ряда, то следует использовать другие методы для проверки сходимости ряда.
Одним из таких методов является признак Даламбера, который записывается следующим образом:
здесь и соответственно n-ый и (n+1)-й члены ряда, а сходимость определяется значением D: Если D 1 – расходится.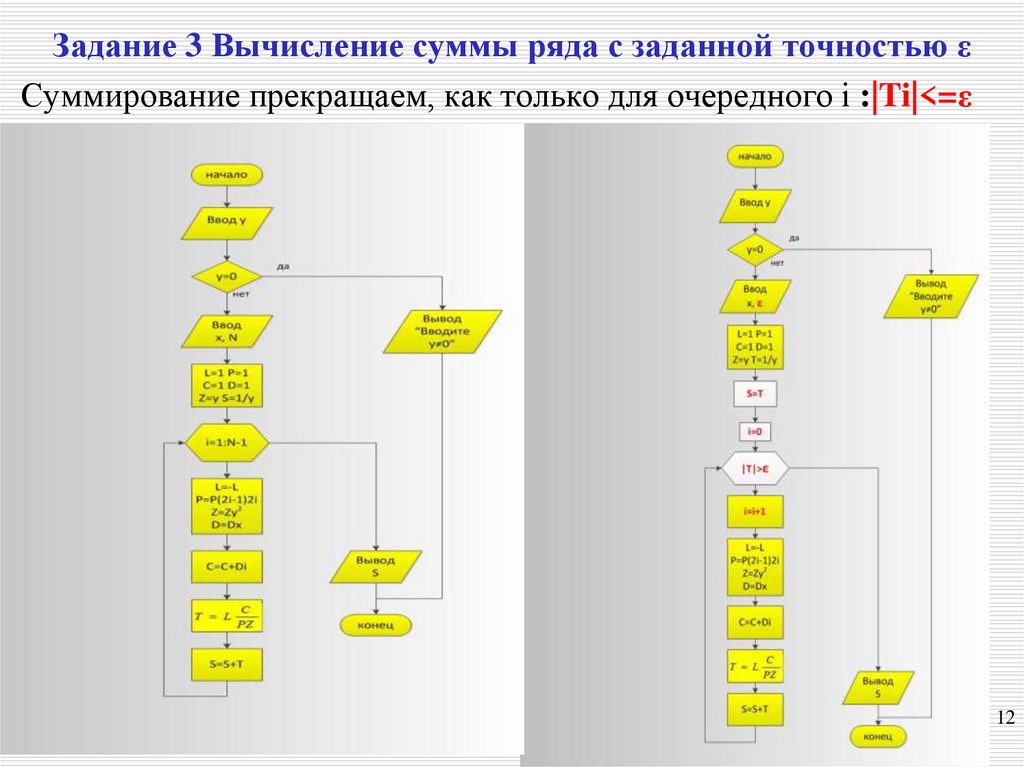 При D = 1 – данный признак не даёт ответа и нужно проводить дополнительные исследования.
При D = 1 – данный признак не даёт ответа и нужно проводить дополнительные исследования.
В качестве примера, исследуем сходимость ряда с помощью признака Даламбера. Сначала запишем выражения для и . Теперь найдем соответствующий предел:
Поскольку , в соответствии с признаком Даламбера, ряд сходится.
Еще одним методом, позволяющим проверить сходимость ряда является радикальный признак Коши, который записывается следующим образом:
здесь n-ый член ряда, а сходимость, как и в случае признака Даламбера, определяется значением D: Если D 1 – расходится. При D = 1 – данный признак не даёт ответа и нужно проводить дополнительные исследования.
В качестве примера, исследуем сходимость ряда с помощью радикального признака Коши. Сначала запишем выражение для . Теперь найдем соответствующий предел:
Читайте также: Что означает три точки в математике
Поскольку 1′ title=’15625/64>1′ /> , в соответствии с радикальным признаком Коши, ряд расходится.
Стоит отметить, что наряду с перечисленными, существуют и другие признаки сходимости рядов, такие как интегральный признак Коши, признак Раабе и др.
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha позволяет протестировать сходимость ряда. При этом, если калькулятор в качестве суммы ряда выдает конкретное число, то ряд сходится. В противном случае, необходимо обращать внимание на пункт «Тест сходимости ряда». Если там присутствует словосочетание «series converges», то ряд сходится. Если присутствует словосочетание «series diverges», то ряд расходится.
Ниже представлен перевод всех возможных значений пункта «Тест сходимости ряда»:
Консультации и решение задач по алгебре, геометрии, анализу, дискретной математике.
Лучшие эксперты в этом разделе
| Коцюрбенко Алексей Владимирович Статус: Модератор Рейтинг: 1690 | w3.org/2000/svg’%20viewBox=’0%200%200%200’%3E%3C/svg%3E» data-lazy-src=»https://rfpro.ru/images/nouser0.jpg»/> | epimkin Статус: Бакалавр Рейтинг: 386 | Roman Chaplinsky / Химик CH Статус: Модератор Рейтинг: 380 |
| Перейти к консультации №: |
Уважаемые эксперты! Пожалуйста, ответьте на вопрос:Укажите, чему равна сумма ряда х в степени n:
1) е в степени x (x-любое)
2) 1/(x+1) (-1 Последнее редактирование 17.11.2016, 16:03 Лысков Игорь Витальевич (Старший модератор)
Состояние: Консультация закрыта
Здравствуйте, Алексей Валентинович!
По-моему, правильный ответ 5).
P. S. Как Вы сами правильно заметили в мини-форуме консультации, всё-таки правильный ответ 3), а не 5).
0
Отправлять сообщения
модераторам могут
только участники портала.
ВОЙТИ НА ПОРТАЛ »
регистрация »
Елена Васильевна
Бакалавр
ID: 398750
Прикрепите фото задания
Гордиенко Андрей Владимирович
Специалист
ID: 17387
Известны следующие “стандартные” разложения:
Профессионал
ID: 304951
Мне не переслать фото.Там написан такой ряд: Сигма от 0 до бесконечности x в степени n. И сумма этого ряда равна одному из четырёх вариантов. Извините, забыл написать пятый вариант
5) Среди предложенных вариантов ответа нет верного
Читайте также: Что значит значок якоря в ворде
Гордиенко Андрей Владимирович
Специалист
ID: 17387
Тогда, по-моему, правильный ответ 5).
Гордиенко Андрей Владимирович
Специалист
ID: 17387
Почему-то невозможно отправить ответ и в этой консультации. 3+. при -1 Специалист
3+. при -1 Специалист
ID: 17387
Даже стыдно стало. Прошу извинить! Ответ, с Вашего согласия, исправлю. На будущее учту.
Возможность оставлять сообщения в мини-форумах консультаций доступна только после входа в систему.
Воспользуйтесь кнопкой входа вверху страницы, если Вы зарегистрированы или пройдите простую процедуру регистрации на Портале.
- Автор: Мария Сухоруких
- Распечатать
Оцените статью:
(0 голосов, среднее: 0 из 5)
Поделитесь с друзьями!
Методы сложения чисел от 1 до 100 – BetterExplained
Существует популярная история о том, что у Гаусса, выдающегося математика, был ленивый учитель. Так называемый воспитатель хотел занять детей, чтобы он мог вздремнуть; он попросил класс сложить числа от 1 до 100.
Гаусс подошел со своим ответом: 5050. Так скоро? Учитель заподозрил обман, но нет. Сложение вручную было для лохов, и Гаусс нашел формулу, позволяющую обойти проблему:
Сложение вручную было для лохов, и Гаусс нашел формулу, позволяющую обойти проблему:
Давайте поделимся несколькими объяснениями этого результата и действительно поймем его интуитивно. Для этих примеров мы добавим 1 к 10, а затем посмотрим, как это применимо к 1 к 100 (или 1 к любому числу).
Техника 1: Парные номера
Парные номера — распространенный подход к этой проблеме. Вместо того, чтобы записывать все числа в один столбец, давайте обернем числа так:
1 2 3 4 5 10 9 8 7 6
Возникает интересный паттерн: сумма каждого столбца равна 11 . По мере увеличения верхней строки нижняя строка уменьшается, поэтому сумма остается прежней.
Поскольку 1 находится в паре с 10 (наше n), мы можем сказать, что в каждом столбце есть (n+1). А сколько у нас пар? Итак, у нас есть 2 равных строки, у нас должно быть n/2 пар.
, что является формулой выше.
Подождите, а как насчет нечетного количества предметов?
Ах, я рад, что вы подняли эту тему. Что, если мы сложим числа от 1 до 9? У нас нет четного количества предметов, которые можно соединить. Многие объяснения просто дадут объяснение выше и остановятся на этом. я не буду.
Что, если мы сложим числа от 1 до 9? У нас нет четного количества предметов, которые можно соединить. Многие объяснения просто дадут объяснение выше и остановятся на этом. я не буду.
Складываем числа от 1 до 9, но вместо того, чтобы начинать с 1, давайте считать с 0:
0 1 2 3 4 9 8 7 6 5
Считая от 0, мы получаем «дополнительный элемент» (всего 10), поэтому у нас может быть четное количество строк. Однако наша формула будет выглядеть немного иначе.
Обратите внимание, что сумма каждого столбца равна n (а не n+1, как раньше), поскольку 0 и 9 сгруппированы. И вместо того, чтобы иметь ровно n элементов в 2 строках (всего n/2 пар), у нас есть n + 1 элемент в 2 строках (всего (n + 1)/2 пар). Если вы подставите эти числа, вы получите:
, что является той же формулой, что и раньше. Меня всегда раздражало, что одна и та же формула работает и для нечетных, и для четных чисел — дробь не получится? Да, вы получаете ту же формулу, но по другим причинам.
Способ 2: Использование двух рядов
Описанный выше метод работает, но вы по-разному обрабатываете нечетные и четные числа. Разве нет лучшего способа? Да.
Вместо того, чтобы зацикливать числа, давайте запишем их в два ряда:
1 2 3 4 5 6 7 8 910 10 9 8 7 6 5 4 3 2 1
Обратите внимание, что у нас есть 10 пар, и каждая пара в сумме дает 10+1.
Сумма всех приведенных выше чисел равна
Но нам нужна сумма только одной строки, а не обеих. Итак, мы делим приведенную выше формулу на 2 и получаем:
Вот это круто (настолько круто, насколько могут быть ряды чисел). Это работает для нечетного или четного количества предметов одинаково!
Техника 3: Создание прямоугольника
Недавно я наткнулся на другое объяснение, свежий подход к старому объяснению спаривания. Разные объяснения работают лучше для разных людей, и мне это нравится больше.
Вместо того, чтобы писать числа, представьте, что у нас есть бобы. Мы хотим добавить 1 боб к 2 бобам, к 3 бобам… вплоть до 5 бобов.
Мы хотим добавить 1 боб к 2 бобам, к 3 бобам… вплоть до 5 бобов.
х х х х х х х х х х х х х х х
Конечно, мы могли бы использовать 10 или 100 бобов, но с 5 вы поняли идею. Как нам посчитать количество бобов в нашей пирамиде?
Ну, сумма явно 1 + 2 + 3 + 4 + 5. Но давайте посмотрим на это по-другому. Допустим, мы зеркально отразим нашу пирамиду (я буду использовать «о» для отраженных бобов), а затем опрокинем ее:
х о х о о о о о х х о о х х о о о о х х х о о о => х х х о о о х х х х о о о о х х х х о о х х х х х о о о о о х х х х х х о
Круто, да? Если вам интересно, действительно ли это совпадает, то это так. Взгляните на нижний ряд правильной пирамиды с 5′x (и 1°). В следующем ряду пирамиды на 1 x меньше (всего 4) и на 1 больше (всего 2), чтобы заполнить пробел. Так же, как и в паре, одна сторона увеличивается, а другая уменьшается.
Теперь пояснение: сколько у нас всего бобов? Ну, это просто площадь прямоугольника.
У нас есть n строк (количество строк в пирамиде мы не меняли), а ширина нашей коллекции (n + 1) единиц, так как 1 «о» стоит в паре со всеми «иксами».
Обратите внимание, что на этот раз нам все равно, будет ли n нечетным или четным — формула общей площади работает просто отлично. Если n нечетно, у нас будет четное количество элементов (n+1) в каждой строке.
Но, конечно, нам не нужна общая площадь (количество иксов и ноликов), нам нужно только количество иксов. Поскольку мы удвоили x, чтобы получить o, x сами по себе составляют лишь половину общей площади:
И мы вернулись к нашей первоначальной формуле. Опять же, количество x в пирамиде = 1 + 2 + 3 + 4 + 5 или сумма от 1 до n.
Метод 4. Усреднение
Все мы знаем, что
среднее = сумма / количество элементов
, что мы можем преобразовать в
сумма = среднее * количество элементов
Чтобы получить среднее значение, обратите внимание, что все числа распределены поровну. Для каждого большого числа на другом конце есть маленькое число. Давайте посмотрим на небольшой набор:
Для каждого большого числа на другом конце есть маленькое число. Давайте посмотрим на небольшой набор:
1 2 3
Среднее значение равно 2. 2 уже находится посередине, а 1 и 3 «сокращаются», поэтому их среднее значение равно 2.
Для четного числа предметов
1 2 3 4
среднее между 2 и 3 — это 2,5. Несмотря на то, что у нас есть дробное среднее, это нормально — поскольку у нас есть даже элементов, когда мы умножаем среднее значение на количество, эта уродливая дробь исчезнет.
Обратите внимание, что в обоих случаях 1 находится по одну сторону от среднего, а N одинаково далеко по другую. Таким образом, мы можем сказать, что среднее значение всего набора на самом деле является средним значением 1 и n: (1 + n)/2.
Подставляем это в нашу формулу
И вуаля! У нас есть четвертый способ думать о нашей формуле.
Так почему же это полезно?
Три причины:
1) Быстрое сложение чисел может быть полезным для оценки. Обратите внимание, что формула расширяется до этого:
Обратите внимание, что формула расширяется до этого:
Допустим, вы хотите сложить числа от 1 до 1000: предположим, вы получаете 1 дополнительного посетителя на свой сайт каждый день — сколько всего посетителей будет через 1000 дней? Так как тысяча в квадрате = 1 миллион, мы получаем миллионов / 2 + 1000/2 = 500 500 .
2) Эта концепция сложения чисел от 1 до N проявляется и в других местах, например, при вычислении вероятности парадокса дня рождения. Твердое понимание этой формулы поможет вашему пониманию во многих областях.
3) Самое главное, этот пример показывает, что есть много способов понять формулу. Может быть, вам нравится метод сопряжения, может быть, вы предпочитаете технику прямоугольника, или, может быть, есть другое объяснение, которое вам подходит. Не отказывайтесь от , если вы не понимаете — попробуйте найти другое объяснение, которое работает. Счастливая математика.
Кстати, есть более подробная информация об истории этой истории и возможной технике, которую использовал Гаусс.
Вариации
Вместо 1 до n, как насчет 5 до n?
Начните с обычной формулы (1 + 2 + 3 + … + n = n * (n + 1) / 2) и вычтите ненужную часть (1 + 2 + 3 + 4 = 4 * (4 + 1) / 2 = 10).
Сумма для 5 + 6 + 7 + 8 + … n = [n * (n + 1) / 2] – 10
И для любого начального числа a:
Сумма от a до n = [n * (n + 1) / 2] – [(a - 1) * a / 2]
Мы хотим избавиться от всех чисел от 1 до — 1.
Как насчет четных чисел, таких как 2 + 4 + 6 + 8 + … + n?
Просто удвойте обычную формулу. Чтобы сложить четные числа от 2 до 50, найдите 1 + 2 + 3 + 4 … + 25 и удвойте его:
Сумма 2 + 4 + 6 + … + n = 2 * (1 + 2 + 3 + … + n/ 2) = 2 * п/2 * (п/2 + 1) / 2 = п/2 * (п/2 + 1)
Итак, чтобы получить четные числа от 2 до 50, нужно сделать 25 * (25 + 1) = 650
Как насчет нечетных чисел, например 1 + 3 + 5 + 7 + … + n?
Это то же самое, что и четная формула, за исключением того, что каждое число на 1 меньше своего аналога (у нас есть 1 вместо 2, 3 вместо 4 и т. д.). Получаем следующее по величине четное число (n + 1) и убираем лишнее (n + 1)/2 «-1″ предметов:
д.). Получаем следующее по величине четное число (n + 1) и убираем лишнее (n + 1)/2 «-1″ предметов:
Сумма 1 + 3 + 5 + 7 + … + n = [(n + 1)/2 * ((n + 1)/2 + 1)] – [(n + 1) / 2]
Чтобы добавить 1 + 3 + 5 + … 13, возьмите следующее наибольшее четное (n + 1 = 14) и выполните
[14/2 * (14/2 + 1)] – 7 = 7 * 8 – 7 = 56 – 7 = 49
Комбинации: четы и смещения
Допустим, вам нужны четы из 50 + 52 + 54 + 56 + … 100. Найдите все четы
2 + 4 + 6 + … + 100 = 50 * 51
и вычесть ненужные
2 + 4 + 6 + … 48 = 24 * 25
Итак, сумма из 50 + 52 + … 100 = (50 * 51) – (24 * 25) = 1950
Фу! Надеюсь это поможет.
Рубиновые умники: вы можете проверить это, используя
(50..100).select {|x| х % 2 == 0 }.inject(:+)
1950 г.
Специалисты по Javascript, сделайте это:
[...Array(51).keys()].map(x => x + 50).filter(x => x % 2 == 0).reduce(( х, у) => х + у) 1950 г. // Примечание: имеется 51 число от 50 до 100 включительно.Забор!
Другие сообщения из этой серии
- Методы сложения чисел от 1 до 100
- Переосмысление арифметики: визуальное руководство
- Quick Insight: интуитивное значение подразделения
- Quick Insight: вычитание отрицательных чисел
- Удивительные закономерности в квадратных числах (1, 4, 9, 16…)
- Развлечение с модульной арифметикой
- Учимся считать (избегая проблемы с ограждением)
- Причудливое введение в системы счисления
- Еще один взгляд на простые числа
- Интуиция для золотого сечения
- Различные интерпретации числа ноль
Как суммировать в Excel Примеры и видео
Примеры показывают, как суммировать в Microsoft Excel с помощью простой функции СУММ или формул, которые суммируют на основе одного или нескольких критериев.
Во-первых, для быстрого обзора посмотрите видео: 7 способов суммирования в Excel. Затем прокрутите вниз, чтобы увидеть больше видеороликов о функции Sum, письменных инструкций и бесплатных книг Excel. Кроме того, внизу страницы есть список тем, если вы ищете конкретную тему «Как суммировать».
Кроме того, внизу страницы есть список тем, если вы ищете конкретную тему «Как суммировать».
Автор: Дебра Далглиш
Обзор: 7 способов суммирования в экселеЧтобы получить краткий обзор 7 различных способов суммирования чисел с помощью функций Excel, вы можете посмотреть это 9-минутное видео. Под видео есть письменные шаги и снимки экрана для всех примеров. Временная шкала видео (синие ссылки ведут к письменным шагам под видео)
|
Суммирование диапазона ячеек — Функция СУММ
Самый быстрый и простой способ суммирования диапазона ячеек – использовать кнопку Excel AutoSum. Он автоматически вводит функцию СУММ Excel в выбранной ячейке. Функция СУММ суммирует одно или несколько чисел в диапазоне ячеек.
В первом примере ниже показано, как использовать функцию автосуммы
- Выберите пустую ячейку в строке под ячейками, которые вы хотите
сумма, ячейка A5 в этом примере.

- Щелкните команду AutoSum на вкладке «Главная» ленты,
или используйте сочетание клавиш: Alt + = - В активной ячейке появится формула СУММ со ссылкой на
ячейки выше. На снимке экрана ниже есть формула СУММ в
ячейка А5: =СУММ(A1:A4)
ПРИМЕЧАНИЕ. Если все ячейки не включаются автоматически, можно расширить кадр, чтобы выбрать их. - Нажмите клавишу Enter, чтобы завершить ввод.
Настройка функции SUM
Вместо использования команды AutoSum для вставки функции SUM можно введите функцию вручную.
Настройка функции СУММ (синтаксис): СУММ(число1 , [число2],…).
- Имеет один обязательный аргумент: число1
- Он также имеет необязательные аргументы (заключенные в квадратные
скобки): [номер2],..

Эти аргументы могут быть ссылками на ячейки или могут быть введены в формулу.
В приведенном выше примере ( =СУММ(A1:A4) ) есть один аргумент — ссылка на ячейки A1:A4.
Исправить числа, которые не складываютсяНекоторые значения Excel выглядят как числа, но не складываются, так как Excel думает, что это текст. Иногда вы можете решить проблему с помощью Paste Специальный. Посмотрите этот короткий видеоурок, чтобы увидеть шаги Для получения письменных инструкций и других способов решения проблемы перейдите на страницу «Числа не складываются». Общий итог по диапазону ячеек Одним быстрым шагом вы можете вычислить строку, столбец и общие итоги для
диапазон ячейки. Посмотрите этот короткий Excel
Видео Grand Totals, чтобы увидеть, как это сделать. Быстрый общий итог для диапазона ячеек
|
ИтогоЧтобы увидеть промежуточный итог в каждой строке списка Excel, вы можете использовать Функция SUM с блокировкой начальной строки как абсолютной ссылки. Ниже приведены немного другие шаги,
Промежуточный итог в списке рабочих листов Для списка рабочих листов (не именованной таблицы Excel) в этом видео показано, как настроить формулу промежуточного итога и заблокировать начальную строку. Промежуточный итог — список рабочих листовДля списка рабочих листов (не именованной таблицы Excel) выполните следующие действия, чтобы создать промежуточный итог. На приведенном ниже снимке экрана суммы вводятся в столбец C, а текущий итог рассчитывается в столбце D.
Как работает формулаФормула использует абсолютную ссылку на строку 2 в качестве отправной точки — C$2 — и относительная ссылка на конечную точку — C2 Это гарантирует, что начальная точка не изменится при копировании
формулу до строк ниже.
Промежуточный итог в таблице ExcelДля именованной таблицы Excel нельзя использовать формулу списка рабочих листов из предыдущего раздела. Сначала я покажу вам задачу с этой формулой, а затем вы увидите формулу, которая работает в именованной таблице. Проблема с промежуточным итогомПосле того, как вы введете формулу в ячейку D2 указанной таблицы Excel, она автоматически заполнится, и промежуточный итог будет выглядеть правильно. Но, как только вы начинаете новую строку внизу таблицы, формула в последней строке меняется. Перед добавлением строки в ячейке D6 была следующая формула:
Как только в строке 7 была запущена следующая запись, формула в D6 автоматически изменилась.
По мере добавления каждой новой строки формулы в нижних строках продолжают изменяться, чтобы показать номер последней строки. Формула промежуточного итога для именованной таблицыЧтобы избежать этой проблемы, мы будем использовать немного другую формулу для промежуточного итога в именованной таблице Excel. На приведенном ниже снимке экрана суммы вводятся в столбце C, а текущий итог рассчитывается в столбце D.
Как работает формулаФормула использует абсолютную ссылку на ячейку заголовка в качестве отправной точки — 1 канадский доллар
Для конечной точки есть ссылка на структурированную таблицу — [@Amt]
На этом снимке экрана показано, что при запуске новой строки в ячейке C6 по-прежнему отображается исходная формула, а суммы промежуточных сумм в каждой строке верны |
Суммирование диапазона ячеек — OFFSET Если вы вставите строку непосредственно над функцией СУММ в предыдущем примере,
новая строка не может быть включена в SUM.
|
Сумма ячеек, соответствующих критериям — СУММЕСЛИВот 3 способа суммирования ячеек, соответствующих критериям, с помощью функции СУММЕСЛИ в Excel: — Точное соответствие критерию — Критерий совпадения в строка – Критерий соответствия с использованием оператор Совет : Для примеров того, как суммировать на основе нескольких критериев, перейдите к ячейкам суммы с сложный раздел множественных критериев , ниже. Настройка функции СУММЕСЛИНастройка функции СУММЕСЛИ (синтаксис): СУММЕСЛИ(диапазон , критерии , [ диапазон_суммы ])
Эти аргументы могут быть ссылками на ячейки или могут быть введены в формулу. Точное соответствие критерию Вы можете рассчитать итог для строк, соответствующих определенному критерию.
Примечание : Вместо того, чтобы вводить критерий в формулу, вы можете указать
в ячейку. Вы можете добавить ячейки, содержащие критерий, как часть содержимого ячейки. В этом примере все заказы Pen, Gel Pen и Pencil будут суммироваться, потому что они содержат строку «ручка».
Примечание : Вместо того, чтобы вводить критерий в формулу, вы можете указать
в ячейку. Например, формула на шаге 9выше можно изменить на: |
Критерий и оператор Вы можете использовать оператор с условием. В приведенных ниже примерах см.
как объединить их в формуле СУММЕСЛИ. Пример 1 Пример 2 Пример 1 — сумма строк больше заданного значенияВ этом примере только строки, в которых количество торговых представителей больше больше или равно десяти, будут включены в общую сумму.
Примечание : Вместо того, чтобы вводить критерий в формулу, вы можете указать
в ячейку. Например, формула на шаге 9выше можно изменить на: Пример 2 — скользящие итоги за 12 месяцев В этом примере только строки за предыдущие 11 месяцев и текущий
месяц, будут включены в общую сумму. Даты находятся в столбце A, и список должен быть отсортирован по дате. Ежемесячный суммы указаны в столбце B.
Как это работает Формула проверяет даты в столбце A, начиная со строки 2 (A$2), и вниз к текущей строке (A2) =СУММЕСЛИ( A$2:A2 Функция ДАТА вычисляет дату на 11 месяцев раньше даты. в текущей строке ДАТА(ГОД(A2),МЕСЯЦ(A2)-11,ДЕНЬ(A2)) Оператор >= проверяет даты, которые больше или равны эта дата, «>=» & ДАТА(ГОД(A2),МЕСЯЦ(A2)-11,ДЕНЬ(A2)) Для строк, соответствующих критерию, формула суммирует суммы в столбце B, начиная со строки 2 (B$2) и заканчивая текущей строкой (B2) B$2:B2 |
Сумма ячеек, соответствующих нескольким критериям — СУММЕСЛИМН В Excel 2007 и более поздних версиях вы можете использовать функцию СУММЕСЛИМН для
вычислить итог для строк, которые соответствуют двум или более критериям. Полную расшифровку видео можно найти на странице суммирования сумм по 2 критериям. СУММЕСЛИМН Настройка функцииНастройка функции СУММЕСЛИМН (синтаксис): СУММЕСЛИМН(диапазон , критерии , [ диапазон_суммы ])
Эти аргументы могут быть ссылками на ячейки или могут быть введены в формулу. Соответствие нескольким критериямВ этом примере функция СУММЕСЛИМН суммирует суммы в столбце D на основе 2 критериев :
Эти критерии вводятся в ячейки F6 (Отправлено) и G6 (10) Выполните следующие действия, чтобы создать формулу СУММЕСЛИМН:
|
Формулы со ссылками на таблицы Если вы создаете формулы со ссылками на таблицы, а затем пытаетесь скопировать эти формулы в соседние столбцы, вы можете столкнуться с проблемами. Проблемы со ссылками на таблицыВ этой сводке продаж есть формула СУММЕСЛИМН в ячейке C5, которая показывает правильную сумму продаж батончиков в Восточном регионе. =СУММЕСЛИМН(Данные_продаж[Количество], Данные_продаж[Регион],$B5, Данные_продаж[Категория],4C$) Однако, если вы наведете указатель на маркер заполнения в ячейке C5 и перетащите вправо, формула покажет неверный итог в ячейке D5. Если вы проверите формулу в ячейке D5, все ссылки на таблицы сместятся на один столбец вправо, потому что формула была перетащена на один столбец вправо. =СУММЕСЛИМН(Данные_продаж[Общая стоимость],Данные_продаж[Категория],$B5, Данные_продаж[Продукт],D$4)
 Ни один из этих критериев не найден, поэтому результат равен нулю. Чтобы предотвратить эту проблему смещения ссылок на таблицы, не перетаскивайте маркер заполнения для копирования. Вместо этого используйте один из следующих методов:
Заполнить справа
Копировать и вставить
 |
СУММЕСЛИМН с несколькими критериями И/ИЛИВ приведенном ниже списке можно использовать формулу СУММЕСЛИМН для суммирования строк, где:
И
Формула в ячейке G9 будет:
Формула с несколькими критериями для И/ИЛИОднако вместо одной категории мы хотели бы рассчитать общее количество для двух и более категорий. В этом примере мы посчитаем общую сумму где:
ИЛИ
Две категории вводятся в ячейки G6:G7 рабочего листа. Массивная формулаЧтобы вычислить итог, мы добавим в формулу СУММЕСЛИМН функцию СУММ, и введите формулу в виде массива.
|
| Сумма ячеек соответствует нескольким критериям —
СУММПРОДУКТ Соответствие нескольким критериям В Excel 2003 и более ранних версиях можно использовать функцию СУММПРОИЗВ для вычисления
общее количество строк, соответствующих двум или более критериям. В этом примере только строки со статусом «Активно». и количество посещений больше или равно десяти будет включено в сумме.
|
Сумма первых 5 номеров в спискеИспользуйте вместе функцию СУММ и функции НАИБОЛЬШИЙ, чтобы сложить наибольшую номера в списке. Версия 1 — несколько лучших номеров Если нужно просуммировать несколько чисел, напр. топ 3, вы можете ввести цифры
в формулу. =СУММ(НАИБОЛЬШИЙ(A1:A7,{1,2,3})) Результат: 70+60+50 = 180 Примечание : Вторые 50 не включаются в результат, хотя он делит 3-е место. Версия 2 — Много лучших номеровЕсли необходимо суммировать много верхних чисел, вы можете включить функцию ДВССЫЛ. в формуле с функцией СУММ. В функции ДВССЫЛ используйте строку числа, которые представляют числа, которые вы хотите включить. В этом примере используются строки 1:10, поэтому первые 10 чисел в указанном диапазоне будут суммироваться.
Версия 3 — Переменные верхние номера Если необходимо суммировать переменное количество верхних чисел, вы можете включить
функция ДВССЫЛ в формуле с функцией СУММ, как показано выше,
и обратитесь к ячейке, содержащей переменную.
|
Сумма сумм в диапазоне датЧтобы суммировать суммы на основе диапазона дат, вы можете использовать функцию СУММЕСЛИМН. в Excel 2007 или более поздних версиях. Посмотрите это видео, чтобы увидеть шаги, и письменные инструкции находятся под видео. Сумма сумм в диапазоне дат Чтобы суммировать суммы за определенный диапазон дат, используйте функцию СУММЕСЛИМН.
(Excel 2007 и более поздние версии) или функцию СУММЕСЛИ. — Всего с СУММЕСЛИМН — Всего с SUMIF В этом примере на лист вводятся даты начала и даты окончания. Даты указаны в столбце A, а проданные единицы — в столбце B. Дополнительные примеры диапазона дат см. на странице Сумма или количество для диапазона дат. Использование СУММЕСЛИМН для вычисления итогового значения для диапазона датВ Excel 2007 и более поздних версиях можно использовать функцию СУММЕСЛИМН для рассчитать итог на основе нескольких критериев. Мы будем использовать формулу СУММЕСЛИМН чтобы суммировать все единицы, где дата продажи:
Вот формула, которая вводится в ячейку D5: =СУММЕСЛИМН($B$2:$B$9,$A$2:$A$9,»>=» & $D$2, $A$2:$A$9,»<=" и $Е$2)
В этом примере результат для выбранного диапазона дат составляет всего Продано 494 единицы. Чтобы проверить, вы можете выбрать ячейки B3: B6 и посмотреть на общее количество отображается в строке состояния Excel. Чтобы получить общее количество единиц для другого диапазона дат, измените дату начала
в ячейке D2 и/или Дата окончания в ячейке E2. Использование СУММЕСЛИ для вычисления итогового значения для диапазона датВ Excel 2003 и более ранних версиях можно использовать функцию СУММЕСЛИ для рассчитать итог по одному критерию. Мы будем использовать одну формулу СУММЕСЛИ чтобы суммировать все единицы, где дата продажи:
Затем мы воспользуемся другой формулой СУММЕСЛИ, чтобы вычесть любые значения, где есть дата
Вот формула, которая вводится в ячейку D5: =СУММЕСЛИ($A$2:$A$9,»>=»
&$D$2,$B$2:$B$9)
В этом примере результат для выбранного диапазона дат составляет всего
Продано 494 единицы. Чтобы получить общее количество единиц для другого диапазона дат, измените дату начала. в ячейке D2 и/или Дата окончания в ячейке E2. |
Суммируйте отфильтрованный список с промежуточным итогомПосле того, как вы отфильтруете строки в списке, вы можете использовать функцию ПРОМЕЖУТОЧНЫЕ.ИТОГИ, вместо функции СУММ для суммирования чисел в видимых строках.
Примечание . В Excel 2003 и более поздних версиях можно использовать формулу: Промежуточные номера функцийПервый аргумент в функции ПРОМЕЖУТОЧНЫЕ.ИТОГИ – это номер функции, который указывает, как числа должны быть рассчитаны. Есть 11 функций который вы можете использовать в качестве первого аргумента в функции ПРОМЕЖУТОЧНЫЕ.ИТОГИ. Список в алфавитном порядке, так что это может помочь вам запомнить некоторые цифры, без обращения к справке Excel каждый раз. Каждая из функций указана дважды. Первая группа функций
под номерами 1-11. Каждая из функций указана дважды. Вторая группа функций номер 101-111. |
Суммировать отфильтрованный список с АГРЕГАТОМФункция АГРЕГАТ, представленная в Excel 2010, аналогична ПРОМЕЖУТОЧНОМУ ИТОГУ. функция, но она имеет больше функций и может игнорировать значения ошибок, а также как скрытые строки в данных. Посмотрите это видео, чтобы узнать, как настроить формулу АГРЕГАТ, и письменные инструкции находятся под видео. Суммирование отфильтрованного списка с AGGREGATE После фильтрации строк в списке можно использовать функцию АГРЕГАТ,
вместо функции СУММ для суммирования чисел в видимых строках. Этот
функция была представлена в Excel 2010. Аналогично функции ПРОМЕЖУТОЧНЫЕ.ИТОГИ, АГРЕГАТ игнорирует скрытые строки и предлагает несколько функций, таких как SUM или AVERAGE, для выбранных данных. Однако у него 19функций по сравнению с ПРОМЕЖУТОЧНЫМИ ИТОГОМИ 11 функций. В отличие от функции ПРОМЕЖУТОЧНЫЕ.ИТОГИ, АГРЕГАТ может быть настроен на игнорирование ошибок, а также скрытые строки и вложенные функции ПРОМЕЖУТОЧНЫЕ.ИТОГИ и АГРЕГАТ. Чтобы суммировать значения в отфильтрованном списке и игнорировать скрытые строки и ошибки:
Завершенная формула: =АГРЕГАТ(9,3,D2:D7) |
Сумма конкретных элементов в отфильтрованном спискеПример 1 Лоран Лонгр создал формулу, позволяющую работать с видимыми строками
после фильтра. Для получения информации см. Техника формулы мощности в этой статье.
на веб-сайте Джона Уокенбаха (больше не доступен). Используя этот метод, СУММПРОИЗВ можно использовать для суммирования видимых элементов. в отфильтрованной таблице. В следующем примере столбец D был отфильтрован для сумм, превышающих 100. Следующая формула суммирует общее количество суммы в строках, содержащих «ручка» в столбце A.
Пример 2 Еще один пример совместного использования СУММПРОИЗВ и ПРОМЕЖУТОЧНЫЙ ИТОГ см. в моем блоге Промежуточный итог и Суммарное произведение с фильтром. В рабочей книге Сэма есть список с полями «Продукт», «Регион» и «Количество». Он создал динамические именованные диапазоны для записей в каждом поле, используя ИНДЕКС и СЧЕТЧИК. Вы можете получить рабочую тетрадь Сэма в разделе «Загрузки» ниже. |
Получить образцы файлов
|
Как суммировать в Excel — Список тем
Вот темы, посвященные суммированию на этой странице
Обзор: 7 способов суммирования в Excel не суммировать
Общая сумма диапазон ячеек
Промежуточный итог
Сумма диапазона ячеек — СМЕЩЕНИЕ
Сумма ячеек, соответствующих одному критерию
0Sum -ячейки, которые соответствуют множественным критериям
Формулы с Ссылками на таблицы
Сумма с множественными и/или критериями
Сумма с Комплексными номерами
Sum TOP 5 номеры в списке
Sum TOP 5 в списке
SUM TOP 5 в списке
SUM TOP 5 в списке
Sum
Сумма сумм в диапазоне дат
Сумма отфильтрованного списка с ПРОМЕЖУТОЧНЫЙ ИТОГ
Сумма отфильтрованного списка с АГРЕГАТ
Сумма конкретных элементов в Отфильтрованный список
Получить образец рабочей книги
Дополнительные руководства по функциям
Список функций
Опции расчета
Формулы, Приступая к работе
Функция ПРОМЕЖУТОЧНЫЙ ИТОГ
СРЕДНЕЕ
СЧЁТ / СЧЁТЕСЛИ
Сумма sql для данных в нескольких столбцах и по строкам с суммой и процентом
Мы видели, как функция суммы используется для получения общего значения столбца в таблице MySQL. Теперь мы узнаем, как получить запрос на сумму в нескольких столбцах и для каждой записи таблицы. Для лучшего понимания немного изменим нашу таблицу учеников, добавив оценки по разным предметам для каждой записи. Теперь таблица будет такой.
Теперь мы узнаем, как получить запрос на сумму в нескольких столбцах и для каждой записи таблицы. Для лучшего понимания немного изменим нашу таблицу учеников, добавив оценки по разным предметам для каждой записи. Теперь таблица будет такой.| id | name | class | social | science | math | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | John Deo | Four | 75 | 84 | 78 | ||||||||||||||||||
| 2 | Max Ruin | Три | 54 | 67 | 85 | ||||||||||||||||||
| 3 | Три | 6 | Krish Star | Four | 50 | 51 | 53 | ||||||||||||||||
| 5 | John Mike | Four | 80 | 78 | 89 | ||||||||||||||||||
| 6 | Alex John | Four | 78 | 60 | 60 | ||||||||||||||||||
| 7 | My John Rob | Five | 77 | 68 | 83 | ||||||||||||||||||
| 8 | Asruid | Five | 55 | 50 | 55 | ||||||||||||||||||
| 9 | Tes Qry | Six | 68 | 60 | 62 | ||||||||||||||||||
| 10 | Big John | Four | 65 | 66 | 76 |
youtube.com/embed/QTmEfTUkhXk» title=»Sum of values of columns in MySQL table with GROUP BY , IN and CASE» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>
Мы напишем запрос для отображения суммы всех оценок каждого ученика. Обратите внимание, что здесь мы не будем использовать функцию sum sql внутри нашего запроса. Вот код.
ВЫБЕРИТЕ идентификатор, имя, класс, (общественное + наука + математика) КАК итого ОТ student_sum
| id | name | class | total |
|---|---|---|---|
| 1 | John Deo | Four | 237 |
| 2 | Max Ruin | Three | 206 |
| 3 | Арнольд | Три | 233 |
| 4 | Криш Стар | Четыре | 154 |
| 5 | John Mike | Four | 247 |
| 6 | Alex John | Four | 198 |
| 7 | My John Rob | Five | 228 |
| 8 | Asruid | Five | 160 |
| 9 | Tes Qry | Six | 190 |
| 10 | Big John | Четыре | 207 |
Несколько столбцов SUM
Связанный учебник
СУММА MySQL
MySQL Макс
MySQL Мин. Среднее значение MySQL
Среднее значение MySQL
ВЫБЕРИТЕ сумму (социальное + математика + естествознание) как общее ОТ student_sum
| всего |
| 2060 |
Расчет процента оценок
Предположим, что полная оценка по каждому предмету равна 95. Итак, чтобы получить процентную оценку каждого учащегося, мы должны умножить 95 на 3 (для трех предметов), а затем разделить это от общего числа и умножить на 100. Вот запрос.ВЫБЕРИТЕ имя, (( социальные сети + естественные науки + математика)/(95*3) * 100) в процентах ОТ `student_sum`
Отображение общей оценки в процентах
И общую оценку, и процент мы можем отобразить следующим образом.
ВЫБЕРИТЕ идентификатор, имя, класс (социальные науки + математика) как общее количество, (( социальные + науки + математика)/(95*3) * 100) AS процент ОТ `student_sum`Выход здесь.
| id | имя | класс | Всего | процент |
|---|---|---|---|---|
| 1 | John Deo | Four | 237 | 83.1579 |
| 2 | Max Ruin | Three | 206 | 72.2807 |
| 3 | Arnold | Three | 233 | 81.7544 |
| 4 | Krish Star | Four | 154 | 54.0351 |
| 5 | John Mike | Four | 247 | 86.6667 |
| 6 | Alex John | Four | 198 | 69.4737 |
| 7 | My John Rob | Five | 228 | 80. 0000 0000 |
| 8 | Asruid | Five | 160 | 56.1404 |
| 9 | Tes Qry | Six | 190 | 66.6667 |
| 10 | Big John | Четыре | 207 | 72,6316 |
ВЫБЕРИТЕ идентификатор, имя, класс (социальные науки + математика) как общее количество, ФОРМАТ((( социальные + естествознание + математика)/(95*3) * 100),2) в процентах ОТ `student_sum`
Сумма данных строки каждой записи
Теперь попробуем отобразить все оценки и их сумму для каждого ученика с помощью группировки. Обратите внимание, что id — уникальный столбец значения в нашей таблице. Вот запросВЫБЕРИТЕ идентификатор, имя, класс, социальные сети, математика, наука, сумма (социальные + математика + наука) как Total from student_sum GROUP BY idВыход здесь
| id | name | class | social | math | science | Total |
|---|---|---|---|---|---|---|
| 1 | John Deo | Four | 75 | 78 | 84 | 237 |
| 2 | Max Ruin | Three | 54 | 85 | 67 | 206 |
| 3 | Arnold | Three | 78 | 90 | 65 | 233 |
| 4 | Krish Star | Четыре | 50 | 53 | 51 | 154 |
| 154 | ||||||
| 154 | ||||||
.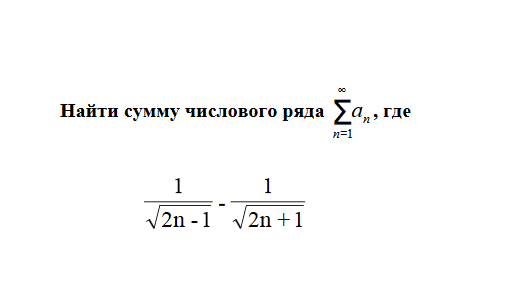 0296 0296 | 89 | 78 | 247 | |||
| 6 | Alex John | Four | 78 | 60 | 60 | 198 |
| 7 | My John Rob | Five | 77 | 83 | 68 | 228 |
| 8 | Asruid | Five | 55 | 55 | 50 | 160 |
| 9 | Tes Qry | Six | 68 | 62 | 60 | 190 |
| 10 | Big John | Four | 65 | 76 | 66 | 207 |
Отображение от наибольшего к наименьшему
Мы можем перечислить, начиная с самой высокой оценки до самой низкой оценки, используя Order By Query.ВЫБЕРИТЕ идентификатор, имя, класс, социальные сети, математика, наука, сумма (социальные + математика + наука) как Total from student_sum GROUP BY id ORDER BY Total DESC
Отображение наивысшей и самой низкой оценки по всем предметам каждого учащегося
ВЫБЕРИТЕ id,name,GREATEST(социальные,науки,математика) как максимальное, НАИМЕНЕЕ(социальные,науки,математика) как min FROM student_sum;
| id | name | max | min |
|---|---|---|---|
| 1 | John Deo | 84 | 75 |
| 2 | Max Ruin | 85 | 54 |
| 3 | Arnold | 90 | 65 |
| 4 | Krish Star | 53 | 50 |
| 5 | John Mike | 89 | 78 |
| 6 | Alex John | 78 | 60 |
| 7 | My John Rob | 83 | 68 |
| 8 | Asruid | 55 | 50 |
| 9 | Tes Qry | 68 | 60 |
| 10 | Big John | 76 | 65 |
Displaying sum of all columns at last row
Как и в MS Excel, мы можем отобразить сумму всех столбцов и сумму всех оценок по предметам, используя UNION. Обратите внимание, что мы должны поддерживать одинаковое количество столбцов при использовании запроса UNION.
Обратите внимание, что мы должны поддерживать одинаковое количество столбцов при использовании запроса UNION.ВЫБЕРИТЕ идентификатор, имя, класс, социальные сети, математика, наука, сумма (социальные + математика + наука) как Total from student_sum GROUP BY id СОЮЗ ВЫБЕРИТЕ '','','Всего',сумма(социальные),сумма(математика),сумма(наука), сумма(социальная)+сумма(математика)+сумма(наука) от student_sumВывод (смотрите последнюю строку)
| id | name | class | social | math | science | Total |
|---|---|---|---|---|---|---|
| 1 | John Deo | Four | 75 | 78 | 84 | 237 |
| 2 | Макс Руин | Три | 54 | 85 | 67 | 206 |
| 3 | Three | 78 | 90 | 65 | 233 | |
| 4 | Krish Star | Four | 50 | 53 | 51 | 154 |
| 5 | John Mike | Four | 80 | 89 | 78 | 247 |
| 6 | Alex John | Four | 78 | 60 | 60 | 198 |
| 7 | My John Rob | Five | 77 | 83 | 68 | 228 |
| 8 | Asruid | Five | 55 | 55 | 50 | 160 |
| 9 | Tes Qry | Six | 68 | 62 | 60 | 190 |
| 10 | Big John | Four | 65 | 76 | 66 | 207 |
| Total | 680 | 731 | 649 | 2060 |
Show Grade based on the total mark ( using CASE statement )
Мы можем отобразить оценку учащегося, используя оператор CASE в нашем запросе. MySQL Case запрос выполняет оператор на основе условия соответствия. Здесь мы сравним общую оценку с установленными оценками для разных уровней оценки и соответственно присвоим ей оценку.
MySQL Case запрос выполняет оператор на основе условия соответствия. Здесь мы сравним общую оценку с установленными оценками для разных уровней оценки и соответственно присвоим ей оценку.Подробнее об операторе CASE WHEN THEN читайте здесь.
Вот наш запрос.ВЫБЕРИТЕ идентификатор, имя, класс, социальные сети, математика, наука, сумма (социальные + математика + наука) как Total , СЛУЧАЙ, КОГДА сумма (социальное + математика + наука) >= 225 THEN 'A' КОГДА сумма (социальное + математика + наука) >=200 ТО 'B' КОГДА сумма (социальное + математика + наука) >=170 ТО 'C' ИНАЧЕ "НЕУДАЧА" КОНЕЦ КАК from student_sum GROUP BY idВыход здесь.
| id | name | class | social | math | science | Total | grade |
|---|---|---|---|---|---|---|---|
| 1 | John Deo | Four | 75 | 78 | 84 | 237 | A |
| 2 | Max Ruin | Three | 54 | 85 | 67 | 206 | B |
| 3 | Arnold | Three | 78 | 90 | 65 | 233 | A |
| 4 | Krish Star | Four | 50 | 53 | 51 | 154 | FAIL |
| 5 | John Mike | Четыре | 80 | 89 | 78 | 247 | A |
| 6 | ALECK JOHLE JOHN | ||||||
. 0296 0296 | 198 | C | |||||
| 7 | My John Rob | Five | 77 | 83 | 68 | 228 | A |
| 8 | Asruid | Five | 55 | 55 | 50 | 160 | FAIL |
| 9 | Tes Qry | Six | 68 | 62 | 60 | 190 | C |
| 10 | Большой Джон | Четырехместный | 65 | 76 | 66 | 207 | B |
| id | имя | социальная | математика | наука | всего< /й>"; foreach ($dbo->query($count) as $row) { echo " | ||
| $row[id] | $row[name] | $row[social] | $row[math]< /td> | $row[наука] | $row[total] |
Имя аргумента | Описание |
|---|---|
номер1 Обязательно | Первый номер, который вы хотите добавить. |
номер2-255 Дополнительно | Это второй номер, который вы хотите добавить. Таким образом можно указать до 255 номеров. |
В этом разделе обсуждаются некоторые рекомендации по работе с функцией СУММ. Многое из этого можно применить и для работы с другими функциями.
Метод =1+2 или =A+B. Хотя вы можете ввести =1+2+3 или =A1+B1+C2 и получить полностью точные результаты, эти методы подвержены ошибкам по нескольким причинам:
- org/ListItem»>
#ЗНАЧ! ошибки от ссылки на текст вместо цифр
Если вы используете формулу вроде:
Ваша формула может не работать, если в ячейках, на которые ссылаются, есть какие-либо нечисловые (текстовые) значения, которые вернут #ЗНАЧ! ошибка. SUM будет игнорировать текстовые значения и даст вам сумму только числовых значений.

#ССЫЛКА! ошибка при удалении строк или столбцов
Если вы удалите строку или столбец, формула не будет обновлена, чтобы исключить удаленную строку, и она вернет #ССЫЛКА! error, когда функция СУММ будет автоматически обновляться.
Формулы не будут обновлять ссылки при вставке строк или столбцов
Если вы вставите строку или столбец, формула не будет обновляться, чтобы включить добавленную строку, где автоматически обновится функция СУММ (если вы не выходите за диапазон, указанный в формуле). Это особенно важно, если вы ожидаете, что ваша формула обновится, а она не обновится, так как это оставит вас с неполными результатами, которые вы можете не уловить.

СУММ с отдельными ссылками на ячейки в сравнении с диапазонами
Используя формулу типа:
=СУММ(А1,А2,А3,В1,В2,В3)
В равной степени подвержен ошибкам при вставке или удалении строк в указанном диапазоне по тем же причинам. Гораздо лучше использовать отдельные диапазоны, например:
=СУММ(A1:A3;B1:B3)
Который будет обновляться при добавлении или удалении строк.

Опечатка . Представьте, что вы пытаетесь ввести больше и/или гораздо большие значения, например:
.Затем попробуйте проверить правильность введенных данных. Гораздо проще поместить эти значения в отдельные ячейки и использовать формулу СУММ. Кроме того, вы можете форматировать значения, когда они находятся в ячейках, что делает их более читабельными, чем когда они находятся в формуле.
Я просто хочу складывать/вычитать/умножать/разделять числа Посмотрите эту серию видео об основах математики в Excel или используйте Excel в качестве калькулятора.
Как показать больше/меньше десятичных разрядов? Вы можете изменить формат номера. Выберите нужную ячейку или диапазон и используйте Ctrl+1 , чтобы вызвать диалоговое окно Формат ячеек , затем щелкните вкладку Число и выберите нужный формат, обязательно указав количество десятичных разрядов, которое вы хотите.
org/ListItem»>Как получить разницу между датами? Как и в случае со временем, вы можете добавлять и вычитать даты. Вот очень распространенный пример подсчета количества дней между двумя датами. Это так же просто, как =B2-A2 . Ключом к работе как с датами, так и с временем является то, что вы начинаете с даты/времени окончания и вычитаете дату/время начала.
Дополнительные способы работы с датами см. в разделе Вычисление разницы между двумя датами.
Как суммировать только видимые ячейки? Иногда, когда вы вручную скрываете строки или используете автофильтр для отображения только определенных данных, вы также хотите суммировать только видимые ячейки.
 Вы можете использовать функцию ПРОМЕЖУТОЧНЫЙ ИТОГ. Если вы используете итоговую строку в таблице Excel, любая функция, выбранная вами в раскрывающемся списке «Итого», будет автоматически введена как промежуточный итог. Узнайте больше о том, как суммировать данные в таблице Excel.
Вы можете использовать функцию ПРОМЕЖУТОЧНЫЙ ИТОГ. Если вы используете итоговую строку в таблице Excel, любая функция, выбранная вами в раскрывающемся списке «Итого», будет автоматически введена как промежуточный итог. Узнайте больше о том, как суммировать данные в таблице Excel.
Как добавить или вычесть время? Вы можете складывать и вычитать время несколькими способами. Например, чтобы получить разницу между 8:00 и 12:00 для целей расчета заработной платы, вы должны использовать: =(«12:00 PM»-«8:00 AM»)*24 , взяв время окончания минус время начала. Обратите внимание, что Excel вычисляет время как часть дня, поэтому вам нужно умножить на 24, чтобы получить общее количество часов. В первом примере мы используем =((B2-A2)+(D2-C2))*24 , чтобы получить сумму часов от начала до конца, за вычетом обеденного перерыва (всего 8,50 часов).
Если вы просто добавляете часы и минуты и хотите отображать их таким образом, то вы можете суммировать и не нужно умножать на 24, поэтому во втором примере мы используем =СУММ(A6:C6) , поскольку нам просто нужно общее количество часов и минут для поставленных задач (5:36 или 5 часов 36 минут).
Для получения дополнительной информации см. : Добавление или вычитание времени.
: Добавление или вычитание времени.
Нужна дополнительная помощь?
Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.
См. также
Узнать больше о СУММ
Функция СУММЕСЛИ складывает только те значения, которые соответствуют одному критерию.
Функция СУММЕСЛИМН складывает только те значения, которые соответствуют нескольким критериям.
Функция СЧЁТЕСЛИ подсчитывает только те значения, которые соответствуют одному критерию.

 n)?
n)? n)?
n)? 02.2018, 13:49
02.2018, 13:49  02.2018, 14:33
02.2018, 14:33  Забор!
Забор!
 Частичное совпадение суммы — совпадение с подстановочным знаком
Частичное совпадение суммы — совпадение с подстановочным знаком 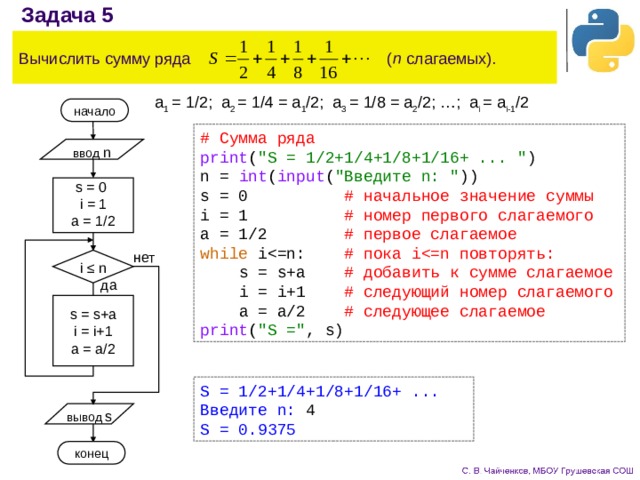

 Под видео есть письменные инструкции.
Под видео есть письменные инструкции. Письменные шаги приведены ниже. Чтобы посмотреть расшифровку видео, перейдите на страницу Running Total Video.
Письменные шаги приведены ниже. Чтобы посмотреть расшифровку видео, перейдите на страницу Running Total Video. Вот формула в ячейке D6 —
начальная точка осталась прежней, а конечная точка находится в текущей
ряд — C6
Вот формула в ячейке D6 —
начальная точка осталась прежней, а конечная точка находится в текущей
ряд — C6 Теперь у него неправильная конечная ссылка на C7 вместо C6:
Теперь у него неправильная конечная ссылка на C7 вместо C6: Он может продолжать суммировать ячейки
A1:A4 и игнорировать A5. Чтобы убедиться, что новые строки включены в итог,
вы можете использовать функцию OFFSET с функцией SUM.
Он может продолжать суммировать ячейки
A1:A4 и игнорировать A5. Чтобы убедиться, что новые строки включены в итог,
вы можете использовать функцию OFFSET с функцией SUM.
 В
В этом примере в итоговую сумму будут включены только строки с заказами пера.
В
В этом примере в итоговую сумму будут включены только строки с заказами пера. Например, формулу на шаге 9 выше можно изменить на:
Например, формулу на шаге 9 выше можно изменить на:  В этом примере
ячейки B2:B10 будут суммированы
В этом примере
ячейки B2:B10 будут суммированы

 Это создает скользящий итог.
Это создает скользящий итог. Посмотрите это короткое видео, чтобы увидеть шаги. Под видео есть письменные инструкции.
Посмотрите это короткое видео, чтобы увидеть шаги. Под видео есть письменные инструкции.
 В этом примере будут проверены ячейки B3:B10 90 218.
В этом примере будут проверены ячейки B3:B10 90 218. В этом видео показана проблема и два способа ее предотвращения. Под видео есть письменные шаги.
В этом видео показана проблема и два способа ее предотвращения. Под видео есть письменные шаги.
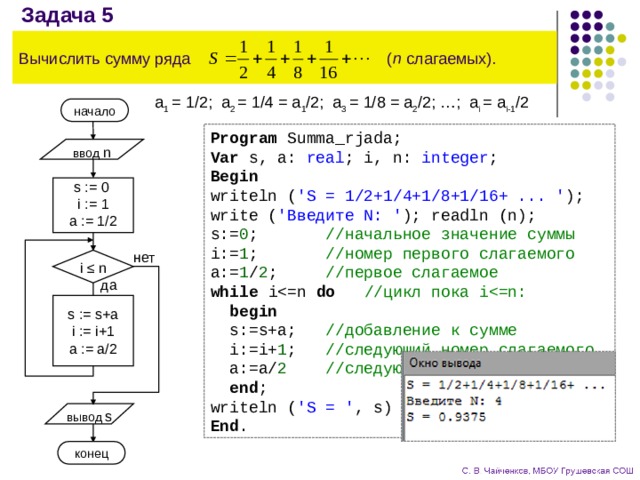 В этом примере будут проверены ячейки C4:C15 — они имеют категорию
В этом примере будут проверены ячейки C4:C15 — они имеют категорию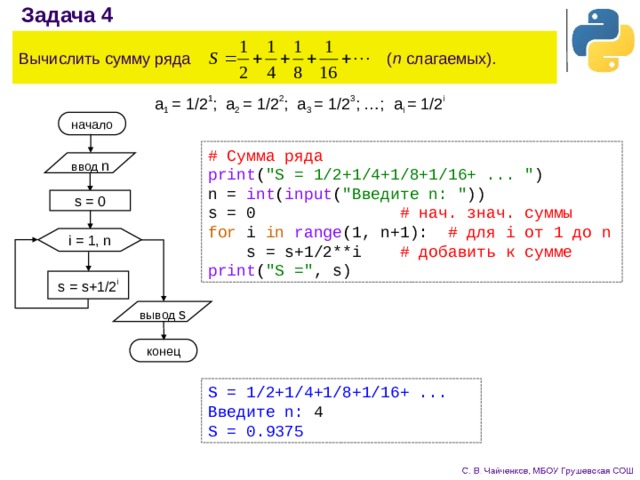 Если вы используете Excel
2007 или более поздней версии следует использовать функцию СУММЕСЛИМН, как описано в
предыдущий раздел.
Если вы используете Excel
2007 или более поздней версии следует использовать функцию СУММЕСЛИМН, как описано в
предыдущий раздел.
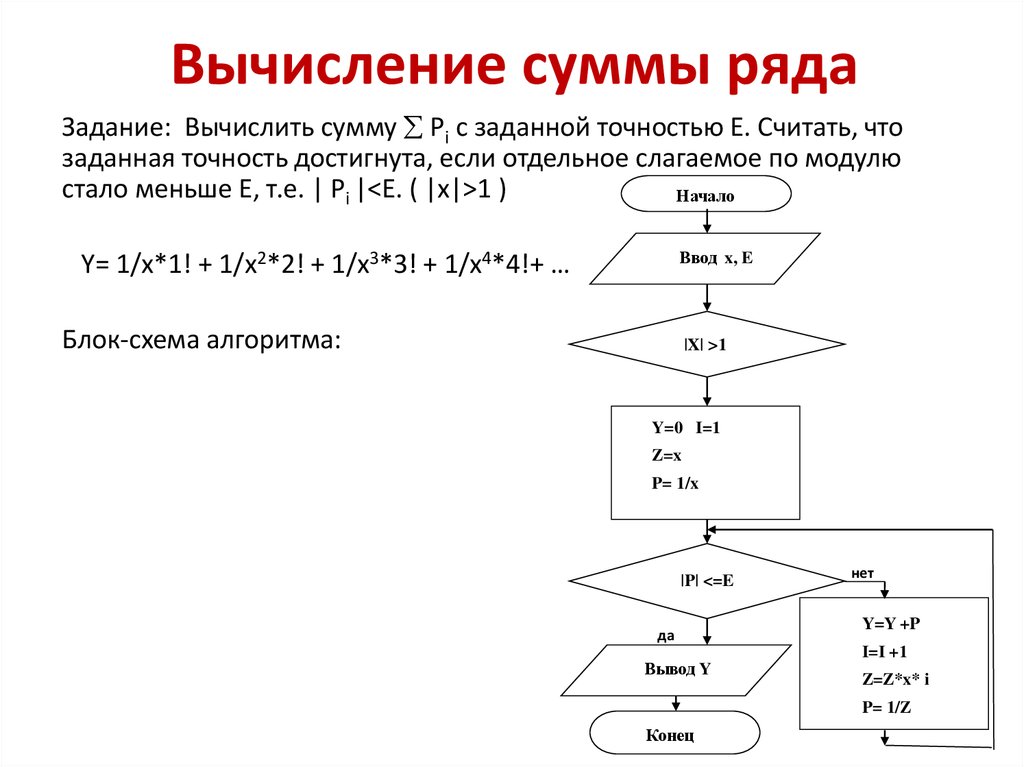 Например:
Например: .
. Ниже приведены два примера:
Ниже приведены два примера:

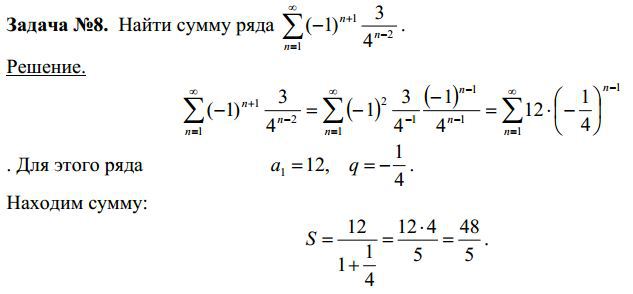 Чтобы проверить, вы можете выбрать ячейки B3: B6 и посмотреть на
общее количество отображается в строке состояния Excel.
Чтобы проверить, вы можете выбрать ячейки B3: B6 и посмотреть на
общее количество отображается в строке состояния Excel.
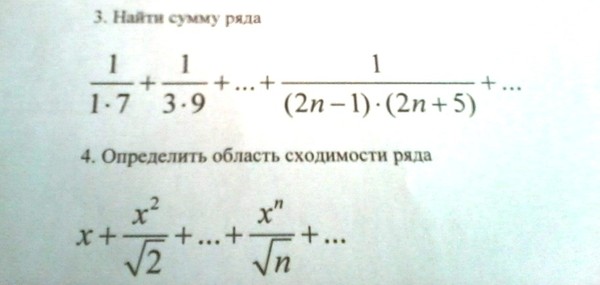


 или вариант 7. В этом примере 3 — второй аргумент, а результат
будет игнорировать скрытые строки, ошибки и вложенные функции АГРЕГАТ и ПРОМЕЖУТОЧНЫЕ ИТОГОВ.
или вариант 7. В этом примере 3 — второй аргумент, а результат
будет игнорировать скрытые строки, ошибки и вложенные функции АГРЕГАТ и ПРОМЕЖУТОЧНЫЕ ИТОГОВ.
 Сэм поделился своим методом выполнения дополнительных сумм или подсчетов на основе видимых данных в отфильтрованной таблице.
Сэм поделился своим методом выполнения дополнительных сумм или подсчетов на основе видимых данных в отфильтрованной таблице. Заархивированный файл имеет формат xlsx и не содержит макросов.
Заархивированный файл имеет формат xlsx и не содержит макросов.