1. Касательные и нормали
М. Борна
Нам часто приходится находить касательные и нормали к кривым, когда мы анализируем силы, действующие на движущееся тело.
Касательная к кривой — это линия, которая касается кривой в одной точке и имеет тот же наклон , что и кривая в этой точке.
нормаль к кривой представляет собой линию , перпендикулярную касательной к кривой.
Касательная
кривой
Нормаль к
кривой
График, показывающий касательную и нормаль к кривой в точке.
Примечание 1: Как мы обсуждалось ранее (в разделе «Наклон касательной к кривой»), мы можем найти наклон касательной в любой точке ( x , y ), используя «dy/dx».
Примечание 2: Чтобы найти уравнение нормали, вспомните условие для двух линий с уклонами м 1 и м 2 быть перпендикулярными (см. Перпендикулярные линии):
м 1 × м 2 = −1
Приложения
Автомобиль занесло при повороте по касательной к двойной кривой из желтых линий.
Тангенс:
- Если мы едем на машине за угол и наезжаем на что-то скользкое на дороге (например, масло, лед, вода или рыхлый гравий) и наша машина начинает скользить, она будет продолжать движение в направлении касательной к кривой.
- Точно так же, если мы возьмем мяч и раскачаем его по кругу, а затем отпустим, он улетит по касательной к кругу движения.
Спицы велосипедного колеса нормальные к ободу.
Нормальный:
- Когда вы быстро едете по круговой дорожке в автомобиле, сила, которую вы чувствуете, толкает вас наружу, равна нормальному к изгибу дороги. Интересно, что сила, заставляющая вас идти за этот угол, на самом деле направлена на 9-ку.0027 центр круга, нормали к кругу.
- Спицы колеса размещаются по нормали к круглой форме колеса в каждой точке, где спица соединяется с центром.
Примеры
Нужна миллиметровка?
Значок миллиметровкиСкачать миллиметровку
1. Найдите градиент из
(i) касательная (ii) обычный
на кривую у = х 92-4(2)`
`=12-8`
`=4`
Наклон нормали определяется с использованием м 1 × м 2 = −1
`m_2=-1/4`
2. Найдите уравнение (i) касательной и (ii) нормали в приведенном выше пример.
Ответить
Используем y
(i) Тангенс имеет наклон «4», поэтому мы имеем:
`у-5=4(х-2)`
дает
`y=4x-3`
или
4 x − y − 3 = 0
(ii) Теперь нормаль к кривой.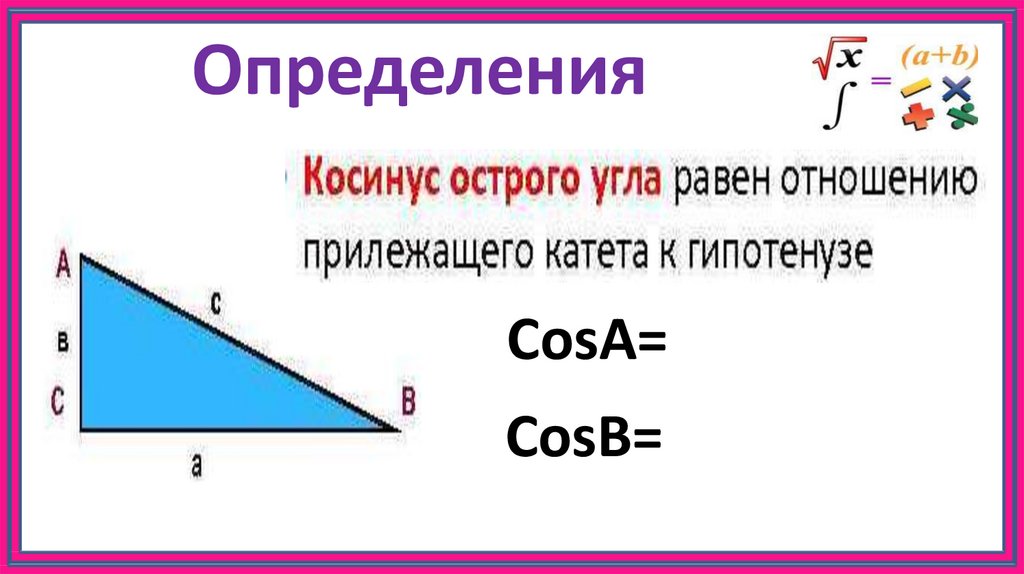
Так как тангенс имеет наклон `4`, мы имеем наклон нормали `m=-1/4`
Таким образом, мы подставляем следующим образом:
`y-5=-1/4(x-2)`
дает
`y=-1/4x+5 1/2`
или
x + 4 y − 22 = 0
3. Эскиз кривая и нормальный в приведенном выше примере.
Ответить
Вот график касательной и нормали к кривой в точке `x=2`.
1212345xyОткрыть изображение на новой страницеГрафик, показывающий касательную (розовый цвет) и нормаль (пунктир) к кривой в точке `(2,5)`
Касательная — это…
Возраст от 16 до 18 лет
Уровень сложности
Матеуш из Технологической академии Эшкрофта, Джозеф из гимназии Эрмистеда, Луис из EMS представили решения этой задачи. Спасибо!
Первое определение касательной было «Касательная — это прямая линия, которая пересекает кривую только в этой
одной точке».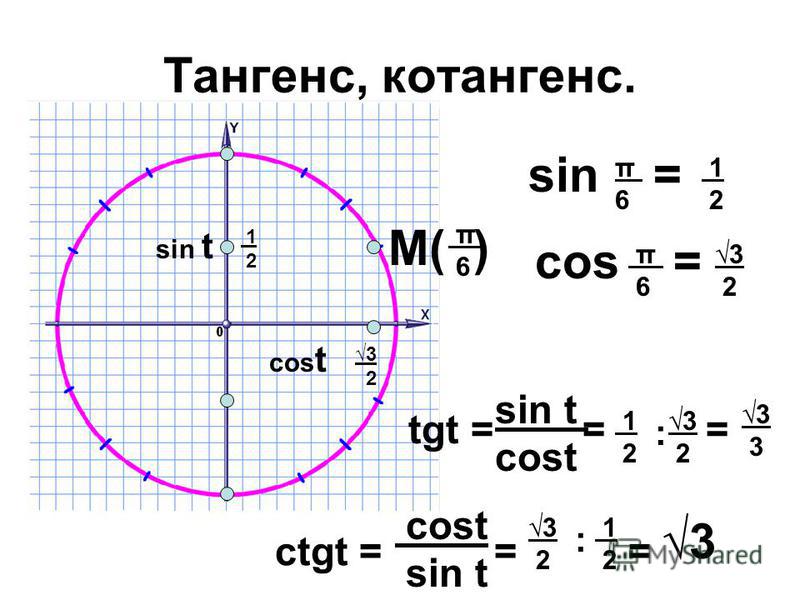
2$). 93-3х+3$. Линия
$y=5$ является касательной в локальном максимуме в точке $(-1,5)$, однако она также пересекает линию
в точке $(2,5)$. Это означает, что она пересекает кривую в двух точках, но является касательной
.
Второе определение касательной звучало так: «Касательная — это прямая линия, которая касается кривой только в этой точке».
Вот контрпример Матеуша:
Это пример, опровергающий определение «Касательная — это прямая, которая касается кривой только в этой точке». Линия y=3x-2 касается кривой и имеет тот же градиент, что и функция в этой точке, однако пересекает кривую более чем в одной точке. Следовательно, второе определение не обязательно верно. 93-0.001x$, что
аналогично, но с другим коэффициентом для члена $x$, эти две точки
находятся в пределах 0,06$ друг от друга, что определенно «близко».
Определение касательной Матеушем:
Более точным определением касательной было бы «прямая линия с тем же градиентом, что и функция, в точке, в которой она проведена, которая не пересекает кривую в точке, в которой она нарисована».