Калькулятор степеней онлайн | umath.ru
Калькулятор степеней поможет просто и быстро возвести число в степень онлайн. При этом показатель степени может быть как положительным, так и отрицательным!
Что такое степень числа?
Как возвести число в степень?
Чтобы понять, как возводить число в степень, рассмотрим несколько простых примеров.
Возведём в пятую степень число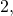 
то есть вычислим значение выражения 
По определению, данному выше, 
Вычислим, чему равно 
то есть чему равно число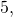 
возведённое в третью степень. 
Отрицательный показатель степени
Показатели степени могут быть не только положительными, но и отрицательными.
![\[a^{-n} = \frac{1}{a^n}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-73b589c14a90741b669884b3c5862de6_l3.png)
Например,
![\[2^{-3} = \frac{1}{2^3} = \frac{1}{8},\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-5a94a73ed14963b56d16c2dec7f319f5_l3.png)
а
![\[5^{-2} = \frac{1}{5^2} = \frac{1}{25}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-cb76185690c4bd183dd6ddff23a54b1d_l3.png)
Как пользоваться калькулятором степеней
Калькулятор помогает возводить число в степень онлайн. Основанием степени могут быть любые целые числа и десятичные дроби. Показатель степени тоже может быть любой десятичной дробью, однако следует помнить о том, что для отрицательных чисел не определена операция возведения в нецелую степень.
При записи дробных чисел можно использовать как точку, так и запятую. В ответе большие числа записываются в так называемом «научном формате», то есть число выглядит как <число>e<количество нулей>. Например, 
, а 
Таблица степеней
Что такое степень числа?
Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a».
\[ \underbrace{a \cdot a \cdot a \cdot a \cdot \cdots \cdot a = a ^{n} }_{n — \text множителей} \]
Запись «an» читается так: «а в степени n» или «n-ая степень числа a».
где:
a — основание степени;
n — показатель степени.
Таблица степеней от 1 до 10
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1n | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2n | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1 024 |
| 3n | 3 | 9 | 27 | 81 | 243 | 729 | 2 187 | 6 561 | 19 683 | 59 049 |
| 4n | 4 | 16 | 64 | 256 | 1 024 | 4 096 | 16 384 | 65 536 | 262 144 | 1 048 576 |
| 5n | 5 | 25 | 125 | 625 | 3 125 | 15 625 | 78 125 | 390 625 | 1 953 125 | 9 765 625 |
| 6n | 6 | 36 | 216 | 1 296 | 7 776 | 46 656 | 279 936 | 1 679 616 | 10 077 696 | 60 466 176 |
| 7n | 7 | 49 | 343 | 2 401 | 16 807 | 117 649 | 823 543 | 5 764 801 | 282 475 249 | |
| 8n | 8 | 64 | 512 | 4 096 | 32 768 | 262 144 | 2 097 152 | 16 777 216 | 134 217 728 | 1 073 741 824 |
| 9n | 9 | 81 | 729 | 6 561 | 59 049 | 531 441 | 4 782 969 | 43 046 721 | 387 420 489 | 3 486 784 401 |
| 10n | 10 | 100 | 1 000 | 10 000 | 100 000 | 1 000 000 | 10 000 000 | 100 000 000 | 1 000 000 000 | 10 000 000 000 |
Таблица степеней от 1 до 10
|
1 1 = 1 1 2 = 1 1 3 = 1 1 4 = 1 1 5 = 1 1 6 = 1 1 7 = 1 1 8 = 1 1 9 = 1 1 10 = 1 |
2 1 = 2 2 2 = 4 2 3 = 8 2 4 = 16 2 6 = 64 2 7 = 128 2 8 = 256 2 9 = 512 2 10 = 1024 |
3 1 = 3 3 2 = 9 3 3 = 27 3 4 = 81 3 5 = 243 3 6 = 729 3 7 = 2187 3 8 = 6561 3 9 = 19683 3 10 = 59049 |
4 1 = 4 4 2 = 16 4 3 = 64 4 4 = 256 4 5 = 1024 4 6 = 4096 4 7 = 16384 4 8 = 65536 4 9 = 262144 4 10 = 1048576 |
5 1 = 5 5 2 = 25 5 3 = 125 5 4 = 625 5 5 = 3125 5 6 = 15625 5 7 = 78125 5 8 = 390625 5 9 = 1953125 5 10 = 9765625 |
|
6 1 = 6 6 2 = 36 6 3 = 216 6 4 = 1296 6 5 = 7776 6 6 = 46656 6 7 = 279936 6 8 = 1679616 6 9 = 10077696 6 10 = 60466176 |
7 1 = 7 7 2 = 49 7 3 = 343 7 4 = 2401 7 5 = 16807 7 6 = 117649 7 7 = 823543 7 8 = 5764801 7 9 = 40353607 7 10 = 282475249 |
8 1 = 8 8 2 = 64 8 3 = 512 8 4 = 4096 8 5 = 32768 8 6 = 262144 8 7 = 2097152 8 8 = 16777216 8 9 = 134217728 8 10 = 1073741824 |
9 1 = 9 9 2 = 81 9 3 = 729 9 4 = 6561 9 5 = 59049 9 6 = 531441 9 7 = 4782969 9 8 = 43046721 9 9 = 387420489 9 10 = 3486784401 |
10 1 = 10 10 2 = 100 10 3 = 1000 10 4 = 10000 10 5 = 100000 10 6 = 1000000 10 7 = 10000000 10 8 = 100000000 10 9 = 1000000000 10 10 = 10000000000 |
Калькулятор степеней онлайн
Входные данные
Число*
Степень*
Точность
1234567
* Обязательные поля для заполненияРезультат
В таблице степеней содержатся значения натуральных положительных чисел от 1 до 10.
Запись 35 читают «три в пятой степени». В этой записи число 3 называют основанием степени, число 5 показателем степени, выражение 35 называют степенью.
Показатель степени указывает сколько множителей в произведение, 35=3×3×3×3×3=243
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
| Назва | Степінь | Число | Префікс | Позначення |
|---|---|---|---|---|
| Один | 0 | 1 | ||
| Десять | 1 | 10 | дека- | да |
| Сто | 2 | 100 | гекто- | г |
| Тисяча | 3 | 1000 | кіло- | к |
| 10000 (міріада) | 4 | 10000 | ||
| Мільйон | 6 | 1000,000 | мега- | М |
| Більйон (мільярд) | 9 | 1000,000,000 | гіга- | Г |
| Трильйон (більйон) | 12 | 1000,000,000,000 | тера- | Т |
| Квадрильйон (більярд) | 15 | 1000,000,000,000,000 | пета- | П |
| Квінтильйон (трильйон) | 18 | 1,000,000,000,000,000,000 | екса- | Е |
| Секстильйон (трильярд) | 21 | 1,000,000,000,000,000,000,000 | зета- | З |
| Септильон (квадрильйон) | 24 | 1,000,000,000,000,000,000,000,000 | йота- | Й |
| Октильйон | 27 | 1,000,000,000,000,000,000,000,000,000 | ксона- | |
| Нонільйон | 30 | 1,000,000,000,000,000,000,000,000,000,000 | векта- | |
| Децильйон | 33 | 1,000,000,000,000,000,000,000,000,000,000,000 | вінка- | |
| Ундецильйон | 36 | 1,000,000,000,000,000,000,000,000,000,000,000,000 | унтра- | |
| Додецильйон | 39 | 1,000,000,000,000,000,000,000,000,000,000,000,000,000 | сампа- | |
| Тредецильйон | 42 | 1,000,000,000,000,000,000,000,000,000,000,000,000,000,000 | роса- | |
| Кватродецильйон | 45 | 1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 | квада- | |
| Квіндецильйон | 48 | 1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 | оба- | |
| Сексдецильйон | 51 | 1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 | ||
| Септемдецильйон | 54 | 1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 | ||
| Октодецильйон | 57 | 1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 | ||
| … | … | … | … | … |
| Гугол | 100 | 10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 | ||
| … | … | … | … | … |
| Техническая информация тут | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица степеней степеней. Степени натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10. Таблица степеней. Поделиться:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Сколько будет 10 в десятой степени?
10000000000 то есть 1 и десять нулей
Всего лишь 10 миллиардов, до трилиона нехватает еще двух нулей.
Есть один верный ответ ДАХРЕНА, тоесть 1000000000000
Зачем так много?
31000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Возведение в степень — Википедия
Графики четырёх функций вида y=ax{\displaystyle y=a^{x}}, a{\displaystyle a} указано рядом с графиком функцииВозведе́ние в сте́пень — арифметическая операция, первоначально определяемая как результат многократного умножения числа на себя. Степень с основанием a{\displaystyle a} и натуральным показателем b{\displaystyle b} обозначается как
- ab=a⋅a⋅…⋅a⏟b,{\displaystyle a^{b}=\underbrace {a\cdot a\cdot \ldots \cdot a} _{b},}
где b{\displaystyle b} — количество множителей (умножаемых чисел)[1][К 1].
Например, 32=3⋅3=9;24=2⋅2⋅2⋅2=16{\displaystyle 3^{2}=3\cdot 3=9;\quad 2^{4}=2\cdot 2\cdot 2\cdot 2=16}
В языках программирования, где написание ab{\displaystyle a^{b}} невозможно, применяются альтернативные обозначения[⇨].
Возведение в степень может быть определено также для отрицательных[⇨], рациональных[⇨], вещественных[⇨] и комплексных[⇨] степеней[1].
Извлечение корня — одна из операций, обратных возведению в степень, она по известным значениям степени c=ab{\displaystyle c=a^{b}} и показателя b{\displaystyle b} находит неизвестное основание a=cb{\displaystyle a={\sqrt[{b}]{c}}}. Вторая обратная операция — логарифмирование, она по известным значениям степени c=ab{\displaystyle c=a^{b}} и основания a{\displaystyle a} находит неизвестный показатель b=logac{\displaystyle b=\log _{a}c}. Задача нахождения числа по известному его логарифму (потенцирование, антилогарифм) решается с помощью операции возведения в степень[⇨]).
Существует алгоритм быстрого возведения в степень, выполняющий возведение в степень за меньшее, чем в определении, число умножений.
Запись an{\displaystyle a^{n}} обычно читается как «a в n{\displaystyle n}-й степени» или «a в степени n». Например, 104{\displaystyle 10^{4}} читается как «десять в четвёртой степени», 103/2{\displaystyle 10^{3/2}} читается как «десять в степени три вторых (или: полтора)».
Для второй и третьей степени существуют специальные названия: возведение в квадрат и в куб соответственно. Так, например, 102{\displaystyle 10^{2}} читается как «десять в квадрате», 103{\displaystyle 10^{3}} читается как «десять в кубе». Такая терминология возникла из древнегреческой математики. Древние греки формулировали алгебраические конструкции на языке геометрической алгебры. В частности, вместо употребления слова «умножение» они говорили о площади прямоугольника или об объёме параллелепипеда: вместо a2{\displaystyle a^{2}}, a3{\displaystyle a^{3}} древние греки говорили «квадрат на отрезке a», «куб на a». По этой причине четвёртую степень и выше древние греки избегали[2].
Основные свойства[править | править код]
Все приведенные ниже основные свойства возведения в степень выполняются для натуральных, целых, рациональных и вещественных чисел[3]. Для комплексных чисел, в силу многозначности комплексной операции, они выполняются только в случае натурального показателя степени[⇨].
Запись anm{\displaystyle a^{n^{m}}} не обладает свойством ассоциативности (сочетательности), то есть, в общем случае,(an)m≠a(nm){\displaystyle (a^{n})^{m}\neq a^{\left({n^{m}}\right)}} Например, (22)3=43=64{\displaystyle (2^{2})^{3}=4^{3}=64}, а 2(23)=28=256{\displaystyle 2^{\left({2^{3}}\right)}=2^{8}=256}. В математике принято считать запись anm{\displaystyle a^{n^{m}}} равнозначной a(nm){\displaystyle a^{\left({n^{m}}\right)}}, а вместо (an)m{\displaystyle (a^{n})^{m}} можно писать просто anm{\displaystyle a^{nm}}, пользуясь предыдущим свойством. Впрочем, некоторые языки программирования не придерживаются этого соглашения.
Возведение в степень не обладает свойством коммутативности (переместительности): вообще говоря, ab≠ba{\displaystyle a^{b}\neq b^{a}}, например, 25=32{\displaystyle 2^{5}=32}, но 52=25.{\displaystyle 5^{2}=25.}
Таблица натуральных степеней небольших чисел[править | править код]
| n | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 | 9 | 27 | 81 | 243 | 729 | 2 187 | 6 561 | 19 683 | 59 049 |
| 4 | 16 | 64 | 256 | 1024 | 4 096 | 16 384 | 65 536 | 262 144 | 1 048 576 |
| 5 | 25 | 125 | 625 | 3125 | 15 625 | 78 125 | 390 625 | 1 953 125 | 9 765 625 |
| 6 | 36 | 216 | 1296 | 7 776 | 46 656 | 279 936 | 1 679 616 | 10 077 696 | 60 466 176 |
| 7 | 49 | 343 | 2401 | 16 807 | 117 649 | 823 543 | 5 764 801 | 40 353 607 | 282 475 249 |
| 8 | 64 | 512 | 4096 | 32 768 | 262 144 | 2 097 152 | 16 777 216 | 134 217 728 | 1 073 741 824 |
| 9 | 81 | 729 | 6561 | 59 049 | 531 441 | 4 782 969 | 43 046 721 | 387 420 489 | 3 486 784 401 |
| 10 | 100 | 1000 | 10 000 | 100 000 | 1 000 000 | 10 000 000 | 100 000 000 | 1 000 000 000 | 10 000 000 000 |
Целая степень[править | править код]
Операция обобщается на произвольные целые числа, включая отрицательные и ноль[4]::
- az={az,z>01,z=0,a≠01a|z|,z<0,a≠0{\displaystyle a^{z}={\begin{cases}a^{z},&z>0\\1,&z=0,a\neq \;0\\{\frac {1}{a^{|z|}}},&z<0,a\neq \;0\end{cases}}}
Результат не определён при a=0{\displaystyle a=0} и z⩽0{\displaystyle z\leqslant 0}.
Рациональная степень[править | править код]
Возведение в рациональную степени p/q,{\displaystyle p/q,} где p{\displaystyle p} — целое число, а q{\displaystyle q} — натуральное, определяется следующим образом[4]:
- apq=(aq)p{\displaystyle a^{p \over q}=({\sqrt[{q}]{a}})^{p}}.
Результат не определён при a=0{\displaystyle a=0} и p/q⩽0.{\displaystyle p/q\leqslant 0.} Для отрицательных a{\displaystyle a} в случае нечётного p{\displaystyle p} и чётного q{\displaystyle q} в результате вычисления степени получаются комплексные числа.
Следствие: an=a1/n.{\displaystyle {\sqrt[{n}]{a}}=a^{1/n}.} Таким образом, понятие рациональной степени объединяет возведение в целочисленную степень и извлечение корня в единую операцию.
Вещественная степень[править | править код]
Если a⩾0,r{\displaystyle a\geqslant 0,r} — вещественные числа, причём r{\displaystyle r} — иррациональное число, возможно определить ar{\displaystyle a^{r}} следующим образом: поскольку любое вещественное число можно приблизить, сверху и снизу, двумя рациональными числами, то есть можно подобрать для r{\displaystyle r} рациональный интервал [p,q]{\displaystyle [p,q]} с любой степенью точности, то общая часть всех соответствующих интервалов [ap,aq]{\displaystyle [a^{p},a^{q}]} состоит из одной точки, которая и принимается за ar{\displaystyle a^{r}}.
Полезные формулы:
- xy=aylogax{\displaystyle x^{y}=a^{y\log _{a}x}}
- xy=eylnx{\displaystyle x^{y}=e^{y\ln x}}
- xy=10ylgx{\displaystyle x^{y}=10^{y\lg x}}
Последние две формулы используют для возведения положительных чисел в произвольную степень на электронных калькуляторах (включая компьютерные программы), не имеющих встроенной функции xy{\displaystyle x^{y}}, и для приближённого возведения в нецелую степень или для целочисленного возведения в степень, когда числа слишком велики для того, чтобы записать результат полностью.
Комплексная степень[править | править код]
Возведение комплексного числа в натуральную степень выполняется обычным умножением, и результат однозначен (см. формулу Муавра). Основой для более общего определения комплексной степени служит экспонента ez{\displaystyle e^{z}}, где e{\displaystyle e} — число Эйлера, z=x+iy{\displaystyle z=x+iy} — произвольное комплексное число[5].
Определим комплексную экспоненту с помощью такого же ряда, как и вещественную:
- ez=1+z+z22!+z33!+z44!+⋯.{\displaystyle e^{z}=1+z+{\frac {z^{2}}{2!}}+{\frac {z^{3}}{3!}}+{\frac {z^{4}}{4!}}+\cdots .}
Этот ряд абсолютно сходится для любого комплексного z,{\displaystyle z,} поэтому его члены можно как угодно перегруппировывать. В частности, отделим от него часть для eiy{\displaystyle e^{iy}}:
- eiy=1+iy+(iy)22!+(iy)33!+(iy)44!+⋯=(1−y22!+y44!−y66!+⋯)+i(y−y33!+y55!−⋯).{\displaystyle e^{iy}=1+iy+{\frac {(iy)^{2}}{2!}}+{\frac {(iy)^{3}}{3!}}+{\frac {(iy)^{4}}{4!}}+\cdots =\left(1-{\frac {y^{2}}{2!}}+{\frac {y^{4}}{4!}}-{\frac {y^{6}}{6!}}+\cdots \right)+i\left(y-{\frac {y^{3}}{3!}}+{\frac {y^{5}}{5!}}-\cdots \right).}
В скобках получились известные из вещественного анализа ряды для косинуса и синуса, и мы получили формулу Эйлера:
- ez=exeyi=ex(cosy+isiny){\displaystyle e^{z}=e^{x}e^{yi}=e^{x}(\cos y+i\sin y)}
Общий случай ab{\displaystyle a^{b}}, где a,b{\displaystyle a,b} — комплексные числа, определяется через представление a{\displaystyle a} в показательной форме: a=rei(θ+2πk){\displaystyle a=re^{i(\theta +2\pi k)}} согласно определяющей формуле[5]:
- ab=(eLn(a))b=(eln(r)+i(θ+2πk))b=eb(ln(r)+i(θ+2πk)).{\displaystyle a^{b}=(e^{\operatorname {Ln} (a)})^{b}=(e^{\operatorname {ln} (r)+i(\theta +2\pi k)})^{b}=e^{b(\operatorname {ln} (r)+i(\theta +2\pi k))}.}
Здесь Ln{\displaystyle \operatorname {Ln} } — комплексный логарифм, ln{\displaystyle \ln } — его главное значение.
При этом комплексный логарифм — многозначная функция, так что, вообще говоря, комплексная степень определена неоднозначно[5]. Неучёт этого обстоятельства может привести к ошибкам. Пример: возведём известное тождество e2πi=1{\displaystyle e^{2\pi i}=1} в степень i.{\displaystyle i.} Слева получится e−2π,{\displaystyle e^{-2\pi },} справа, очевидно, 1. В итоге: e−2π=1,{\displaystyle e^{-2\pi }=1,} что, как легко проверить, неверно. Причина ошибки: возведение в степень i{\displaystyle i} даёт и слева, и справа бесконечное множество значений (при разных k{\displaystyle k}), поэтому правило (ab)c=abc{\displaystyle \left(a^{b}\right)^{c}=a^{bc}} здесь неприменимо. Аккуратное применение формул определения комплексной степени даёт слева и справа e−2πk;{\displaystyle e^{-2\pi k};} отсюда видно, что корень ошибки — путаница значений этого выражения при k=0{\displaystyle k=0} и при k=1.{\displaystyle k=1.}
Потенцирование (от нем. potenzieren[К 2]) — нахождение числа по известному значению его логарифма, то есть решение уравнения logax=b{\displaystyle \log _{a}x=b}. Из определения логарифма вытекает, что x=ab{\displaystyle x=a^{b}}, таким образом, возведение a{\displaystyle a} в степень b{\displaystyle b} может быть названо другими словами «потенцированием b{\displaystyle b} по основанию a{\displaystyle a}».
Антилогарифм — результат потенцирования, то есть нахождения числа по известному значению его логарифма[6]. Как самостоятельное понятие используется в логарифмических таблицах, логарифмических линейках, микрокалькуляторах.
Согласно сказанному выше, антилогарифм по основанию a{\displaystyle a} для числа b{\displaystyle b} равен ab{\displaystyle a^{b}}:
- antlogab=ab.{\displaystyle \operatorname {ant} \log _{a}{b}=a^{b}.}
Разновидности[править | править код]
Поскольку в выражении xy{\displaystyle x^{y}} используются два символа (x{\displaystyle x} и
Чему будет равно 10 в минус 6 степени?? 10 в минус 10 степени?? Скажите пожалуйста!!!!))
10 в 6 степени (просто прибавляей 6 нулей к 10) 10000000 а так как степень четная, то минус опускается)
Десять в минус какой-то степени, это 1 деленная на 1 с количеством нулей равным степени. Например, 10 в минус 2 степени = 0,01
Если единицу разделить на миллион это и будет 10 в минус шестой степени. А вам зачем столько мало надо? Берите миллион, не мелочитесь..
10 в минус 6 степени равно 1/10^6 10 в минус 10 степени равно 1/10^10
десять в минус шестой степени, это одна десятая в шестой степени, т. е. 1/1000000 а десять в минус десятой, это одна десятая в десятой степени, т. е. 1/10000000000