что это такое и как его найти?
Модуль — математическое понятие, которое проходят в шестом классе. Сам по себе числовой модуль не представляет собой ничего сложного, это одна из простейших тем в начальной математике. Но если случайно пропустить изучение нужного параграфа, то можно столкнуться с непониманием темы. Поэтому напомним, что именно называется модулем, как его найти для разных чисел, и что представляет собой это понятие по сути.
Модуль с точки зрения геометрии
Забегая вперед, попробуем сразу понять, что же представляет собой модуль на практике — так будет легче уловить его смысл. Нарисуем на листе бумаги прямую координат, возьмем нуль за точку отсчета, а по правую и по левую стороны на одинаковом расстоянии поставим некие две точки — например, 5 и -5.
Модулем будет считаться именно фактическое расстояние до нуля от -5 и от 5. Очевидно, что это расстояние будет совершенно одинаковым. Поэтому в обоих случаях модуль будет равняться числу «5» — и неважно, какой знак стоит перед исходным числом, которое мы рассматриваем.

Как найти модуль числа?
Теперь, когда мы визуально представляем, что же такое модуль, будет проще понять формулировку из учебника. Она гласит, что модулем некоего числа является само это число, если оно положительное, число, противоположное исходному числу, если оно отрицательное, и нуль, если модуль мы ищем для нуля.
Это можно сформулировать и иначе — модулем любого числа будет само это число в абсолютном выражении, то есть без учета знака. Записывается модуль так — по обе стороны от нужного числа ставятся вертикальные линии, например, модуль для числа «5» будет равен «5», а записываться он будет, как |5|.
Из всего, что мы рассказали выше, можно вывести несколько строгих правил для модулей.
- Может ли модуль быть отрицательным? Нет! Модуль может быть только положительным. Даже если речь идет об отрицательном числе, например, -7, то его модуль будет равен |7| — числу, противоположному исходному.
- Для нуля модуль всегда будет равен нулю. Верно и другое — нуль может быть модулем исключительно в том случае, если вычисляется он для числа нуль, и ни в каком другом.
- Если нужно найти модуль для выражения типа a*b, то есть модуль произведения, то можно сначала найти модуль а, затем модуль b, и перемножить их друг на друга.
- То же самое касается и деления — если нам нужно разделить y на z и найти модуль получившегося числа, то можно взять модуль y и разделить его на модуль z. Результат будет одним и тем же.
Похожие статьи
infoogle.ru
Как найти модуль числа 🚩 википедия числа 🚩 Математика
Автор КакПросто!
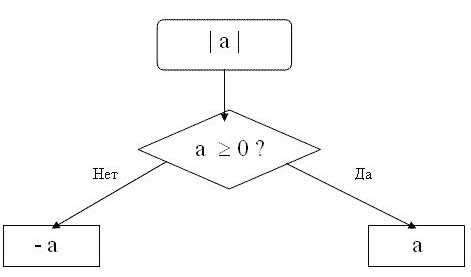
Модуль числа n представляет собой количество единичных отрезков от начала координат до точки n. Причем не важно, в какую сторону будет отсчитываться это расстояние – вправо или влево от нуля.
Статьи по теме:
Инструкция
Модуль числа также принято называть абсолютной величиной этого числа. Он обозначается короткими вертикальными линиями, проведенными слева и справа от числа. Например, модуль числа 15 записывается следующим образом: |15|. Помните, что модуль может быть только положительным числом или нулем. Модуль положительного числа равен самому числу. Модуль нуля равен нулю. То есть для любого числа n, которое больше либо равно нулю, будет справедлива следующая формула |n| = n. Например, |15| = 15, то есть модуль числа 15 равен 15-ти.Модулем отрицательного числа будет то же число, но с противоположным знаком. То есть для любого числа n, которое меньше нуля, будет справедлива формула |n| = -n. Например, |-28| = 28. Модуль числа -28 равен 28-ми.
Можно находить модули не только для целых, но и для дробных чисел. Причем в отношении дробных чисел действуют те же правила. Например, |0,25| = 25, то есть модуль числа 0,25 будет равен 0,25. А |-¾| = ¾, то есть модуль числа -¾ будет равен ¾.
При работе с модулями полезно знать, что модули противоположных чисел всегда равны друг другу, то есть |n| =|-n|. Это является основным свойством модулей. Например, |10| = |-10|. Модуль числа 10 равен 10-ти, точно так же, как модуль числа -10. Кроме того, |a — b| = |b — a|, так как расстояние от точки a до точки b и расстояние от b до a равны друг другу. Например, |25 — 5| = |5 — 25|, то есть |20| = |- 20|.
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Как найти модуль комплексного числа 🚩 Математика
Если вам нужно назвать расстояние между двумя городами, то можно дать ответ, состоящий из одного числа в милях, километрах или в других единицах измерения линейных расстояний. Однако если вы должны описать, как добраться из одного города в другой, то необходимо дать больше информации, чем просто расстояние между двумя точками на карте. В этом случае стоит сказать о направлении, в котором надо двигаться и о времени движения.
Вид информации, которая выражает одномерное измерение, в науке называется скалярной величиной. Скаляры – это числа, используемые в большинстве математических расчетов. К примеру, масса и скорость, которыми обладает тот или иной объект являются скалярными величинами.
Для того чтобы успешно анализировать природные явления, мы должны работать с абстрактными объектами и методами, способными представлять многомерные величины. Здесь необходимо отказываться от скалярных чисел в пользу комплексных. Они дают возможность выразить два измерения одновременно.
Комплексные числа легче понять, когда они представлены в графическом виде. Если нарисовать линию, имеющую определенную длину и направление, то это и будет графическое представление комплексного числа. Оно также широко известно в физике как вектор.
Такие типы чисел, как целые, рациональные, иррациональные и реальные знакомы детям со школы. Им всем присуща одномерность. Прямолинейность числовой прямой иллюстрирует это графически. Вы можете перемещаться вверх или вниз по ней, но все «движения» по этой линии будут ограничиваются горизонтальной осью. Одномерных, скалярных цифр вполне достаточно для подсчета количества предметов, выражения веса или измерения постоянного напряжения батареи. Но они не могут обозначать что-то более сложное. Скалярами невозможно одновременно выразить расстояние и направление между двумя городами, или амплитуду с фазой. Представлять эти виды чисел необходимо уже в виде многомерной области значений. Другими словами, нам нужны векторные величины, которые могут иметь не только величину, но и направление распространения.
Скалярное число является типом математического объекта, который люди привыкли использовать в повседневной жизни — это температура, длина, вес и т.д. Комплексное число представляет собой значение, которое включает в себя два типа данных.
Вектор является графическим изображением комплексного числа. Он выглядит, как стрелка с начальной точкой, определенной длиной и направлением. Иногда слово «вектор» используется в радиотехнике, где он выражает фазовый сдвиг между сигналами.
www.kakprosto.ru
Как найти модуль скорости | Сделай все сам
Скорость тела характеризуется направлением и модулем. Иными словами,

Инструкция
1. Введите систему координат, касательно которой вы будете определять направление и модуль скорости . Если в задаче теснее задана формула зависимости скорости от времени, вводить систему координат не надобно – предполагается, что она теснее есть.
2. По имеющейся функции зависимости скорости от времени дозволено обнаружить значение скорости в всякий момент времени t. Пускай, скажем, v=2t?+5t-3. Если требуется обнаружить модуль скорости в момент времени t=1, примитивно подставьте это значение в уравнение и посчитайте v: v=2+5-3=4.
3. Когда задача требует обнаружить скорость в исходный момент времени, подставьте в функцию t=0. Таким же образом дозволено обнаружить время, подставив вестимую скорость. Так, в конце пути тело остановилось, то есть, его скорость стала равна нулю. Тогда 2t?+5t-3=0. Отсель t=[-5±?(25+24)]/4=[-5±7]/4. Получается, что либо t=-3, либо t=1/2, а от того что время не может быть негативным, остается только t=1/2.
4. Изредка в задачах уравнение скорости дается в завуалированной форме. Скажем, в условии сказано, что тело двигалось равноускоренно с негативным убыстрением -2 м/с?, а в первоначальный момент скорость тела составляла 10 м/с. Негативное убыстрение обозначает, что тело равномерно замедлялось. Из этих условий дозволено составить уравнение для скорости : v=10-2t. С всей секундой скорость будет уменьшаться на 2 м/с, пока тело не остановится. В конце пути скорость обнулится, следственно легко обнаружить всеобщее время движения: 10-2t=0, откуда t=5 секунд. Через 5 секунд позже начала движения тело остановится.
5. Помимо откровенного движения тела, существует еще и движение тела по окружности. В всеобщем случае оно является криволинейным. Тут появляется центростремительное убыстрение, которое связано с линейной скоростью формулой a(c)=v?/R, где R – радиус. Комфортно рассматривать также угловую скорость ?, причем v=?R.
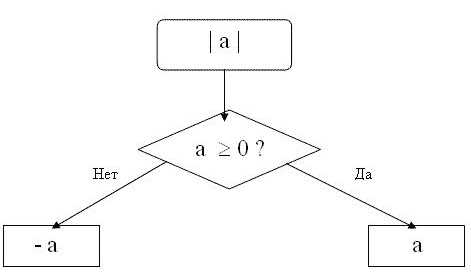
Модуль числа n представляет собой число единичных отрезков от начала координат до точки n. Причем не главно, в какую сторону будет отсчитываться это расстояние – вправо либо налево от нуля.
Инструкция
1. Модуль числа также принято называть безусловной величиной этого числа . Он обозначается короткими вертикальными линиями, проведенными слева и справа от числа . Скажем, модуль числа 15 записывается дальнейшим образом: |15|.
2. Помните, что модуль может быть только позитивным числом либо нулем. Модуль позитивного числа равен самому числу. Модуль нуля равен нулю. То есть для всякого числа n, которое огромнее либо равно нулю, будет объективна дальнейшая формула |n| = n. Скажем, |15| = 15, то есть модуль числа 15 равен 15-ти.
3. Модулем негативного числа будет то же число, но с противоположным знаком. То есть для всякого числа n, которое поменьше нуля, будет объективна формула |n| = -n. Скажем, |-28| = 28. Модуль числа -28 равен 28-ми.
4. Дозволено находить модули не только для целых, но и для дробных чисел. Причем в отношении дробных чисел действуют те же правила. Скажем, |0,25| = 25, то есть модуль числа 0,25 будет равен 0,25. А |-?| = ?, то есть модуль
5. При работе с модулями пригодно знать, что модули противоположных чисел неизменно равны друг другу, то есть |n| =|-n|. Это является основным свойством модулей. Скажем, |10| = |-10|. Модуль числа 10 равен 10-ти, верно так же, как модуль числа -10. Помимо того, |a – b| = |b – a|, потому что расстояние от точки a до точки b и расстояние от b до a равны друг другу. Скажем, |25 – 5| = |5 – 25|, то есть |20| = |- 20|.
Для нахождения метаморфозы скорости определитесь с типом движения тела. В случае если движение тела равномерно, изменение скорости равно нулю. Если тело движется с убыстрением, то изменение его скорости в весь момент времени дозволено узнать, если отнять от мгновенной скорости в данный момент времени его исходную скорость.
Вам понадобится
- секундомер, спидометр, радар, рулетка, акселерометр.
Инструкция
1. Определение метаморфозы скорости произвольно движущегося по прямой траекторииС поддержкой спидометра либо радара измерьте скорость тела в начале и конце отрезка пути. После этого от финального итога отнимите первоначальный, это и будет изменение скорости тела.
2. Определение метаморфозы скорости тела, движущегося с ускорениемНайдите убыстрение тела. Используйте акселерометр либо динамометр. Если знаменита масса тела, тогда силу, действующую на тело, поделите на его массу (a=F/m). Позже этого измерьте время, за которое происходил процесс метаморфозы скорости . Дабы обнаружить изменение скорости , умножьте значение убыстрения на время, за которое происходило это
3. Определение метаморфозы скорости
тела при поворотеЕсли изменилась не только величина, но и направление скорости , то обнаружьте ее изменение через векторную разность исходной и финальной скорости . Для этого измерьте угол между векторами. После этого от суммы квадратов скоростей отнимите удвоенное их произведение, умноженное на косинус угла между ними: v1?+v2?-2v1v2•Cos(?). Из полученного числа извлеките квадратный корень.Видео по теме
Для определения скорости разных видов движения потребуются различные формулы. Дабы определить скорость равномерного движения, расстояние поделите на время его прохождения. Среднюю скорость движения находите сложением всех отрезков, которое прошло тело, на всеобщее время движения. При равноускоренном движении узнайте убыстрение, с которым двигалось тело, а при свободном падении высоту, с которой оно предисловие движение.

Вам понадобится
- дальномер, секундомер, акселерометр.
Инструкция
1. Скорость равномерного движения и средняя скоростьИзмерьте расстояние с поддержкой дальномера, которое прошло тело, а время, за которое оно его одолело, с поддержкой секундомера. Позже этого поделите расстояние, пройденное телом на время его прохождения, итогом будет скорость равномерного движения (v=S/t). Если тело движется неравномерно, произведите те же измерения и примените ту же формулу – тогда получите среднюю скорость тела. Это значит, что если бы тело по данному отрезку пути двигалось с полученной скоростью, оно было бы в пути время, равное измеренному. Если тело движется по окружности, измерьте ее радиус и время прохождения полного цикла, после этого радиус умножьте на 6,28 и поделите на время (v=6,28•R/t). Во всех случаях итог получится в метрах в секунду. Для перевода в километры в час помножьте его на 3,6.
2. Скорость равноускоренного движенияИзмерьте убыстрение тела с поддержкой акселерометра либо динамометра, если знаменита масса тела. Секундомером замерьте время движения тела и его исходную скорость, если тело не начинает двигаться из состояния покоя. Если же тело двигается из состояния покоя, она равна нулю. Позже этого узнайте скорость тела, прибавив к исходной скорости произведение убыстрения на время (v=v0+at).
3. Скорость вольно падающего телаС поддержкой дальномера измерьте высоту, с которой падает тело в метрах. Дабы узнать скорость, с которой оно долетит до поверхности Земли (без контроля сопротивления воздуха), умножьте высоту на 2 и на число 9,81 (убыстрение свободного падения). Из итога извлеките квадратный корень. Дабы обнаружить скорость тела на всякий высоте, применяйте ту же методологию, только от исходной высоты, отнимайте нынешнюю и полученное значение подставляйте взамен высоты.
Видео по теме
Человек привык воспринимать представление “скорость ” как что-то больше примитивное, чем это есть на самом деле. Подлинно, проносящийся на перекрестке автомобиль движется с определенной скорость ю, в то время как человек стоит и отслеживает за ним. Но если человек находится в движении, то умнее говорить не об безусловной скорости, а об относительной ее величине. Обнаружить относительную скорость дюже легко.

Инструкция
1. Дозволено продолжить рассмотрение темы движущегося на перекрестка на автомобиле. Человек же, стоя на красном свете светофора, стоит и глядит на проезжающий автомобиль. Человек статичен, следственно примем его за систему отсчета. Система отсчета – такая система, касательно которой движется какое-нибудь тело либо другая физическая точка.
2. Возможен, автомобиль движется со скорость ю 50 км/ч. Но, возможен, что человек побежал следом автомобилю (дозволено, скажем, взамен автомобиля представить маршрутку либо проезжающий мимо автобус). Скорость бега человека 12 км/ч. Таким образом, скорость данного механического транспортного средства представится человеку не столь и стремительной, как было прежде, когда он стоял! В этом каждая и суть относительной скорости. Относительная скорость неизменно измеряется касательно подвижной системы отсчета. Таким образом, скорость автомобиля не будет для пешехода 50 км/ч, а 50 – 12 = 38 км/ч.
3. Дозволено разглядеть еще один живой пример. Довольно припомнить всякий из моментов, когда человек, сидя у окна автобуса, отслеживает за проносящимися мимо автомобилями. Подлинно, из окна автобуса их скорость кажется примитивно потрясающей. И это не изумительно, чай, если принять автобус за систему отсчета, то скорость автомобиля и скорость автобуса надобно будет сложить. Возможен, что автобус движется со скорость ю 50 км/ч, а машины 60 км/ч. Тогда 50 + 60 = 110 км/ч. Именно с такой скорость ю эти самые автомобили проносятся мимо автобуса и пассажиров в нем.Эта же скорость будет объективна и действительна и в том случае, если за систему отсчета принять всякий из проезжающих мимо автобусов автомобилей.
Кинематика постигает разные виды движения тела с заданной скоростью, направлением и траекторией. Дабы определить его расположение касательно точки начала пути, надобно обнаружить перемещение тела .

Инструкция
1. Движение тела происходит по некоторой траектории. В случае откровенного движения ею является прямая линия, следственно обнаружить перемещение тела достаточно примитивно: оно равно пройденному пути. В отвратном случае определить его дозволено по координатам исходного и финального расположения в пространстве.
2. Величина перемещения физической точки является векторной, от того что она имеет направление. Следственно, дабы обнаружить ее числовое значение, нужно вычислить модуль вектора, соединяющего точки начала пути и его окончания.
3. Разглядим двухмерное координатное пространство. Пускай тело проделало путь от точки A (x0, y0) до точки B (x, y). Тогда, дабы обнаружить длину вектора АВ, опустите проекции его концов на оси абсцисс и ординат. Геометрически проекции касательно той и иной координатной оси дозволено представить в виде катетов прямоугольного треугольника с длинами:Sx = x – x0;Sy = y – y0, где Sx и Sy – проекции вектора на соответствующих осях.
4. Модуль вектора, т.е. длина перемещения тела , в свою очередь, является гипотенузой этого треугольника, длину которой легко определить по теореме Пифагора. Он равен квадратному корню из суммы квадратов проекций:S = ?(Sx? + Sy?).
5. В трехмерном пространстве:S = ?(Sx? + Sy? + Sz?), где Sz = z – z0.
6. Это формула является всеобщей для всякий разновидности движения. Вектор перемещения владеет несколькими свойствами: • его модуль не может превышать длину пройденного пути;• проекция перемещения может быть как позитивной, так и негативной величиной, в то время как величина пути неизменно огромнее нуля;• в всеобщем случае перемещение не совпадает с траекторией движения тела , а его модуль не равен пути.
7. В частном случае откровенного движения тело перемещается только по одной оси, скажем, оси абсцисс. Тогда длина перемещения равна разности финальной и исходной первой координаты точек:S = x – x0.
От модуля исходной скорости во многом зависят колляции движения тела. Для того дабы обнаружить эту величину, нужно воспользоваться дополнительными измерениями либо данными. Величина модуля исходной скорости может являться основополагающей колляцией, скажем, для огнестрельного оружия.

Вам понадобится
- – рулетка;
- – дальномер;
- – секундомер;
- – акселерометр;
- – спидометр;
- – угломер;
- – хронограф.
Инструкция
1. Вначале определитесь с типом движения. Если оно равномерное, то довольно измерить длину пути, по которому переместилось тело, сделав это рулеткой, дальномером либо иным доступным методом, и поделить это значение на время, за которое это перемещение осуществлялось. От того что движение равномерное, то модуль скорости на протяжении каждого пути будет идентичен, так что полученная скорость будет равна исходной.
2. При равноускоренном откровенном движении измерьте при помощи акселерометра убыстрение тела, а с подмогой секундомера время его движения, спидометром финальную скорость в конце отрезка пути. Обнаружьте значение модуля исходной скорости, отняв от финальной скорости произведение убыстрения на время движения v0=v-a*t. Если незнакомо значение убыстрения, измеряйте расстояние, которое покрыло тело за время t. Сделайте это при помощи рулетки либо дальномера.
3. Зафиксируйте значение финальной скорости. Обнаружьте исходную скорость, отняв от удвоенного значения расстояния S, поделенного на время, значение финальной скорости v, v0=2S/t-v. Когда значение финальной скорости измерить трудно, а убыстрение знаменито, воспользуйтесь иной формулой. Для этого измеряйте перемещение тела, а также время, которое оно было в пути. От значения перемещения отнимите произведение убыстрения на квадрат времени, поделенное на 2, а итог поделите на время, v0=(S-at?/2)/t либо v0=S/t-at/2.
4. Когда тело начинает движение под углом к горизонту, на него воздействует сила тяжести. Для того дабы обнаружить модуль исходной скорости, при помощи угломера замеряйте угол к горизонту, под которым тело начинает двигаться. При помощи рулетки либо дальномера замеряйте расстояние, на котором тело упадет на поверхность земли. Дабы определить модуль исходной скорости, расстояние S поделите на синус удвоенного угла ?. Из полученного итога извлеките квадратный корень, v0=?(S/sin(2?)).
5. Дабы измерить модуль исходной скорости пули, выпущенной из стрелкового оружия, используйте хронограф. Для этого установите его так, как указано в его инструкции, от того что хронографы бывают различных типов. Позже этого сделайте выстрел из оружия, на табло хронографа появится итог. Выстрелите еще несколько раз и возьмите среднее значение показаний хронографа. Это и будет модуль исходной скорости пули, выпущенного из данного типа стрелкового оружия.
jprosto.ru
Содержание
Инструкция
|
completerepair.ru
Как найти модуль скорости
Скорость тела характеризуется направлением и модулем. Иными словами, модуль скорости – это число, которое показывает, насколько быстро тело передвигается в пространстве. Перемещение предполагает изменение координат.Инструкция
- Введите систему координат, относительно которой вы будете определять направление и модуль скорости. Если в задаче уже задана формула зависимости скорости от времени, вводить систему координат не нужно – предполагается, что она уже есть.
- По имеющейся функции зависимости скорости от времени можно найти значение скорости в любой момент времени t. Пусть, например, v=2t²+5t-3. Если требуется найти модуль скорости в момент времени t=1, просто подставьте это значение в уравнение и посчитайте v: v=2+5-3=4.
- Когда задача требует найти скорость в начальный момент времени, подставьте в функцию t=0. Таким же образом можно найти время, подставив известную скорость. Так, в конце пути тело остановилось, то есть, его скорость стала равна нулю. Тогда 2t²+5t-3=0. Отсюда t=[-5±√(25+24)]/4=[-5±7]/4. Получается, что либо t=-3, либо t=1/2, а поскольку время не может быть отрицательным, остается только t=1/2.
- Иногда в задачах уравнение скорости дается в завуалированной форме. Например, в условии сказано, что тело двигалось равноускоренно с отрицательным ускорением -2 м/с², а в начальный момент скорость тела составляла 10 м/с. Отрицательное ускорение означает, что тело равномерно замедлялось. Из этих условий можно составить уравнение для скорости: v=10-2t. С каждой секундой скорость будет уменьшаться на 2 м/с, пока тело не остановится. В конце пути скорость обнулится, поэтому легко найти общее время движения: 10-2t=0, откуда t=5 секунд. Через 5 секунд после начала движения тело остановится.
- Помимо прямолинейного движения тела, существует еще и движение тела по окружности. В общем случае оно является криволинейным. Здесь возникает центростремительное ускорение, которое связано с линейной скоростью формулой a(c)=v²/R, где R – радиус. Удобно рассматривать также угловую скорость ω, причем v=ωR.
completerepair.ru
Как найти модуль вектора
В математике и физике «модулем» принято называть абсолютное значение какой-либо величины, не учитывающее ее знака. Применительно к вектору это означает, что его направление следует игнорировать, считая обычным отрезком прямой. В этом случае задача нахождения модуля сводится к вычислению длины такого отрезка, заданного координатами исходного вектора.Инструкция
- Используйте для вычисления длины (модуля) вектора теорему Пифагора — это наиболее простой и понятный метод вычисления. Чтобы это сделать рассмотрите треугольник, составленный из самого вектора и его проекций на оси прямоугольной двухмерной (Декартовой) системы координат. Это прямоугольный треугольник, в котором катетами будут являться проекции, а гипотенузой — сам вектор. Согласно теореме Пифагора для нахождения нужной вам длины гипотенузы следует сложить квадраты длин проекций и извлечь из результата квадратный корень.
- Рассчитайте длины проекций для использования в формуле из предыдущего шага. Для этого следует найти разности между координатами двух точек, образующих исходный вектор, вдоль соответствующих осей. Если обозначить начальную точку координатами (X₁,Y₁), а конечную — (X₂,Y₂), то длина проекции на ось абсцисс будет равна X₁-X₂, а на ось ординат — Y₁-Y₂. При этом не имеет значения координаты которой точки считать вычитаемым, а которой — уменьшаемым, так как в формуле будут использоваться их квадраты, что автоматически отбросит знаки этих величин.
- Подставьте полученные значения в выражение, сформулированное в первом шаге. Искомый модуль вектора в двухмерных прямоугольных координатах будет равен квадратному корню из суммы возведенных в квадрат разностей координат начальной и конечной точек вектора вдоль соответствующих осей: √((X₁-X₂)²+(Y₁-Y₂)²).
- Если вектор задан в трехмерной системе координат, то используйте аналогичную формулу, добавив в нее третье слагаемое, которое образуется координатами вдоль оси аппликат. Например, если обозначить начальную точку вектора координатами (X₁,Y₁,Z₁), а конечную — (X₂,Y₂,Z₂), то формула вычисления модуля вектора примет такой вид: √((X₁-X₂)²+(Y₁-Y₂)²+(Z₁-Z₂)²).
completerepair.ru

