Формулы сложения аргументов
$$sin(\alpha + \beta) = sin \alpha cos \beta + cos \alpha sin \beta$$
$$cos(\alpha + \beta) = cos \alpha cos \beta — sin \alpha sin \beta$$
$$tg(\alpha + \beta)= \frac{tg \alpha + tg \beta}{1 — tg \alpha tg \beta}$$
$$ctg(\alpha + \beta)= \frac{ctg \alpha ctg \beta -1}{ctg \alpha + ctg \beta}$$
$$sin(\alpha — \beta) = sin \alpha cos \beta — cos \alpha sin \beta$$
$$cos(\alpha — \beta) = cos \alpha cos \beta + sin \alpha sin \beta$$
$$tg(\alpha — \beta)= \frac{tg \alpha — tg \beta}{1 + tg \alpha tg \beta}$$
$$ctg(\alpha — \beta)= \frac{ctg \alpha ctg \beta +1}{ctg \alpha — ctg \beta}$$
Формулы суммы тригонометрических функций
$$sin\alpha + sin\beta = 2sin \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$
$$cos\alpha + cos\beta = 2cos \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$
$$tg\alpha + tg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$
$$ctg\alpha + ctg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$
$$(sin\alpha + cos\alpha)^2= 1+sin2\alpha$$
Формулы разности тригонометрических функций
$$sin\alpha — sin\beta = 2sin \frac{\alpha — \beta }{2} \cdot cos \frac{\alpha + \beta }{2}$$
$$cos\alpha — cos\beta = -2sin \frac{\alpha + \beta }{2} \cdot sin \frac{\alpha — \beta }{2}$$
$$tg\alpha — tg\beta = \frac{sin(\alpha — \beta) }{cos \alpha cos \beta}$$
$$ctg\alpha — ctg\beta = — \frac{sin(\alpha — \beta) }{sin \alpha sin \beta}$$
$$(sin\alpha + cos\alpha)^2= 1-sin2\alpha$$
Формулы произведения тригонометрических функций
$$sin\alpha \cdot sin\beta = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}$$
$$sin\alpha \cdot cos\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}$$
$$cos\alpha \cdot cos\beta = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}$$
\begin{align} tg\alpha \cdot tg\beta & = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)}\\ &= \frac{tg\alpha + tg\beta}{ctg\alpha + ctg\beta} \end{align}
\begin{align} ctg\alpha \cdot ctg\beta & = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)}\\ &= \frac{ctg\alpha + ctg\beta}{tg\alpha + tg\beta} \end{align}
$$tg\alpha \cdot ctg\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}$$
© 2012–2021 100formul.
{2}(\alpha)
$$
$$
\operatorname{tg}(\alpha)=\frac{\sin (\alpha)}{\cos (\alpha)}=\frac{1}{\operatorname{ctg}(\alpha)}
$$
Формулы суммы и разности (16 шт)
$$
\sin (\alpha+\beta)=\sin (\alpha) \cdot \cos (\beta)+\cos (\alpha) \cdot \sin (\beta)
$$
$$
\sin (\alpha-\beta)=\sin (\alpha) \cdot \cos (\beta)-\cos (\alpha) \cdot \sin (\beta)
$$
$$
\cos (\alpha+\beta)=\cos (\alpha) \cdot \cos (\beta)-\sin (\alpha) \cdot \sin (\beta)
$$
$$
\cos (\alpha-\beta)=\cos (\alpha) \cdot \cos (\beta)+\sin (\alpha) \cdot \sin (\beta)
$$
$$
\operatorname{tg}(\alpha+\beta)=\frac{\operatorname{tg}(\alpha)+\operatorname{tg}(\beta)}{1-\operatorname{tg}(\alpha) \cdot \operatorname{tg}(\beta)} \operatorname{tg}(\alpha-\beta)=\frac{\operatorname{tg}(\alpha)-\operatorname{tg}(\beta)}{1+\operatorname{tg}(\alpha) \cdot \operatorname{tg}(\beta)}
$$
$$ \sin (\alpha)+\sin (\beta)=2 \cdot \sin \left(\frac{\alpha+\beta}{2}\right) \cdot \cos \left(\frac{\alpha-\beta}{2}\right) $$
$$ \sin (\alpha)-\sin (\beta)=2 \cdot \cos \left(\frac{\alpha+\beta}{2}\right) \cdot \sin \left(\frac{\alpha-\beta}{2}\right) $$
$$ \cos (\alpha)+\cos (\beta)=2 \cdot \cos \left(\frac{\alpha+\beta}{2}\right) \cdot \cos \left(\frac{\alpha-\beta}{2}\right) $$
$$ \cos (\alpha)-\cos (\beta)=-2 \cdot \sin \left(\frac{\alpha+\beta}{2}\right) \cdot \sin \left(\frac{\alpha-\beta}{2}\right) $$
$$ \operatorname{ctg}(\alpha)+\operatorname{ctg}(\beta)=\frac{\sin (\beta+\alpha)}{\sin (\alpha) \cdot \sin (\beta)} \quad \operatorname{ctg}(\alpha)-\operatorname{ctg}(\beta)=\frac{\sin (\beta-\alpha)}{\sin (\alpha) \cdot \sin (\beta)} $$
Формулы понижения степени (10 шт)
$$
\sin ^{2}(\alpha)=\frac{1-\cos (2 \alpha)}{2} \quad \cos ^{2}(\alpha)=\frac{1+\cos (2 \alpha)}{2}
$$
$$
\operatorname{tg}^{2}(\alpha)=\frac{1-\cos (2 \alpha)}{1+\cos (2 \alpha)} \quad \operatorname{ctg}^{2}(\alpha)=\frac{1+\cos (2 \alpha)}{1-\cos (2 \alpha)}
$$
$$
\cos ^{3}(\alpha)=\frac{1}{4}(3 \cdot \cos (\alpha)+\cos (3 \alpha))
$$
$$
\sin ^{3}(\alpha)=\frac{1}{4}(3 \cdot \sin (\alpha)-\sin (3 \alpha))
$$
$$
\cos ^{4}(\alpha)-\sin ^{4}(\alpha)=\cos (2 \alpha)
$$
$$
\cos ^{4}(\alpha)+\sin ^{4}(\alpha)=1-\frac{\sin ^{2}(2 \alpha)}{2}
$$
$$
\cos ^{6}(\alpha)+\sin ^{6}(\alpha)=1-\frac{3}{4} \sin ^{2}(2 \alpha)
$$
$$
\cos ^{6}(\alpha)-\sin ^{6}(\alpha)=\cos (2 \alpha) \cdot\left[1-\frac{1}{4} \sin ^{2}(2 \alpha)\right]
$$
Формулы для функций кратных аргументов (11 шт)
$$
\sin (2 \alpha)=2 \cdot \sin (\alpha) \cdot \cos (\alpha)
$$
$$
\cos (2 \alpha)=\cos ^{2}(\alpha)-\sin ^{2}(\alpha)=2 \cdot \cos ^{2}(\alpha)-1=1-2 \cdot \sin ^{2}(\alpha)
$$
$$
\operatorname{tg}(2 \alpha)=\frac{2 \cdot \operatorname{tg}(\alpha)}{1-\operatorname{tg}^{2}(\alpha)} \quad \operatorname{ctg}(2 \alpha)=\frac{\operatorname{ctg}^{2}(\alpha)-1}{2 \cdot \operatorname{ctg}(\alpha)}
$$
$$
\sin (3 \alpha)=3 \cdot \sin (\alpha)-4 \cdot \sin ^{3}(\alpha)
$$
$$
\cos (3 \cdot \alpha)=4 \cdot \cos ^{3}(\alpha)-3 \cdot \cos (\alpha)
$$
$$
\operatorname{tg}(3 \alpha)=\frac{3 \cdot \operatorname{tg}(\alpha)-\operatorname{tg}^{3}(\alpha)}{1-3 \cdot \operatorname{tg}^{2}(\alpha)}=\operatorname{tg}(\alpha) \cdot \operatorname{tg}\left(\frac{\pi}{3}+\alpha\right) \cdot \operatorname{tg}\left(\frac{\pi}{3}-\alpha\right)
$$
$$
\operatorname{ctg}(3 \cdot \alpha)=\frac{3 \cdot \operatorname{ctg}(\alpha)-\operatorname{ctg}^{3}(\alpha)}{1-3 \cdot \operatorname{ctg}^{2}(\alpha)}
$$
Формулы произведения функций (6 шт)
$$
\sin (\alpha) \cdot \sin (\beta)=\frac{1}{2}(\cos (\alpha-\beta)-\cos (\alpha+\beta))
$$
$$
\cos (\alpha) \cdot \cos (\beta)=\frac{1}{2}(\cos (\alpha-\beta)+\cos (\alpha+\beta))
$$
$$
\sin (\alpha) \cdot \cos (\beta)=\frac{1}{2}(\sin (\alpha-\beta)+\sin (\alpha+\beta))
$$
$$
\operatorname{tg}(\alpha) \cdot \operatorname{tg}(\beta)=\frac{\operatorname{tg}(\alpha)+\operatorname{tg}(\beta)}{\operatorname{ctg}(\alpha)+\operatorname{ctg}(\beta)} \quad \operatorname{ctg}(\alpha) \cdot \operatorname{ctg}(\beta)=\frac{\operatorname{ctg}(\alpha)+\operatorname{ctg}(\beta)}{\operatorname{tg}(\alpha)+\operatorname{tg}(\beta)}
$$
$$
\operatorname{ctg}(\alpha) \cdot \operatorname{tg}(\beta)=\frac{\operatorname{ctg}(\alpha)+\operatorname{tg}(\beta)}{\operatorname{tg}(\alpha)+\operatorname{ctg}(\beta)}
$$
Формулы, связывающие все тригонометрические функции с тангенсом половинного угла (3 шт)
$$ \sin (\alpha)=\frac{2 \cdot \operatorname{tg}\left(\frac{\alpha}{2}\right)}{1+\operatorname{tg}^{2}\left(\frac{\alpha}{2}\right)} \quad \cos (\alpha)=\frac{1-\operatorname{tg}^{2}\left(\frac{\alpha}{2}\right)}{1+\operatorname{tg}^{2}\left(\frac{\alpha}{2}\right)} \quad \operatorname{tg}(\alpha)=\frac{2 \cdot \operatorname{tg}\left(\frac{\alpha}{2}\right)}{1-\operatorname{tg}^{2}\left(\frac{\alpha}{2}\right)} $$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Завершите более 100 формул тригонометрии от начального до продвинутого
Формулы тригонометрии очень важны для решения любых тригонометрических вопросов.
Итак, мы привели здесь полный список формул тригонометрии, которые используются в вопросах тригонометрии. Мы включили сюда все формулы тригонометрии.
Тригонометрия и тригонометрические формулы
Тригонометрия — это раздел математики, который имеет дело с тремя боковыми фигурами, такими как треугольник. Треугольник – это двумерная фигура, у которой три стороны. Тригонометрия помогает понять треугольники и использовать ее для решения задач в нашей повседневной жизни, таких как измерение расстояния, измерение скорости, измерение угла и т. д.
История тригонометрических соотношений
Первое использование понятия «синус» в том виде, в каком мы его используем сегодня, было в работе Арьябхаты «Арьябхатиям» в 500 г. н.э. Арьябхата использовал слово ардха-джья для полуаккорда, которое со временем было сокращено до джья или дживы. Когда Арьябхатиям был переведен на арабский язык, слово джива было сохранено как есть. Слово джива было переведено как синус, что означает кривая, когда арабская версия была переведена на латынь.
Вскоре слово синус, также использовавшееся как синус, стало распространенным в математических текстах по всей Европе. Английский профессор астрономии Эдмунд Гюнтер (1581–1626) впервые употребил сокращенное число 9.0011 обозначение «грех».
Термины «косинус» и «тангенс» возникли гораздо позже. Функция косинуса возникла из-за необходимости вычислить синус дополнительного угла. Арьябхатта назвал его котийа . Название cosinus произошло от Эдмунда Гюнтера. В 1674 году английский математик сэр Джонас Мур впервые использовал сокращенную запись «cos».
Формула тригонометрии
Итак, вот все формулы тригонометрии от основ до продвинутых.
1. Тригонометрические соотношения
2.Краткие названия тригонометрических отношений .
3.Тригонометрия Связь с другими соотношениями тригонометрии
4.Теорема Пифагора
5.Тригонометрическая таблица
6.Тригонометрические отношения дополнительных углов
7.Тождества тригонометрии
8.Тригонометрические функции
9.
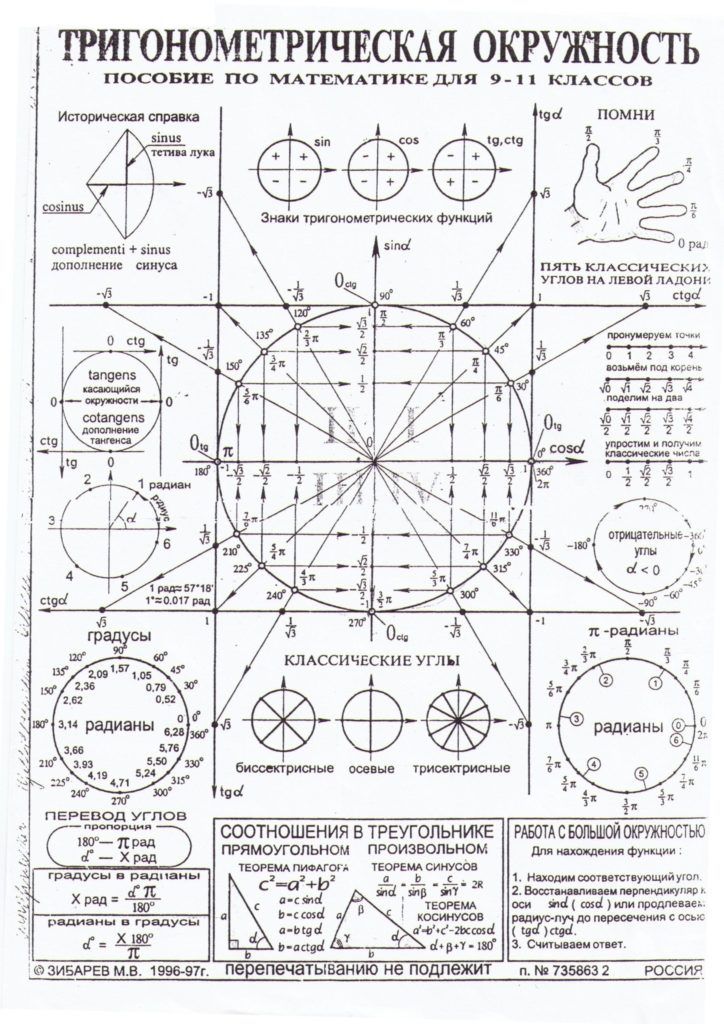Углы любого треугольника – законы синуса и законы синусов любого треугольника. косинуса
10. Обратные тригонометрические функции/формулы
Тригонометрические отношения
Для прямоугольного треугольника мы можем вычислить тригонометрические отношения следующим образом. Рассмотрим прямоугольный треугольник, как показано на рисунке . Треугольники имеют три стороны как AB, BC, CA и три угла как A, B, C. Тригонометрические отношения можно найти как под: —
Примечание: Сторона AB примыкает к углу A,
Примечание: Сторона BC противоположна углу A,
Примечание: Сторона AC является гипотенузой, так как эта сторона противоположна углу B (прямой угол 90°). ).
Синус ∠A = (Сторона, противоположная углу A) / Гипотенуза = \(\frac{BC}{AC}\)
Косинус ∠A = (Сторона, прилегающая к углу A)/ Гипотенуза = \(\frac{AB }{AC}\)
Тангенс ∠A = (сторона, противоположная углу A)/ (сторона, прилегающая к углу A) = \(\frac{BC}{AB}\)
косеканс ∠A = (гипотенуза)/ (Сторона, противоположная углу A) = \(\frac{AC}{BC}\)
секанс ∠A = (гипотенуза) / (сторона, примыкающая к углу A) = \(\frac{AC}{AB}\)
котангенс ∠A = (сторона, примыкающая к углу A) / (сторона, противолежащая углу A ) = \(\frac{AB}{BC}\)
Краткие названия тригонометрических соотношений
Здесь приведены краткие названия тригонометрических отношений .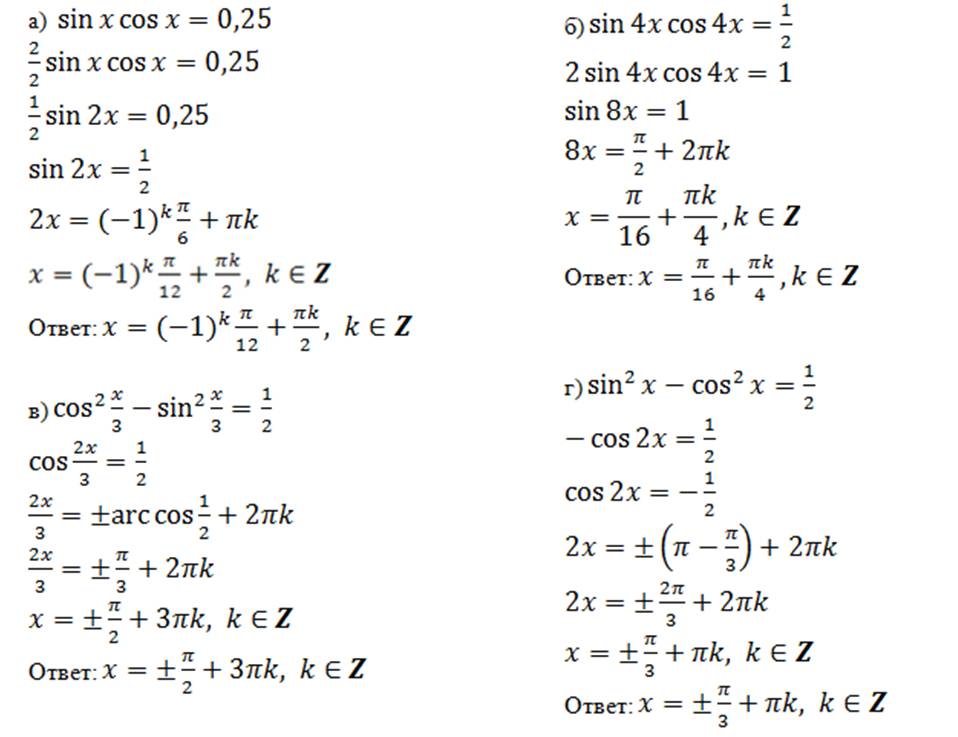
| Полное название тригонометрического отношения | Краткое название тригонометрического отношения | |||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | Синус 9 θ | 068 Sin θ | ||||||||||||||||||||||||||||||||||||||||||||||||
| 2. | Cosine θ | Cos θ | ||||||||||||||||||||||||||||||||||||||||||||||||
| 3. | Tangent θ | Tan θ | ||||||||||||||||||||||||||||||||||||||||||||||||
| 4. | Cosecant θ | Cosec θ | ||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | Секанс θ | Сек θ | ||||||||||||||||||||||||||||||||||||||||||||||||
| 6. | Котангенс θ | Cot θ | 90s в форме отношения сторон треугольника. Пусть угол равен θ (тета), а P = перпендикуляр треугольника относительно угла θ и B = основание треугольника относительно угла θ. Sin θ = \(\frac{P}{H}\) Пифагор ТеоремаТеорема Пифагора: Для прямоугольного треугольника, как указано ниже, квадрат длины гипотенузы всегда равен сумме квадратов двух других сторон. (CA) 2 = (AB) 2 + (BC) 2 Тригонометрическая таблицаТригонометрическая таблица используется для получения значений тригонометрических отношений под определенным углом, которые определены в таблице. используя таблицу тригонометрии, мы можем легко вычислить значения тригонометрических соотношений при углах – 0°, 30°, 45°, 60°, 90°, 180°, 270°, 360° Таблица тригонометрии 1 : Угол составляют от 0° до 90° [Углы в градусах] – первые три тригонометрических соотношения
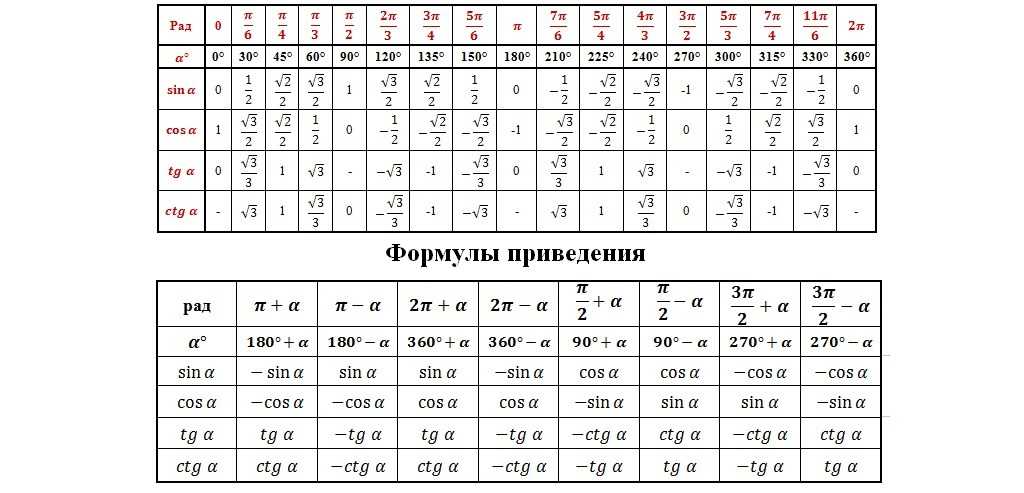
Trigonometry Table 2 : Angle are from 0° to 360° [ Angles are in degree ] – All trigonometric ratios
Trigonometry Table 3 : Angle are from 0 to 2π [ Angles are in radian ]
Тригонометрические соотношения отношение друг к другуВсе шесть тригонометрических соотношений связаны друг с другом обратной величиной следующим образом: Sin θ = \(\frac{1}{Cosec \ θ }\) θ }\) Tan θ = \(\frac{Sin\ θ}{Cos \ θ }\) Тригонометрическое отношение дополнительных/дополнительных углов Вот все формулы тригонометрии дополнительных и дополнительных углов. B. Тригонометрические формулы дополнительных углов Тригонометрические тождестваТригонометрические тождества – это отношения между всеми тригонометрическими отношениями одного или нескольких углов. Всего существует три тригонометрических тождества. Все тригонометрические тождества представлены ниже: — a) Sin 2 A +Cos 2 A = 1 Тригонометрические формулы угла в виде градусов и радианов Иногда мы используем углы в виде градусов, но некоторые вопросы решает угол в радианах. Шестидесятеричная система (градусы) Столетняя система Круговая система Связь между градусами и радианами Угол дуги Соотношение Тригонометрические функцииВот формулы тригонометрии, связанные с суммой и произведением двух углов тригонометрических отношений Sin ( x + y ) = Sin x cos y + cos x cos y Tan (A+B) = \( \frac{ \ ( \ tan \ A \ + \ tan \ B \ ) }{ \ ( \ 1 \ – \ tan \ A \ tan \ B \ ) \ } \) Tan (A-B) = \ (\frac{\tan{A}\ -\ \tan{B}}{1+\tan{A}\tan{B}} \) Tan ( \( \frac{π}{4} \) + x ) = \( \frac{( \ 1 \ + \ tan \ x \ ) \ }{ \ ( \ 1 \ – \ tan \ x \ )} \) 92 \ A \ ) \ } \) Sin (-x) = – sin x Cos (-x) = Cos x Tan (-x) = – tan x Тригонометрическая формула произведений тригонометрических отношений Формула тригонометрии, состоящая из произведения двух отношений, также полезна при решении вопросов тригонометрии.
Тригонометрические формулы — список всех тригонометрических формулТригонометрические формулы — это наборы различных формул, включающих тригонометрические тождества, используемые для решения задач, основанных на сторонах и углах прямоугольного треугольника. Кроме того, существует множество тригонометрических тождеств и формул, которые можно использовать для упрощения выражений, решения уравнений и вычисления интегралов. Эти формулы тригонометрии включают тригонометрические функции, такие как синус, косинус, тангенс, косеканс, секанс и котангенс для заданных углов. Давайте подробно изучим эти формулы, включающие тождества Пифагора, тождества произведения, тождества кофункций (углы сдвига), тождества суммы и разности, тождества двойного угла, тождества половинного угла и т.
Что такое формулы тригонометрии?Тригонометрические формулы — это математические выражения, связывающие углы и стороны прямоугольного треугольника. Они используются в тригонометрии для решения широкого круга задач, связанных с углами, расстояниями и высотами. Используя эти формулы, можно найти недостающую сторону или угол в прямоугольном треугольнике. Помимо основных формул, таких как теорема Пифагора, существует множество тригонометрических тождеств и формул, которые можно использовать для упрощения выражений, решения уравнений и вычисления интегралов. Эти формулы являются важным инструментом для инженеров, математиков и ученых, работающих в различных областях. Список всех формул тригонометрииДавайте посмотрим на приведенные ниже наборы различных формул тригонометрии.
Некоторые основные формулы тригонометрии можно увидеть на изображении ниже. Рассмотрим их подробно в следующих разделах. Основные формулы тригонометрииОсновные формулы тригонометрии используются для нахождения соотношения между отношениями треугольников и отношением соответствующих сторон прямоугольного треугольника. В тригонометрии используются шесть основных тригонометрических отношений, также называемых тригонометрическими функциями: синус, косинус, секанс, косеканс, тангенс и котангенс, которые записываются как sin, cos, sec, csc, tan, cot. Тригонометрические функции и тождества выводятся с использованием прямоугольного треугольника в качестве эталона. Мы можем узнать значения синуса, косинуса, тангенса, секанса, косеканса и котангенса, учитывая размеры прямоугольного треугольника, используя формулы тригонометрии как, Формулы тригонометрических соотношений
Взаимные тождества Косеканс, секанс и котангенс являются обратными величинами основных тригонометрических отношений синуса, косинуса и тангенса соответственно.
Пифагорейские тождестваТеорема Пифагора гласит, что «в прямоугольном треугольнике, если ‘c’ — это гипотенуза, а ‘a’ и ‘b’ — два катета, то c 2 = a 2 + b 2 «. Используя эту теорему и тригонометрические соотношения, выводятся тождества Пифагора. Эти тождества используются для преобразования одного коэффициента триггера в другой. Триггерные тождества Пифагора упомянуты ниже:
Таблица тригонометрических соотношений Вот таблица тригонометрических формул для углов, которые обычно используются для решения тригонометрических задач.
Формулы единичного круга Единичная окружность — это окружность радиусом 1 с центром в начале координат плоскости. Вот некоторые формулы, связанные с единичным кругом:
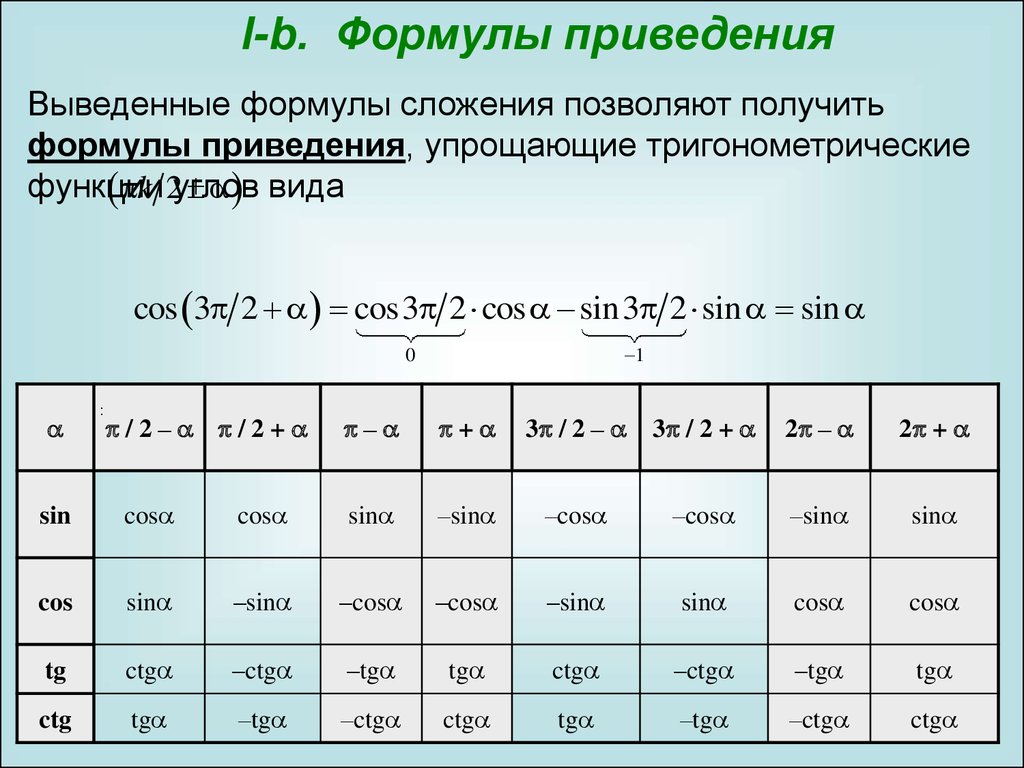
Тригонометрические периодические тождества (в радианах) Тригонометрические формулы, включающие периодические тождества, используются для сдвига углов на π/2, π, 2π и т. д. Все тригонометрические тождества цикличны по своей природе, что означает, что они повторяются через точку. Этот период различен для разных формул тригонометрии периодических тождеств. Например, tan 30° = tan 210°, но это неверно для cos 30° и cos 210°. Вы можете обратиться к формулам тригонометрии, приведенным ниже, чтобы проверить периодичность функций синуса и косинуса в разных квадрантах. Первый квадрант:
Второй квадрант:
Третий квадрант:
Четвертый квадрант:
Идентичности кофункций (в градусах)Тригонометрические формулы тождеств кофункций обеспечивают взаимосвязь между различными тригонометрическими функциями. Формулы тригонометрии кофункций представлены в градусах ниже:
Тождества кофункций в радианах можно получить, заменив 90° на π/2 в приведенных выше формулах. Тождества суммы и разностиТождества суммы и разности включают тригонометрические формулы sin(x + y), cos(x — y), cot(x + y) и т. д.
Множественные и субмножественные углыТригонометрические формулы для кратных и дольных углов могут быть использованы для расчета значения тригонометрических функций для половинного угла, двойного угла, тройного угла и т. д. Полуугольные тождестваТригонометрические формулы половинного угла включают x/2 и выглядят следующим образом.
Тождества двойного угла Формулы тригонометрии двойного угла используются для нахождения двойного угла (2x) тригонометрических функций.
Трехугольные тождестваТриггерные формулы для триггерного угла (3x) следующие:
Идентичность суммы и произведения Тригонометрические формулы для суммы или произведения тождеств используются для представления суммы любых двух тригонометрических функций в форме их произведения или наоборот. Произведение для суммирования формул
Формулы суммы в произведениеКомбинация двух острых углов A и B может быть представлена через тригонометрические соотношения в приведенных ниже тригонометрических формулах.
Формулы обратной тригонометрии Используя формулы обратной тригонометрии, тригонометрические соотношения инвертируются для создания обратных тригонометрических функций, таких как sin θ = x и θ = sin −1 x. Здесь x может иметь значения в целых числах, десятичных дробях, дробях и показателях степени.
Законы синусов и косинусовЗакон синуса: Закон синуса и закон косинуса определяют отношение между сторонами и углами треугольника. Закон синусов дает отношение сторон и угла, противолежащего стороне. В качестве примера берется отношение стороны «а» и противолежащего ей угла «А». (sin A)/a = (sin B)/b = (sin C)/c Закон косинуса: Закон косинуса помогает найти длину стороны для заданных длин двух других сторон и прилежащий угол. Например, длину «а» можно найти с помощью двух других сторон «b» и «с» и прилежащего к ним угла «А».
где, a, b, c — длины сторон треугольника, а A, B, C — углы треугольника. ☛ Связанные темы:
Примеры использования формул тригонометрии
перейти к слайдуперейти к слайдуперейти к слайду Разбивайте сложные концепции с помощью простых визуальных средств. Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций. Записаться на бесплатный пробный урок Практические вопросы по тригонометрическим формулам
перейти к слайдуперейти к слайду Часто задаваемые вопросы по тригонометрическим формуламЧто такое тригонометрические формулы?Тригонометрические формулы — это формулы, используемые для решения задач на основе сторон и углов прямоугольного треугольника. Эти формулы можно использовать для вычисления тригонометрических отношений (также называемых тригонометрическими функциями), sin, cos, tan, csc, sec и cot. Что такое Основная формула тригонометрии?Основные формулы тригонометрии включают представление основных тригонометрических соотношений в терминах отношения соответствующих сторон прямоугольного треугольника. Они задаются следующим образом: sin θ = Противоположная сторона/Гипотенуза, cos θ = Прилегающая сторона/Гипотенуза, tan θ = Противоположная сторона/Прилегающая сторона. Какие пифагорейские тождества используются в тригонометрии?Три фундаментальные формулы тригонометрии, включающие пифагорейские тождества, задаются следующим образом: Что такое формулы тригонометрических отношений? В тригонометрии используются три основные функции: синус, косинус и тангенс.
Что такое тригонометрические формулы для четных и нечетных тождеств?Тригонометрические формулы, включающие четные и нечетные тождества, задаются следующим образом:
Что такое тригонометрические формулы сложения?Тригонометрические формулы для тригонометрических соотношений, когда углы складываются, задаются следующим образом:
К какому треугольнику применимы тригонометрические формулы? Формулы тригонометрии применимы к прямоугольным треугольникам. |
)
} \)
∞
Итак, вот все формулы тригонометрии для углов в виде градусов и радианов.
Вот тригонометрические формулы произведения тригонометрических отношений.
д., в следующих разделах.
д.
Все взаимные тождества также получены с использованием прямоугольного треугольника в качестве эталона. Эти взаимные тригонометрические тождества выводятся с использованием тригонометрических функций. Формулы тригонометрии на взаимных тождествах, приведенные ниже, часто используются для упрощения тригонометрических задач.
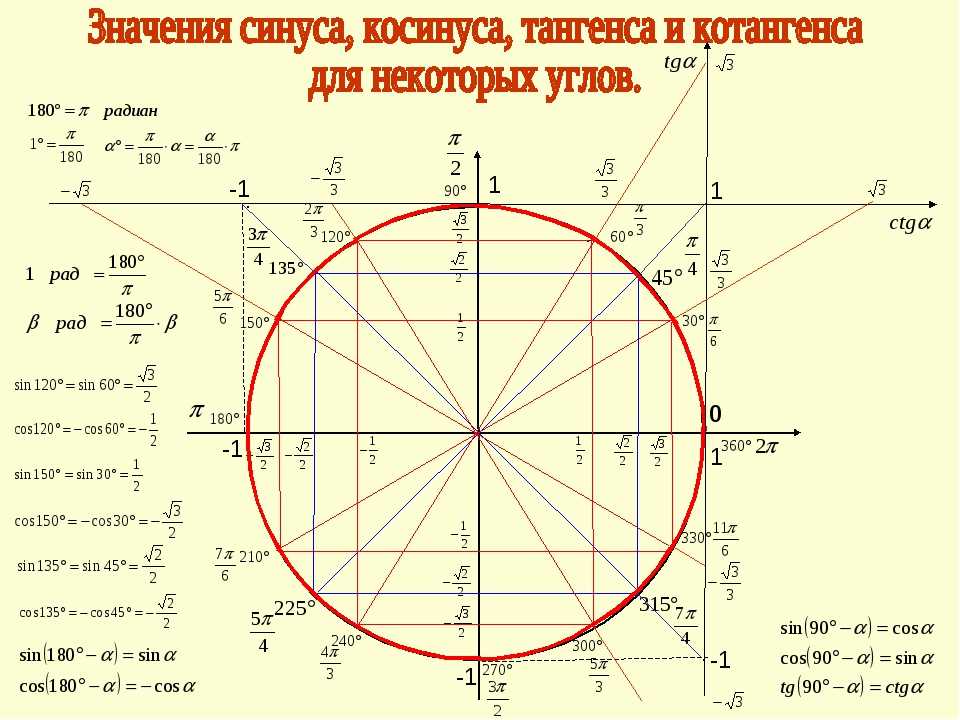
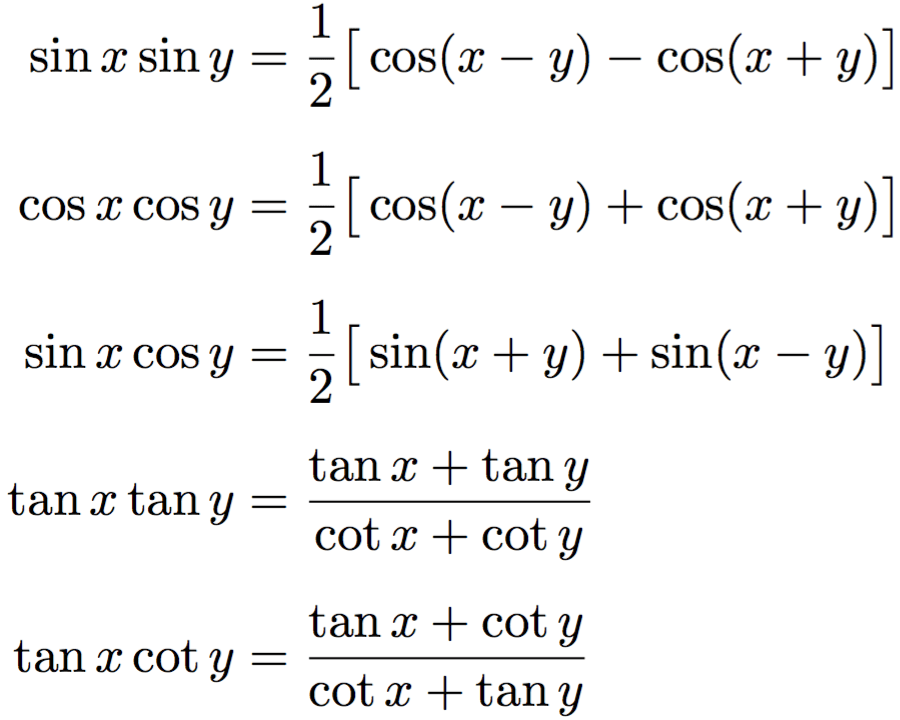
Формулы тригонометрических соотношений имеют следующий вид: