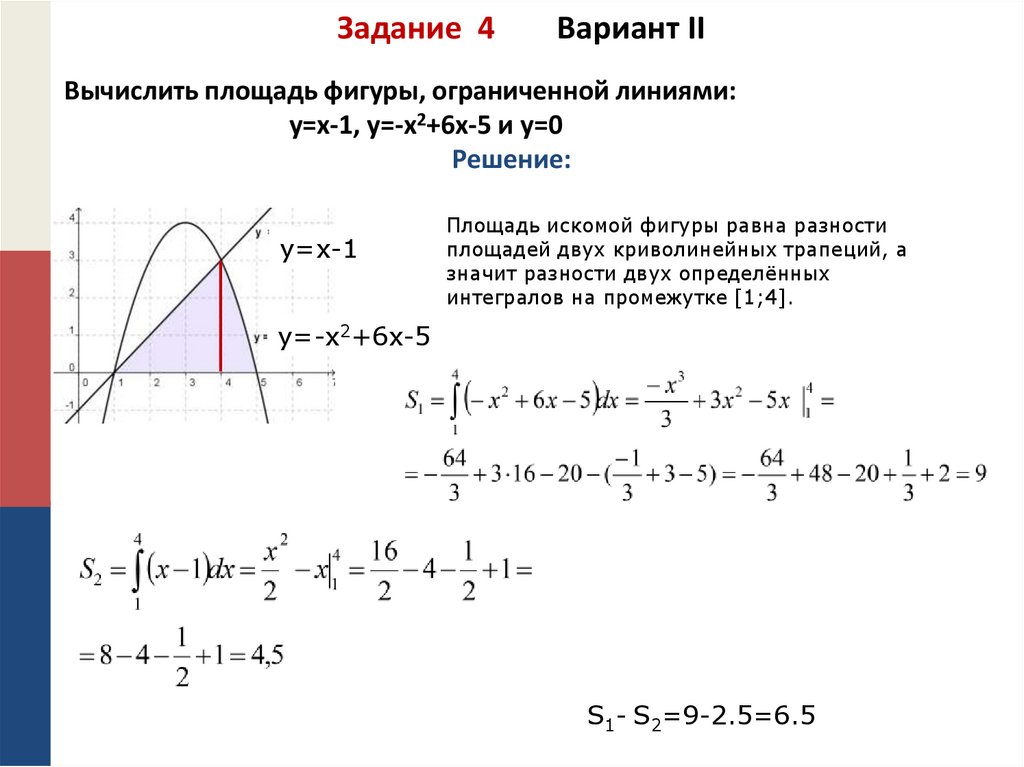
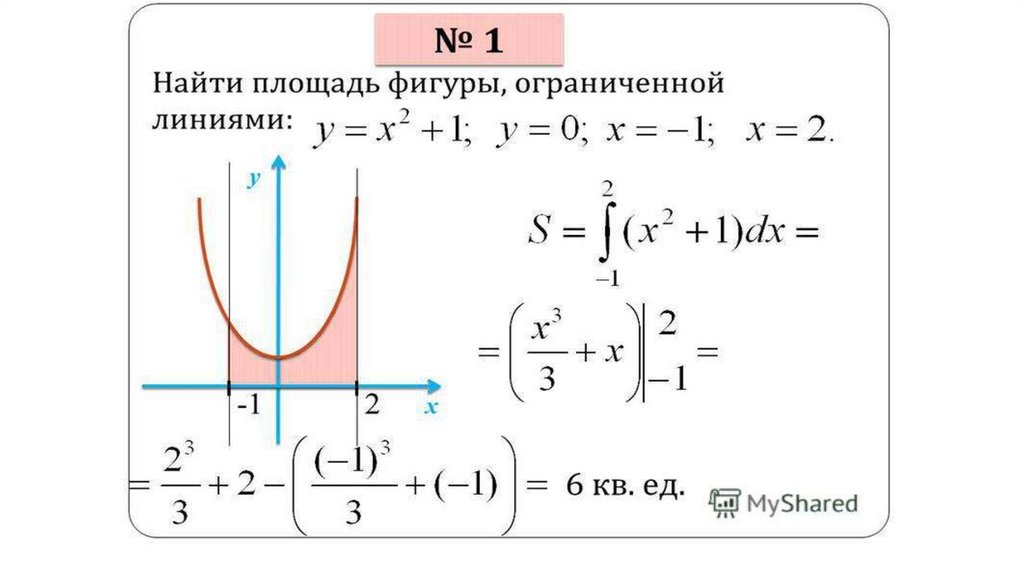
Вычисление площади фигуры, ограниченной параметрически заданной кривой
Когда мы выясняли геометрический смысл определенного интеграла, у нас получилась формула, с помощью которой можно найти площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми x=a, x=b, а также непрерывной (неотрицательной или неположительной) функцией y=f(x). Иногда удобнее задавать функцию, ограничивающую фигуру, в параметрическом виде, т.е. выражать функциональную зависимость через параметр t. В рамках данного материала мы покажем, как можно найти площадь фигуры, если она ограничена параметрически заданной кривой.
После объяснения теории и выведения формулы мы разберем несколько характерных примеров на нахождение площади таких фигур.
Основная формула для вычисления
Допустим, что у нас имеется криволинейная трапеция, границами которой являются прямые x=a, x=b, ось Ox и параметрически заданная кривая x=φ(t)y=ψ(t), а функции x=φ(t) и y=ψ(t) являются непрерывными на интервале α; β, α<β, x=φ(t) будет непрерывно возрастать на нем и φ(α)=a, φ(β)=b.
Чтобы вычислить площадь трапеции при таких условиях, нужно использовать формулу S(G)=∫αβψ(t)·φ'(t)dt.
Мы вывели ее из формулы площади криволинейной трапеции S(G)=∫abf(x)dx методом подстановки x=φ(t)y=ψ(t):
S(G)=∫abf(x)dx=∫αβψ(t)d(φ(t))=∫αβψ(t)·φ'(t)dt
Определение 2Учитывая монотонное убывание функции x=φ(t) на интервале β; α, β<α, нужная формула принимает вид S(G)=-∫βαψ(t)·φ'(t)dt.
Если функция x=φ(t) не относится к основным элементарным, то нам понадобится вспомнить основные правила возрастания и убывания функции на интервале, чтобы определить, будет ли она возрастающей или убывающей.
Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой
В этом пункте мы разберем несколько задач на применение формулы, выведенной выше.
Условие: найдите площадь фигуры, которую образует линия, заданная уравнениями вида x=2cos ty=3sin t.
Решение
У нас есть параметрически заданная линия. Графически ее можно отобразить в виде эллипса с двумя полуосями 2 и 3. См на иллюстрацию:
Графически ее можно отобразить в виде эллипса с двумя полуосями 2 и 3. См на иллюстрацию:
Попробуем найти площадь 14 полученной фигуры, которая занимает первый квадрант. Область находится в интервале x∈a; b=0; 2. Далее умножим полученное значение на 4 и найдем площадь целой фигуры.
Вот ход наших вычислений:
x=φ(t)=2cos ty=ψ(t)=3sin tφα=a⇔2cos α=0⇔α=π2+πk, k∈Z,φβ=b⇔2cos β=2⇔β=2πk, k∈Z
При k, равном 0, мы получим интервал β; α=0; π2. Функция x=φ(t)=2cos t на нем будет монотонно убывать (подробнее см. статью об основных элементарных функциях и их свойствах). Значит, можно применить формулу вычисления площади и найти определенный интеграл, используя формулу Ньютона-Лейбница:
-∫0π23 sin t·2cos t’dt=6∫0π2sin2t dt=3∫0π2(1-cos(2t)dt==3·t-sin(2t)20π2=3·π2-sin2·π22-0-sin2·02=3π2
Значит, площадь фигуры, заданной исходной кривой, будет равна S(G)=4·3π2=6π.
Ответ: S(G)=6π
Уточним, что при решении задачи выше можно было взять не только четверть эллипса, но и его половину – верхнюю или нижнюю.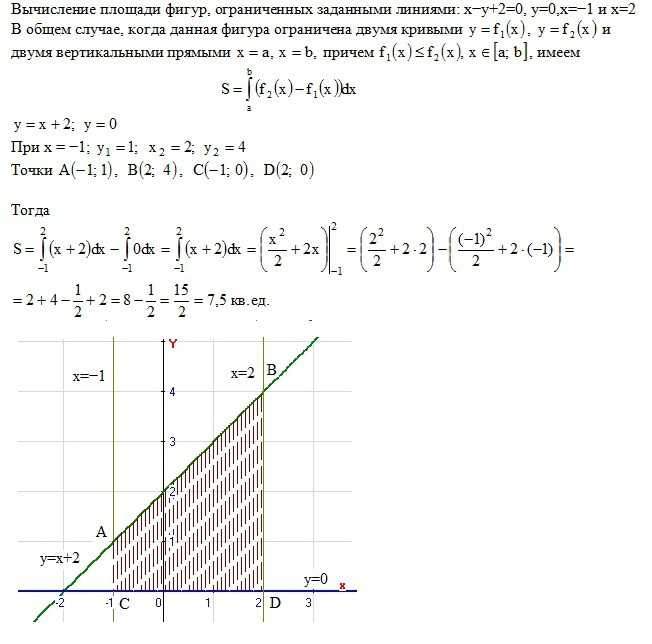 Одна половина будет расположена на интервале x∈a; b=-2; 2. В этом случае у нас бы получилось:
Одна половина будет расположена на интервале x∈a; b=-2; 2. В этом случае у нас бы получилось:
φ(α)=a⇔2cos α=-2⇔α=π+πk, k∈Z,φ(β)=b⇔2cos β=2⇔β=2πk, k∈Z
Таким образом, при k равном 0, мы получили β; α=0; π. Функция x=φ(t)=2cos t на этом интервале будет монотонно убывать.
После этого вычисляем площадь половины эллипса:
-∫0π3sin t·2cos t’dt=6∫0πsin2t dt=3∫0π(1-cos(2t)dt==3·t-sin(2t)20π=3·π-sin2·π2-0-sin2·02=3π
Важно отметить, что можно взять только верхнюю или нижнюю часть, а правую или левую нельзя.
Можно составить параметрическое уравнение данного эллипса, центр которого будет расположен в начале координат. Оно будет иметь вид x=a·cos ty=b·sin t. Действуя так же, как и в примере выше, получим формулу для вычисления площади эллипса Sэлипса=πab.
Задать окружность, центр которой расположен в начале координат, можно с помощью уравнения x=R·cos ty=R·sin t, где t является параметром, а R – радиусом данной окружности. Если мы сразу воспользуемся формулой площади эллипса, то то у нас получится формула, с помощью которой можно вычислить площадь круга с радиусом R: Sкруга=πR2.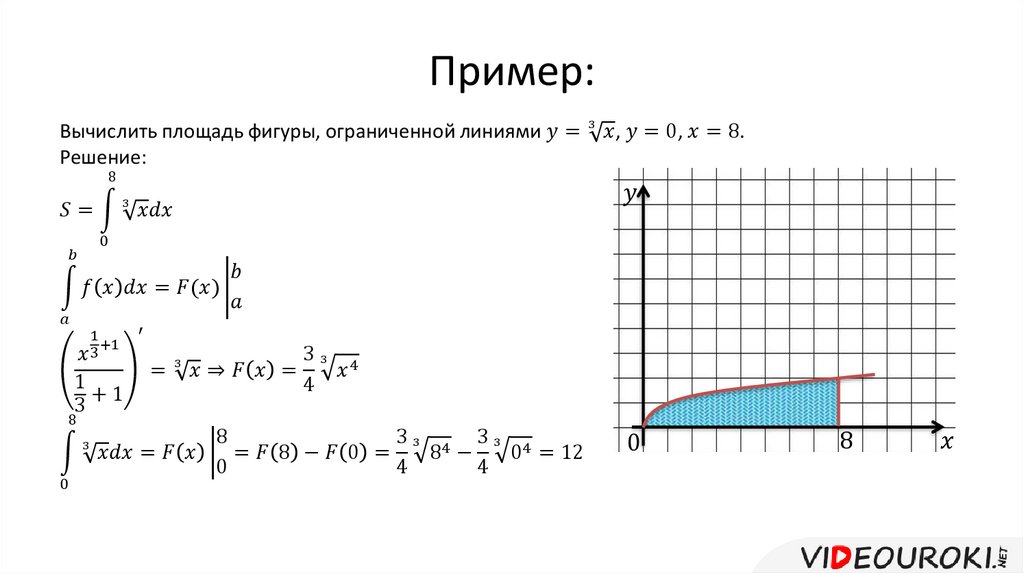
Разберем еще одну задачу.
Пример 2Условие: найдите, чему будет равна площадь фигуры, которая ограничена параметрически заданной кривой x=3cos3ty=2sin3t.
Решение
Сразу уточним, что данная кривая имеет вид вытянутой астроиды. Обычно астроида выражается с помощью уравнения вида x=a·cos3ty=a·sin3t.
Теперь разберем подробно, как построить такую кривую. Выполним построение по отдельным точкам. Это самый распространенный метод, который применим для большинства задач. Более сложные примеры требуют проведения дифференциального исчисления, чтобы выявить параметрически заданную функцию.
У нас x=φ(t)=3cos3t, y=ψ(t)=2sin3t.
Данные функции являются определенными для всех действительных значений t. Для sin и cos известно, что они являются периодическими и их период составляет 2 пи. Вычислив значения функций x=φ(t)=3cos3t, y=ψ(t)=2sin3t для некоторых t=t0∈0; 2π π8, π4, 3π8, π2,…, 15π8, получим точки x0; y0=(φ(t0); ψ(t0)).
Составим таблицу итоговых значений:
| t0 | 0 | π8 | π4 | 3π8 | π2 | 5π8 | 3π4 | 7π8 | π |
| x0=φ(t0) | 3 | 2.36 | 1.06 | 0.16 | 0 | -0.16 | -1.06 | -2.36 | -3 |
| y0=ψ(t0) | 0 | 0.11 | 0.70 | 1.57 | 2 | 1.57 | 0.70 | 0.11 | 0 |
| t0 | 9π8 | 5π4 | 11π8 | 3π2 | 13π8 | 7π4 | 15π8 | 2π |
| x0=φ(t0) | -2.36 | -1.06 | -0.16 | 0 | 0.16 | 1.06 | 2.36 | 3 |
| y0=ψ(t0) | -0.11 | -0.70 | -1.57 | -2 | -1.57 | -0.70 | -0.11 | 0 |
После этого отметим нужные точки на плоскости и соединим их одной линией.
Теперь нам надо найти площадь той части фигуры, что находится в первой координатной четверти. Для нее x∈a; b=0; 3:
φ(α)=a⇔3cos3t=0 ⇔α=π2+πk, k∈Z,φ(β)=b⇔3cos3t=3⇔β=2πk, k∈Z
Если k равен 0, то у нас получится интервал β; α=0; π2, и функция x=φ(t)=3cos3t на нем будет монотонно убывать. Теперь берем формулу площади и считаем:
-∫0π22sin3t·3cos3t’dt=18∫0π2sin4t·cos2tdt==18∫0π2sin4t·(1-sin2t)dt=18∫0π2sin4tdt-∫0π2sin6tdt
У нас получились определенные интегралы, которые можно вычислить с помощью формулы Ньютона-Лейбница. Первообразные для этой формулы можно найти, используя рекуррентную формулу Jn(x)=-cos x·sinn-1(x)n+n-1nJn-2(x), где Jn(x)=∫sinnxdx.
∫sin4tdt=-cos t·sin3t4+34∫sin2tdt==-cos t·sin3t4+34-cos t·sin t2+12∫sin0tdt==-cos t·sin3t4-3cos t·sin t8+38t+C⇒∫0π2sin4tdt=-cos t·sin3t4-3cos t·sin t8+38t0π2=3π16∫sin6tdt=-cos t·sin5t6+56∫sin4tdt⇒∫0π2sin6tdt=-cos t·sin5t60π2+56∫0π2sin4tdt=56·3π16=15π96
Мы вычислили площадь четверти фигуры. Она равна 18∫0π2sin4tdt-∫0π2sin6tdt=183π16-15π96=9π16.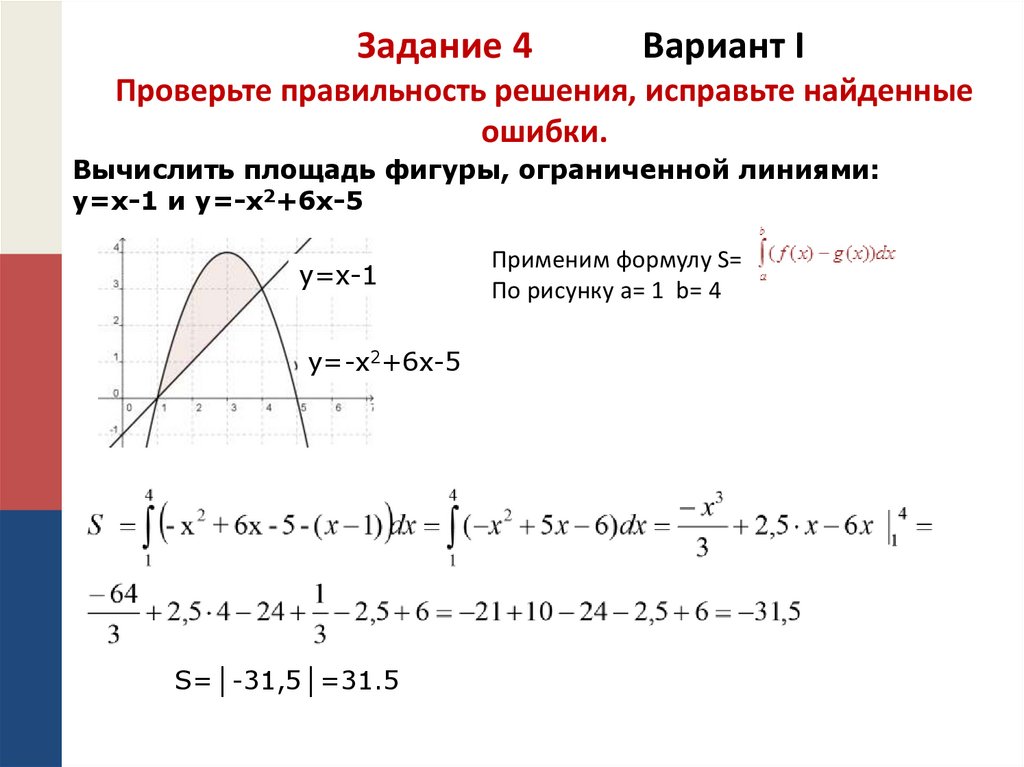
Если мы умножим это значение на 4, получим площадь всей фигуры – 9π4.
Точно таким же образом мы можем доказать, что площадь астроиды, заданной уравнениями x=a·cos3ty=a·sin3t, можно найти по формуле Sастроиды=3πa28, а площадь фигуры, которая ограничена линией x=a·cos3ty=b·sin3t, считается по формуле S=3πab8.
Калькулятор площади между двумя кривыми
Калькулятор площади между двумя кривыми
y = f(x) =
y = g(x) =
На интервале:
вложенный в curvesпользовательский ввод
Как использовать этот калькулятор 9000 7
Решение
Вернуться к калькулятору
Заполните поля ввода для расчета решения.
Хотите неограниченный доступ к калькуляторам, ответам и шагам решения?
Присоединяйтесь сейчас
100% без риска. Отменить в любое время.
Площадь между двумя кривыми Урок
Какова площадь между двумя кривыми?
Заштрихованная желтым цветом область на изображении ниже является примером области между двумя кривыми. Эта область представляет собой двумерное пространство, ограниченное кривой верхней функции, кривой нижней функции, левой конечной точкой интервала и правой конечной точкой интервала.
Эта область представляет собой двумерное пространство, ограниченное кривой верхней функции, кривой нижней функции, левой конечной точкой интервала и правой конечной точкой интервала.
Почему мы изучаем площадь между двумя кривыми?
Когда мы впервые узнаем об интегралах для нахождения площади под кривой, мы получаем первое представление о полезности исчисления для работы со сложными системами реального мира. Основным примером этого является использование суммы Римана для аппроксимации расстояния, пройденного транспортным средством, путем нахождения площади под кривой зависимости скорости от времени.
Но что мы могли сделать, найдя площадь между две кривые ? Ну, допустим, по выходным таскаем гоночные машины по трассе. Перед каждой гонкой мы гарантируем, что наша система сбора данных внутри автомобиля настроена на запись нашей скорости через заданные промежутки времени в течение всей продолжительности каждого заезда против нашего соперника, с которым мы участвуем.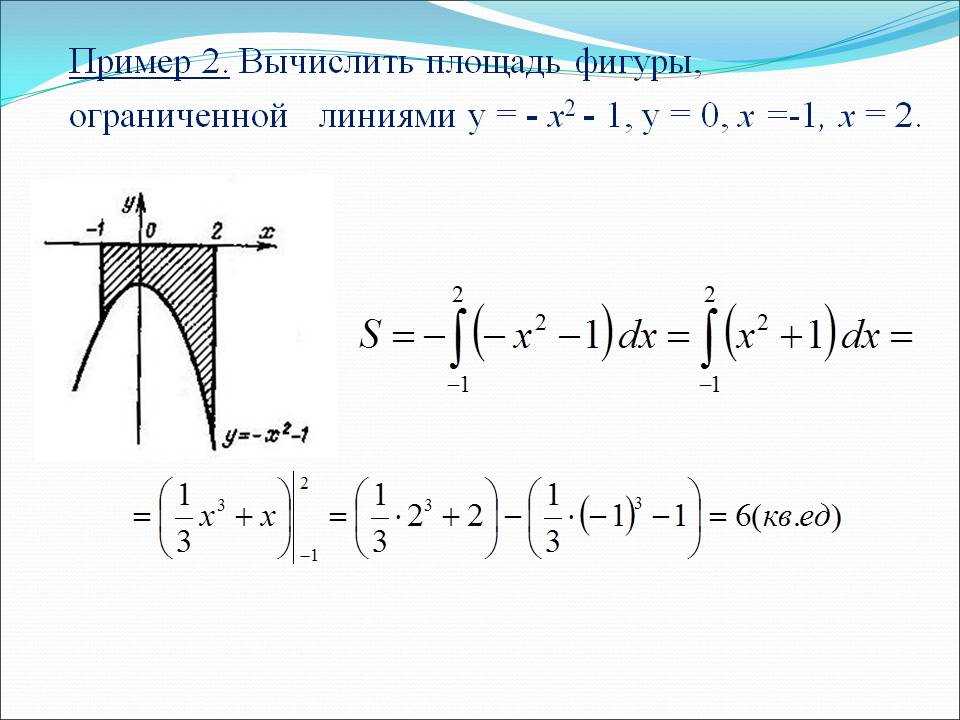 У нашего оппонента такая же система сбора данных, которая записывает те же данные в те же промежутки времени.
У нашего оппонента такая же система сбора данных, которая записывает те же данные в те же промежутки времени.
После каждой гонки на четверть мили мы хотели бы узнать дистанцию разрыва между нашей машиной и нашим соперником. Для этого мы собираем данные (скорость в зависимости от времени) от обеих машин и находим площадь между две кривые скорости на протяжении всей рассматриваемой дистанции в четверть мили. Это покажет нам взаимное смещение наших машин, когда победитель доедет до финиша.
Другими словами, найдя площадь между этими двумя кривыми скорости, мы можем определить расстояние разрыва между двумя автомобилями в течение заданного интервала времени в гонке.
Как рассчитать площадь между двумя кривыми
Формула для расчета площади между двумя кривыми: 9{b} \left( \text{Верхняя функция} — \text{Нижняя функция} \right) \; dx, \hspace{3ex} a \leq x \leq b \end{align}$$
Где A площадь между кривыми, a левая конечная точка интервала, b правая конечная точка интервала, Верхняя функция — это функция x , которая имеет большее значение на интервале, а Нижняя функция — это функция x , которая имеет меньшее значение на интервале.
Мы можем указать интервал x = [a, b] (что эквивалентно a ≤ x ≤ b ) при нахождении площади между двумя кривыми. Однако, если две кривые имеют по крайней мере две точки пересечения, мы также можем использовать интервал, определяющий площадь, заключенную между двумя кривыми.
Давайте посмотрим на изображение ниже в качестве примера. Синяя кривая представляет f(x) = x , а красная кривая представляет g(x) = x 3 . Кривые этих двух функций пересекаются в трех точках: х = -1 , х = 0 и х = 1 . Следовательно, площадь, ограниченная ими, определяется интервалом x = [-1, 1] .
Замкнутая область между f(x) = x (синий) и g(x) = x 3 (красный) Зная интервал, на котором мы решаем, мы должны определить верхнюю и нижнюю функции для подинтервал(ы). В некоторых случаях будет только один подинтервал, который сам является основным интервалом. В других случаях будет более одного подинтервала, где кривые пересекают друг друга и меняют положение в качестве верхней и нижней функций, как, например, на изображении непосредственно выше.
Мы можем визуально определить верхнюю и нижнюю функции для каждого подинтервала, просмотрев график кривых. Если график кривых недоступен, мы можем оценить значение каждой функции в середине каждого подинтервала. Например, подинтервал x = [2, 4] имеет среднюю точку x = 3 . Поэтому мы подставим x = 3 в каждую функцию и оценим, какое из них имеет большее значение, а какое меньшее в этой точке.
Зная верхнюю и нижнюю функции для одного или нескольких подинтервалов, мы можем установить формулу площади для каждого подинтервала. После решения каждого интеграла формулы площади мы суммируем результаты каждого, чтобы определить общую площадь между кривыми на нашем интервале. Для проблемы с 92 = x\\ \\ & \hspace{3ex} \text{Решая относительно x, получаем: } \: x = 0,00000, \: x = 1,00000\\ \\ & \hspace{3ex} \text{Наш подынтервал (s): } \:x = [0,000, 1,000]\\ \\ \\ & \text{3.) Теперь мы должны определить верхнюю и нижнюю функции для площади} \\ \\ & \hspace{3ex } \text{формульные интегралы).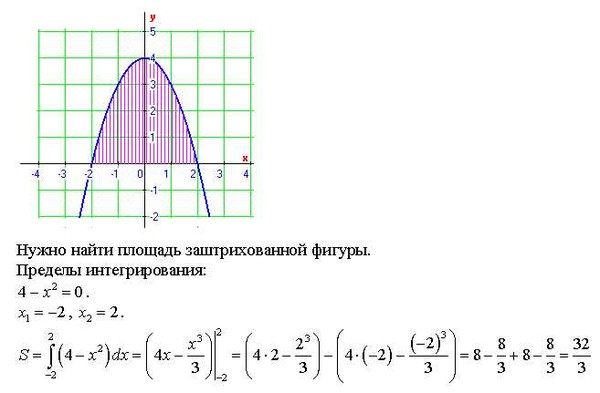 {1,00000} = 0,16667\\ \\ \\ & \text{5.) Суммируя результаты определенного интеграла, получаем:} \\ \\ & \ hspace{3ex} A = \fbox{0.16667}\\ & \end{align}$$
{1,00000} = 0,16667\\ \\ \\ & \text{5.) Суммируя результаты определенного интеграла, получаем:} \\ \\ & \ hspace{3ex} A = \fbox{0.16667}\\ & \end{align}$$
Калькулятор площади между двумя кривыми в основном построен с использованием языков веб-программирования HTML (язык разметки гипертекста), CSS (каскадные таблицы стилей) и JS (JavaScript). HTML строит архитектуру, CSS создает все свойства визуального стиля калькулятора, а JS обеспечивает функциональность вычислений.
При нажатии кнопки «Рассчитать» активируется функция JS. Введенные пользователем значения считываются и используются для того же самого процесса, который описан в примерах выше. Различные промежуточные значения сохраняются и форматируются для шагов решения.
Неопределенные интегралы выполняются CAS (система компьютерной алгебры) на основе JS. CAS применяет интегральные правила, рассматривая каждый символ как символ, обеспечивая почти идеальную точность. Этот процесс известен как символьные вычисления.
Окончательный ответ округляется и форматируется, затем форматируются все шаги решения. Ответ и шаги печатаются в области решения и визуализируются механизмом рендеринга LaTeX (язык/технология математического визуального рендеринга).
Изучение математики еще никогда не было таким простым.
Получите неограниченный доступ к более чем 165 персонализированным урокам и 69 интерактивным калькуляторам.
Присоединяйтесь к Voovers+ сегодня
100% без риска. Отменить в любое время.
Калькулятор площади прямоугольника
Создано Bogna Szyk и Hanna Pamula, PhD
Отзыв от Jack Bowater
Последнее обновление: 09 февраля 2023 г.
Содержание:- Что такое прямоугольник?
- Как найти площадь прямоугольника?
- Формулы прямоугольника
- Вычисление прямоугольника: найти A (площадь)
- Вычисление прямоугольника: найти P (периметр)
- Вычисление прямоугольника: найти D (диагональ)
- Золотой прямоугольник
- Свойства прямоугольника
- Прямоугольник против другого формы.
 Является ли квадрат прямоугольником?
Является ли квадрат прямоугольником? - Странный забавный факт: какая страна имеет самую прямоугольную форму в мире?
- Прямоугольники
- Прямоугольники в повседневной жизни: прямоугольная форма тела, прямоугольный бассейн, прямоугольная скатерть…
- Часто задаваемые вопросы
Если вам нужно узнать площадь ковра, посылки, экрана телевизора, прямоугольного бассейна или окна, этот калькулятор площади прямоугольника решит вашу проблему в мгновение ока. !
Все, что вам нужно сделать, это ввести длину и ширину (или диагональ) и позволить этому прямоугольнику вычислить значения P (периметр) и A (площадь).
Продолжайте читать, если вы хотите понять, что такое прямоугольник, вас интересует определение прямоугольника, формулы и свойства прямоугольника… Или вы просто хотите узнать, как найти площадь прямоугольника.
Что такое прямоугольник?
Прямоугольник — это четырехугольник с четырьмя прямыми углами . Мы можем также определить его по-другому: параллелограмм, содержащий прямой угол — если один угол прямой, другие должны быть такими же. При этом каждая сторона прямоугольника имеет ту же длину, что и противоположная ей сторона. Он также имеет неравные смежные стороны, в отличие от квадрата, частного случая прямоугольника.
Мы можем также определить его по-другому: параллелограмм, содержащий прямой угол — если один угол прямой, другие должны быть такими же. При этом каждая сторона прямоугольника имеет ту же длину, что и противоположная ей сторона. Он также имеет неравные смежные стороны, в отличие от квадрата, частного случая прямоугольника.
Если вы немного знаете латынь, название формы обычно многое объясняет. Слово прямоугольник происходит от латинского прямоугольный . Это комбинация rectus (что означает «правильный, прямой») и angulus (угол), поэтому оно может служить простым базовым определением прямоугольника.
Прямоугольник является примером четырехугольника. Вы можете использовать наш четырехугольник калькулятор, чтобы найти площадь других типов четырехугольника.
Как найти площадь прямоугольника?
На изображении выше показан типичный прямоугольник. У него четыре стороны и четыре прямых угла. Длины его сторон обозначим через a и b , а длина диагонали обозначается d .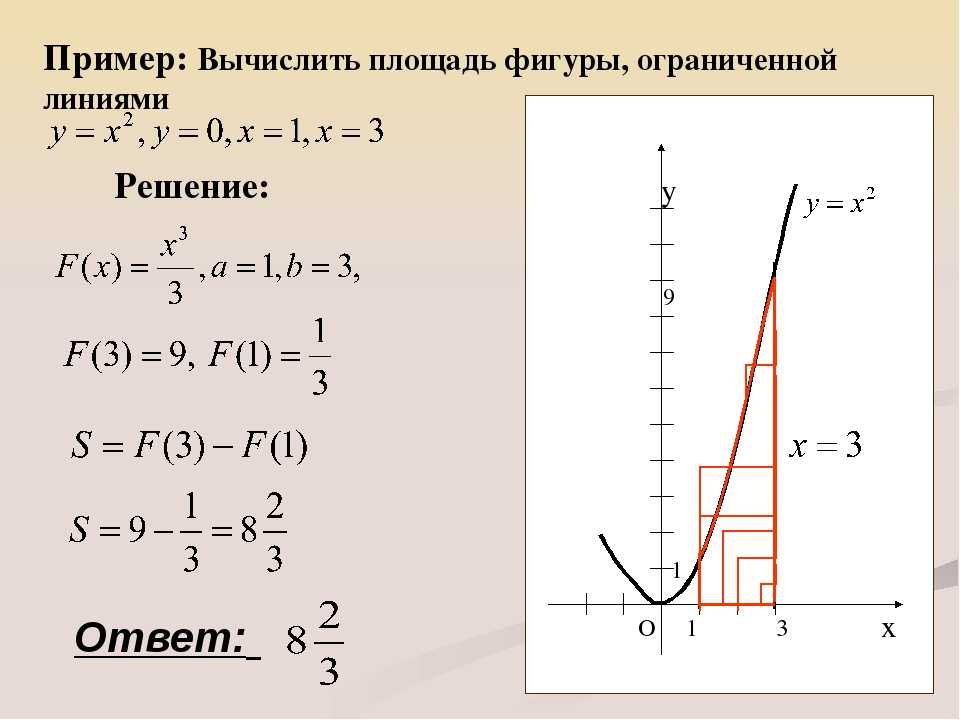
Если все стороны прямоугольника имеют одинаковую длину, мы называем его квадратом .
Площадь прямоугольника — это пространство, ограниченное его сторонами или, другими словами, в пределах периметра прямоугольника. Чтобы найти площадь прямоугольника, все, что вам нужно сделать, это умножить стороны прямоугольника a и b :
Площадь = a × b
Формулы прямоугольников
В нашем калькуляторе прямоугольников реализованы следующие формулы:
Для площади прямоугольника :
A = a × bДля периметра прямоугольника :
P = 2 × (a + b)Для диагонали прямоугольника :
d² = a² + b²
d = √(a² + b²)
Расчет прямоугольника: найти A (площадь)
Поскольку мы знаем формулу площади прямоугольника A = a × b , покажем на примере, как можно вычислить это свойство:
- Выберем длину прямоугольника – например,
a = 5 см.
- Определите ширину прямоугольника – например,
b = 6 см. - Умножьте эти два значения:
A = 5 см × 6 см = 30 см². - Площадь прямоугольника 30 см².
Расчет прямоугольника: найти P (периметр)
Давайте узнаем, как найти периметр прямоугольника. Как обычно, периметр представляет собой сумму всех сторон фигуры:
P = a + b + a + b
… что можно записать как:
P = 2 × (a + b )
Возьмем для примера тот же прямоугольник:
- Выберем длину прямоугольника –
a = 5 смв нашем случае. - Определите ширину прямоугольника – например,
b = 6 см. - Добавьте эти два значения:
а + b = 5 + 6 = 11 см. - Умножьте результат на 2:
P = 2 × 11 = 22 см. - Поехали! Периметр нашего прямоугольника равен 22 см.
Расчет прямоугольника: найти D (диагональ)
Диагональ прямоугольника — это отрезок, соединяющий две противоположные вершины прямоугольника. Вычислим длину диагонали примерного прямоугольника:
Вычислим длину диагонали примерного прямоугольника:
- Выберем длину прямоугольника – например,
а = 5 см. - Определитесь с шириной прямоугольника – например,
b = 6 см. - Вычислить
aв степени двойки:a² = 25 см². - Вычислите
bв степени двойки:b² = 36 см². - Сложите эти два значения:
a² + b² = 25 + 36 = 61 см². - Наконец, извлеките квадратный корень из результата:
d = √(a² + b²) = √61 ~ 7,81 см. - Длина диагонали 7,81 см.
Естественно, вместо того, чтобы вычислять все эти значения вручную, вы можете использовать эту область калькулятора прямоугольника. Вы также можете использовать его в обратном порядке — например, для вычисления ширины прямоугольника с известными длиной и периметром.
Золотой прямоугольник
На рисунке выше показан особый тип прямоугольника, называемый золотым прямоугольником (узнайте с помощью нашего калькулятора золотого прямоугольника). Такой прямоугольник удовлетворяет следующему условию:
Такой прямоугольник удовлетворяет следующему условию:
(a + b) / a = a / b = ϕ
, где φ — золотое сечение, равное 1,618. Узнайте больше об этом особом соотношении с помощью нашего калькулятора золотого сечения.
Как вы, наверное, помните из калькулятора отношений, отношение — это отношение между двумя величинами, часто представленное в виде дроби.
Знаете ли вы, что золотой треугольник можно построить, используя только линейку и циркуль ? Это всего несколько шагов!
- Нарисуйте квадрат.
- Проведите линию от середины одной стороны квадрата до противоположного угла. Наш калькулятор средней точки может помочь вам с этим шагом.
- Нарисуйте круг с радиусом, равным этой линии, с центром в средней точке, как показано на рисунке выше.
- Точка, в которой круг встречается с расширенной стороной квадрата, является следующим углом золотого прямоугольника.
- Найдите последнюю вершину и завершите золотой прямоугольник.

Таадааах! Это было не так сложно, не так ли?
Свойства прямоугольника
Прямоугольники обладают многими интересными свойствами:
- Цикличность – это означает, что все углы лежат на одной окружности.
- Равноугольный – все его углы равны 90 градусов.
- Прямолинейный – его стороны сходятся под прямым углом.
- Две линии отражательной симметрии – вертикальная и горизонтальная через центр.
- Две диагонали, которые делят друг друга пополам . Длину диагонали можно найти по теореме Пифагора.
- Противоположные стороны прямоугольника параллельны друг другу и имеют одинаковую длину.
Другие менее известные прямоугольные свойства:
- Пересечение диагоналей — это центр описанной окружности — существует окружность с центром в этой точке, которая проходит через четыре угла.

- В прямоугольнике с разной длиной сторон (попросту говоря, не в квадрате) невозможно провести вписанную окружность.
- Прямые, соединяющие середины сторон прямоугольника, образуют ромб, площадь которого составляет половину площади прямоугольника. Стороны фигуры параллельны диагоналям.
Можно придумать и свои собственные свойства, например, о вращении прямоугольника — по стороне или диагонали, чтобы получился цилиндр или конус соответственно.
Прямоугольник против других форм. Является ли квадрат прямоугольником?
TL;DR:
- Является ли квадрат прямоугольником? ДА .
- Является ли прямоугольник параллелограммом? ДА .
- Является ли прямоугольник ромбом? В целом – НЕТ. Только если это квадрат (все углы ромба 90 градусов).
- Является ли ромб прямоугольником? В целом – НЕТ. Только если это квадрат (все стороны прямоугольника равны по длине).

- Является ли прямоугольник четырехугольником? ДА , конечно.
- Является ли прямоугольник трапецией? ДА .
Хотите знать, является ли квадрат прямоугольником или прямоугольник параллелограммом? Взгляните на картинку ниже, и у вас больше не должно быть никаких сомнений относительно отношений между четырехугольниками:
Источник: WikimediaКак читать эту диаграмму? Начнем с нашего прямоугольника. Непосредственно к фигуре присоединены три фигуры: квадрат, параллелограмм и равнобедренная трапеция. Таким образом, если фигура находится выше интересующей нас формы, например, квадрата и прямоугольника, мы можем сказать, что:
- Каждый квадрат является прямоугольником , а квадрат является частным случаем прямоугольника .
Для двух других цифр аналогично:
- Каждый прямоугольник является параллелограммом и прямоугольник является частным случаем параллелограмма .

- Каждый прямоугольник является трапецией и прямоугольник является частным случаем трапеции .
Странный забавный факт: какая страна имеет самую прямоугольную форму в мире?
Существует множество различных рейтингов, оценивающих страны по площади, населению, уровню образования или лауреатам Нобелевской премии.
Но задумывались ли вы когда-нибудь кто победит в конкурсе на самую прямоугольную страну? Австралийский геостатистик Дэвид Бэрри рассчитал параметр прямоугольности для всех стран мира и составил рейтинг.
Он выяснил, что самой прямоугольной страной является Египет, тогда как титул «наименее прямоугольной страны в мире» достается Мальдивским островам (впрочем, автор допускает, что расчеты для стран, состоящих из множества мелких островов, могут быть ужасно неверными). Взгляните на таблицу ниже и проверьте первые десять стран, а также наименее прямоугольные.
Ранг | Страна | Округлость | Изображение 9 0560 |
|---|---|---|---|
1 | Египет | 0,955 | |
2 | Ватикан | 0,948 | |
3 | Синт-Мартен | 0,937 | 9 0573 |
4 | Лесото | 0,936 | |
5 | 9 0004 Йемен | 0,928 | |
6 | Гана | 0,924 | |
7 | Македония | 0,921 | |
8 | Кот-д’Ивуар | 0,919 | |
9 | 9 0004 Польша | 0,919 | |
10 | Науру | 0,917 9058 0 | |
. | |||
169 | США 9 0007 | 0,735 | |
… | |||
206 90 580 | Тувалу | 0,240 | |
207 | Маршалловы Острова | 0,201 | |
208 | Мальдивы | 0,018 | 9 0573 |
Египет является лидером, но это не должно удивлять никого, кто проверяет форму этой страны на карте. USA находится в середине рейтинга, в основном из-за эксцентричности Аляски и Гавайев. Сбивает с толку то, что вторая самая прямоугольная страна — Ватикан — является в то же время четвертой самой круглой страной, и Польша , 5 место по округлости, 9 место по прямоугольности.
Как вообще возможно быть прямоугольным и круглым одновременно?! Как вы можете догадаться, все дело в определении прямоугольности и округлости, которое может быть неадекватным для сложных или разрозненных форм — и такими примерами обычно являются границы стран, содержащие острые края, маленькие острова или колонии где-то на другой стороне. земного шара.
земного шара.
Если вам интересна эта тема, вы можете ознакомиться с этим объяснением и обсуждением результатов.
Можно подумать, что мир было бы легче рисовать, если бы каждая страна была прямоугольником… Или нет?
Шаблоны прямоугольников
Форма прямоугольника используется во многих периодических шаблонах мозаики. Его можно использовать для стен из кирпича, напольной плитки, тротуара или различной мозаики. Ниже вы найдете несколько популярных рисунков:
- Укладка в стопку – самый распространенный и простой узор укладки плитки, так как плитка укладывается прямыми линиями.
- Текучая связка – типична для дорожных покрытий, плитки и кирпичной кладки.
- Елочка – с таким рисунком хорошо смотрятся деревянные полы.
- Корзиночное плетение – часто используется для коридоров или дорожек на открытом воздухе.
Конечно, плитка бывает всех форм и размеров – довольно популярны шестиугольные и восьмиугольные с квадратами. Для пятиугольника форма должна быть неправильной, чтобы образовался мозаичный узор.
Для пятиугольника форма должна быть неправильной, чтобы образовался мозаичный узор.
Прямоугольники в повседневной жизни: прямоугольное телосложение, прямоугольный бассейн, прямоугольная скатерть…
Телосложение типа — одна из самых искомых проблем, связанных с прямоугольниками. Все, что вам нужно сделать, это измерить свой бюст, талию, бедра и высоту бедер и ввести значения в инструмент. Тогда вы получите информацию о том, какая у вас форма тела.
Например, прямоугольная фигура определяется как «мальчишеский» тип телосложения — ваши бедра, талия и бюст примерно одного размера. Ваше тело имеет правильные пропорции и спортивный вид.
Удивительно, но нас окружают прямоугольные объекты. Вот почему наш калькулятор прямоугольников может быть полезен не только на уроках математики, но и в решении повседневных задач. Конечно, идеального прямоугольника в реальности не найти, так как он всегда имеет третье измерение; но если оно мало по сравнению с двумя другими измерениями, приближение достаточно хорошее.
Прямоугольные скатерти – учитывая размер вашего стола, вы можете узнать, какая скатерть вам нужна, сколько кружева или подшивочной ленты вам потребуется.
Двери или оконное стекло – шторм или мяч для гольфа разбили ваше оконное стекло? Рассчитайте площадь и оцените стоимость ремонта, учитывая цену за кв.м или кв.м.
Экраны электронных устройств — планшетов, смартфонов, телевизоров — используйте этот калькулятор площади прямоугольника, чтобы оценить, сколько места на стене займет ваш экран — или насколько большой экран телефона, который вы хотите купить.
Доски, зеркала, рамы, холст, листы бумаги, блокноты, конверты, деньги, флажки, прямоугольные бассейны… Это бесконечный список!
Посмотри. Можете ли вы найти больше прямоугольных объектов вокруг вас? Что вы можете!
FAQ
Как найти периметр и площадь прямоугольника?
Чтобы найти периметр, нужно сложить все стороны прямоугольника:
P = a + b + a + b
Чтобы найти площадь прямоугольника, нужно умножить меньшую и длинную стороны :
A = a × b
Какова площадь прямоугольника размером 3 фута на 4 дюйма?
Это 144 квадратных дюйма ! Чтобы найти площадь этого прямоугольника, вам нужно:
- Преобразовать футов в дюймы.


 Является ли квадрат прямоугольником?
Является ли квадрат прямоугольником?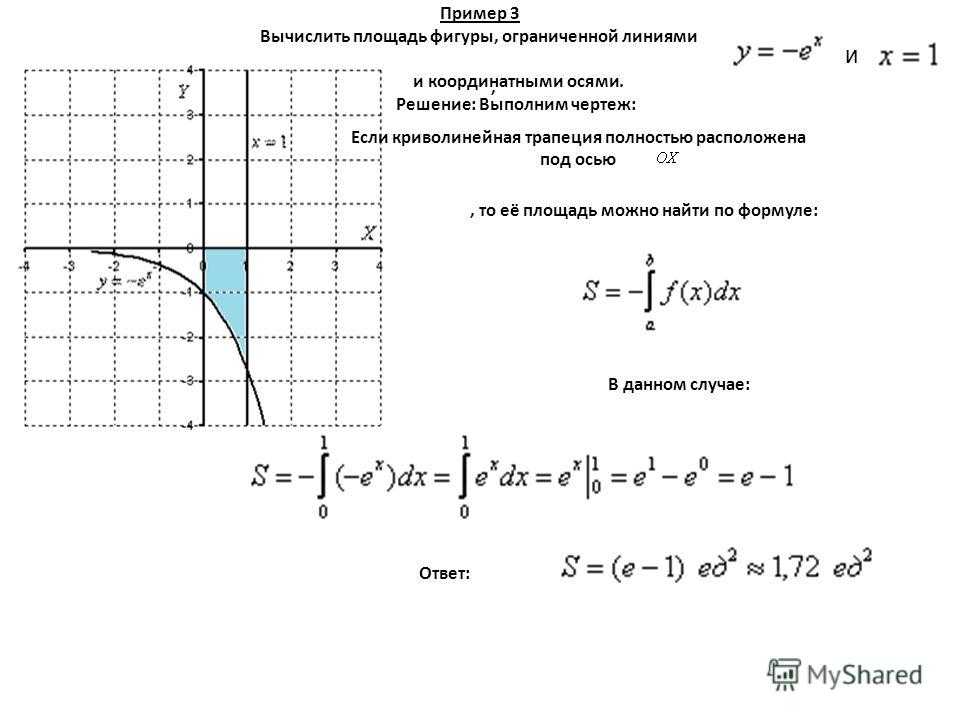

 Индекс 1 — идеальный прямоугольник, 0 — бесконечное число бесконечно малых островков. Таблица адаптирована с веб-страницы г-на Барри как изображение мира ниже.
Индекс 1 — идеальный прямоугольник, 0 — бесконечное число бесконечно малых островков. Таблица адаптирована с веб-страницы г-на Барри как изображение мира ниже.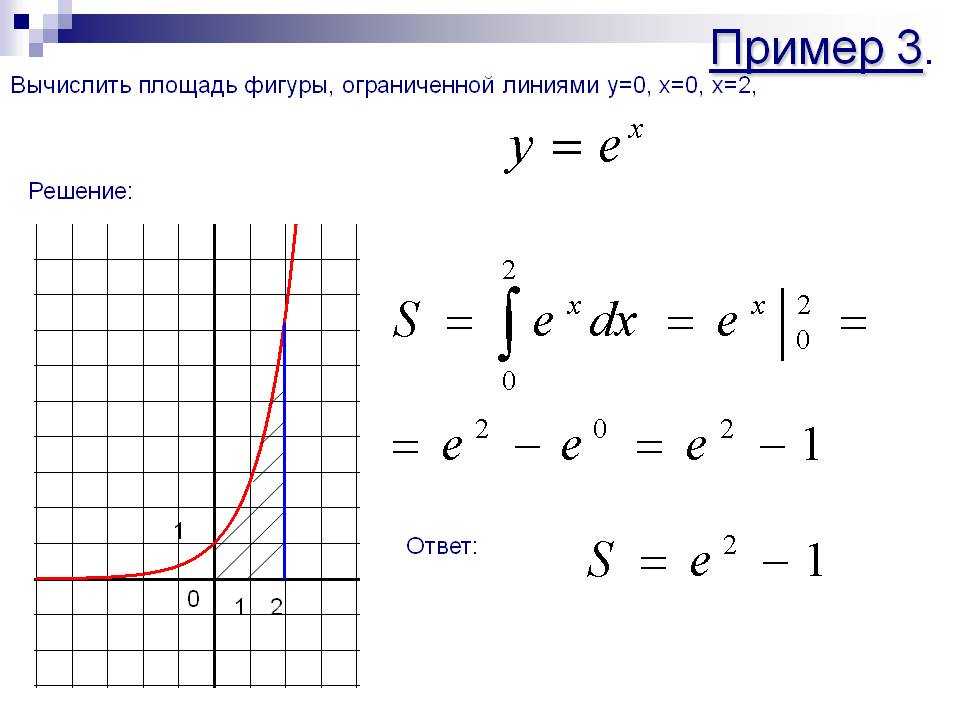 ..
..