Четное число | Математика
Что такое четное число, какое число называется четным, можно ли вывести все четные числа!? Вывести все однозначные, двузначные , трехзначные , четырехзначные четные числа.
Скопировать ссылку
Что такое четное число Определение Что такое четное число!? Есть несколько способов заполнить, Что такое четное число
Любое число, которое делится на 2 без остатка будет четным!
Как еще можно определить, что это четное число!?
Любое число, которое оканчивается цифрой :
2 , 4 , 6 , 8 , 0
будет четным.
наименьшее(целое,положительное) четное число
Изначально, вопрос был «наименьшее четное число«, но все же нужно уточнить, что это должно звучать так:наименьшее(целое,положительное) четное числоЭто 2
Четное число число делится
Четное число делится как минимум на 2 и на себя! И главный признак четного числа — как было сказано выше, что оно(число) должно делиться на 2.
вывести все четные числа
Когда вы ищите вывести все четные числа, то, что конкретно вы имеете ввиду говоря эту фразу!!?Если произвести математическую операцию и вывести все четные числа например через цикл, то у вас памяти на компьютере не хватит открыть такую страницу… потому, что все четные числа будут стремиться к бесконечности…
Однозначные положительные четные числа
А вот вывести все четные цифры — это вполне возможно, потому, что их не так много… их всего 4 :
2 , 4 , 6 , 8
Скопировать ссылку
четные числа до 100
Вот интересный вопрос : четные числа до 100 — включая 100 или нет!? Вручную я выводить четные числа до 100 не буду у нас есть «php», а там есть циклЕще более интересный вопрос — сколько четных чисел от 0 до 100 , слева выведем нумерацию по счету.
 ..
..
Форма скрыта
1). 2
2). 4
3). 6
4). 8
5). 10
6). 12
7). 14
8). 16
9). 18
10). 20
11). 22
12). 24
13). 26
14). 28
15). 30
16). 32
17). 34
18). 36
19). 38
20). 40
21). 42
22). 44
23). 46
24). 48
25). 50
26). 52
27). 54
28). 56
29). 58
30). 60
31). 62
32). 64
33). 66
34). 68
35). 70
36). 72
37). 74
38). 76
39). 78
40). 80
41). 82
42). 84
43). 86
44). 88
45). 90
46). 92
47). 94
48). 96
49). 98
Если интересно, то эти четные числа сегментированы программой:
for ($i=2; $i < 100; $i += 2)
{
$COUNT ++;
$echo .= ‘<red>’.$COUNT.'</red>). ‘ .$i.»\n»;
}
echo $echo;
Скопировать ссылку
Четные двузначные числа
Вывести все двухзначные четные двухзначные числа. Двузначные это от 10 до 99 :
10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98,
Скопировать ссылку
Четные трехзначные числа
Вывести все трехзначные четные двухзначные числа. Двузначные это от 100 до 999 :
Двузначные это от 100 до 999 :
100, 102, 104, 106, 108, 110, 112, 114, 116, 118, 120, 122, 124, 126, 128, 130, 132, 134, 136, 138, 140, 142, 144, 146, 148, 150, 152, 154, 156, 158, 160, 162, 164, 166, 168, 170, 172, 174, 176, 178, 180, 182, 184, 186, 188, 190, 192, 194, 196, 198, 200, 202, 204, 206, 208, 210, 212, 214, 216, 218, 220, 222, 224, 226, 228, 230, 232, 234, 236, 238, 240, 242, 244, 246, 248, 250, 252, 254, 256, 258, 260, 262, 264, 266, 268, 270, 272, 274, 276, 278, 280, 282, 284, 286, 288, 290, 292, 294, 296, 298, 300, 302, 304, 306, 308, 310, 312, 314, 316, 318, 320, 322, 324, 326, 328, 330, 332, 334, 336, 338, 340, 342, 344, 346, 348, 350, 352, 354, 356, 358, 360, 362, 364, 366, 368, 370, 372, 374, 376, 378, 380, 382, 384, 386, 388, 390, 392, 394, 396, 398, 400, 402, 404, 406, 408, 410, 412, 414, 416, 418, 420, 422, 424, 426, 428, 430, 432, 434, 436, 438, 440, 442, 444, 446, 448, 450, 452, 454, 456, 458, 460, 462, 464, 466, 468, 470, 472, 474, 476, 478, 480, 482, 484, 486, 488, 490, 492, 494, 496, 498, 500, 502, 504, 506, 508, 510, 512, 514, 516, 518, 520, 522, 524, 526, 528, 530, 532, 534, 536, 538, 540, 542, 544, 546, 548, 550, 552, 554, 556, 558, 560, 562, 564, 566, 568, 570, 572, 574, 576, 578, 580, 582, 584, 586, 588, 590, 592, 594, 596, 598, 600, 602, 604, 606, 608, 610, 612, 614, 616, 618, 620, 622, 624, 626, 628, 630, 632, 634, 636, 638, 640, 642, 644, 646, 648, 650, 652, 654, 656, 658, 660, 662, 664, 666, 668, 670, 672, 674, 676, 678, 680, 682, 684, 686, 688, 690, 692, 694, 696, 698, 700, 702, 704, 706, 708, 710, 712, 714, 716, 718, 720, 722, 724, 726, 728, 730, 732, 734, 736, 738, 740, 742, 744, 746, 748, 750, 752, 754, 756, 758, 760, 762, 764, 766, 768, 770, 772, 774, 776, 778, 780, 782, 784, 786, 788, 790, 792, 794, 796, 798, 800, 802, 804, 806, 808, 810, 812, 814, 816, 818, 820, 822, 824, 826, 828, 830, 832, 834, 836, 838, 840, 842, 844, 846, 848, 850, 852, 854, 856, 858, 860, 862, 864, 866, 868, 870, 872, 874, 876, 878, 880, 882, 884, 886, 888, 890, 892, 894, 896, 898, 900, 902, 904, 906, 908, 910, 912, 914, 916, 918, 920, 922, 924, 926, 928, 930, 932, 934, 936, 938, 940, 942, 944, 946, 948, 950, 952, 954, 956, 958, 960, 962, 964, 966, 968, 970, 972, 974, 976, 978, 980, 982, 984, 986, 988, 990, 992, 994, 996, 998,
Скопировать ссылку
Четные четырехзначные числа
Вывести все четырехзначные четные двухзначные числа.
1000, 1002, 1004, 1006, 1008, 1010, 1012, 1014, 1016, 1018, 1020, 1022, 1024, 1026, 1028, 1030, 1032, 1034, 1036, 1038, 1040, 1042, 1044, 1046, 1048, 1050, 1052, 1054, 1056, 1058, 1060, 1062, 1064, 1066, 1068, 1070, 1072, 1074, 1076, 1078, 1080, 1082, 1084, 1086, 1088, 1090, 1092, 1094, 1096, 1098, 1100, 1102, 1104, 1106, 1108, 1110, 1112, 1114, 1116, 1118, 1120, 1122, 1124, 1126, 1128, 1130, 1132, 1134, 1136, 1138, 1140, 1142, 1144, 1146, 1148, 1150, 1152, 1154, 1156, 1158, 1160, 1162, 1164, 1166, 1168, 1170, 1172, 1174, 1176, 1178, 1180, 1182, 1184, 1186, 1188, 1190, 1192, 1194, 1196, 1198, 1200, 1202, 1204, 1206, 1208, 1210, 1212, 1214, 1216, 1218, 1220, 1222, 1224, 1226, 1228, 1230, 1232, 1234, 1236, 1238, 1240, 1242, 1244, 1246, 1248, 1250, 1252, 1254, 1256, 1258, 1260, 1262, 1264, 1266, 1268, 1270, 1272, 1274, 1276, 1278, 1280, 1282, 1284, 1286, 1288, 1290, 1292, 1294, 1296, 1298, 1300, 1302, 1304, 1306, 1308, 1310, 1312, 1314, 1316, 1318, 1320, 1322, 1324, 1326, 1328, 1330, 1332, 1334, 1336, 1338, 1340, 1342, 1344, 1346, 1348, 1350, 1352, 1354, 1356, 1358, 1360, 1362, 1364, 1366, 1368, 1370, 1372, 1374, 1376, 1378, 1380, 1382, 1384, 1386, 1388, 1390, 1392, 1394, 1396, 1398, 1400, 1402, 1404, 1406, 1408, 1410, 1412, 1414, 1416, 1418, 1420, 1422, 1424, 1426, 1428, 1430, 1432, 1434, 1436, 1438, 1440, 1442, 1444, 1446, 1448, 1450, 1452, 1454, 1456, 1458, 1460, 1462, 1464, 1466, 1468, 1470, 1472, 1474, 1476, 1478, 1480, 1482, 1484, 1486, 1488, 1490, 1492, 1494, 1496, 1498, 1500, 1502, 1504, 1506, 1508, 1510, 1512, 1514, 1516, 1518, 1520, 1522, 1524, 1526, 1528, 1530, 1532, 1534, 1536, 1538, 1540, 1542, 1544, 1546, 1548, 1550, 1552, 1554, 1556, 1558, 1560, 1562, 1564, 1566, 1568, 1570, 1572, 1574, 1576, 1578, 1580, 1582, 1584, 1586, 1588, 1590, 1592, 1594, 1596, 1598, 1600, 1602, 1604, 1606, 1608, 1610, 1612, 1614, 1616, 1618, 1620, 1622, 1624, 1626, 1628, 1630, 1632, 1634, 1636, 1638, 1640, 1642, 1644, 1646, 1648, 1650, 1652, 1654, 1656, 1658, 1660, 1662, 1664, 1666, 1668, 1670, 1672, 1674, 1676, 1678, 1680, 1682, 1684, 1686, 1688, 1690, 1692, 1694, 1696, 1698, 1700, 1702, 1704, 1706, 1708, 1710, 1712, 1714, 1716, 1718, 1720, 1722, 1724, 1726, 1728, 1730, 1732, 1734, 1736, 1738, 1740, 1742, 1744, 1746, 1748, 1750, 1752, 1754, 1756, 1758, 1760, 1762, 1764, 1766, 1768, 1770, 1772, 1774, 1776, 1778, 1780, 1782, 1784, 1786, 1788, 1790, 1792, 1794, 1796, 1798, 1800, 1802, 1804, 1806, 1808, 1810, 1812, 1814, 1816, 1818, 1820, 1822, 1824, 1826, 1828, 1830, 1832, 1834, 1836, 1838, 1840, 1842, 1844, 1846, 1848, 1850, 1852, 1854, 1856, 1858, 1860, 1862, 1864, 1866, 1868, 1870, 1872, 1874, 1876, 1878, 1880, 1882, 1884, 1886, 1888, 1890, 1892, 1894, 1896, 1898, 1900, 1902, 1904, 1906, 1908, 1910, 1912, 1914, 1916, 1918, 1920, 1922, 1924, 1926, 1928, 1930, 1932, 1934, 1936, 1938, 1940, 1942, 1944, 1946, 1948, 1950, 1952, 1954, 1956, 1958, 1960, 1962, 1964, 1966, 1968, 1970, 1972, 1974, 1976, 1978, 1980, 1982, 1984, 1986, 1988, 1990, 1992, 1994, 1996, 1998, 2000, 2002, 2004, 2006, 2008, 2010, 2012, 2014, 2016, 2018, 2020, 2022, 2024, 2026, 2028, 2030, 2032, 2034, 2036, 2038, 2040, 2042, 2044, 2046, 2048, 2050, 2052, 2054, 2056, 2058, 2060, 2062, 2064, 2066, 2068, 2070, 2072, 2074, 2076, 2078, 2080, 2082, 2084, 2086, 2088, 2090, 2092, 2094, 2096, 2098, 2100, 2102, 2104, 2106, 2108, 2110, 2112, 2114, 2116, 2118, 2120, 2122, 2124, 2126, 2128, 2130, 2132, 2134, 2136, 2138, 2140, 2142, 2144, 2146, 2148, 2150, 2152, 2154, 2156, 2158, 2160, 2162, 2164, 2166, 2168, 2170, 2172, 2174, 2176, 2178, 2180, 2182, 2184, 2186, 2188, 2190, 2192, 2194, 2196, 2198, 2200, 2202, 2204, 2206, 2208, 2210, 2212, 2214, 2216, 2218, 2220, 2222, 2224, 2226, 2228, 2230, 2232, 2234, 2236, 2238, 2240, 2242, 2244, 2246, 2248, 2250, 2252, 2254, 2256, 2258, 2260, 2262, 2264, 2266, 2268, 2270, 2272, 2274, 2276, 2278, 2280, 2282, 2284, 2286, 2288, 2290, 2292, 2294, 2296, 2298, 2300, 2302, 2304, 2306, 2308, 2310, 2312, 2314, 2316, 2318, 2320, 2322, 2324, 2326, 2328, 2330, 2332, 2334, 2336, 2338, 2340, 2342, 2344, 2346, 2348, 2350, 2352, 2354, 2356, 2358, 2360, 2362, 2364, 2366, 2368, 2370, 2372, 2374, 2376, 2378, 2380, 2382, 2384, 2386, 2388, 2390, 2392, 2394, 2396, 2398, 2400, 2402, 2404, 2406, 2408, 2410, 2412, 2414, 2416, 2418, 2420, 2422, 2424, 2426, 2428, 2430, 2432, 2434, 2436, 2438, 2440, 2442, 2444, 2446, 2448, 2450, 2452, 2454, 2456, 2458, 2460, 2462, 2464, 2466, 2468, 2470, 2472, 2474, 2476, 2478, 2480, 2482, 2484, 2486, 2488, 2490, 2492, 2494, 2496, 2498, 2500, 2502, 2504, 2506, 2508, 2510, 2512, 2514, 2516, 2518, 2520, 2522, 2524, 2526, 2528, 2530, 2532, 2534, 2536, 2538, 2540, 2542, 2544, 2546, 2548, 2550, 2552, 2554, 2556, 2558, 2560, 2562, 2564, 2566, 2568, 2570, 2572, 2574, 2576, 2578, 2580, 2582, 2584, 2586, 2588, 2590, 2592, 2594, 2596, 2598, 2600, 2602, 2604, 2606, 2608, 2610, 2612, 2614, 2616, 2618, 2620, 2622, 2624, 2626, 2628, 2630, 2632, 2634, 2636, 2638, 2640, 2642, 2644, 2646, 2648, 2650, 2652, 2654, 2656, 2658, 2660, 2662, 2664, 2666, 2668, 2670, 2672, 2674, 2676, 2678, 2680, 2682, 2684, 2686, 2688, 2690, 2692, 2694, 2696, 2698, 2700, 2702, 2704, 2706, 2708, 2710, 2712, 2714, 2716, 2718, 2720, 2722, 2724, 2726, 2728, 2730, 2732, 2734, 2736, 2738, 2740, 2742, 2744, 2746, 2748, 2750, 2752, 2754, 2756, 2758, 2760, 2762, 2764, 2766, 2768, 2770, 2772, 2774, 2776, 2778, 2780, 2782, 2784, 2786, 2788, 2790, 2792, 2794, 2796, 2798, 2800, 2802, 2804, 2806, 2808, 2810, 2812, 2814, 2816, 2818, 2820, 2822, 2824, 2826, 2828, 2830, 2832, 2834, 2836, 2838, 2840, 2842, 2844, 2846, 2848, 2850, 2852, 2854, 2856, 2858, 2860, 2862, 2864, 2866, 2868, 2870, 2872, 2874, 2876, 2878, 2880, 2882, 2884, 2886, 2888, 2890, 2892, 2894, 2896, 2898, 2900, 2902, 2904, 2906, 2908, 2910, 2912, 2914, 2916, 2918, 2920, 2922, 2924, 2926, 2928, 2930, 2932, 2934, 2936, 2938, 2940, 2942, 2944, 2946, 2948, 2950, 2952, 2954, 2956, 2958, 2960, 2962, 2964, 2966, 2968, 2970, 2972, 2974, 2976, 2978, 2980, 2982, 2984, 2986, 2988, 2990, 2992, 2994, 2996, 2998, 3000, 3002, 3004, 3006, 3008, 3010, 3012, 3014, 3016, 3018, 3020, 3022, 3024, 3026, 3028, 3030, 3032, 3034, 3036, 3038, 3040, 3042, 3044, 3046, 3048, 3050, 3052, 3054, 3056, 3058, 3060, 3062, 3064, 3066, 3068, 3070, 3072, 3074, 3076, 3078, 3080, 3082, 3084, 3086, 3088, 3090, 3092, 3094, 3096, 3098, 3100, 3102, 3104, 3106, 3108, 3110, 3112, 3114, 3116, 3118, 3120, 3122, 3124, 3126, 3128, 3130, 3132, 3134, 3136, 3138, 3140, 3142, 3144, 3146, 3148, 3150, 3152, 3154, 3156, 3158, 3160, 3162, 3164, 3166, 3168, 3170, 3172, 3174, 3176, 3178, 3180, 3182, 3184, 3186, 3188, 3190, 3192, 3194, 3196, 3198, 3200, 3202, 3204, 3206, 3208, 3210, 3212, 3214, 3216, 3218, 3220, 3222, 3224, 3226, 3228, 3230, 3232, 3234, 3236, 3238, 3240, 3242, 3244, 3246, 3248, 3250, 3252, 3254, 3256, 3258, 3260, 3262, 3264, 3266, 3268, 3270, 3272, 3274, 3276, 3278, 3280, 3282, 3284, 3286, 3288, 3290, 3292, 3294, 3296, 3298, 3300, 3302, 3304, 3306, 3308, 3310, 3312, 3314, 3316, 3318, 3320, 3322, 3324, 3326, 3328, 3330, 3332, 3334, 3336, 3338, 3340, 3342, 3344, 3346, 3348, 3350, 3352, 3354, 3356, 3358, 3360, 3362, 3364, 3366, 3368, 3370, 3372, 3374, 3376, 3378, 3380, 3382, 3384, 3386, 3388, 3390, 3392, 3394, 3396, 3398, 3400, 3402, 3404, 3406, 3408, 3410, 3412, 3414, 3416, 3418, 3420, 3422, 3424, 3426, 3428, 3430, 3432, 3434, 3436, 3438, 3440, 3442, 3444, 3446, 3448, 3450, 3452, 3454, 3456, 3458, 3460, 3462, 3464, 3466, 3468, 3470, 3472, 3474, 3476, 3478, 3480, 3482, 3484, 3486, 3488, 3490, 3492, 3494, 3496, 3498, 3500, 3502, 3504, 3506, 3508, 3510, 3512, 3514, 3516, 3518, 3520, 3522, 3524, 3526, 3528, 3530, 3532, 3534, 3536, 3538, 3540, 3542, 3544, 3546, 3548, 3550, 3552, 3554, 3556, 3558, 3560, 3562, 3564, 3566, 3568, 3570, 3572, 3574, 3576, 3578, 3580, 3582, 3584, 3586, 3588, 3590, 3592, 3594, 3596, 3598, 3600, 3602, 3604, 3606, 3608, 3610, 3612, 3614, 3616, 3618, 3620, 3622, 3624, 3626, 3628, 3630, 3632, 3634, 3636, 3638, 3640, 3642, 3644, 3646, 3648, 3650, 3652, 3654, 3656, 3658, 3660, 3662, 3664, 3666, 3668, 3670, 3672, 3674, 3676, 3678, 3680, 3682, 3684, 3686, 3688, 3690, 3692, 3694, 3696, 3698, 3700, 3702, 3704, 3706, 3708, 3710, 3712, 3714, 3716, 3718, 3720, 3722, 3724, 3726, 3728, 3730, 3732, 3734, 3736, 3738, 3740, 3742, 3744, 3746, 3748, 3750, 3752, 3754, 3756, 3758, 3760, 3762, 3764, 3766, 3768, 3770, 3772, 3774, 3776, 3778, 3780, 3782, 3784, 3786, 3788, 3790, 3792, 3794, 3796, 3798, 3800, 3802, 3804, 3806, 3808, 3810, 3812, 3814, 3816, 3818, 3820, 3822, 3824, 3826, 3828, 3830, 3832, 3834, 3836, 3838, 3840, 3842, 3844, 3846, 3848, 3850, 3852, 3854, 3856, 3858, 3860, 3862, 3864, 3866, 3868, 3870, 3872, 3874, 3876, 3878, 3880, 3882, 3884, 3886, 3888, 3890, 3892, 3894, 3896, 3898, 3900, 3902, 3904, 3906, 3908, 3910, 3912, 3914, 3916, 3918, 3920, 3922, 3924, 3926, 3928, 3930, 3932, 3934, 3936, 3938, 3940, 3942, 3944, 3946, 3948, 3950, 3952, 3954, 3956, 3958, 3960, 3962, 3964, 3966, 3968, 3970, 3972, 3974, 3976, 3978, 3980, 3982, 3984, 3986, 3988, 3990, 3992, 3994, 3996, 3998, 4000, 4002, 4004, 4006, 4008, 4010, 4012, 4014, 4016, 4018, 4020, 4022, 4024, 4026, 4028, 4030, 4032, 4034, 4036, 4038, 4040, 4042, 4044, 4046, 4048, 4050, 4052, 4054, 4056, 4058, 4060, 4062, 4064, 4066, 4068, 4070, 4072, 4074, 4076, 4078, 4080, 4082, 4084, 4086, 4088, 4090, 4092, 4094, 4096, 4098, 4100, 4102, 4104, 4106, 4108, 4110, 4112, 4114, 4116, 4118, 4120, 4122, 4124, 4126, 4128, 4130, 4132, 4134, 4136, 4138, 4140, 4142, 4144, 4146, 4148, 4150, 4152, 4154, 4156, 4158, 4160, 4162, 4164, 4166, 4168, 4170, 4172, 4174, 4176, 4178, 4180, 4182, 4184, 4186, 4188, 4190, 4192, 4194, 4196, 4198, 4200, 4202, 4204, 4206, 4208, 4210, 4212, 4214, 4216, 4218, 4220, 4222, 4224, 4226, 4228, 4230, 4232, 4234, 4236, 4238, 4240, 4242, 4244, 4246, 4248, 4250, 4252, 4254, 4256, 4258, 4260, 4262, 4264, 4266, 4268, 4270, 4272, 4274, 4276, 4278, 4280, 4282, 4284, 4286, 4288, 4290, 4292, 4294, 4296, 4298, 4300, 4302, 4304, 4306, 4308, 4310, 4312, 4314, 4316, 4318, 4320, 4322, 4324, 4326, 4328, 4330, 4332, 4334, 4336, 4338, 4340, 4342, 4344, 4346, 4348, 4350, 4352, 4354, 4356, 4358, 4360, 4362, 4364, 4366, 4368, 4370, 4372, 4374, 4376, 4378, 4380, 4382, 4384, 4386, 4388, 4390, 4392, 4394, 4396, 4398, 4400, 4402, 4404, 4406, 4408, 4410, 4412, 4414, 4416, 4418, 4420, 4422, 4424, 4426, 4428, 4430, 4432, 4434, 4436, 4438, 4440, 4442, 4444, 4446, 4448, 4450, 4452, 4454, 4456, 4458, 4460, 4462, 4464, 4466, 4468, 4470, 4472, 4474, 4476, 4478, 4480, 4482, 4484, 4486, 4488, 4490, 4492, 4494, 4496, 4498, 4500, 4502, 4504, 4506, 4508, 4510, 4512, 4514, 4516, 4518, 4520, 4522, 4524, 4526, 4528, 4530, 4532, 4534, 4536, 4538, 4540, 4542, 4544, 4546, 4548, 4550, 4552, 4554, 4556, 4558, 4560, 4562, 4564, 4566, 4568, 4570, 4572, 4574, 4576, 4578, 4580, 4582, 4584, 4586, 4588, 4590, 4592, 4594, 4596, 4598, 4600, 4602, 4604, 4606, 4608, 4610, 4612, 4614, 4616, 4618, 4620, 4622, 4624, 4626, 4628, 4630, 4632, 4634, 4636, 4638, 4640, 4642, 4644, 4646, 4648, 4650, 4652, 4654, 4656, 4658, 4660, 4662, 4664, 4666, 4668, 4670, 4672, 4674, 4676, 4678, 4680, 4682, 4684, 4686, 4688, 4690, 4692, 4694, 4696, 4698, 4700, 4702, 4704, 4706, 4708, 4710, 4712, 4714, 4716, 4718, 4720, 4722, 4724, 4726, 4728, 4730, 4732, 4734, 4736, 4738, 4740, 4742, 4744, 4746, 4748, 4750, 4752, 4754, 4756, 4758, 4760, 4762, 4764, 4766, 4768, 4770, 4772, 4774, 4776, 4778, 4780, 4782, 4784, 4786, 4788, 4790, 4792, 4794, 4796, 4798, 4800, 4802, 4804, 4806, 4808, 4810, 4812, 4814, 4816, 4818, 4820, 4822, 4824, 4826, 4828, 4830, 4832, 4834, 4836, 4838, 4840, 4842, 4844, 4846, 4848, 4850, 4852, 4854, 4856, 4858, 4860, 4862, 4864, 4866, 4868, 4870, 4872, 4874, 4876, 4878, 4880, 4882, 4884, 4886, 4888, 4890, 4892, 4894, 4896, 4898, 4900, 4902, 4904, 4906, 4908, 4910, 4912, 4914, 4916, 4918, 4920, 4922, 4924, 4926, 4928, 4930, 4932, 4934, 4936, 4938, 4940, 4942, 4944, 4946, 4948, 4950, 4952, 4954, 4956, 4958, 4960, 4962, 4964, 4966, 4968, 4970, 4972, 4974, 4976, 4978, 4980, 4982, 4984, 4986, 4988, 4990, 4992, 4994, 4996, 4998, 5000, 5002, 5004, 5006, 5008, 5010, 5012, 5014, 5016, 5018, 5020, 5022, 5024, 5026, 5028, 5030, 5032, 5034, 5036, 5038, 5040, 5042, 5044, 5046, 5048, 5050, 5052, 5054, 5056, 5058, 5060, 5062, 5064, 5066, 5068, 5070, 5072, 5074, 5076, 5078, 5080, 5082, 5084, 5086, 5088, 5090, 5092, 5094, 5096, 5098, 5100, 5102, 5104, 5106, 5108, 5110, 5112, 5114, 5116, 5118, 5120, 5122, 5124, 5126, 5128, 5130, 5132, 5134, 5136, 5138, 5140, 5142, 5144, 5146, 5148, 5150, 5152, 5154, 5156, 5158, 5160, 5162, 5164, 5166, 5168, 5170, 5172, 5174, 5176, 5178, 5180, 5182, 5184, 5186, 5188, 5190, 5192, 5194, 5196, 5198, 5200, 5202, 5204, 5206, 5208, 5210, 5212, 5214, 5216, 5218, 5220, 5222, 5224, 5226, 5228, 5230, 5232, 5234, 5236, 5238, 5240, 5242, 5244, 5246, 5248, 5250, 5252, 5254, 5256, 5258, 5260, 5262, 5264, 5266, 5268, 5270, 5272, 5274, 5276, 5278, 5280, 5282, 5284, 5286, 5288, 5290, 5292, 5294, 5296, 5298, 5300, 5302, 5304, 5306, 5308, 5310, 5312, 5314, 5316, 5318, 5320, 5322, 5324, 5326, 5328, 5330, 5332, 5334, 5336, 5338, 5340, 5342, 5344, 5346, 5348, 5350, 5352, 5354, 5356, 5358, 5360, 5362, 5364, 5366, 5368, 5370, 5372, 5374, 5376, 5378, 5380, 5382, 5384, 5386, 5388, 5390, 5392, 5394, 5396, 5398, 5400, 5402, 5404, 5406, 5408, 5410, 5412, 5414, 5416, 5418, 5420, 5422, 5424, 5426, 5428, 5430, 5432, 5434, 5436, 5438, 5440, 5442, 5444, 5446, 5448, 5450, 5452, 5454, 5456, 5458, 5460, 5462, 5464, 5466, 5468, 5470, 5472, 5474, 5476, 5478, 5480, 5482, 5484, 5486, 5488, 5490, 5492, 5494, 5496, 5498, 5500, 5502, 5504, 5506, 5508, 5510, 5512, 5514, 5516, 5518, 5520, 5522, 5524, 5526, 5528, 5530, 5532, 5534, 5536, 5538, 5540, 5542, 5544, 5546, 5548, 5550, 5552, 5554, 5556, 5558, 5560, 5562, 5564, 5566, 5568, 5570, 5572, 5574, 5576, 5578, 5580, 5582, 5584, 5586, 5588, 5590, 5592, 5594, 5596, 5598, 5600, 5602, 5604, 5606, 5608, 5610, 5612, 5614, 5616, 5618, 5620, 5622, 5624, 5626, 5628, 5630, 5632, 5634, 5636, 5638, 5640, 5642, 5644, 5646, 5648, 5650, 5652, 5654, 5656, 5658, 5660, 5662, 5664, 5666, 5668, 5670, 5672, 5674, 5676, 5678, 5680, 5682, 5684, 5686, 5688, 5690, 5692, 5694, 5696, 5698, 5700, 5702, 5704, 5706, 5708, 5710, 5712, 5714, 5716, 5718, 5720, 5722, 5724, 5726, 5728, 5730, 5732, 5734, 5736, 5738, 5740, 5742, 5744, 5746, 5748, 5750, 5752, 5754, 5756, 5758, 5760, 5762, 5764, 5766, 5768, 5770, 5772, 5774, 5776, 5778, 5780, 5782, 5784, 5786, 5788, 5790, 5792, 5794, 5796, 5798, 5800, 5802, 5804, 5806, 5808, 5810, 5812, 5814, 5816, 5818, 5820, 5822, 5824, 5826, 5828, 5830, 5832, 5834, 5836, 5838, 5840, 5842, 5844, 5846, 5848, 5850, 5852, 5854, 5856, 5858, 5860, 5862, 5864, 5866, 5868, 5870, 5872, 5874, 5876, 5878, 5880, 5882, 5884, 5886, 5888, 5890, 5892, 5894, 5896, 5898, 5900, 5902, 5904, 5906, 5908, 5910, 5912, 5914, 5916, 5918, 5920, 5922, 5924, 5926, 5928, 5930, 5932, 5934, 5936, 5938, 5940, 5942, 5944, 5946, 5948, 5950, 5952, 5954, 5956, 5958, 5960, 5962, 5964, 5966, 5968, 5970, 5972, 5974, 5976, 5978, 5980, 5982, 5984, 5986, 5988, 5990, 5992, 5994, 5996, 5998, 6000, 6002, 6004, 6006, 6008, 6010, 6012, 6014, 6016, 6018, 6020, 6022, 6024, 6026, 6028, 6030, 6032, 6034, 6036, 6038, 6040, 6042, 6044, 6046, 6048, 6050, 6052, 6054, 6056, 6058, 6060, 6062, 6064, 6066, 6068, 6070, 6072, 6074, 6076, 6078, 6080, 6082, 6084, 6086, 6088, 6090, 6092, 6094, 6096, 6098, 6100, 6102, 6104, 6106, 6108, 6110, 6112, 6114, 6116, 6118, 6120, 6122, 6124, 6126, 6128, 6130, 6132, 6134, 6136, 6138, 6140, 6142, 6144, 6146, 6148, 6150, 6152, 6154, 6156, 6158, 6160, 6162, 6164, 6166, 6168, 6170, 6172, 6174, 6176, 6178, 6180, 6182, 6184, 6186, 6188, 6190, 6192, 6194, 6196, 6198, 6200, 6202, 6204, 6206, 6208, 6210, 6212, 6214, 6216, 6218, 6220, 6222, 6224, 6226, 6228, 6230, 6232, 6234, 6236, 6238, 6240, 6242, 6244, 6246, 6248, 6250, 6252, 6254, 6256, 6258, 6260, 6262, 6264, 6266, 6268, 6270, 6272, 6274, 6276, 6278, 6280, 6282, 6284, 6286, 6288, 6290, 6292, 6294, 6296, 6298, 6300, 6302, 6304, 6306, 6308, 6310, 6312, 6314, 6316, 6318, 6320, 6322, 6324, 6326, 6328, 6330, 6332, 6334, 6336, 6338, 6340, 6342, 6344, 6346, 6348, 6350, 6352, 6354, 6356, 6358, 6360, 6362, 6364, 6366, 6368, 6370, 6372, 6374, 6376, 6378, 6380, 6382, 6384, 6386, 6388, 6390, 6392, 6394, 6396, 6398, 6400, 6402, 6404, 6406, 6408, 6410, 6412, 6414, 6416, 6418, 6420, 6422, 6424, 6426, 6428, 6430, 6432, 6434, 6436, 6438, 6440, 6442, 6444, 6446, 6448, 6450, 6452, 6454, 6456, 6458, 6460, 6462, 6464, 6466, 6468, 6470, 6472, 6474, 6476, 6478, 6480, 6482, 6484, 6486, 6488, 6490, 6492, 6494, 6496, 6498, 6500, 6502, 6504, 6506, 6508, 6510, 6512, 6514, 6516, 6518, 6520, 6522, 6524, 6526, 6528, 6530, 6532, 6534, 6536, 6538, 6540, 6542, 6544, 6546, 6548, 6550, 6552, 6554, 6556, 6558, 6560, 6562, 6564, 6566, 6568, 6570, 6572, 6574, 6576, 6578, 6580, 6582, 6584, 6586, 6588, 6590, 6592, 6594, 6596, 6598, 6600, 6602, 6604, 6606, 6608, 6610, 6612, 6614, 6616, 6618, 6620, 6622, 6624, 6626, 6628, 6630, 6632, 6634, 6636, 6638, 6640, 6642, 6644, 6646, 6648, 6650, 6652, 6654, 6656, 6658, 6660, 6662, 6664, 6666, 6668, 6670, 6672, 6674, 6676, 6678, 6680, 6682, 6684, 6686, 6688, 6690, 6692, 6694, 6696, 6698, 6700, 6702, 6704, 6706, 6708, 6710, 6712, 6714, 6716, 6718, 6720, 6722, 6724, 6726, 6728, 6730, 6732, 6734, 6736, 6738, 6740, 6742, 6744, 6746, 6748, 6750, 6752, 6754, 6756, 6758, 6760, 6762, 6764, 6766, 6768, 6770, 6772, 6774, 6776, 6778, 6780, 6782, 6784, 6786, 6788, 6790, 6792, 6794, 6796, 6798, 6800, 6802, 6804, 6806, 6808, 6810, 6812, 6814, 6816, 6818, 6820, 6822, 6824, 6826, 6828, 6830, 6832, 6834, 6836, 6838, 6840, 6842, 6844, 6846, 6848, 6850, 6852, 6854, 6856, 6858, 6860, 6862, 6864, 6866, 6868, 6870, 6872, 6874, 6876, 6878, 6880, 6882, 6884, 6886, 6888, 6890, 6892, 6894, 6896, 6898, 6900, 6902, 6904, 6906, 6908, 6910, 6912, 6914, 6916, 6918, 6920, 6922, 6924, 6926, 6928, 6930, 6932, 6934, 6936, 6938, 6940, 6942, 6944, 6946, 6948, 6950, 6952, 6954, 6956, 6958, 6960, 6962, 6964, 6966, 6968, 6970, 6972, 6974, 6976, 6978, 6980, 6982, 6984, 6986, 6988, 6990, 6992, 6994, 6996, 6998, 7000, 7002, 7004, 7006, 7008, 7010, 7012, 7014, 7016, 7018, 7020, 7022, 7024, 7026, 7028, 7030, 7032, 7034, 7036, 7038, 7040, 7042, 7044, 7046, 7048, 7050, 7052, 7054, 7056, 7058, 7060, 7062, 7064, 7066, 7068, 7070, 7072, 7074, 7076, 7078, 7080, 7082, 7084, 7086, 7088, 7090, 7092, 7094, 7096, 7098, 7100, 7102, 7104, 7106, 7108, 7110, 7112, 7114, 7116, 7118, 7120, 7122, 7124, 7126, 7128, 7130, 7132, 7134, 7136, 7138, 7140, 7142, 7144, 7146, 7148, 7150, 7152, 7154, 7156, 7158, 7160, 7162, 7164, 7166, 7168, 7170, 7172, 7174, 7176, 7178, 7180, 7182, 7184, 7186, 7188, 7190, 7192, 7194, 7196, 7198, 7200, 7202, 7204, 7206, 7208, 7210, 7212, 7214, 7216, 7218, 7220, 7222, 7224, 7226, 7228, 7230, 7232, 7234, 7236, 7238, 7240, 7242, 7244, 7246, 7248, 7250, 7252, 7254, 7256, 7258, 7260, 7262, 7264, 7266, 7268, 7270, 7272, 7274, 7276, 7278, 7280, 7282, 7284, 7286, 7288, 7290, 7292, 7294, 7296, 7298, 7300, 7302, 7304, 7306, 7308, 7310, 7312, 7314, 7316, 7318, 7320, 7322, 7324, 7326, 7328, 7330, 7332, 7334, 7336, 7338, 7340, 7342, 7344, 7346, 7348, 7350, 7352, 7354, 7356, 7358, 7360, 7362, 7364, 7366, 7368, 7370, 7372, 7374, 7376, 7378, 7380, 7382, 7384, 7386, 7388, 7390, 7392, 7394, 7396, 7398, 7400, 7402, 7404, 7406, 7408, 7410, 7412, 7414, 7416, 7418, 7420, 7422, 7424, 7426, 7428, 7430, 7432, 7434, 7436, 7438, 7440, 7442, 7444, 7446, 7448, 7450, 7452, 7454, 7456, 7458, 7460, 7462, 7464, 7466, 7468, 7470, 7472, 7474, 7476, 7478, 7480, 7482, 7484, 7486, 7488, 7490, 7492, 7494, 7496, 7498, 7500, 7502, 7504, 7506, 7508, 7510, 7512, 7514, 7516, 7518, 7520, 7522, 7524, 7526, 7528, 7530, 7532, 7534, 7536, 7538, 7540, 7542, 7544, 7546, 7548, 7550, 7552, 7554, 7556, 7558, 7560, 7562, 7564, 7566, 7568, 7570, 7572, 7574, 7576, 7578, 7580, 7582, 7584, 7586, 7588, 7590, 7592, 7594, 7596, 7598, 7600, 7602, 7604, 7606, 7608, 7610, 7612, 7614, 7616, 7618, 7620, 7622, 7624, 7626, 7628, 7630, 7632, 7634, 7636, 7638, 7640, 7642, 7644, 7646, 7648, 7650, 7652, 7654, 7656, 7658, 7660, 7662, 7664, 7666, 7668, 7670, 7672, 7674, 7676, 7678, 7680, 7682, 7684, 7686, 7688, 7690, 7692, 7694, 7696, 7698, 7700, 7702, 7704, 7706, 7708, 7710, 7712, 7714, 7716, 7718, 7720, 7722, 7724, 7726, 7728, 7730, 7732, 7734, 7736, 7738, 7740, 7742, 7744, 7746, 7748, 7750, 7752, 7754, 7756, 7758, 7760, 7762, 7764, 7766, 7768, 7770, 7772, 7774, 7776, 7778, 7780, 7782, 7784, 7786, 7788, 7790, 7792, 7794, 7796, 7798, 7800, 7802, 7804, 7806, 7808, 7810, 7812, 7814, 7816, 7818, 7820, 7822, 7824, 7826, 7828, 7830, 7832, 7834, 7836, 7838, 7840, 7842, 7844, 7846, 7848, 7850, 7852, 7854, 7856, 7858, 7860, 7862, 7864, 7866, 7868, 7870, 7872, 7874, 7876, 7878, 7880, 7882, 7884, 7886, 7888, 7890, 7892, 7894, 7896, 7898, 7900, 7902, 7904, 7906, 7908, 7910, 7912, 7914, 7916, 7918, 7920, 7922, 7924, 7926, 7928, 7930, 7932, 7934, 7936, 7938, 7940, 7942, 7944, 7946, 7948, 7950, 7952, 7954, 7956, 7958, 7960, 7962, 7964, 7966, 7968, 7970, 7972, 7974, 7976, 7978, 7980, 7982, 7984, 7986, 7988, 7990, 7992, 7994, 7996, 7998, 8000, 8002, 8004, 8006, 8008, 8010, 8012, 8014, 8016, 8018, 8020, 8022, 8024, 8026, 8028, 8030, 8032, 8034, 8036, 8038, 8040, 8042, 8044, 8046, 8048, 8050, 8052, 8054, 8056, 8058, 8060, 8062, 8064, 8066, 8068, 8070, 8072, 8074, 8076, 8078, 8080, 8082, 8084, 8086, 8088, 8090, 8092, 8094, 8096, 8098, 8100, 8102, 8104, 8106, 8108, 8110, 8112, 8114, 8116, 8118, 8120, 8122, 8124, 8126, 8128, 8130, 8132, 8134, 8136, 8138, 8140, 8142, 8144, 8146, 8148, 8150, 8152, 8154, 8156, 8158, 8160, 8162, 8164, 8166, 8168, 8170, 8172, 8174, 8176, 8178, 8180, 8182, 8184, 8186, 8188, 8190, 8192, 8194, 8196, 8198, 8200, 8202, 8204, 8206, 8208, 8210, 8212, 8214, 8216, 8218, 8220, 8222, 8224, 8226, 8228, 8230, 8232, 8234, 8236, 8238, 8240, 8242, 8244, 8246, 8248, 8250, 8252, 8254, 8256, 8258, 8260, 8262, 8264, 8266, 8268, 8270, 8272, 8274, 8276, 8278, 8280, 8282, 8284, 8286, 8288, 8290, 8292, 8294, 8296, 8298, 8300, 8302, 8304, 8306, 8308, 8310, 8312, 8314, 8316, 8318, 8320, 8322, 8324, 8326, 8328, 8330, 8332, 8334, 8336, 8338, 8340, 8342, 8344, 8346, 8348, 8350, 8352, 8354, 8356, 8358, 8360, 8362, 8364, 8366, 8368, 8370, 8372, 8374, 8376, 8378, 8380, 8382, 8384, 8386, 8388, 8390, 8392, 8394, 8396, 8398, 8400, 8402, 8404, 8406, 8408, 8410, 8412, 8414, 8416, 8418, 8420, 8422, 8424, 8426, 8428, 8430, 8432, 8434, 8436, 8438, 8440, 8442, 8444, 8446, 8448, 8450, 8452, 8454, 8456, 8458, 8460, 8462, 8464, 8466, 8468, 8470, 8472, 8474, 8476, 8478, 8480, 8482, 8484, 8486, 8488, 8490, 8492, 8494, 8496, 8498, 8500, 8502, 8504, 8506, 8508, 8510, 8512, 8514, 8516, 8518, 8520, 8522, 8524, 8526, 8528, 8530, 8532, 8534, 8536, 8538, 8540, 8542, 8544, 8546, 8548, 8550, 8552, 8554, 8556, 8558, 8560, 8562, 8564, 8566, 8568, 8570, 8572, 8574, 8576, 8578, 8580, 8582, 8584, 8586, 8588, 8590, 8592, 8594, 8596, 8598, 8600, 8602, 8604, 8606, 8608, 8610, 8612, 8614, 8616, 8618, 8620, 8622, 8624, 8626, 8628, 8630, 8632, 8634, 8636, 8638, 8640, 8642, 8644, 8646, 8648, 8650, 8652, 8654, 8656, 8658, 8660, 8662, 8664, 8666, 8668, 8670, 8672, 8674, 8676, 8678, 8680, 8682, 8684, 8686, 8688, 8690, 8692, 8694, 8696, 8698, 8700, 8702, 8704, 8706, 8708, 8710, 8712, 8714, 8716, 8718, 8720, 8722, 8724, 8726, 8728, 8730, 8732, 8734, 8736, 8738, 8740, 8742, 8744, 8746, 8748, 8750, 8752, 8754, 8756, 8758, 8760, 8762, 8764, 8766, 8768, 8770, 8772, 8774, 8776, 8778, 8780, 8782, 8784, 8786, 8788, 8790, 8792, 8794, 8796, 8798, 8800, 8802, 8804, 8806, 8808, 8810, 8812, 8814, 8816, 8818, 8820, 8822, 8824, 8826, 8828, 8830, 8832, 8834, 8836, 8838, 8840, 8842, 8844, 8846, 8848, 8850, 8852, 8854, 8856, 8858, 8860, 8862, 8864, 8866, 8868, 8870, 8872, 8874, 8876, 8878, 8880, 8882, 8884, 8886, 8888, 8890, 8892, 8894, 8896, 8898, 8900, 8902, 8904, 8906, 8908, 8910, 8912, 8914, 8916, 8918, 8920, 8922, 8924, 8926, 8928, 8930, 8932, 8934, 8936, 8938, 8940, 8942, 8944, 8946, 8948, 8950, 8952, 8954, 8956, 8958, 8960, 8962, 8964, 8966, 8968, 8970, 8972, 8974, 8976, 8978, 8980, 8982, 8984, 8986, 8988, 8990, 8992, 8994, 8996, 8998, 9000, 9002, 9004, 9006, 9008, 9010, 9012, 9014, 9016, 9018, 9020, 9022, 9024, 9026, 9028, 9030, 9032, 9034, 9036, 9038, 9040, 9042, 9044, 9046, 9048, 9050, 9052, 9054, 9056, 9058, 9060, 9062, 9064, 9066, 9068, 9070, 9072, 9074, 9076, 9078, 9080, 9082, 9084, 9086, 9088, 9090, 9092, 9094, 9096, 9098, 9100, 9102, 9104, 9106, 9108, 9110, 9112, 9114, 9116, 9118, 9120, 9122, 9124, 9126, 9128, 9130, 9132, 9134, 9136, 9138, 9140, 9142, 9144, 9146, 9148, 9150, 9152, 9154, 9156, 9158, 9160, 9162, 9164, 9166, 9168, 9170, 9172, 9174, 9176, 9178, 9180, 9182, 9184, 9186, 9188, 9190, 9192, 9194, 9196, 9198, 9200, 9202, 9204, 9206, 9208, 9210, 9212, 9214, 9216, 9218, 9220, 9222, 9224, 9226, 9228, 9230, 9232, 9234, 9236, 9238, 9240, 9242, 9244, 9246, 9248, 9250, 9252, 9254, 9256, 9258, 9260, 9262, 9264, 9266, 9268, 9270, 9272, 9274, 9276, 9278, 9280, 9282, 9284, 9286, 9288, 9290, 9292, 9294, 9296, 9298, 9300, 9302, 9304, 9306, 9308, 9310, 9312, 9314, 9316, 9318, 9320, 9322, 9324, 9326, 9328, 9330, 9332, 9334, 9336, 9338, 9340, 9342, 9344, 9346, 9348, 9350, 9352, 9354, 9356, 9358, 9360, 9362, 9364, 9366, 9368, 9370, 9372, 9374, 9376, 9378, 9380, 9382, 9384, 9386, 9388, 9390, 9392, 9394, 9396, 9398, 9400, 9402, 9404, 9406, 9408, 9410, 9412, 9414, 9416, 9418, 9420, 9422, 9424, 9426, 9428, 9430, 9432, 9434, 9436, 9438, 9440, 9442, 9444, 9446, 9448, 9450, 9452, 9454, 9456, 9458, 9460, 9462, 9464, 9466, 9468, 9470, 9472, 9474, 9476, 9478, 9480, 9482, 9484, 9486, 9488, 9490, 9492, 9494, 9496, 9498, 9500, 9502, 9504, 9506, 9508, 9510, 9512, 9514, 9516, 9518, 9520, 9522, 9524, 9526, 9528, 9530, 9532, 9534, 9536, 9538, 9540, 9542, 9544, 9546, 9548, 9550, 9552, 9554, 9556, 9558, 9560, 9562, 9564, 9566, 9568, 9570, 9572, 9574, 9576, 9578, 9580, 9582, 9584, 9586, 9588, 9590, 9592, 9594, 9596, 9598, 9600, 9602, 9604, 9606, 9608, 9610, 9612, 9614, 9616, 9618, 9620, 9622, 9624, 9626, 9628, 9630, 9632, 9634, 9636, 9638, 9640, 9642, 9644, 9646, 9648, 9650, 9652, 9654, 9656, 9658, 9660, 9662, 9664, 9666, 9668, 9670, 9672, 9674, 9676, 9678, 9680, 9682, 9684, 9686, 9688, 9690, 9692, 9694, 9696, 9698, 9700, 9702, 9704, 9706, 9708, 9710, 9712, 9714, 9716, 9718, 9720, 9722, 9724, 9726, 9728, 9730, 9732, 9734, 9736, 9738, 9740, 9742, 9744, 9746, 9748, 9750, 9752, 9754, 9756, 9758, 9760, 9762, 9764, 9766, 9768, 9770, 9772, 9774, 9776, 9778, 9780, 9782, 9784, 9786, 9788, 9790, 9792, 9794, 9796, 9798, 9800, 9802, 9804, 9806, 9808, 9810, 9812, 9814, 9816, 9818, 9820, 9822, 9824, 9826, 9828, 9830, 9832, 9834, 9836, 9838, 9840, 9842, 9844, 9846, 9848, 9850, 9852, 9854, 9856, 9858, 9860, 9862, 9864, 9866, 9868, 9870, 9872, 9874, 9876, 9878, 9880, 9882, 9884, 9886, 9888, 9890, 9892, 9894, 9896, 9898, 9900, 9902, 9904, 9906, 9908, 9910, 9912, 9914, 9916, 9918, 9920, 9922, 9924, 9926, 9928, 9930, 9932, 9934, 9936, 9938, 9940, 9942, 9944, 9946, 9948, 9950, 9952, 9954, 9956, 9958, 9960, 9962, 9964, 9966, 9968, 9970, 9972, 9974, 9976, 9978, 9980, 9982, 9984, 9986, 9988, 9990, 9992, 9994, 9996, 9998,
Скопировать ссылку
Вопросы о четных числах.
 Четные числа — довольно простой вопрос, и написал данную страницу лишь потому, что количество поисковых запросов касающихся понятию четного числа и около, достигает почти 100 000. Вы только вдумайтесь это число! Не поленился и посчитал…до 19 строки дошел, потом притомился…
Четные числа — довольно простой вопрос, и написал данную страницу лишь потому, что количество поисковых запросов касающихся понятию четного числа и около, достигает почти 100 000. Вы только вдумайтесь это число! Не поленился и посчитал…до 19 строки дошел, потом притомился…
четно ли число
Как я уже написал выше, чтобы узнать «четно ли число» — это число должно отвечать одному из условий описанных в первом пункте.Скопировать ссылку
Поиск четных чисел онлайн в заданном приделе.
Если вам требуется найти четные числа в пределе от одного числа до другого, то далее вы можете найти эти четные числа.
Как найти четные числа в пределе от одного числа до другого!?
Для нахождения всех чисел в вашем предел чисел, вам нужно:
В первом поле введите число от которого начнем считать искать все четные числа.
Во втором поле введите число до которого будем считать.
И нажмите кнопку найти все четные.
Теги :
четные числа
четно ли число
четные числа цифры
найди четные числа
четные целые числа
является четным числом
наименьшее четное число
четное число число делится
четные трехзначные числа
количество четных чисел
каждое четное число
n четное число
следующее четное число
таблица четных чисел
последовательность четных чисел
вывести все четные числа
кратное четное число
четные числа до 100
задача четные числа
четные числа это какие
запиши четные числа
любое четное число
найдите наименьшее четное число
первое четное число
четные числа таблица
Четные и нечетные числа. Понятие о десятичной записи числа
Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.
Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.
Например: -24, 0, 6, 38 — все это четные числа.
m = 2k — общая формула написания четных чисел, где k — целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.
Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.
Пример нечетных чисел: 3, 1, 7 и 35.
n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k — целое число.
Сложение и вычитание четных и нечетных чисел
В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.
Операция | Результат | Пример |
Четное + Четное | ||
Четное + Нечетное | Нечетное | |
Нечетное + Нечетное |
Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.
Умножение четных и нечетных чисел
При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.
Операция | Результат | Пример |
Четное * Четное | ||
Четное * Нечетное | ||
Нечетное * Нечетное | Нечетное |
А теперь рассмотрим дробные числа.
Десятичная запись числа
Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.
Например: 3,14; 5,1; 6,789 — это все
С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.
Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.
Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.
А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом — дробную.
Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.
Ответы к с. 66212. Какое число получится: чётное или нечётное, если нечётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи три примера, подтверждающих твоё предположение.
При делении нечётного числа на нечётное число результат всегда будет нечётным числом.
45 : 5 = 9 55 : 11 = 5 63 : 7 = 9
213. Какое число получится: чётное или нечётное, если чётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи несколько примеров, подтверждающих твоё предположение. Обсуди результат с соседом по парте.
Какое число получится: чётное или нечётное, если чётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи несколько примеров, подтверждающих твоё предположение. Обсуди результат с соседом по парте.
При делении чётного числа на нечётное число результат всегда будет чётным числом.
54 : 9 = 6 50 : 5 = 10 96 : 3 = 32
214.
Можешь ли ты привести пример такого случая деления, когда нечётное число делится нацело на чётное число? Почему? Вспомни, как можно получить делимое из делителя и значения частного.
Делимое можно получить, умножив делитель на значение частного. По условию делитель является чётным числом. Мы знаем, что если чётное число умножить на чётное или нечётное число, то результатом будет всегда чётное число. В нашем же случае делимое должно быть нечётным числом. Это означает, что никакое значение частного в этом случае подобрать нельзя и привести пример такого случая деления невозможно.
215.
Представь число 2873 в виде суммы круглых десятков и однозначного числа. Чётным или нечётным числом является каждое из слагаемых? Чётным или нечётным числом будет значение их суммы? На какую цифру может оканчиваться запись чётного числа? А нечётного?
2873 = 2870 + 3
Первое слагаемое – чётное число, второе слагаемое – нечётное число.
2873 – нечётное число.
Нечётное число 2873 заканчивается на нечётную цифру 3, запись чётного числа 2870 — на чётную цифру 0.
Запись чётного числа может оканчиваться чётными цифрами (0, 2, 4, 6, 8), а запись нечётного числа — нечётными числами (1, 3, 5, 7, 9).
216. Выпиши чётные числа в один столбик, а нечётные — в другой.
2844 57893
67586 9231
10050 9929
217.
Сколько существует чётных двузначных натуральных чисел? А сколько таких же нечётных чисел?
Самое маленькое двузначное чётное число 10, а самое большое – нечётное число 99. Всего их 99 – 10 + 1 = 90. Чётные и нечётные числа в натуральном ряду чередуются, поэтому чётных двузначных чисел столько же сколько и нечётных, то есть 45, поскольку 90 : 2 = 45.
Чётные и нечётные числа в натуральном ряду чередуются, поэтому чётных двузначных чисел столько же сколько и нечётных, то есть 45, поскольку 90 : 2 = 45.
218.
Запиши самое большле чётное шестизначное число.
Что означают чётные и нечётные числа в духовной нумерологии. В изучении это очень важная тема! Чем по своей СУТИ чётные числа отличаются от нечётных чисел?
Чётные числа
Общеизвестно, что чётные числа — те, которые делятся на два. То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.
А что означают чётные числа относительно ? Какова нумерологическая суть деления на два? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.
У несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».
А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии. Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.
Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?
Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.
Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе… надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.
Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.
Нечётные числа
Нечётные числа — те, которые не делятся на два: числа 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 и так далее. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.
Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого — чётное… Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?
Видимые совпадения материальной логики и духовной происходят очень часто. Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел , никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.
Возьмём для примера — число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.
Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!
Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!
Парадоксальность — вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них…
Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.
Чётные и нечётные числа в нумерологии
Подведём итоги. В чём главное отличие чётных чисел от нечётных?
Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…
Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…
Нечётные числа — взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь…
Обратите внимание!
В магазины уже поступила моя книга под названием «Духовная нумерология. Язык чисел». На сегодняшний день это самое полное и востребованное из всех существующих эзотерических пособий о смысле чисел. Подробнее об этом, а также для заказа книги пройдите по следующей ссылке: ««
———————————————————————————————
Определения
- Чётное число — целое число, которое делится без остатка на 2: …, −4, −2, 0, 2, 4, 6, 8, …
- Нечётное число — целое число, которое не делится без остатка на 2: …, −3, −1, 1, 3, 5, 7, 9, …
В соответствии с этим определением нуль является чётным числом.
Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .
В разных странах существуют связанные с количеством даримых цветов традиции.
В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли.
Например, вполне допустимо подарить юной даме букет из 12 или 14 цветов или срезов кустового цветка, если они имеют множество бутонов , у которых они, в принципе, не подсчитываются.
Тем более это относится к б́ольшему количеству цветов (срезов), даримых в других случаях.
Примечания
Wikimedia Foundation . 2010 .
Смотреть что такое «Чётные и нечётные числа» в других словарях:
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19). … … Википедия
… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19). … … Википедия
… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Слегка избыточное число, или квазисовершенное число избыточное число, сумма собственных делителей которого на единицу больше самого числа. До настоящего времени не было найдено ни одного слегка избыточного числа. Но со времён Пифагора,… … Википедия
Целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… …
Целые (0, 1, 2,…) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы. … … Большая советская энциклопедия
… … Большая советская энциклопедия
Книги
- Математические лабиринты и ребусы, 20 карточек , Барчан Татьяна Александровна, Самоделко Анна. В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20…
Дарят четное или нечетное число. Имеет ли значение количество цветов в букете
Выбрать примету, более подходящую к данной ситуации, например такую: если Вам подарили четное (парное) количество цветков, то это означает, что Вы всегда будете в паре и никогда не будете страдать от одиночества. К тому же на западе подсчет идет в дюжинах (аналог нашим десяткам, только равен числу 12). А это все четные количества, заметьте. Вот и получается, что в любом случае Вы в плюсе: у Вас и чудный букет, и прекрасное будущее, и отличное настроение.
Вариант 3. Не считать цветы в букетеСамый простой и верный способ — не считайте цветы вовсе. Самое главное, что Вам подарили прекрасный букет, да и глупо расстраиваться из-за каких-то примет. Еще и давать кому-то возможность Вас огорчить, если допустить, что четное количество было вручено намеренно. Недоброжелателей в жизни хватает, так ведь? В таком случае, зачем давать кому-то повод манипулировать Вами? Допустим, захотел недруг подпортить Вам праздник и подарил 30 роз, или гвоздик, или хризантем, полагаясь на то, что Вы расстроитесь. А Вы, увидев это, радостно и восторженно начинаете благодарить и целовать его. Теперь уже его очередь грустить. А сами, если уж таки верите в приметы, отделили один цветок и забыли.
Самое главное, что Вам подарили прекрасный букет, да и глупо расстраиваться из-за каких-то примет. Еще и давать кому-то возможность Вас огорчить, если допустить, что четное количество было вручено намеренно. Недоброжелателей в жизни хватает, так ведь? В таком случае, зачем давать кому-то повод манипулировать Вами? Допустим, захотел недруг подпортить Вам праздник и подарил 30 роз, или гвоздик, или хризантем, полагаясь на то, что Вы расстроитесь. А Вы, увидев это, радостно и восторженно начинаете благодарить и целовать его. Теперь уже его очередь грустить. А сами, если уж таки верите в приметы, отделили один цветок и забыли.
Не позволяйте кому бы то ни было (людям или стереотипам) портить Вам настроение и омрачать торжество, влиять на Ваши эмоции. Будьте выше этого, будьте мудрее и сильнее. А цветы — это одно из средств, с помощью которых накапливаются положительные эмоции. Вот и заряжайтесь позитивом! Они приносят счастье, радость и уют в дом. Дарите их и принимайте с благодарностью, и неважно, сколько там штук, привезла ли их служба доставки или они были вручены собственноручно, главное — внимание, забота и уважение, оказанное Вам таким презентом. Цените то, что имеете, и будьте счастливы!
Цените то, что имеете, и будьте счастливы!
Делайте такие подарки, не зависимо от того, праздник сегодня или обычный будний день. Букет — это терапия, инструмент, который лечит от плохого настроения, доставляя радость, как дарящему человеку, так и получающему.
Так что же делать, если подарили четное количество цветов? Выбор в Ваших руках:
- разделить букет на две части;
- поверить в «парную» примету, что четное количество цветов — к счастью;
- обмануть недоброжелателей и продемонстрировать свое актерское мастерство, разыграв перед ними бурную радость и тем самым расстроив их планы;
- не считать цветы в букетах, а просто радоваться тому, что Вам сделали такой нежный подарок, что о Вас заботятся, о Вас думают;
- дарить цветы родным, близким, знакомым, дарить охапками, букетами, поштучно, дарить по поводу и без, дарить радость и получать от этого удовольствие!
Дарить четное число цветов — нельзя . Пожалуй, это самое распространенное суеверие, которые соблюдают практически все. Откуда пошло поверье, что четное количество цветов приносит несчастье и действительно ли стоит верить данной примете?
Откуда пошло поверье, что четное количество цветов приносит несчастье и действительно ли стоит верить данной примете?
Четное количество цветов — можно ли дарить
Обычно букет из четного количества цветов приносят на могилу умершего человека. А вот живым принято дарить нечетное количество. Примета эта возникла еще в период языческой Руси. Волхвы олицетворяли четные числа с завершенностью жизненного цикла, то есть с концом, смертью. Нечетные, напротив, символизировали начало жизни и были оберегом от злых духов.
Интересно, что такая примета о цветах существует практически только в России. К примеру, в странах бывшего СССР, в Европе, США и Японии мужчины не видят ничего дурного в том, чтобы подарить своей женщины букет из четырех или восьми роз. В Японии считают, что четное количество цветов олицетворяет гармонию. Такие букеты принято дарить тем, кто не нашел свою вторую половинку. Японцы придерживаются такого принципа: каждой твари по паре, и поэтому даря четное количество цветов, желают человеку найти свой пару.
Значение цветов в букете
В флористике существует свой язык цветов. Количество цветов в букете имеет следующие значения:
- 1 цветок дарится в знак внимания.
- 3 цветка — в знак уважения.
- 5 — в знак признания.
- 7 — в знак обожания.
- 9 в букете означает — «я у ваших ног».
- 11 — проявление любви, верности и преданности.
- 13, по мнению флористов, уместно дарить на годовщину знакомства, свадьбы и по случаю любой значимой даты для любящей пары.
Суеверие о четном количестве цветов в букете так сильно укоренилась в нашем сознании, что, наверно, никакие доказательства его несостоятельности не поменяют мнения. Желаем удачи и не забывайте нажимать на кнопки и
04.03.2015 09:46
Диффенбахия — неприхотливое растение, которое сейчас можно увидеть во многих домах. Она обладает сильными энергетическими…
Декабрист — это красивое растение, но специалисты по биоэнергетике советуют не спешить покупать его себе. ..
..
В разных странах существуют различные поверья и приметы. Одно из многих поверий, отличающих жителей стран бывшего СНГ от жителей стран Европы, — это предрассудки, связанные с количеством цветов в букете.
Сколько цветов можно дарить
Одни люди считают, что живым можно дарить только нечетное количество цветов. Другие ни за что не подарят близкому человеку два, четыре или шесть цветков, потому что верят: букеты с четным количеством цветов носят только на могилы.
Суеверие, связанное с количеством цветков в букете, появилось на Руси в те времена, когда она еще была языческой. Волхвы, которые несли ответственность за соблюдение религиозных обрядов , считали четные числа завершенными, мертвыми. Именно отсюда взялась известная пословица: «Беда не приходит одна».
Нечетные числа, напротив, символизировали жизнь, развитие и процветание. Бытует мнение о том, что данное поверье пришло к нам из Японии. Японский иероглиф, обозначающий цифру 4, очень похож на иероглиф, символизирующий понятие «смерть».
В искусстве составления подарочного букета существует множество других, не менее важных правил. Например, цветы считаются как четные и нечетные до дюжины. После дюжины количество цветов перестает иметь значение.
Запрет на использование четного количества цветов в подарочных букетах закрепился лишь на территории бывшего СНГ. В других странах мира большой популярностью пользуются букеты, состоящие из двух, четырех, шести и восьми цветков.
Букеты, составленные из нечетного количества цветков , трактуются следующим образом:
Чтобы не попасть в неудобную ситуацию, сделай выбор в пользу большого букета, состоящего из множества мелких цветков. Их точно никто считать не станет. В крайнем случае, если ты незнакома с традициями страны, в которой оказалась, подари живые цветы в горшочке, они всегда будут желанным подарком, символизирующим долголетие и крепость.
По российским, украинським и, например, французским традициям — четное количество цветов могут приносить на похороны, а живому человеку пристало дарить цветы только в нечетном количестве.
Почти на всей теретории Европы, США и некоторых восточных странах все с точностью до наоборот, дарят четное количество цветов, потому что это приносит счастье.
Израильтяне – дарят только четное количество цветов, а вот на похороны и вовсе цветы не приносят. В Грузии считают, что все связанное с семейными ценностями приносит счастье, поэтому парное количестко цветов – удачное сочетание, а на кладбище несут нечетное количество цветов «чтобы покойный пару не забрал с собой».
Корни всех этих традиций и предрассудков нужно искать в дохристианском мире.
Каждая страна (регион) прошли свой путь развития и поэтому часто возникают подобные несовпадения и противоречия.
Языческие верования трактуют четные числа – как символы смерти и зла. Помните поговорку «беда не приходит одна»?
Многими древними культурами, парные числа связывались с законченностью, завершением, в данном случае – жизненного пути.
Нечетное число, напротив, символ счастья, успеха, везения.
Нечетные числа нестабильны, они символизируют движение, жизнь, развитие.
Четные – символ умиротворенности и покоя.
Для древних пифагорейцев олицетворением добра, жизни, света были нечетные числа, а еще они символизировали правую сторону (сторону удачи). Неудачливую же левую сторону, и вместе с ней смерть, зло, тьму – символизировали четные числа. Не отсюда ли пошло знаменитое «встать с левой ноги», символизирующее неудачное начало дня?
В древней Руси только погибшем на войне, защищавшим родину возлагали два цветка: «одна покойнику, другая – богу».
Сейчас же всем умершим принято возлагать чётное количество цветов.
Подарочный букет в современной России подчиняется несложному правилу: «нечетно до дюжины», то есть количество цветов имеет значение, если их три, пять, семь, девять или одиннадцать. Четное число в десять или меньше стеблей принято приносить в знак скорби на траурные церемонии. Если же в букете двенадцать и больше цветов, их число не несет никакой смысловой нагрузки.
На языке знаков у каждого числа есть своё значение, и с этим можно воспользоваться, что бы придать букету правильный смысл. Так, если вы дарите один цветок, то это значит, что человек, которому вы его дарите единственный для вас. Подарив три цветка, можно выразить своё желание уехать с любимым человеком на край света. Ну а пять, значит: « Я тебя люблю».
Так, если вы дарите один цветок, то это значит, что человек, которому вы его дарите единственный для вас. Подарив три цветка, можно выразить своё желание уехать с любимым человеком на край света. Ну а пять, значит: « Я тебя люблю».
Мало кто знает, что семь цветков раньше дарили только в день обручения.
Стереотип при покупке, оформлении доставки букетов – обязательно нечетное число цветов. Флористы и эзотерики уверяют, что именно оно несет в себе особый положительный заряд от дарителя к одариваемому. Однако и четное число бутонов не должно пугать вас. О числовом таинстве в языке цветов и о прочтении различного количества цветов в букете расскажет NameWoman.
Четное число цветов не принято брать при составлении букета только в
том случае, если в композиции задействовано менее 10 цветков . Т.е.
траурное значение будут иметь числа 2, 4, 6, 8. А вот четное количество цветов,
начиная от десяти, имеет вполне благоприятную трактовку. Впрочем, на западе,
например, классические свадебные букеты
состоят из десятка, дюжины или половины дюжины цветов – 10, 12, 6.
Язык цветов в числах
1 – романтичное и, казалось бы, скромное число, которое на языке цветов означает не много ни мало, как «все, что есть у меня – это ты» или «ты – самое важное для меня».
3 – число цветов, означающее романтичный порыв «готов уехать с тобой хоть на край света».
5 – небольшой букет для первого признания в серьезных чувствах, цвету подтвердят слова «я люблю тебя».
7 – букет на счастье, волшебное число-талисман на день обручения или предложения руки и сердца.
9 – букет для друга или подруги, коллеги, цветы говорят о чувстве глубокого уважения.
10 – букет-поддержка, цветы выражают желание дарителя помочь одариваемому, сделать для него что-нибудь приятное, оказаться рядом в непростое время. Если вы заказываете доставку цветов близкому человеку, находящемуся далеко от вас, в другом городе или даже в другой стране, то счастливая дюжина бутонов – лучший вариант.
11 – букет-признание,
но не в любви, а в настоящей крепкой дружбе. Именно столько цветов можно
подарить своей лучшей подруге или дорогой сестре.
Именно столько цветов можно
подарить своей лучшей подруге или дорогой сестре.
12 – букет, признающий то, что любовный союз пары оказался довольно тяжелым, но даритель хочет показать, что верит в лучшее будущее и в то, что чувства и стремления помогут все исправить.
13 – чертова дюжина является нечетным числом в букете, несущим негативный посыл, говорит о ненависти и презрении. Доставку такого невеселого букета могут заказать при разрыве отношений.
14 – число, повторяющее значение 1 цветка.
15 – букет говорит о дружбе, которая началась с непростых отношений, о принятии человека после ссоры, о прощении, о вновь заслуженном уважении.
От 20 цветов дарят букеты с числом бутонов, соответствующих числу прожитых лет. Особенно эффектен такой подарок на юбилей. При этом, если вы боитесь смутить одариваемого четным числом, добавляют еще один цветок – как знак уже начатого нового года . Именно такое решение предлагают флористы магазинов, занимающихся составлением букетов и
Четные числа от 1 до 30.
 Четные и нечетные числа. Понятие о десятичной записи числа. Смотреть что такое «Чётные и нечётные числа» в других словарях
Четные и нечетные числа. Понятие о десятичной записи числа. Смотреть что такое «Чётные и нечётные числа» в других словаряхЧто означают чётные и нечётные числа в духовной нумерологии. В изучении это очень важная тема! Чем по своей СУТИ чётные числа отличаются от нечётных чисел?
Чётные числа
Общеизвестно, что чётные числа — те, которые делятся на два. То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.
А что означают чётные числа относительно ? Какова нумерологическая суть деления на два? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.
У несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».
А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии. Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.
Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.
Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?
Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.
Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе… надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.
Нечётные числа
Нечётные числа
— те, которые не делятся на два: числа 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 и так далее. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.
С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.
Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого — чётное… Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?
Видимые совпадения материальной логики и духовной происходят очень часто. Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел , никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.
Возьмём для примера — число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.
Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!
Парадоксальность — вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел
надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них…
В толковании нечётных чисел
надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них…
Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.
Чётные и нечётные числа в нумерологии
Подведём итоги. В чём главное отличие чётных чисел от нечётных?
Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…
Нечётные числа — взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь…
Обратите внимание!
В магазины уже поступила моя книга под названием «Духовная нумерология. Язык чисел». На сегодняшний день это самое полное и востребованное из всех существующих эзотерических пособий о смысле чисел. Подробнее об этом,
а также для заказа книги пройдите по следующей ссылке:
««
Язык чисел». На сегодняшний день это самое полное и востребованное из всех существующих эзотерических пособий о смысле чисел. Подробнее об этом,
а также для заказа книги пройдите по следующей ссылке:
««
———————————————————————————————
Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.
Например: -24, 0, 6, 38 — все это четные числа.
m = 2k — общая формула написания четных чисел, где k — целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.
Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.
Пример нечетных чисел: 3, 1, 7 и 35.
n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k — целое число.
Сложение и вычитание четных и нечетных чисел
В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.
Операция | Результат | Пример |
Четное + Четное | ||
Четное + Нечетное | Нечетное | |
Нечетное + Нечетное |
Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.
Умножение четных и нечетных чисел
При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.
Операция | Результат | Пример |
Четное * Четное | ||
Четное * Нечетное | ||
Нечетное * Нечетное | Нечетное |
А теперь рассмотрим дробные числа.
Десятичная запись числа
Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.
Например: 3,14; 5,1; 6,789 — это все
С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.
Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.
Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.
А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом — дробную.
Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.
Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.
212. Какое число получится: чётное или нечётное, если нечётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи три примера, подтверждающих твоё предположение.
При делении нечётного числа на нечётное число результат всегда будет нечётным числом.
45 : 5 = 9 55 : 11 = 5 63 : 7 = 9
213.
Какое число получится: чётное или нечётное, если чётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи несколько примеров, подтверждающих твоё предположение. Обсуди результат с соседом по парте.
Обсуди результат с соседом по парте.
При делении чётного числа на нечётное число результат всегда будет чётным числом.
54 : 9 = 6 50 : 5 = 10 96 : 3 = 32
214.
Можешь ли ты привести пример такого случая деления, когда нечётное число делится нацело на чётное число? Почему? Вспомни, как можно получить делимое из делителя и значения частного.
Делимое можно получить, умножив делитель на значение частного. По условию делитель является чётным числом. Мы знаем, что если чётное число умножить на чётное или нечётное число, то результатом будет всегда чётное число. В нашем же случае делимое должно быть нечётным числом. Это означает, что никакое значение частного в этом случае подобрать нельзя и привести пример такого случая деления невозможно.
215.
Представь число 2873 в виде суммы круглых десятков и однозначного числа. Чётным или нечётным числом является каждое из слагаемых? Чётным или нечётным числом будет значение их суммы? На какую цифру может оканчиваться запись чётного числа? А нечётного?
2873 = 2870 + 3
Первое слагаемое – чётное число, второе слагаемое – нечётное число.
2873 – нечётное число.
Нечётное число 2873 заканчивается на нечётную цифру 3, запись чётного числа 2870 — на чётную цифру 0.
Запись чётного числа может оканчиваться чётными цифрами (0, 2, 4, 6, 8), а запись нечётного числа — нечётными числами (1, 3, 5, 7, 9).
216. Выпиши чётные числа в один столбик, а нечётные — в другой.
2844 57893
67586 9231
10050 9929
217.
Сколько существует чётных двузначных натуральных чисел? А сколько таких же нечётных чисел?
Самое маленькое двузначное чётное число 10, а самое большое – нечётное число 99. Всего их 99 – 10 + 1 = 90. Чётные и нечётные числа в натуральном ряду чередуются, поэтому чётных двузначных чисел столько же сколько и нечётных, то есть 45, поскольку 90 : 2 = 45.
218.
Запиши самое большле чётное шестизначное число.
Определения
- Чётное число — целое число, которое делится без остатка на 2: …, −4, −2, 0, 2, 4, 6, 8, …
- Нечётное число — целое число, которое не делится без остатка на 2: …, −3, −1, 1, 3, 5, 7, 9, …
В соответствии с этим определением нуль является чётным числом.
Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .
В разных странах существуют связанные с количеством даримых цветов традиции.
В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли.
Например, вполне допустимо подарить юной даме букет из 12 или 14 цветов или срезов кустового цветка, если они имеют множество бутонов , у которых они, в принципе, не подсчитываются.
Тем более это относится к б́ольшему количеству цветов (срезов), даримых в других случаях.
Примечания
Wikimedia Foundation . 2010 .
Смотреть что такое «Чётные и нечётные числа» в других словарях:
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19). … … Википедия
… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19). … … Википедия
… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Слегка избыточное число, или квазисовершенное число избыточное число, сумма собственных делителей которого на единицу больше самого числа. До настоящего времени не было найдено ни одного слегка избыточного числа. Но со времён Пифагора,… … Википедия
Целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… …
Целые (0, 1, 2,…) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы. … … Большая советская энциклопедия
… … Большая советская энциклопедия
Книги
- Математические лабиринты и ребусы, 20 карточек , Барчан Татьяна Александровна, Самоделко Анна. В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20…
Открытый урок на тему «Четные и нечетные числа» | План-конспект урока по математике (2 класс) на тему:
Тема: Чётные и нечётные числа.
Цель: знакомство с чётными и нечётными числами .
Задачи:
- познакомить с чётными и нечётными числами;
- закрепить знания таблицы умножения;
- закрепить знания таблицы умножения и деления с числом 2;
- расширять кругозор учащихся;
- прививать интерес к предмету.
- решать простые задачи на деление, основываясь на знании взаимосвязи умножения и деления.
- развивать интеллектуальные и коммуникативные общеучебные умения.
- развивать организационные общеучебные умения, в том числе самостоятельно оценивать результаты своих действий, самого себя, находить и исправлять собственные ошибки.

Оборудование: учебник «Математика» ( авторы Т. Е. Демидова, С. А. Козлова) , детская энциклопедия «Я познаю мир», рисунки, изречения Пифагора.
Ход урока
I. Организация урока (Мотивация, ведущая к выдвижению гипотез решения проблем):
-Добрый день, дорогие ребята. Поприветствуем друг друга хорошим настроением, добрыми улыбками. А сейчас урок математики.
Вступительный рассказ учителя.
Изучать науку математику люди начали очень давно. Греки обогнали в математике все другие народы.
— Как вы думаете? Почему? Вы спросите почему?
— Да потому, что они хорошо умели спорить.
В древние времена Греция состояла из многих маленьких государств. Каждый раз, когда приходилось решать какой-нибудь важный государственный вопрос, горожане собирались на площадь, обсуждали, спорили, голосовали
Древние греки считали, что спор помогает найти самое лучшее, самое правильное решение. Они даже придумали следующее изречение:
В споре рождается истина»
И в науке греки стали поступать так же, как на народном собрании. Они не просто заучивали правила, а спорили друг с другом, старались найти в рассуждениях ошибки.
Они не просто заучивали правила, а спорили друг с другом, старались найти в рассуждениях ошибки.
Едва родившись, греческая математика сразу семимильными шагами пошла вперёд. Ей помогали чудесные сапоги- скороходы, которых раньше у других народов не было. Они назывались «Рассуждение», «Доказательство».
- ( Краткий рассказ о Пифагоре. «Первый греческий учёный, который начал рассуждать о числах явился Пифагор. Затем он пришёл к выводу, что всё на свете можно выразить с помощью чисел.
- «ЧИСЛА ПРАВЯТ МИРОМ» — провозгласил он»
II .Математическая разминка. Рассуждаем и доказываем.
Представьте, что мы юные Пифагоры . Я предлагаю всем надеть на головы вот такие головные уборы. Вот и мы сейчас с вами займёмся рассуждениями и доказательствами.
1) Проверяем таблицу умножения на 2 (работа в парах)
(каждая пара задаёт друг другу выражение на знание таблицы умножения
на 2 и вычисляет значение)
2) Составь выражение и посчитай:
— сколько лапок у 3 гусят? 2*3 = 6
— сколько лапок у 2 котят? 4*2 = 8
— сколько крыльев у 4 утят? 2*4 = 8
3) Определите истинные высказывания и докажите, что они истинные
Квадрат – это четырёхугольник?. .. И
.. И
(это геометрическая фигура, которая имеет четыре угла)
10см=10л Л 1кг=1л Л
(нельзя сравнивать разные величины)
Сложение – это математическое действие?… И (Составьте выражения на сложение)
Периметр квадрата со стороной 3 см равен 12 см И
10- однозначное число Л
(нет, потому что стоит из двух знаков 1 и 0)
Одинаковые слагаемые можно заменить действием умножения И
Пример: 4+4=8 по4 взяли 2 раза 2+2+2+2+2=10 по2 взяли 5раз
4·2=8 2·5=10
От перестановки множителей произведение не изменяется И
2·7=7·2 2·6=6·2
Умножение с нулём и единицей
1·а=а а·1=а 0·а=0 а·0=0
III. Формулирование темы и целей урока
Какие из этих предметов используются только по два?
ТАПОК ПЕРЧАТКА
НОСОК ВАРЕЖКА
ШАПКА ШАРФ
Работа с учебником
- Задание 1 (стр.
 66)
66)
Как разложить варежки по 2 (парами)?
(Проанализировать вместе с детьми задание и рисунок. Сделать вывод, как должны производить деление: варежки разложить парами в соответствии с их цветами, при этом варежка останется без пары.)
Практическая работа
(Варежки разложить в классе не можем, заменим их кругами.)
Возьми 7 кружков и разложи их по 2.
Сколько пар получилось?(получилось 3 пары)
Сколько кружков осталось без пары? (один кружок остался без пары)
(Дети раскладывают на партах 7 кружков по 2. Делают вывод: 7 по 2 не делится, один кружок остается.)
- Задание 2 (стр. 66)
Попробуйте разложить:
а) по два 4 красных кружка, 6 синих кружков, 10 зеленых кружков;
б) 3 красных кружка, 5 синих кружков, 9 зеленых кружков.
Практическая работа
а) дети раскладывают красные, синие, зеленые кружки по 2;
(Дети самостоятельно на партах раскладывают кружки, а два человека работают у доски. После того, как задание выполнено, они объясняют, как делили кружки «по 2».
После того, как задание выполнено, они объясняют, как делили кружки «по 2».
Учитель записывает на доске числа в две строчки:4 6 10
3 5 9
Остальные ребята оценивают выполненное задание, выставляют оценку.
Дети делают вывод сами:
Какие кружки удалось разложить парами?
а) 6, 4, 10- удалось разложить парами ( делятся на 2)
Какие кружки не удалось разложить парами?
б) 3, 9, 5 – нельзя разложить парами ( не делятся на 2)
IV. «Открытие» нового знания
Сравнивают свой вывод с учебником на стр. 66
(дети читают из оранжевой рамочки учебника 1 строчка))
-Как называются числа, которые делятся на 2?
(Числа, которые делятся на 2 называются — чётными)
(Учитель записывает на доске числа:
4, 6, 10- чётные числа
-Как называются числа, которые не делятся на 2)
(Числа, которые не делятся на 2 называются -нечётными)
(Учитель записывает на доске числа:
3, 5, 7, 10-нечётные числа
В тетрадях появляется запись:
4, 6, 10- чётные числа
3, 5, 7, 9- нечётные числа
Что нового мы узнали? (мы узнали, что числа бывают чётные и нечётные)
Чему мы будем учиться? (мы будем учиться определять чётные и нечётные числа)
V. Применяем новые знания
Применяем новые знания
- Задание 3 (стр. 66).
(Дети читают про себя числа:)
1,2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18.
-Назовите сначала чётные числа.
(дети читают по очереди и записывают в тетрадь)
2,4,6,8,10,12,14,16,18.
-Теперь назовите нечётные числа.
(дети читают по очереди и записывают в тетрадь)
1,3,5,7,9,11,13,15,17.
-Какой вывод можем сделать?
(дети из оранжевой рамочки учебника читают вывод)
Вывод: Четные и нечетные числа в числовом ряду чередуются.
ФИЗМИНУТКА
Если я называю чётное число, вы приседаете.
Если называю нечётное число – 1 хлопок
2, 3, 1, 12, 14, 5, 11, 16, 9, 8, 7, 20, 6, 4, 10, 13, 15, 18, 17, 19
VI. Первичное закрепление
(использование нового знания при решении задач)
Задание 5 (а) стр. 67.
(Прочитайте и объясните задание. Как будем его выполнять?)
(Ответы детей, составление плана действий, выполнение задания в тетрадях, на доске)
— Что мы будем делать? (мы будем решать задачу)
(прочитайте задачу про себя)
Восемь ребят разделились в группы по 2 человека. Сколько групп получилось.
Сколько групп получилось.
— Что нам надо сделать? (Сделать рисунок и решить задачу.)
— Что нам известно из условия задачи?
Нам известно, что 8 ребят разделились в группы по 2 человека
Практическая работа (в тетрадях и на доске появляется рисунок)
О О О О О О О О
-Что надо найти в задаче?
Нам надо найти сколько групп получилось.
-Как это показать на рисунке?
Нам надо кружочки разделить по 2(на доске и в тетрадях дети делят
по 2 при помощи вертикальных линий )
О О/ О О/ О О/ О О
-Как записать решение при помощи выражения?
8:2=4(г.)
Ответ: 4 группы получилось.
Оценить работу учащихся. Какую оценку заслужил?
— Ещё во времена Пифагора продавцу на базаре приходилось раскладывать товар попарно и иногда яблок в мешке или баранок оказывалось больше и оставались лишние. И Пифагор стал думать о свойствах чётных и нечётных чисел.
VII. Выполнение задания 4.
Выполни действия:
а) умножь на 2 все четные числа в числовом ряду от 1 до 10. Расскажи, какие получились числа – четные или нечетные?
Расскажи, какие получились числа – четные или нечетные?
б) умножь на 2 все нечетные числа в этом же ряду. Расскажи, какие получились числа – четные или нечетные?
Дети записывают в тетрадь
а) 2 4 6 8 10
4 8 12 16 20
б) 1 3 5 7 9
2 6 10 14 18
Делают вывод: записанные числа четные и нечетные.
Какое число, четное или нечетное получается при умножении любого числа на 2?
Вывод: При умножении любого числа на 2 получается четное число.
.
VIII .Закрепление нового материал
Игра «Найди лишнее»
1) 2 4 7 6 8 10 (все числа чётные, а число 7 нечётное)
-Какие числа называются чётными?
(Числа, которые делятся на 2 называются – чётными
2) 1 3 5 7 9 4 (все числа нечётные, а число 4 чётное )
— Какие числа называются нечётными?
(Числа, которые не делятся на 2 называются – нечётными)
— Где мы можем встретиться с расположениями чётных и нечётных чисел.
(Нумерация домов на улицах нашего посёлка).
— Как располагаются чётные и нечётные числа в числовом ряду?
(Чётные и нечётные числа в числовом ряду чередуются
ХI . Итог урока:
— Чему учились сегодня на уроке?
(Мы учились определять чётные и нечётные числа)
-Какое задание захотелось выполнить еще раз?
-Где мы можем применить полученные знания
Х. Предполагаемая домашняя работа
1) Задание 6, 8, стр. 67.
2) Задание 9 (по желанию), стр. 67.
3) Запомнить вывод в оранжевой рамочке на стр. 66
ХI. Чтобы убедиться, что материал вами усвоен, предлагаю «блиц-опрос»
Он сложил 2 чётных числа и получил снова чётное число. То же самое вышло, когда он сложил 2 нечётных числа. А от сложения чётного числа с нечётным получилось нечётное. Такое много раз случалось и у египтян, и у вавилонян, греков живших до Пифагора.
- какое число получится, если
а) сложить два четных числа;
три четных числа;
два нечетных числа;
три нечетных числа.
б) из четного вычесть четное;
из нечетного вычесть четное;
из нечетного вычесть нечетное.
(Обоснуйте свои ответы)
(после каждого ответа на доске выставляются карточки с буквами
Ч – четное, Н – нечетное)
ч ч ч н ч н ч
А теперь получите оценку за урок.
(карточки переворачиваются, там слово МОЛОДЦЫ)
Рефлексия. Группы оценивают работу каждого участника. Учитель оценивает работу групп в целом.
— Оцените своё участие в уроке, используя условные обозначения:
Мне было очень интересно.
Мне было скучно.
Я затруднялся, работая в группе
Спасибо, ребята, вам за урок. Вы сегодня очень хорошо работали. Мне с вами было интересно.
- Фронтальная работа
а) соревнования по группам
«Кто первый решит?»
18 : 9 = 2 4 – 2 = 8 5 – 2 = 10
8 : 2 = 4 12 : 2 = 6 10 : 5 = 2
2 – 3 = 6 2 – 2 = 4 6 – 2 = 12
16 : 2 = 8 14 : 7 = 2 16 : 8 = 2
6 : 2 = 3 18 : 2 = 9 2 – 8 = 16
10 : 2 = 5 14 : 2 = 7 9 – 2 = 18
Что можно сказать об ответах, которые получились в 1, 2, 3 столбиках? Что это за числа?
Физминутка
Мы устали, засиделись
Мы устали, засиделись,
Нам размяться захотелось.
Отложили мы тетрадки,
Приступили мы к зарядке
(Одна рука вверх, другая вниз, рывками менять руки.)
То на стену посмотрели,
То в окошко поглядели.
Вправо, влево поворот.
(Повороты корпусом.)
А потом наоборот.
Приседанья начинаем,
Ноги до конца сгибаем.
Вверх и вниз, вверх и вниз,
Приседать не торопись!
(Приседанья.)
И в последний раз присели,
А теперь за парты сели.
(Дети садятся за парты.)
- Фронтальная работа, на перестановку четырех элементов.
№ 9 (стр. 67)
Сколько различных четных и двузначных чисел можно написать с помощью цифр 1, 3, 2, 0, если:
а) цифры в числе могут повторяться;
б) цифры в числе не повторяются.
Последовательность работы:
а) на доске записаны цифры 1, 3, 2, 0
Детям предлагается назвать все возможные способы получения двухзначных чисел, когда цифры в числе повторяются, отобрать из них только четные. Получается, что возможен только один вариант – 22.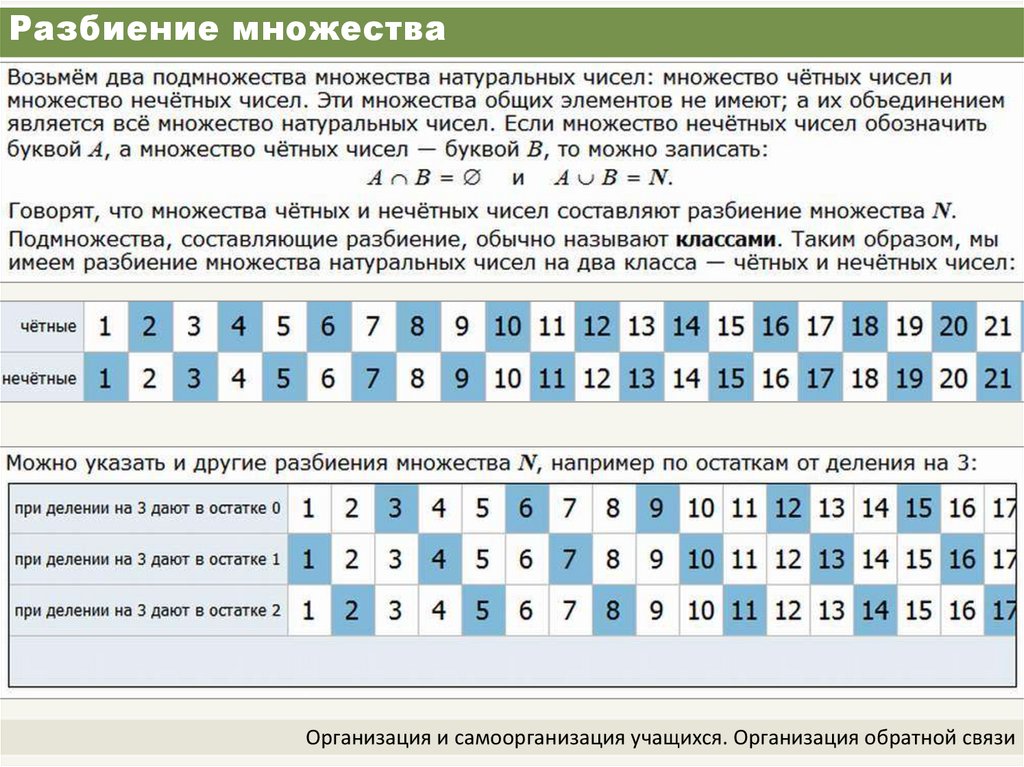
б) устанавливается закономерность, по которой записываются двузначные числа, когда цифры в числе не повторяются (фиксируется первая цифра, а вторые меняются), при этом двузначные числа должны быть четными. Из всех возможных вариантов выбираются следующие числа: 10, 12, 20, 30, 32.
- Познакомиться с понятиями четности-нечетности
(учить видеть, что:
- сумма двух четных чисел – четное число;
- сумма двух нечетных чисел – четное число;
- сумма четного и нечетного чисел – нечетное число).
Тип урока :изучение нового материала с элементами исследовательской деятельности .
Формы обучения: работа под руководством учителя , групповая , самостоятельная работа, фронтальная.
The Amazing 5 Even Numbers
Представляем Четные и нечетные числа Различать четные и нечетные числа — важный навык, который необходим детям.
помочь им понять нашу систему счисления и помочь в их подготовке к группированию
операции с целыми числами. Это также поможет подготовить их к обучению делению,
простые числа и даже квадратные корни.
Это также поможет подготовить их к обучению делению,
простые числа и даже квадратные корни.
Некоторые дети очень плохо понимают четные и нечетные числа. Этот концепция важна, потому что она помогает учащемуся увидеть закономерность в числа. Это предшественник для подсчета пропусков, деления и простых чисел. Так, важно убедиться, что дети понимают это на раннем этапе.
Четные числа — это целые числа, которые делятся на 2 без остатка. Этот означает, что число можно разделить на пары или две равные группы без остатки. Примеры четных чисел: 2, 6, 10, 20, 50 и т. д.
Что такое четное число в математике?
Число, которое можно разделить на две половины, т.е. на две равные части. Это называется четное число. Другими словами, четные числа точно делится на 2. Это означает, что остаток будет 0.
Что такое четные числа вообще?
Целые числа, в которых вместо единицы стоят цифры 0, 2, 4, 6 или 8, считаются
четные числа. Четные числа всегда заканчиваются последней цифрой 0, 2, 4, 6 или
8. Некоторые примеры четных чисел: 2, 4, 6, 8, 10, 12, 14 и 16.
Некоторые примеры четных чисел: 2, 4, 6, 8, 10, 12, 14 и 16.
Это четные числа, так как их легко разделить на 2. Это следует отметить, что наименьшее положительное четное натуральное число равно 2. Если вы выберите число, которое не может быть разделено на 2,
, оно будет известно как нечетное число Например: 1, 3, 5, 7, 9и т. д.
Как узнать, четное число или нечетное?
Чтобы узнать, является ли заданное число четным или нечетным, необходимо проверить число на месте единицы (или единицы). Это конкретное число на своем месте скажет вам, является ли число нечетным или четным.
- Четный числа заканчиваются на 0, 2, 4, 6, 8
- Нечетный Номера заканчиваются на 1, 3, 5, 7, 9
Если цифра единицы (или цифра единицы) равна 1, 3, 5, 7 или 9, то число
назвал нечетное число . Если устройство
цифра 0, 2, 4, 6 или 8, то число называется четным номер . Это простые приемы для определения чисел
четные они или нечетные.
Подумайте о следующих числах 3, 845 и 917, которые оканчиваются на нечетную число, то есть 3, 5 и 7. Следовательно, данные числа 3, 845 и 917 нечетны. числа. Таким образом, эти числа не являются четными числами. Точно так же 8 и 322 являются четными числами, поскольку они заканчиваются на 8 и 2.
НольНоль — четное число, потому что нечего спаривать и ничего не осталось над. Значит, четно. Для математиков ноль — четное число. потому что любое число, которое можно разделить на два, чтобы получить другое целое число, даже. Ноль проходит этот тест, потому что если вы разделите ноль пополам, вы получите ноль. Нам следует запомните 0, 2, 4, 6, 7 и 8 как четные, а 1, 3, 5, 7 и 9 как нечетные.
Список четных чисел до 100
Список четных чисел до 100 приведен ниже:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100
Свойства четных чисел
Свойство дополнения
Ниже приведены три важных свойства четных чисел: Добавление четного и другого четного числа всегда приведет к четному номер
Пример: четный + четный = четный, 14 + 6 = 20
Свойство вычитания
Вычитание четного числа из другого четного числа всегда приводит к четное число.
Пример: четный – четный = четный, 16 – 6 = 10
Свойство умножения
Умножение четного числа на другое четное число всегда приводит к четное число.
Пример: четное × четное = четное, 6 × 4 = 24
Краткое изложение фактов
Сумма из двух или более четных чисел всегда четно
Четный числа при делении на 2 не оставляют остатка
Четный числа кратны двум
Есть не являются остатком. Да, это правда!
Четный числа при умножении на любое число всегда дают четное число
произведение двух или более четных чисел всегда четно
Свойство дополнения
- Когда
сложение четного и нечетного числа (или наоборот), в результате
число всегда будет нечетным.

Примеры:
9 + 4 = 13
3 + 20 = 23
Добавление четное число и другое четное число, приведет к числу, которое всегда даже.
Примеры:
14+6 =20
Добавление нечетное число и другое нечетное число всегда будут приводить к числу это даже.
Примеры:
11 + 13=24
Свойство вычитания
- Если вы вычесть четное число из четного числа, ответ будет четным числом
- Если вы из нечетного числа вычесть нечетное, получится четное число
- Если вы из нечетного числа вычесть четное, получится нечетное число
- Если вы из четного числа вычесть нечетное, получится нечетное число
- Вычитание четное число из нечетного числа (или наоборот) приведет к числу это всегда странно.
Примеры:
7 – 4= 3
8 – 5= 3
Вычитание четное число из другого четного числа приведет к числу, которое всегда даже.
Пример:
12 – 8= 4
Вычитание
нечетное число из другого нечетного числа, приведет к числу, которое
всегда даже.
Примеры:
23 –11 = 12
Свойство умножения
Умножение четное число и другое четное число всегда приводят к четному количество.
Примеры:
8 × 2= 16
10 × 6= 60
Умножение четное число и нечетное число всегда будут давать четное число.
Примеры:
4 × 5= 20
8 × 5= 40
Умножение нечетное число и другое нечетное число всегда дадут вам нечетное число.
Примеры:
3 × 5= 15
3 × 5= 15
Четные числа от 40 до 60
Давайте посмотрим на список четных чисел между 40 и 60. 42, 44, 46, 48, 50, 52, 54, 56, 58 Таким образом, всего 9четные числа от 40 до 60. Пройдите примеры и решения четного числа, приведенные ниже, для лучшее понимание.
Пример 1:Некоторые четные числа Решенные задачи
Все ли числа четные?
Решение:
Нет, список целых чисел, которые точно делятся на два, называется четные числа.
Пример 2: Запишите любые четыре последовательных четных числа между числами от 13 до 21.
Решение:
Пусть А = {13, 14, 15, 16, 17, 18, 19, 20, 21}
Следовательно, 14, 16, 18, 20 — это 4 последовательных четных числа.
Пример 3:
Выберите правильный ответ. Сумма двух четных чисел
А) Всегда четное число
B) Всегда нечетное число
C) иногда бывает нечетным, а иногда четным
г) Может быть ни нечетным, ни четным Решение:
Правильный ответ — вариант а). Четное число + Четное число = Четное число
Пример 4: −24, 0, 6 и 38 — все четные числа?
Да, все числа -24, 0, 6 и 38 четные.
Пример 5: Является ли 2 четным числом?Да, 2 — четное число, поскольку 2 точно делится на 2.
Пример 6: Какие четные числа находятся между 1 и 50?Список четных чисел от 1 до 50: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48
Пример 7: Какое четное простое число?2 — единственное четное простое число.
Пример 8. Если сложить два четных числа, получится:
- Всегда даже
- Всегда нечетный
- Иногда четные и иногда нечетные
- 0
- четный + четный = четный
Например, 2 + 6 = 8.
 Значит, ответ всегда четный.
Значит, ответ всегда четный.
Пример 9. Какое из следующих чисел четное?
- 9 × 14
- 15 × 17
- 17 × 9
- 11 × 19
9 × 14 = 126 четно, потому что нечетное × четное = четное 15 × 17 = 255 нечетно, потому что нечетное × нечетное = нечетное 17 × 9 = 153 нечетно, потому что нечетное × нечетное = нечетное 11 × 19=209 нечетно, потому что нечетное × нечетное = нечетное
значит ответ А.
Пример 10. Какое из следующих чисел является четным?
а.5+16 б.22+12 с.13+44 д.11+4Ответ б. Почему?
Как записать общую форму четного числа?
Общая форма четного числа — 2k, где k — целое число.
Рабочие листы по четным числам
- Что четные числа от 1 до 100?
- Как узнать, является ли число четным?
- Можешь ли ты угадай первое четное число?
- Имя наименьшее четное число?
Все дело в четных числах. Надеемся, вам понравилось. Чтобы еще больше попрактиковаться в четных числах и узнать о
другие интересные концепции математики, продолжайте посещать LearningMole.
Надеемся, вам понравилось. Чтобы еще больше попрактиковаться в четных числах и узнать о
другие интересные концепции математики, продолжайте посещать LearningMole.
Share :
Сумма четных чисел — Формула и примеры решения
Сумму четных чисел от 2 до бесконечности можно легко получить, используя AP (арифметическую прогрессию). Однако мы также можем использовать формулу суммы всех натуральных чисел, чтобы найти сумму четных чисел. Мы уже знаем, что четные числа — это числа, которые полностью делятся на 2. К таким числам относятся 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24… И так вперед. Теперь все, что нам нужно, это определить сумму этих чисел. Кроме того, оцените сумму нечетных чисел здесь.
Воспоминания учеников о том, что они впервые изучали четные числа по предмету математики, восходят к самым ранним школьным дням. Следовательно, значение или определение четного числа для студентов сейчас не нужно. Потому что все студенты знают, что числа, которые делятся на 2, являются четными числами, такими как 2, 8, 22, 252, 398 и т. д., потому что все эти числа можно разделить на 2.
д., потому что все эти числа можно разделить на 2.
В этих числах есть одна интересная вещь. это означает, что четные числа, и это то, что ученикам действительно легко найти сумму прогрессивных четных чисел, таких как 10 + 12 + 14 + 16 и так далее до бесконечности. Но для этого вам необходимо знать формулу арифметической прогрессии, и поэтому Веданту предлагает учащимся формулу нахождения суммы четных чисел вместе с ее решенным примером.
Формула суммы четных чисел
Стандартной формулой для определения суммы четных чисел является n (n+1), где n представляет собой натуральное число. Мы можем определить эту формулу, используя формулу суммы натуральных чисел, например
S = 1 + 2+3+4+5+6+7, 8, 9…+n
S= n (n+1) ÷ 2
Чтобы вычислить сумму последовательных четных чисел, нам нужно умножить приведенную выше формулу на 2. Таким образом,
Se = n (n+1)
Выведем эту формулу, используя AP.
Формула суммы четных чисел с использованием арифметической прогрессии
Пусть сумма первых n четных чисел равна Sn
Sn = 2+4+6+8+10+12+14+16………………….. +(2н)……. (1)
По AP мы знаем, что для любой последовательности сумма чисел равна назначенной;
Sn=1÷2 × n (2a+ (n-1) d)….. (2)
Где,
n = количество цифр в ряду
a = 1-й член АП
d = Разница в AP
Таким образом, если мы поместим значения в уравнении 2 в отношении уравнения 1, например;
a=2, d = 2
Предположим, что последний член, l = (2n)
Таким образом, сумма будет:
Sn = ½ n (2,2+ (n-1)2)
Sn = n÷2 (4+2n-2)
Sn = n÷2 (2+2n)
Sn = n (n+1)
Сумма n четных чисел = n (n+1)
Сумма первых десяти четных чисел
Ниже приведена таблица сумм от 1 до 10 последовательных четных чисел:
Number of Consecutive Even Numbers (n) | Sum of Even Numbers (Sn = n (n+1)) | Verify | |||||
1 | 1(1+1)= 1 × 2 = 2 | 2 | |||||
2 | 2 (2 + 1) = 2 × 3 = 6 | 4 2 + 4 = 69000 | 4 2 + 4 = 69000 | 49927 2 + 4 = 69000 | 4 2 + 4 = 2 | .3(3+1)=3×4 = 12 | 2+4+6 = 12 |
4 | 4(4+1) = 4 x 5 = 20 | 2+4+6+8=20 | |||||
5 | 5(5 +1) = 5 x 6 = 30 | 2+4+6+8+10 = 30 | |||||
6 | 6 (6+1) = 6 x 7 = 42 | 444444444444444444444444444444444444444444444444444444444444444444444444 2+4+6+8+10+12 = 42 | |||||
7 | 7(7+1) = 7×8 = 56 | 2+4+6+8+10+12+14 = 56 | |||||
8 | 8(8+1) = 8 x 9 = 72 | ||||||
9 | 9(9+1) = 9 x 10 = 90 | 2+4+1+2+8 +16+18=90 | |||||
10 | 10(10+1) = 10 x 11 =110 | +1+4+61+1+84 +20= 110 |
Решенные примеры
Пример:
Определить сумму четных чисел от 1 до 100.
Решение:
Нам известно, что существует 50 четных чисел от 1 до 100.
Таким образом, n = 50
Используя формулу суммы четных чисел, т.е. Пример:
Определить сумму четных чисел от 1 до 200?
Решение:
Мы знаем, что от 1 до 200 всего 100 четных чисел.
Следовательно, n =100
Используя известную нам формулу суммы четных чисел;
Sn = n (n+1)
Sn = 100 (100+1)
= 100 x 101
= 10100
квадрат
Решение:
Сумма квадратов из 3 нечетных чисел = N (2n+1) (2n-1) ÷ 5
= 5 (2 x 5+1) (2 x 5-1) ÷ 5
= 5 (11) (9) ÷ 5
Решение:
Сумма квадратов из трех нечетных чисел = N (2n + 1) (2n-1) ÷ 3
= 3 (2 x 3 + 1) (2 x 3-1) ÷ 3
= 5 (7) (5) / 5
= 35
, чтобы доказать = 1² + 5² + 7²
= 1 + 25 + 49
= 35
Преимущества наличия формулы для суммы ровных чисел
Вам может быть интересно, зачем добавить. еще одна формула в список формул, которые вам уже предстоит выучить. Потому что кажется, что нет необходимости в формуле суммы четных чисел, потому что мы можем просто сложить ее. И да, это правда, что мы можем сложить его легко, но что, когда дано так много четных чисел, то сложение полной суммы либо занимает слишком много времени, с большими шансами ошибок, либо становится просто невозможным для нас. решать.
еще одна формула в список формул, которые вам уже предстоит выучить. Потому что кажется, что нет необходимости в формуле суммы четных чисел, потому что мы можем просто сложить ее. И да, это правда, что мы можем сложить его легко, но что, когда дано так много четных чисел, то сложение полной суммы либо занимает слишком много времени, с большими шансами ошибок, либо становится просто невозможным для нас. решать.
И, следовательно, формула действительно помогает в этой ситуации, потому что формула позволяет легко вычислить сумму любых чисел. Кроме того, с точки зрения экзамена это снова очень полезно, потому что вопросы, в которых учащиеся правильно выполнили все шаги, тогда и только тогда учащийся получает полные оценки за этот конкретный вопрос. А еще, решение вопроса на сумму четных чисел без формулы занимает столько времени, что тоже не хорошо для экзамена.
Преимущества наличия примеров для суммы четных чисел
В предмете математики примеры играют жизненно важную роль для учащихся. Потому что одной формулы или даже объяснения темы недостаточно. Поскольку оба они только говорят студентам, что делать и как делать, то есть говорят о подходе к решению вопроса. Но не обязательно показывает, как это сделать практически.
Потому что одной формулы или даже объяснения темы недостаточно. Поскольку оба они только говорят студентам, что делать и как делать, то есть говорят о подходе к решению вопроса. Но не обязательно показывает, как это сделать практически.
И поэтому в таких ситуациях на помощь учащимся приходят примеры. Потому что пример показывает, что говорит обычное объяснение и формула. То есть он показывает, как решить вопрос, реализуя данную формулу поэтапно. Изучая примеры, учащиеся могут узнать, как решать конкретный вопрос, особенно вопросы различных типов, применяя формулу.
Примеры знакомят учащихся со всеми возможностями вопросов на нахождение суммы четных чисел. И, следовательно, Веданту предоставляет учащимся подробные примеры, решаемые шаг за шагом.
Освоение темы суммы четных чисел
Математика является практическим предметом, поэтому ученикам требуется как можно больше практики. Кроме того, это лучший способ запомнить формулу суммы четных чисел. Решая больше вопросов, вы улучшаете ясность в отношении различных типов вопросов, а также повышаете скорость решения вопросов учащимися.
Решая больше вопросов, вы улучшаете ясность в отношении различных типов вопросов, а также повышаете скорость решения вопросов учащимися.
Но самое главное, это повышает уверенность учеников в решении вопросов. А значит, отработка вопросов на сумму четных чисел — лучший способ освоить тему.
Интересные факты
0 не входит в четное число.
Сумма двух или более четных чисел всегда четна.
Четные числа при делении ровно на 2 не оставляют остатка.
Произведение двух или более четных чисел всегда четно.
Четные числа от 1 до 100, определение, примеры и ответы на вопросы
Четные числа
Четные числа: Целое число можно разделить на четное и нечетное. Если число при делении на 2 не оставляет остатка, то число называется четным. Если целое число при делении на 2 оставляет какой-либо остаток, то это число idd. Чтобы понять четные числа намного проще и лучше, вы должны знать таблицы/кратные 2 и основные методы деления. Например:
Если число при делении на 2 не оставляет остатка, то число называется четным. Если целое число при делении на 2 оставляет какой-либо остаток, то это число idd. Чтобы понять четные числа намного проще и лучше, вы должны знать таблицы/кратные 2 и основные методы деления. Например:
Давайте поговорим о числах 4, 19, 54 и 488.
Вы можете легко узнать, что 4 — четное число, если знаете таблицы 2. Точно так же вы можете легко узнать, что 19 — это четное число. нечетное число, так как оно не делится на 2. 19÷2= 9, оставив 1 в качестве остатка или частного.
Теперь, если у нас есть такие числа, как 54 и 488,
54÷2= 27 Так что в приведенных выше примерах только 19не четное число. Вы можете легко определить четное число, прочитав эту статью. В этом уроке мы расскажем все о четных числах, определениях, примерах, свойствах и важных моментах.
Четное число Определение
Четным числом считается любое число, которое полностью делится на 2, или число, которое можно разделить на две равные группы или пары без остатка, называется четным числом. Ниже приведены некоторые примеры. Проверьте, является ли число четным или нет.
Ниже приведены некоторые примеры. Проверьте, является ли число четным или нет.
8, если мы разделим 8 на 2, т.е. 8 ÷ 2=4, а остаток равен 0. Таким образом, данное число 8 является четным числом.
12, если мы разделим 12 на 2, т. е. 12 ÷ 2 = 6, то снова в остатке будет 0. Таким образом, данное число 12 является четным числом.
15, если мы разделим 15 на 2, то есть 15 ÷ 2, то в остатке получится 1, поэтому данное число 15 не является четным числом. Это нечетное число.
21, Если мы проверим делимость 21 тем же методом, то есть 21 ÷ 2 дает остаток 1. Таким образом, 21 не является четным числом. Это нечетное число.
Как вы заметили, те числа, которые не делятся на 2, оставляют остаток, следовательно, они являются нечетными, а не четными числами.
Четное число также может быть определено как четное целое число в форме n=2k , где k — целое число.
Как легко найти четные числа?
Самый простой способ определить, является ли данное число четным или нет. Сначала мы должны посмотреть на последнюю цифру данного числа:
Сначала мы должны посмотреть на последнюю цифру данного числа:
- Если последняя цифра числа заканчивается на 0, 2, 4, 6 или 8. Это четное число.
- Если последняя цифра числа заканчивается на 1, 3, 5, 7 или 9. Это нечетное число.
Например,
58 — четное число, поскольку последняя цифра числа 58 — 8.
366 — четное число, поскольку последняя цифра числа 366 равна 6. последняя цифра 987654 — 4.
23 — нечетное число, так как последняя цифра 23 — 3, поэтому 23 — нечетное число.
487 тоже нечетное число, так как последняя цифра 7, а значит, это тоже нечетное число.
Even Numbers 1 to 100
| List of Even Numbers 1 to 100 | |||||
| 2 | 22 | 42 | 62 | 82 | |
| 4 | 24 | 44 | 64 | ||
| 46 | 66 | 86 | |||
| 8 | 28 | 48 | 68 | 88 | |
| 10 | 30 | 50 | 70 | 90 | |
| 12 | 4497979797979797979797979797979797979797979. 9000 9000 9000 9000 | 444444444444444444444444444444444444444444444444444444444444444444444444444444444444н.0344 52 | 72 | 92 | |
| 14 | 34 | 54 | 74 | 94 | |
| 16 | 36 | 56 | 76 | 96 | |
| 18 | 4 9000 3894494949474747474747474747474747474747474747474747474747474747474747474747474747474747474747474747474747474749н. 0004 0004 | 78 | 98 | ||
| 20 | 40 | 60 | 80 | 100 | |
Even Numbers 1 to 200
| Список четных чисел с 1 до 200 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 22 | 42 9747 | 42 747 | 44444444444444444444444444444444444444444444444444444444444444444444444444н.0004 | 82 | 102 | 122 | 142 | 162 | 182 | |
| 4 | 24 | 44 | 64 | 84 | 104 | 124 | 144 | 164 | 164 | 444444444444444444444444444444444444444444444444444444444444444444444444444444444444444н.||
| 6 | 26 | 46 | 66 | 86 | 106 | 126 | 146 | 166 | 186 | ||
| 8 | 28 | 48 | 68 | 4 9000 888 974474474474474444444444444444444444444444444444444444444444444444444444444444447н0003 108 | 128 | 148 | 168 | 188 | |||
| 10 | 30 | 50 | 70 | 90 | 110 | 130 | 150 | 170 | |||
| 32 | 52 | 72 | 92 | 112 | 132 | 152 | 172 | 192 | |||
| 14 | 34 | 54 | 74 | 94 | 114 | 134 | 154 | 174 | 194 | ||
| 16 | 36 | 56 | 76 | 96 | 116 | 136 | 156 | 176 | 196 | ||
| 18 | 38747474747447447447447444744744744744744744744744744744744744749444749344934493444474749н. 0004 0004 | 78 | 98 | 118 | 138 | 158 | 178 | 198 | |||
| 20 | 40 | 60 | 80 | 100 | 120 | 1400044449| 160 | 449 | 44 160 | 44940003 160 | 4494440004 | 200 |
Свойства четных чисел
1. Свойства сложения:
а) Сложение двух четных чисел всегда дает четное число.
Например, 8+6=14, 14+82=96, 12+6=18
b) Сложение четного и нечетного числа или наоборот дает нечетное число.
Например, 4+9=13, 11+10=21, 22+3=25
c) Сумма двух нечетных чисел всегда дает четное число.
Например, 7+3=10, 9+9=18, 43+65=108
2. Свойства вычитания:
а) Разница между двумя четными числами дает четное число.
Например, 16-4=12, 88-8=80, 442-322=120
b) Разница между четным и нечетным числом или наоборот дает нечетное число.
Например, 32-9=23, 19-10=9, 40-7=33
c) Разница между двумя нечетными числами дает четное число.
Например, 7-3=4, 11-9=2, 47-5=42
3. Свойства умножения.
а) Умножение двух четных чисел всегда является четным числом.
Например, 8 X 2 = 16, 14 X 4 = 56, 2 X 2 = 4
б) Произведение четного числа на нечетное дает четное число.
Например, 4 х 7 = 28, 3 х 6 = 18, 12 х 5 = 60
c) Умножение двух нечетных чисел всегда дает нечетное число. Иногда это не будет считаться свойством четных чисел.
For example, 5 X 5=25, 11 X 11=121, 13 X 3=39
Summary of Properties of Even Numbers
| Properties of Addition: | |||||||||||
1. | Even + Even | Even | |||||||||
| 2. | Even + Odd | Odd | |||||||||
| 3. | Odd + Odd | Even | |||||||||
| Properties of Subtraction: | |||||||||||
| 1. | Even — Even | Even | |||||||||
| 2. | Even — Odd | ODD | |||||||||
| 3. | ODD — ODD | даже | |||||||||
| Properties Multiplation | |||||||||||
| Properties | 479797|||||||||||
.0356| 1. |  Even X Even | Even | 2. | Even X Odd | Even | 3. | Нечетные X Нечетные | Нечетные | | ||
Четные простые числа
Знаете ли вы, что простое число имеет только два делителя: 1 и само себя. Принимая во внимание, что четное число делится на 2. Если число считается четным простым числом, оно должно соответствовать обоим вышеуказанным критериям. Следовательно, только 2 может быть четным простым числом. Поскольку все остальные четные числа делятся на 2, они не могут быть простыми числами.
Важные моменты по четным числам:
- При счете каждое альтернативное число является четным числом, начиная с 2, и нечетным числом, начиная с 1.
- 0 «Ноль» — это четное число.

- Наименьшее четное число 2.
- Единственное четное простое число 2.
Четные числа — Решенные вопросы
Q1: Как узнать сумму n 35 четных чисел?
Ответ: Сумма n четных чисел рассчитывается по формуле S= n (n+1)
Q2: Найдите сумму первых десяти четных чисел.
Ответ: Сумма первых десяти четных чисел вычисляется по формуле S= n(n+1)
Итак, здесь нам нужно найти сумму первых десяти четных чисел т.е. n =10
Подставляя n=10 в формулу
S=10(10+1)
=10(11)
=110 – ответ , 10, 12, 14, 16, 18 и 20.
2+4+6+8+10+12+14+16+18+20=110, следовательно, сумма первых десяти четных чисел равна 110
Q3: Найдите четное число из заданного набора чисел 633, 524, 873, 448, 87, 222, 65, 14872, 8945, 25648.
Ответ: Четные числа из списка: 524, 448, 222, 14872 и 25648.
Итак, общее количество бутылок с водой в их доме равно 84 (четным) + 60 (четным) = четным, т.е. 144
Q4. Запишите любые восемь последовательных четных чисел от 50 до 70.
Ответ: Все числа от 50 до 70 равны 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69 и 70. Восемь последовательных четных чисел от 50 до 70: 52, 54, 56, 58, 60, 62, 64 и 68.
Q5: Камаль покупает 84 новые бутылки с водой, а его брат Сатьям также приносит домой 60 новых бутылок с водой. Является ли общее количество бутылок с водой в их доме четным числом?
Ответ: Камаль купил 84 бутылки с водой, т.е. четное число.
Количество бутылок с водой, принесенных Satyam, равно 60, что также является четным числом.
Итак, общее количество бутылок с водой в их доме равно
84 (четные) + 60 (четные) = четные, т. е. 144
е. 144
Q6: Найдите сумму всех четных чисел от 1 до 20?
Ответ: Всего между числами от 1 до 200 100 четных чисел.
Здесь n = 100
Используя формулу S = n(n+1), , мы можем вычислить сумму всех четных чисел от 1 до 200.
Так как n= 100
S = N (N+1)
S = 100 (100+1)
S = 100 (101)
Итак, здесь S = 100 x 101
= 10100
Следовательно, сумма четные числа от 1 до 200 равны 10 100.
Q7: Какое утверждение является правильным?
- Произведение двух четных чисел всегда является четным числом.
- Сумма двух четных чисел всегда является нечетным числом.
Ответ: Правильный ответ — Утверждение 1.
Здесь, если мы рассмотрим утверждение 1, т.е. Чет X Чет = Чет, что верно. Например, 6 X 6 = 36, 8 X 6 = 48.
Но утверждение 2 неверно, так как Чет + Чет = Чет,
Например, 4+8=12, 10+12=22. После сложения двух четных чисел сумма также будет четным числом, а не нечетным.
После сложения двух четных чисел сумма также будет четным числом, а не нечетным.
Q8: Выберите правильный вариант. Разница между двумя четными числами:
а) Всегда четное число
б) Всегда нечетное число
в) Может быть как нечетным, так и четным
г) Ничего из вышеперечисленного правильно.
Ответ: Правильный ответ вариант а). Как четное число — четное число = четное. Например, 8 — 4 = 4, 18 — 6 = 12
Q9: Является ли ноль (0) четным числом? Обосновать ответ.
Ответ: Да, ноль (0) — четное число. Четное число всегда должно делиться на 2. Итак, когда 0 делится на 2, результирующий остаток в частном также равен нулю, который является целым числом, тем самым классифицируя его как четное число .
Q10: Какова сумма 4 последовательных четных чисел от 20 до 30? , сумма первых четырех последовательных четных чисел от 20 до 30 равна 22 + 24 + 26 + 28 = 100.
Читайте также:
Четные/нечетные числа — ACT Math
Все ресурсы ACT Math
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
ACT Math Help » Арифметика » Целые числа » Четные/нечетные числа
Решение:
Возможные ответы:
Правильный ответ:
Объяснение:
Добавьте цифры единиц:
Так как нет цифры десятков для переноса, продолжайте добавлять цифры десятков:
Ответ: .
Сообщить об ошибке
В одной средней школе каждый должен сдавать латынь или греческий. Студентов, изучающих латынь, больше, чем студентов, изучающих греческий. Если есть студенты, изучающие греческий язык, сколько всего студентов?
Если есть студенты, изучающие греческий язык, сколько всего студентов?
Возможные ответы:
Правильный ответ:
Объяснение:
Если есть студенты, изучающие греческий язык, значит, есть или студенты, изучающие латынь. Однако вопрос спрашивает, сколько всего учеников в школе, поэтому вы должны сложить эти два значения вместе, чтобы получить:
или всего учеников.
Сообщить об ошибке
Найдите сумму 13 и 19.
Возможные ответы:
Правильный ответ:
Объяснение:
Перепишите вопрос в виде математического выражения.
Добавьте цифру единиц.
Поскольку это число больше , при добавлении следующего члена переносите разряд десятков.
Добавьте цифру десятков с переносом.
Объедините цифру десятков и цифру единиц. Ответ .
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы получить нечетный результат от сложения, у нас должно быть одно нечетное и одно четное число, таким образом, вы знаете из первого пункта о том, что только одно из двух значений является нечетным. Теперь, чтобы получить четный результат, у вас может быть два четных или два нечетных. Итак, предположим, что имеет два нечетных значения, это означает, что должно быть четным. Таким образом, у вас есть:
Теперь, если мы предположим, что имеет два четных значения, мы должны тогда знать, что это нечетное. Таким образом, мы имеем:
Прежде всего, вы можете исключить два ответа, которые говорят, что данное значение положительно или отрицательно. Этого нельзя сказать по нашим данным. Далее, не может быть четного случая. Оно всегда будет нечетным (следовательно, правильный ответ таков). Наконец, не может быть, чтобы даже всегда было . Во втором вышеприведенном случае у вас будет два четных числа, сложенных вместе, что даст вам четное число. Затем вы добавите нечетное, что даст вам нечетное.
Этого нельзя сказать по нашим данным. Далее, не может быть четного случая. Оно всегда будет нечетным (следовательно, правильный ответ таков). Наконец, не может быть, чтобы даже всегда было . Во втором вышеприведенном случае у вас будет два четных числа, сложенных вместе, что даст вам четное число. Затем вы добавите нечетное, что даст вам нечетное.
Сообщить об ошибке
Выберите ответ, который лучше всего решает следующее уравнение:
Возможные ответы:
Правильный ответ:
917 Объяснение:
Есть два способа решить эту проблему. Сначала вы можете сделать это алгебраически, разделив обе части на 13:
Но есть и другой способ, который, если вы понимаете нечетные числа, еще быстрее. Из всех ответов выше только один нечетный. Вы знаете, что данное уравнение должно быть нечетным — любое нечетное число, умноженное на нечетное число, даст нечетное число. Если вы умножите нечетное число на четное число, вы получите четное число.
Если вы умножите нечетное число на четное число, вы получите четное число.
Сообщить об ошибке
Найдите в следующем уравнении:
Возможные ответы:
Правильный ответ:
7 Объяснение:
Есть два способа решить эту задачу:
1. Используйте правило, согласно которому любые два нечетных числа, умноженные вместе, дадут еще одно нечетное число.
Используя это правило, только один ответ является нечетным числом (29), которое даст другое нечетное число (493) при умножении на заданное нечетное число (17).
2. Решение алгебраически:
Отчет о ошибке
Решение для уравнения в Фоллвинге:
Возможные ответы:
Правильный ответ:
777 2 Правильный ответ:7 777 . Объяснение:
Объяснение:
Есть два способа решить эту задачу:
1. Используйте правило, согласно которому любые два нечетных числа, умноженные вместе, дадут еще одно нечетное число.
Используя это правило, только один ответ является нечетным числом (85), которое даст другое нечетное число (7,735) при умножении на заданное нечетное число (91).
2. Решите алгебраически:
Сообщить об ошибке
Если и являются нечетными целыми числами, какое из следующих чисел не обязательно нечетное?
Возможные ответы:
Правильный ответ:
Объяснение:
Со многими вопросами, подобными этому, может быть проще подставить числа, чем иметь дело с теоретическими переменными. Однако, учитывая, что этот вопрос требует выражения, которое не всегда является четным или нечетным, а только не обязательно нечетным, теоретический путь может быть нашим единственным выбором.
Поэтому наш лучший подход — просто анализировать каждый вариант ответа.
: Поскольку нечетное, тоже нечетное, так как и нечетное число, умноженное на нечетное число, дает нечетный продукт. Так как также является нечетным, умножение его на даст снова нечетный продукт, поэтому это выражение всегда нечетное.
: Поскольку нечетное число, умножив его на 2, вы получите четное число. Вычитание этого числа из также даст нечетный результат, поскольку нечетное число минус четное число дает нечетное число. Поэтому этот ответ тоже всегда нечетный.
: Поскольку оба числа нечетные, их произведение также всегда будет нечетным.
: Поскольку нечетное число, умножив его на 2, вы получите четное число. Поскольку это нечетное число, вычитание его из нашего четного числа даст нечетное число, поскольку четное число минус нечетное число всегда будет нечетным. Поэтому этот ответ всегда будет нечетным.
: Поскольку оба числа нечетные, сумма будет четной. Однако деление четного числа на другое четное число (в нашем случае на 2) не всегда дает четное или нечетное число. Например, 5 и 7 оба нечетные. Их сумма 12 четна. Деление на 2 дает 6, четное число. Однако числа 5 и 9 тоже нечетные. Их сумма, 14, четна, но деление на 2 дает 7, нечетное число. Следовательно, это выражение не обязательно всегда нечетное или всегда четное, и поэтому является нашим ответом.
Однако деление четного числа на другое четное число (в нашем случае на 2) не всегда дает четное или нечетное число. Например, 5 и 7 оба нечетные. Их сумма 12 четна. Деление на 2 дает 6, четное число. Однако числа 5 и 9 тоже нечетные. Их сумма, 14, четна, но деление на 2 дает 7, нечетное число. Следовательно, это выражение не обязательно всегда нечетное или всегда четное, и поэтому является нашим ответом.
Сообщить об ошибке
У Теодора есть драже. У Порции в три раза больше. У Харви их в пять раз больше, чем у нее. Каково общее количество драже во всей группе?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти ответ на этот вопрос, подсчитайте общее количество мармеладок для каждого человека:
Порция: * <количество мармеладок Теодора>, то есть или
Харви: * <количество мармеладок у Порции>, то есть или
Итого:
(Не забывайте, что эти оригиналы нужны для Теодора!)
6Сообщить об ошибке 0 7
Найдите произведение и .
Возможные ответы:
Правильный ответ:
Объяснение:
Преобразуйте произведение в выражение и умножьте на единицу оба числа.
Цифра единиц окончательного ответа — это цифра единиц от умножения 3 и 7, то есть 1. Цифра десятков, 2, будет перенесена в следующий расчет.
Умножьте число десятков от 13 до 7 и добавьте перенос.
Значение 9 — это разряд десятков окончательного ответа.
Объедините цифру десятков с цифрой единиц. Ответ .
Сообщить об ошибке
← Предыдущая 1 2 3 Следующая →
Уведомление об авторских правах
Все математические ресурсы ACT
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Учиться по понятиям
Простые числа – Элементарная математика
Значение
Неформальный смысл
Построение чисел из меньших строительных блоков: Любое счетное число, кроме 1, может быть построено путем сложения двух или более меньших счетных чисел. Но только некоторые счетных чисел могут быть составлены путем умножения двух или более меньших счетных чисел.
Но только некоторые счетных чисел могут быть составлены путем умножения двух или более меньших счетных чисел.
Простые и составные числа: Мы можем построить 36 из 9 и 4 путем умножения; или мы можем построить его из 6 и 6; или с 18 и 2; или даже путем умножения 2 × 2 × 3 × 3. Числа, такие как 10, 36 и 49, из которых могут быть составлены как произведения меньших счетных чисел, называются составными числами.
Некоторые числа нельзя составить таким образом из более мелких частей. Например, он единственный способ построить 7 путем умножения и использования только при подсчете чисел равно 7 × 1. Чтобы «построить» 7, мы должны использовать 7! Так что на самом деле мы не собираем его из более мелких строительных блоков; нам это нужно для начала. Такие числа называются простых чисел.
Неформально простые числа — это числа, которые нельзя получить путем умножения других чисел. Это хорошо передает идею, но не является достаточно хорошим определением, потому что в нем слишком много лазеек. Число 7 может быть составлено как произведение других чисел: например, это 2 × 3. Чтобы уловить идею о том, что «7 не делится на 2», мы должны четко указать, что мы ограничиваем числа, включающие только счетные числа: 1, 2, 3….
Это хорошо передает идею, но не является достаточно хорошим определением, потому что в нем слишком много лазеек. Число 7 может быть составлено как произведение других чисел: например, это 2 × 3. Чтобы уловить идею о том, что «7 не делится на 2», мы должны четко указать, что мы ограничиваем числа, включающие только счетные числа: 1, 2, 3….
Формальное определение
Простое число — это положительное целое число, имеющее ровно два различных целочисленных множителя (или делителя), а именно 1 и само число.
Разъяснение двух распространенных заблуждений
Два распространенных заблуждения:
- Число 1 — это , а не простое число.
- Число 2 является простым. (Это единственное четное простое число.)
Что ж, определение исключает это. В нем говорится «два различных целочисленных множителей», и единственный способ записать 1 в виде произведения целых чисел — это 1 × 1, в котором множителей — это одинаковых множителей, то есть не различных. Даже неформальная идея исключает это: его нельзя построить путем умножения других (целых) чисел.
Даже неформальная идея исключает это: его нельзя построить путем умножения других (целых) чисел.
Но зачем исключать?! Студенты иногда утверждают, что 1 «ведет себя» так же, как и все остальные простые числа: его нельзя «разорвать на части». И часть неформального понятия прайма — мы не можем составить 1, кроме как с помощью его, поэтому он должен быть строительным блоком — кажется, делает его простым. Почему не включает его в ?
Математика не произвольна. Чтобы понять, почему полезно исключить 1 из , рассмотрим вопрос «Сколькими способами можно записать 12 в виде произведения, используя только простые числа?» Вот несколько способов записать 12 как произведение, но они не ограничиваются простыми числами.
- 3 × 4
- 4 × 3
- 1 × 12
- 1 х 1 х 12
- 2 × 6
- 1 × 1 × 1 × 2 × 6
Использование 4, 6 и 12 явно нарушает ограничение «использование только простых чисел». Но как насчет этих?
Но как насчет этих?
- 3 × 2 × 2
- 2 × 3 × 2
- 1 × 2 × 3 × 2
- 2 × 2 × 3 × 1 × 1 × 1 × 1
Ну, если мы включим 1, есть бесконечно много способов записать 12 как произведение простых чисел. На самом деле, если мы назовем 1 простым числом, то существует бесконечно много способов записать 9.1572 любое число как произведение простых чисел. Включение 1 упрощает вопрос. При его исключении остаются только эти случаи:
- 3 × 2 × 2
- 2 × 3 × 2
- 2 × 2 × 3
Это гораздо более полезный результат, чем представление каждого числа в виде произведения простых чисел бесконечным числом способов, поэтому мы определяем простое число таким образом, что оно исключает 1.
Число 2 — это простых чисел. Почему?
Студенты иногда считают, что все простые числа нечетные. Если кто-то работает только по «шаблонам», это легко сделать, поскольку 2 — это единственное исключение , единственное четное простое число. Одно доказательство: поскольку 2 является делителем каждого четного числа, каждое четное число, большее 2, имеет не менее 91 572 трех 91 575 различных положительных делителей.
Одно доказательство: поскольку 2 является делителем каждого четного числа, каждое четное число, большее 2, имеет не менее 91 572 трех 91 575 различных положительных делителей.
Еще один распространенный вопрос: «Все четные числа делятся на 2, значит, они не простые; 2 четно, так как же оно может быть простым?» Каждое целое число делится само на себя и на 1; все они делятся на что-то . Но если число делится на только на само по себе и на 1, то оно простое. Итак, поскольку все других четных чисел делятся сами на себя, на 1, и на 2 , все они составные (точно так же, как все положительные числа, кратные 3, кроме самого 3, составные).
Математическая основа
Уникальная факторизация простых чисел и деревья множителей
Вопрос «Сколькими способами можно записать число в виде произведения, используя только простые числа?» (посмотрите, почему 1 не простое число) становится даже еще интереснее, если мы спросим себя, достаточно ли различны 3 × 2 × 2 и 2 × 2 × 3, чтобы считать их « различными способами». Если мы рассмотрим только набор используемых чисел — другими словами, если мы проигнорируем то, как эти числа устроены, — мы придем к замечательному и очень полезному факту (доказуемому).
Если мы рассмотрим только набор используемых чисел — другими словами, если мы проигнорируем то, как эти числа устроены, — мы придем к замечательному и очень полезному факту (доказуемому).
- Каждое целое число больше 1 можно разложить на уникальный набор простых чисел. Для любого целого числа существует только один набор из простых множителей.
Простые числа и прямоугольники
Можно расположить 12 квадратных плиток в виде трех отдельных прямоугольников.
Семь квадратных плиток можно сложить разными способами, но только одна из них образует прямоугольник.
Сколько существует простых чисел?
От 1 до 10 4 простых числа: 2, 3, 5 и 7.
От 11 до 20 опять 4 простых числа: 11, 13, 17 и 19.
От 21 до 30 только 2 простых числа: 23 и 29.
От 31 до 40 снова только 2 простых числа: 31 и 37.
От 91 до 100 только одно простое число: 97.
Похоже, они редеют. Кажется, это даже имеет смысл; по мере того, как числа становятся больше, появляется больше маленьких строительных блоков, из которых они могут быть сделаны.
Останавливаются ли когда-нибудь простые числа? Предположим на мгновение, что они в конце концов остановятся. Другими словами, предположим, что 91 572 — это 91 575 «наибольшего простого числа» — назовем его 91 572 p 9.1575 . Итак, если бы мы перемножили вместе все известные нам простые числа (все от 2 до p ), а затем прибавили 1 к этому произведению, мы бы получили новое число — назовем его q — которое не делится ни на одно из известных нам простых чисел. (Деление на любое из этих простых чисел даст в остатке 1.) Таким образом, либо q само является простым числом (и, безусловно, больше, чем p ), либо оно делится на какое-то простое число, которое мы еще не перечислили (что, следовательно, , также должно быть больше стр. ). В любом случае, предположение о существовании наибольшего простого числа — p якобы было нашим наибольшим простым числом — приводит к противоречию! Так что это предположение должно быть неверным: 91 572 — это 91 575, а не «наибольшее простое число»; простые числа никогда не останавливаются.
Предположим, что 11 — это самое большое простое число.
- 2 × 3 × 5 × 7 × 11 + 1 = 2311 — Прайм!
- Никакое число (кроме 1) не делит 2311 с нулевым остатком, поэтому 11 не является самым большим простым числом.
Предположим, что 13 — самое большое простое число.
- 2 × 3 × 5 × 7 × 11 × 13 + 1 = 30031 — Не простых!
- Но 59 × 509 = 30031, и 59, и 509 — простые числа, и оба больше 13, поэтому 13 — не самое большое простое число.
Q1 Какова сумма любых двух i Нечетных чисел ii Четных чисел…
Перейти к
- Упражнение 3.1
- Упражнение 3.2
- Упражнение 3.3
- Упражнение 3.
 4
4 - Упражнение 3.5
- Упражнение 3.6
- Упражнение 3.7
- Зная наши цифры
- Целые числа
- Игра с числами
- Основные геометрические идеи
- Понимание элементарных форм
- Целые числа
- Фракции
- Десятичные
- Обработка данных
- Измерение
- Алгебра
- Соотношение и пропорция
- Симметрия
- Практическая геометрия
Главная >
Решения НЦЭРТ
Класс 6
Математика
>
Глава 3. Игра с числами
>
Упражнение 3.2
>
Вопрос 1
Игра с числами
>
Упражнение 3.2
>
Вопрос 1
Вопрос 1 Упражнение 3.2
В1) Чему равна сумма любых двух
(i) Нечетных чисел?
(ii) Четные числа?
Ответ:
РЕШЕНИЕ:
(i) Сумма любых двух нечетных чисел является четным числом.
пример: 1+3=4, 3+5=8
(ii) Сумма любых двух четных чисел является четным числом.
Пример: 4+4=8, 2+2=4
Расшифровка видео
привет, ребята добро пожаловать на домашнее задание сегодня мы делаем вопрос номер один, который является суммой любых двух первых нечетные числа, поэтому давайте возьмем в качестве примера любые два нечетных числа, поэтому три три — нечетное число, а пять — так что пять — это также n число, поэтому теперь мы добавим их оба, так что три плюс пять, что даст нам 8, оба нечетные, но ответ 8, что является четным, так что сумма любых двух нечетных чисел четная, давайте перейдем ко второй части, какова сумма любых двух четных чисел, так что теперь давайте возьмем любые два четных числа, поэтому давайте возьмем 8 и давайте возьмем 4, так что сумма означает прибавление так что 8 плюс 4 равно 12 12 тоже четно поэтому сумма любых двух четных чисел тоже четно так что ответ на оба этих вопроса четный спасибо ребята за просмотр видео если у вас есть сомнения дайте мне знать в комментариях ниже i’ свяжусь с вами как можно скорее большое спасибо
Связанные вопросы
Q2) Укажите, являются ли следующие утверждения верными или неверными: (i) сумма трех нечетных чисел равна е. ..
..
Q5) Какое самое большое простое число между 1 и 10?
Q3) Числа 13 и 31 являются простыми числами. Оба эти числа имеют одинаковые цифры 1 и 3. Найдите s…
Q11) Запишите пять пар простых чисел меньше 20, сумма которых делится на 5.
Q6) Выразите следующее в виде суммы двух нечетных простых чисел. (i) 44 (ii) 36 (iii) 24 (iv) 18
Q7) Назовите три пары простых чисел, разность которых равна 2. [Примечание: два простых числа, разность которых…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Задание
Задание 3.


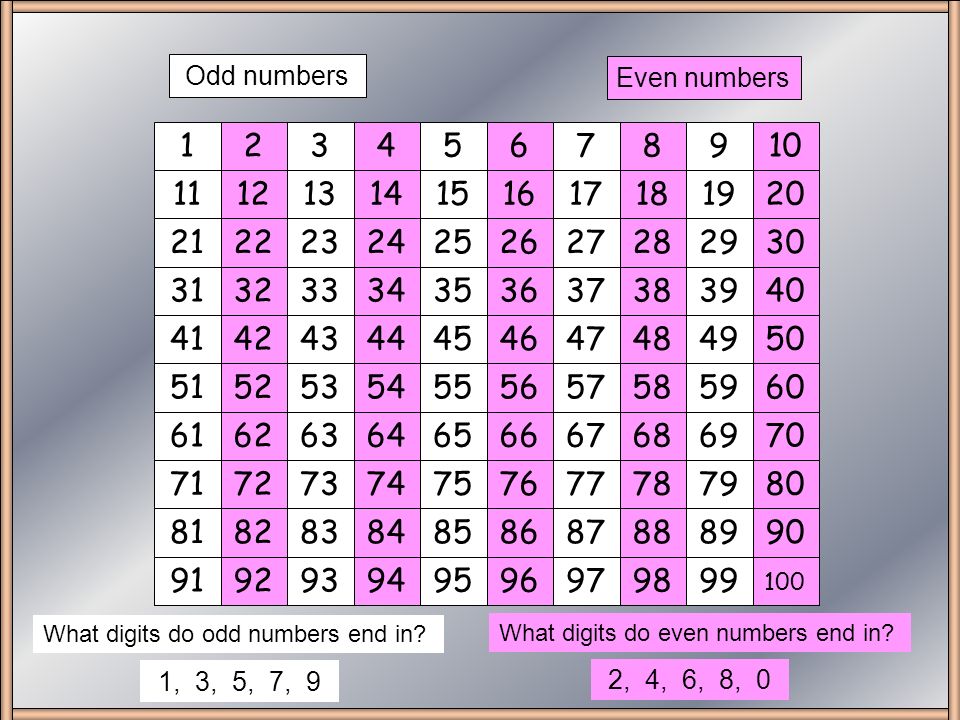 66)
66)

 Значит, ответ всегда четный.
Значит, ответ всегда четный.
 0004
0004 0004
0004
 4
4