определение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Определение 1Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Определение 6Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.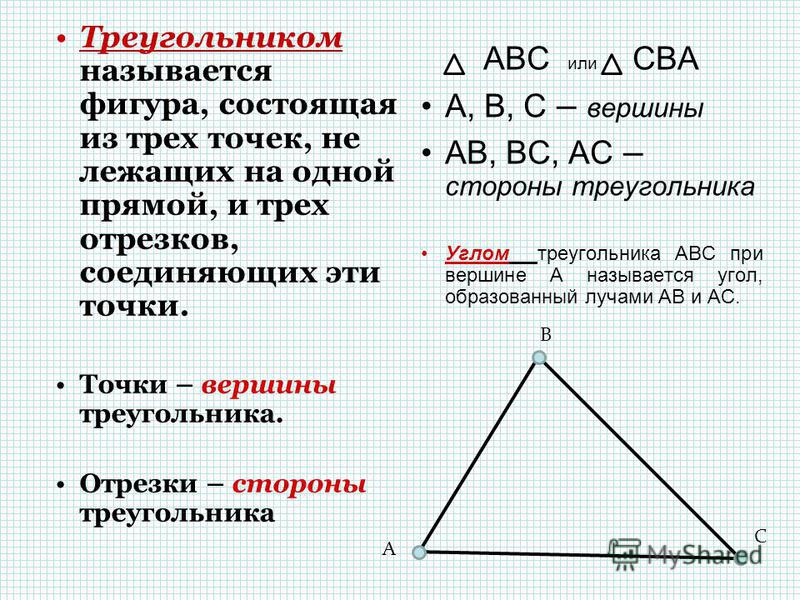
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
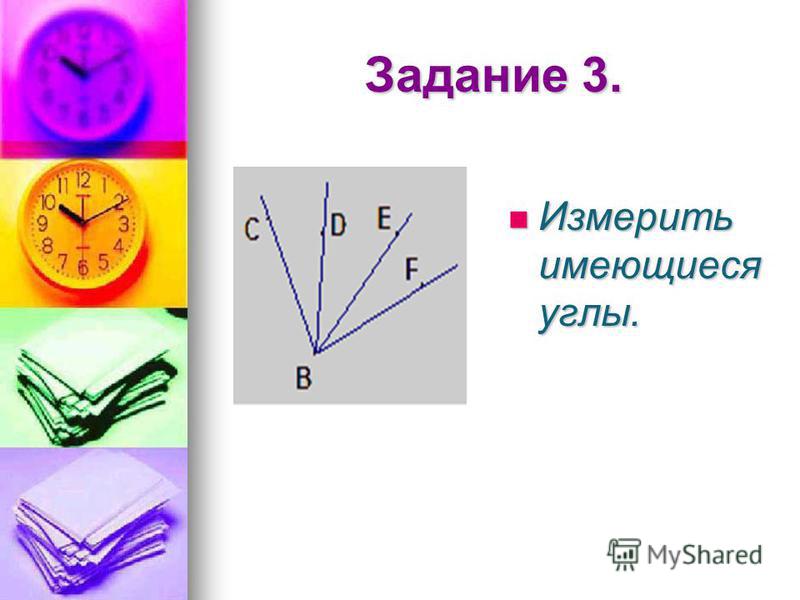
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Определение 8Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Определение 9 Минутой называют одну шестидесятую часть градуса. Определение 10Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение:
1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» .
Определение 11Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600.
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов.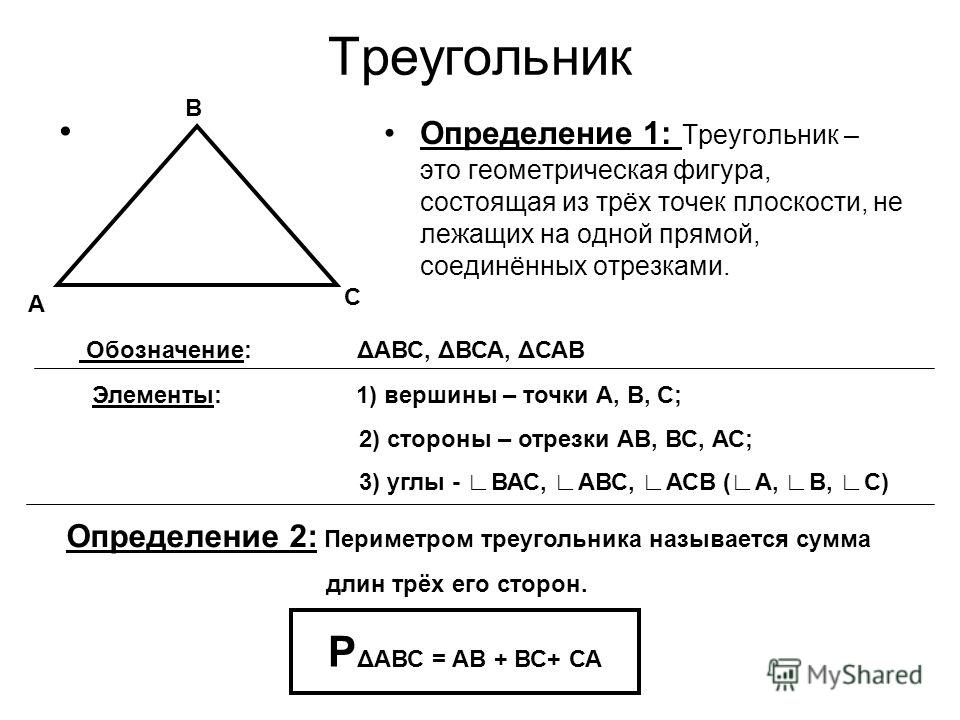 Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.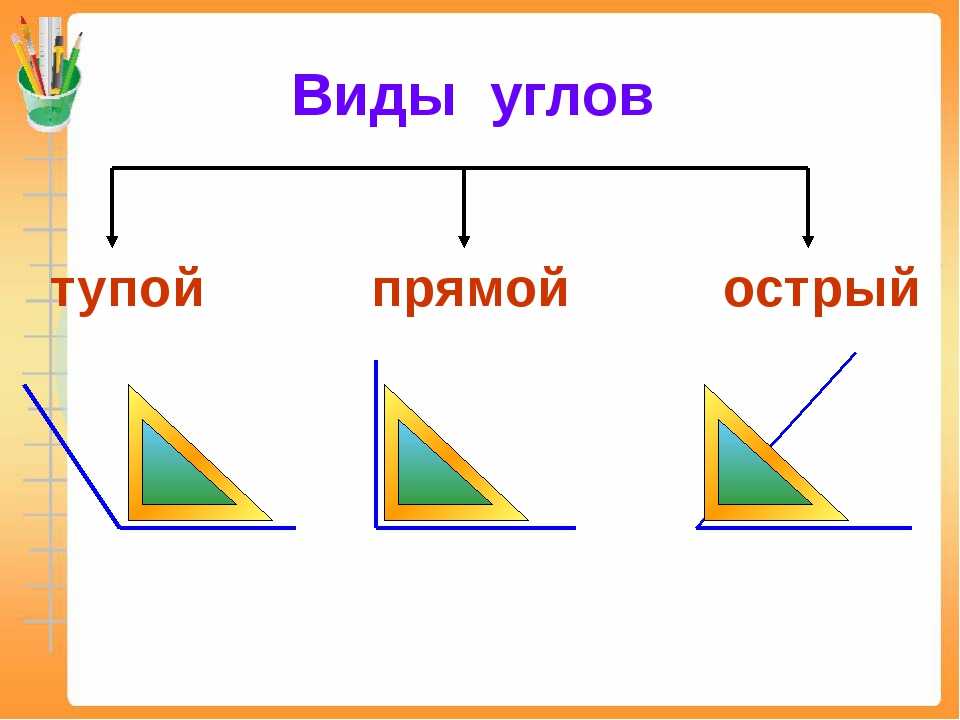
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Решение задач
от 1 дня / от 150 р.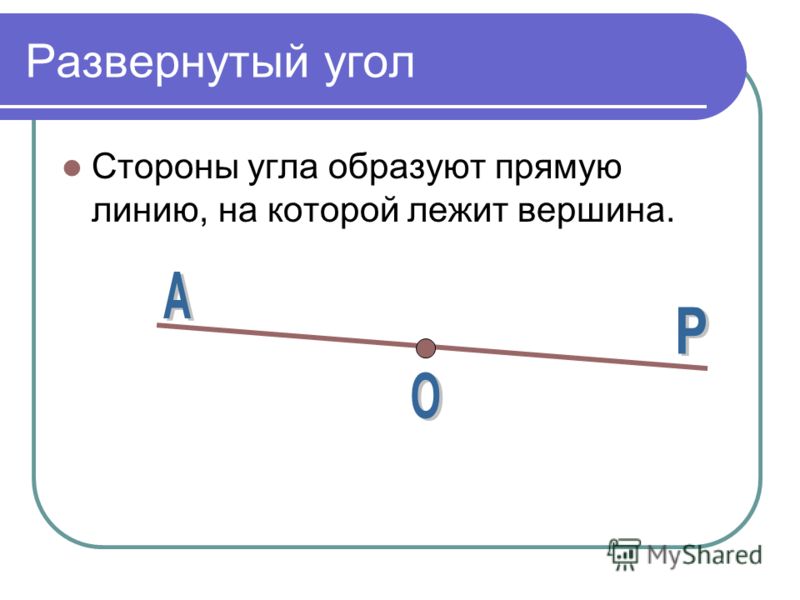
определение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Определение 1Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Определение 6Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Ниже показано на рисунке.
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу.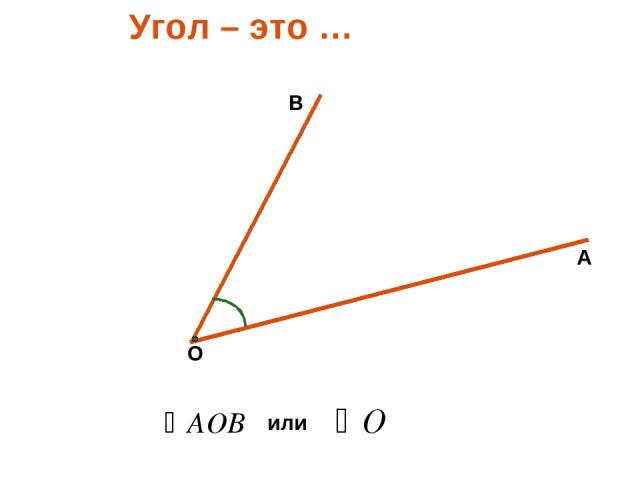 Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Определение 8Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Определение 9Минутой называют одну шестидесятую часть градуса.
Определение 10Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение:
1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» .
Определение 11Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600.
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
Обозначение угла принимается за «рад».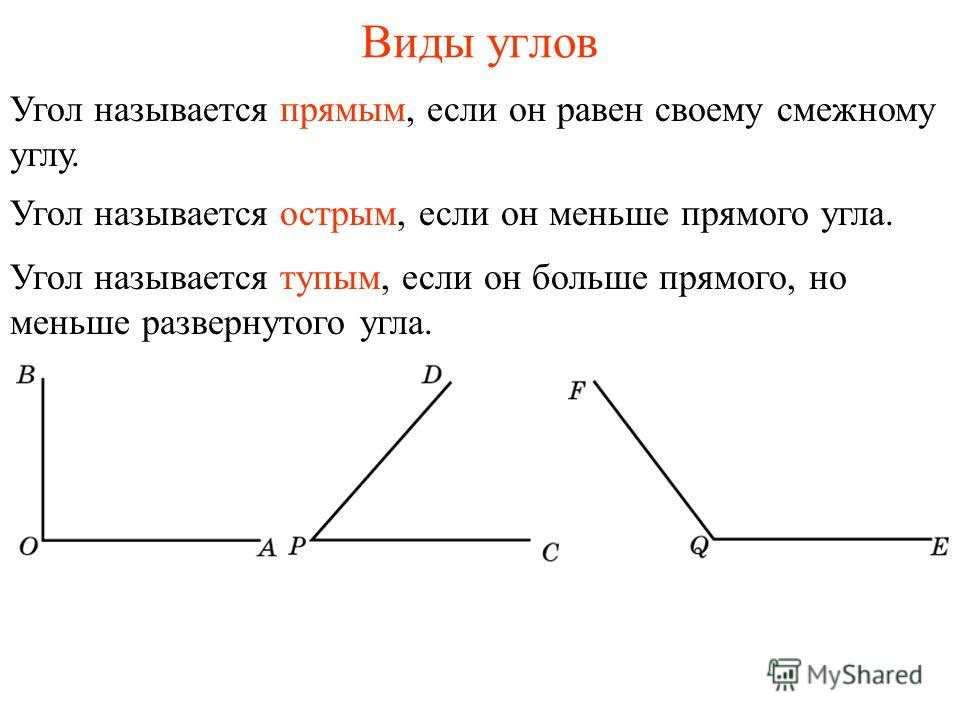 То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного.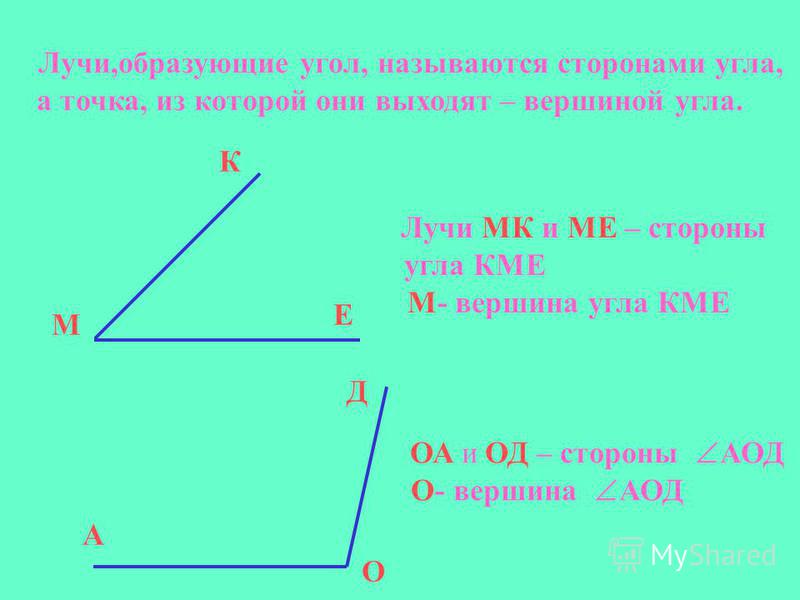 На чертеже изображено правильное обозначение острых, равных и неравных углов.
На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.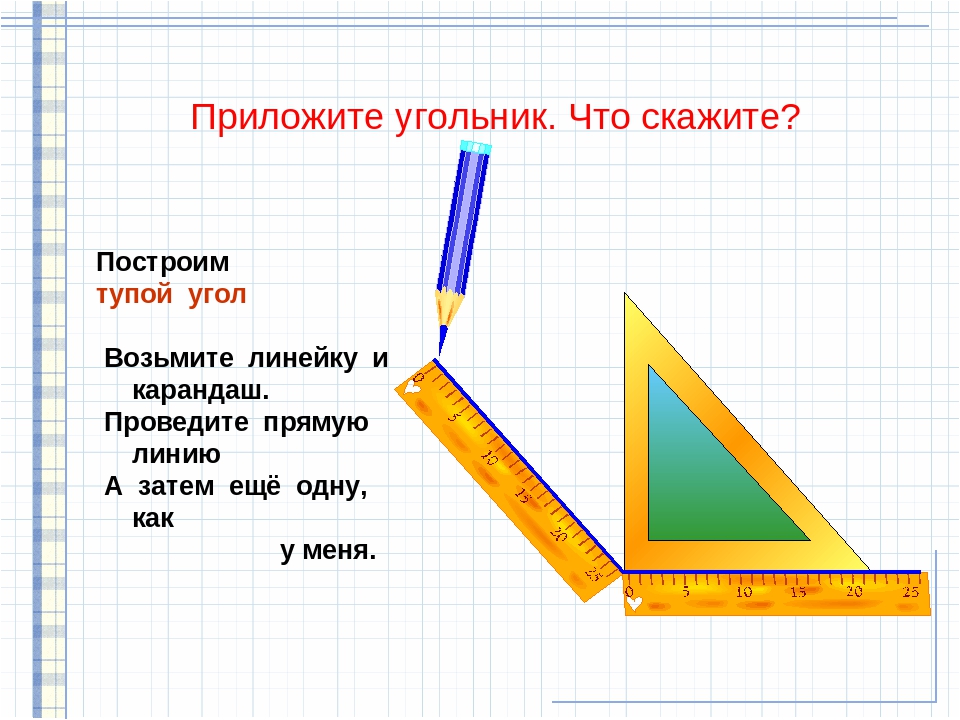 Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
определение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Определение 1Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Определение 6Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Определение 8Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Определение 9Минутой называют одну шестидесятую часть градуса.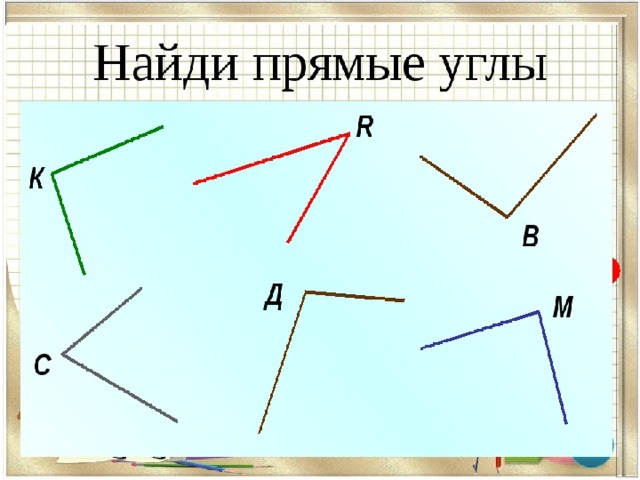
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение:
1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» .
Определение 11Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600.
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла.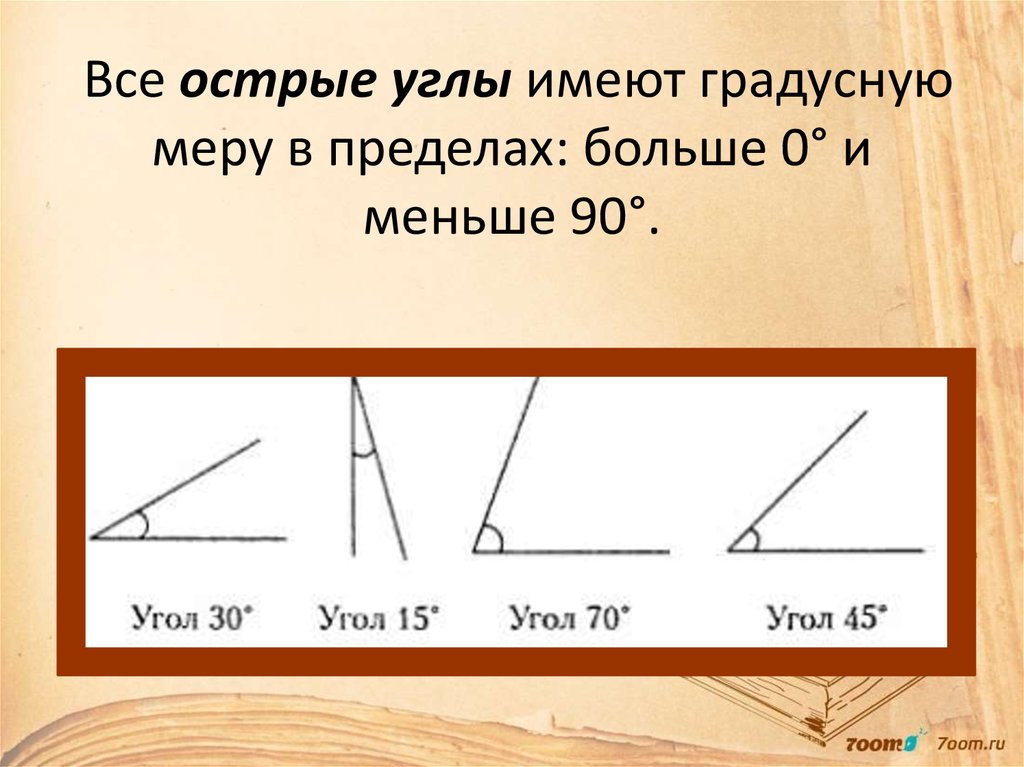 Они считаются подобными.
Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение.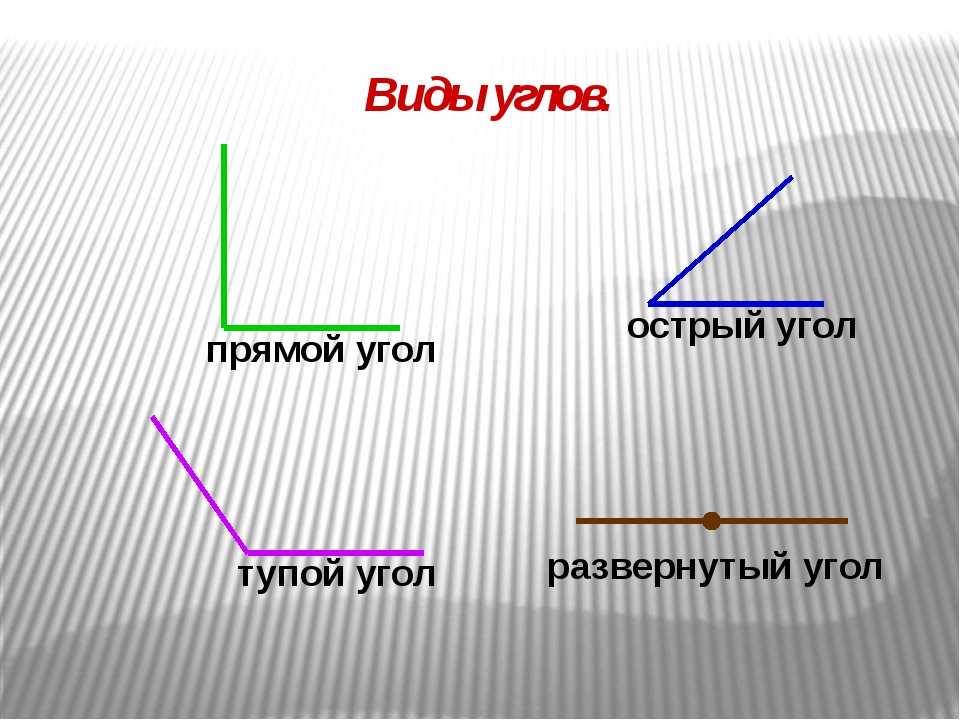 Ниже приведен рисунок, где показано их обозначение.
Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.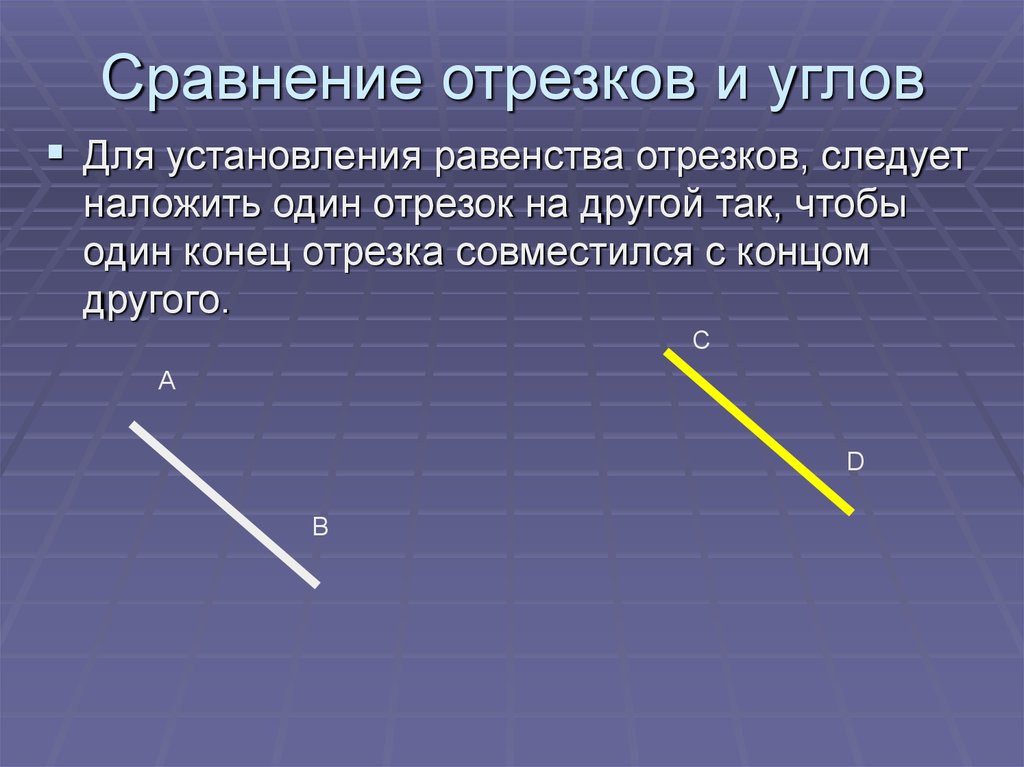 Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
определение угла, измерение углов, обозначения и примеры. Прямой, тупой, острый и развернутый угол Тупой отрезок
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD.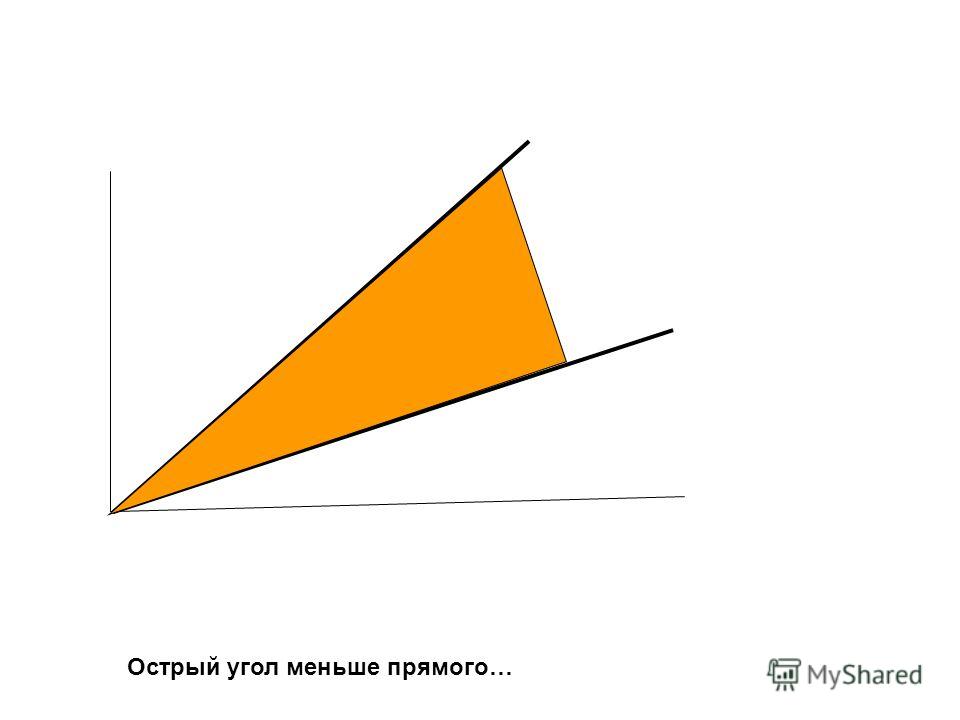 Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные
конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или
разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или
проверки любых углов — длинна сторон не ограничена.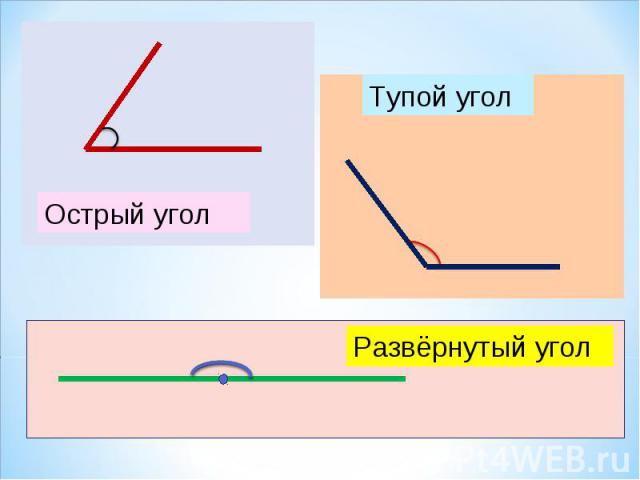 Основной инструмент для измерений — рулетка.
Основной инструмент для измерений — рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы . В виде формулы записывается это так:
a²+b²=c²
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих
стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно
больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250
см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат
(умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 —
это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра
должна составлять диагональ между нашими отметками.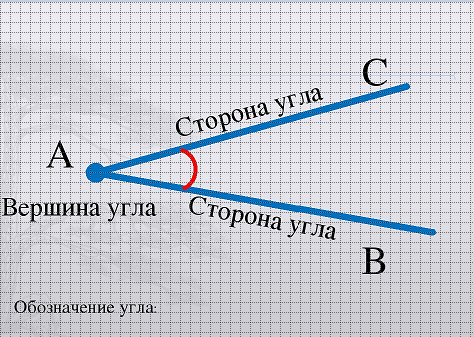 Если измерение рулеткой показывает другую длину диагонали —
проверяемый угол развернут и имеет отклонение от 90°.
Если измерение рулеткой показывает другую длину диагонали —
проверяемый угол развернут и имеет отклонение от 90°.
Калькулятор расчета диагонали прямого угла
Внимание! Для работы калькулятора необходимо включить поддержку JavaScript в вашем браузере!
Длина a
Длина b
Диагональ c
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же,
не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно
лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у
прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого
метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны
быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее.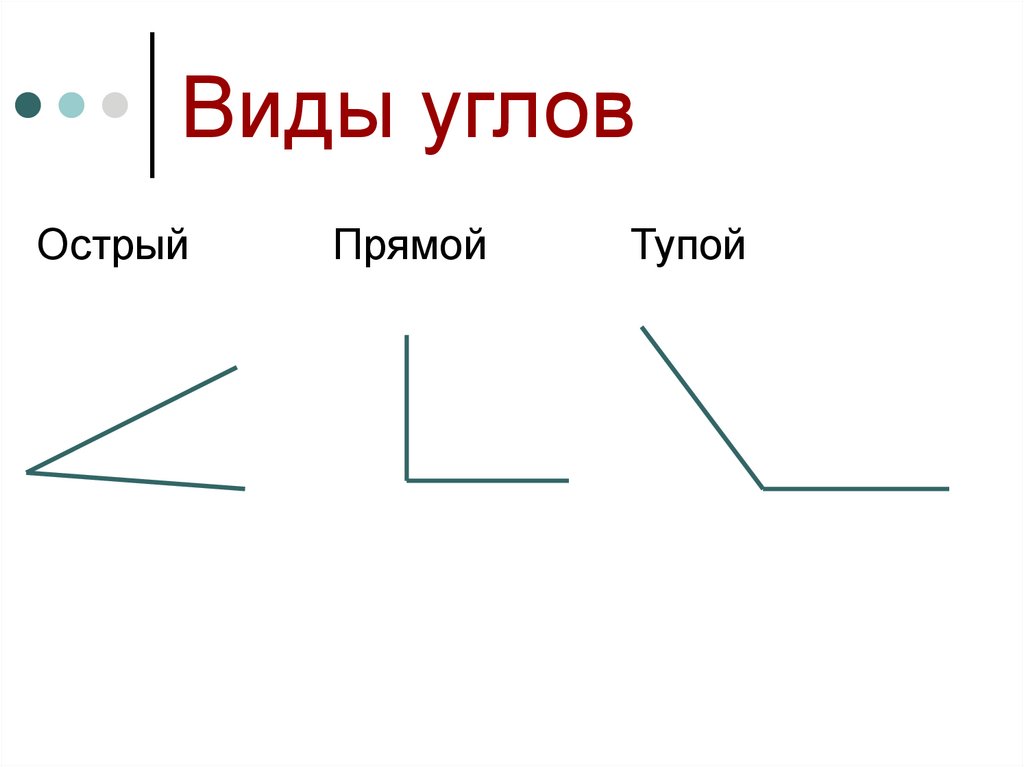 Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.
Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако
это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или
линиями на полу — задача посложнее.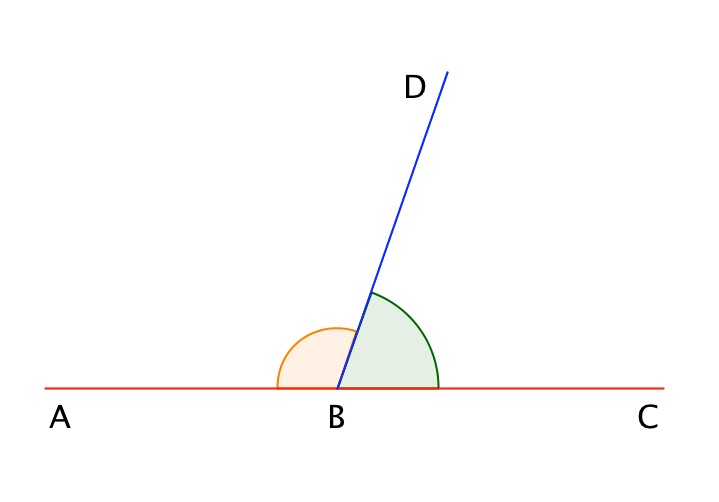
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!
Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных
фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные
или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается
прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить
45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим
два угла по 45 градусов.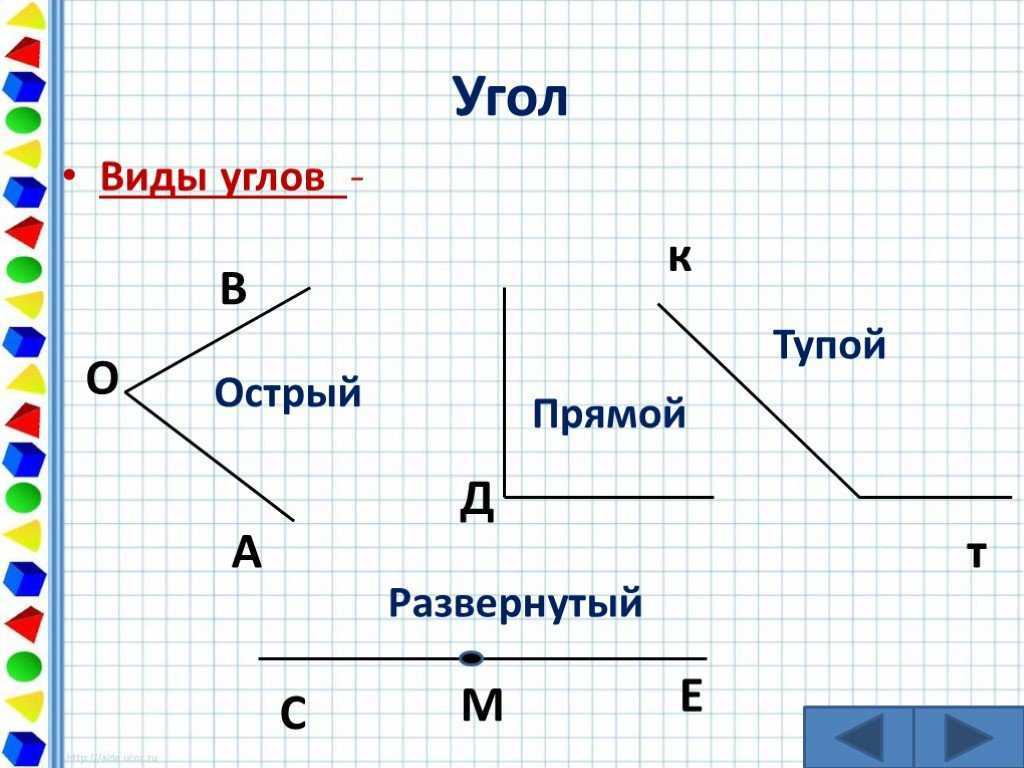 Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм
вам понятен.
Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм
вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
ПРЯМОЙ, ая, ое; прям, пряма, прямо, прямШы и прямы. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
прямой угол — — Тематики нефтегазовая промышленность EN right angle …
Угол, равный своему смежному. * * * ПРЯМОЙ УГОЛ ПРЯМОЙ УГОЛ, угол, равный своему смежному … Энциклопедический словарь
Угол, равный своему смежному; в градусном измерении равен 90° … Естествознание. Энциклопедический словарь
См. Угол … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
1) угол, равный своему смежному. 2) Внесистемная ед. плоского угла. Обозначение L. 1 L = 90° = ПИ/2 рад 1,570 796 рад (см. Радиан) … Большой энциклопедический политехнический словарь
2) Внесистемная ед. плоского угла. Обозначение L. 1 L = 90° = ПИ/2 рад 1,570 796 рад (см. Радиан) … Большой энциклопедический политехнический словарь
Прямая, прямое; прям, пряма, прямо. 1. Ровно вытянутый в каком–н. направлении, не кривой, без изгибов. Прямая линия. «Прямая дорога обрывалась и уж шла вниз.» Чехов. Прямой нос. Прямая фигура. 2. Беспересадочный (ж.–д. и разг.). Прямой маршрут.… … Толковый словарь Ушакова
ПРЯМОЙ, ая, ое; прям, пряма, прямо, прямы и прямы. 1. Ровно идущий в каком н. направлении, без изгибов. Прямая линия (линия, образом к рой может служить бесконечная туго натянутая нить). Провести прямую (т. е. прямую линию; сущ.). Дорога идёт… … Толковый словарь Ожегова
угол основного профиля витка — (αb) Угол между основным профилем витка эвольвентного червяка и прямой, составляющей с осью червяка прямой угол скрещивания. Примечание Угол прямолинейного основного профиля витка эвольвентного червяка αb равен основному углу подъема… … Справочник технического переводчика
Книги
- Таблицы для численного решения граничных задач теории гармонических функций , Канторович Л.
 В., Крылов В. И., Чернин К. Е.. Граничные задачи для гармонических функций часто возникают при математическом анализе многих важных вопросов физики и техники (задачи расчета электрического и теплового поля, задачи…
В., Крылов В. И., Чернин К. Е.. Граничные задачи для гармонических функций часто возникают при математическом анализе многих важных вопросов физики и техники (задачи расчета электрического и теплового поля, задачи… - Математика. 2 класс. Учебник. В 2-х частях. Часть 2 , Моро М.И.. Учебник «Математика» входит в образовательную систему» Школа России» . Материал учебника позволяет реализовать системно-деятельностный подход, организовать дифференцированное обучение и…
Каждый угол, в зависимости от его величины, имеет своё название:
| Вид угла | Размер в градусах | Пример |
|---|---|---|
| Острый | Меньше 90° | |
| Прямой | Равен 90°. На чертеже прямой угол, обычно обозначают символом , проведённым от одной стороны угла до другой. | |
| Тупой | Больше 90°, но меньше 180° | |
| Развёрнутый | Равен 180° Развёрнутый угол равен сумме двух прямых углов, а прямой угол составляет половину развёрнутого угла. | |
| Выпуклый | Больше 180°, но меньше 360° | |
| Полный | Равен 360° |
Два угла называются смежными , если у них одна сторона общая, а две другие стороны составляют прямую линию:
Углы MOP и PON смежные, так как луч OP — общая сторона, а две другие стороны — OM и ON составляют прямую.
Общая сторона смежных углов называется наклонной к прямой , на которой лежат две другие стороны, только в том случае, когда смежные углы не равны между собой. Если смежные углы равны, то их общая сторона будет перпендикуляром .
Сумма смежных углов равна 180°.
Два угла называются вертикальными , если стороны одного угла дополняют до прямых линий стороны другого угла:
Углы 1 и 3, а также углы 2 и 4 — вертикальные.
Вертикальные углы равны.
Докажем, что вертикальные углы равны:
Сумма ∠1 и ∠2 составляет развёрнутый угол.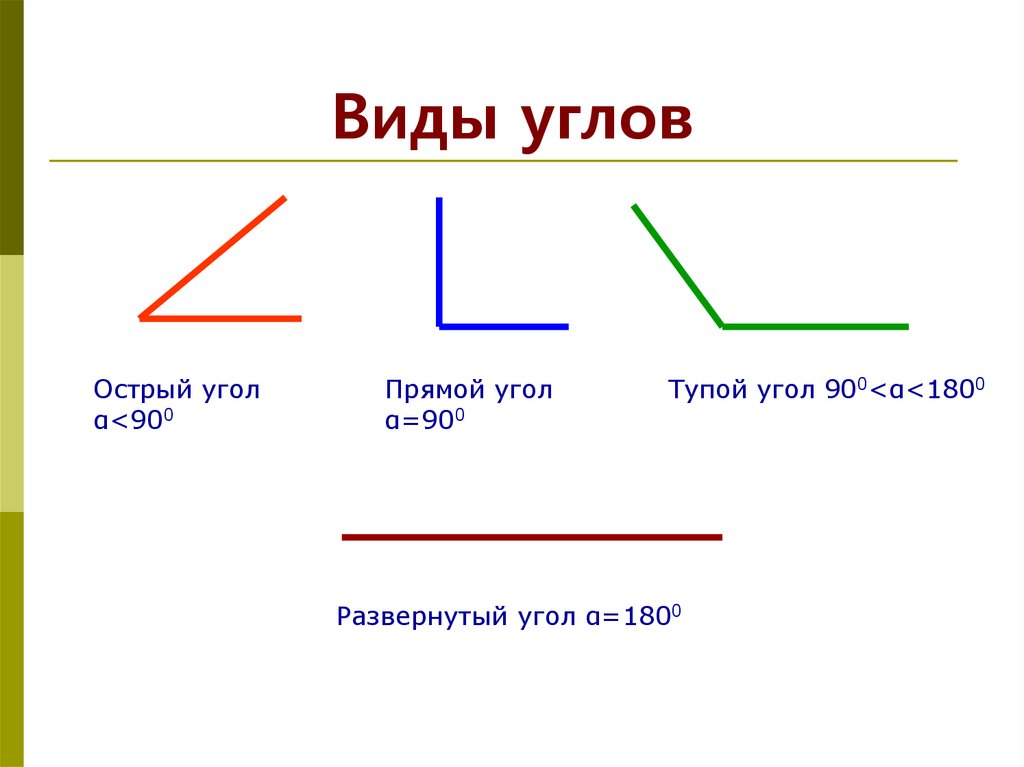 И сумма ∠3 и ∠2 составляет развёрнутый угол. Значит, эти две суммы равны:
И сумма ∠3 и ∠2 составляет развёрнутый угол. Значит, эти две суммы равны:
∠1 + ∠2 = ∠3 + ∠2.
В этом равенстве слева и справа есть по одинаковому слагаемому — ∠2. Равенство не нарушится, если это слагаемое в левой и в правой части опустить. Тогда мы получаем.
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).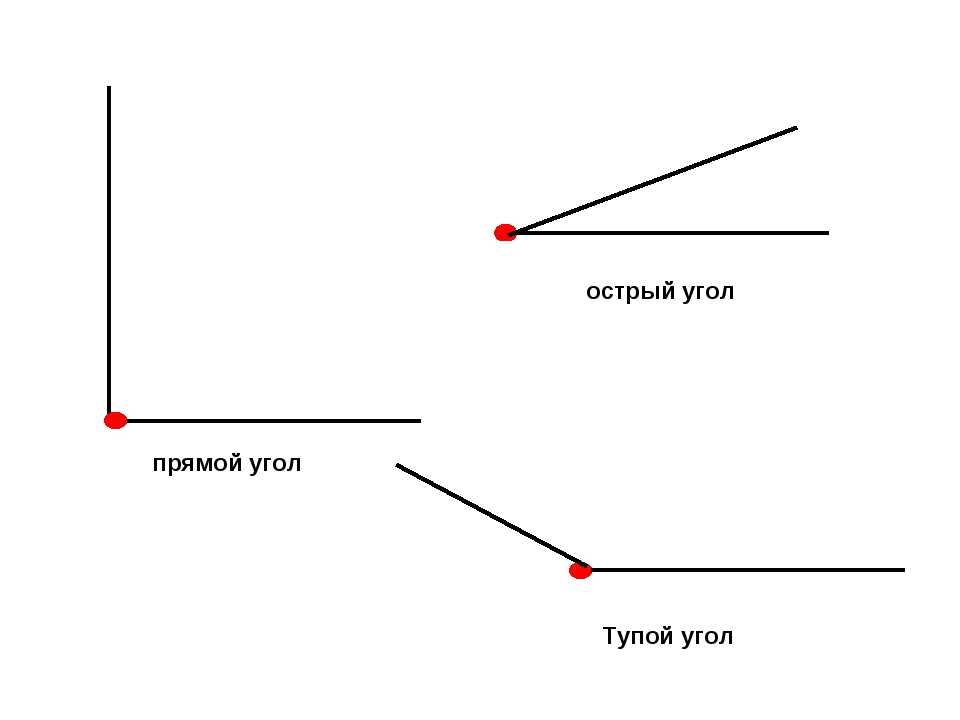
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
определение угла, измерение углов, обозначения и примеры. Прямой и развернутый угол Что называется развернутым углом
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам .
В морской терминологии углы обозначаются румбами .
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation
.
2010
.
Смотреть что такое «Развернутый угол» в других словарях:
Угол, равный двум прямым. *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
угол — ▲ разность направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона. образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… …
Угол — Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми. УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
Геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки.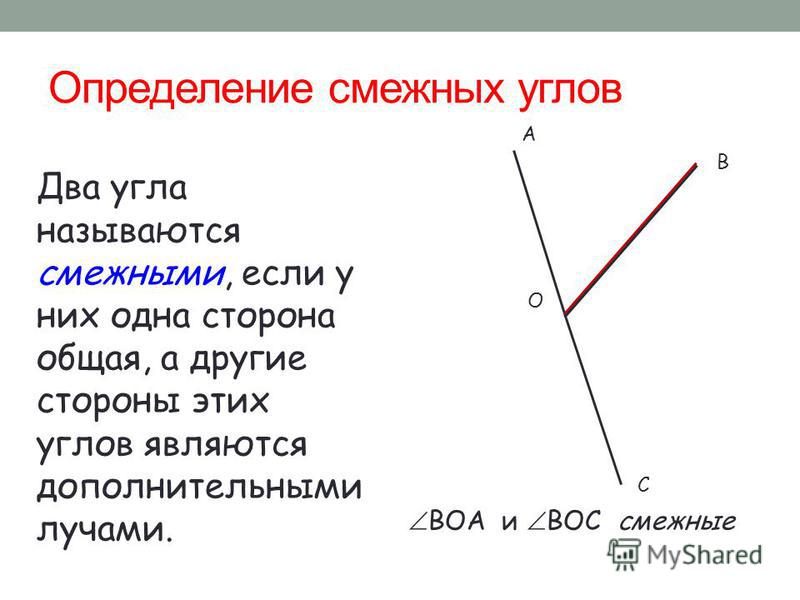 Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия
Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия
Угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь
Раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия
поперек — ▲ под углом максимум, косой угол поперечный. поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
градус — а, м. 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка
Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном… … Википедия
«Основные понятия геометрии» — Признак равенства треугольника. Отрезки. Геометрия. Смежные и вертикальные углы. Построение параллельных прямых. Построение треугольника. Выводы. Прямые параллельны. Вершины. Простейшие геометрические фигуры. Какая фигура называется треугольником. Равные отрезки имеют равные длины. Угол – это геометрическая фигура, которая состоит из точки и двух лучей.
Угол – это геометрическая фигура, которая состоит из точки и двух лучей.
«Геометрия в таблицах» — Координаты точки и координаты вектора в пространстве Скалярное произведение векторов в пространстве Движение Цилиндр Конус Сфера и шар Объем прямоугольного параллелепипеда Объем прямой призмы и цилиндра Объем наклонной призмы Объем пирамиды Объем конуса Объем шара и площадь сферы. Таблицы геометрия.
«Геометрия 8 класс» — Каждое утверждение опирается на уже доказанные. У любого здания есть фундамент. Понятие теоремы. Аксиома -утверждение, истинность которых принимается без доказательств. Каждое математическое утверждение, получаемое путем логического доказательства, есть теорема. Так перебирая теоремы, можно добраться до аксиом.
«Геометрия это наука» — Геометрия состоит из двух разделов: планиметрии и стереометрии. Какая геометрическая фигура была отличительным знаком пифагорейцев? Какую форму, по мнению пифагорейцев, имела вся Вселенная? Ответ: 580 – 500 гг. до н. эры. Когда существовала Древняя Греция? Введение. Ответ: «Плоскомерие». Объяснение устройства мира пифагорейцы тесно связывали с геометрией.
Ответ: «Плоскомерие». Объяснение устройства мира пифагорейцы тесно связывали с геометрией.
«Геометрические термины» — Конус. Пирамида. Радиус и центр. Диагональ. Геометрия. Квадрат. Ромб. Куб. Трапеция. Возникновение геометрических терминов. Точка. Линия. Цилиндр. Гипотенуза и катет. Сфера. Призма. Из истории геометрических терминов.
«Что изучает геометрия» — Слово «параллельный» происходит от греческого «параллелос» — идти рядом. История геометрии. Преобразования в основном ограничивались подобием. L=(Р1+Р2)/2 L – длина окружности Р1 — периметр большого квадрата Р2 — периметр малого квадрата. Vпрям. Геометрия в Древней Греции. Муза геометрии, Лувр. Мы узнаем откуда пришла, и какой раньше была геометрия.
Всего в теме 24 презентации
Что такое угол?
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160).
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
Этот угол обозначают так: АОВ.
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.
Например, вместо «угол АОВ» пишут короче: «угол О».
Вместо слова «угол» пишут знак .
Например, AОВ, O.
На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла.
Как и все геометрические фигуры, углы сравниваются с помощью наложения.
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
Например, на рисунке 162 ABC = MNK.
Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Пишут: COP
Прямой и развернутый угол
Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164).
164).
Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165).
Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166).
Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми.
Прямым углом называют половину развернутого угла.
Чертежный треугольник
Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо:
а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА;
б) провести вдоль второй стороны треугольника луч ОВ.
В результате получим прямой угол АОВ.
Вопросы к теме
1.Что такое угол?
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Нам с вами уже известно, что любой угол делит плоскость на две части.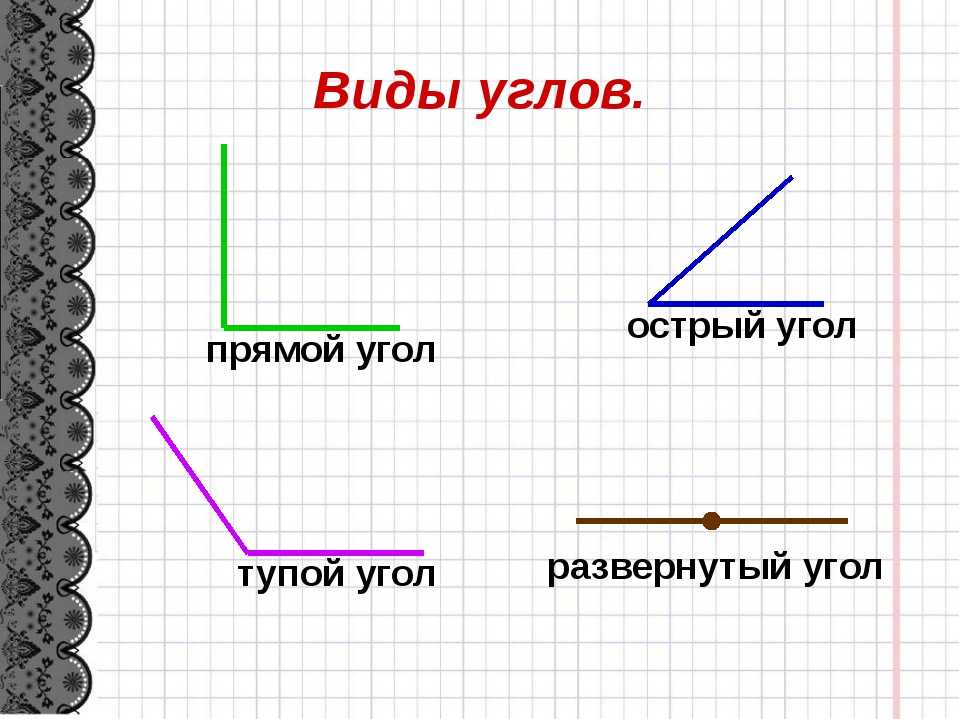 Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О.
Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных.
Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла.
А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым.
Свойства развернутого угла
Развернутый угол обладает такими свойствами:
Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую;
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.
Измерение углов
Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам.
То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид: « ° ».
Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным.
А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°.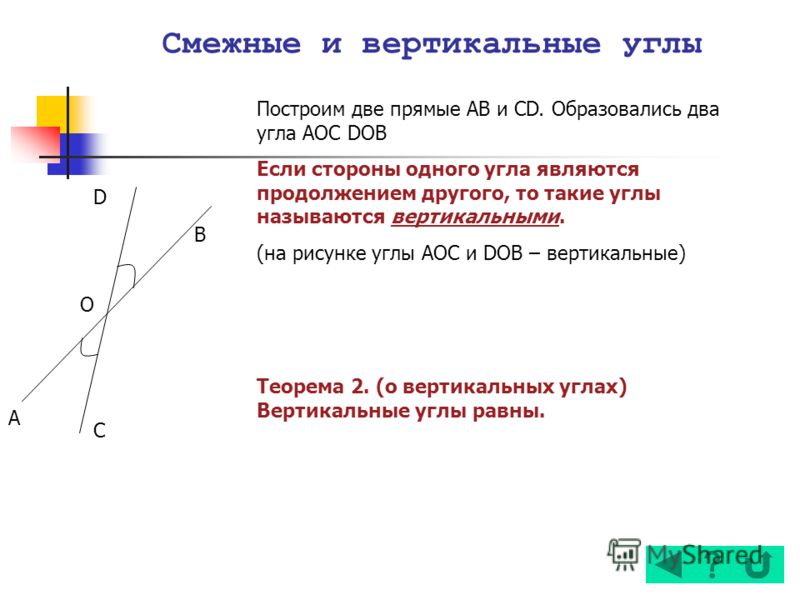 Это и есть развернутый угол.
Это и есть развернутый угол.
Практическое задание
1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения.
1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ?
1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD.
1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170).
1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях.
1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения.
1620. Укажите прямые углы в классной комнате.
а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1.
1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600?
1630. Найдите пропущенное число:
а) 2 5 3 б) 2 3 5
13 6 12 1
2 3? 42?
1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года?
1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м.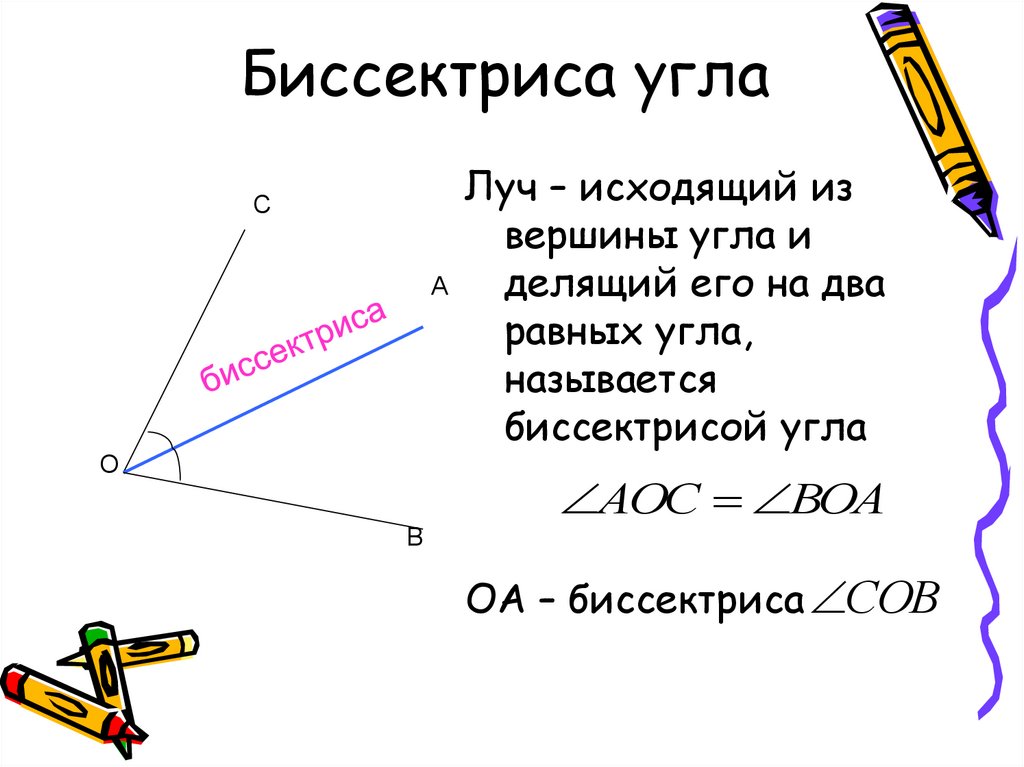 Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
1635. Найдите с помощью микрокалькулятора:
а) 4,5% от 168; в) 28,3% от 569,8;
б) 147,6% от 2500; г) 0,09% от 456 800.
1636. Решите задачу:
1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось?
1637. Выполните действия:
1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85;
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)).
1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла.
1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК?
1640. Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь.
1642. Найдите значение выражения:
а) 14,791: а + 160,961: b, если а = 100, b = 10;
б) 361,62с + 1848: d, если с = 100, d =100.
1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день?
1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке?
1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики?
1646. Найдите, сколько составляют:
а) 1% от тонны; в) 5% от 7 т;
б) 1% от литра; г) 6% от 80 км.
1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т?
1648. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения .
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым .
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.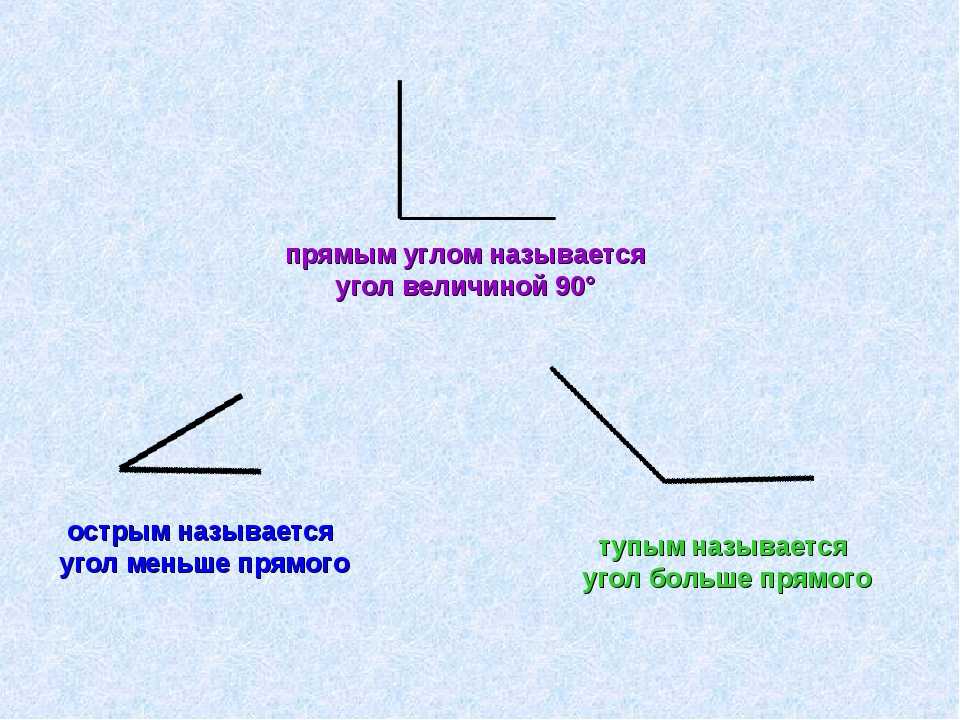
Определение 6
Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7
Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные .
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус .
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты.
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение:
1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» .
Определение 11
Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».
В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла.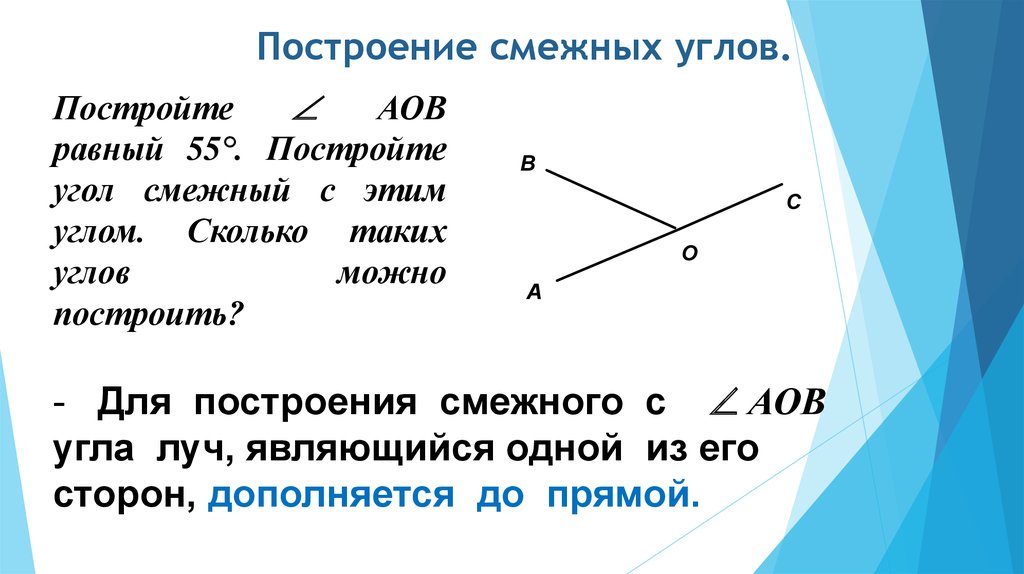 Они считаются подобными.
Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Геометрическая фигура угол — определение угла, измерение углов, обозначения и примеры. Геометрическая фигура угол: определение угла, измерение углов, обозначения и примеры Обозначение угла в ворде
В этой статье мы всесторонне разберем одну из основных геометрических фигур – угол. Начнем со вспомогательных понятий и определений, которые нас приведут к определению угла. После этого приведем принятые способы обозначения углов. Далее подробно разберемся с процессом измерения углов. В заключении покажем как можно отметить углы на чертеже. Все теорию мы снабдили необходимыми чертежами и графическими иллюстрациями для лучшего запоминания материала.
Навигация по странице.
Определение угла.
Угол является одной из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур как точка, прямая и плоскость. Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и .
Итак, будем отталкиваться от понятий точки, прямой на плоскости и плоскости.
Дадим сначала определение луча.
Пусть нам дана некоторая прямая на плоскости. Обозначим ее буквой a . Пусть O – некоторая точка прямой a . Точка O разделяет прямую a на две части. Каждая из этих частей вместе с точкой О называется лучом , а точка О называется началом луча . Еще можно услышать, что луч называют полупрямой .
Для краткости и удобства ввели следующие обозначения для лучей: луч обозначают либо малой латинской буквой (например, луч p
или луч k
), либо двумя большими латинскими буквами, первая из которых соответствует началу луча, а вторая обозначает некоторую точку этого луча (например, луч ОА
или луч СD
). Покажем изображение и обозначение лучей на чертеже.
Покажем изображение и обозначение лучей на чертеже.
Теперь мы можем дать первое определение угла.
Определение.
Угол – это плоская геометрическая фигура (то есть целиком лежащая в некоторой плоскости), которую составляют два несовпадающих луча с общим началом. Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла .
Возможен случай, когда стороны угла составляют прямую линию. Такой угол имеет свое название.
Определение.
Если обе стороны угла лежат на одной прямой, то такой угол называется развернутым .
Предлагаем Вашему вниманию графическую иллюстрацию развернутого угла.
Для обозначения угла используют значок угла «». Если стороны угла обозначены малыми латинскими буквами (например, одна сторона угла k
, а другая h
), то для обозначения этого угла после значка угла записывают подряд буквы, соответствующие сторонам, причем порядок записи значения не имеет (то есть, или ). Если стороны угла обозначены двумя большими латинскими буквами (к примеру, одна сторона угла OA
, а вторая сторона угла OB
), то угол обозначают следующим образом: после значка угла записывают три буквы, участвующие в обозначении сторон угла, причем буква, отвечающая вершине угла, располагается посередине (в нашем случае угол будет обозначен как или ). Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла , а другую – внешней областью угла . Следующее изображение разъясняет, какая часть плоскости отвечает внутренней области угла, а какая — внешней.
Любую из двух частей, на которые развернутый угол разделяет плоскость, можно считать внутренней областью развернутого угла.
Определение внутренней области угла приводит нас ко второму определению угла.
Определение.
Угол – это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла.
Следует отметить, что второе определение угла строже первого, так как содержит больше условий. Однако не следует отметать первое определение угла, также не следует рассматривать первое и второе определения угла по отдельности. Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Дадим еще определения смежных и вертикальных углов.
Определение.
Смежные углы – это два угла, у которых одна сторона общая, а две другие образуют развернутый угол.
Из определения следует, что смежные углы дополняют друг друга до развернутого угла.
Определение.
Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого.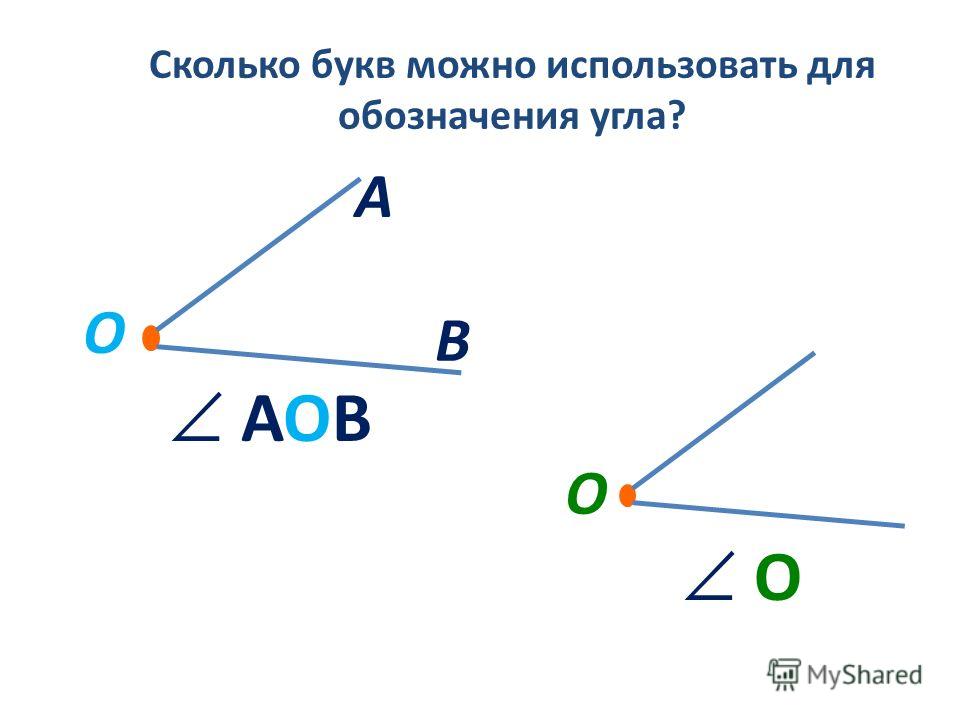
На рисунке изображены вертикальные углы.
Очевидно, что две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов.
Сравнение углов.
В этом пункте статьи мы разберемся с определениями равных и неравных углов, а также в случае неравных углов разъясним, какой угол считается большим, а какой меньшим.
Напомним, что две геометрические фигуры называются равными, если их можно совместить наложением.
Пусть нам даны два угла. Приведем рассуждения, которые помогут нам получить ответ на вопрос: «Равны эти два угла или нет»?
Очевидно, что мы всегда можем совместить вершины двух углов, а также одну сторону первого угла с любой из сторон второго угла. Совместим сторону первого угла с той стороной второго угла, чтобы оставшиеся стороны углов оказались по одну сторону от прямой, на которой лежат совмещенные стороны углов. Тогда, если две другие стороны углов совместятся, то углы называются равными .
Если же две другие стороны углов не совместятся, то углы называются неравными , причем меньшим считается тот угол, который составляет часть другого (большим является тот угол, который полностью содержит другой угол).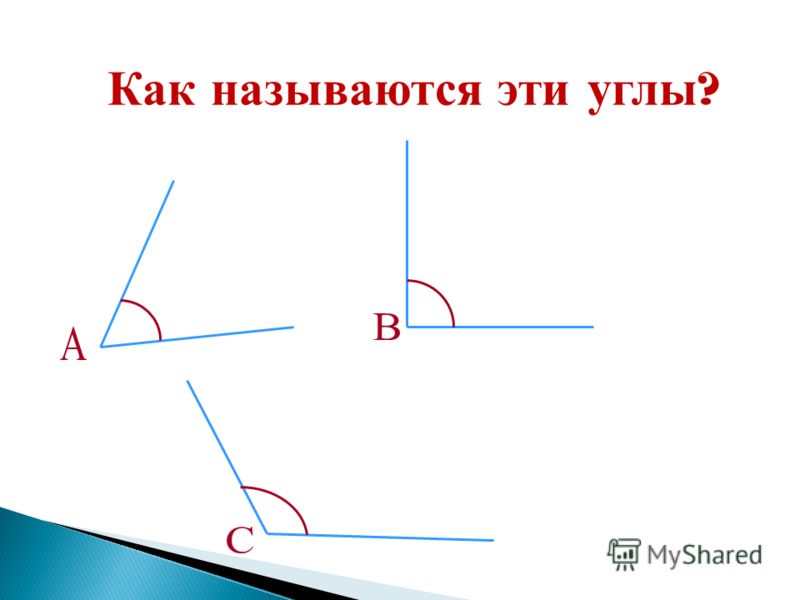
Очевидно, что два развернутых угла равны. Также очевидно, что развернутый угол больше любого неразвернутого угла.
Измерение углов.
Измерение углов основывается на сравнении измеряемого угла с углом, взятым в качестве единицы измерения. Процесс измерения углов выглядит так: начиная от одной из сторон измеряемого угла, его внутреннюю область последовательно заполняют единичными углами, плотно укладывая их один к другому. При этом запоминают количество уложенных углов, которое и дает меру измеряемого угла.
Фактически, в качестве единицы измерения углов может быть принят любой угол. Однако существует множество общепринятых единиц измерения углов, относящихся к различным областям науки и техники, они получили специальные названия.
Одной из единиц измерения углов является градус .
Определение.
Один градус – это угол, равный одной сто восьмидесятой части развернутого угла.
Градус обозначают символом «», следовательно, один градус обозначается как .
Таким образом, в развернутом угле мы можем уложить 180 углов в один градус. Это будет выглядеть как половинка круглого пирога, разрезанная на 180 равных кусочков. Очень важно: «кусочки пирога» плотно укладываются один к другому (то есть, стороны углов совмещаются), причем сторона первого угла совмещается с одной стороной развернутого угла, а сторона последнего единичного угла совпадет с другой стороной развернутого угла.
При измерении углов выясняют, сколько раз градус (или другая единица измерения углов) укладывается в измеряемом угле до полного покрытия внутренней области измеряемого угла. Как мы уже убедились, в развернутом угле градус укладывается ровно 180 раз. Ниже приведены примеры углов, в которых угол в один градус укладывается ровно 30 раз (такой угол составляет шестую часть развернутого угла) и ровно 90 раз (половина развернутого угла).
Для измерения углов, меньших одного градуса (или другой единицы измерения углов) и в случаях, когда угол не удается измерить целым числом градусов (взятых единиц измерения), приходится использовать части градуса (части взятых единиц измерения). Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определение.
Минута – это одна шестидесятая часть градуса.
Определение.
Секунда – это одна шестидесятая часть минуты.
Иными словами, в минуте содержится шестьдесят секунд, а в градусе – шестьдесят минут (3600 секунд). Для обозначения минут используют символ «», а для обозначения секунд – символ «» (не путайте со знаками производной и второй производной). Тогда при введенных определениях и обозначениях имеем , а угол, в котором укладываются 17 градусов 3 минуты и 59 секунд, можно обозначить как .
Определение.
Градусной мерой угла называется положительное число, которое показывает сколько раз градус и его части укладываются в данном угле.
Например, градусная мера развернутого угла равна ста восьмидесяти, а градусная мера угла равна .
Для измерения углов существуют специальные измерительные приборы, наиболее известным из них является транспортир.
Если известно и обозначение угла (к примеру, ) и его градусная мера (пусть 110 ), то используют краткую запись вида и говорят: «Угол АОВ равен ста десяти градусам».
Из определений угла и градусной меры угла следует, что в геометрии мера угла в градусах выражается действительным числом из интервала (0, 180] (в тригонометрии рассматривают углы с произвольной градусной мерой, их называют ). Угол в девяносто градусов имеет специальное название, его называют прямым углом . Угол меньший 90 градусов называется острым углом . Угол больший девяноста градусов называется тупым углом . Итак, мера острого угла в градусах выражается числом из интервала (0, 90) , мера тупого угла – числом из интервала (90, 180) , прямой угол равен девяноста градусам. Приведем иллюстрации острого угла, тупого угла и прямого угла.
Из принципа измерения углов следует, что градусные меры равных углов одинаковы, градусная мера большего угла больше градусной меры меньшего, а градусная мера угла, который составляют несколько углов, равна сумме градусных мер составляющих углов. На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
Таким образом, сумма смежных углов равна ста восьмидесяти градусам , так как они составляют развернутый угол.
Из этого утверждения следует, что . Действительно, если углы АОВ и СОD – вертикальные, то углы АОВ и ВОС — смежные и углы СОD и ВОС также смежные, поэтому, справедливы равенства и , откуда следует равенство .
Наряду с градусом удобна единица измерения углов, называемая радианом . Радианная мера широко используется в тригонометрии. Дадим определение радиана.
Определение.
Угол в один радиан – это центральный угол , которому соответствует длина дуги, равная длине радиуса соответствующей окружности.
Дадим графическую иллюстрацию угла в один радиан. На чертеже длина радиуса OA (как и радиуса OB ) равна длине дуги AB , поэтому, по определению угол AOB равен одному радиану.
Для обозначения радианов используют сокращение «рад». Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Стоит отдельно отметить, что величина угла, выраженная в радианах, не зависит от длины радиуса окружности. Это связано с тем, что фигуры, ограниченные данным углом и дугой окружности с центром в вершине данного угла, подобны между собой.
Измерение углов в радианах можно выполнять так же, как и измерение углов в градусах: выяснить, сколько раз угол в один радиан (и его части) укладываются в данном угле. А можно вычислить длину дуги соответствующего центрального угла, после чего разделить ее на длину радиуса.
Для нужд практики полезно знать, как соотносятся между собой градусная и радианная меры, так как довольно часть приходится осуществлять . В указанной статье установлена связь между градусной и радианной мерой угла, и приведены примеры перевода градусов в радианы и обратно.
Обозначение углов на чертеже.

На чертежах для удобства и наглядности углы можно отмечать дугами, которые принято проводить во внутренней области угла от одной стороны угла до другой. Равные углы отмечают одинаковым количеством дуг, неравные углы – различным количеством дуг. Прямые углы на чертеже обозначают символом вида «», который изображают во внутренней области прямого угла от одной стороны угла до другой.
Если на чертеже приходится отмечать много различных углов (обычно больше трех), то при обозначении углов кроме обычных дуг допустимо использование дуг какого-либо специального вида. К примеру, можно изобразить зубчатые дуги, или нечто подобное.
Следует отметить, что не стоит увлекаться с обозначением углов на чертежах и не загромождать рисунки. Рекомендуем обозначать только те углы, которые необходимы в процессе решения или доказательства.
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.

- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
Если в документах Microsoft Word Вам приходиться работать не только с текстом, но иногда необходимо показать элементарные расчеты, или вставить в текст определенный символ, тогда не найдя его на клавиатуре, Вы зададитесь вопросом: как добавить его в документ?
Сделать это довольно просто, поскольку в текстовом редакторе Ворд есть специальная таблица, в которой Вы точно найдете все необходимое. В данной статье мы с Вами рассмотрим, как, используя ее, можно вставить в документ Ворд примерно равно.
Установите курсор в том месте документа, куда будете его добавлять. Затем перейдите на вкладку «Вставка» и в группе «Символы» нажмите на одноименную кнопку. В выпадающем списке выберите пункт «Другие» .
Откроется вот такое окно. В нем в поле «Шрифт»
выберите «(обычный текст)»
, в поле «Набор»
– «математические операторы»
.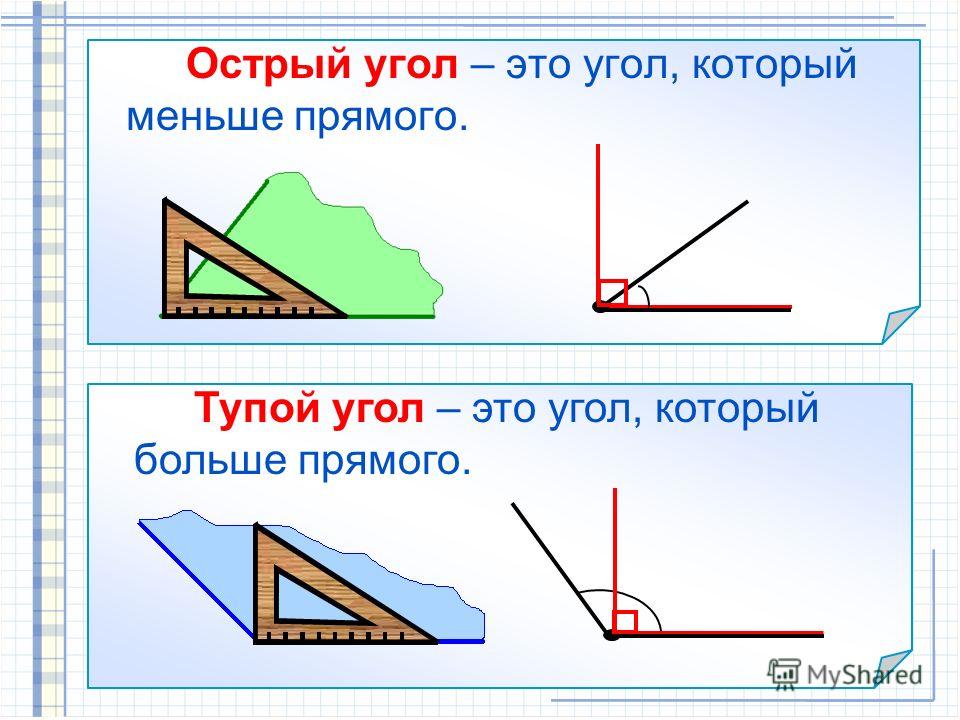 Дальше найдите в списке то, что нужно, кликните по нему и затем нажмите кнопку «Вставить»
.
Дальше найдите в списке то, что нужно, кликните по нему и затем нажмите кнопку «Вставить»
.
После того, как значок будет добавлен в документ, закройте данное окно, нажав на соответствующую кнопку в правом нижнем углу.
Если Вам часто приходится добавлять в документ различные знаки, которые напечатать напрямую с клавиатуры не получится, и приходится искать их в упомянутой таблице, тогда можете воспользоваться горячими клавишами, для вставки подходящего знака в документ.
Найдите символ в списке и кликните по нему мышкой. Затем внизу в поле «Сочетание клавиш» посмотрите, какая комбинация для него используется.
В нашем случае, это «2248, Alt+X» . Сначала наберите число «2248» , а потом нажмите «Alt+X» .
Замечу, что не для всех знаков есть сочетания, но его можно назначить самостоятельно, кликнув по кнопке «Сочетание клавиш» .
Если у Вас, как и в примере, знак приблизительно нужно поставить сразу после какой-нибудь цифры, то сочетание получится другое. В примере получилось «32248»
.
В примере получилось «32248»
.
Поэтому, после того, как Вы нажмете «Alt+X» , может вставится не то, что Вы хотите.
Для того чтобы добавить именно приблизительно-равно, поставьте пробел после той цифры, где он должен стоять и наберите сочетание «2248» . Затем нажимайте «Alt+X» .
Символ будет вставлен. Теперь можно поставить курсив перед добавленным знаком и нажать «Backspace» , чтобы удалить пробел.
Вот так, используя один из способов, можно поставить значок приблизительно равно в документ Ворд.
Оценить статью:
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения .
Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения .
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым .
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A .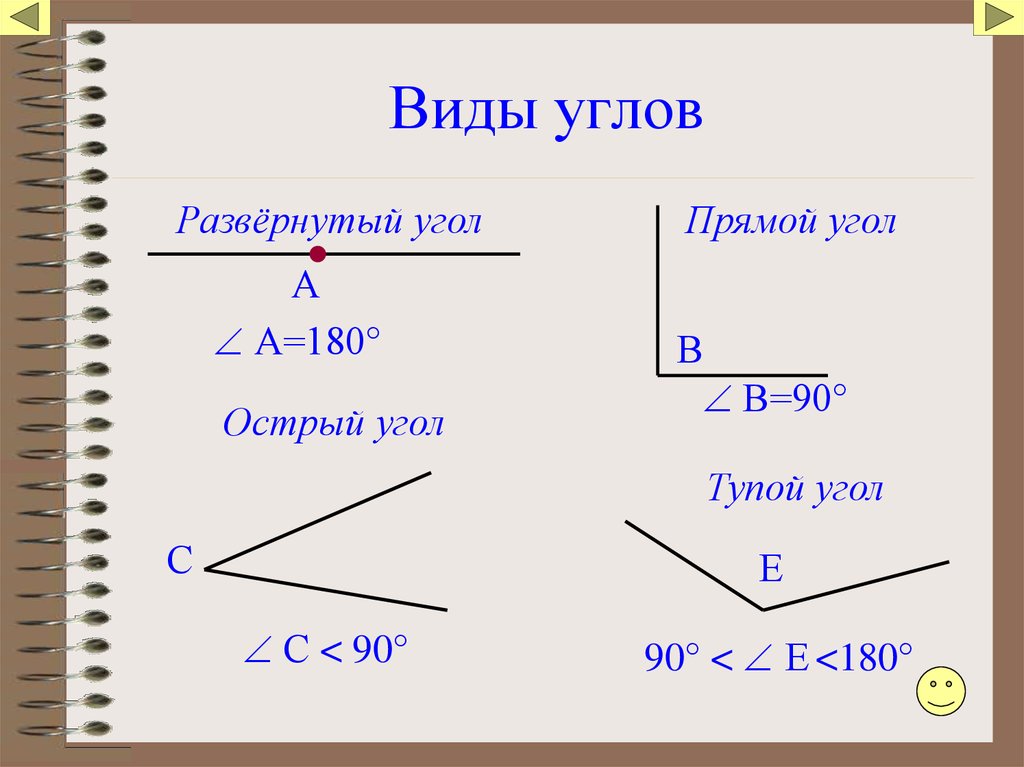 Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение 6
Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7
Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают.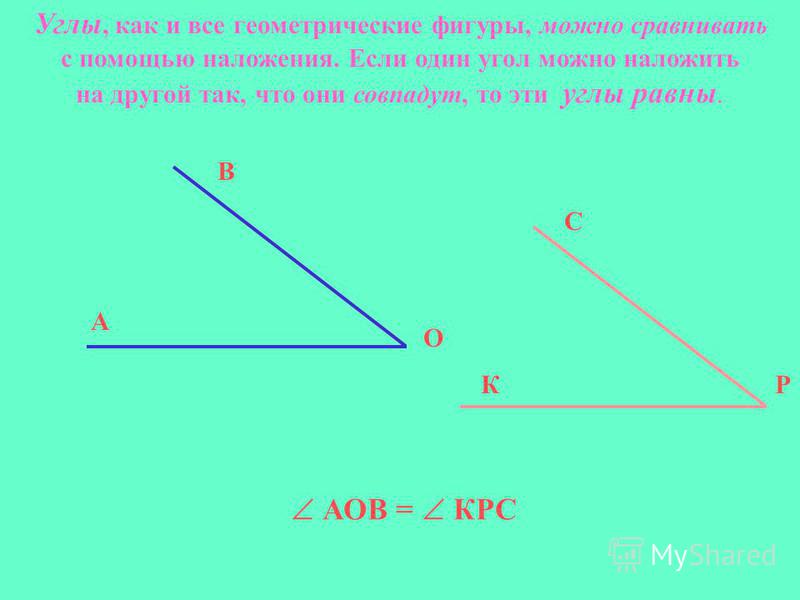 Такое же свойство применимо для сравнения углов.
Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные .
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Они специализируются на других названиях.
Чаще всего используют понятие градус .
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты.
Определение 9
Минутой называют одну шестидесятую часть градуса.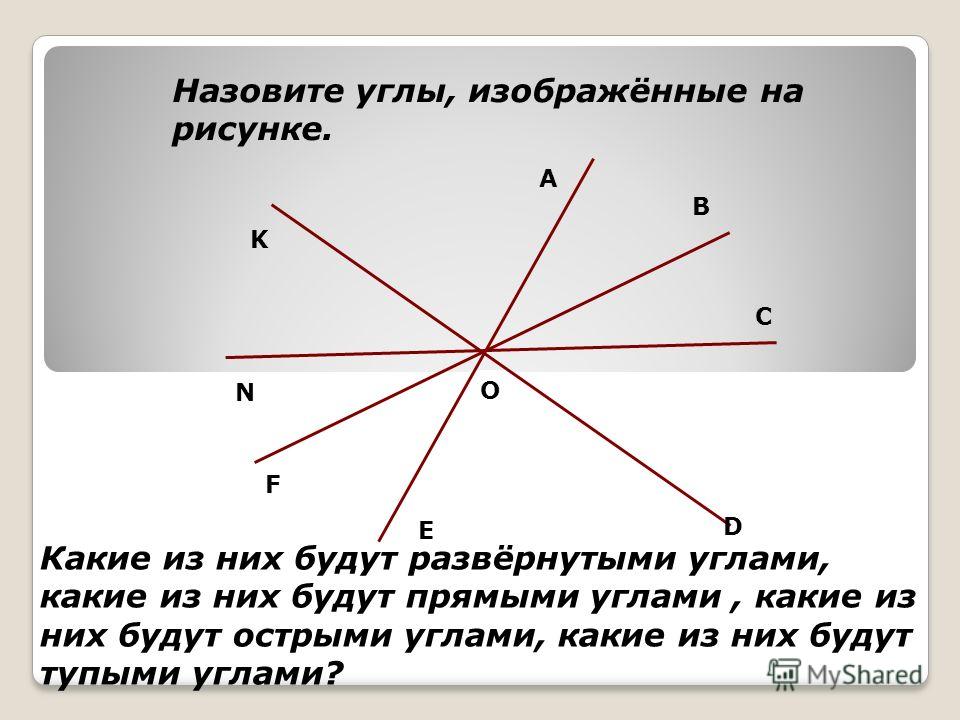
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение:
1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» .
Определение 11
Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».
В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Очень часто слышу вопрос «Как получитьсимвол галочки в Ворде?» Ответы — один мудренее другого! Проще всего нажать клавишу Альт и, не отпуская её, набрать на боковой цифровой клавиатуре число 10003. Можно так же набрать число 2713 и потом нажать Альт икс. Просто оба эти числа равны между собой: 10003 (десятичное) = 2713 (шестнадцатиричное).
Когда много работаешь в программах Ворд и Ексель, начинаешь понимать, что бросать клавиатуру, хвататься за мышь, а потом снова переходить к «клаве» — неудобно, неэргономично, не… — продолжите сами. Наверное для этого и придуманы разные сочетания кнопок, «горячие» клавиши и т.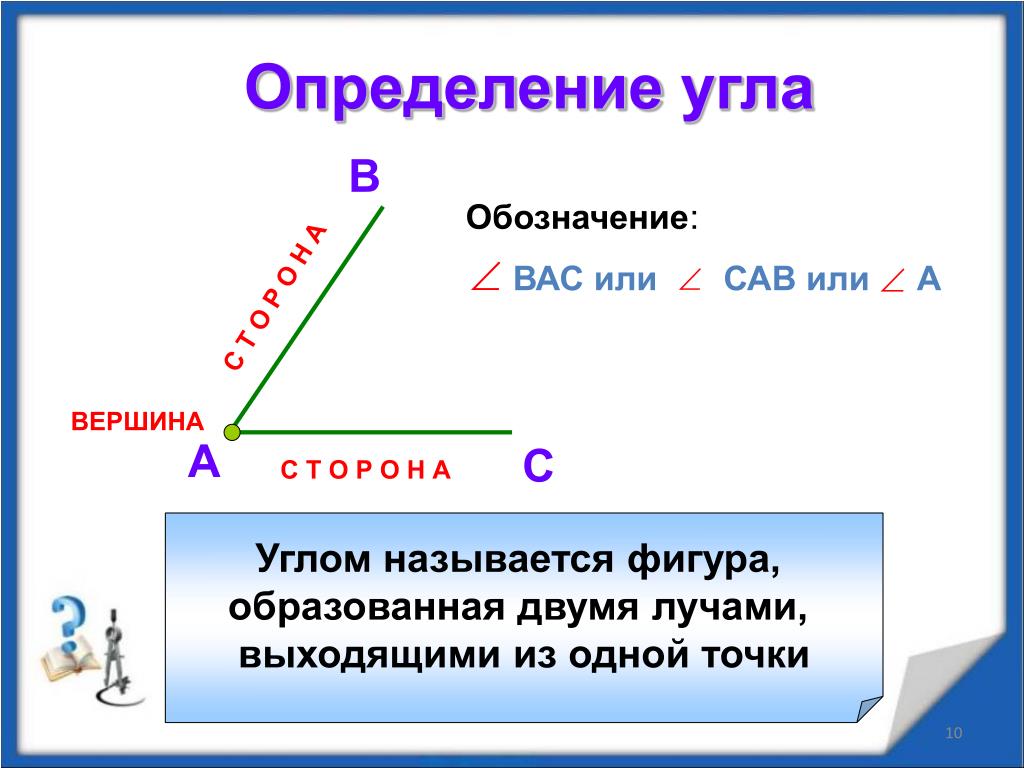 п. В этом плане мне очень нравится функциональная клавиша F4, нажатие на которую повторяет любое действие, которое только что выполнялось. Например, вам надо 8 слов в разных местах текста выделить полужирным шрифтом. Первое слово вы можете сделать сделать «жирным» щелкнув по букве » ж » в меню или нажав одновременно две клавиши Ctrl и b (русская буква и). Для остальных слов достаточно правой рукой щелкнуть мышью по любому месту в нужном слове, а левой рукой нажать клавишу F4. «И так сэм раз».
п. В этом плане мне очень нравится функциональная клавиша F4, нажатие на которую повторяет любое действие, которое только что выполнялось. Например, вам надо 8 слов в разных местах текста выделить полужирным шрифтом. Первое слово вы можете сделать сделать «жирным» щелкнув по букве » ж » в меню или нажав одновременно две клавиши Ctrl и b (русская буква и). Для остальных слов достаточно правой рукой щелкнуть мышью по любому месту в нужном слове, а левой рукой нажать клавишу F4. «И так сэм раз».
Многие вздрагивают при слове «макрос», а между тем в них нет ничего страшного и опасного. Вообще, макросы — это очень полезная вещь! Создать макрос в Ворде — проще простого. Допустим, вам часто требуется при наборе текста вставлять название организации: ООО «Рога и Копыта» . Или печатать в конце документа: Исполнитель — Вася Пупкин . Рассмотрим, как набрать первый текст нажатием всего двух клавиш, а второй — одним нажатием на кнопку с любым рисунком, созданную на панели быстрого доступа.
Итак, давайте попробуем: открываем Ворд и выбираем «Сервис-Макросы» или «Вид-Макросы» (в зависимости от того 2003-й или 2007-й) и жмем «Запись макроса…». В появившемся окне можно придумать название макросу и сделать его описание, но можно оставить предложенное по умолчанию название «Макрос1» и ничего не описывать — кому как нравится. Но нажать на значок с изображением клавиатуры или молотка надо обязательно. В первом случае вам будет предложено придумать любое сочетание клавиш, а во втором — кнопку на панели. Для первого текста выбираем сочетание Ctrl+P (что бы легче вспомнить, берем первую букву Рогов), затем нажимаем «Назначить» и «Закрыть». Окно при этом исчезает, а рядом с курсором появляется пиктограмма магнитофонной кассеты, это означает, что «все ходы записываются». В 2003-м Ворде при этом еще появляется малюсенькая плавающая панель. В первый и последний раз (потом это за вас будет делать компьютер) набираем нужный текст с названием фирмы и останавливаем запись. В старом Ворде — просто нажав квадратик на плавающей панели, а в новом — зайдя в меню «Вид-Макросы-Остановить запись». Теперь и всегда (до переустановки Офиса или удаления макроса) нажатие выбранного вами сочетания клавиш выдаст вам то, что вы набрали во время записи макроса.
Теперь и всегда (до переустановки Офиса или удаления макроса) нажатие выбранного вами сочетания клавиш выдаст вам то, что вы набрали во время записи макроса.
Если на начальной стадии вы нажмете на молоток, то в 2003-м появится окно Настройка со стандартным значком макроса, который надо, схватив мышкой, перетащить в любое место верхней панели меню, а затем, щелкнув по кнопке «Изменить выделенный объект» и по строке «Выбрать значок для кнопки» выбрать смайлик или любой понравившийся вам рисунок. Если же нажать на строку «Изменить значок на кнопке…», то откроется простенький графический редактор, в котором можно самому нарисовать значок на свой вкус.
В 2007-м похожий путь: при выборе молотка появляется Настройка панели быстрого доступа, где надо, выделив в левом окошке макрос и нажать кнопку «Добавить». После этого стандартный значок макроса с вашим названием добавится в правое окно, где его можно снова выделить и нажать кнопку «Изменить». Выбор рисунков будет побольше, чем в старом Ворде, но зато убрана возможность нарисовать свой значок и размещать его можно только на панели быстрого доступа.
Дальнейшие действия такие же, что и в 2003-м: набор нужного текста и остановка записи. Подобных макросов можно наделать сколько угодно, в результате вы получите возможность одним щелчком по вашему значку (которого, заметьте, нет ни у кого из ваших коллег!) получать нужный текст или любую последовательность операций.
Как и что надо набрать на клавиатуре, чтобы получить в текстовом документе изображение сердечка? Проще всего нажать клавишу Alt и не отпуская её нажать цифру 3 на правой части клавиатуры. Другой способ: набрать число 2665 и нажать сочетание клавиш Alt+х. Так же для получения сердечек можно набрать числа 2765, 2764 или 2661. Очень похожа на сердечко одна из букв грузинского алфавита ღ, получить которую можно набрав код 10Е5 (Е — латинское) и нажав Alt+х.
Вообще для получения любого символа достаточно набрать его
ASCII
-код и нажать
Alt+х.
Например, чтобы напечатать знак доллара «$», проще и быстрее не переходя на английский шрифт набрать число 24, а затем нажать
Alt+х.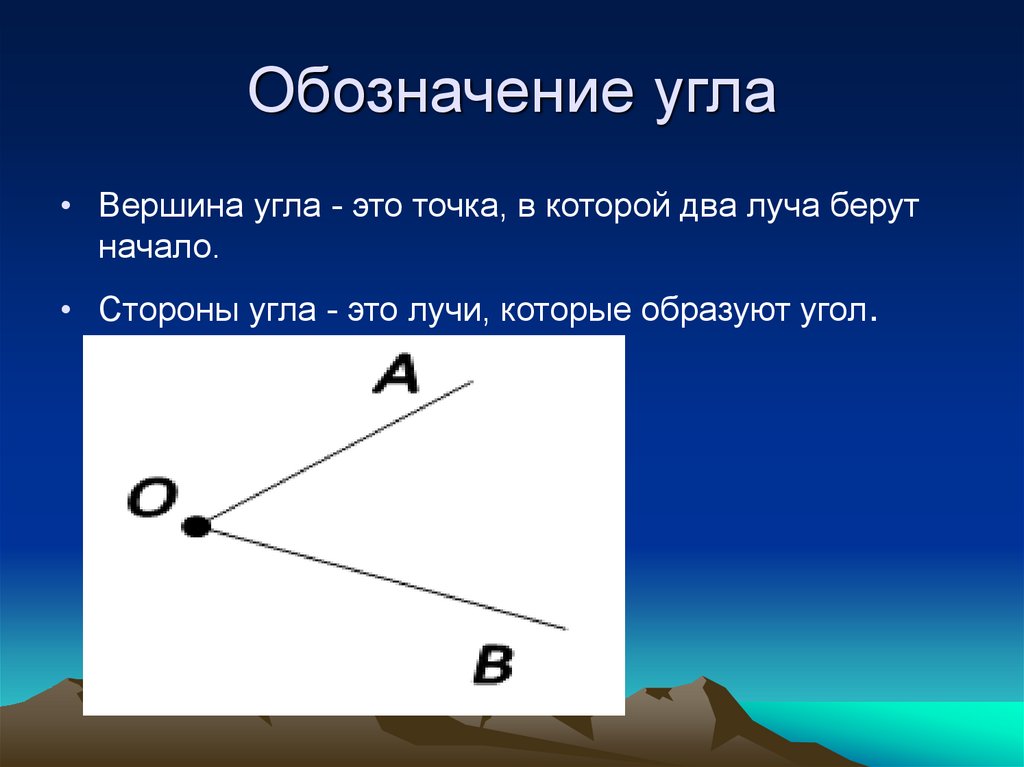 Можно быстро получить знак суммы «∑»
(код — 2211), символ угла «∠»
(код — 2220), приблизительного равенства
«
≈
»
(код — 2248), различные стрелки и т.д. Именно поэтому иногда вместо слова «собака» говорят «сорок альт икс» имея ввиду @.
Можно быстро получить знак суммы «∑»
(код — 2211), символ угла «∠»
(код — 2220), приблизительного равенства
«
≈
»
(код — 2248), различные стрелки и т.д. Именно поэтому иногда вместо слова «собака» говорят «сорок альт икс» имея ввиду @.
Вот таблица кодов некоторых символов:
Код | Символ | Код | Символ | Код | Символ | Код | Символ |
23 | # | 2020 | † | 2194 | ↔ | 2265 | ≥ |
24 | $ | 2030 | ‰ | 2195 | ↕ | 2640 | ♀ |
26 | & | 2122 | ™ | 2211 | ∑ | 2642 | ♂ |
27 | » | 2190 | ← | 2220 | 2660 | ♠ | |
40 | @ | 2191 | 2248 | ≈ | 2663 | ♣ | |
60 | ` | 2192 | → | 2260 | ≠ | 2665 | |
394 | Δ | 2193 | ↓ | 2264 | ≤ | 2666 | ♦ |
Угол — геометрическая фигура
Угол — геометрическая фигура, образованная двумя лучами.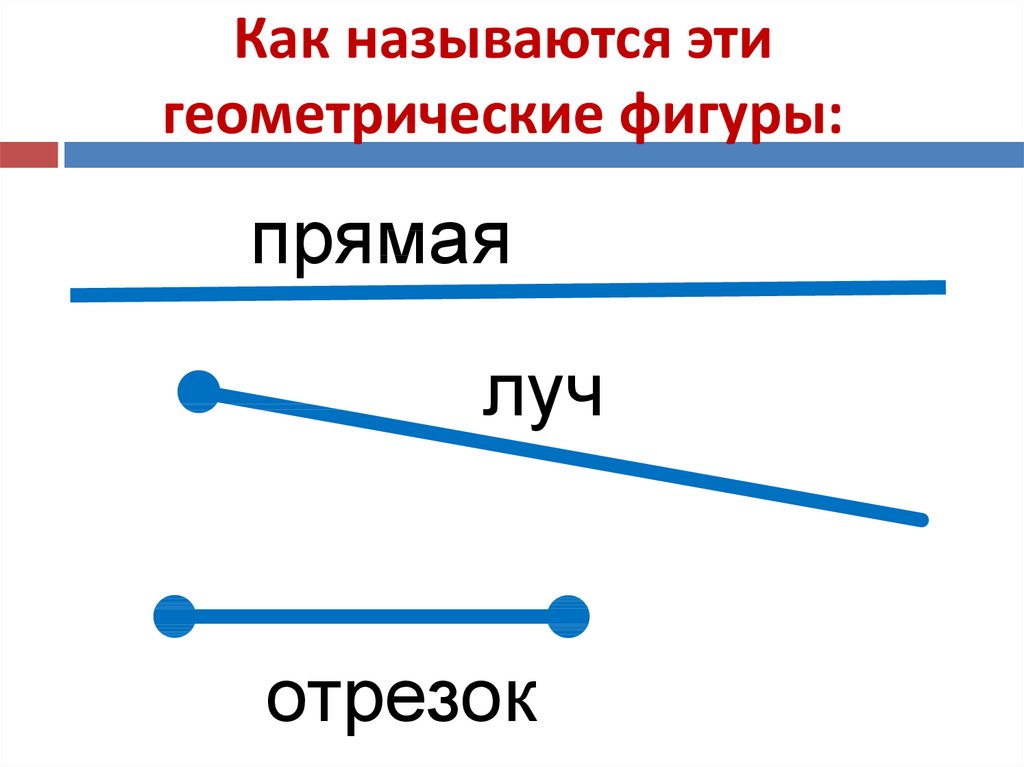 Начальная точка у них одна. Эта точка называется вершиной угла, лучи называются сторонами угла. Стороны угла делят плоскость на 2 области, их называют плоскими углами или просто углами. Меньший угол называется внутренним углом , а больший называется внешним углом .
Начальная точка у них одна. Эта точка называется вершиной угла, лучи называются сторонами угла. Стороны угла делят плоскость на 2 области, их называют плоскими углами или просто углами. Меньший угол называется внутренним углом , а больший называется внешним углом .
Углы также могут обозначаться тремя точками. Скажем, АВС . В этой записи B — вершина, а A и C — точки, лежащие на разных лучах угла. Чтобы упростить и быстро записать, углы обычно определяются с нижними греческими буквами: α — Alpha , β — Beta , γ — Гамма , θ — Theta 9004, 111111111111111111111111111111111111111111111111111111111. — fi и т.д. Угол обозначается двухстрочным символом, обозначающим угол.
На рисунке вы видите два лучей AB и AC с вершиной в точке A Сформируя два угла: α — Внутренний угол , β — Внешний.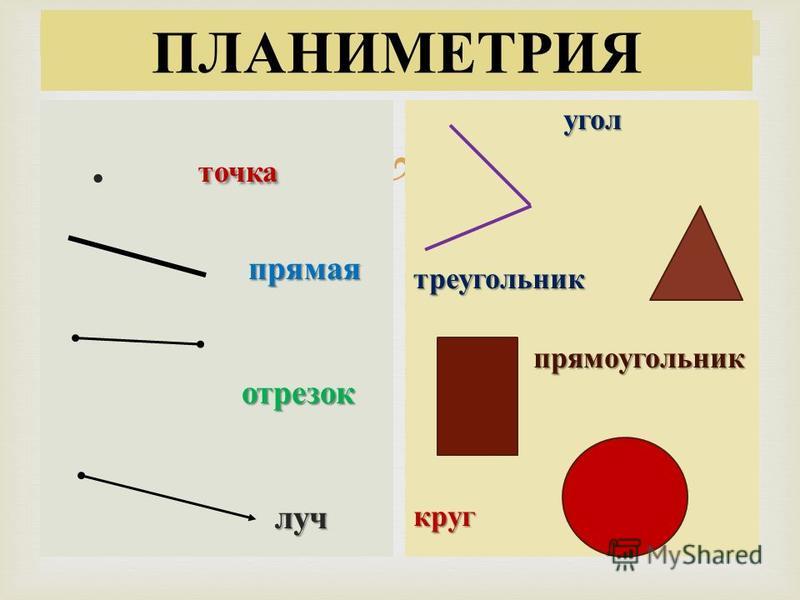 угол .
угол .
Измеритель угла
Измеритель угла позволяет сравнивать углы между собой. Это значит, что зная меру угла, мы можем сказать, что этот угол либо больше другого, либо меньше, либо они равны. Существует несколько мер углов:
- в градусах, минутах, секундах;
- в радианах;
- по очереди;
В математике более распространен первый тип меры угла — градуса , минуты , секунды . Давайте узнаем это в деталях. Посмотрите на часы, показанные ниже.
Если вы посмотрите на часы, вы увидите стрелки часов в виде лучей, начальная точка которых совпадает с центром циферблата. Полный оборот стрелки составляет 360 градусов . Степень определяется символом °. Если стрелка делает половину оборота, она перемещается на 180 градусов или 180°. Если он делает четверть, он перемещается на 90 °. На картинке ниже вы можете увидеть, какое время соответствует каждому углу, когда время меняется. Это означает, что 15:00 соответствует углу 90°, 18:00 соответствует углу 180°, 21:00 — 270° и 24:00 — 360°. Сумма внешнего и внутреннего углов всегда должна быть 360°.
Это означает, что 15:00 соответствует углу 90°, 18:00 соответствует углу 180°, 21:00 — 270° и 24:00 — 360°. Сумма внешнего и внутреннего углов всегда должна быть 360°.
Вы подробно изучите угловую меру в других разделах математики: геометрия и тригонометрия .
Типы углов
В зависимости от величины угла различают следующие типы углов:
Нулевой угол
Нулевой угол — это угол, две стороны которого совпадают. Из вершины выходят два равнонаправленных луча. Нулевой угол равен 0°.
Острый угол
Острый угол лежит от 0° до 90°, где 0 и 90 не входят в эту систему координат.
Острый угол легко запомнить. Все острые предметы имеют острый угол, как клюв птицы, шило, кухонный нож. Вы можете видеть желтую рамку на картинке, показывающую максимальную меру прямого угла.
Прямой угол
Прямой угол — это угол, перпендикулярные стороны которого равны 90°.
Прямой угол — это маленький квадрат в нижней части угла, как показано ниже.
Тупой угол
Тупой угол лежит между 90° и 180°, где 90° и 180° не включены.
Косой угол
Косой угол означает угол, отличный от 0°, 90°, 180° или 270°.
Прямой угол
Прямой угол равен 180°, его лучи направлены в противоположные стороны.
Угол выпуклости
Угол выпуклости — это угол от 0° до 180°, включая значения посадки.
Невыпуклый или вогнутый угол
Невыпуклый угол или вогнутый угол — это угол, лежащий в пределах 180° и 360°, где граничные значения не включены.
Полный угол
Полный угол — это угол с двумя совпадающими сторонами. Он противоположен нулевому углу. Полный угол равен 360°.
Нулевой и полный углы имеют одинаковые стороны.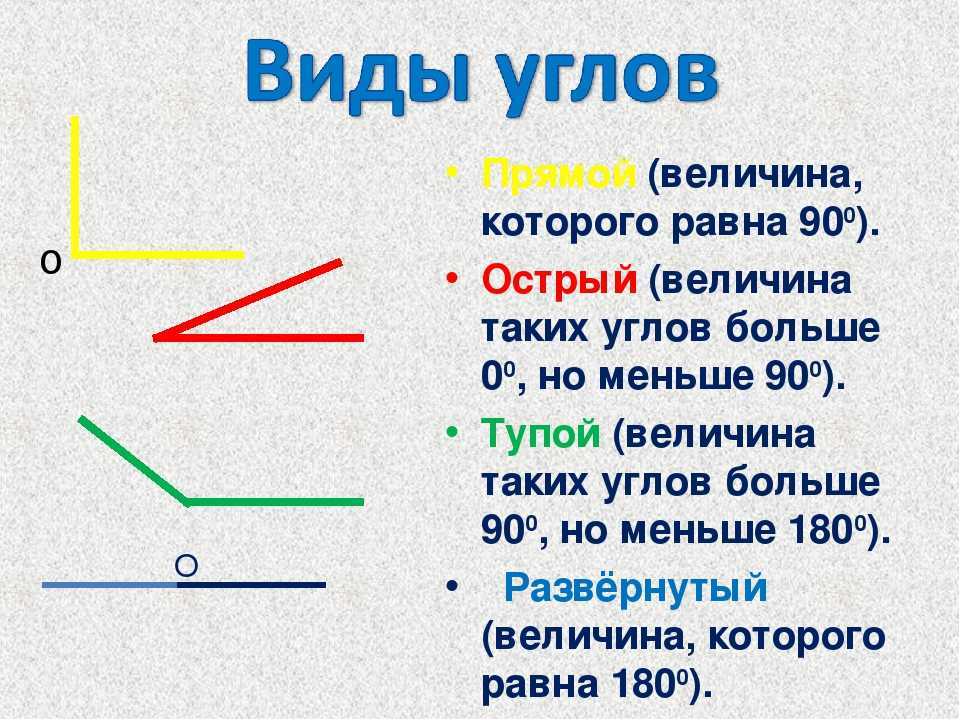 Нулевой угол — это внутренний угол, равный 0°, а полный угол — это внешний угол, равный 360°.
Нулевой угол — это внутренний угол, равный 0°, а полный угол — это внешний угол, равный 360°.
Посмотрите на картинку и посчитайте количество углов каждого типа?
- Угол нулевой — 2;
- Острый угол — 3;
- Угол прямой — 2;
- Угол тупой — 2;
- Косой угол — 6;
- Угол прямой — 1;
- Угол выпуклый — 10;
- Угол вогнутый — 1;
- Полный угол — 1;
Вам нравится этот урок?
thumb_up thumb_down
54
12
Basic Geometric Shapes
- 1.Simplest geometric shapes
- 2.Angle — geometric shape
- 3.All about geometric shape triangles
- 4. Четырехугольники
Углы и пары углов
Углы, которые они образуют, не менее важны, чем лучи и отрезки. Без них не было бы ни одной из известных вам геометрических фигур (за исключением разве что круга).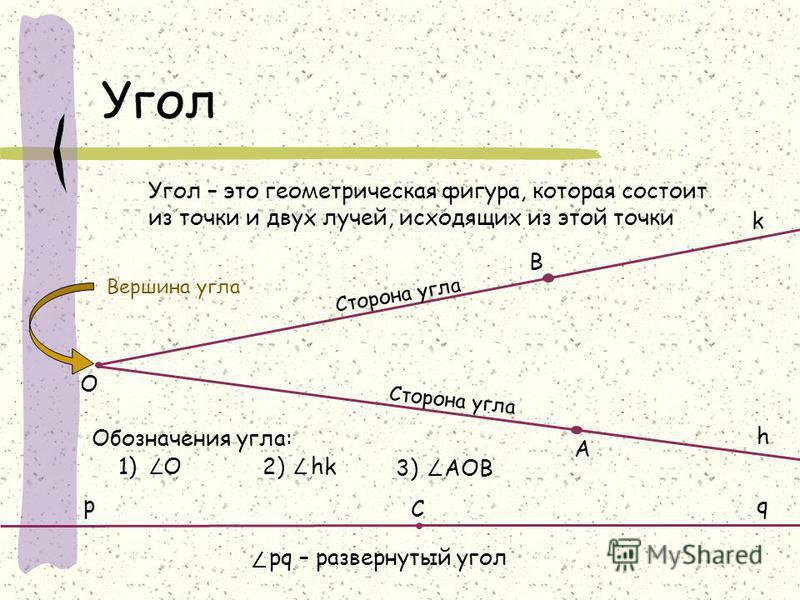
Углы
Два луча с одинаковыми концами образуют угол. Эта конечная точка называется вершиной , а лучи называются сторонами угла. В геометрии угол измеряется в градуса от 0° до 180°. Число градусов указывает величину угла. На рисунке 1 лучи АВ и АС образуют угол. — это вершина. и являются сторонами угла.
Рисунок 1 ∠BAC.Символ ∠ используется для обозначения угла. Символ м ∠ иногда используется для обозначения меры угла.
Угол может называться по-разному (рис. 2).
Рисунок 2 Различные названия одного и того же угла.
- По букве вершины — следовательно, угол на рисунке можно обозначить ∠ A .
- По цифре (или строчной букве) внутри — поэтому угол на рисунке можно обозначить как ∠1 или ∠ x .
- По буквам трех точек, которые его образуют, поэтому угол на рисунке можно назвать ∠ BAC или ∠ CAB .
 Буква центра всегда является буквой вершины.
Буква центра всегда является буквой вершины.
Пример 1: На рисунке 3(a) используйте три буквы для переименования ∠3; (b) используйте один номер для переименования ∠ KMJ .
Рисунок 3 Различные названия одного и того же угла
(a) ∠3 совпадает с ∠ IMJ или ∠ JMI;
(б) ∠ KMJ совпадает с ∠ 4 .
Постулат 9 (постулат транспортира): Предположим, что O является точкой на . Рассмотрим все лучи с конечной точкой O , лежащие по одну сторону от . Каждому лучу может быть сопоставлено ровно одно вещественное число от 0° до 180°, как показано на рис. 4. Положительная разность между двумя числами, представляющими два разных луча, является мерой угла, сторонами которого являются два луча.
Рисунок 4 Использование постулата транспортира
Пример 2: Используйте рисунок 5 , чтобы найти следующее: (a) м ∠ SON , (b) м ∠ ROT и (c) м ∠ 4 E MO.
Рисунок 5 Использование постулата о транспортире.
- (а)
м ∠ SON = 40° −0°
м ∠ SON = 40°
- (б)
м ∠ ROT = 160° −70°
м ∠ ROT = 90°
- (с)
м ∠ МОЭ = 180° −105°
м ∠ МОЭ = 75°
Постулат 10 (постулат сложения углов): Если лежит между и , то m ∠ AOB + м ∠ BOC = м ∠ AOC (рис. 6).
Рисунок 6 Сложение углов.
Пример 3: На рисунке 7, если м ∠1 = 32° и м ∠2 = 45°, найдите м ∠ NEC .
Рисунок 7 Сложение углов.
Потому что между и , по Постулат 10 ,
Биссектриса угла
Биссектриса угла — это луч, который делит угол на два равных угла.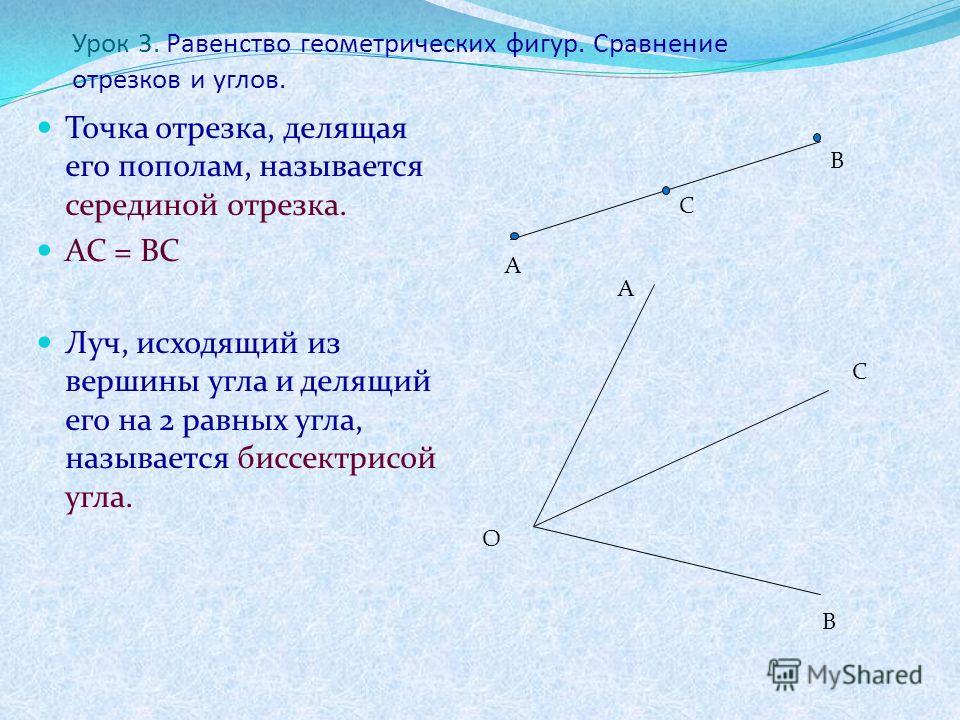 На рисунке 8 это биссектриса ∠ XOZ , потому что = м ∠ XOY = м ∠ YOZ .
На рисунке 8 это биссектриса ∠ XOZ , потому что = м ∠ XOY = м ∠ YOZ .
Теорема 5: Угол, который не является прямым, имеет ровно одну биссектрису.
Некоторым углам даются специальные названия, основанные на их размерах.
Прямой угол
А прямой угол имеет меру 90°. Символ внутри угла указывает на то, что угол образован прямым. На рисунке 9 ∠ ABC — прямой угол.
Рисунок 9 Прямой угол.Теорема 6: Все прямые углы равны.
Острый угол
Острый угол — это любой угол, градусная мера которого меньше 90°. На Рисунке 10 ∠ b означает остроту.
Рисунок 10 Острый угол.
Тупой угол
Тупой угол — это угол, градусная мера которого больше 90°, но меньше 180°. На рисунке 11 ∠4 тупой.
На рисунке 11 ∠4 тупой.
Рисунок 11 Тупой угол.
Угол прямой
В некоторых текстах по геометрии угол с мерой 180° называется прямым углом . На рисунке 12 ∠ BAC представляет собой прямой угол.
Рисунок 12 Прямой угол
Пример 4: Используйте рисунок 13, чтобы определить каждый названный угол как острый, прямой, тупой или прямой: (a) ∠ BFD , (b) ∠ AFE , (c) ∠ BFC , (d) ∠ ДФА .
Рисунок 13 Классификация уголков
- (а)
м ∠ BFD = 90° (130° − 40° = 90°), поэтому ∠ BFD — прямой угол.
- (б)
м ∠ AFE = 180 °, значит ∠ AFE прямой угол.
- (с)
м ∠ BFC = 40° (130° − 90° = 40°), поэтому ∠ BFC — острый угол.
- (г)
м ∠ DFA = 140° ( 180 ° − 40° = 140°), поэтому ∠ DFA — тупой угол.
Mathwords: Геометрическая фигура
Mathwords: Геометрическая фигура
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Что такое геометрические фигуры? Определение, типы, свойства, факты
Геометрические фигуры Определение
Геометрические фигуры — это замкнутые фигуры, созданные с использованием точек, отрезков, окружностей и кривых.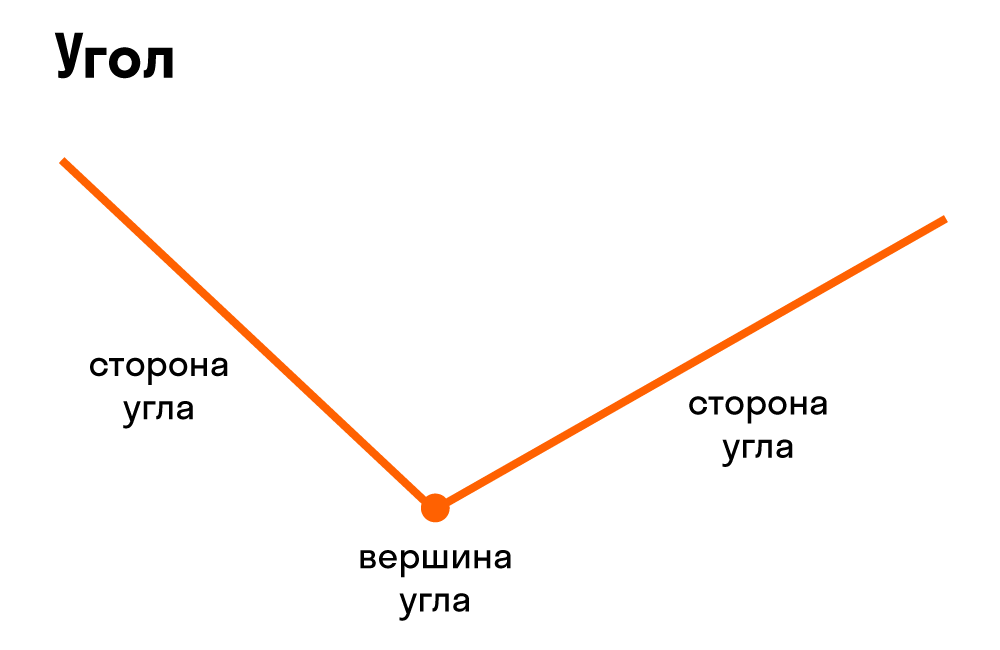 Такие формы можно увидеть повсюду вокруг нас.
Такие формы можно увидеть повсюду вокруг нас.
Примерами геометрических фигур являются круг, прямоугольник, треугольник и т. д. Пицца круглая, а ее ломтики треугольные. Точно так же двери и окна являются примерами прямоугольников.
У правильной формы все стороны равны. Например, квадрат или правильный шестиугольник. Неправильные формы имеют стороны разной величины. Например, разносторонний треугольник.
Некоторые из наиболее популярных фигур описаны ниже:
- Прямоугольник
Прямоугольник — это фигура, которая получается в результате соединения четырех разных точек четырьмя разными линиями. В прямоугольнике противоположные стороны параллельны и равны по длине. Все углы в прямоугольнике прямые. Отличие прямоугольника от квадрата в том, что в прямоугольнике два параллельных отрезка длиннее двух других, а в квадрате все отрезки имеют одинаковую длину.
Примерами прямоугольных объектов являются экраны ноутбуков, мобильные экраны и т. д.
д.
- Квадрат
Квадрат — это четырехсторонняя геометрическая фигура, образованная соединением четырех отрезков прямой равной длины. Подобно прямоугольнику, отрезки, образующие квадрат, лежат под прямым углом друг к другу. Примерами квадратных объектов являются кубик Рубика, игральные кости, шахматные доски и т. д.
- Круг
Круг — это геометрическая фигура, состоящая из прямых линий. Можно считать, что окружность составлена из бесчисленных точек, расположенных на одинаковом расстоянии от центральной точки.
Примерами круглых объектов являются целые пиццы и колеса.
- Треугольник
Треугольник состоит из трех соединенных отрезков. Это сложная геометрическая фигура, поскольку она может иметь переменные углы и размеры.
Примерами треугольных объектов являются кусочки пиццы, начос, праздничные шапочки и т. д.
Примечательно, что название треугольника меняется в зависимости от его углов и размера сторон. Например, когда два отрезка треугольника образуют прямой угол, такой треугольник называется прямоугольным. Вот как это выглядит:
Любой треугольник с углами меньше 90 градусов называется остроугольным. Точно так же треугольник с одним углом больше 90 градусов называется тупоугольным треугольником. В равноугольном треугольнике все внутренние углы равны 60 градусов, а все стороны равны по длине. Обратитесь к диаграмме ниже, чтобы лучше понять.
Применение геометрических фигур в реальной жизни
Геометрия — это изучение формы и пространства. Это помогает нам понять другие математические концепции, а также приложения в реальной жизни. Геометрию можно использовать для проектирования зданий, мостов, автомобилей и даже одежды. Принципы геометрии также используются в других разделах математики, таких как тригонометрия и исчисление.
Ниже приведены некоторые из реальных применений:
Квадраты: Квадраты можно найти в природе, например, кристаллы квадратной формы. Квадраты также используются в искусстве. Ярким примером является известная картина Пита Мондриана «Композиция с красным, синим и желтым».
Квадраты также используются в искусстве. Ярким примером является известная картина Пита Мондриана «Композиция с красным, синим и желтым».
Прямоугольники: Многие искусственные объекты, такие как телевизоры, книги и компьютерные мониторы, имеют прямоугольную форму. Есть много реальных примеров прямоугольников, таких как банкноты, сотовые телефоны и обложки книг.
Круги: Круги можно увидеть повсюду вокруг нас, от пиццы, которую мы едим, до циферблата часов.
Треугольники: Треугольники можно найти во многих местах. Большинство крыш имеют треугольную форму, называемую фронтонами. Треугольники могут помочь поддерживать такие конструкции, как мосты и здания. Есть даже некоторые чипы, которые имеют форму треугольников.
Овалы/эллипсы: Овал или эллипс представляет собой вытянутый круг (яйцевидной формы), длина которого больше ширины.
Примеры трехмерных фигур
Трехмерные фигуры представляют собой группу вершин, линии, соединяющие вершины, и грани, заключенные в эти линии.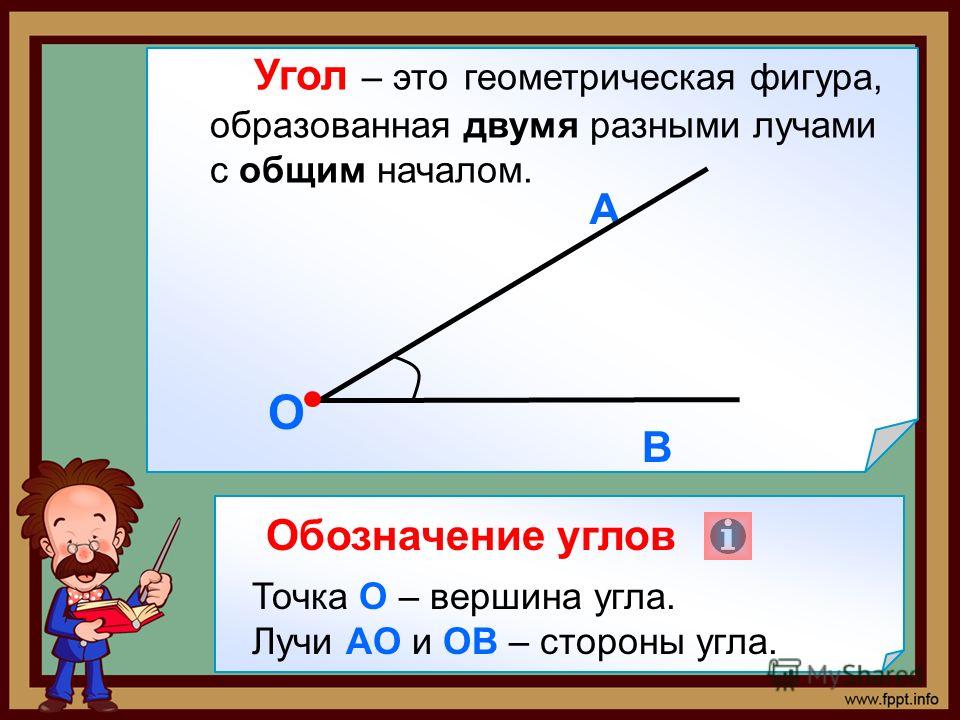 Они имеют длину, ширину и высоту и занимают некоторый объем. Для многих трехмерных фигур грани двумерны. Кроме того, некоторые фигуры в трех измерениях имеют криволинейные поверхности.
Они имеют длину, ширину и высоту и занимают некоторый объем. Для многих трехмерных фигур грани двумерны. Кроме того, некоторые фигуры в трех измерениях имеют криволинейные поверхности.
В трех измерениях основными фигурами являются:
- Кубик: Кубик Рубика, кубик сахара
- Конус: Конус для мороженого, пирамидка
- Кубовид: Деревянная прямоугольная коробка, спичечный коробок
- Цилиндр: Рулон туалетной бумаги; банка газировки
- Сфера: Футбол, Баскетбол
Решаемые примеры
Пример 1. Сколько сторон у десятиугольника?
Решение : У десятиугольника десять сторон и десять вершин.
Пример 2: Как называется треугольник, у которого только две равные стороны?
Решение : Треугольник, у которого только две равные стороны, называется равнобедренным.
Пример 3: конус имеет двумерную или трехмерную форму?
Решение : Конус представляет собой трехмерную фигуру.
Практические задачи
Две равные стороны
Четыре равные стороны
Четыре неравные стороны
Ни одна из этих
Правильный ответ: Четыре равные стороны
Квадрат в геометрии — это плоская фигура, имеющая четыре равные стороны и четыре прямых угла.
радиус
кривая
диаметр
хорда
Правильный ответ: радиус
Расстояние от центра круга до его внешней границы называется радиусом круга. Диаметр круга всегда вдвое больше его радиуса.
одномерная фигура
трехмерная фигура
двумерная фигура
Ничего из перечисленного
Правильный ответ: трехмерная фигура
Куб – это трехмерная фигура. У него шесть граней, восемь вершин и двенадцать ребер. Каждая грань куба представляет собой квадрат, и все ребра имеют одинаковую длину.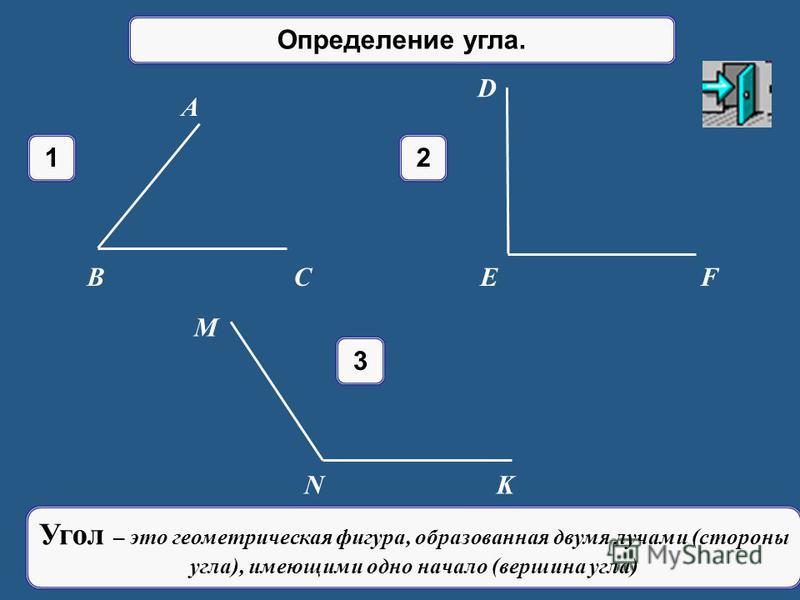 У куба шесть квадратных граней.
У куба шесть квадратных граней.
открытая форма
неправильная форма
правильная форма
замкнутая кривая
Правильный ответ: правильная форма
Стороны равностороннего треугольника имеют одинаковую длину. Итак, равносторонний треугольник – это правильная фигура.
Заключение
Геометрические фигуры являются частью нашей повседневной жизни. Учащимся они помогают заложить основу для более сложных понятий, таких как пространственные отношения.
Часто задаваемые вопросы
Основные геометрические фигуры?
Основными геометрическими формами являются круг, квадрат, прямоугольник, треугольник и т. д. Эти формы могут быть расположены в различных комбинациях.
Как образуются геометрические фигуры?
Геометрические фигуры формируются с помощью линий, точек или кривых. Мы должны помнить, что эти формы должны соответствовать математическому определению. Если форму нельзя определить математически, она не является геометрической.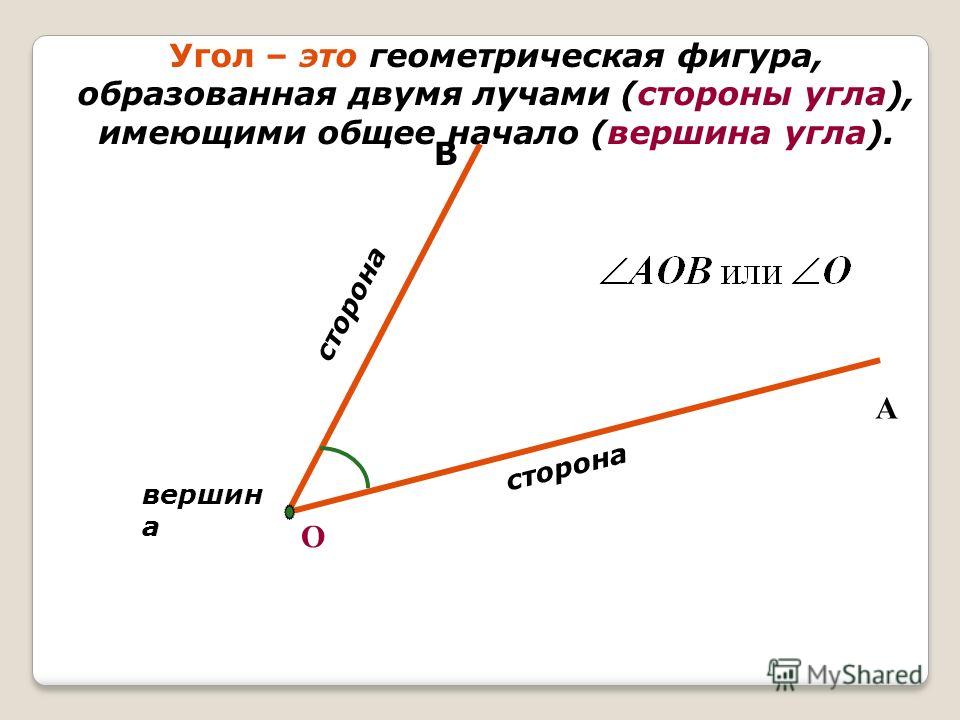
Какие примеры фигур не являются геометрическими?
В природе можно найти негеометрические формы. Например, галька, реки и т. д.
Как определить многоугольник?
Многоугольник — это фигура, состоящая из прямых линий без кривых. У него нет открытых сторон. «Многоугольник» — это широкий термин, обозначающий различные формы, такие как квадраты, треугольники и прямоугольники.
Геометрические фигуры — определение, список, типы, свойства
Любой объект вокруг нас с фиксированной структурой можно считать геометрической формой. Эти формы состоят из линий, кривых, углов и поверхностей. Некоторыми из известных геометрических фигур являются квадрат, прямоугольник, круг, цилиндр и т. д. Многоугольник — это геометрическая форма с 3 или более сторонами. Некоторые из распространенных многоугольников — треугольник, квадрат, ромб, трапеция и т. д.
В этой статье мы рассмотрим различные двухмерные и трехмерные геометрические фигуры и их свойства.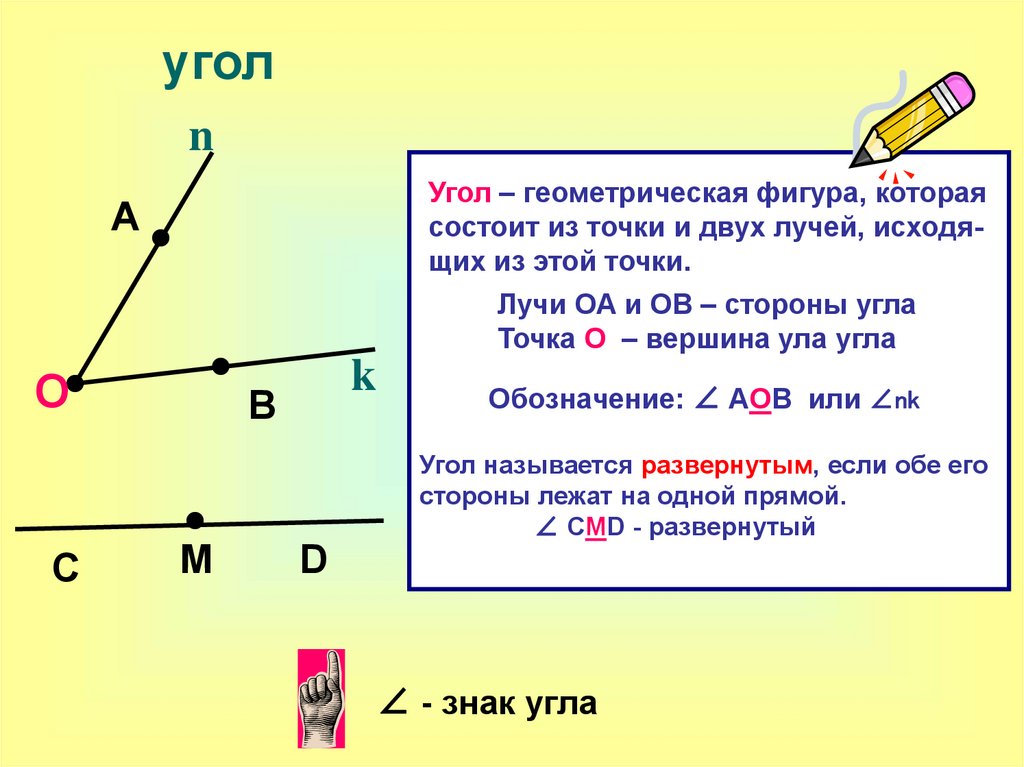 На их основе мы решим несколько примеров для лучшего понимания концепции.
На их основе мы решим несколько примеров для лучшего понимания концепции.
| 1. | Что такое геометрические фигуры? |
| 2. | Типы геометрических фигур |
| 3. | Список и свойства геометрических фигур |
| 4. | Часто задаваемые вопросы о геометрических фигурах |
Что такое геометрические фигуры?
Геометрические фигуры – это любая структура, открытая или замкнутая, имеющая определенную форму и свойства, состоящая из линий, кривых и точек. Некоторыми из известных геометрических фигур являются квадрат, прямоугольник, круг, конус, цилиндр, сфера и т. д. Все эти формы обладают некоторыми свойствами, которые делают их уникальными и отличными от других форм.
Геометрические фигуры определяются как фигуры, замкнутые границей, которая образована путем объединения определенного количества кривых, точек и отрезков линий.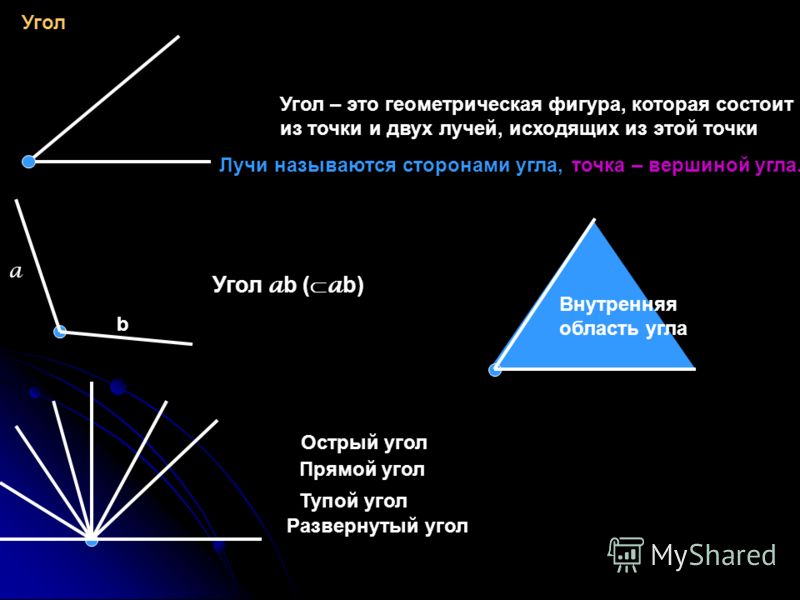 Каждая фигура имеет уникальное имя, такое как круг, квадрат, треугольник, прямоугольник и т. д. В реальной жизни нас окружают различные основные геометрические фигуры, например, кусок пиццы имеет форму треугольника, двери или окна в форме треугольника. форма прямоугольника и многое другое.
Каждая фигура имеет уникальное имя, такое как круг, квадрат, треугольник, прямоугольник и т. д. В реальной жизни нас окружают различные основные геометрические фигуры, например, кусок пиццы имеет форму треугольника, двери или окна в форме треугольника. форма прямоугольника и многое другое.
Типы геометрических фигур
В геометрии, когда объект или форма не соединены с обоих концов, это считается открытой геометрической формой. Когда объект или форма соединены с обоими концами, это считается замкнутой геометрической формой. Существует два типа геометрических фигур, которые классифицируются как:
- Двумерные: Это двумерные фигуры, которые имеют только оси x и y. Это плоские структуры с 2 измерениями. Например, треугольник, квадрат, прямоугольник и т. д.
- Трехмерный: Это трехмерные фигуры, которые имеют оси x, y и z. Ось Z представляет высоту объекта. Это твердые структуры с 3 измерениями. Например, куб, прямоугольный параллелепипед и т.
 д.
д.
Чтобы нарисовать любую из этих геометрических фигур, мы должны начать с линии, кривой или отрезка. Таким образом, на основе количества и расположения линий мы можем создавать различные типы геометрических фигур и фигур, например, путем соединения четырех отрезков линий образуется прямоугольная форма. Треугольник можно получить, соединив отрезки по три линии и так далее.
Посмотрите на приведенную ниже схему, которая представляет различные двухмерные и трехмерные геометрические фигуры.
Двумерные геометрические фигуры
Давайте узнаем о пяти основных двумерных геометрических фигурах.
- Треугольник: Треугольник представляет собой замкнутую двумерную геометрическую фигуру с тремя сторонами. Например, эскиз кусочка пиццы, формы начос и т. д.
- Квадрат: Квадрат представляет собой двумерную геометрическую фигуру, образованную четырьмя сторонами одинаковой длины. Например, формы шахматной доски и карромной доски.

- Прямоугольник: прямоугольник представляет собой четырехстороннюю двумерную геометрическую фигуру, в которой длины противоположных сторон равны. Например, экраны ноутбуков и т. д.
- Круг: Круг представляет собой замкнутую двухмерную геометрическую фигуру круглой формы. Круг не имеет ни линий, ни углов. Например, основа для пиццы, колесо и т. д.
- Овал: Овал похож на круг, но его форма слегка вытянута. Овал не имеет прямых линий и углов. Например, форма числа ноль (0).
Трехмерные геометрические фигуры
Давайте теперь познакомимся с шестью основными трехмерными геометрическими фигурами.
- Куб: Куб представляет собой трехмерную геометрическую фигуру, состоящую из шести квадратов с равными сторонами. Например, игральные кости, кубик Рубика и т. д.
- Кубоид: кубоид — это трехмерная геометрическая фигура, состоящая из шести прямоугольников. Например, книга, коробка и т. д.
- Цилиндр: Цилиндр представляет собой твердую трехмерную геометрическую фигуру, которая имеет два одинаковых круглых плоских конца.
 Например, банки с прохладительными напитками, лапша для бассейна и т. д.
Например, банки с прохладительными напитками, лапша для бассейна и т. д. - Сфера: Сфера представляет собой твердую трехмерную геометрическую фигуру, похожую на шар. Например, футбол, баскетбол и т. д.
- Полушарие: Полушарие — это геометрическая фигура, которая составляет половину сферы. Например, тарелки для супа.
- Конус: Конус представляет собой трехмерную геометрическую форму с плоским круглым основанием и заостренным краем наверху, называемым вершиной. Например, рожки для мороженого, клоунские шляпы и т. д.
Список и свойства геометрических фигур
Существует множество основных геометрических фигур, которые можно сформировать. Некоторые из них двумерные, а некоторые трехмерные. Список геометрических фигур вместе с их гранями, ребрами и вершинами приведен ниже:
| Наименование | Тип | Края | Вершины | Лица |
|---|---|---|---|---|
| Площадь | 2D | 4 | 4 | — |
| Прямоугольник | 2D | 4 | 4 | — |
| Треугольник | 2D | 3 | 3 | — |
| Круг | 2D | Изогнутый | 0 | — |
| Пентагон | 2D | 5 | 5 | — |
| Шестигранник | 2D | 6 | 6 | — |
| Куб | 3D | 12 | 8 | 6 |
| Прямоугольный | 3Д | 12 | 8 | 6 |
| Конус | 3D | 1 | 1 | 2 |
| Цилиндр | 3D | 2 | 0 | 3 |
| Сфера | 3D | Изогнутый | 0 | 1 |
► Похожие статьи
- Кольцо
- Усеченный конус
- Трапеция
- Параллелограмм
Примеры геометрических фигур
Пример 1: Приведите список геометрических фигур с двумя примерами из жизни.

Решение: Ниже приведен список геометрических фигур с примерами из жизни:
Список 2D геометрических фигур:
- Треугольник: квадрат, дорожные знаки
- Квадрат: клавиши виртуальной клавиатуры, шахматная доска
- Прямоугольник: банкнота доллара, карты UNO
- Круг: Алфавит O, обеденные тарелки
- Овал: глаза человека, орбита Земли вокруг Солнца.
Список трехмерных геометрических фигур:
- Куб: кости, кубики льда
- Кубовидный: кирпичи, тряпка
- Цилиндр: прямые трубы, соломинки
- Сфера: апельсины, баскетбол
- Полусфера: миски, иглу
- Конус: колпачки для вечеринок, воронка
Пример 2: Ответьте на следующие вопросы, исходя из своего понимания геометрических фигур.
а) Я круглой формы (2D) без прямых линий и с одной полностью плоской поверхностью.
 Кто я?
Кто я?
б) Я замкнутая двумерная фигура, образованная тремя прямыми линиями. Кто я?Решение:
а) Окружность: Окружность представляет собой двумерную геометрическую фигуру с нулевым количеством прямых линий и одной полной круглой плоской поверхностью.
б) Треугольник: Треугольник представляет собой двумерную геометрическую фигуру с тремя прямыми линиями.Пример 3: Запишите количество прямых линий в следующих геометрических фигурах.
а) Треугольник
б) прямоугольник
в) Квадрат
г) КругРешение:
а) Треугольник: Треугольник состоит из трех прямых линий.
б) Прямоугольник: прямоугольник состоит из четырех прямых линий.
в) Квадрат: Квадрат состоит из четырех прямых линий. Все четыре линии равны.
г) Круг: Круг не имеет прямых линий. Он круглой формы.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.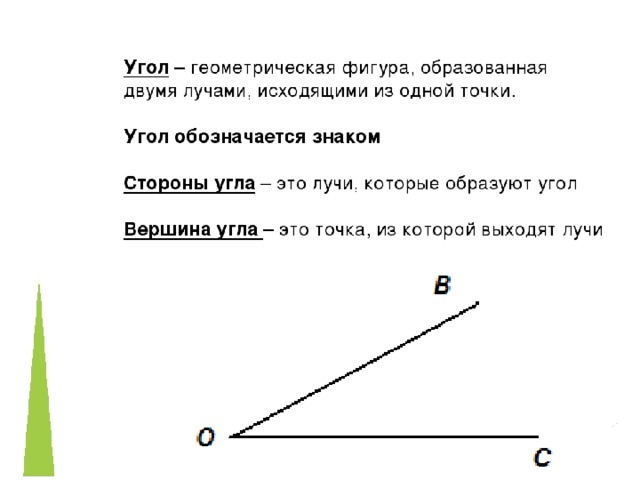
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по геометрическим фигурам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о геометрических фигурах
Что такое геометрические фигуры в геометрии?
Геометрические фигуры также известны как геометрические фигуры, состоящие из комбинации линий или кривых. В реальной жизни нас окружают геометрические фигуры, например, окна в форме квадратов или двери в форме прямоугольников и т. д.
Какие существуют типы геометрических фигур?
Существуют два типа геометрических фигур: двумерные и трехмерные геометрические фигуры. Двумерные фигуры — это замкнутые фигуры с длиной и шириной, такие как квадрат и прямоугольник. Трехмерные фигуры также являются замкнутыми фигурами, имеющими длину, ширину и высоту, например параллелепипед и куб.
Является ли прямая геометрической фигурой?
Прямая линия — это одномерная геометрическая фигура, имеющая только длину. Когда много прямых линий соединяются вместе, они образуют фигуры, такие как квадраты, треугольники и т. д.
Что такое трехмерные геометрические фигуры?
В геометрии трехмерная геометрическая фигура представляет собой твердую фигуру или фигуру с тремя измерениями: длиной, шириной и высотой. Например, цилиндр, сфера, параллелепипед и т. д.
Что такое двумерные геометрические фигуры?
Двумерная геометрическая фигура — это форма, которая имеет длину и ширину, но не имеет высоты или глубины. Круг, квадрат, прямоугольник, треугольник — вот несколько примеров двумерной формы.
Как называются геометрические фигуры?
Ниже приведен список некоторых основных геометрических фигур:
- Треугольник
- Прямоугольник
- Куб
- Прямоугольный
- Сфера
- Площадь
- Ромб
- Трапеция
Какие основные геометрические фигуры?
Существует множество геометрических фигур в зависимости от их размеров. Круг, треугольник, квадрат, прямоугольник — вот лишь некоторые из основных двумерных фигур. Куб, прямоугольный параллелепипед, сфера, конус и цилиндр — вот лишь некоторые из основных трехмерных фигур или форм.
Круг, треугольник, квадрат, прямоугольник — вот лишь некоторые из основных двумерных фигур. Куб, прямоугольный параллелепипед, сфера, конус и цилиндр — вот лишь некоторые из основных трехмерных фигур или форм.
Каковы примеры основных геометрических фигур в реальной жизни?
Ниже перечислены несколько примеров геометрических фигур из реальной жизни:
- Круг: печенье, колеса велосипеда
- Квадрат: квадратная плитка на полу, квадратные бумажные салфетки
- Прямоугольник: учебники, сотовые телефоны, телеэкран
- Треугольник: сэндвич разрезанный по диагонали, дорожные знаки
Какая польза от геометрических фигур?
Геометрические формы освежают наши зрительные чувства логичным, практичным и интересным способом. Они придают ощущение порядка и аккуратности как работе, так и повседневной жизни.
Почему геометрические фигуры важны для детей?
Изучение геометрических фигур помогает детям идентифицировать визуальную информацию, а также помогает им в организации и обучении навыкам в различных областях. Дети развивают навыки распознавания лиц и навигации, если они могут классифицировать и сравнивать различные формы.
Дети развивают навыки распознавания лиц и навигации, если они могут классифицировать и сравнивать различные формы.
Скачать БЕСПЛАТНО учебные материалы
Рабочие листы по геометрическим фигурам
Введение в геометрию | SkillsYouNeed
Когда вы начинаете изучать геометрию, важно знать и понимать некоторые основные понятия.
Эта страница поможет вам понять концепцию размеров в геометрии и понять, работаете ли вы в одном, двух или трех измерениях.
Здесь также объясняются некоторые основные термины и указываются ссылки на другие страницы для получения дополнительной информации.
На этой странице рассматриваются точки, линии и плоскости.
На других страницах этой серии рассказывается об углах и формах, включая многоугольники, круги и другие изогнутые формы, а также трехмерные формы.
Что такое геометрия?
Геометрия , н. та часть математики, которая рассматривает свойства точек, линий, поверхностей и твердых тел…
Английский словарь Чемберса, издание 1989 г. узоры и то, как они сочетаются друг с другом в пространстве. Вы обнаружите, что наши страницы геометрии содержат множество диаграмм, которые помогут вам понять предмет.
узоры и то, как они сочетаются друг с другом в пространстве. Вы обнаружите, что наши страницы геометрии содержат множество диаграмм, которые помогут вам понять предмет.
Когда вы сталкиваетесь с проблемой, связанной с геометрией, может быть очень полезно нарисовать себе схему.
Работа в разных измерениях
Нет, не пространственно-временной континуум! Мы говорим о формах, которые находятся в одном, двух и трех измерениях.
То есть объекты, имеющие длину (одно измерение), длину и ширину (два измерения) и длину, ширину и глубину или высоту (три измерения).
Очки: особый случай: без размеров
Точка — это отдельное место в пространстве. Он часто изображается точкой на странице, но на самом деле не имеет реального размера или формы.
Вы не можете описать точку с точки зрения длины, ширины или высоты, поэтому безразмерная . Однако точка может быть описана координатами. Координаты не определяют ничего о точке, кроме ее положения в пространстве относительно точки отсчета с известными координатами.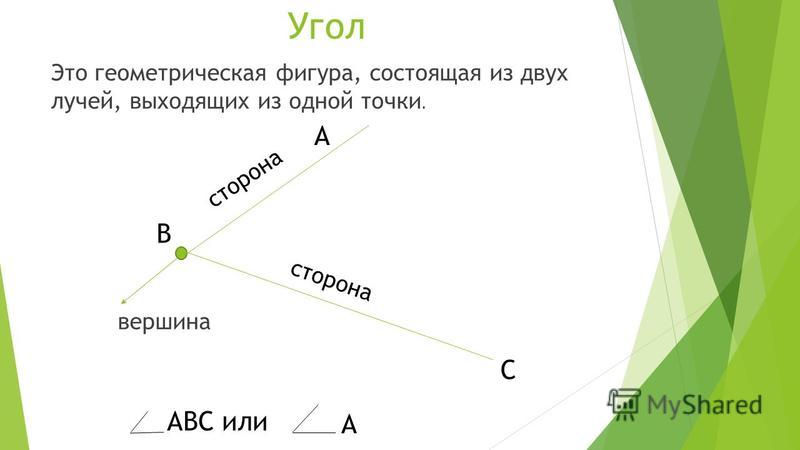 Вы столкнетесь с координатами точек во многих приложениях, например, когда вам 9 лет.0003 рисование графиков или чтение карт.
Вы столкнетесь с координатами точек во многих приложениях, например, когда вам 9 лет.0003 рисование графиков или чтение карт.
Почти все в геометрии начинается с точки, будь то линия или сложная трехмерная фигура.
Линии: одно измерение
Линия — это кратчайшее расстояние между двумя точками. У него есть длина, но нет ширины, что делает его одномерным.
Везде, где встречаются или пересекаются две или более линий, существует точка, и говорят, что две линии имеют общую точку:
Отрезки и лучи
Есть два вида линий: те, которые имеют определенную начальную и конечную точки, и те, которые продолжаются вечно.
Линии, которые перемещаются между двумя точками, называются отрезками . Они начинаются в определенной точке, а идут в другую, конечную точку. Как и следовало ожидать, они нарисованы как линия между двумя точками.
Второй тип линий называется луч , и они продолжаются вечно. Их часто рисуют в виде линии, начинающейся от точки со стрелкой на другом конце:
Их часто рисуют в виде линии, начинающейся от точки со стрелкой на другом конце:
Параллельные и перпендикулярные линии
Есть два типа линий, которые особенно интересны и/или полезны в математике. Параллельные линии никогда не встречаются и не пересекаются. Они просто идут вечно бок о бок, как железнодорожные пути. Чтобы показать, что линии параллельны на диаграмме, принято добавлять «перья», которые выглядят как наконечники стрел.
Перпендикулярные линии пересекаются под прямым углом, 90°:
Плоскости и двумерные формы
Теперь, когда мы разобрались с одним измерением, пришло время перейти к двум.
Плоскость представляет собой плоскую поверхность, также известную как двухмерная. Технически он неограничен, что означает, что он бесконечно продолжается в любом заданном направлении, и поэтому его невозможно нарисовать на странице.
Одним из ключевых элементов геометрии является количество измерений, в которых вы работаете в любой момент времени.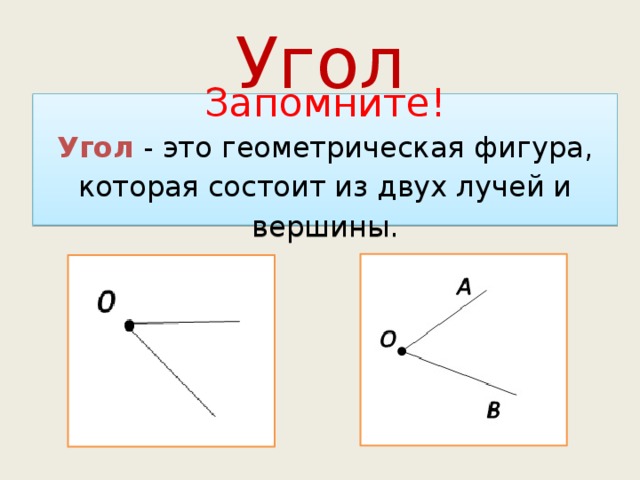 Если вы работаете в одной плоскости, то это либо одна (длина), либо две (длина и ширина). При наличии более чем одной плоскости она должна быть трехмерной, так как высота/глубина также задействованы.
Если вы работаете в одной плоскости, то это либо одна (длина), либо две (длина и ширина). При наличии более чем одной плоскости она должна быть трехмерной, так как высота/глубина также задействованы.
К двумерным фигурам относятся многоугольники, такие как квадраты, прямоугольники и треугольники, которые имеют прямые линии и точки в каждом углу.
Подробнее о полигонах читайте на нашей странице Полигоны . К другим двумерным фигурам относятся круги и любые другие формы, включающие кривую. Вы можете узнать больше об этом на нашей странице Изогнутые формы .
Три измерения: многогранники и изогнутые формы
Наконец, есть еще трехмерные формы , такие как кубы, сферы, пирамиды и цилиндры.
Чтобы узнать больше об этом, посетите нашу страницу Трехмерные фигуры .
Знаки, символы и терминология
Фигура, показанная здесь, представляет собой неправильный пятиугольник, пятиугольник с разными внутренними углами и длинами линий (подробнее об этих формах см. на нашей странице Многоугольники ).
на нашей странице Многоугольники ).
Градусы ° являются мерой вращения и определяют размер угла между двумя сторонами.
Углы обычно обозначаются в геометрии с помощью сегмента окружности (дуги), если они не являются прямыми углами, когда они «квадратичны». Угловые метки в примере показаны зеленым цветом. Смотрите нашу страницу на Angles для получения дополнительной информации.
Засечки (показаны оранжевым цветом) обозначают стороны фигуры равной длины (стороны фигуры конгруэнтны или совпадают). Одиночные линии показывают, что две вертикальные линии имеют одинаковую длину, а двойные линии показывают, что две диагональные линии имеют одинаковую длину. Нижняя горизонтальная линия в этом примере имеет длину, отличную от остальных 4 линий, и поэтому не отмечена. Галочки также могут называться ‘ отметки штриховки ’.
Вершина — это точка пересечения линий (линии также называются лучами или ребрами). Множественное число вершины — это вершины. В примере есть пять вершин, помеченных буквами A, B, C, D и E. В геометрии принято называть вершины буквами.
Множественное число вершины — это вершины. В примере есть пять вершин, помеченных буквами A, B, C, D и E. В геометрии принято называть вершины буквами.
В закрытой форме, такой как в нашем примере, математическое соглашение гласит, что буквы всегда должны располагаться по порядку по часовой стрелке или против часовой стрелки. Нашу фигуру можно описать «ABCDE», но было бы неправильно помечать вершины так, чтобы фигура была, например, «ADBEC». Это может показаться неважным, но в некоторых сложных ситуациях крайне важно избежать путаницы.
Символ угла ‘∠’ используется как сокращенный символ в геометрии при описании угла. Выражение ∠ABC является сокращением для описания угла между точками A и C в точке B. Средняя буква в таких выражениях всегда является вершиной описываемого вами угла — порядок сторон не важен. ∠ABC совпадает с ∠CBA, , и оба описывают вершину B в этом примере.
Если вы хотите записать измеренный угол в точке B в сокращенной форме, вы должны использовать:
m∠ABC = 128° (m просто означает «мера»)
или
m∠CBA = 128°
м∠BCD=104°
Почему эти концепции важны?
Точки, линии и плоскости лежат в основе почти всех других понятий геометрии.

 В., Крылов В. И., Чернин К. Е.. Граничные задачи для гармонических функций часто возникают при математическом анализе многих важных вопросов физики и техники (задачи расчета электрического и теплового поля, задачи…
В., Крылов В. И., Чернин К. Е.. Граничные задачи для гармонических функций часто возникают при математическом анализе многих важных вопросов физики и техники (задачи расчета электрического и теплового поля, задачи…
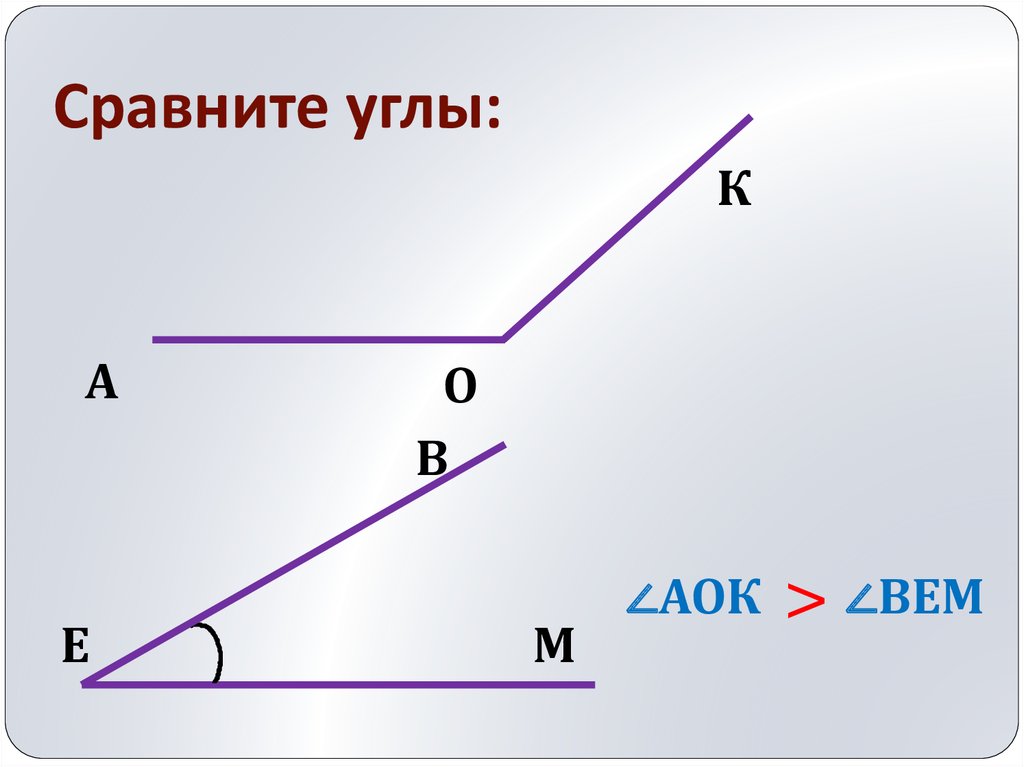
 Буква центра всегда является буквой вершины.
Буква центра всегда является буквой вершины. д. Формально геометрическая фигура — это любое множество
точки на плоскости или в пространстве.
д. Формально геометрическая фигура — это любое множество
точки на плоскости или в пространстве. д.
д.
 Например, банки с прохладительными напитками, лапша для бассейна и т. д.
Например, банки с прохладительными напитками, лапша для бассейна и т. д.
 Кто я?
Кто я?