123 четное или нечетное: Сумма нечётного натурального числа и простого числа равно 123. Найти эти числа.

Конспект урока по математике 3 класс УМК «Школа России» Тема: Четные и нечетные числа

 Математика                      Урок№11          ТЕМА:ЧЕТНЫЕ И НЕЧЕТНЫЕ ЧИСЛА

Цель:  познакомить с понятиями «чётные» и «нечётные» числа.

Задачи: создать условия для определения  чётное число или нечётное; закрепить знание таблиц умножения с числом 2; совершенствовать вычислительные навыки и умения решать текстовые задачи;

Планируемые результаты:

Познавательные умения:

– объяснить значение понятий “чётное число”, “нечётное число”, “кратное число” и использовать их в активном словаре;

– определять чётные и нечётные числа в пределах 100 и обосновывать своё мнение.

Регулятивные умения:

– выполнять учебное задание в соответствии с целью;

– соотносить учебное задание с известным правилом.

Коммуникативные умения:

– формулировать понятные высказывания, обосновывать своё мнение, используя термины, в рамках учебного диалога

 

 

Ход урока

1. Самоопределение к деятельности.

Ну-ка, юный мой дружок,

Ты готов начать урок?

Всё в порядке на столе?

Есть порядок в голове?

2. Актуализация опорных знаний.

Начнем урок мы как всегда с гимнастики для ума

1. Какое число лишнее?  Почему?

12, 16, 9, 18, 24, 21.- на доске

2.Проверка таблицы умножения на 2( мяч)

3.Назовите какая картинка лишняя?

Носок, ботинок, шапка, варежка, перчатка. (Шапка.)-на доске

– Какие из этих предметов всегда используют только по два?

Минутка чистописания.

— Отгадайте загадку и скажите, какую цифру мы будем прописывать на минутке чистописания.

— Если ДВА перевернуть
И внимательно взглянуть,
Так и сяк взглянуть опять,
То получим цифру…(Пять)

-Где в жизни нам встречается цифра 5?

3. Целеполагание

У цифры » два» есть свой секрет

Она гордится этим.

А мы узнаем тот секрет, 

О нём расскажем  всем мы!

-Сегодня цифра 2 нам откроет новый секрет о числах

Вернемся к нашим числам. На какие группы можно разделить эти числа?

-Кто догадался, над чем сегодня мы будем работать?

1. Коля разделил 6 тетрадей поровну — себе и своему другу Диме. Сколько тетрадей получил каждый?
2. Затем Коля разделил 5карандашей. Сколько конфет достанется каждому? Можно ли разделить конфеты поровну?

 — Значит, есть числа, которые делятся на 2 , и числа, которые не делятся.
 — Кто знает, как называются такие числа? («четные» и «нечетные»).
 — Какие новые понятия мы узнали на уроке? («Четные» и « нечетные» числа»).
 — Какую поставите цель вашей дальнейшей деятельности?
Цель: выяснить, какие числа относятся к четным, а какие к нечетным, узнаем особенности четных и нечетных чисел.

 — Из каких источников мы можем получить информацию по данной теме?
 (интернет, взрослые, словари, у учителя, из учебника).
4. Открытие новых знаний.

— Ребята сейчас я вам расскажу одну удивительную историю, внимательно послушайте и скажите, какие числа называются четными, а какие нечетными.

— Однажды в городе Математики произошла удивительная история. Числа, которые жили в этом городе, были очень дружные. Они часто ходили в гости друг к другу, собирались вместе и придумывали различные игры.

Один раз они решили поиграть в игру «Прятки», но в итоге все числа перессорились и даже стали жить на разных сторонах улиц.

— Улица, на которой живут числа 2,4,6,8,10 называться – ЧЁТНАЯ, а числа называются чётными.

-Улица, на которой живут числа1,3,5,7,9 стала называться–НЕЧЁТНАЯ , а числа —

нечётными .

— Какие числа называются четными?

— Какие нечетными?

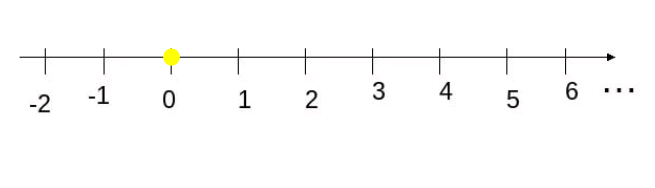
Слайд 2  — Назовите на числовой прямой четные и нечетные числа.

Слайд 3. Запишите числа от 10 до 19. Обведите кружком четные числа. Подчеркните нечетные числа. Проверка по слайду

(Работа по учебнику)
-Прочитайте теоретический материал на с.20
— Так какие же числа называются «четными»? (правило, например: 2 4 6 8 10). А «нечетными»? (1 3 5 7 9).
Приступаем к реализации данной цели.
 — Где в жизни нам пригодятся эти знания? (ответы детей)Хотите узнать?
 — Номера домов, четная, нечетная сторона улиц. В поездах номера спальных мест: нижние «нечетные», а верхние « четные». Такт в танце на 4 и 8 считают, расписание приема врачей. Кто вяжет четное количество рядов и нечетное.

 

-Как легче определить многозначные числа, четное или нечетное?

На доске:234, 357, 846, 539

Признак   чётности.
Если  в десятичной  форме  числа  последняя (0,2,4,6,8) , то число четное.

Рубрика: «Это интересно» Слайд5.6

Слайд 7.Свойства четных и нечетных чисел

1.      Сумма двух четных чисел =четное число

2.      Сумма двух нечетных чисе =четное число

3.      Суммачетного и нечетного чисел =нечетное число

 

Игра-считалка (видео)

Задание № 2 с последующей проверкой..

Работа в парах (Листочки)

— Узнаем какие числа чётные или нечётные получаются при умножении числа на число два.

План работы в паре

1.У вас записаны числа: 1 группа (2, 4, 6, 10, 14, 18), 2 группа нечётные числа (1,3,5,7,9,11)

2.Умножьте их на число два.

. Пронаблюдайте за результатами – какие числа получились: чётные или нечётные.

-Что было общего в примерах? Почему у вас получились такие числа?

6. Подумайте, как вы расскажите об этом одноклассникам.

Учитель раздаёт детям листки с заготовкой для вывода, дети вписывают пропущённые слова. Учитель координирует деятельность групп.

Дети озвучивают свои выводы. Что делали? К какому выводу вы пришли?

Вывод. 1 группа. При умножении чётного числа на 2 получается всегда чётное число.

Вывод. 2 группа. При умножении нечётного числа на 2 получается всегда чётное число

Вывод:При умножении и четных и нечетных чисел на 2 в результате получаются четные числа

-Ребята, а как вы думаете, о-четное или нечетное число? Докажите.

5.Ф и з к у л ь т м и н у т к а

6. Работа над пройденным материалом.

1. Решение задач. №4

Прочитай условие задачи.

1ящик – 6 кг

3ящика — ? кг

6 х 3 = 18(кг)

Ответ: всего 18кг огурцов привезли в школьный буфет.

2. Решение примеров №6 по вариантам

7. Итоги урока. Рефлексия.

-Какую учебную задачу ставили перед собой? Выполнили задачу?

— Какие числа называются чётными?

— Какие числа называются нечётными.

-Что повторяли сегодня на уроке?

-Оцените свою работу на уроке  светофориками.

8.Домашнее задание.

С.20 №5 , 4 (составить две обратные задачи)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

234

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                                      357

 

846

 

539

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2                                                                                    

4

6

10

14

15

Вывод: при умножении чётного числа на 2 получается всегда ………………………. .число.     

 

 

3

5

7

9

11

13

Вывод: при умножении нечётного числа на 2 получается всегда ……………………….число

 

 

2                                                                                    

4

6

10

14

15

Вывод: при умножении чётного числа на 2 получается всегда ………………………..число

 

 

3

5

7

9

11

13

Вывод: при умножении нечётного числа на 2 получается всегда ……………………….число

 

 

Основы штрихкодирования. — ФПФЭ

Штриховой Код EAN13 является непрерывным, имеет фиксированную длину и высокую плотность записи позволяет отобразить 13 цифр от 0 до 9.

Рис.1. Пример штрихового кода EAN

Кодовое обозначение может выражаться восемью (EAN8) или тринадцатью (EAN13) цифрами, причем во втором случае реально кодируется только двеннадцать цифр. Знаки штрихового Кода EAN состоят из двух штрихов и двух промежутков.

Штриховое изображение всех 12-ти (8-ми) цифр составляет в целом символ кода EAN.

Краевые знаки (удлиненные штрихи — знаки начала и конца символа) определяют его границы; делится символ на две части разделительным знаком (удлиненные штрихи в центре символа), как показано на рисунке 2.

Рис.2. Стуктура штрихового кода EAN-13

Таблица 1. Характеристика позиций полного и сокращенного кодов в системе EAN

Возможен вариант, когда для кода страны-изготовителя отводится два знака, а для кода предприятия — пять.

Необходимо также помнить, что штриховой код не несет в себе информации по классификации товара, т.е. и код страны (первые 2-3 цифры), и код предприятия (следующие 4-5 цифр), и код изделия (следующие пять цифр) уникальные (единственные и неповторимые) для этого изделия и являются в это же время номером товара в том банке данных, где он зарегестрирован.

Поэтому первые 2-3 цифры — это код страны или, другими словами, номер страны в международном банке данных.

Возьмем, к примеру цифровой код 4||018993||404787||. Первые две цифры (40), если читать слева направо, обозначают страну изготовителя (или продавца) продукта («флаг страны»), в данном случае — Германии. Следующие пять (18993) — фирму-изготовителя. Еще пять (40478) — наименование товара. И, наконец, последняя цифра (7) — контрольная, используемая для проверки правильности считывания предыдущих цифр кода сканирующей системой. Контрольную цифру кода можно определить самому с помощью следующих математических действий.

Расчет контрольной цифры для кода EAN-13

Складываем цифры, стоящие на четных позициях, затем на нечетных позициях:
Теперь складываем результат сложения цифр на четных позициях, помноженный на три и результат сложения цифр на нечетных позициях:
(33*3) + 24 = 123Контрольное число представляет собой разницу между окончательной суммой (123) и ближайшим к ней наибольшим числом, кратным десяти (в данном случае — 130):
130 — 123 = 7Полученная в результате последняя семерка и соответствует контрольной цифре.

Расчет контрольной цифры для кода EAN-8

Расчет абсолютно идентичен рассмотренному выше.

Структура штрихового кода

Из изложенного выше мы уже знаем что весь символ штрихового кода делится на левую и правую части. В кодировании знаков левой половины заключена возможность проверки на нечетность, т. е. если пересчитать все темные модули штрихов в левой половине кода. то сумма их составит нечетное число, а если то же самое проделать с правой половиной, то в результате подсчета всех темных модулей штрихов получим в сумме четное число, так как правая часть наделена возможностью проверки на четность.

Эта возможность проверки на четность и нечетность введена для исключения ошибки и самопроверки при считывании хода с помощью технических устройств. После считывания код попадает в компьютер и проверяется на правильность (наличие ошибок), посредством про-верки на четность/нечетность, если это условие не выполняется, то значит при считывании произошла ошибка и необходимо еще раз считать код с помощью специального технического устройства.

Также при штриховом кодировании введен еще один термин или понятие. В зависимости от выполнении правила четности/нечетности левой или правой половины кода цифровые знаки называются знаками четного или нечетного паритета. Паритет говорит нам о том. что если он четный, то сумма темных модулей двух штрихов, которыми закодированна данная цифра есть число четное, и наоборот — если паритет нечетный. Это правило относится к каждому цифровому знаку.

Сочетание штрихов и пробелов, а также их расстановка внутри кажого цифрового знака, в зависимости от вида паритета записывается в виде комбинаций кода A, B или C, которые приведены в таблице 2.

Таблица 2. Перевод цифр в двоичную систему записи в зависимости от четности паритета

Цифра	Код цифры в двоичной системе
	Комбинация A	Комбинация B	Комбинация C
	нечетный паритет	четный паритет	четный паритет
0	0001101	0100111	1110010
1	0011001	0110011	1100110
2	0010011	0011011	1101100
3	0111101	0100001	1000010
4	0100011	0011101	1011100
5	0110001	0111001	1001110
6	0101111	0000101	1010000
7	0111011	0010001	1000100
8	0110111	0001001	1001000
9	0001011	0010111	1110100

Каждая цифра кода представляет собой сочетание штрихов и пробелов, исполняемых в комбинациях A, B или C, тип комбинации определяется первой цифрой префикса — «флага» страны.

Итак, любой символ кода EAN-13 состоит из шести цифровых знаков переменного паритета (исполненных в комбинациях A или B) в левой половине символа кода, а также шести цифровых знаков четного паритета (исполненных только в комбинации C) в правой половине символа кода, двух краевых и одного разделительного знаков.

Цифра, стоящая на 13-й позиции (она-же первая при чтении кода слева направо) определяет, в какой комбинации A или B, согласно паритета цифрового знака, будет исполнена каждая из цифр левой половины символа кода. По таблице 2.

Таблица 2. Исполнение цифровых знаков в комбинациях A и B в 7-12 позициях

Теперь рассмотрим пример кодирования кода EAN-13, который рассматривали выше: 4||018993||404787||.

В итоге мы получаем штриховой код, который приведен ниже. Распечатайте и считайте его!

Оригинал статьи читайте на KAZUS.RU .

Задания для подготовки к ОГЭ по информатике (№2 «Значение логического выражения»)

1. За­да­ние 2 № 798. Для ка­ко­го из при­ведённых чисел ис­тин­но вы­ска­зы­ва­ние:

НЕ (число 10) И (число нечётное)?

1) 22

2) 13

3) 9

4) 6

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(число И (число нечётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку 22 — чётное число.

2) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 13

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния.

4) Ложно, по­сколь­ку 6 — чётное число.

Ответ: 3

2. За­да­ние 2 № 242. Для ка­ко­го из при­ведённых чисел ложно вы­ска­зы­ва­ние: (число ИЛИ НЕ (число чётное)?

1) 123

2) 56

3) 9

4) 8

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ис­тин­но тогда, когда ис­тин­но хотя бы одно вы­ска­зы­ва­ние. За­пи­шем вы­ра­же­ние в виде

(число ИЛИ (число нечётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: 123 — нечётное.

2) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: 56 мень­ше 40 и 56 — чётное.

3) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: 9 — нечётное.

4) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: 8 мень­ше 40.

 Ответ: 2

3. За­да­ние 2 № 363. Для ка­ко­го из при­ведённых имён ис­тин­но вы­ска­зы­ва­ние:

НЕ (Пер­вая буква глас­ная) И НЕ (По­след­няя буква со­глас­ная)?

1) Анна

2) Роман

3) Олег

4) Та­тья­на

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(Пер­вая буква со­глас­ная) И (По­след­няя буква глас­ная)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: а — со­глас­ная.

2) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: н — глас­ная.

3) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: о — со­глас­ная и г — глас­ная.

4) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния.

Ответ: 4

4. За­да­ние 2 № 102. Для ка­ко­го из при­ведённых зна­че­ний числа X ис­тин­но вы­ска­зы­ва­ние: (X И НЕ (X

1) 4

2) 5

3) 6

4) 7

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(X И (X = 6)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 4 не мень­ше 6.

2) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 5 не мень­ше 6.

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: 6 мень­ше 7 и 6 не мень­ше 6.

4) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 7 мень­ше 7.

Ответ: 3

5. За­да­ние 2 № 703. Для ка­ко­го из при­ведённых чисел ложно вы­ска­зы­ва­ние:

НЕ (число 50) ИЛИ (число чётное)?

1) 123

2) 56

3) 9

4) 8

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда лож­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(число = ИЛИ (число чётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: 123 не мень­ше 50 и 123 — нечётное число.

2) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: 56 — чётное.

3) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: 9 — нечётное число.

4) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: 8 не мень­ше 50.

Ответ: 1

6. За­да­ние 2 № 182. Для ка­ко­го из при­ведённых чисел ис­тин­но вы­ска­зы­ва­ние: НЕ (число И (число чётное)?

1) 24

2) 45

3) 74

4) 99

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(число = 50) И (число чётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 24 боль­ше или равно 50.

2) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 45 мень­ше или равно 50.

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: 74 — чётное И 74 боль­ше или равно 50.

4) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 99 — нечётное.

Ответ: 3

7. За­да­ние 2 № 503. Для ка­ко­го из при­ведённых имён ложно вы­ска­зы­ва­ние:

НЕ ((Пер­вая буква глас­ная) И (По­след­няя буква со­глас­ная))?

1) Ва­лен­ти­на

2) Гер­ман

3) Ана­ста­сия

4) Яков

По­яс­не­ние.

Ло­ги­че­ское «И» ложно толь­ко тогда, когда ложны хотя бы одно из вы­ска­зы­ва­ний. По­сколь­ку перед конъ­юнк­ци­ей стоит от­ри­ца­ние, нужно найти вы­ра­же­ние, для ко­то­ро­го конъ­юнк­ция будет ис­тин­на.

1) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ния: в — со­глас­ная.

2) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: г — со­глас­ная.

3) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: я — глас­ная.

4) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: я — глас­ная и в — со­глас­ная.

 Ответ: 4

8. За­да­ние 2 № 1013. Для какой из пе­ре­чис­лен­ных ниже фа­ми­лий рус­ских пи­са­те­лей и по­этов ис­тин­но вы­ска­зы­ва­ние:

НЕ (ко­ли­че­ство глас­ных букв чётно) И НЕ (пер­вая буква со­глас­ная)?

1) Есе­нин

2) Одо­ев­ский

3) Тол­стой

4) Фет

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. Про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Есе­нин — ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния.

2) Одо­ев­ский — ложно, по­сколь­ку ложно вы­ска­зы­ва­ние «НЕ (ко­ли­че­ство глас­ных букв чётно)».

3) Тол­стой — ложно, по­сколь­ку ложно вы­ска­зы­ва­ние «НЕ (пер­вая буква со­глас­ная)».

4) Фет — ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния.

Ответ: 1

9. За­да­ние 2 № 403. Для ка­ко­го из при­ведённых имён ис­тин­но вы­ска­зы­ва­ние:

НЕ (Пер­вая буква со­глас­ная) И НЕ (По­след­няя буква глас­ная)?

1) Юлиан

2) Кон­стан­тин

3) Ека­те­ри­на

4) Свет­ла­на

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(Пер­вая буква глас­ная) И (По­след­няя буква со­глас­ная)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния.

2) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: к — глас­ная.

3) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: а — со­глас­ная.

4) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: с — со­глас­ная и а — глас­ная.

Ответ: 1

10. За­да­ние 2 № 965. Для ка­ко­го из при­ведённых чисел ложно вы­ска­зы­ва­ние:

НЕ (число 50) ИЛИ (число чётное)?

1) 123

2) 56

3) 9

4) 8

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. Пре­об­ра­зу­ем вы­ра­же­ние:

(число ИЛИ (число чётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния.

2) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: 56 — чётное.

3) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: 9 не боль­ше 50.

4) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния.

Ответ: 1

11. За­да­ние 2 № 1136. Для ка­ко­го из при­ведённых чисел ис­тин­но вы­ска­зы­ва­ние:

(Пер­вая цифра чётная) И НЕ(Сумма цифр чётная)?

1) 648

2) 452

3) 357

4) 123

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. Про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние.

2) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния.

3) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние.

4) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние.

Ответ: 2

12. За­да­ние 2 № 1255. Для ка­ко­го из при­ведённых имён ЛОЖНО вы­ска­зы­ва­ние:

НЕ(Пер­вая буква глас­ная) ИЛИ (По­след­няя буква глас­ная)?

1) Анна

2) Мак­сим

3) Та­тья­на

4) Егор

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(Пер­вая буква со­глас­ная) ИЛИ (По­след­няя буква глас­ная)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

 1) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: а — глас­ная.

2) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: м — со­глас­ная.

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: т — со­глас­ная и а — глас­ная.

4) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: е — глас­ная и р — со­глас­ная.

Ответ: 4

13. За­да­ние 2 № 142. Для ка­ко­го из при­ведённых чисел ис­тин­но вы­ска­зы­ва­ние: НЕ (число И НЕ (число чётное)?

1) 123

2) 106

3) 37

4) 8

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(число = 100) И (число нечётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: 123 не мень­ше 100 и 123 — нечётное число.

2) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 106 — чётное.

3) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 37 не мень­ше 100.

4) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 8 — нечётное.

Ответ: 1

14. За­да­ние 2 № 1033. Для какой из пе­ре­чис­лен­ных ниже фа­ми­лий рус­ских пи­са­те­лей и по­этов ис­тин­но вы­ска­зы­ва­ние:

НЕ (ко­ли­че­ство глас­ных букв нечётно) И НЕ (пер­вая буква со­глас­ная)?

1) Есе­нин

2) Одо­ев­ский

3) Тол­стой

4) Фет

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. Про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Есе­нин — ложно, по­сколь­ку ложно вы­ска­зы­ва­ние «НЕ (ко­ли­че­ство глас­ных букв нечётно)».

2) Одо­ев­ский — ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния.

3) Тол­стой — ложно, по­сколь­ку ложно вы­ска­зы­ва­ние «НЕ (пер­вая буква со­глас­ная)».

4) Фет — ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния.

Ответ: 2

15. За­да­ние 2 № 483. Для ка­ко­го из при­ведённых имён ложно вы­ска­зы­ва­ние:

НЕ (Пер­вая буква со­глас­ная) ИЛИ НЕ (По­след­няя буква глас­ная)?

1) Егор

2) Тимур

3) Вера

4) Лю­бовь

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(Пер­вая буква глас­ная) ИЛИ (По­след­няя буква со­глас­ная)

и про­ве­рим все ва­ри­ан­ты от­ве­та.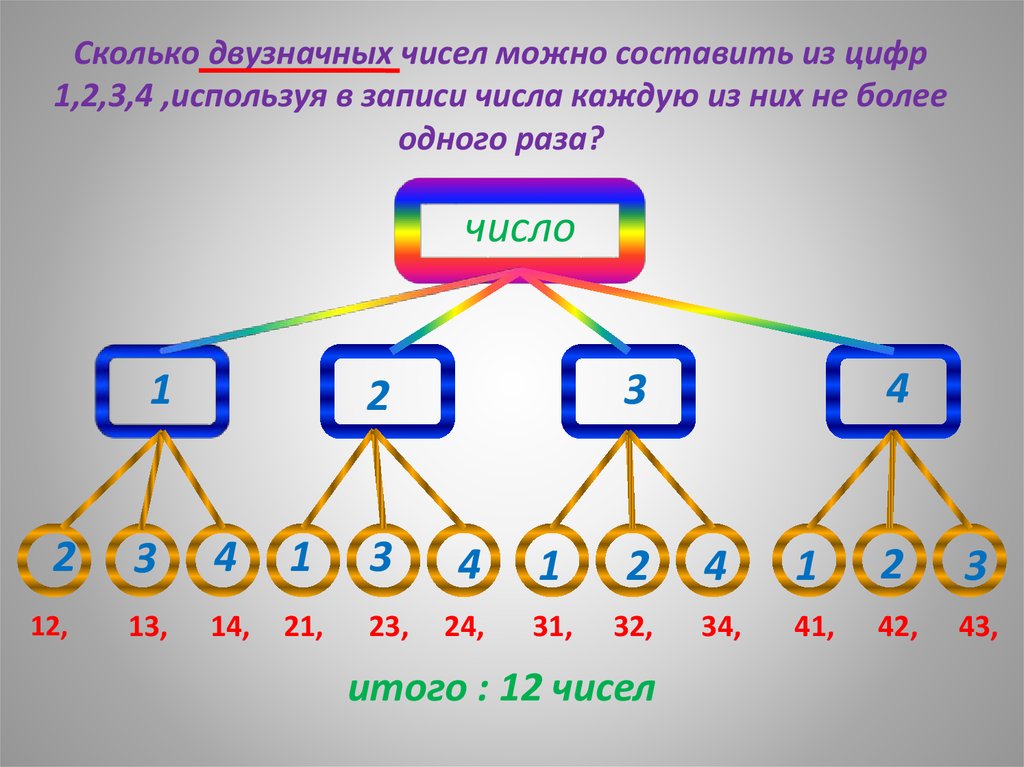

1) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: е — глас­ная.

2) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: р — со­глас­ная.

3) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: в — со­глас­ная и а — глас­ная.

4) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: ь — со­глас­ная.

Ответ: 3

16. За­да­ние 2 № 2. Для ка­ко­го из при­ведённых зна­че­ний числа X ложно вы­ска­зы­ва­ние:

НЕ (X ИЛИ (X

1) 7

2) 6

3) 5

4) 4

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(X = 6) ИЛИ (X

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: 7 боль­ше 6.

2) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: 6 не мень­ше 6.

3) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: 5 не боль­ше 6 и 5 не мень­ше 5.

4) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: 4 мень­ше 5.

Ответ: 3

17. За­да­ние 2 № 343. Для ка­ко­го из при­ведённых имён ис­тин­но вы­ска­зы­ва­ние:

НЕ (Пер­вая буква глас­ная) И НЕ (По­след­няя буква со­глас­ная)?

1) Инна

2) Нелли

3) Иван

4) Потап

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(Пер­вая буква со­глас­ная) И (По­след­няя буква глас­ная)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: и — глас­ная.

2) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: н — со­глас­ная и и — глас­ная.

3) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: н — со­глас­ная.

4) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: п — со­глас­ная.

Ответ: 2

18. За­да­ние 2 № 543. Для ка­ко­го из дан­ных слов ис­тин­но вы­ска­зы­ва­ние:

НЕ (окан­чи­ва­ет­ся на мяг­кий знак) И (ко­ли­че­ство букв чётное)?

1) сен­тябрь

2) ав­густ

3) де­кабрь

4) май

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(не окан­чи­ва­ет­ся на мяг­кий знак) И (ко­ли­че­ство букв чётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: сен­тябрь окан­чи­ва­ет­ся на мяг­кий знак.

2) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: ав­густ не окан­чи­ва­ет­ся на мяг­кий знак и имеет шесть букв.

3) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: де­кабрь окан­чи­ва­ет­ся на мяг­кий знак.

4) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: в слове май три буквы.

Ответ: 2

19. За­да­ние 2 № 1116. Для ка­ко­го из при­ведённых зна­че­ний числа X ложно вы­ска­зы­ва­ние:

НЕ (X

1) 4

2) 5

3) 6

4) 7

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» лож­но толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. Про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, по­сколь­ку ис­тин­но вы­ска­зы­ва­ние (X

2) Ис­тин­но, по­сколь­ку ис­тин­но вы­ска­зы­ва­ние (X

3) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния.

4) Ис­тин­но, по­сколь­ку ис­тин­но вы­ска­зы­ва­ние НЕ (X

Ответ: 3

20. За­да­ние 2 № 463. Для ка­ко­го из при­ведённых имён ложно вы­ска­зы­ва­ние:

НЕ (Пер­вая буква со­глас­ная) ИЛИ НЕ (По­след­няя буква глас­ная)?

1) Пимен

2) Кри­сти­на

3) Ирина

4) Алек­сандр

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(Пер­вая буква глас­ная) ИЛИ (По­след­няя буква со­глас­ная)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: н — со­глас­ная.

2) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: к — со­глас­ная и а — глас­ная.

3) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: и — глас­ная.

4) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: а — глас­ная и р — со­глас­ная.

Ответ: 2

21. За­да­ние 2 № 222. Для ка­ко­го из при­ведённых чисел ложно вы­ска­зы­ва­ние:

НЕ (число ИЛИ НЕ (число чётное)?

1) 123

2) 56

3) 9

4) 8

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ис­тин­но тогда, когда ис­тин­но хотя бы одно вы­ска­зы­ва­ние. За­пи­шем вы­ра­же­ние в виде

(число = 10) ИЛИ (число нечётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: 123 не мень­ше 10.

2) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: 56 не мень­ше 10.

3) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: 9 — нечётное.

4) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: 8 не мень­ше 10 и 8 — нечётное.

Ответ: 4

22. За­да­ние 2 № 623. Для ка­ко­го из дан­ных слов ис­тин­но вы­ска­зы­ва­ние:

НЕ (уда­ре­ние на пер­вый слог) И (ко­ли­че­ство букв чётное)?

1) ко­ро­ва

2) козел

3) кошка

4) конь

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(уда­ре­ние не на пер­вый слог) И (ко­ли­че­ство букв чётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: в слове ко­ро­ва уда­ре­ние не на пер­вый слог и ко­ли­че­ство букв чётное.

2) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: в слове козел пять букв.

3) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: в слове кошка пять букв.

4) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: в слове конь уда­ре­ние на пер­вый слог.

Ответ: 1

23. За­да­ние 2 № 643. Для ка­ко­го из дан­ных слов ис­тин­но вы­ска­зы­ва­ние:

(уда­ре­ние на пер­вый слог) И НЕ (ко­ли­че­ство букв чётное)?

1) ко­ро­ва

2) козел

3) кошка

4) конь

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(уда­ре­ние на пер­вый слог) И (ко­ли­че­ство букв нечётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: в слове ко­ро­ва шесть букв.

2) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: в слове козел уда­ре­ние не на пер­вый слог.

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: в слове кошка пять букв и уда­ре­ние на пер­вый слог.

4) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: в слове конь че­ты­ре буквы.

Ответ: 3

24. За­да­ние 2 № 42. Для ка­ко­го из при­ведённых зна­че­ний числа X ис­тин­но вы­ска­зы­ва­ние:

(X И НЕ (X

1) 9

2) 8

3) 7

4) 6

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(X И (X = 7)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние.

2) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние.

3) Ис­тин­но, ис­тин­ны оба вы­ра­же­ния: 7 мень­ше 8 и 7 не мень­ше 7.

4) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние.

Ответ: 3

25. За­да­ние 2 № 423. Для ка­ко­го из при­ведённых имён ложно вы­ска­зы­ва­ние:

НЕ (Пер­вая буква глас­ная) ИЛИ НЕ (По­след­няя буква со­глас­ная)?

1) Арина

2) Вла­ди­мир

3) Раиса

4) Яро­слав

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(Пер­вая буква со­глас­ная) ИЛИ (По­след­няя буква глас­ная)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: а — глас­ная.

2) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: в — со­глас­ная.

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: р — со­глас­ная и а — глас­ная.

4) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: я — глас­ная и в — со­глас­ная.

Ответ: 4

26. За­да­ние 2 № 322. Для ка­ко­го из при­ведённых чисел ис­тин­но вы­ска­зы­ва­ние:

НЕ (Пер­вая цифра чётная) И (По­след­няя цифра нечётная)?

1) 1234

2) 6843

3) 3561

4) 4562

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(Пер­вая цифра нечётная) И (По­след­няя цифра нечётная)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 4 — нечётное.

2) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 6 — нечётное.

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: 3 — нечётное и 1 — нечётное.

4) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: 4 — чётное и 2 — чётное.

Ответ: 3

27. За­да­ние 2 № 921. Для ка­ко­го из при­ведённых чисел ис­тин­но вы­ска­зы­ва­ние:

НЕ (число И (число чётное)?

1) 8

2) 15

3) 21

4) 36

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(X = 20) И (число чётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 8 не боль­ше 20.

2) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 15 не боль­ше 20.

3) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 21 — нечётное.

4) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: 36 боль­ше 20 и 36 — чётное.

Ответ: 4

28. За­да­ние 2 № 22. Для ка­ко­го из при­ведённых зна­че­ний числа X ис­тин­но вы­ска­зы­ва­ние:

НЕ (X И (X

1) 5

2) 6

3) 7

4) 8

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(X = 6) И (X

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 5 не мень­ше 6.

2) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: 6 не мень­ше 6 и 6 мень­ше 7.

3) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 7 мень­ше 7.

4) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 8 мень­ше 7.

 Ответ: 2

29. За­да­ние 2 № 383. Для ка­ко­го из при­ведённых имён ис­тин­но вы­ска­зы­ва­ние:

НЕ (Пер­вая буква со­глас­ная) И НЕ (По­след­няя буква глас­ная)?

1) Ольга

2) Ми­ха­ил

3) Ва­лен­ти­на

4) Ян

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(Пер­вая буква глас­ная) И (По­след­няя буква со­глас­ная)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: а — со­глас­ная.

2) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: м — глас­ная.

3) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: в — глас­ная.

4) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: я — глас­ная и н — со­глас­ная.

Ответ: 4

30. За­да­ние 2 № 1096. Для ка­ко­го из ука­зан­ных зна­че­ний числа X ис­тин­но вы­ска­зы­ва­ние:

(X

1) 1

2) 2

3) 3

4) 4

По­яс­не­ние.

Пре­об­ра­зу­ем вы­ска­зы­ва­ние:

(X

(X 2)

2 X

 

Та­ко­му не­ра­вен­ству удо­вле­тво­ря­ет толь­ко X = 2. Ответ: 2

31. За­да­ние 2 № 122. Для ка­ко­го из при­ведённых зна­че­ний числа X ложно вы­ска­зы­ва­ние:

НЕ (X ИЛИ (X

1) 4

2) 5

3) 6

4) 7

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(X = 7) ИЛИ (X

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: 4 мень­ше 6.

2) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: 5 мень­ше 6.

3) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: 6 не боль­ше 7 и 6 не мень­ше 6.

4) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: 7 не мень­ше 7.

Ответ: 3

32. За­да­ние 2 № 443. Для ка­ко­го из при­ведённых имён ложно вы­ска­зы­ва­ние:

НЕ (Пер­вая буква глас­ная) ИЛИ НЕ (По­след­няя буква со­глас­ная)?

1) Эду­ард

2) Ан­ге­ли­на

3) Ка­ри­на

4) Никон

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

 (Пер­вая буква со­глас­ная) ИЛИ (По­след­няя буква глас­ная)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

 1) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: э — глас­ная и д — со­глас­ная.

2) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: а — глас­ная.

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: к — со­глас­ная и а — глас­ная.

4) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: в — со­глас­ная.

 Ответ: 1

33. За­да­ние 2 № 162. Для ка­ко­го из при­ведённых чисел ис­тин­но вы­ска­зы­ва­ние:

(число И НЕ (число чётное)?

 1) 156

2) 105

3) 23

4) 10

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

 (число И (число нечётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

 1) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 156 мень­ше 100.

2) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 105 мень­ше 100.

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: 23 мень­ше 100 и 23 — нечётное.

4) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 10 — нечётное.

Ответ: 3

34. За­да­ние 2 № 583. Для ка­ко­го из дан­ных слов ис­тин­но вы­ска­зы­ва­ние:

НЕ (есть ши­пя­щие) И (окан­чи­ва­ет­ся на глас­ную)?

Ши­пя­щие звуки — это [ж], [ш], [ч’], [щ’].

1) лю­бовь

2) от­вра­ще­ние

3) за­бо­та

4) от­чуждённость

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(нет ши­пя­щих) И (окан­чи­ва­ет­ся на глас­ную)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: лю­бовь не окан­чи­ва­ет­ся на глас­ную.

2) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: в слове от­вра­ще­ние есть ши­пя­щие.

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: в слове за­бо­та нет ши­пя­щих и оно окан­чи­ва­ет­ся на глас­ную.

4) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: слово от­чуждённость не окан­чи­ва­ет­ся на глас­ную и в нём есть ши­пя­щие.

Ответ: 3

35. За­да­ние 2 № 62. Для ка­ко­го из при­ведённых зна­че­ний числа X ис­тин­но вы­ска­зы­ва­ние:

НЕ(X 5) И (X 4)?

1) 4

2) 5

3) 6

4) 7

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(X = И (X 4)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 4 боль­ше 4.

2) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: 5 не боль­ше 5 и 5 боль­ше 4.

3) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 6 не боль­ше 5.

4) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 7 не боль­ше 5.

Ответ: 2

36. За­да­ние 2 № 1053. Для ка­ко­го из при­ведённых имён ис­тин­но вы­ска­зы­ва­ние:

НЕ (Тре­тья буква глас­ная) И (По­след­няя буква со­глас­ная)?

1) Иван

2) Ксе­ния

3) Ма­ри­на

4) Мат­вей

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. Таким об­ра­зом, в ис­ко­мом имени тре­тья буква долж­на быть со­глас­ной, а по­след­няя − также со­глас­ной. Под такие усло­вия под­хо­дит толь­ко имя «Мат­вей».

Ответ: 4

37. За­да­ние 2 № 766. Для ка­ко­го из дан­ных слов ис­тин­но вы­ска­зы­ва­ние:

НЕ (тре­тья буква глас­ная) И НЕ (по­след­няя со­глас­ная)?

1) слива

2) инжир

3) ана­нас

4) киви

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(тре­тья буква со­глас­ная) И (по­след­няя ­глас­ная)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: и — глас­ная.

2) Ложно, по­сколь­ку ложно по­след­нее вы­ска­зы­ва­ние: р — со­глас­ная.

3) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния.

4) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния.

Ответ: 4

38. За­да­ние 2 № 563. Для ка­ко­го из дан­ных слов ис­тин­но вы­ска­зы­ва­ние:

(окан­чи­ва­ет­ся на мяг­кий знак) И НЕ (ко­ли­че­ство букв чётное)?

1) сен­тябрь

2) ав­густ

3) де­кабрь

4) май

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(окан­чи­ва­ет­ся на мяг­кий знак) И (ко­ли­че­ство букв нечётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: в слове сен­тябрь во­семь букв.

2) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: ав­густ не окан­чи­ва­ет­ся на мяг­кий знак.

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: де­кабрь окан­чи­ва­ет­ся на мяг­кий знак и имеет семь букв.

4) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: май не окан­чи­ва­ет­ся на мяг­кий знак.

Ответ: 3

39. За­да­ние 2 № 1073. Для ка­ко­го из при­ведённых имён ложно вы­ска­зы­ва­ние:

(Тре­тья буква глас­ная) ИЛИ НЕ (По­след­няя буква глас­ная)?

1) Елена

2) Та­тья­на

3) Мак­сим

4) Ста­ни­слав

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. Про­ве­рим все ва­ри­ан­ты от­ве­та.

 1) Елена — ис­ти­но, по­сколь­ку ис­ти­но вы­ска­зы­ва­ние «(Тре­тья буква глас­ная)».

2) Та­тья­на — ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния.

3) Мак­сим — ис­ти­но, по­сколь­ку ис­ти­но вы­ска­зы­ва­ние «НЕ (По­след­няя буква глас­ная)».

4) Ста­ни­слав — ис­ти­но, по­сколь­ку ис­ти­ны оба вы­ска­зы­ва­ния.

Ответ: 2

40. За­да­ние 2 № 860. Для ка­ко­го из при­ведённых зна­че­ний числа X ложно вы­ска­зы­ва­ние:

НЕ (X = 5) ИЛИ (X 6)?

1) 4

2) 5

3) 6

4) 7

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. Про­ве­рим все ва­ри­ан­ты от­ве­та.

За­пи­шем вы­ра­же­ние в виде

(X ≠ 5) ИЛИ (X 6)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, ис­тин­но пер­вое вы­ска­зы­ва­ние, 4 не равно 5.

2) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние, 5 равно 5, и ложно вто­рое, 5 не боль­ше 6.

3) Ис­тин­но, ис­тин­но пер­вое вы­ска­зы­ва­ние, 6 не равно 5.

4) Ис­тин­но, ис­тин­но пер­вое вы­ска­зы­ва­ние, 7 не равно 5.

Ответ: 2

41. За­да­ние 2 № 901. Для ка­ко­го из при­ведённых чисел ложно вы­ска­зы­ва­ние:

НЕ (число 30) ИЛИ (число чётное)?

1) 28

2) 34

3) 17

4) 45

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(число ИЛИ (число чётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние, 28 мень­ше 30.

2) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­сказ­вы­а­ник: 34 —чётное.

3) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: число мень­ше 17 мень­ше 30.

4) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: 45 боль­ше 30 и 45 не яв­ля­ет­ся чётным.

Ответ: 4

42. За­да­ние 2 № 282. Для ка­ко­го из при­ведённых зна­че­ний числа X ис­тин­но вы­ска­зы­ва­ние: НЕ (X И (X

1) 5

2) 2

3) 3

4) 4

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(X = 3) И (X

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 5 мень­ше 4.

2) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 2 не мень­ше 3.

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: 3 не мень­ше 3 и 3 мень­ше 4.

4) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 4 мень­ше 4.

Ответ: 3

43. За­да­ние 2 № 881. Для ка­ко­го из при­ведённых чисел ложно вы­ска­зы­ва­ние: НЕ (число 30) ИЛИ (число нечётное)?

1) 28

2) 34

3) 17

4) 45

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(число ИЛИ (число нечётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние, 28 мень­ше 30.

2) Ложно, по­сколь­ку ложны оба вы­сказ­вы­а­ния: 34 не мень­ше 30 и 34 не яв­ля­ет­ся нечётным число.

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ни­ея: число мень­ше 30 и 17 — нечётное.

4) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние, 45 — нечётное.

Ответ: 2

44. За­да­ние 2 № 746. Для ка­ко­го из дан­ных слов ис­тин­но вы­ска­зы­ва­ние:

НЕ (тре­тья буква глас­ная) И (по­след­няя со­глас­ная)?

1) слива

2) инжир

3) ана­нас

4) киви

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(тре­тья буква со­глас­ная) И (по­след­няя со­глас­ная)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: и — глас­ная.

2) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния.

3) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: а — глас­ная.

4) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния.

Ответ: 2

45. За­да­ние 2 № 663. Для ка­ко­го из при­ведённых на­зва­ний ложно вы­ска­зы­ва­ние:

НЕ (Ко­ли­че­ство букв чётное) ИЛИ (Пер­вая буква со­глас­ная)?

1) Омск

2) Ива­но­во

3) Москва

4) Ки­ровск

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(Ко­ли­че­ство букв нечётное) ИЛИ (Пер­вая буква со­глас­ная)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: в слове Омск че­ты­ре буквы, пер­вая глас­ная.

2) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: в слове Ива­но­во семь букв, пер­вая глас­ная.

3) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: в слове Москва шесть букв, пер­вая со­глас­ная.

4) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: в слове Ки­ровск семь букв, пер­вая со­глас­ная.

Ответ: 1

46. За­да­ние 2 № 603. Для ка­ко­го из дан­ных слов ис­тин­но вы­ска­зы­ва­ние:

НЕ (есть ши­пя­щие) И НЕ (окан­чи­ва­ет­ся на глас­ную)?

Ши­пя­щие звуки — это [ж], [ш], [ч’], [щ’].

1) лю­бовь

2) от­вра­ще­ние

3) за­бо­та

4) от­чуждённость

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(нет ши­пя­щих) И (окан­чи­ва­ет­ся на со­глас­ную)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: слово лю­бовь окан­чи­ва­ет­ся на со­глас­ную и в нём нет ши­пя­щих.

2) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: в слове от­вра­ще­ние есть ши­пя­щие и оно окан­чи­ва­ет­ся на глас­ную.

3) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: слово за­бо­та окан­чи­ва­ет­ся на глас­ную.

4) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: в слове от­чуждённость есть ши­пя­щие.

Ответ: 1

47. За­да­ние 2 № 941. Для ка­ко­го из при­ведённых чисел ис­тин­но вы­ска­зы­ва­ние:

НЕ (число

1) 8

2) 15

3) 21

4) 36

По­яс­не­ние.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда, когда ис­тин­ны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(X = 20) И (число нечётное)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 8 не боль­ше 20.

2) Ложно, по­сколь­ку ложно пер­вое вы­ска­зы­ва­ние: 15 не боль­ше 20.

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: 21 боль­ше 20 и 21 — нечётное.

4) Ложно, по­сколь­ку ложно вто­рое вы­ска­зы­ва­ние: 36 — чётное.

Ответ: 3

48. За­да­ние 2 № 683. Для ка­ко­го из при­ведённых на­зва­ний ложно вы­ска­зы­ва­ние:

(Ко­ли­че­ство букв чётное) ИЛИ (По­след­няя буква глас­ная)?

1) Москва

2) Омск

3) Дубна

4) Но­во­куз­нецк

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. За­пи­шем вы­ра­же­ние в виде

(Ко­ли­че­ство букв чётное) ИЛИ (По­след­няя буква глас­ная)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: в слове Москва чётное ко­ли­че­ство букв.

2) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: в слове Омск чётное ко­ли­че­ство букв.

3) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: в слове Дубна по­след­няя буква глас­ная.

4) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: в слове Но­во­куз­нецк 11 букв и по­след­няя буква со­глас­ная.

Ответ: 4

49. За­да­ние 2 № 523. Для ка­ко­го из при­ведённых имён ложно вы­ска­зы­ва­ние:

НЕ ((Пер­вая буква со­глас­ная) И (По­след­няя буква глас­ная))?

1) Дарья

2) Павел

3) Абрам

4) Ан­фи­са

По­яс­не­ние.

Пре­об­ра­зу­ем И в ИЛИ по пра­ви­лам Де Мор­га­на:

НЕ(Пер­вая буква со­глас­ная) ИЛИ НЕ(По­след­няя буква глас­ная)

(Пер­вая буква глас­ная) ИЛИ (По­след­няя буква со­глас­ная)

 

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. Про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: д — со­глас­ная и я — глас­ная.

2) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: л — со­глас­ная.

3) Ис­тин­но, по­сколь­ку ис­тин­ны оба вы­ска­зы­ва­ния: а — глас­ная и м — со­глас­ная.

4) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние: а — глас­ная.

Ответ: 1

50. За­да­ние 2 № 840. Для ка­ко­го из при­ведённых зна­че­ний числа X ложно вы­ска­зы­ва­ние:

(X = 9) ИЛИ НЕ (X

1) 8

2) 9

3) 10

4) 11

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ложно толь­ко тогда, когда ложны оба вы­ска­зы­ва­ния. Пе­ре­пи­шем вы­ра­же­ние в виде

(X = 9) ИЛИ (X = 10)

и про­ве­рим все ва­ри­ан­ты от­ве­та.

1) Ложно, по­сколь­ку ложны оба вы­ска­зы­ва­ния: 8 не равно 9 и 8 не боль­ше 10.

2) Ис­тин­но, по­сколь­ку ис­тин­но пер­вое вы­ска­зы­ва­ние, 9 равно 9.

3) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние 10 равно 10.

4) Ис­тин­но, по­сколь­ку ис­тин­но вто­рое вы­ска­зы­ва­ние: 11 боль­ше 10.

Ответ: 1

Задание 2
№ задания	Ответ	№ задания	Ответ

Нечетные числа От 1 до 1000

Нечетные числа вообще могут быть определены разными способами. Один из способов понять нечетные числа: любое число, не кратное 2, называется нечетным числом. Нечетные числа от 1 до 1000 — это набор всех чисел, не кратных 2, лежащих в диапазоне от 1 до 1000, таких как 11, 103, 999 и т. д. Нечетные числа от 1 до 1000 также могут быть идентифицированы как все числа в этом диапазоне, заканчивающиеся нечетными цифрами, такими как 1, 3, 5, 7 и 9.

1.	Список нечетных чисел от 1 до 1000
2.	Сумма нечетных чисел от 1 до 1000
3.	Часто задаваемые вопросы о нечетных числах от 1 до 1000

Список нечетных чисел от 1 до 1000

В этом разделе мы перечислим все нечетные числа от 1 до 1000. Всего существует 500 нечетных чисел от 1 до 1000. Мы знаем, что нечетные числа всегда заканчиваются нечетной цифрой, такой как 1, 3, 5, 7 и 9.. Следовательно, наименьшее нечетное число в этом диапазоне от 1 до 1000 равно 1, а наибольшее нечетное число — 999. Алгоритм, используемый для перечисления нечетных чисел, заключается в добавлении 2 к предыдущему нечетному числу. Например, 1 — первое нечетное число, за ним следуют 1 + 2 = 3, 3 + 2 = 5 и так далее. Основываясь на этой логике, давайте теперь посмотрим на список всех нечетных чисел от 1 до 1000, как показано ниже.

1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49,

51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99,

101, 103, 105, 107 , 109, 111, 113, 115, 117, 119, 121, 123, 125, 127, 129, 131, 133, 135, 137, 139, 141, 143, 145, 147, 149,

3,1 55 ,157,159,161,163,165,167,169,171,173,175,177,179,181,183,185,187,189,191,193,195,197,199,

30 , 205, 207, 209, 211, 213, 215, 217, 219, 221, 223, 225, 227, 229, 231, 233, 235, 237, 239, 241, 243, 245, 247, 249,

251, 253, 255, 257, 259, 261, 263, 265, 267, 269, 271, 273, 275, 277, 279, 281, 283, 285, 287, 289, 291, 293, 295, 297, 2 ,

301, 303, 305, 307, 309, 311, 313, 315, 317, 319, 321, 323, 325, 327, 329, 331, 333, 335, 337, 339, 341, 343, 47 34 , 349,

351, 353, 355, 357, 359, 361, 363, 365, 367, 369, 371, 373, 375, 377, 379, 381, 383, 385, 387, 389, 3,3 99 5 , 397, 399,

401, 403, 405, 407, 409, 411, 413, 415, 417, 419, 421, 423, 425, 427, 429, 431, 433, 435, 437, 439, 441, 443, 445, 447, 449,

451, 453, 455, 457, 459, 461, 463, 465, 467, 469, 471, 473, 475, 477, 479, 481, 5, 483, 87 , 489, 491, 493, 495, 497, 499,

501, 503, 505, 507, 509, 511, 513, 515, 517, 519, 521, 523, 525, 527, 529, 3,5 3 53 , 537, 539, 541, 543, 545, 547, 549,

551, 553, 555, 557, 559, 561, 563, 565, 567, 569, 571, 573, 575, 577, 579, 83 , 585, 587, 589, 591, 593, 595, 597, 599,

601, 603, 605, 607, 609, 611, 613, 615, 617, 619, 621, 623, 625, 627, 629, 631, 633, 635, 637, 639, 641, 643, 645, 647, 649,

651, 653, 655, 657, 659, 661, 65,6, 67 66 , 669, 671, 673, 675, 677, 679, 681, 683, 685, 687, 689, 691, 693, 695, 697, 699,

701, 703, 705, 707, 709, 711, 71 51 , 717, 719, 721, 723, 725, 727, 729, 731, 733, 735, 737, 739, 741, 743, 745, 747, 749,

751, 753, 755, 757, 759, 736 , 765, 767, 769, 771, 773, 775, 777, 779, 781, 783, 785, 787, 789, 791, 793, 795, 797, 799,

801, 803, 805, 807, 807, 807, 811, 813, 815, 817, 819, 821, 823, 825, 827, 829, 831, 833, 835, 837, 839, 841, 843, 845, 847, 849,

851, 85, 8, 55 , 859, 861, 863, 865, 867, 869, 871, 873, 875, 877, 879, 881, 883, 885, 887, 889, 891, 893, 895, 897, 899,

901, 05 , 907, 909, 911, 913, 915, 917, 919, 921, 923, 925, 927, 929, 931, 933, 935, 937, 939, 941, 943, 945, 947, 949,

9 95 , 955, 957, 959, 961, 963, 965, 967, 969, 971, 973, 975, 977, 979, 981, 983, 985, 987, 989, 991, 993, 995, 997, 999.

Сумма нечетных чисел от 1 до 1000

Мы будем находить сумму нечетных чисел от 1 до 1000, используя формулу суммы нечетных чисел. Согласно формуле суммы нечетных чисел, сумма первых n нечетных чисел определяется как n ² , где n — натуральное число, представляющее количество терминов. Таким образом, сумма первых n нечетных чисел будет представлена ​​как 1 + 3 + 5 +…+ n слагаемых = n ² .

Мы знаем, что самое маленькое и самое большое нечетное число в диапазоне от 1 до 1000 будет 1 и 999. Таким образом, первый член равен 1, а последний член равен 999. Количество нечетных чисел от 1 до 1000 равно 500, следовательно, количество членов n = 500.

Используя формулу суммы первых n нечетных чисел, и подставив значение n = 500, сумма нечетных чисел от 1 до 1000 будет рассчитана следующим образом:

Сумма = 1 + 3 + … + 999 = n ²
Сумма = 500 ² = 250000

Следовательно, сумма нечетных чисел от 1 до 1000 равна 250000.

Статьи по теме

Проверьте эти статьи, связанные с концепцией нечетных чисел от 1 до 1000.

• Нечетные числа
• Нечетные числа от 1 до 100
• Четные и нечетные числа
• Целые числа

абстрактная алгебра — нечетные/четные перестановки

Результаты естественным образом следуют из рассмотрения действия $ S_n $ на расположения:

Список $ [k_1, \ldots, k_n] $, составленный путем взятия $ 1, 2, \ldots , n $ в некотором порядке называется расположением. 9{-1} (j) $ .]

Также $ \sigma * ( \tau * [k_1, \ldots, k_n] ) = (\sigma \tau) * [k_1, \ldots, k_n] $

[ Поскольку в $[k_1, \ldots, k_n] \rightsquigarrow \sigma * (\tau * [k_1, \ldots, k_n])$ $k_i$ сначала отправляется в слот $ \tau(i) $, а затем в слот $ \sigma(\tau(i)) $. И $ [k_1, \ldots, k_n] \rightsquigarrow (\sigma \ tau)*[k_1, \ldots, k_n] $ имеет тот же эффект. ]

Мы будем писать $ «\, [k_1, \ldots, k_n] \stackrel{\sigma}{\rightsquigarrow} [l_1, \ldots, l_n]»$ для обозначения $«\, [l_1 , \ldots, l_n] = \sigma * [k_1, \ldots, k_n]» $.

---

Пример 1 . Цикл $(1\,\,2\,\,3\,\,4) = (1\,\,4)(1\,\,3)(1\,\,2)$. Это легко проверить, но вот один из способов, которым мы можем придумать разложение:

Итак, $$ (1 \, \, 2 \, \, 3 \, \, 4)*[1, 2,3,4] = (1 \, \, 4)*\bigg( (1 \, \, 3) * ( (1 \, \, 2) * [1,2,3,4]) \bigg )$$

т. е.

$$(1 \, \, 2 \, \, 3 \, \, 4)*[1,2,3,4] = (1 \, \, 4) (1 \ , \, 3) (1 \, \, 2) * [1,2,3,4] $$

т.е.

$$ (1 \, \, 2 \, \, 3 \, \, 4) = (1 \, \, 4) (1 \, \, 3) (1 \, \, 2) $$

Это предполагает в целом $ (a_1 \, \, a_2 \, \, \ldots \, \, a_k) = (a_1 \, \, a_k) (a_1 \, \, a_{k-1}) \ldots (a_1 \, \, а_2)$, что легко проверить.

Также любой $\sigma\in S_n$ является произведением непересекающихся циклов, и каждый цикл разлагается на $ (a_1 \, \, a_2 \, \, \ldots \, \, a_k) = (a_1 \, \, a_k) (a_1 \, \, a_{k-1}) \ldots (a_1 \, \, a_2) $. Таким образом, каждый $\sigma\in S_n$ является произведением транспозиций.

---

Пример 2 .

Так

$$ (1 \, \, 4) = (1 \, \, 2) (2 \, \, 3) (3 \, \, 4) (2 \, \, 3) (1 \, \, 2) $$

Аналогично, в общем случае любая транспозиция является произведением нечетного числа «элементарных транспозиций» [ т.е. транспозиций вида $ (j \, \, j+1) $ ]

---

Для $\sigma\in S_n$ пара $i \sigma(j)$, называется инверсией в $\sigma$. Также $\text{inv}(\sigma)$ обозначает количество инверсий в $\sigma$. 9{\ текст {инв} (\ сигма)} $. Перестановки со знаком $1$ называются четными, а со знаком $(-1)$ нечетными.

Под «инверсией в расположении $[k_1, \ldots, k_n]$» мы будем понимать инверсию в $ \sigma = \begin{pmatrix} 1 &2 &\ldots &n \\ k_1 &k_2 &\ldots &k_n \end{pmatrix} $ [ , то есть пара $ k_i, k_j $ в $[k_1, \ldots, k_n]$, где большее из двух находится слева от меньшего ]. Точно так же имеет значение и знак расположения.

---

Уведомление для любых $ (j \, \, j+1) \in S_n $, $ [k_1, \ldots, k_n] \rightsquigarrow (j \, \, j+1)*[k_1, \ldots, k_n] $ изменяет количество инверсий на $ \pm 1 $ (и, следовательно, меняет знак).

Следовательно, для любой транспозиции $ \tau \in S_n $ запись ее в виде произведения нечетного числа элементарных транспозиций (пример 2) дает $ [k_1, \ldots, k_n] \rightsquigarrow \tau * [k_1, \ldots , k_n] $ меняет знак.

---

Пусть $ \tau_1, \ldots, \tau_k \in S_n $ — транспозиции. Глядя на их произведение $\sigma=\tau_1\ldots\tau_k$, 9{к-1} $.

---

Ref : Аналогичное обсуждение можно найти в «Курсе алгебры» Э.Б.Винберга.

БЕСПЛАТНЫХ снежков Математика с четными и нечетными числами

1-й класс • Математика 1-го класса • 2-й класс • Математика 2-го класса • 3-й класс • Математика 3-го класса • БЕСПЛАТНЫЕ распечатки • Математика • Математика Разное. • Зима

16 января 2021 г.

Бет Горден

Помогите детям узнать о четных и нечетных числах с помощью этой милой бесплатной распечатки Математическая игра в снежки . Бросай снежков в зависимости от того, являются ли они четными или нечетными числами в этом веселом математическом задании для детского сада , 1-го, 2-го и 3-го классов! Просто распечатайте PDF-файл с нечетными и четными числами , и вы готовы играть и учиться с забавными зимними печатными формами .

Pdd и даже игры для печати

Мы любим игривые детские математические игры в нашем доме. Не только математические задания для дошкольников помогают детям оставаться заинтересованными и готовыми учиться, но они также помогают детям лучше запоминать содержание! Это упражнение по сортировке четных или нечетных чисел помогает детсадовцам и ученикам 1-го класса практиковаться в определении, являются ли числа четными или нечетными. Упражнение с четными и нечетными числами — отличный способ помочь детям запомнить, какие числа четные, а какие нечетные.

Независимо от того, являетесь ли вы родителем, учителем или учеником на дому, эта зимняя математика наверняка доставит вам удовольствие дома, в качестве математического центра в вашем классе или в качестве дополнения к учебной программе по математике на дому.

Winter Printables

Начните с прокрутки вниз сообщения, под условиями использования, и нажмите на текстовую ссылку, которая говорит >> _____ <<. Файл PDF откроется в новом окне, чтобы вы могли сохранить халяву и распечатать шаблон.

 

Зимняя математика

Просто распечатайте три страницы:

• Коврик для сортировки зимних сцен
• Пронумерованные снежки для сортировки
• Ключ ответа с объяснением четных/нечетных чисел

Вырежьте снежки, и вы готовы к игре. Его можно легко хранить в большом пакете с застежкой-молнией или в защитной пленке для страниц.

Математика снежков

Для выполнения задания ваш ребенок будет сортировать пронумерованные снежки, стараясь, чтобы снежок «попал» в нужную крепость.

Например, если вы подняли 4 снежка, 4 будет четным. Вы бы «кинули» его в ровную снежную крепость.

Зимние развлечения

• Зимний рецепт снежной слизи Занятие для детей
• Как легко сделать снежную глину для рождественских украшений
• FUN Snowman Launcher – зимние развлечения для дошкольников
• Рецепт тающей слизи снеговика и задание
• Приготовление исторической снежной конфеты (с 2 рецептами!)
• Пистолет для рисования снега
• НЯМ! Как сделать снежное мороженое всего из 2 ингредиентов!
• Chilly Snow Dough Antarctica Занятия для дошкольников
• 30+ января Занятия для детей
• Поделка с рождественским украшением безделушка с БЕСПЛАТНЫМИ распечатками
• Деятельность Мартина Лютера Кинга
• Поздравительные открытки ручной работы со снеговиком Зимние поделки для детей

Зимняя наука

Ищете больше развлечений  Зимние научные проекты для детей ? У нас есть много интересных идей, которые вы можете попробовать!

• Супер крутой снежный вулкан Научный эксперимент
• Зимний эксперимент с тающим снеговиком
• Извержение снеговика с простым научным зимним экспериментом со снеговиком для детей
• Тающая слизь снеговика Рецепт
• Легко взрывающийся снеговик — Зимний научный эксперимент
• Снеговик, измеряющий снегопад – Зимнее задание STEM
• Зимние мраморные открытки, созданные с помощью науки
• Зимний научный эксперимент с извергающимся снегом
• Как сделать мороз в консервной банке. Зимний научный эксперимент

 

Распечатки со снеговиком

Ищете рабочие листы со снеговиком и идеи для занятий со снеговиком? Вам понравятся эти ресурсы!

Зимние распечатки

• Build-a-Snowman Winter CVC Words Activity
• Снеговик Части речи Зимние рабочие листы
• Игра «Зрение в словах для детского сада Arctic Animals»
• Игра «Горячий шоколад» или «Варежка: звуки начала»
• Hot Cocoa Winter Rhyming Words Puzzles, игра с зимними рифмованными словами или эти зимние головоломки с рифмованными словами в шляпе
• Снежинка Зимние составные слова Распечатки и упражнения
• Саморегулирующиеся зимние сапоги. Алфавит. Игра 9.0103
• Пазлы из смеси варежек — зимние развлечения для детского сада
• Зимние слоги Печатная деятельность
• Рабочие листы слов «Взгляд пингвина»

Математика снеговика

• Зимняя математика Рассказ о времени Рабочие листы и упражнения
• Карточки со снеговиком
• Умножение снеговика
• Winter Snowballs Нечетные и четные игры для печати
• Счет карточек со снеговиком Упражнение
• Снеговик по математике или эта сборка снеговика по математике для занятий сложением и вычитанием
• Занятия со снеговиком для дошкольников – посчитайте до 10
• Очень милые рабочие листы по зимнему счету для дошкольников
• Практическое занятие по счету снеговиков для юных учащихся
• Пазлы на умножение снеговиков
• Бесплатная печатная книга для подсчета снеговиков

 

Зимняя математика

• Пазлы в форме милого снеговика
• Зимнее математическое задание с карточками с шаблонами Snap Cube
• Математика горячего шоколада – Семейства фактов сложения и вычитания
• Математическая игра варежки для дошкольников
• Фракция Снежинки Активность
• Зимние цвета – игра «Собери пингвинов» или эта игра «Собери варежки»
• Коврики из зимнего пластилина варежки
• Карточки с математическими клипсами Penguin для печати для счета до 20
• Зимняя математика – головоломки с пропуском счета
• Таблица сотен Зимняя раскраска по номерам или эти более простые рабочие листы зимней раскраски по номерам
• Рабочие листы Snowman, работающие над разрядным значением
• Рабочие наборы с пропуском счета для полярных животных

 

• Снеговик Набор рабочих листов с большим количеством страниц по математике, грамоте и многому другому для детей от 3 до 8 лет.
• Посмотрите еще больше идей в этой зимней теме
• Действия пингвинов в День осведомленности о пингвинах 20 января
• Простые зимние раскраски
• Зимние рабочие листы для дошкольников
• Не пропустите эти фантастические зимние книги для чтения вслух, веселые зимние книжки с картинками или эти зимние книги для дошкольников
• Сверните и промокните листы зимних заданий или эти зимние распечатки для изучения цветных слов с помощью маркеров бинго
• Зимние рабочие листы для детского сада и дошкольников
• Рабочие листы «Животные Арктики» — огромный набор с заданиями по математике и грамотности для малышей, дошкольников, первоклассников и первоклассников
• Зимние птицы Рабочий лист для работы с буквами, счета, сложения и многого другого! (огромный пакет!)
• Жизненный цикл пингвинов Страницы рабочего листа
• Последовательность Как слепить снеговика Листы

Четные и нечетные числа Snowball Math Activity

Используя ресурсы с моего сайта, вы соглашаетесь со следующим: этот пост, чтобы получить свою собственную копию)

Это ЗАПРЕЩЕНО продавать, размещать, воспроизводить или хранить на любом другом сайте (включая блог, Facebook, Dropbox и т. д.)

Все предоставленные материалы защищены авторским правом. Пожалуйста, ознакомьтесь с Условиями использования.

Графика Приобретено и используется с разрешения Graphics by Pretty Grafik на Mygrafico.com

Я предлагаю бесплатные печатные материалы, чтобы благословить своих читателей И обеспечить свою семью. Ваши частые посещения моего блога и поддержка покупок через партнерские ссылки и рекламу, так сказать, поддерживают меня. Спасибо!

>> Четные нечетные снежки

<<

Вам также может понравиться

2 сентября 2021 г.

15 января 2021 г.

5 января 2021 г.

15 июня 2022 г.

23 сентября 2019 г.

21 февраля 2022 г.

29 марта 2021 г.

5 июля 2021 г.

Об авторе

Бет Горден

Бет Горден — творческий многозадачный создатель 123 Homeschool 4 Me. Будучи занятой матерью шести детей, занимающейся домашним обучением, она стремится создавать практические учебные задания и рабочие листы, которые детям понравятся, чтобы сделать обучение УДОВЛЕТВОРИТЕЛЬНЫМ! Она создала более 1 миллиона страниц печатных материалов, чтобы научить детей азбуке, естественным наукам, английской грамматике, истории, математике и многому другому! Бет также является создателем 2 дополнительных сайтов с еще большим количеством образовательных мероприятий и БЕСПЛАТНЫХ печатных материалов: www.

No related posts.