Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | ||
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
1.
 4 Умножение | СНКГ
4 Умножение | СНКГПросмотр навигации
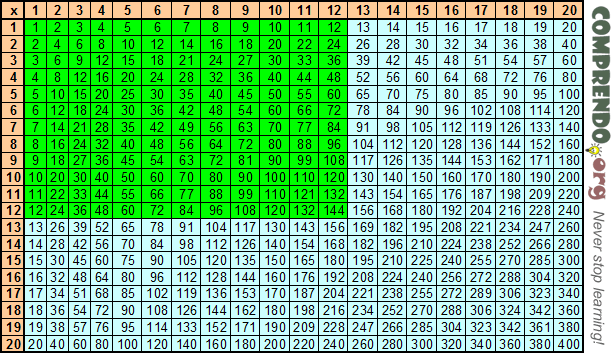
УМНОЖЕНИЕ: ПОВТОРНОЕ СЛОЖЕНИЕ
. Умножение — это более простой способ многократного сложения. Предположим, Рон может сделать 30 отжиманий за одну минуту. Если бы он поддерживал постоянный темп, сколько отжиманий он мог бы сделать за пять минут? Вы можете сложить 30 + 30 + 30 + 30 + 30 или умножить 30 × 5, чтобы получить 150 отжиманий. Некоторые слова и символы, используемые при умножении умножить на , произведение , знака «×» или точки вроде «•». Иногда перемножаемые числа заключаются в скобки (30)(5)=150.
Пример 1. Каждый член вашей бригады из шести человек несет по пять литров воды. Сколько литров воды в общей сложности у вашей команды?
Задача на умножение будет 5 × 6 = 30.
Этот процесс аналогичен шестикратному прибавлению 5.
Когда речь идет о больших числах, умножение намного проще, чем многократное сложение.
Пример 2 – Умножьте 17 на 63.
Шаг 1. Умножьте верхнее число на число в разряде единиц, что равно 3.
17 × 3 = 51
Шаг 2. Умножьте на число в разряде единиц Десятки или 60, поставив «0» в разряде единиц и умножив 17 × 6.
17 × 60 = 1020
Шаг 3. Сложите их вместе.
17 × 63 = 51 + 1020 = 1071
Пример 3. Умножьте 374 × 261.
Выполните те же действия, что и выше.
Шаг 1. Умножьте 374 на 1,
Шаг 2. Умножьте на 60. Поставьте «0» в разряде единиц, а затем умножьте 374 на 6.
Шаг 3. Умножьте на 200. Поставьте «0» в разряде единиц и десятков, а затем умножьте 374 на 2. .
Шаг 4. Добавьте числа.
374 + 22 440 + 74 800 = 97 614
Ответ на 374 × 261 равен 97 614.
Умножение чисел со знаком
При умножении двух чисел с одинаковым знаком ответ будет положительным числом. Положительное число, умноженное на положительное число, всегда дает положительный ответ.

 3
3 14159..
14159..