17 число четное или нечетное число: Таблица нечётных чисел от 0 до 100

Содержание

Четные и нечетные числа | Образовательная социальная сеть

Районная научно — практическая конференция учащихся и педагогов

Предмет «математика»

Номинация «Реферат проблемно — поискового характера»

Тема: «Четные и нечетные числа»

Автор: Шнякина Алина учащаяся 5 класса

МОБУ «Рыбкинская средняя общеобразовательная школа»

Учитель: Окшина Л.А.

2011 – 2012 учебный год

МОБУ «Рыбкинская средняя общеобразовательная школа»

Чётные и нечётные числа.

/Реферат/

Работу выполнила

ученица 5 класса

Шнякина Алина.

Работу проверил

учитель математики

Окшина Л. А.

с. Рыбкино 2012г.

Оглавление

Введение 4

Основная часть 5

Определение. Свойства. 5

Традиции 6

Пифагорейская теория чисел 8

Нумерология 10

Вывод 12

Литература 13

Введение.

Цель: узнать, почему четным и нечетным числам приписывают различный смысл.

Задачи:

Найти определение и свойства четных и нечетных чисел.
Какие традиции в различных странах связаны с числами?
Как четные и нечетные числа применяются в нумерологии?

План:

Введение.
Основная часть.

Определение. Свойства;

Традиции;
Пифагорейская теория чисел;
Нумерология.

Вывод.

Актуальность.

Еще в древности люди отмечали влияние чисел и зависимость судьбы от совпадения или, наоборот, невыпадения определенных чисел, а также цикличность всего происходящего в мире. Не философы и не мыслители, скорее всего, вообще в своей массе простые и не слишком образованные люди очень верно выражали это в сказках и мифах, где чаще всего фигурируют тройка и семерка.

В сказках жили-были три богатыря, трое или семеро сыновей, семь гномов, а царство числилось тридевятым! Чтобы не сглазить свою удачу, люди традиционно трижды сплевывали (и сейчас тоже!) через левое плечо или стучали по дереву. Особо любимые числа часто встречаются в пословицах и поговорках: «Бог троицу любит», «семеро одного не ждут», «семь раз отмерь, один раз отрежь»…

Почему в основном в сказках применяются нечетные числа?

Почему на день рождения дарят нечетное число цветов? И еще много вопросов встало передо мною.

Я решила узнать об этом. Нашла материал и начала своё исследование.

Основная часть.

Определение.

Чётное число — целое число, которое делится без остатка на 2: например: 2, 4, 6, 8, …
Нечётное число — целое число, которое не делится без остатка на 2: например: 1, 3, 5, 7, 9, …

В соответствии с этим определением нуль является чётным числом.

Если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.

42, 104, 11110, 9115817342 — чётные числа.

31, 703, 78527, 2356895125 — нечётные числа

Свойства.

Сложение и вычитание:

Чётное ± Чётное = Чётное
Чётное ± Нечётное = Нечётное
Нечётное ± Чётное = Нечётное
Нечётное ± Нечётное = Чётное

Умножение:

Чётное × Чётное = Чётное
Чётное × Нечётное = Чётное
Нечётное × Нечётное = Нечётное

Деление:

Чётное / Чётное — однозначно судить о чётности результата невозможно (если результат целое число, то оно может быть как чётным, так и нечётным)
Чётное / Нечётное = если результат целое число, то оно Чётное
Нечётное / Чётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
Нечётное / Нечётное = если результат целое число, то оно Нечётное.

Традиции.

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В разных странах существуют традиции, связанные с количеством даримых цветов.

Например, в Европе, США и некоторых государствах востока существует поверье, что четное количество цветов приносит счастье.

По российским традициям четное количество цветов приносят на похороны, а живому человеку пристало дарить цветы только в нечетном количестве.
Существует несколько версий о происхождении этой традиции.
Языческие верования трактуют четные числа – как символы смерти и зла. Помните поговорку «беда не приходит одна»? Именно из следования этой традиции и пошел обычай дарить живым людям только четное количество цветов.

Многими древними культурами, парные числа связывались с законченностью, завершением, в данном случае – жизненного пути. Нечетное число, (кроме 13) напротив, символ счастья, успеха, везения. Нечетные числа нестабильны, они символизируют движение, жизнь, смех. Четные – символ умиротворенности и покоя.

Для древних пифагорейцев олицетворением добра, жизни, света были нечетные числа, а еще они символизировали правую сторону (сторону удачи). Неудачливую же левую сторону, и вместе с ней смерть, зло, тьму – символизировали четные числа.

Не отсюда ли пошло знаменитое «встать с левой ноги», символизирующее неудачное начало дня? В японской культуре числа 1,3,5 обозначают мужское начало «янь» и говорят о жизни, силе, движении. Числа 2,4,6, — это женское начало «инь», покой, пассивность. В Японии не принято дарить живым людям четыре цветка, потому что число 4 символизирует смерть.

Израильтяне, наоборот – дарят четное количество цветов, а вот на похороны цветы не приносят. В Грузии считают, что все связанное с семейными ценностями приносит счастье, поэтому два цветка (пара) – удачное сочетание, а на кладбище несут нечетное количество цветов «чтобы покойный пару не забрал с собой». Европеец и американец может с наилучшими намерениями подарить русской девушке 8 или 10 роз, и искренне удивиться ее реакции.

Стоит отметить, что столь придирчивый счет цветов имеет место лишь до дюжины. После этого количества не имеет значение четное или нет количество стеблей в букете. Ведь, пресловутый «миллион алых роз» — имеет четное количество цветов.

Во многих сказках^[1] мы встречаем разные числа. Чаще всего это числа ТРИ и СЕМЬ.

Число «3» издревле считали магическим. Даже в библии бог предстает в триедином лице. 3- это божественное совершенство. Известно выражение: Бог троицу любит.

Цифра «3» в сказках наталкивает читателя на мысль о волшебстве, о совершенстве. Ведь в русских сказках всегда желания исполняются только в третий раз.

«Три девицы под окном

Пряли поздно вечерком».

«И очутятся на бреге,

В чешуе как жар горя,

Тридцать три богатыря.»

7 – число особое. Так, известно, что жрецы Вавилона поклонялись семи богам. Символика числа 7 характерна и для библейских сюжетов. Богословы трактуют это число как соединение числа 3-божественного совершенства и 4 –мирового порядка.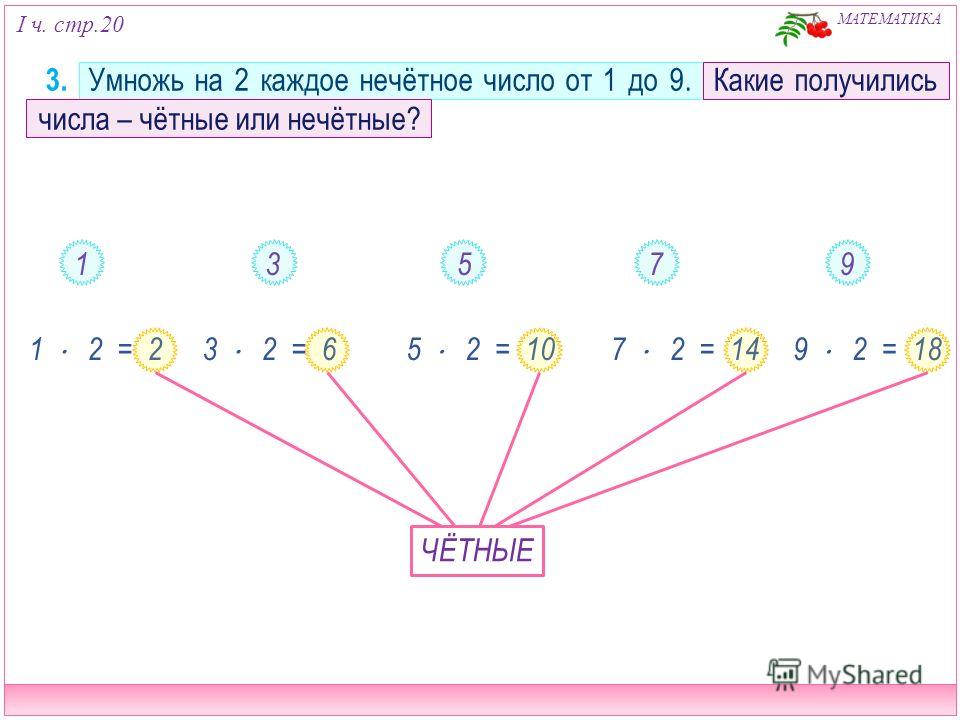

В русских поговорках и пословицах слово «семь» часто выступает в значении «много»: «Семеро одного не ждут», «Семь раз отмерь – один раз отрежь», «Семь бед – один ответ», «Лук от семи недуг» и т. д. В сказке А.С. Пушкина число 7 тоже имеет значение «много»: «семь богатырей, семь румяных усачей».

В приданое царевне было дано «семь торговых городов да сто сорок теремов».

А вот с четными числами есть суеверное представление: оно связано со смертью, с нечистой силой.

Значит, выбор числительных в сказках основан на народном представлении о значении чисел.

Пифагорейская теория чисел.

Пифагор^[2] определяя число как энергию и считал, что через науку о числах раскрывается тайна Вселенной, ибо число заключает в себе тайну вещей.

Проникая в свойства чисел, объясняя их различные сочетания, Пифагор пытался создать науку всех наук. Все числа он разделил на два вида: четные и нечетные, и с удивительной чуткостью выявил свойства чисел каждой группы. Четные числа обладают следующими свойствами: любое число может быть разделено на две равные части, обе из которых либо четны, либо нечетны. Например, 14 делится на две равные части 7 + 7, где обе части нечетные; 16 = 8 + 8, где обе части четные. Пифагорейцы рассматривали четное число, прототипом которого была дуада^[3], неопределенным и женским.

Четные числа Пифагор делил на 3 класса: четно-четные, четно-нечетные, нечетно-нечетные.

Четно – четные — числа, которые представляют собой удвоение чисел, начиная с единицы. Таким образом, это 1,2,4,8,16,32,64,128,512 и 1024. Совершенство этих чисел Пифагор видел в том, что они могут делиться пополам и еще раз, и так далее до получения единицы.

Четно-нечетные числа — это числа, которые будучи разделены пополам не делятся.

Нечетно-нечетные числа неоднократно делятся пополам, но при делении не придут к 1.

Нечетные числа не могут быть разделены равным образом, то есть поровну. Пифагор объяснял неспособность таких чисел делится пополам следующим образом: поскольку 1 всегда остается не делимой, нечетное число таким же образом не может быть делимым. Если нечетное число попытаться разделить поровну, то получается два четных числа, а последнее из них единица, которая является неделимой. Например, 9 есть 4+4+1.

Нечетные числа имеют и такое свойство — если какое-либо нечетное число разделить на две части, одна всегда будет четной, а другая — всегда нечетной.

Пифагорейцы рассматривали нечетное число, прототипом которого была монада^[4], определенным и мужским, хотя по поводу 1 (единицы) среди них существовали определенные разногласия.

Нечетные числа делятся на 3 общих класса: несоставные, составные и несоставные — составные.

Несоставные числа — это такие числа, которые не имеют других делителей, кроме себя самого и единицы. Это числа 3,5,7,11,13,17 и т.д.

Составные числа — это числа, делимые не только сами на себя, но и на некоторые другие числа. Такими числами являются те из нечетных чисел, которые не входят в группу несоставных. Это числа 9,15,21,25,27,33,39 и т.д.

Несоставные — составные числа — эта числа, не имеющие общего делителя, хотя каждое из них делимо.

Обычаем у пифагорейцев было приношение высшим богам нечетного числа предметов, в то время как богиням и подземным духам приносить четное число.

Все числа представляют собой чет и нечет, точно так же и все вещи и процессы соединяют в себе противоположности – начало и конец, предел и бесконечность. Каждое явление или вещь Пифагор рассматривал как примирение противоположностей – гармонию. Поиск внутреннего различия и гармонии всей реальности посредством числа объединял Бога, душу и природу в единое целое. Знать природу и числа, ее определяющие, значит, по мнению ученого, знать Бога.

Нумерология.^[5]

А можно ли узнать, сколько радостей, счастливых дней, бед и несчастий предназначено в жизни каждому из нас? В поисках ответа люди издавна по своим наблюдениям стали приписывать цифрам особый магический смысл. Это позволило растолковать зависимость явлений от чисел и объяснить их законы. Так зарождалась наука о числах – нумерология. Особая роль в становлении нумерологии принадлежит великому Пифагору – древнегреческому философу и математику, который объединил математику с науками о природе человека.

Нумерология утверждает, что числа обладают определенными свойствами, которые они распространяют на все предметы и явления мира.

Чётные и нечётные числа применяются в нумерологии.

Во вселенной существуют пары противоположностей, которые являются важным фактором ее устройства. Основные свойства, которые нумерология приписывает нечетным (1, 3, 5, 7, 9) и четным (2, 4, 6, 8) числам, как парам противоположностей, следующие:

1 — активный, целеустремленный, властный, черствый, руководящий, инициативный;

2 — пассивный, восприимчивый, слабый, сочувствующий, подчиненный;

3 — яркий, веселый, артистичный, удачливый, легко добивающийся успеха;

4 — трудолюбивый, скучный, безынициативный, несчастный, тяжелый труд и частое поражение;

5 — подвижный, предприимчивый, нервный, неуверенный;

6 — простой, спокойный, домашний, устроенный; материнская любовь;

7 — уход от мира, мистика, тайны;

8 — мирская жизнь; материальная удача или поражение;

9 — интеллектуальное и духовное совершенство.

Нечетные числа обладают гораздо более яркими свойствами. Рядом с энергией «1», блеском и удачливостью «3», авантюрной подвижностью и многогранностью «5», мудростью «7» и совершенством «9» четные числа выглядят не столь ярко. Насчитывается 10 основных пар противоположностей, существующих во Вселенной. Среди этих пар: четное — нечетное, один — много, правое — левое, мужское — женское, добро — зло. Один, правое, мужское и доброе ассоциировалось с нечетными числами; много, левое, женское и злое — с четными.

Мужские свойства нечетных чисел вытекают из того факта, что они сильнее четных. Если четное число расщепить пополам, то, кроме пустоты, посередине ничего не останется. Нечетное число разбить непросто, потому что посередине остается точка. Если же соединить вместе четное и нечетное числа, то победит нечетное, так как результат всегда будет нечетным. Именно поэтому нечетные числа обладают мужскими свойствами, властными и резкими, а четные — женскими, пассивными и воспринимающими.

Нечетных чисел нечетное число: их пять. Четных чисел четное число — четыре.
Нечетные числа — солнечные, электрические, кислотные и динамичные. Они являются слагаемыми; их с чем либо складывают. Четные числа — лунные, магнетические, щелочные и статичные. Они являются вычитаемыми, их уменьшают. Они остаются без движения, потому что имеют четные группы пар (2 и 4; 6 и 8).

Если мы сгруппируем нечетные числа, одно число всегда останется без своей пары (1 и 3; 5 и 7; 9). Это делает их динамичными. Два подобных числа (два нечетных числа или два четных) не являются благоприятными.

четное + четное = четное (статичное) 2+2=4

четное + нечетное = нечетное (динамичное) 3+2=5

нечетное + нечетное = четное (статичное) 3+3=6

Некоторые числа дружественны, другие — противостоят друг другу. Взаимоотношения чисел определяются отношениями между планетами, которые ими управляют (подробности в разделе «Совместимость чисел»). Когда два дружественных числа соприкасаются, их сотрудничество не очень продуктивно. Подобно друзьям, они расслабляются — и ничего не происходит. Но когда в одной комбинации находятся враждебные числа, они заставляют друг друга быть настороже и побуждают к активным действиям; таким образом, эти два человека работают намного больше. В таком случае, враждебные числа оказываются на самом деле друзьями, а друзья — настоящими врагами, тормозящими прогресс. Нейтральные числа остаются неактивными. Они не дают поддержки, не вызывают и не подавляют активность.

Вывод.

В ходе работы я выяснила, что не зря Пифагор сказал «Число есть всё». Нечетные числа, особенно 3 и 7, являлись символом полноты, счастья. В сказках часто встречается тройка персонажей. А в радуге не случайно семь цветов, на свете семь чудес света, в неделе 7 дней. В Библии есть упоминание о семи светильниках, семи ангелах, о семи годах изобилия и семи – голода.

Еще с древних времен остались обычаи дарить четное или нечетное количество цветов, хотя в разных странах по — разному.

И еще я выяснила, что есть целая наука, которая занимается числами. Это нумерология. Числовые совпадения встречаются сплошь и рядом – в номерах телефонов и автомобилей, в адресах и номерах этажей, в датах рождения. Это не случайные совпадения, а вполне определенная зависимость, так называемая магия чисел. Числа не только позволяют измерять количества, но и обозначают свойства и качественные характеристики, обращают наше внимание на различные явления и могут о многом рассказать. Числа магическим, неотвратимым образом влияют на нашу жизнь, на самые разные события, и невозможно отрицать, что магия чисел существует. Надо только найти ключ к их тайному коду.

Я поняла, что, изучая числа и их роль, можно лучше понять историю своего народа по сказкам. Зная дату рождения, можно определить характер человека. Поэтому работа над этим рефератом мне очень понравилась.

Литература.

Людмила Большедворова. Нумерология. Коды жизни и судьбы. Введение. Немного о нумерологии.
Пропп В.Я. «Исторические корни Волшебной сказки»
http://ru. wikipedia.org
http://www.opakyl.ru/number.php?id=10
http://numerology.astrostar.ru/number/133702.html
http://ru.math.wikia.com/wiki/
http://skazvikt.ucoz.ru

[1] Пропп В.Я. «Исторические корни Волшебной сказки»

[2] Пифагор Самосский ( 570—490 гг. до н. э.) – древнегреческий философ, математик и мистик, создатель религиозно – философской школы пифагорейцев.

[3] Дуада — символ деления единого на противоположности.

[4] Монада (греч. monas — единица, единое)

[5] Людмила Большедворова. Нумерология. Коды жизни и судьбы. Введение. Немного о нумерологии.

Чётные и нечётные числа. Традиции русской народной свадьбы

ВикиЧтение

Традиции русской народной свадьбы
Соколова Алла Леонидовна

Содержание

Чётные и нечётные числа

При анализе свадебных обычаев становится понятно, что русские люди считали нечётные числа благоприятными. Да и в наше время крепка эта примета: «нечет» символизирует жизнь, а «чёт» – наоборот. Это наглядно демонстрирует современное правило о количестве цветов в букетах (на праздники мы дарим букеты с нечётным числом цветом, а на похороны выбираем чётное количество).

Перечислим свадебные поверья, связанные с «нечетом»:

Наиболее благоприятными числами для сватовства считались 3, 7, 9, 11;

На сговоре должно было присутствовать нечётное число гостей;

Число подвод свадебного поезда должно быть нечётным;

Каравай должно печь нечётное количество женщин;

Практически любая свадьба праздновалась три дня (реже пять или семь дней).

Вполне возможно, это правило могло распространяться и на другие свадебные события.

Данный текст является ознакомительным фрагментом.

ПРИЛОЖЕНИЕ 2 Зависимость числа убитых и оставшихся без крова от тоннажа бомбового груза; и оценки, вытекающие из теорий Линдемана и Блэкетта

ПРИЛОЖЕНИЕ 2 Зависимость числа убитых и оставшихся без крова от тоннажа бомбового груза; и оценки, вытекающие из теорий Линдемана и Блэкетта 1. Теорииа) Теория профессора Блэкетта, изложенная в его «Заметках о некоторых аспектах методологии исследования операций;

Кафедра Ваннаха: Мир без числа e

Кафедра Ваннаха: Мир без числа e Автор: Ваннах МихаилОпубликовано 19 октября 2011 годаОдним из самых популярных жанров ныне является альтернативная история. Ну, какие книги лидируют в магазинах на тему Великой Отечественной войны? Да рассуждения о том, как славно/ужасно было

Пушкин А. С. – Гоголю, март – первые числа (не позднее 7) апреля 1834

Пушкин А. С. – Гоголю, март – первые числа (не позднее 7) апреля 1834 Март – первые числа (не позднее 7) апреля 1834 г. Петербург [257]Вы правы – я постараюсь. До свидания.А.

24. Поход глазами туристов. Коммуникативные отношения в группе Игоря Дятлова на основании анализа походных фотоснимков.

Доказательство наличия у членов группы большего числа фотоаппаратов, нежели зафиксировано материалами уголовного дела

24. Поход глазами туристов. Коммуникативные отношения в группе Игоря Дятлова на основании анализа походных фотоснимков. Доказательство наличия у членов группы большего числа фотоаппаратов, нежели зафиксировано материалами уголовного дела Уже после завершения

И тяжбам несть числа

И тяжбам несть числа Инновационные сервисы Google ставят сложные юридические вопросы, требующие решений креативных и вместе с тем практических. В поисках таких решений мы работаем там, где область передовых технологий соприкасается с областью действующих законодательных

М. И. ГОГОЛЬ 1825-го года. Июня 10-го числа. <Нежин>

М. И. ГОГОЛЬ 1825-го года. Июня 10-го числа. <Нежин> Письмо ваше, дражайшая маминька, (писанное 24 мая), я получил 3-го июня и спешу отвечать вам. — Я не знаю, получили ли вы прежние два письма, которые я к вам писал одно последних чисел мая, а другое первых июня. Вы не поверите,

А. С. ДАНИЛЕВСКОМУ 1825-го года, августа 17 числа, Гимназия

А. С. ДАНИЛЕВСКОМУ 1825-го года, августа 17 числа, Гимназия Ты не поверишь, как я был раздосадован, узнавши, как ты был в Гимназии и мне не удалось тебя видеть. А мне бы весьма хотелось тебе порассказать и пересказать много разных разностей, из коих некоторые для тебя были бы

А. П. ТОЛСТОМУ Фрейвалдау. Июнь — не помню числа <18 июня н. ст. 1846>

А. П. ТОЛСТОМУ Фрейвалдау. Июнь — не помню числа <18 июня н. ст. 1846> Наконец, пишу к вам из Греффенберга, куда прибыл благополучно, отдохнул два дни и вот уже другой день начал лечение. От дороги ли, [или] а может быть, отчасти, и от грубиевского прописания, которое я выполнял

Ю. Ф. САМАРИНУ <20-ые числа августа н. ст. 1846. Остенде.>

Ю. Ф. САМАРИНУ <20-ые числа августа н. ст. 1846. Остенде.> В проезд мой через Париж я познакомился с вашим братцем и от него получил ваше письмо, за которое вас благодарю очень, потому что оно доставило мне короткое знакомство с вами, [Далее начато: Вы сделали] введя меня в ваши

<ОТВЕТ НА АНКЕТУ ЖУРНАЛА «ЧИСЛА»>

<ОТВЕТ НА АНКЕТУ ЖУРНАЛА «ЧИСЛА»> Что вы думаете о своем творчестве? Разбросанным в пыли по магазинам, Где их никто не брал и не берет — Моим стихам, как драгоценным винам, Настанет свой черед. Марина ЦветаеваМосква 1913—Париж

<Двадцатые числа декабря 1911 г.

Москва>

<Двадцатые числа декабря 1911 г. Москва> <В Париж>[41]Ну не ожидал я от Вас, Елизавета Яковлевна, моя добрая, хорошая, распрекрасная, такого сюрприза, какой Вы сделали мне Вашим глубоко философским письмом.— К чему вся эта философия?Не проще ли было бы сказать на словах

Формула для нечетных чисел — Что такое формула для нечетных чисел? Примеры

Прежде чем приступить к изучению формулы нечетных чисел, давайте вспомним, что такое нечетные числа. Нечетные числа — это целые числа, которые нельзя точно разделить на 2. Например, числа 1, 3, 5, 7, 9,… — нечетные числа. Формула нечетных чисел помогает представить нечетное число в целом. Давайте узнаем о формуле для нечетных чисел с несколькими примерами в конце.

Какая формула для нечетных чисел?

Нечетное число всегда может быть выражено как 1 плюс или минус четное число.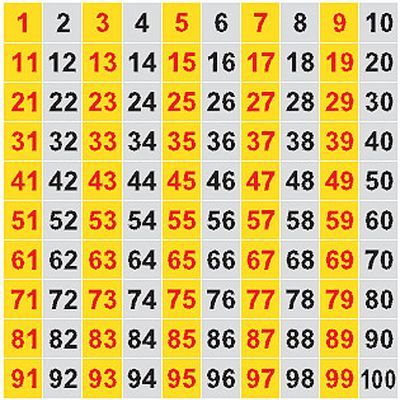 Мы знаем, что четное число имеет вид 2n, где n — целое число. Таким образом, формула для нечетных чисел может быть представлена следующим образом:

Формула для нечетных чисел = 2n ± 1

, где n ∈ W (целые числа)

Еще один способ проверить, является ли число нечетным. может напрямую разделить его на 2. Если число делится точно, это четное число, в противном случае это нечетное число.

Формула суммы нечетных чисел

Мы только что прочитали об общей формуле для нахождения последовательности нечетных чисел. Мы также можем формулу суммы n нечетных чисел выразить как:

Сумма n нечетных чисел = n ² , где n — натуральное число. Чтобы вычислить сумму первых n нечетных чисел вместе, фактически не складывая их по отдельности. т. е. 1 + 3+ 5 +………..n членов = n ²
Сумма нечетных чисел от 1 до l= [(1+l)/2] ² Чтобы найти сумму всех последовательных нечетных чисел от 1 до l, сложите 1 и l. Получите половину. Возведите его в квадрат, чтобы получить ответ.
Сумма квадратов n нечетных чисел1 ² + 3 ² + 5 ² +………..(2n-1) ² слагаемых = n(4n ² — 1)/3
Сумма кубов n нечетных чисел 1 ³ + 3 ³ + 5 ³ +………..(2n-1) ³ = n ² (2n ² -1)

Рассмотрим применение формулы для нечетных чисел в следующем разделе.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Забронируйте бесплатный пробный урок

Примеры формулы для нечетных чисел

Пример 1: Проверьте, является ли 23 нечетным числом, используя формулу для нечетных чисел.

Решение:

Чтобы найти: Проверьте, является ли 23 нечетным числом.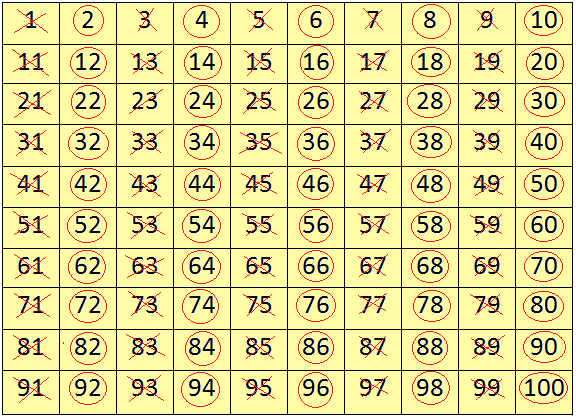
При делении 23 на 2 в остатке остается 1.
Таким образом, мы заключаем, что 23 — нечетное число.

Ответ: 23 — нечетное число.

Пример 2: Используя формулу для нечетных чисел, решите следующее.

а) 1+ 3 + 5 + 7 + ……………….40 слагаемых Найдите сумму 40 слагаемых.

б) Найдите сумму нечетных чисел от 1 до 51.

Решение:

. =26 ² = 676

Пример 3: Сумма 3 последовательных нечетных чисел равна 21. Найдите 3 числа, используя формулу для нечетных чисел.

Решение: Пусть 3 последовательных нечетных числа равны 2n+1, 2n+3 и 2n +5

дано: (2n+1) + (2n+3) + (2n +5) = 21

6n + 9 = 21

6n = 12

n = 2

Таким образом, 2n + 1 = 5
2n + 3 = 7
2n + 5 = 9

Следовательно, 3 последовательных нечетных числа — это 5, 7 и 9.

Часто задаваемые вопросы о формуле нечетных чисел

Как определить ряд нечетных чисел с помощью формулы нечетных чисел?

Чтобы определить ряд нечетных чисел, мы будем использовать формулу нечетных чисел, которая может быть выражена как:
Нечетные числа = 2n + 1, где n ∈ W (целые числа)

Какие существуют способы определения нечетных чисел?

Чтобы идентифицировать нечетное число, мы можем напрямую разделить его на 2. Если число точно делится на 2, оно не является нечетным. Например, 4 не является нечетным числом, поскольку оно точно делится на 2.

Что представляет n в формуле для нечетных чисел (2n+1)?

Чтобы найти серию нечетных чисел, мы используем общую формулу нечетных чисел (2n+1). Здесь n представляет целые числа. Для определения суммы по n нечетным числам мы используем формулу n

2 , где n — натуральное число.

Сумма нечетных чисел – формула, доказательство, примеры

Нечетные числа определяются как любое число, которое не кратно 2 или имеет нечетную цифру разряда единиц, например 3, 45, 67 и т. д. Сумма нечетные числа — это общая сумма нечетных чисел, взятых вместе для любого заданного диапазона. Мы узнаем о сумме нечетных чисел и сумме первых n нечетных чисел, используя формулы и примеры в этой статье.

1.	Сумма нечетных чисел Определение
2.	Формула суммы n нечетных чисел
3.	Доказательство суммы первых n нечетных чисел
4.	Часто задаваемые вопросы о сумме нечетных чисел

Сумма нечетных чисел Определение

Сумма нечетных чисел определяется как сумма нечетных чисел, взятых вместе и сложенных для вычисления результата. Сумма нечетных чисел начинается с 1 и доходит до бесконечности. Мы можем найти сумму нечетных чисел для любого диапазона, например от 1 до 100, от 1 до 50 и т. д., используя формулу суммы n нечетных чисел, включающую концепцию арифметической прогрессии, обсуждаемую в следующем разделе.

Формула суммы n нечетных чисел

Мы знаем, что нечетное число имеет общую форму (2n — 1), где n — целое число. Кроме того, последовательные нечетные числа имеют общую разность 2. Следовательно, ряды нечетных чисел образуют арифметическую прогрессию. Формула суммы n нечетных чисел описывается следующим образом:
Сумма n нечетных чисел = n ², где n — натуральное число, представляющее количество терминов.

Таким образом, чтобы вычислить сумму первых n нечетных чисел без фактического сложения их по отдельности, мы можем использовать формулу суммы n нечетных чисел, т. е. 1 + 3 + 5 +……….. .n членов = n

2 .

Сумма первых n нечетных чисел Доказательство

Теперь выведем формулу суммы n нечетных натуральных чисел. Мы знаем, что ряд нечетных чисел задается как 1, 3, 5,… (2n — 1), что образует арифметическую прогрессию с общей разностью 2. Пусть сумма первых n нечетных чисел представлена в виде S _n = 1 + 3 + 5 +…+ (2n — 1). Здесь 1 представляет первое нечетное число, а (2n — 1) представляет последнее нечетное число.

Таким образом, первый член (a) = 1, последний член (l) = 2n — 1 и обычная разность (d) = 2,

Сумма n членов АП определяется по формуле S _n = n/2 × [a + l].

Подставляя значения ‘a’ и ‘l’ в приведенную выше формулу, мы получаем

S _n = n/2 × [1 + (2n — 1)]
S _n = n/2 × [2n]
S _n = n × n
S _n = n ²

Таким образом, при n = 1 S ₁ = 1 ² = 1
когда n = 2, S ₂ = 2 ² = 4
когда n = 3, S ₃ = 3 ² = 9

Таким образом, мы доказали, что сумма первых n нечетных чисел равна n ² . Давайте возьмем пример, чтобы понять это.

Пример: Найдите сумму нечетных чисел от 1 до 50.

Мы знаем, что существует 25 нечетных чисел от 1 до 50. Таким образом, используя формулу суммы n нечетных чисел, которая равна n ² , мы получить, S ₂₅ = 25 ² = 625.

Альтернативно мы можем показать это, используя формулу S _n = n/2 × [a + l]. Мы знаем, что сумма нечетных чисел от 1 до 50 представляется как S _n = 1 + 3 + … + 49.
Таким образом, a = 1, l = 49 и n = 25.
S ₂₅ = (25/2) × [1 + 49]
= (25/2) × 50
= 25 × 25 = 625

Таким образом, сумма нечетных чисел от 1 до 50 равна 625.

Статьи по теме

Проверьте эти статьи, связанные с понятием суммы нечетных чисел.

Нечетные числа
Натуральные числа
Арифметическая прогрессия
Сумма n членов AP

Часто задаваемые вопросы о сумме нечетных чисел

Что такое сумма нечетных чисел?

Сумма нечетных чисел определяется как сложение или суммирование всех нечетных чисел, присутствующих в заданном диапазоне. Например, чтобы вычислить сумму нечетных чисел от 1 до 10, мы рассмотрим все нечетные числа в этом диапазоне и сложим их. 1 + 3 + 5 + 7 + 9= 25.

Какова формула суммы нечетных чисел?

Мы знаем, что ряды нечетных чисел всегда находятся в AP, так как общая разность между ними равна 2. Формула для нахождения суммы нечетных чисел: S _n = n/2 × [a + l], где ‘a ‘ — первое нечетное число, «l» — последнее нечетное число, а «n» — количество нечетных чисел в этом диапазоне. Другая формула для вычисления суммы нечетных чисел: S _n = n ² .

Как найти сумму нечетных чисел?

Сумму нечетных чисел можно рассчитать по формуле S _n = n/2 × [a + l], где «a» — первое нечетное число, «l» — последнее нечетное число, а «n» — количество нечетных чисел или S _n = n ² . Чтобы вычислить сумму нечетных чисел от 1 до 20, мы будем использовать S _n = n ², где n = 10, поскольку существует 10 нечетных чисел от 1 до 20. Таким образом, S ₁₀ = 10 ² = 100.

Какая формула для суммы первых n нечетных чисел?

Формула для суммы первых n нечетных чисел задается как S _n = n ², где n представляет количество нечетных чисел.

Как найти сумму первых n нечетных чисел?

Чтобы найти сумму первых n нечетных чисел, мы можем использовать формулу S _n = n ² . Например, чтобы вычислить сумму нечетных чисел от 1 до 10, мы знаем, что n = 5. Таким образом, S ₅ = 5 ² = 25.

Чему равна сумма первых n нечетных натуральных чисел?

Сумма первых n нечетных натуральных чисел может быть представлена как 1 + 3 + 5 + … + (2n — 1), где 1 — первое нечетное число, а (2n — 1) — последнее нечетное число. В этом AP-ряду n натуральных чисел. Сумма n членов АП определяется по формуле S _n = n/2 × [a + l], где a — первое нечетное число, а l — последнее нечетное число. Таким образом, сумма первых n нечетных натуральных чисел рассчитывается как
.