Перевод десятичных чисел в дробь: онлайн калькулятор
Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.
Представление дробей
Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби:
- 0,5 = 1/2;
- 0,25 = 1/4;
- 1,375 = 11/8.
И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа.
Избавляемся от запятой
Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая.
Такое преобразование осуществляется в три шага:
Шаг 1: Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1.
Шаг 2: После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:
- 0,5/1 = 5/10;
- 0,25/1 = 2,5/10 = 25/100;
- 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.
Шаг 3: Сокращаем полученные дроби до удобоваримого вида:
- 5/10 = 1 × 5 / 2 × 5 = 1/2;
- 25/100 = 1 × 25 / 4 × 25 = 1/4;
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8.
Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей.
Избавляемся от запятой еще проще
Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс.
И вновь мы выполняем три шага.
Шаг 1: Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.
Шаг 2: Теперь нам достаточно представить дробь в виде C/10n, где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:
- для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/103 = 1375/1000;
- для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/106 = 625/1000000.
По сути, 10n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.
Шаг 3: Сокращаем нули и получаем итоговый результат:
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
- 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.
Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.
Преобразование на слух
Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби.
0,025 = 25/1000 = 1/40
Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости.
Примеры использования дробей в повседневной жизни
На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач. Рассмотрим пару примеров.
Работа
Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.
0,4 = 4/10 = 2/5
Быт
К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:
0,12 = 12/100 = 3/25
Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.
Заключение
Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.
Десятичные дроби — как решать примеры 5, 6 класс
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной.
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
| Основные свойства |
|---|
|
Обыкновенная и десятичная дробь — давние друзья.
Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Как решаем:
- Знаменатель равен 10 — это один ноль.
- Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
- В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.
Ответ: 16/10 = 1,6.
Пример 2. Перевести 37/1000 в десятичную дробь.
Как решаем:
- Знаменатель равен 1000 — это три нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Так как в числителе только две цифры, то на пустующие места пишем нули.
- В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.
Ответ: 37/1000 = 0,037.
Приходите решать увлекательные задачки с красочными героями и в интерактивном формате. Запишите вашего ребенка на бесплатный вводный урок в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
и т. д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
1% = 1/100 = 0,01
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
0,15 = 0,15 · 100% = 15%.
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого.
Преобразование десятичных дробей
Быстрая напоминалка:
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Как решаем:
- Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
- А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.
Ответ: 5,4 = 5 2/5.
Пример 2.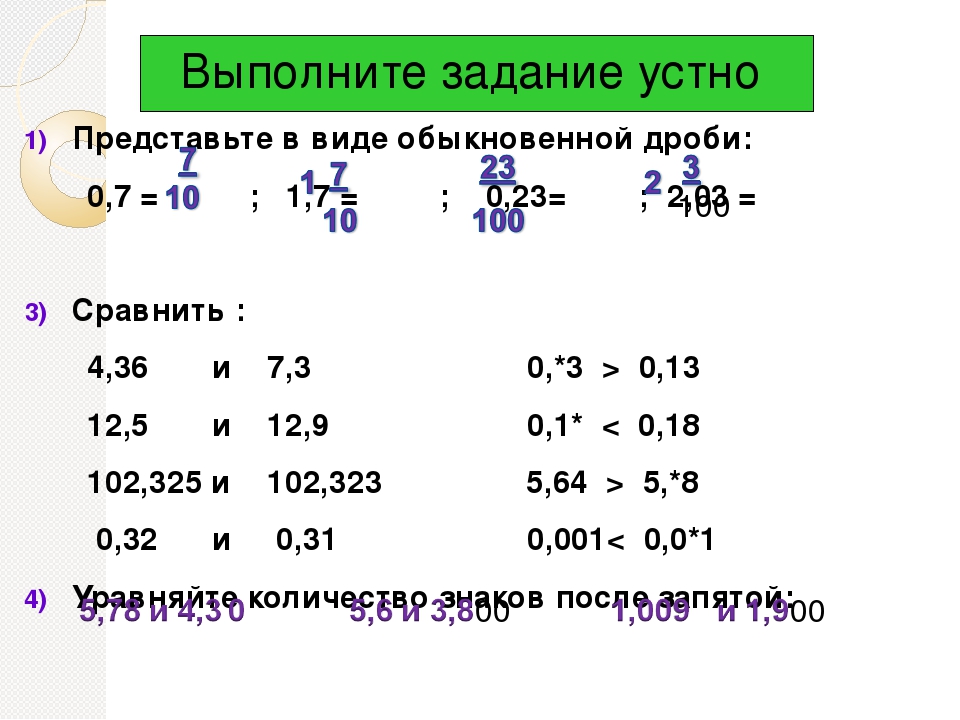
Перевести 4,005 в смешанное число.
Как решаем:
- Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как решаем:
- Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
- Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.
Ответ: 5,60 = 5 6/10.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.
Например:Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
- Разделить целую часть десятичной дроби на это число.
- Поставить запятую в частном и продолжить вычисление, как при обычном делении.
Как решаем:
- Записать деление уголком.
- Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
- Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
- Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:
Ответ: 4,8 : 2 = 2,4.
Пример 2. Разделить 183,06 на 45.
Как решаем:
- Записать деление уголком.
- Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
- Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
- Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.Как решаем:
- Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
- Разделить дробь по правилам:
Ответ: 0,25 : 3/4 = 1/3.
Пример 2. Разделить 2,55 на 1 1/3.
Как решаем:
- Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
- Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
- Разделить дробь по правилам:
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Как решаем:
- Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
- Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.
Ответ: 2/5 ∗ 0,8 = 0,32.
Пример 2. Умножить 0,28 на 6 1/4.
Как решаем:
- Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
- Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом.
А еще помогут догнать сверстников и справиться со сложной контрольной.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
Перевод десятичной дроби в обыкновенную
Любую десятичную дробь можно представить в виде обыкновенной дроби. Для этого надо просто записать её со знаменателем.
Главное правило в переводе десятичной дроби в обыкновенную — как читается десятичная дробь, так и пишется обыкновенная. Например:
2,3 — две целых три десятых.
Так как дробь имеет целую часть, то перевести её мы можем или в смешанное число или в неправильную дробь:
Если у десятичной дроби нет целой части, например:
0,75 — ноль целых семьдесят пять сотых,
то её можно сразу перевести в правильную обыкновенную дробь и, если нужно (по необходимости), сократить:
Перевод обыкновенной дроби в десятичную
Не любую обыкновенную дробь можно перевести в десятичную, так как чтобы записать обыкновенную дробь в виде десятичной, надо привести её к знаменателю, представляющему собой единицу с одним или несколькими нулями, например: 10, 100, 1000 и т.
д. Если разложить такой знаменатель на простые множители, то получится одинаковое количество двоек и пятёрок:
10 = 2 · 5;
100 = 10 · 10 = 2 · 5 · 2 · 5;
1000 = 10 · 10 · 10 = 2 · 5 · 2 · 5 · 2 · 5.
Никаких других простых множителей эти разложения не содержат, следовательно:
Обыкновенную дробь можно представить в виде десятичной только в том случае, если её знаменатель не содержит никаких других множителей, кроме 2 и 5.
Возьмём дробь:
При разложении её знаменателя на простые множители получается произведение 2 · 2:
Если домножить его на две пятёрки, чтобы уравнять количество пятёрок с двойками, то получится один из нужных знаменателей — 100. Чтобы получить дробь равную данной, то числитель тоже надо будет умножить на произведение двух пятёрок:
| 3 | = | 3 · 5 · 5 | = | 75 | = | 0,75. |
| 4 | 2 · 2 · 5 · 5 | 100 |
Рассмотрим ещё одну дробь:
При разложении её знаменателя на простые множители получается произведение 2 · 7, содержащее число 7:
Множитель 7 будет присутствовать в знаменателе, на какие бы целые числа его ни умножали, поэтому произведение, содержащее только двойки и пятёрки никогда не получится. Значит данную дробь нельзя привести ни к одному из нужных знаменателей: 10, 100, 1000 и так далее. То есть её нельзя представить в виде десятичной.
Обыкновенную несократимую дробь нельзя представить в виде десятичной, если её знаменатель содержит хотя бы один простой множитель, отличный от 2 и 5.
Обратите внимание, что в правиле написано только о несократимых дробях, потому что некоторые дроби после сокращения, можно представить в виде десятичных. Рассмотрим две дроби:
Первая дробь является несократимой и, как мы уже выяснили, её нельзя представить в виде десятичной.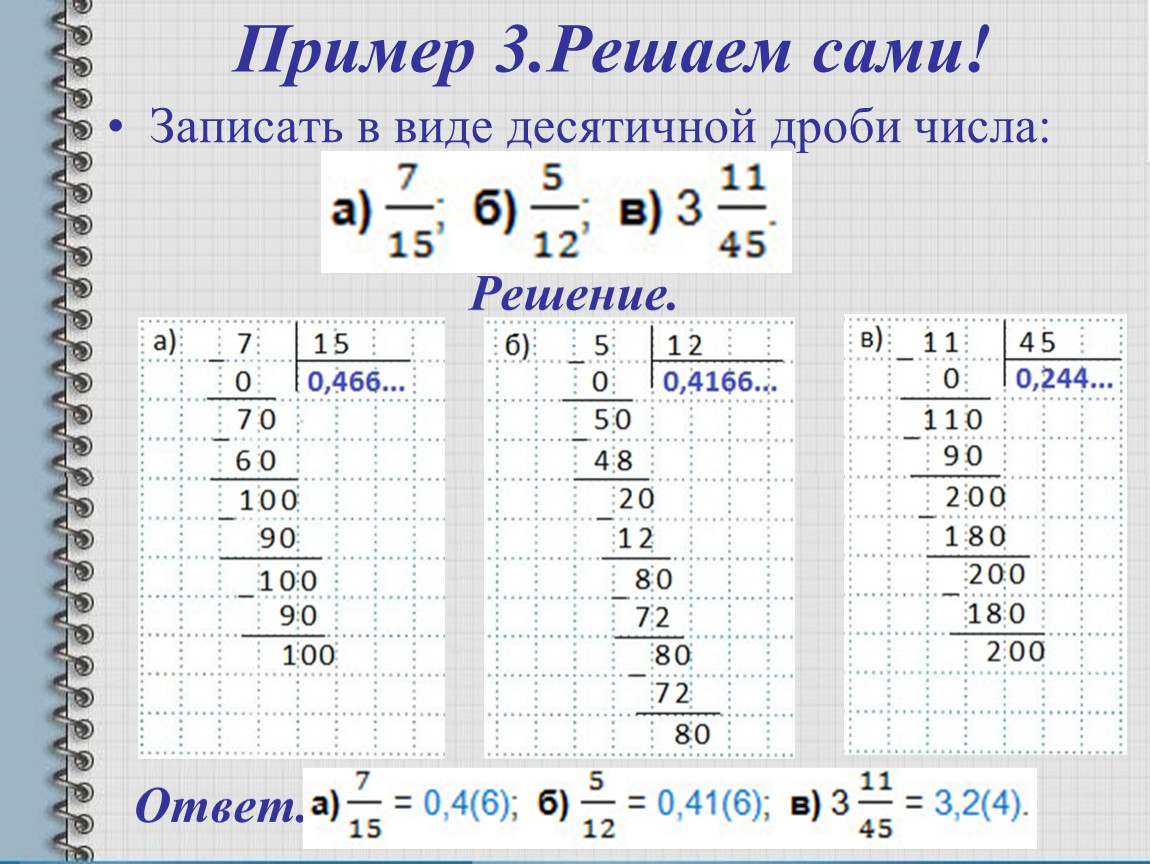
Во второй дроби числитель и знаменатель можно сократить на 7, то есть на тот простой множитель, который мешает в первой дроби:
| 7 | = | 7 : 7 | = | 1 | . |
| 14 | 14 : 7 | 2 |
Теперь осталось только умножить оба члена дроби на 5, чтобы получить 10 в знаменателе, и можно будет переводить дробь в десятичную:
| 1 | = | 1 · 5 | = | 5 | = | 0,5. |
| 2 | 2 · 5 | 10 |
Превращение десятичной дроби в обыкновенную и наоборот
Содержание:
Десятичную дробь представляют в виде
обыкновенной дроби, записав ее со знаменателем. При этом число целых
искомой обыкновенной дроби равно числу целых десятичной дроби. В числителе искомой дроби пишем цифры, стоящие
после запятой (десятичные знаки), а в знаменателе записываем 1 с количеством нулей, которое равно количеству
десятичных знаков.
Далее, если возможно, производят сокращение дроби.
Если десятичные знаки начинаются нулями, их в числитель обыкновенной дроби писать не нужно.
Для превращения обыкновенной дроби в десятичную имеется несколько способов.
Первый способ
Чтобы обратить обыкновенную дробь в десятичную, нужно числитель разделить на знаменатель.
Пример
Задание. Представить обыкновенную дробь $\frac{3}{25}$ в виде десятичной.
Решение. Поделим числитель на знаменатель в столбик:
Таким образом, $\frac{3}{25}=3:25=0,12$
Ответ. $\frac{3}{25}=0,12$
Второй способ
Чтобы превратить обыкновенную дробь в десятичную, нужно помножить числитель и знаменатель указанной дроби на такое число, чтобы в знаменателе получилось число, кратное десяти (если это возможно).
Слишком сложно?
Превращение десятичной дроби в обыкновенную, превращение обыкновенной дроби в десятичную не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание.
Представить дробь
$\frac{3}{25}$ в виде десятичной.
Решение. Знаменатель заданной дроби равен 25, если это число умножить на 4, то получим в результате 100. То есть
$$\frac{3}{25}=\frac{3 \cdot 4}{25 \cdot 4}=\frac{12}{100}=0,12$$Ответ. $\frac{3}{25}=\frac{12}{100}=0,12$
Замечание
Следует иметь в виду, что не всякая обыкновенная дробь представима в виде конечной десятичной. В виде конечной десятичной дроби можно представить только те обыкновенные дроби, которые после сокращения в знаменателе содержат только простые множители 2 и 5.
Если знаменатель несократимой необратимой дроби содержит хотя бы один простой множитель, отличный от 2 и 5, то она не может быть представлена конечной десятичной дробью.
Читать следующую тему: действия над десятичными дробями.
Дроби
Дроби это тема об которую спотыкается половина жителей нашей планеты. Если спросить у людей с какой темы у них начались проблемы с математикой, то большинство из них ответят — с дробей.
Этих людей нельзя упрекнуть. Дроби действительно тема не из простых. Тема дробей требует много терпения и внимания, особенно если человек изучает её впервые.
Но есть и хорошие новости. Если вы наберётесь терпения и освоите дроби, то уверяем, что дальнейшее изучение математики станет для вас простым и интересным.
А если вы ещё хорошо изучили предыдущий урок, который назывался деление, то можете быть уверены, что дроби вы освоили уже наполовину.
Что такое дробь?Если говорить простым языком, то дробь это часть чего-либо. Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение.
Рассмотрим пример из жизни. Мы купили себе пиццу, чтобы съесть её в течении дня. Допустим мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку.
Посмотрите на этот рисунок. Представьте, что это наша пицца, разделённая на четыре куска.
Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы.
Допустим мы съели один кусок. Как его записать? Очень просто. Сначала рисуется маленькая линия:
Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка:
А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу:
Такие записи называют дробями. Дробь состоит из числителя и знаменателя.
Число, которое записывается сверху, называется числителем дроби.
Число, которое записывается снизу, называется знаменателем дроби.
В нашем примере числитель дроби это единица, а знаменатель дроби — четвёрка. Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — всё это синонимы.
Теперь представьте, что мы съели ещё один кусок той же самой пиццы, которая была разделена на четыре куска. Как записать такую дробь?
Очень просто. Сверху записываем 2 (поскольку уже съедено два куска), а внизу записываем 4 (поскольку всего кусков было 4):
Эта дробь читается так: «две четвёртых» либо «два куска из четырёх» либо «две четвёртые доли».
Теперь представьте, что пиццу мы разделили не на четыре части, а на три.
Допустим мы съели один кусок этой пиццы. Как записать такую дробь?
Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается число 3, поскольку пицца разделена на три части, а сверху этой линии записывается число 1, поскольку съеден один кусок:
Эта дробь читается так: «Одна третья» либо «Один кусок из трёх» либо «Одна третья доля» либо «Треть».
Если мы съедим два куска пиццы, то такая дробь будет называться «две третьих» и записываться следующим образом:
Теперь представьте, что пиццу мы разделили на две части, или как говорят в народе: «Пополам»:
Допустим, из этих двух кусков мы съели один кусок.
Как записать такую дробь?
Опять же рисуем линию. Внизу этой линии записываем число 2, поскольку пицца разделена на две части, а вверху записываем число 1, поскольку съеден один кусок:
Эта дробь читается так: «одна вторая» либо «один кусок из двух» либо «одна вторая доля» либо «половина».
Дроби, которые мы сейчас рассмотрели, называют обыкновенными.
Вообще, дроби бывают двух видов: обыкновенные и десятичные. На данный момент мы рассматриваем обыкновенные дроби. Обыкновенная дробь это дробь, которая состоит из числителя и знаменателя. Десятичные дроби рассмотрим немного позже.
Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться.
На следующем рисунке представлены три пиццы, которые разделены по разному. У первой пиццы знаменателем будет 2. У второй пиццы знаменателем будет 3. У третьей пиццы знаменателем будет 4.
Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли (одну часть из двух), или как говорят в народе «половину» пиццы.
С помощью переменных дробь можно записать так:
где a — это числитель, b — знаменатель.
Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают правильными и неправильными.
Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными:
Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята.
Например, если пицца разделена на четыре части, и мы возьмём (одну четвёртую), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными.
С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными:
Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.
Теперь возьмём к примеру неправильную дробь и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.
Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной.
Например:
Вообще, такие дроби даже не должны называться дробями. И вот почему. Рассмотрим к примеру дробь . Применим её к нашей пицце.
Допустим, мы хотим съестьпиццы. В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим этупиццы, то съедим не часть пиццы, а всю пиццу целиком. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.
Дробь означает деление
Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.
Например, рассмотрим дробь . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:
Можно сделать вывод, что любое деление чисел можно записать с помощью дробей.
Например:
Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби».
Выделение целой части дроби
Вычислим дробь . Пять разделить на два будет два и один в остатке:
5 : 2 = 2 (1 в остатке)
Проверка: (2 × 2) + 1 = 4 + 1 = 5
Но сейчас мы имеем дело с дробями, значит и отвечать надо в дробном виде. Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.
Представьте, что у вас есть 5 яблок и вы решили поделиться ими со своим другом. Причём поделиться по-честному, чтобы каждому досталось поровну. Как разделить эти 5 яблок?
Очевидно, что каждому из вас достанется по два яблока, а оставшееся одно яблоко вы разрежете ножом пополам и тоже разделите между собой:
Посмотрите внимательно на этот рисунок. На нём показано, как пять яблок разделены между вами и вашим другом.
Очевидно, что каждому досталось по два целых яблока и по половинке яблока.
Теперь возвращаемся к дроби и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:
Схематически это выглядит так:
Процедуру, которую мы сейчас провели, называют выделением целой части дроби.
В нашем примере мы выделили целую часть дроби и получили новую дробь . Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная.
В нашем примере целая часть это 2, а дробная часть это
Обязательно запомните эти понятия! А лучше запишите в свою рабочую тетрадь.
Выделить целую часть можно только у неправильных дробей. Напомним, что неправильная дробь это дробь, у которой числитель больше знаменателя.
Например, следующие дроби являются неправильными, и у них выделена целая часть:
Чтобы выделить целую часть, достаточно знать, как делить числа уголком. Например, выделим целую часть у дроби . Записываем уголком данное выражение и решаем:
После того, как решение примера завершается, новую дробь собирают подобно детскому конструктору. Важно понимать, что куда относить. Частное относят к целой части, остаток относят в числитель дробной части, делитель относят в знаменатель дробной части.
В принципе, если вы хорошо знаете таблицу умножения, и можете быстро в уме выполнять элементарные вычисления, то можно обойтись без записей уголком. В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.
Но если вы только начинаете изучать математику, советуем записывать каждую мелочь.
Рассмотрим ещё один пример на выделение целой части. Пусть требуется выделить целую часть дроби
Записываем уголком данное выражение и решаем.
Потом собираем смешанную дробь:
Получили:
Перевод смешанного числа в неправильную дробь
Любое смешанное число получается в результате выделения целой части в неправильной дроби. Например, рассмотрим неправильную дробь . Если выделить в ней целую часть, то получается
Но возможен и обратный процесс — любое смешанное число можно перевести в неправильную дробь. Для этого целую часть надо умножить на знаменатель дробной части и полученный результат прибавить к числителю дробной части. Полученный результат будет числителем новой дроби, а знаменатель останется без изменений.
Например, переведём смешанное число в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:
2 × 3 = 6
Затем к 6 прибавляем числитель дробной части:
6 + 1 = 7
Полученная семёрка будет числителем новой дроби, а знаменатель 3 останется без изменений:
Подробное решение выглядит так:
А с помощью переменных перевод смешанного числа в неправильную дробь можно записать так:
Пример 2.
Перевести смешанное число в неправильную дробь.
Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем без изменений:
Основное свойство дроби
Основное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Это означает, что значение дроби не изменится.
Например, рассмотрим дробь . Умножим её числитель и знаменатель на одно и то же число, например на число 2
Получили новую дробь . Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (один кусок из двух), а второй иллюстрирует дробь (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры.
Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.
Рассмотрим дробь . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2
Получили новую дробь . Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (четыре куска из восьми), а второй иллюстрирует дробь (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному.
Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.
Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно!
Сокращение дробей
Дроби можно сокращать. Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь выглядит намного проще и красивее, чем дробь .
Если при решении примеров получается большая и некрасивая дробь, то нужно попытаться её сократить.
Сокращение дроби опирается на основное свойство дроби. Поэтому, прежде чем изучать сокращение дробей, обязательно изучите основное свойство дроби.
Деление числителя и знаменателя на их наибольший общий делитель называется сокращением дроби.
Пример 1. Сократить дробь
Итак, нужно разделить числитель и знаменатель дроби на наибольший общий делитель чисел 2 и 4.
В данном случае дробь простая и для неё НОД ищется легко. НОД чисел 2 и 4 это число 2. Значит, числитель и знаменатель дроби надо разделить на 2
В результате дробь обратилась в более простую дробь . Значение исходной дроби при этом не изменилось, поскольку сокращение подразумевает деление числителя и знаменателя на одно и то же число. А это действие, как было указано ранее, не меняет значение дроби.
На рисунке представлены дроби и в виде кусочков пиццы. До сокращения и после сокращения они имеют одинаковые размеры. Разница лишь в том, что раздéланы они по-разному.
Пример 2. Сократим дробь
Чтобы сократить дробь , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40.
НОД чисел 20 и 40 это число 20. Поэтому делим числитель и знаменатель дроби на 20
Пример 3. Сократим дробь
Чтобы сократить дробь , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36.
НОД чисел 32 и 36 это число 4. Поэтому делим числитель и знаменатель дроби на 4
Если в числителе и знаменателе располагаются простые числа, то такую дробь сократить нельзя — она не сокращается. Такие дроби называют несократимыми. Например, следующие дроби являются несократимыми:
Напомним, что простыми называются числа, которые делятся только на единицу и самих себя.
Второй способ сокращения дроби
Второй способ является короткой версией первого способа. Суть его заключается в том, что пропускается подробное разъяснение того, на что был разделён числитель и знаменатель.
К примеру, вернёмся к дроби . Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4
Теперь представьте, что в данном выражении отсутствует конструкция , и сразу записан ответ .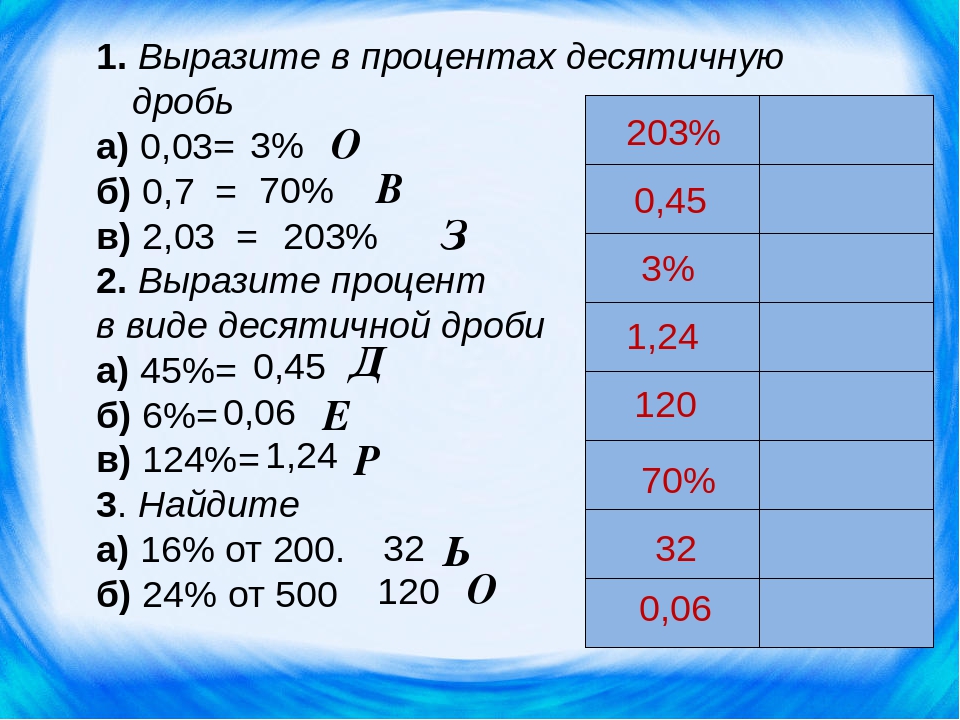
Получится следующее выражение:
Суть в том что число, на которое разделили числитель и знаменатель, хранят в уме. В нашем случае числитель и знаменатель делят на 4 — это число и будем хранить в уме.
Сначала делим числитель на число 4. Полученный ответ записываем рядом с числителем, предварительно зачеркнув его:
Затем таким же образом делим знаменатель на число 4. Полученный ответ записываем рядом со знаменателем, предварительно зачеркнув его:
Затем собираем новую дробь. В числитель отправляем новое число 8 вместо 32, а в знаменатель отправляем новое число 9 вместо 36
Происходит своего рода замена одной дроби на другую. Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Также, дроби можно сокращать, предварительно разложив на простые множители числитель и знаменатель.
Например, сократим дробь , предварительно разложив на простые множители числитель и знаменатель:
Итак, мы разложили числитель и знаменатель дроби на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.
Давайте сократим по тройке в числителе и в знаменателе. Для этого разделим эти тройки на 3 (на их наибольший общий делитель). Получим следующее выражение:
Сократить можно ещё по тройке в числителе и в знаменателе:
Дальше сокращать больше нéчего. Последнюю тройку в знаменателе просто так сократить нельзя, поскольку в числителе нет множителя, который можно было бы сократить вместе с этой тройкой.
Записываем новую дробь, в числителе и в знаменателе которой будут новые множители.
Получили ответ . Значит, при сокращении дроби получается новая дробь .
Не рекомендуется пользоваться вторым способом сокращения дроби и способом разложения на простые множители числителя и знаменателя, если человек только нáчал изучать математику.
Практика показывает, что это оказывается сложным на первых этапах.
Поэтому, если испытываете затруднения при использовании второго способа, то пользуйтесь старым добрым способом сокращения: делите числитель и знаменатель дроби на их наибольший общий делитель. Выражение в таком случае получается простым, понятным и красивым. Так, предыдущий пример может быть решён старым способом и будет выглядеть так:
Сравните это выражение с выражением, которое мы получили, когда пользовались вторым способом:
Первое выражение намного понятнее, аккуратнее и короче. Не правда ли?
Задания для самостоятельного решения
Задание 1. Запишите в виде дроби следующий рисунок:
Задание 2. Запишите в виде дроби следующий рисунок:
Задание 3. Запишите в виде дроби следующий рисунок:
Задание 4. Запишите в виде дроби следующий рисунок:
Задание 5. Запишите в виде дроби следующий рисунок:
Задание 6.
Выделите целые части в следующих дробях:
Задание 7. Выделите целые части в следующих дробях:
Задание 8. Переведите смешанные дроби в неправильные:
Задание 9. Переведите смешанные дроби в неправильные, не расписывая как целая часть умножается на знаменатель дробной части и полученный результат складывается с числителем дробной части
Задание 10. Сократите следующую дробь на 3
Задание 11. Сократите следующую дробь на 3 вторым способом
Задание 12. Сократите следующую дробь на 5
Задание 13. Сократите следующую дробь на 5 вторым способом
Задание 14. Сократите следующие дроби:
Задание 15. Сократите следующие дроби вторым способом:
Задание 16. Запишите в виде дроби следующий рисунок:
Задание 17. Запишите в виде дроби следующий рисунок:
Задание 18. Запишите в виде дроби следующий рисунок:
Задание 19. Запишите в виде дроби следующий рисунок:
Задание 20.
Запишите в виде дроби следующий рисунок:
Задание 21. Изобразите в виде рисунка следующую дробь:
Задание 22. Изобразите в виде рисунка следующую дробь:
Задание 23. Изобразите в виде рисунка следующую дробь:
Задание 24. Изобразите в виде рисунка следующую дробь:
Задание 25. Изобразите в виде рисунка следующую дробь:
Задание 26. Изобразите в виде рисунка следующую дробь:
Задание 27. Изобразите в виде рисунка следующую дробь:
Задание 28. Изобразите в виде рисунка следующую дробь:
Задание 29. Изобразите в виде рисунка следующую дробь:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
6.
3.4. Как записать число в виде десятичной дробиАвтор Татьяна Андрющенко На чтение 3 мин. Просмотров 3.4k. Опубликовано
Чтобы рациональное число m/n записать в виде десятичной дроби, нужно числитель разделить на знаменатель. При этом частное записывается конечной или бесконечной десятичной дробью.
Решение. Разделим в столбик числитель каждой дроби на ее знаменатель: а) делим 6 на 25; б) делим 2 на 3; в) делим 1 на 2, а затем получившуюся дробь припишем к единице — целой части данного смешанного числа.
Несократимые обыкновенные дроби, знаменатели которых не содержат других простых делителей, кроме 2 и 5, записываются конечной десятичной дробью.
В примере 1 в случае а) знаменатель 25=5·5; в случае в) знаменатель равен 2, поэтому, мы получили конечные десятичные дроби 0,24 и 1,5.
В случае б) знаменатель равен 3, поэтому результат нельзя записать в виде конечной десятичной дроби.
А можно ли без деления в столбик обратить в десятичную дробь такую обыкновенную дробь, знаменатель которой не содержит других делителей, кроме 2 и 5? Разберемся! Какую дробь называют десятичной и записывают без дробной черты? Ответ: дробь со знаменателем 10; 100; 1000 и т.д. А каждое из этих чисел — это произведение равного количества «двоек» и «пятерок». На самом деле: 10=2·5; 100=2·5·2·5; 1000=2·5·2·5·2·5 и т.д.
Следовательно, знаменатель несократимой обыкновенной дроби нужно будет представить в виде произведения «двоек» и «пятерок», а затем домножить на 2 и (или) на 5 так, чтобы «двоек» и «пятерок» стало поровну. Тогда знаменатель дроби будет равен 10 или 100 или 1000 и т.д. Чтобы значение дроби не изменилось — числитель дроби умножим на то же число, на которое умножили знаменатель.
Пример 2. Представить в виде десятичной дроби следующие обыкновенные дроби:
Решение.
Каждая из данных дробей является несократимой. Разложим знаменатель каждой дроби на простые множители.
20=2·2·5. Вывод: не хватает одной «пятерки».
8=2·2·2. Вывод: не хватает трех «пятерок».
25=5·5. Вывод: не хватает двух «двоек».
Замечание. На практике чаще не используют разложение знаменателя на множители, а просто задаются вопросом: на сколько нужно умножить знаменатель, чтобы в результате получилась единица с нулями (10 или 100 или 1000 и т.д.). А затем на это же число умножают и числитель.
Так, в случае а) (пример 2) из числа 20 можно получить 100 умножением на 5, поэтому, на 5 нужно умножить числитель и знаменатель.
В случае б) (пример 2) из числа 8 число 100 не получится, но получится число 1000 умножением на 125. На 125 умножается и числитель (3) и знаменатель (8) дроби.
В случае в) (пример 2) из 25 получится 100, если умножить на 4.
Значит, и числитель 8 нужно умножить на 4.
Бесконечная десятичная дробь, у которой одна или несколько цифр неизменно повторяются в одной и той же последовательности, называется периодической десятичной дробью. Совокупность повторяющихся цифр называется периодом этой дроби. Для краткости период дроби записывают один раз, заключая его в круглые скобки.
В случае б) (пример 1) повторяющаяся цифра одна и равна 6. Поэтому, наш результат 0,66… запишется так: 0,(6). Читают: нуль целых, шесть в периоде.
Если между запятой и первым периодом есть одна или несколько не повторяющихся цифр, то такая периодическая дробь называется смешанной периодической дробью.
Несократимая обыкновенная дробь, знаменатель которой вместе с другими множителями содержит множитель 2 или 5, обращается в смешанную периодическую дробь.
Пример 3.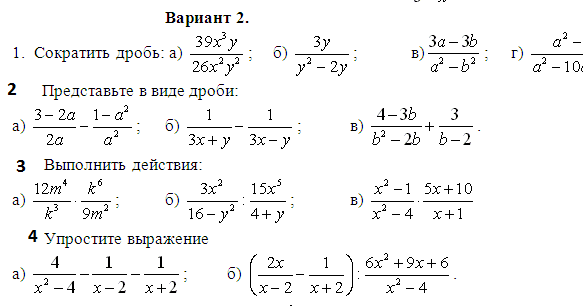
Записать в виде десятичной дроби числа:
Любое рациональное число можно записать в виде бесконечной периодической десятичной дроби.
Пример 4. Записать в виде бесконечной периодической дроби числа:
Решение.
ЕГЭ 2021 года по математике, профиль и баллы, таблицы
Москва, 12.06.2021, 12:05:32, редакция ПРОНЕДРА.РУ, автор Ирина Орлонская.
В понедельник, 7 июня, выпускники 11 классов будут сдавать ЕГЭ по математике. Это второй обязательный экзамен, который сдают школьники в 2021 году.
Экзамен по математике предстоит сдавать всем выпускникам 11 класса без исключения. На образовательных сайтах встречается множество противоречивой информации о возможных результатах экзаменов. Путаница возникает из-за того, что существует два уровня математического ЕГЭ: основной (базовый), и вариативный (профильный).
В зависимости от уровня, различаются и баллы ЕГЭ по математике в 2020 — 2021 году.
Профильная математика, особенности и баллы
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:
- часть 1 содержит 8 заданий (задания 1–8) с кратким ответом в виде целого числа или конечной десятичной дроби;
- часть 2 содержит 4 задания (задания 9–12) с кратким ответом в виде целого числа или конечной десятичной дроби и 7 заданий (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий).
Таким образом, за решение первой части можно набрать 8 первичных баллов → 39 тестовых.
Баллы ЕГЭ по математике (профиль) 2020 — 2021
Результаты ЕГЭ по математике профильного уровня (тестовые баллы) также могут быть условно сопоставлены со школьными оценками. Официальный перевод баллов в отметки не применяется с 2008 года. Таблица дает наглядное представление о реальном уровне знаний по математике, который необходим абитуриенту для поступления в профильный вуз.
70 — 80 тестовых баллов — это показатель отличного знания школьной программы.
РАСПРЕДЕЛЕНИЕ БАЛЛОВ В 2021 ГОДУ ПО ПРОФИЛЬНОЙ МАТЕМАТИКЕ
1 балл — за 1-12 задания.
2 балла — 13-15.
З балла — 16, 17.
4 балла — 18, 19.
Всего: 32 балла
Первичные баллы — своеобразная условная оценка, выставляемая за правильные ответы на экзаменационные задания. Количество баллов зависит от уровня ЕГЭ по математике: базовый или профильный. На профильном уровне 19 заданий разделены на 4 группы сложности, верный ответ может принести от 1 до 4 баллов.
Стоит знать, что баллы можно получить даже за неправильный ответ: эксперты оценивают обоснованность и логичность рассуждений, и могут начислить несколько драгоценных первичных баллов, влияющих на итоговый результат. Для борьбы со списыванием введено отдельное правило для задач, требующих развернутого решения: если ученик ограничится только кратким ответом, не приводя логику рассуждений, баллов за задание он не получит.
Максимальное количество первичных баллов за правильное и полное решение 19-ти экзаменационных задач — 32.
Соответствие первичных баллов тестовым
Что такое 2/5 из 12? (Вычислите 2/5 из 12)
В этой статье мы покажем вам, как именно вычислить 2/5 от 12, чтобы вы могли быстро и легко вычислить дробную часть любого числа! Приступим к математике!
Хотите быстро узнать или показать студентам, как конвертировать 2/5 из 12? Воспроизведите это очень быстрое и веселое видео прямо сейчас!
Вы, наверное, знаете, что число над чертой дроби называется числителем, а число под ним — знаменателем.Чтобы вычислить дробь любого числа, нам сначала нужно преобразовать это целое число в дробь.
Вот вам небольшой совет. Любое число можно преобразовать в дробь, если в качестве знаменателя использовать 1:
12 / 1
Итак, теперь, когда мы преобразовали 12 в дробь, чтобы получить ответ, мы помещаем дробь 2/5 рядом с нашей новой дробью, 12/1, чтобы мы могли умножить эти две дроби.
Правильно, все, что вам нужно сделать, это преобразовать целое число в дробь, а затем умножить числители и знаменатели. Давайте посмотрим:
2 х 12 / 5 х 1 знак равно 24 / 5
Как видите, в этом случае числитель выше знаменателя.Это означает, что мы можем упростить ответ до смешанного числа, также известного как смешанная дробь.
Для этого нам нужно преобразовать неправильную дробь в смешанную дробь. Мы не будем здесь подробно объяснять это, потому что у нас есть другая статья, которая уже охватывает это для 24/5. Нажмите здесь, чтобы узнать, как преобразовать 24/5 в смешанную дробь.
Полный и упрощенный ответ на вопрос, что составляет 2/5 из 12:
4 4/5
Надеюсь, это руководство помогло вам понять, как найти дробную часть любого целого числа.Теперь вы можете попробовать больше чисел, чтобы попрактиковаться в новых навыках дробления.
Цитируйте, ссылайтесь или ссылайтесь на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
«Что такое 2/5 из 12?». VisualFractions.com . По состоянию на 12 июня 2021 г. https://visualfractions.com/calculator/fraction-of-number/what-is-2-5-of-12/.
«Что такое 2/5 из 12?». VisualFractions.com , https://visualfractions.com/calculator/fraction-of-number/what-is-2-5-of-12/. По состоянию на 12 июня 2021 г.
Что такое 2/5 из 12 ?. VisualFractions.com. Получено с https://visualfractions.com/calculator/fraction-of-number/what-is-2-5-of-12/.
Калькулятор дробей числа
Дробь числа
Введите числитель, знаменатель и целое число
Вычисление следующей дроби числа
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами.Он также показывает подробную пошаговую информацию о процедуре расчета дроби.
Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т.е. для пяти сотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .
Десятичные числа (десятичные числа) вводятся с десятичной точкой . , и они автоматически переводятся в дроби — i.
1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное в дробное: 0.625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Задачи на дроби в словах:
следующие математические задачи »
| Параметр | Описание |
|---|---|
| Неправильное преобразование | Если дробь смешанная, отображаются шаги для преобразования в неправильную дробь. |
| Неправильная фракция | Если дробь смешанная, значения окончательной неправильной дроби. |
| Добавить | Показывает фактические шаги сложения. |
| Наименьшее общее кратное (LCM) | Показывает вычисленное наименьшее общее кратное. Это наименьшее число, при котором обе дроби делятся поровну. |
| Ответ | Показывает решение. Обратите внимание, это решение не упрощено. |
| Наибольший общий делитель | Используется для упрощения ответа. Наибольшее или наибольшее целое число, которое разделит числитель и знаменатель без получения дроби. |
| Разделить на GCD | Показывает числитель и знаменатель, разделенные на НОД, чтобы уменьшить дробь. |
| Ответ (упрощенный) | Решение в правильном или неправильном формате. |
| Ответ (смешанный) | Если раствор является неправильной дробью, отображается преобразованная смешанная дробь. Смешанная фракция показывает дробь с целой частью в дополнение к оставшейся части фракции. |
Это дробь слева от операнда сложения.Простой в использовании калькулятор дробей [для деления, умножения и упрощения дробей]
Калькулятор дробей складывает, вычитает, умножает и делит дроби с одинаковыми или разными знаменателями.
Это также позволит нам упростить дроби, преобразовать дроби в десятичные и десятичные в дроби.
Сначала просто введите значения a, b, c, d для дробей \ (\ frac {a} {b} \) и \ (\ frac {c} {d} \), затем математическую операцию по вашему желанию. выполнить (+, -, x, /).Калькулятор моментально и точно выполнит операцию и выдаст ответ в простейшей форме. Вы также можете использовать калькулятор, чтобы проверить свою работу, которую вы проделали вручную.
Сложение и вычитание дробей Подобные (общие) знаменателиСложите или вычтите числители, оставив знаменатели неизменными.
Пример: \ (\ frac {3} {5} + \ frac {4} {5} \)
Поскольку знаменатель равен 5 в обеих дробях, сложите 3 и 4, чтобы получить 7.
Знаменатель остается равным 5, поэтому ответ равен 7/5.
Поскольку знаменатель равен 6 в обеих дробях, вычтите 5 из 7, чтобы получить 2. Тогда дробь будет \ (\ frac {2} {6} \).
Но теперь мы можем упростить \ (\ frac {2} {6} \). Чтобы упростить, поищите общий фактор. Обратите внимание, что 2 равномерно делится как на 2, так и на 6. Следовательно, разделите числитель и знаменатель на 2, чтобы получить \ (\ frac {1} {3} \). Теперь дробь упрощена.
В отличие от знаменателейЧтобы сложить и вычесть отличные знаменатели, сначала вычислите общий знаменатель.Самый простой способ сделать это — умножить два знаменателя. Это не всегда дает наименьший общий знаменатель, но вы можете упростить его после сложения и вычитания.
Пример: \ (\ frac {2} {5} + \ frac {4} {7} \)
Общий знаменатель равен 5 (7) = 35. Поскольку знаменатель в первой дроби умножается на 7, числитель также нужно умножить на 7, чтобы получить \ (\ frac {14} {35} \).
Поскольку знаменатель второй дроби умножается на 5, числитель должен быть таким же, чтобы получить \ (\ frac {20} {35} \).
Теперь добавьте \ (\ frac {14} {35} + \ frac {20} {35} = \ frac {34} {35} \)
Вычитание выполняется таким же образом, просто вычтите две дроби после перезаписи дроби с их общими знаменателями. Если вам нужно упростить, не забудьте разделить на наибольший общий множитель.
При умножении дробей просто умножайте числители и знаменатели.Тогда упростите. Вы также можете сначала упростить, прежде чем умножать.
Пример: \ (\ frac {2} {9} \ times \ frac {4} {7} \)
Умножьте 2 и 4, чтобы получить 8. Затем умножьте 9 и 7, чтобы получить 63. Результат: \ ( \ frac {8} {63} \). Нет необходимости в упрощении, поскольку наибольший общий делитель равен 1.
Теперь предположим, что мы хотим разделить \ (\ frac {2} {9} \ div \ frac {4} {7} \).
При делении дробей возьмите первую дробь и умножьте на обратную величину второй. Обратное просто меняет местами числитель и знаменатель.Проблема деления превращается в проблему умножения.
\ (\ frac {2} {9} \ times \ frac {7} {4} \) 2 × 7 = 14 и 9 × 4 = 36. Итак, ответ \ (\ frac {14} { 36} \). Но обратите внимание, что это не в простейшей форме. Наибольший общий делитель равен 2, поэтому деление обоих на 2 дает упрощенный ответ \ (\ frac {7} {18} \).
Калькулятор преобразования дробей в десятичные принимает любую дробь и преобразует ее в десятичную.
Метод преобразования дроби в десятичную довольно прост. Просто разделите числитель на знаменатель.
Замените \ (\ frac {14} {25} \) на десятичное число.
Разделите 14 на 25, чтобы получить 0,56. Вы можете сделать это на калькуляторе или вручную с помощью длинного деления.
Некоторые фракции не так просто обрабатывать вручную, особенно те, которые не завершаются. На этом калькуляторе с ними работать намного проще.
Но если вы решите вручную, калькулятор станет отличным инструментом для мгновенной проверки вашей работы.
Преобразование десятичных знаков в дроби является обратным преобразованию дробей в десятичные. Калькулятор быстро выполнит это и даст точные результаты, просто введя десятичное значение.
Чтобы преобразовать вручную, возьмите десятичную дробь и преобразуйте ее в целое число, затем разделите на 10, возведенное в число десятичных знаков, перемещенных вправо для преобразования числа. Оттуда вы можете упростить дробь, если это необходимо.
Пример:
Преобразует 0,68 в дробь. Чтобы изменить 0,68 на целое число, переместите десятичную запятую на 2 разряда вправо, чтобы получить 68.
Поскольку мы переместили 2 десятичных разряда, разделите 68 на 10 во второй степени, которая равна 100.
Это дает нам \ (\ гидроразрыв {68} {100} \). Теперь мы можем упростить дробь, найдя общий множитель. Если вы не знаете наибольшего общего множителя, вы можете начать с деления на любой общий множитель. Замечания 68 и 100 делятся на 2. Это уменьшает дробь до 34/50.Отсюда обратите внимание, что 34 и 50 делятся на 2. Это сводится к \ (\ frac {17} {25} \), что является упрощенным ответом.
Вы можете проверить свои ручные вычисления с помощью этого калькулятора или просто ввести информацию для вашей конкретной проблемы, чтобы получить почти мгновенные и точные результаты!
Преобразование дробей в десятичное
Преобразование дробей в десятичноеТаблицы преобразования дробей в десятичные
Важное примечание: любой диапазон чисел, равный подчеркнутому , означает, что эти числа повторяются.Например, 0. 09 означает 0,0 .
… Перечислены только дроби с наименьшим числом. Например, чтобы найти 2/8, сначала упростите его до 1/4, а затем выполните поиск.
в таблице ниже.
| дробь = десятичная | |||
| 1/1 = 1 | |||
| 1/2 = 0.5 | |||
| 1/3 = 0. 3 | 2/3 = 0. 6 | ||
| 1/4 = 0,25 | 3/4 = 0,75 | ||
| 1/5 = 0,2 | 2/5 = 0,4 | 3/5 = 0. 6 | 4/5 = 0,8 |
| 1/6 = 0,1 6 | 5/6 = 0,8 3 | ||
| 1/7 = 0. 142857 | 2/7 = 0. 285714 | 3/7 = 0. 428571 | 4/7 = 0. 571428 |
| 5/7 = 0. 714285 | 6/7 = 0. 857142 | ||
| 1/8 = 0,125 | 3/8 = 0,375 | 5/8 = 0,625 | 7/8 = 0,875 |
| 1/9 = 0. 1 | 2/9 = 0. 2 | 4/9 = 0. 4 | 5/9 = 0. 5 |
| 7/9 = 0. 7 | 8/9 = 0. 8 | ||
| 1/10 = 0,1 | 3/10 = 0,3 | 7/10 = 0,7 | 9/10 = 0,9 |
1/11 = 0. 09 | 2/11 = 0. 18 | 3/11 = 0. 27 | 4/11 = 0. 36 |
| 5/11 = 0. 45 | 6/11 = 0. 54 | 7/11 = 0. 63 | |
| 8/11 = 0. 72 | 9/11 = 0. 81 | 10/11 = 0. 90 | |
| 1/12 = 0,08 3 | 5/12 = 0,41 6 | 7/12 = 0,58 3 | 11/12 = 0.91 6 |
| 1/16 = 0,0625 | 3/16 = 0,1875 | 5/16 = 0,3125 | 7/16 = 0,4375 |
| 11/16 = 0,6875 | 13/16 = 0,8125 | 15/16 = 0,9375 | |
| 1/32 = 0,03125 | 3/32 = 0,09375 | 5/32 = 0,15625 | 7/32 = 0.21875 |
| 9/32 = 0,28125 | 11/32 = 0,34375 | 13/32 = 0,40625 | |
| 15/32 = 0,46875 | 17/32 = 0,53125 | 19/32 = 0,59375 | |
| 21/32 = 0,65625 | 23/32 = 0,71875 | 25/32 = 0,78125 | |
27/32 = 0. 84375 | 29/32 = 0, | 31/32 = 0,96875 |
Нужно преобразовать повторяющееся десятичное число в дробь? Следуйте этим примерам:
Обратите внимание на следующий шаблон для повторения десятичных знаков:
0. 2 2222222 … = 2/9
0. 54 545454 … = 54/99
0. 298 298298 … = 298/999
Деление на 9 вызывает повторяющийся узор.
Обратите внимание на шаблон, если перед повторяющимся десятичным знаком нули:
0.0 2 2222222 … = 2/90
0,000 54 545454 … = 54/99000
0,00 298 298298 … = 298/99900
Добавление нулей в знаменатель добавляет ноль перед повторяющейся десятичной дробью.
Чтобы преобразовать десятичную дробь, которая начинается с неповторяющейся части , например 0,21 456 456456456456 …, в дробную часть, запишите ее как сумму неповторяющихся
часть и повторяющаяся часть.
0,21 + 0,00 456 456456456456…
Затем преобразуйте каждый из этих десятичных знаков в дроби. Первая десятичная дробь имеет
делитель мощности десять. Второй десятичный знак (который повторяется) сверяется в соответствии с шаблоном
приведено выше.
21/100 + 456/99900
Теперь сложите эти дроби, выразив их общим делителем
20979/99900 + 456/99900
и добавить.
21435/99900
Наконец, упростите его до самых низких значений
1429/6660
и проверьте на своем калькуляторе или с длинным делением.
= 0,2145645645 …
Вы МОЖЕТЕ делать дроби: 2 — разные имена, одинаковые дроби | Джордж Пит Калеодис | Startup
В прошлый раз мы обсуждали части дроби — знаменатель (нижнее число, которое говорит нам, сколько частей составляет целое) и числитель (верхняя часть, которая говорит нам, как многие части мы обсуждаем в данный момент).
Математики вроде меня ЛЮБЯТ определения.
Фактически, большая часть высшей математики сводится к простому формулированию определений и демонстрации того, как они совпадают с другими определениями (мы называем это «математическими доказательствами»).Обычно в математике мы определяем вещи до того, как начинаем их использовать. В данном случае, хотя мы уже использовали их некоторое время, не мешало бы остановиться здесь и формально определить, что мы подразумеваем под «дробью»:
Определение: A дробь — это частное (результат деления) двух целых чисел (круглые числа без десятичных частей).
Например, если мы рассмотрим этот моноблок, который подозрительно похож на прямоугольник, который я нарисовал в Microsoft Word:
ммм.. .delicious текстовый процессор candyи разделите его на 5 равных частей:
ммм. . .Вкусная конфета для текстового процессора, разделенная на пятые части, каждая часть представляет собой 1/5 («одну пятую») шоколадного батончика.
Таким образом, две из этих частей составляют 2/5 («две пятых») моноблока и т. Д.
Мы называем такие выражения, как «1/5» и «2/5». »,« Дроби ». Мы можем думать о них как о сумме, которую мы получаем, когда делим верхнее число на нижнее число.
Если этот шоколадный батончик весит 15 унций, мы ожидаем, что 1/5 леденца будет весить 15/5 = 3 унции.Таким образом, вес синей части выше будет 2 * 3 унции = 6 унций. Если бы этот шоколадный батончик содержал 300 калорий, мы ожидали бы, что 1/5 шоколадного батончика будет содержать 300/5 = 60 калорий, поэтому синяя часть выше будет содержать 2 * 60 = 120 калорий. Если бы этот шоколадный батончик стоил 1 доллар, можно было бы ожидать, что 1/5 часть шоколадного батончика будет стоить 1/5 доллара. Таким образом, стоимость синей части выше будет 2 * (1/5) доллара = 2/5 доллара.
А теперь давайте предположим, что мы берем конфетку выше и разрезаем каждую из этих 5 частей на две равные части.
Тогда вместо шоколадного батончика, разрезанного на 5 пятых, у нас есть шоколадный батончик, разрезанный на 10 десятых.Вместо 2 закрашенных частей из 5 всего у нас есть 4 закрашенных части из 10 полных частей:
Обратите внимание, что размер заштрихованной части шоколадного батончика не изменился. т изменился. 2/5 всего моноблока — это то же количество леденца, что и 4/10 всего леденца.
Мы можем символически резюмировать то, что мы сделали, следующим образом:
Эти две дроби представляют собой одинаковую сумму 2/5 = 4/10. 2/5 и 4/10 представляют одно и то же число.(Попробуйте ввести их в калькулятор. 2/5 и 4/10 дадут вам 0,4.)
Если весь моноблок весит 15 унций, мы ожидаем, что 1/10 моноблока будет весить 15/10 = 1,5. унция $ 12.99 Таким образом, вес синей части будет 4 * 1,5 унции = 6 унций. (Те же 6 унций, что и несколько минут назад! Прокрутите вверх и посмотрите.) Если бы этот шоколадный батончик содержал 300 калорий, мы ожидали бы, что 1/10 шоколадного батончика будет содержать 300/10 = 30 калорий, поэтому синяя часть выше будет содержат 4 * 30 = 120 калорий.
(Те же 120 калорий, что и несколько минут назад! Прокрутите вверх и посмотрите.) Если бы этот шоколадный батончик стоил 1 доллар, можно было бы ожидать, что 1/10 часть шоколадного батончика будет стоить 1/10 доллара. Таким образом, стоимость синей части выше будет 4 * (1/10) доллара = 4/10 доллара. (Это должна быть та же сумма денег, что и несколько минут назад, поэтому 4/10 = 2/5 долларов.)
Давайте еще раз посмотрим на последнюю строку на графике выше:
Мы разделили каждую из 5 частей. конфеты на 2 части, что даст нам 10 одинаковых кусочков. Это включало разделение каждой из 2 синих частей, в результате чего мы получали 4 синих части. В цифре 2 не было ничего волшебного.Мы могли бы разделить каждый кусок конфет на 3 части:
Итак, 2/5 конфет — это такое же количество конфет, как 6/15 конфет. Мы могли бы разделить каждую часть на 7 частей:
Итак, 2/5 шоколадного батончика — это такое же количество леденцов, как 14/35 шоколадного батончика. Мы могли бы разделить каждую часть на ☺ частей:
Итак, 2/5 конфет — это такое же количество конфет, как (2☺) / (5☺).
Мы называем списки дробей типа 2/5, 4/10, 6/15, 14/35, (2☺) / (5☺) «эквивалентными дробями», потому что, хотя они выглядят по-разному, они представляют собой одно и то же число.
Определение: Эквивалентные дроби — это дроби, представляющие одно и то же количество.
Выше мы обнаружили, что для любой дроби мы можем получить эквивалентную дробь, умножив числитель и знаменатель на одинаковую величину. Вот еще несколько примеров:
1/4 и 2/8 — эквивалентные дроби.
2/9 и 10/45 — эквивалентные дроби.
3/8 и 12/32 — эквивалентные дроби.
Когда мы сделаем достаточно этого, мы замечаем закономерность.Выражение паттерна способом, включающим все возможности в одном кратком утверждении, называется «теоремой».
Теорема: Если a и b — целые числа, то a / b эквивалентно (ac) / (bc) (при условии, что c не равно нулю).
Мы можем использовать эту теорему для преобразования дробей в другие эквивалентные дроби в любое удобное для нас время.
Один простой повседневный пример, конечно же, связан с деньгами.
Пример: Что больше денег — десять центов или четверть?
Вы уже запомнили ответ на этот вопрос.Но как бы вы объяснили ребенку или инопланетной форме жизни, почему четверть доллара стоит больше десяти центов? Вы конвертируете!
одна четверть = 1/4 доллара = (1 * 25) / (4 * 25) = 25/100 доллара = 25 центов
одна копейка = 1/10 доллара = (1 * 10) / (10 * 10) = 10/100 доллара = 10 центов
Поскольку 25 центов больше, чем 10 центов, четверть — это больше денег, чем десять центов.
Преобразуя обе дроби в эквивалентные дроби с одинаковым знаменателем, мы можем сравнивать два разных типа монет.Мы называем этот же знаменатель «общим знаменателем», и это предмет нашего следующего обсуждения.
А пока займитесь этими упражнениями. Если вы подпишетесь на меня в Твиттере @caleodis, я буду рад ответить вам в DM.
Упражнения:
- Перечислите 3 дроби, эквивалентные 3/4.
- Эквивалентны ли дроби 26/39 и 16/24? Почему или почему нет?
- Эквивалентны ли дроби 2/3 и 3/4? Почему или почему нет?
- Найдите дробь, эквивалентную 4/7, знаменатель которой равен 84.
- Найдите дробь, эквивалентную 4/7, числитель которой равен 84.
- Без использования калькулятора решите, какая дробь больше: 5/7 или 4/5?
- Сокращенная дробь — это дробь, числитель и знаменатель которой не имеют делителей, кроме 1. Найдите сокращенную дробь, эквивалентную 120/168.
- Найдите уменьшенную дробь, эквивалентную 73/73.
- Дроби, числители которых больше знаменателя, называются неправильными дробями. (Они представляют числа больше 1, что, как можно было бы утверждать, вовсе не дроби — опять же, математики все любят определения.) Запишите неправильную дробь 12/8 как сумму целого числа и правильной дроби.
- Запишите неправильную дробь 21/6 как сумму целого числа и правильной дроби.
- Джордж «дробь под любым другим именем все равно означает, что я получаю меньше, чем целый пирог» Калеодис
Что такое дробь? — Определение, факты и пример
Что такое дробь?
Фракции представляют собой равных части целого или совокупности.
Дробь целого : Когда мы делим целое на равные части, каждая часть является частью целого.
Например ,
Фрагмент коллекции : Фракции также представляют собой части набора или коллекции.
Например ,
Всего 5 детей.
3 из 5 — девушки. Итак, доля девушек составляет три пятых ( 3 ⁄ 5 ).
2 из 5 — мальчики. Итак, доля мальчиков составляет две пятых ( 2 ⁄ 5 ).
Дробное обозначение
Дробь состоит из двух частей. Число в верхней части строки называется числителем.
Он сообщает, сколько равных частей взяты из целого. Число под чертой называется знаменателем. Он показывает общее делимое количество равных частей целого или общее количество равных частей, которые есть в коллекции.
Дроби на числовой строке : Дроби могут быть представлены на числовой строке, как показано ниже.
Например,
Примеры из жизни
Самыми распространенными примерами дробей из реальной жизни являются равные кусочки пиццы, фруктов, торта, плитки шоколада и т. Д.
Без примеров
Когда части целого разделены неравномерно, они не образуют дробей.
Виды фракций
Дроби единицы Дроби с числителем 1 называются единичными дробями. | Правильные дроби Дроби, у которых числитель меньше знаменателя, называются правильными дробями. |
