2 делить на 3: как разделить 2 на 3 в столбик сколько будет???

2 делить на 3 корня из 2

Вы искали 2 делить на 3 корня из 2? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 2 корня из 3 делить на 2, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «2 делить на 3 корня из 2».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 2 делить на 3 корня из 2,2 корня из 3 делить на 2,3 корень из 2 поделить на 2,3 корня из 2 делить на 2.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 2 делить на 3 корня из 2. Просто введите задачу в окошко и нажмите «решить» здесь (например, 3 корень из 2 поделить на 2).

Где можно решить любую задачу по математике, а так же 2 делить на 3 корня из 2 Онлайн?

Решить задачу 2 делить на 3 корня из 2 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Деление дробей — как делить дроби 🤔

Понятие дроби

Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. В 5 классе ребята это уже знают.

Дроби бывают двух видов:

1. Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
2. Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.

Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.

Основные свойства дроби 1. Дробь не имеет значения, при условии, если делитель равен нулю. 2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля. 3. Две дроби a/b и c/d называются равными, если a * d = b * c. 4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Деление дробных чисел

Деление — арифметическое действие, по которому можно узнать, сколько раз одно число содержится в другом. А еще деление — это обратное действие умножения.

Свойства деления:

1. При делении на единицу получится такое же число:

2. На ноль делить нельзя.

3. Когда делим ноль на любое число, всегда получаем ноль:

4. Когда делим любое число на само себя получаем единичку:

5. Когда делим сумму на какое-либо число, можно разделить на него каждое слагаемое, а потом сложить полученное:

• (a + b) : c = a : c + b : c.

6. Когда делим разность на какое-нибудь число, можно разделить на него уменьшаемое и вычитаемое отдельно и из первого частного вычесть второе:

• (a — b) : c = a : c — b : c.

7. Когда делим произведение двух множителей на число, можно разделить на него любой из множителей и частное умножить на второй множитель:

• (a * b) : c = (a : c) · b = a * (b : c).

Деление обыкновенных дробей

Как делить дробь на дробь? Выполняем следующую последовательность действий:

• числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
• знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Как делить дроби с разными знаменателями? Тут все просто: пользуемся правилами выше, поскольку на практике нам неважно, одинаковые знаменатели или нет.

Деление дроби на натуральное число

Для деления дроби на натуральное число нужно:

• представить данный делитель в виде неправильной дроби, где числитель равен этому числу, а знаменатель единица;
• произвести деление по предыдущему правилу.
  

Деление натурального числа на дробь

Чтобы поделить натуральное число на обыкновенную дробь нужно:

• знаменатель делителя умножить на число;
• числитель делителя записать в знаменатель.
  

Деление на смешанное число

Для деления смешанных чисел необходимо:

• представить числа в виде неправильных дробей
• разделить то, что получилось друг на друга.
  

Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:

Приходите практиковаться в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

2 Делить на 3 сколько будет

Калькулятор наследства позволяет рассчитать долю в наследственной массе. Для расчета необходимо заполнить три параметра.

Доля наследодателя в объекте имущества

Как правило по наследству переходят определенные объекты имущества: квартира, дача, машина и т.д. В большинстве случаев, доля наследодателя не равна 100%, потому что имущество совместное. Например, отец владел дачей вместе с матерью в равных долях, соответственно его доля в собственности на дачу составляет 50% или ½ часть. Кстати, доли в собственности чаще всего выражаются в простых дробях: 2/3, ¼ и т.п.

Размер доли

Укажите размер доли наследодателя в объекте имущества. Если доля равно 100%, то укажите 1/1

Количество наследников

Укажите количество наследников, включая Вас. Определить всех наследников можно по схеме.

Я имею долю в жилой квартире 12 и мой супург так же имел 12. Супруг умер, у него двое родителей притендуют на его долю в наследстве. Как правильно разделить его 12 доли на три равные части?

1/2 делится на 3 и = 1/6 каждому. Просите суд (если это вам нужно) чтобы выплатить денежную компенсацию за эти доли родителям. У вас не было детей ? а то они тоже должны иметь долю.

Здравствуйте.Все наследники получат по 16 части.

Спасибо за ответ!

Похожие вопросы

адвокат Шевченко Ольга Павловна:

По поводу материнского капитала, нет никаких изменений в законе на данный момент. По поводу квартиры, продажа квартиры в отсутствие согласия всех собственников абсолютно невозможна.

юрист Харченко Ольга Валерьевна:

Юрий, здравствуйте! Конечно, выгоднее продавать всю квартиру целиком, а не треть доли, а деньги разделить. А обезопасить себя от махинаций, на мой взгляд.

адвокат Шевченко Ольга Павловна:

Если речь идёт о разделе имущества супругов, доля делится поровну между ними. Следует заключить соглашение о разделе имущества

юрист Соловьева Наталья Викторовна:

В данном случае, если есть возможность подтвердить, что дети не проживали в спорном жилом помещении (лучше конечно регистрация по месту пребывания)

юрист Швецова Ирина Владимировна:

Добрый день НАследниками первой очереди по закону являются супруга, дети и родители умершего. Если бывший супруг не написал завещания,

Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей. Если дробь имеет вид «смешанной дроби», то также заполните поле, соответствующее целой части дроби. Если у дроби нет целой части, т.е. дробь имеет вид «простой дроби», то оставьте данное поле пустым. Затем нажмите кнопку «Вычислить».

Вид дроби: простые дроби смешанные дроби

Дробью в математике называется число, представляющее часть единицы или несколько её частей. Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби – количество взятых этих частей целого.

Дроби бывают правильными и неправильными. Правильной называется дробь, у которой числитель меньше знаменателя. Если у дроби числитель больше знаменателя, то такая дробь называется неправильной.

Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть,называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь (см. пример ниже).

Дробь 1	Дробь 2	Результат

правила, методы, примеры как делить квадратные корни

Наличие квадратных корней в выражении усложняет процесс деления, однако существуют правила, с помощью которых работа с дробями становится значительно проще.

Единственное, что необходимо все время держать в голове —  подкоренные выражения делятся на подкоренные выражения, а множители на множители. В процессе деления квадратных корней мы упрощаем дробь. Также, напомним, что корень может находиться в знаменателе.

Метод 1. Деление подкоренных выражений

Алгоритм действий:

Записать дробь

Если выражение не представлено в виде дроби, необходимо его так записать, потому так легче следовать принципу деления квадратных корней.

Пример 1

144÷36, это выражение следует переписать так: 14436

Использовать один знак корня

В случае если и в числителе, и знаменателе присутствует квадратные корни, необходимо записать их подкоренные выражения под одним знаком корня, чтобы сделать процесс решения проще.

Напоминаем, что подкоренным выражением (или числом) является выражением под знаком корня.

Пример 2

14436. Это выражение следует записать так: 14436

Разделить подкоренные выражения

Просто разделите одно выражение на другое, а результат запишите под знаком корня.

Пример 3

14436=4, запишем это выражение так: 14436=4

Упростить подкоренное выражение (если необходимо)

Если подкоренное выражение или один из множителей представляют собой полный квадрат, упрощайте такое выражение.

Напомним, что полным квадратом является число, которое представляет собой квадрат некоторого целого числа.

Пример 4

4 — полный квадрат, потому что 2×2=4. Из этого следует:

4=2×2=2. Поэтому 14436=4=2.

Метод 2. Разложение подкоренного выражения на множители

Алгоритм действий:

Записать дробь

Перепишите выражение в виде дроби (если оно представлено так). Это значительно облегчает процесс деления выражений с квадратными корнями, особенно при разложении на множители. 

Пример 5

8÷36, переписываем так 836

Разложить на множители каждое из подкоренных выражений

Число под корнем разложите на множители, как и любое другое целое число, только множители запишите под знаком корня.

Пример 6

Упростить числитель и знаменатель дроби

Для этого следует вынести из-под знака корня множители, представляющие собой полные квадраты. Таким образом, множитель подкоренного выражения станет множителем перед знаком корня.

Пример 7

2266×62×2×2, из этого следует: 836=226

Рационализировать знаменатель (избавиться от корня)

В математике существуют правила, по которым оставлять корень в знаменателе — признак плохого тона, т.е. нельзя. Если в знаменателе присутствует квадратный корень, то избавляйтесь от него. 

Умножьте числитель и знаменатель на квадратный корень, от которого необходимо избавиться.

Пример 8

В выражении 623 необходимо умножить числитель и знаменатель на 3, чтобы избавиться от него в знаменателе:

623×33=62×33×3=669=663

Упростить полученное выражение (если необходимо)

Если в числителе и знаменателе присутствуют числа, которые можно и нужно сократить. Упрощайте такие выражения, как и любую дробь.

Пример 9

26 упрощается до 13; таким образом 226упрощается до 123=23

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание  

Метод 3. Деление квадратных корней с множителями

Алгоритм действий:

Упростить множители

Напомним, что множители представляют собой числа, стоящие перед знаком корня. Для упрощения множителей понадобится разделить или сократить их. Подкоренные выражения не трогайте!

Пример 10

432616. Сначала сокращаем 46: делим на 2 и числитель, и знаменатель: 46=23.

Упростить квадратные корни

Если числитель нацело делится на знаменатель, то делите. Если нет, то упрощайте подкоренные выражения, как и любые другие.

Пример 11

32 делится нацело на 16, поэтому: 3216=2

Умножить упрощенные множители на упрощенные корни

Помним про правило: не оставлять в знаменателе корни.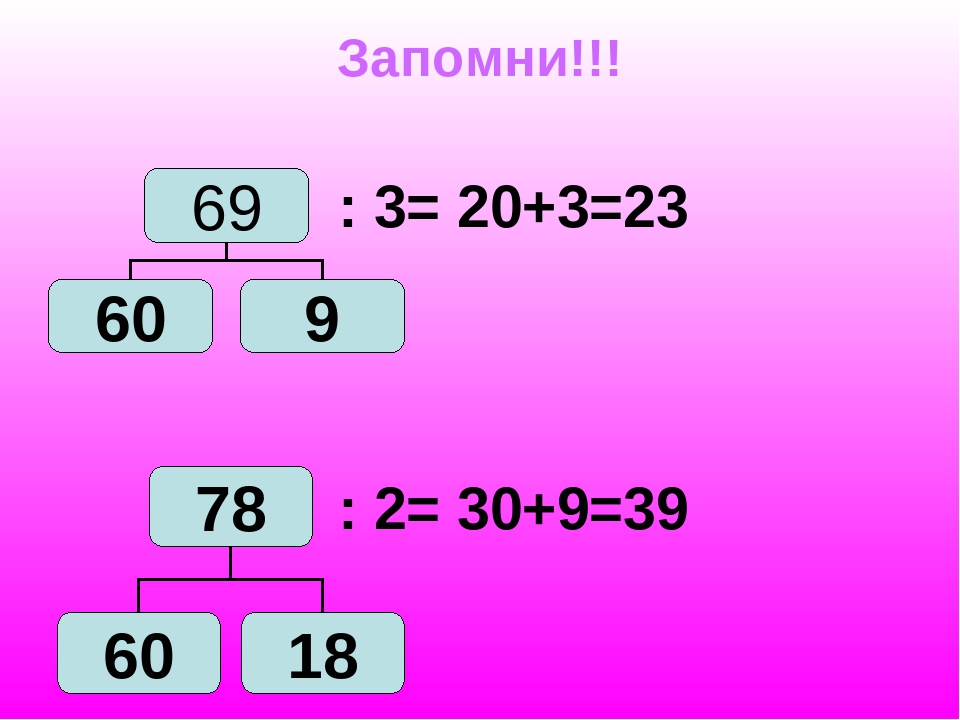 Поэтому просто перемножаем числитель и знаменатель на этот корень.

Пример 12

Рационализировать знаменатель (избавиться от корня в знаменателе)

Пример 13

4327. Следует умножить числитель и знаменатель на 7, чтобы избавиться от корня в знаменателе.

437×77=43×77×7=42149=4217

Метод 4. Деление на двучлен с квадратным корнем

Алгоритм действий:

Определить, находится ли двучлен (бином) в знаменателе

Напомним, что двучлен представляет собой выражение, которое включает 2 одночлена. Такой метод имеет место быть только в случаях, когда в знаменателе двучлен с квадратным корнем.

Пример 14

15+2— в знаменателе присутствует бином, поскольку есть два одночлена.

Найти выражение, сопряженное биному

Напомним, что сопряженный бином является двучленом с теми же одночленами, но с противоположными знаками. Чтобы упростить выражение и избавиться от корня в знаменателе, следует перемножить сопряженные биномы.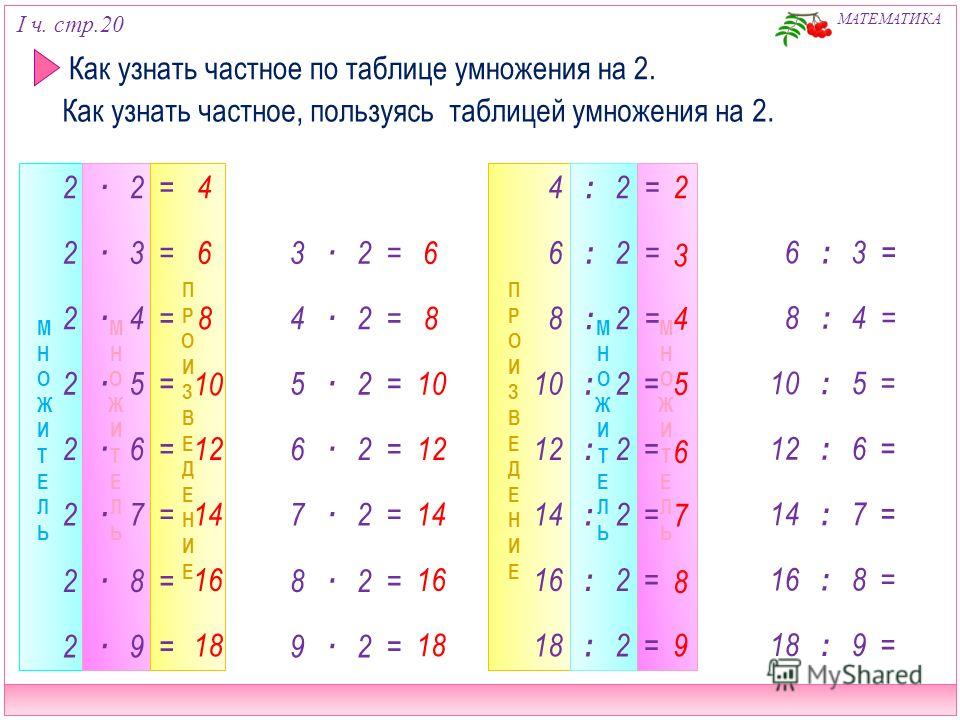

Пример 15

5+2и 5-2 — сопряженные биномы.

Умножить числитель и знаменатель на двучлен, который сопряжен биному в знаменателе

Такая опция поможет избавиться от корня в знаменателе, поскольку произведение сопряженных двучленов равняется разности квадратов каждого члена биномов: (a-b)(a+b)=a2-b2

Пример 16

15+2=1(5-2)(5-2)(5+2)=5-2(52-(2)2=5-225-2=5-223.

Из этого следует: 15+2=5-223.

Советы: 

1. Если вы  работаете с квадратными корнями смешанных чисел, то преобразовывайте их в неправильную дробь. 
2. Отличие сложения и вычитания от деления — подкоренные выражения в случае деления не рекомендуется упрощать (за счет полных квадратов).
3. Никогда (!) не оставляйте корень в знаменателе.
4. Никаких десятичных дробей или смешанных перед корнем — необходимо преобразовать их в обыкновенную дробь, а потом упростить.
5. В знаменателе сумма или разность двух одночленов? Умножьте такой бином на сопряженный ему двучлен и избавьтесь от корня в знаменателе.

Свойства деления. Деление произведения, суммы и разности на число

Деление произведения на число

Произведение можно разделить на число двумя способами:

1) Чтобы разделить произведение на какое-нибудь число, можно сначала вычислить значение произведения (выполнить умножение) и полученный результат разделить.

Например, чтобы найти значение выражения:

(12 · 5) : 3,

можно сначала умножить  12  на  5:

12 · 5 = 60

и полученное произведение разделить на  3:

60 : 3 = 20,

значит  (12 · 5) : 3 = 60 : 3 = 20.

Если один из сомножителей делится на число, на которое надо разделить произведение, то можно воспользоваться вторым способом нахождения частного от деления произведения на число.

2) Чтобы разделить произведение на какое-нибудь число, можно разделить на это число один любой сомножитель, оставив другие без изменений.

Например, чтобы найти значение выражения:

(8 · 20) : 4,

можно сначала разделить любой из сомножителей  (8  или  20)  на  4:

8 : 4 = 2

и полученное частное умножить на другой сомножитель:

2 · 20 = 40,

значит  (8 · 20) : 4 = (8 : 4) · 20 = 2 · 20 = 40.

Данное выражение можно решить ещё так:

(8 · 20) : 4 = 8 · (20 : 4) = 8 · 5 = 40.

Деление числа на произведение

Число можно разделить на произведение двумя способами:

1) Чтобы разделить какое-нибудь число на произведение, можно сначала вычислить значение произведения (выполнить умножение), а затем разделить число на полученный результат.

Например, чтобы найти значение выражения:

60 : (3 · 2),

можно сначала умножить  3  на  2:

3 · 2 = 6

и разделить  60  на полученный результат:

60 : 6 = 10,

значит  60 : (3 · 2) = 60 : 6 = 10.

Если число, которое нужно разделить на произведение, делится на каждый сомножитель, из которого состоит данное произведение, то можно воспользоваться вторым способом нахождения частного от деления числа на произведение.

2) Чтобы разделить какое-нибудь число на произведение, можно разделить это число на первый сомножитель, полученное частное разделить на второй сомножитель, это частное на третий и т. д.

Например, чтобы найти значение выражения:

120 : (5 · 3),

можно сначала разделить  120  на  5:

120 : 5 = 24,

а теперь, полученное частное  24  разделить на  3:

24 : 3 = 8,

значит  120 : (5 · 3) = (120 : 5) : 3 = 24 : 3 = 8.

Так как от перестановки множителей произведение не изменится, то множители можно поменять местами:

120 : (3 · 5)

и разделить  120  сначала на  3,  а затем полученный результат разделить на  5:

120 : (3 · 5) = (120 : 3) : 5 = 40 : 5 = 8.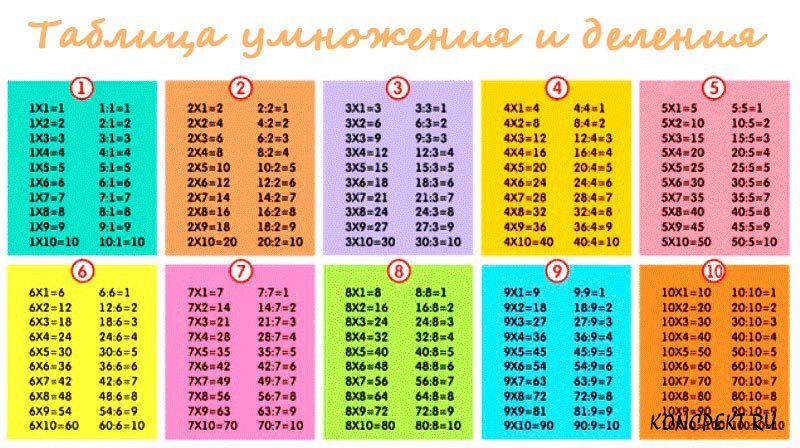

Получается, что не важно на какой множитель сначала делить число, результат будет одинаковым:

120 : (5 · 3) = (120 : 5) : 3 = 24 : 3 = 8

тоже самое, что и

120 : (5 · 3) = (120 : 3) : 5 = 40 : 5 = 8.

Из данного примера можно сделать вывод, что значение частного не изменится от порядка выполнения действий.

Деление суммы на число

Сумму можно разделить на число двумя способами:

1) Чтобы разделить сумму на какое-нибудь число, можно сначала вычислить значение суммы (выполнить сложение) и полученный результат разделить.

Например, чтобы найти значение выражения:

(15 + 12) : 3,

можно сначала сложить числа  15  и  12:

15 + 12 = 27

и полученную сумму разделить на  3:

27 : 3 = 9,

значит  (15 + 12) : 3 = 27 : 3 = 9.

Если все слагаемые в записи суммы делятся на число, на которое надо разделить сумму, то можно воспользоваться вторым способом нахождения частного от деления суммы на число.

2) Чтобы разделить сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно и полученные частные сложить.

Например, чтобы найти значение выражения:

(42 + 28 + 70) : 7,

можно каждое слагаемое разделить на число  7:

42 : 7 = 6,    28 : 7 = 4   и   70 : 7 = 10;

и полученные частные  (6,  4  и  10)  сложить:

6 + 4 + 10 = 20,

значит  (42 + 28 + 70) : 7 = 42 : 7 + 28 : 7 + 70 : 7 = 6 + 4 + 10 = 20.

Деление разности на число

Разность можно разделить на число двумя способами:

1) Чтобы разделить разность на какое-нибудь число, можно сначала вычислить значение разности (выполнить вычитание) и полученный результат разделить.

Например, чтобы найти значение выражения:

(24 — 8) : 2,

можно сначала вычесть из  24  число  8:

24 — 8 = 16,

и полученную разность разделить на  2:

16 : 2 = 8,

значит  (24 — 8) : 2 = 16 : 2 = 8.

Если и уменьшаемое и вычитаемое в записи разности делятся на число, на которое надо разделить разность, то можно воспользоваться вторым способом нахождения частного от деления разности на число.

2) Чтобы разделить разность на какое-нибудь число, можно разделить на это число отдельно уменьшаемое и вычитаемое, а потом из первого частного вычесть второе.

Например, чтобы найти значение выражения:

(42 — 28) : 7,

можно отдельно уменьшаемое и вычитаемое разделить на число  7:

42 : 7 = 6,   28 : 7 = 4

и найти разность полученных частных:

6 — 4 = 2,

значит  (42 — 28) : 7 = 42 : 7 — 28 : 7 = 6 — 4 = 2.

Общие формулы свойств деления

Все свойства деления можно представить в виде формул:

Распределительные свойства
(a + b) : c = a : c + b : c
(a — b) : c = a : c — b : c
(a · b) : c = (a : c) · b = (b : c) · a
a : (b · c) = (a : b) : c = (a : c) : b
Действия с единицей и нулём
a : 1 = a
a : a = 1
0 : a = 0 (a ≠ 0)
На нуль делить нельзя

Раздел земельного участка в 2021 г.

1. Проживём.com≫
2. Земля≫
3. Разделение

Рубрика обновлена: 29 декабря 2020 г.

Девяткин АлександрЗемельный юрист. Стаж работы с земельными участками с 2005 г.

Здравствуйте. Раздел земельных участков регулируется статьей 11.4. Земельного Кодекса РФ. Крайне советую прочитать эту небольшую статью, чтобы иметь хотя-бы небольшое представление об этой процедуре.

Если нужна бесплатная юридическая консультация, напишите онлайн юристу справа или позвоните по телефонам (круглосуточно и без выходных для всех регионов РФ): 8 (499) 938-45-78 — Москва и обл.; 8 (812) 425-62-89 — Санкт-Петербург и обл.; 8 (800) 350-24-83 — все регионы РФ.

Как правильно оформить в 2021 году

Для начала изучите требования к участку, прежде чем его разделить.

Я опубликовал 2 инструкции, т.к. многое зависит от количества собственников. Инструкции подходят для разных видов участков — ИЖС, ЛПХ, СНТ и т.п.

Вариант №1 — когда участком владеет несколько собственников

Как разделить участок, если им владеет несколько собственников — инструкция подходит как при общей долевой собственности, так и при совместной. Оформление уложил в 4 этапа.

Вариант №2 — когда один собственник

Как разделить участок, если им владеет один собственник. В этом случае разделить участок легче, инструкции по ссылке всего в 3 этапа.

Другие статьи

Как оформить земельный участков в собственность — инструкция, законы, стоимость.Как перевести земельный участок: с ЛПХ в ИЖС; с ИЖС в ЛПХ; с ИЖС в «коммерческую недвижимость»

Требования к участкам

Не каждый участок можно разделить, для этого есть определенные требования:

• Участок должен стоять на кадастровом учете — п. 7 ст. 1 Федерального закона от 13. 07.2015 № 218-ФЗ.

  Я опубликовал подробную инструкцию с картинками — как проверить есть ли земельный участок в кадастровом учете.

  Если участок не стоит на кадастровом учете, для начала нужно это исправить. И только потом участок можно разделить. Постановка земельного участка на кадастровый учет.

• У участка должны быть определены границы — пп. 3 и 9 п. 4 ст. 8 Федерального закона от 13.07.2015 № 218-ФЗ.

  У меня также есть отдельная инструкция — как узнать определены ли границы у земельного участка.

  Если кратко, найдите участок на публичной кадастровой карте Росреестра. Чтобы не искать, можете нажать кнопку «лупа» слева и ввести кадастровый номер участка. Если участок имеет границы, на кадастровой карте он будет подсвечен желтым. Если границы не уточнены, будет написано «Ничего не найдено» или «Без координат границ». В этом случае сначала нужно установить границы участка и только потом заниматься переводом с ЛПХ в ИЖС.

  Примеры участков

  (нажмите на картинки, чтобы их увеличить)

  Границы определены

  Границы не определены

• Если собственников несколько, все они должны быть согласны на раздел. Им потребуется подписать соглашение о разделе участка. Если кто-либо не согласен, придется обращаться в суд и делить участок по решению суда. Это указано в п. 5 и 8 ст. 11.2 ЗК РФ.
• Полученные участки не должны быть меньше минимальной площади, которая установлена местными органами власти — ст. 11.9 ЗК РФ.

  Минимальная площадь в населенных пунктах разная, потому что ее устанавливают местные органы власти. Она также зависит от категории участка и вида его разрешенного использования. Например, минимальный размер участка ИЖС или ЛПХ в Люберецком районе Московской области — 4 сотки, а в Балашихинском районе по таким же участкам — 6 соток. В п. Лесколово Ленинградской области для ИЖС — минимум 6 соток, для ЛПХ — минимум 10 соток. Поэтому, нельзя разделить участок в 10 соток на два участка, если местной администрацией установлен минимальный размер в 6 соток.

Другие статьи

Как уточнить границы земли на местности — закажите у кадастрового инженера «вынос точек в натуру»Проверка земли на обременение/ограничение — онлайн способ.

• К каждому участку должен быть доступ/проход, иначе его не поставят на кадастровый учет — пп. 26 п. 1 ст. 26 Закона о регистрации недвижимости. Если на участок не получится сделать проход с улицы (дороги), его нужно сделать через соседний полученный участок.

  Ниже я нарисовал как собственникам можно разделить участок в зависимости от его расположения.

  Пример №1

  (нажмите на картинки, чтобы их увеличить)

  Первый вариант — к каждому участку есть доступ с дороги

  Второй вариант — доступ ко второму участку осуществлен через сервитут

  Пример №2

  Первый вариант

  Второй вариант

• Нельзя разделить участок с видом разрешенного использования «Для ведения крестьянско-фермерского хозяйства». Прямой запрет указан в п. 1 ст. 9 Федерального закона о крестьянском (фермерском) хозяйстве.

Показать остальные комментарии

ДЕЛЕНИЕ НА 8: НАЦЕЛО И С ОСТАТКОМ

Благодарен вашему журналу за публикацию моего материала о признаке делимости целых чисел на 7 (см. «Наука и жизнь» № 10, 1997 г.). Рискну предложить еще один новый признак делимости, но уже на 8.

Я перелистал много книг по занимательной математике, но такого признака не нашел нигде.

Общепринятый признак делимости на 8 выглядит так: число делится на 8 в том и только в том случае, если его последние три цифры образуют число, делящееся на 8.

Этот способ деления основан на том, что все числа, кратные 1000, делятся на 8 без остатка.

Значит, определение признака делимости на 8 любых многозначных целых чисел сводится в итоге к определению признака делимости на 8 трехзначных чисел.

Трехзначные числа и будем рассматривать.

Б. А. Кордемский сводит делимость уже трехзначных чисел к делимости двузначных (образованных цифрами сотен и десятков): «На 8 делится всякое трехзначное число, у которого двузначное число, образованное цифрами сотен и десятков, сложенное с половиной числа единиц, делится на 4».

Он приводит пример с числом 592. Применяя к нему признак делимости, получаем:

59 + 1 = 60,

где 1 — это 2:2, половина числа единиц.

Число 60 делится на 4, значит, число 592 делится на 8 без остатка.

При данном методе определения остатка от деления надо учитывать, что трехзначные числа, оканчивающиеся нечетной цифрой (1, 3, 5, 7, 9), надо сначала «округлить» в разряде единиц до ближайшей большей или меньшей четной цифры и в конечном результате опять же учесть эту единицу, то есть прибавить ее или отнять. Это первое.

Второе: в некоторых случаях сумма двузначного числа, образованного цифрами сотен и десятков, и половины единиц будет также трехзначным числом, что опять же не совсем удобно. Это будет происходить с рядом чисел в промежутке от 968 до 999.

Однако всех этих неудобств — прибавления (вычитания) 1 и оперирования трехзначными числами — можно избежать.

Вспомним, что четное число сотен — 2, 4, 6, 8 (200, 400, 600, 800) делится на 8 без остатка. Следовательно, у таких, к примеру, чисел, как 059, 237, 461, 632, 844, определить остаток от деления на 8 можно сразу по двузначному числу, составленному из десятков и единиц, то есть по числам 59, 37, 61, 32, 44. Достаточно в уме разделить эти двузначные числа на 8.

Если цифры сотен в трехзначных исходных числах нечетны (1, 3, 5, 7, 9), то опять же делим на 8 двузначные числа, образованные десятками и единицами, но в этом случае прибавляем (или отнимаем) к двузначным числам цифру 4. Этот факт следует из того, что все целые нечетные сотни (100, 300, 500, 700, 900) при делении на 8 дают один остаток — 4.

Для примера возьмем числа 165, 371, 587, 716, 923. «Превратим» их в двузначные числа, прибавляя (можно отнимая) 4:

69, 75, 91, 20, 27.

Делить эти двузначные числа на 8 опять же просто. Остатки от делений и будут остатками от деления на 8 исходных трехзначных чисел.

А как поступить, если трехзначное число 997?

Выше говорилось, что цифру 4 можно не только прибавлять, но и отнимать от двузначного числа. Значит, делить на 8 будем уже число 93: 97- 4 = 93.

Так происходит «избавление» от трехзначных чисел.

Обобщая все вышесказанное, алгоритм упрощенного признака делимости на 8 целых чисел можно записать так: отделяем, отсчитывая справа, три цифры исходного числа; если третья справа цифра четная (0, 2, 4, 6, 8), то делим на 8 только число, образованное двумя крайними правыми цифрами; остаток от этого деления и будет остатком от деления на 8 всего исходного числа; если третья справа цифра в исходном числе нечетная (1, 3, 5, 7, 9), делим на 8 число, образованное двумя крайними правыми цифрами, плюс (минус) 4; остаток от деления этой суммы и даст остаток от деления на 8 всего исходного целого числа.

Как видно, этот признак делимости совсем прост, и для его освоения понадобятся минимальные усилия и знание элементарной арифметики.

Литература

Кордемский Б. А. Математическая смекалка. М., 1991.

Воробьев Н. Н. Признаки делимости. М., 1980.

Гарднер М. Математические досуги. М., 1995.

Калькулятор дробей

Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.

Правила для выражений с дробями:

Дроби — используйте косую черту «/» между числителем и знаменателем, т.е.е., для пяти сотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.
Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).

Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .

Десятичные числа (десятичные числа) вводятся с десятичной запятой . , и они автоматически конвертируются в дроби — то есть 1,45 .

Двоеточие : и косая черта / являются символом деления. Может использоваться для деления смешанных чисел 1 2/3: 4 3/8 или может использоваться для записи сложных дробей i.1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное дробное: 0,625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4 ​​
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3

Калькулятор следует известным правилам для порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.

Дроби в словесных задачах:

следующие математические задачи »

2 разделить на что равно 3? (Найдите недостающий номер)

2 разделить на 3? Если вы хотите решить эту словесную проблему, то вы попали в нужное место. Если у вас есть число 2 и вы хотите разделить его на что-то, чтобы получить ответ 3, то этот быстрый урок по уравнениям покажет вам, как именно найти это недостающее число «что-то».

Прежде всего, мы можем записать эту проблему и использовать букву X в качестве недостающего числа, которое мы хотим найти:

2 / Икс = 3

Первый шаг — умножить обе части этого уравнения на недостающее число X. Мы еще не знаем, что такое X, поэтому мы делаем это, добавляя X в скобках:

2 (Х) / Икс = 3 (Х)

Если вы новичок в уравнениях, это может показаться немного запутанным, но на самом деле мы говорим, что 2 — это то же самое, что и 3, умноженные на X.

Чтобы найти X, нам нужно разделить обе части на наш окончательный ответ, 3:

2 / 3 знак равно 3 (Х) / 3

Итак, наш окончательный ответ на 2, разделенный на 3, будет:

0. 6667 = Х

В этих ответах мы округляем их максимум до 4 знаков после запятой, потому что некоторые вычисления могут иметь длинные десятичные ответы. Если вы хотите проверить, близок ли ответ, вы можете разделить 2 на 0,6667:

.

2 / 0,6667 = 2,9999

Надеюсь, теперь вы точно знаете, как решать подобные математические задачи в будущем.Могу я просто сказать тебе разделить 2 на 3? Да, но разве вы не рады, что научились этому процессу?

Попробуйте сами и попробуйте вычислить пару из них без использования нашего калькулятора. Возьмите карандаш и лист бумаги и выберите пару цифр.

Цитируйте, ссылайтесь или ссылайтесь на эту страницу

Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте инструмент ниже, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!

• 2 разделить на то, что равно 3?

• «2 разделить на 3 равно 3?». VisualFractions.com . По состоянию на 3 июня 2021 г. https://visualfractions.com/calculator/divided-by-what/2-divided-by-what-equals-3/.

• «2 разделить на 3 равно 3?». VisualFractions.com , https: // visualfractions.ru / калькулятор / разделить-на-чем / 2-разделить-на-что-равно-3 /. По состоянию на 3 июня 2021 г.

• 2 разделить на то, что равно 3 ?. VisualFractions.com. Получено с https://visualfractions.com/calculator/divided-by-what/2-divided-by-what-equals-3/.

Калькулятор

Делится на то, что равно

Калькулятор остатка

Этот калькулятор частного и остатка поможет вам разделить любое число на целое и вычислить результат в виде целых чисел. В этой статье мы объясним вам, как использовать этот инструмент и каковы его ограничения. Мы также предоставим вам пример, который лучше проиллюстрирует его назначение.

Дивиденды, делитель, частное и остаток

Когда вы выполняете деление, вы обычно можете записать эту операцию следующим образом:

а / п = д + р / п

где:

• a — это начальное число, которое вы хотите разделить, называемое делимым .
• n — это число, на которое вы делите; он называется делителем .
• q — результат деления с округлением до ближайшего целого числа; оно называется частным .
• r — это остаток этой математической операции.

При выполнении деления с остатками на нашем калькуляторе важно помнить, что все эти значения должны быть целыми числами. В противном случае результат будет правильным с точки зрения формул, но не будет иметь математического смысла.

Не забудьте проверить наш калькулятор по модулю для практического применения калькулятора с остатками.

Как рассчитать остаток

1. Начните с записи вашей проблемы. Например, вы хотите разделить 346 на 7.
2. Решите, какое из чисел является делимым, а какое — делителем. Делимое — это число, над которым выполняется операция — в данном случае 346. Делитель — это число, которое фактически «выполняет работу», в данном случае 7.
3. Произведите деление — можете использовать любой калькулятор. Вы получите результат, который, скорее всего, не является целым числом — в этом примере 49.4285714.
4. Округлите это число в меньшую сторону. В нашем примере вы получите 49.
5. Умножьте число, полученное на предыдущем шаге, на делитель. В нашем случае 49 * 7 = 343 .
6. Вычтите число из предыдущего шага из вашего дивиденда, чтобы получить остаток. 346 - 343 = 3 .
7. Вы всегда можете воспользоваться нашим калькулятором с остатками и сэкономить время 🙂

FAQ

Как вы решаете китайские задачи теоремы об остатках?

1. Убедитесь, что у вас есть неизвестный , равный двум или более различным модулям , например. грамм. x = d mod a, e mod b и f mod c.
2. Убедитесь, что все модули имеют одинаковый наибольший общий делитель .
3. Умножаем каждый по модулю на все остальные по модулю, кроме одного, , пока не будут найдены все комбинации . Для указанных выше модулей это будет: b c, a c, a * b.
4. Разделите каждое число на пропущенный модуль . Если он равен остатку от этого модуля, например (b * c) / a = d, оставьте число как есть.
5. Если остаток не равен остатку по модулю, используйте метод проб и ошибок, чтобы найти положительное целое число, чтобы умножить его на так, чтобы шаг 4 стал истинным.
6. Сложите все числа вместе, как только шаг 4 верен для всех комбинаций.

Какие еще уловки?

Полезно запомнить некоторые оставшиеся ярлыки, чтобы сэкономить ваше время в будущем. Во-первых, если число делится на 10 , то остаток равен последней цифре этого числа . Точно так же, если число делится на 9, складывайте каждую из цифр друг с другом, пока у вас не останется одно число (например, 1164 превратится в 12, которое, в свою очередь, превратится в 3), которое является остатком.Наконец, вы можете умножить десятичную дробь частного на делитель, чтобы получить остаток.

Как интерпретировать остаток?

Изучение того, как вычислить остаток, включает , многие из которых используют в реальном мире , и это то, чему вас учат школа, что вы обязательно будете использовать в повседневной жизни. Допустим, вы купили 18 пончиков для своего друга, но появилось только 15 из них, у вас осталось 3 . Или сколько денег у вас осталось после покупки пончиков? Если максимальное количество обезьян в бочке составляет 150, а в районе 183 обезьяны, сколько обезьян будет в меньшей группе?

Как превратить остаток в десятичную дробь?

1. Настройте деление, добавив десятичный знак, а затем ноль после столбца единицы делимого (если ваш дивиденд уже является десятичным, добавьте дополнительный ноль в конец).
2. Выполните деление как обычно , пока не останется остаток.
3. Вместо того, чтобы писать остаток после частного, переместите остаток выше добавленного вами нуля .
4. Если есть остаток от этого деления, добавьте еще один ноль к делимому и прибавьте к нему остаток.
5. Продолжайте таким же образом до тех пор, пока не будет: либо нет остатка, цифра или цифры повторяются бесконечно, либо вы не достигнете желаемой степени точности (3 десятичных знака обычно нормально).
6. Результат после десятичной точки — это остаток в виде десятичной дроби.

Что такое частное и остаток?

Частное составляет , количество раз, когда деление завершается полностью , а остаток — это сумма, которая остается , которая не полностью входит в делитель . Например, 127, разделенное на 3, составляет 42 R 1, поэтому 42 — это частное, а 1 — остаток.

Как записать остаток в виде дроби?

После того, как вы нашли остаток от деления, вместо R, за которым следует остаток после частного, просто запишите дробь, где остаток делится на делитель исходного уравнения .Это так просто!

Как писать остатки?

Есть 3 способа записи остатка: с R, в виде дроби и в виде десятичной дроби . Например, 821, разделенное на 4, будет записано как 205 R 1 в первом случае, 205 ¹ / ₄ во втором и 205,25 в третьем.

Какой остаток от деления 26 на 6?

Остаток 2 . Чтобы решить эту проблему, найдите наибольшее кратное 6, которое меньше 26.В данном случае это 24. Затем вычтите 24 из 26, чтобы получить остаток, который равен 2.

Каков остаток от деления 599 на 9?

Остаток 5 . Чтобы вычислить это, сначала разделите 599 на 9, чтобы получить наибольшее кратное 9 перед 599. 5/9 <1, поэтому перенесите 5 в десятки, 59/9 = 6 r 5, поэтому перенесите 5 в цифры. 59/9 = 6 r 5 снова, поэтому наибольшее кратное 66. Умножьте 66 на 9, чтобы получить 594, и вычтите это из 599, чтобы получить 5, остаток.

Как рассчитать остаток от деления 24 на 7?

1. Вычтите 7 из 24 несколько раз , пока результат не станет меньше 7.
2. 24 минус 3 умножить на 7 равно 3.
3. Оставшееся число, 3 , является остатком.
4. Это может быть выражено как ³ / ₇ в дробной форме или как 0,42857 в десятичной форме.

Дивизион ÷ | Основы арифметики

На этой странице представлены основные сведения о Дивизионе (÷) .

См. Другие наши арифметические страницы для обсуждения и примеров: Сложение ( + ), Вычитание (-) и Умножение ( × ).

Дивизион

Обычный письменный символ деления — (÷). В электронных таблицах и других компьютерных приложениях используется символ «/» (косая черта).

Деление — это противоположность умножения в математике.

Деление часто считается самой сложной из четырех основных арифметических функций. На этой странице объясняется, как выполнять расчеты деления. Когда мы хорошо разбираемся в методе и правилах, мы можем без ошибок использовать калькулятор для более сложных вычислений.

Дивизион позволяет нам разделить или «поделиться» числами, чтобы найти ответ. Например, давайте посмотрим, как мы можем найти ответ на 10 ÷ 2 (десять, разделенные на два). Это то же самое, что «разделить» 10 сладостей между 2 детьми. У обоих детей должно получиться одинаковое количество конфет. В этом примере ответ — 5.

---

Некоторые быстрые правила о делении:

---

• Если вы разделите 0 на другое число, ответ всегда будет 0. Например: 0 ÷ 2 = 0.То есть 0 сладостей делятся поровну между 2 детьми — каждый ребенок получает 0 сладостей.

• Когда вы делите число на 0, вы вообще не делите (это большая проблема в математике). 2 ÷ 0 невозможно. У вас есть 2 сладости, но нет детей, чтобы разделить их между собой. Нельзя делить на 0.

• Когда вы делите на 1, ответ будет таким же, как и число, которое вы делили. 2 ÷ 1 = 2. Две сладости, разделенные на одного ребенка.

• Когда вы делите на 2, вы уменьшаете число вдвое.2 ÷ 2 = 1.

• Любое число, разделенное на такое же число, равно 1. 20 ÷ 20 = 1. Двадцать конфет, разделенных на двадцать детей — каждый ребенок получает по одной конфете.

• Номера должны быть разделены в правильном порядке. 10 ÷ 2 = 5, тогда как 2 ÷ 10 = 0,2. Десять сладостей, разделенных на двоих детей, сильно отличаются от двух сладостей, разделенных на 10 детей.

• Все дроби, такие как ½, ¼ и ¾, являются суммами деления. ½ — это 1 ÷ 2. Одна конфета, разделенная на двоих детей.Смотрите нашу страницу Дроби для получения дополнительной информации.

Множественное вычитание

Так же, как умножение — это быстрый способ вычисления множественных сложений, деление — это быстрый способ выполнения множественных вычитаний.

Например:

Если у Джона есть 10 галлонов топлива в машине и он использует 2 галлона в день, сколько дней до того, как он закончится?

Мы можем решить эту проблему, выполнив серию вычитаний или посчитав в обратном порядке с шагом 2.

• В день 1 Джон начинает с 10 галлонов и заканчивается 8 галлонами. 10-2 = 8
• В день 2 Джон начинает с 8 галлонов и заканчивается 6 галлонами. 8 — 2 = 6
• В день 3 Джон начинает с 6 галлонов и заканчивается 4 галлонами. 6 — 2 = 4
• В день 4 Джон начинает с 4 галлонов и заканчивается 2 галлонами. 4 — 2 = 2
• В день 5 Джон начинает с 2 галлонов и заканчивается 0 галлонами. 2 — 2 = 0

У Джона заканчивается топливо на 5-й день.

Более быстрый способ выполнить этот расчет — разделить 10 на 2. То есть сколько раз 2 уходит в 10 или сколько партий по два галлона в десяти галлонах? 10 ÷ 2 = 5.

Таблица умножения (см. Умножение) может помочь нам найти ответ на простые вычисления деления.

В приведенном выше примере нам нужно было вычислить 10 ÷ 2 . Для этого с помощью таблицы умножения найдите столбец для 2 (заштрихованный красным заголовок). Двигайтесь вниз по столбцу, пока не найдете искомый номер: 10 . Переместитесь по строке влево, чтобы увидеть ответ (заштрихованный красным заголовок) 5 .

Таблица умножения

×	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

Мы можем выполнить другие простые вычисления деления, используя тот же метод. Например, 56 ÷ 8 = 7 . Найдите 7 в верхней строке, посмотрите вниз по столбцу, пока не найдете 56 , затем найдите соответствующий номер строки, 8 .

Если возможно, вам следует попытаться запомнить приведенную выше таблицу умножения, потому что она значительно ускоряет решение простых вычислений умножения и деления.

---

Деление больших чисел

Вы можете использовать калькулятор для вычисления деления, особенно когда вы делите большие числа, которые труднее вычислить в уме.Однако важно понимать, как выполнять расчеты деления вручную. Это полезно, когда у вас нет калькулятора под рукой, но также важно для того, чтобы вы правильно использовали калькулятор и не допускали ошибок. Деление может показаться устрашающим, но на самом деле, как и в большинстве арифметических операций, оно логично.

Как и всю математику, проще всего понять, если мы рассмотрим пример:

Машине Дэйва нужны новые шины. Ему нужно заменить все четыре шины на машине, а также запасную.

Дэйв получил предложение в местном гараже на сумму 480 фунтов стерлингов, включая шины, установку и утилизацию старых шин. Сколько стоит каждая шина?

Задача, которую нам нужно вычислить, — это 480 ÷ 5 . Это то же самое, что сказать, сколько раз 5 перейдет в 480?

Условно мы пишем это как:

Мы работаем слева направо в логической системе.

Мы начинаем с деления 4 на 5 и сразу же решаем задачу. 4 не делится на 5, чтобы получить целое число, так как 5 больше 4.

Язык, который мы используем в математике, может сбивать с толку. Другой способ взглянуть на это — спросить: «Сколько раз 5 переходит в 4?».

Мы знаем, что 2 дважды переходит в 4 (4 ÷ 2 = 2), и мы знаем, что 1 переходит в 4 четыре раза (4 ÷ 1 = 4), но 5 не переходит в 4, потому что 5 больше 4.

Число, на которое мы делим (в данном случае 5), должно войти в число, на которое мы делим (в данном случае 4) целое количество раз. Как вы увидите, это необязательно должно быть точное целое число.

Поскольку 5 не переходит в 4, мы помещаем 0 в первый столбец (сотни). Для получения помощи с столбцами сотен, десятков и единиц см. Нашу страницу на числах .

	Сот	Десятки	шт.
	0
5	4	8	0

Затем мы переместимся вправо, чтобы включить столбец десятков.Теперь мы можем увидеть, сколько раз 5 переходит в 48.

5 переходит в 48, так как 48 больше 5. Однако нам нужно выяснить, сколько раз оно идет.

Если мы обратимся к нашей таблице умножения, мы увидим, что 9 × 5 = 45 и 10 × 5 = 50 .

Число

48 , которое мы ищем, находится между этими двумя значениями. Помните, что нас интересует целое число , умноженное на , из которого 5 переходит в 48. Десять раз — это слишком много.

Мы можем видеть, что 5 переходит в 48 целое число (9) раз, но не точно, с оставшимися 3.

9 × 5 = 45
48-45 = 3

Теперь мы можем сказать, что 5 делится на 48 девять раз, но с остатком 3. Остаток — это то, что остается, когда мы вычитаем найденное число из числа, на которое делим: 48-45 = 3 .

Итак, 5 × 9 = 45, + 3, чтобы получить 48.

Мы можем ввести 9 в столбец десятков в качестве ответа для второй части вычисления и поставить остаток перед нашим последним числом в столбце единиц.Наше последнее число становится 30.

	Сот	Десятки	шт.
	0	9
5	4	8	30

Теперь разделим 30 на 5 (или узнаем, сколько раз 5 делится на 30). Используя нашу таблицу умножения, мы можем увидеть, что ответ — ровно 6 без остатка. 5 × 6 = 30. Мы пишем 6 в столбце единиц нашего ответа.

	Сот	Десятки	шт.
	0	9	6
5	4	8	30

Поскольку остатков нет, мы закончили расчет и получили ответ 96 .

Новые шины

Дэйва будут стоить фунтов стерлингов 96 каждая. 480 ÷ 5 = 96 и 96 × 5 = 480 .

---

Отдел рецептов

Наш последний пример деления основан на рецепте. Часто при приготовлении рецепты сообщают вам, сколько еды они собираются приготовить, например, чтобы накормить 6 человек.

Ингредиенты, указанные ниже, необходимы для изготовления 24 сказочных лепешек, однако мы хотим приготовить только 8 сказочных лепешек. Мы немного изменили ингредиенты для удобства этого примера (оригинальный рецепт на сайте BBC Food).

Первое, что нам нужно установить, это сколько восьмерок в 24 — используйте приведенную выше таблицу умножения или свою память.3 × 8 = 24 — если мы разделим 24 на 8, мы получим 3. Следовательно, нам нужно разделить каждый ингредиент ниже на 3, чтобы получить правильное количество смеси, чтобы сделать 8 сказочных лепешек.

Состав

• 120 г сливочного масла, размягченного при комнатной температуре
• 120 г сахарной пудры
• 3 яйца от кур на свободном выгуле, слегка взбитые
• 1 чайная ложка ванильного экстракта
• 120 г муки самоподнимания
• 1-2 столовые ложки молока

Масло сливочное, сахар и мука все одинаковые, 120гр.Следовательно, необходимо всего один раз проработать 120 ÷ 3, так как ответ будет одинаковым для этих трех ингредиентов.

Как и раньше, мы начинаем с левого столбца (сотни) и делим 1 на 3. Однако 3 ÷ 1 не идет, поскольку 3 больше 1. Затем мы смотрим, сколько умножений 3 получается в 12. Используя таблицу умножения при необходимости мы можем увидеть, что 3 переходит в 12 ровно 4 раза по без остатка.

120 г ÷ 3, следовательно, 40 г. Теперь мы знаем, что нам понадобится 40 г масла, сахара и муки.

Исходный рецепт требует 3 яйца, и мы снова делим на 3. Итак, 3 ÷ 3 = 1, поэтому необходимо одно яйцо.

Далее рецепт требует 1 чайную ложку ванильного экстракта. Нам нужно разделить одну чайную ложку на 3. Мы знаем, что деление можно записать в виде дроби, поэтому 1 ÷ 3 то же самое, что third (одна треть). Вам понадобится чайной ложки ванильного экстракта, хотя на самом деле сложно точно отмерить чайной ложки!

Оценка может быть полезной, а единицы измерения можно менять!

---

Мы можем взглянуть на это с другой стороны, если знаем, что одна чайная ложка равна 5 мл или 5 миллилитрам.(Если вам нужна помощь с единицами измерения, см. Нашу страницу, посвященную системам измерения , . ) Если мы хотим быть более точными, мы можем попробовать разделить 5 мл на 3. 3 делится на 5 один раз (3) с оставшимися 2. 2 ÷ 3 — это то же самое, что и so, поэтому 5 мл, разделенное на 3, дает 1 ⅔ мл, что в десятичных дробях составляет 1,666 мл. Мы можем использовать наши навыки оценки и сказать, что одна чайная ложка, разделенная на три, немного больше полутора миллилитров. Если у вас на кухне есть крошечные мерные ложки, вы можете быть очень точными!

Мы можем оценить ответ, чтобы убедиться, что мы правы.Три партии по 1,5 мл дают нам 4,5 мл. Итак, три партии «чуть больше 1,5 мл» дают нам около 5 мл. Рецепты редко являются точной наукой, поэтому небольшие оценки могут быть забавой и хорошей практикой для нашей ментальной арифметики.

Следующий рецепт требует 1-2 ст. Л. Молока. Это от 1 до 2 столовых ложек молока. У нас нет точного количества, и то, сколько молока вы добавите, будет зависеть от консистенции вашей смеси.

Мы уже знаем, что 1 ÷ 3 — это, а 2 ÷ 3 -. Поэтому нам понадобится – столовой ложки молока, чтобы испечь восемь сказочных лепешек. Давайте посмотрим на это с другой стороны. Одна столовая ложка равна 15 мл. 15 ÷ 3 = 5, поэтому ⅓ – столовой ложки равно 5–10 мл, что соответствует 1–2 чайным ложкам!

---

Дополнительная литература по навыкам, которые вам нужны

---

Основы счета
Часть необходимых навыков Руководство по счету

Эта электронная книга содержит рабочие примеры и простые для понимания объяснения, чтобы показать вам, как использовать основные математические операции и начать манипулировать числами.Он также включает в себя примеры из реальной жизни, чтобы прояснить, насколько эти концепции полезны в реальной жизни.

Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.

---

Что такое два и три?

Что такое длинное деление? — Определение и примеры

Деление в длину — это метод, с помощью которого человек может решать более сложные задачи деления, используя только карандаш и бумагу. В этом уроке будет дано определение деления в столбик, показано, как выполнять операцию, и приведено несколько примеров. В конце будет викторина, чтобы вы попрактиковались.

Соотношение дробей и десятичных знаков

Посмотрите этот видеоурок, чтобы узнать, как использовать дробные и десятичные дроби для решения задач.Узнайте, как переключаться между ними, чтобы использовать наиболее подходящий для вашей проблемы.

Посмотрите этот видеоурок, чтобы узнать, как можно разделить любое число на 1. Изучите правило, которое позволит вам мгновенно решить любую задачу деления на 1.

Правильные дроби: определение и примеры

В этом уроке мы обсудим, что делает правильные дроби правильными.Мы увидим, как они сравниваются с неправильными дробями, а также рассмотрим несколько примеров.

Делитель в математике: определение и пример

Математический язык часто может усложнять простые операции. В этом уроке будет представлено определение термина «делитель» вместе с примером, на котором сложное слово кажется довольно простым.

Умножение на дву- и трехзначные числа: Урок для детей

Умножение можно производить разными способами с разными цифрами.В этом уроке вы узнаете, как умножать двузначные и трехзначные числа на двузначные числа, используя как стандартную, так и развернутую форму умножения.

Как завершить приговор о разделении

Если вы когда-либо покупали еду для вечеринки или делились едой с семьей или друзьями, вы, возможно, не осознавали, что используете умножение и деление. В этом уроке вы узнаете, как завершить предложение о делении с помощью умножения.

Как оценивать коэффициенты

Может показаться безумным думать, что вы можете быстро оценить ответ на что-то вроде 81837/95, но к концу этого урока вы сможете легко оценить частные для простых и более сложных задач деления.После урока проверьте свои новые знания на практических примерах.

Как найти, произнести и написать, кратное 5

В этом уроке вы узнаете, как найти число, кратное 5. Вы узнаете, как легко произносить и записывать числа, получаемые при умножении числа на 5.

Что такое произведение по математике? — Определение и обзор

В математике термин «продукт» относится к ответу на задачу умножения.В этом уроке мы более подробно определим этот термин и приведем несколько примеров его использования. Затем будет викторина, чтобы проверить ваше понимание.

Изучение фактов умножения на 10 с помощью подсчета пропусков

Факты умножения могут быть не вашим любимым занятием на уроках математики, но это очень важно знать! В этом уроке мы будем использовать подсчет пропусков как метод для изучения ваших фактов умножения от 0 до 10.

Моделирование изменений состояния: тепло и энергия

Материя существует в разных фазах, но также может переходить из одной фазы в другую.Это не волшебство, это энергия! В этом уроке вы узнаете, как энергия может переводить материю из одного состояния в другое и как называются эти фазовые изменения.

Решение задач с разделительными словами

Проблемы с разделением слов. .. Эти три слова вызывают у вас желание выдернуть волосы? Не бойся! В этом уроке вы узнаете четыре простых шага, которые помогут вам решить эти ужасные проблемы с разделением слов.

География и климат средних колоний

Во многих отношениях Средние колонии представляли собой смесь южных колоний и Новой Англии.В этом уроке мы сосредоточимся на том, как география и климат помогли сформировать это сочетание.

Решение проблем со словами: шаги и примеры

Посмотрите этот видео-урок, чтобы узнать, как решать задачи со словами, следуя этому трехэтапному процессу. Узнайте, как визуализировать свою проблему, чтобы полностью ее понять. Затем научитесь писать и решать свои уравнения.

Арифметика с целыми числами

Есть четыре основных математических операции: сложение, вычитание, умножение и деление.Эти четыре операции используются в широком спектре повседневных навыков и являются фундаментальными блоками арифметики.

Наибольший общий делитель: определение и формула

Наибольший общий делитель, также известный как наибольший общий делитель, можно найти с помощью различных методов. Этот урок будет посвящен как методу факторизации простых чисел, так и алгоритму Евклида.

Напишите и решите реальную задачу для 1/2, разделенной на 3. Затем объясните значение частного

Привет, Даяна,

Давайте посмотрим на ваш вопрос:

Напишите проблему, которая может возникнуть в реальной жизни, используя числа 1/2 и 3. Вам нужно разделить. Вы должны объяснить, что означает частное.

Я не хочу давать ответ прямо, поэтому я проведу вас через решение аналогичного вопроса с другими числами.

Напишите и решите реальную задачу для 3/4, разделенного на 4. Затем объясните значение частного.

Один из способов думать о разделении — это делиться чем-то поровну. Итак, что вы могли бы разделить поровну?

В этой проблеме все, что мы разделяем поровну, должно быть частью, а не целым. Какие вещи мы обычно воспринимаем как части? Что ж, о еде поговорим по частям. Это может быть 3/4 пиццы или 3/4 части пирожного. Мы также измеряем некоторые виды продуктов питания в частях фунта, особенно объемные продукты или сладости.Есть материалы, которые мы покупаем частями целого, например, отрезки ленты, веревки или ткани, которые можно купить как части двора. Ваша задача со словом может включать в себя разделение любого из этих элементов на равные части. Вот два примера:

Дайанна и трое друзей купили пакет конфет весом 3/4 фунта в продуктовом магазине. Если они хотят разделить это поровну, сколько конфет получит каждый человек?

3/4 ÷ 4

3/4 × 1/4 = 3/16

Частное 3/16. Это означает, что каждый получит 3/16 фунта конфет.

Дайанна имеет доску 3/4 ярда. длинный. Если она разрежет его на четыре равных части, какой длины будет каждая часть?

3/4 ÷ 4

3/4 × 1/4 = 3/16

Частное 3/16. Это означает, что длина каждой доски будет 3/16 ярда. после того, как Даянна отрежет его.

* Обратите внимание, что значение частного меняется в зависимости от проблемы со словом.

Чтобы решить вашу проблему, выполните следующие действия:

1) Подумайте, какие реальные предметы мы используем как части целого.

2) Напишите задачу, в которой этот элемент разделяется или разделяется поровну.

3) Когда вы закончите деление на дроби, расскажите читателю, что означает ответ или частное.

Удачи!

Деление дробей на целые числа

Этот урок учит, как делить дроби на целые числа (делить деления), используя математику в уме. Мы используем аналогию с разделением кусков пирога поровну между определенным количеством людей.

В видео я объясняю две разные ситуации деления, когда нам не нужно использовать «правило» или ярлык для дробного деления, а вместо этого можно использовать мысленную математику.Первый — когда дробь делится на целое число. Второй — когда ответом на дробное деление является целое число.

Сначала давайте разделим кусков пирога равномерно. среди определенное количество человек . Это означает, что дробь делится на целое число .
4 5 пирога делится между двумя людьми. Каждый получает 2 5 пирога. 4 5 ÷ 2 = 2 5 Чек: 2 5 × 2 = 4 5	9 10 делится между тремя людьми. Каждый получает 3 10 пирога. 9 10 ÷ 3 = 3 10 Чек: 3 10 × 3 = 9 10
Обратите внимание, как мы можем проверить по каждому деление на умножение!

1.Раскрасьте долю каждого человека другим цветом и напишите предложение о разделении.

а. 4 6 пирога делится между четырьмя людьми.	б. 3 5 пирога делится между тремя людьми.
г. 6 9 пирога делится между двумя людьми.	г. 6 10 пирога делится между тремя людьми.
e. 6 12 пирога делится между тремя людьми.	ф. 15 20 пирога делится между пятью людьми.

2. Составьте разделительное предложение для каждой задачи. и решите это.

а. Осталось 6/9 пиццы больше, и три человека делят его поровну. Сколько получает каждый?

б. Пирог разрезан на 20 частей, а теперь осталось штук 12. Четыре человека делят эти поровну. Какую долю оригинального торта получает каждый человек?

Затем мы делим единичные дроби на такие дроби, как 1/2, 1/3, 1/5, 1/8, 1/12 и т. Д. (В форме 1 / n ).
Половина разделена равно среди четыре человека. Каждому человеку достается 1/8 от суммы. Вы понимаете, почему? 1 2 ÷ 4 = 1 8 Проверить: 1 8 × 4 = 4 8 = 1 2	Пятая часть делится между тремя людьми. Каждый человек получает 1/15. Чтобы увидеть это, разделите каждого пятый (цветной и неокрашенный) на три новые части. 1 5 ÷ 3 = 1 15 Проверить: 1 15 × 3 = 3 15 = 1 5

3.Разделите единичную дробь поровну среди людей. Напишите предложение о разделении. Напишите предложение умножения
, чтобы проверить свое деление.

а. Разделитесь на двух человек. Чек: × 2 =	б. Разделитесь на двух человек. 1 3 ÷ 2 = Чек: × 2 =	c. Разделитесь на двух человек. 1 5 ÷ 2 = Чек: × ____ =
d. Разделитесь на двух человек. ÷ 2 =	e. Разделитесь на пять человек. ÷ 5 =	f. Разделитесь на четырех человек.
г. Разделитесь на четырех человек.	час Разделитесь на трех человек.	я. Разделитесь на трех человек.
Вот ярлык для деления дроби единицы 1/ n на целое число м : 1 n ÷ м = 1 м × № . Пример. 1 8 ÷ 7 = 1 56 . Умножьте знаменатель дробь единицы на делитель, чтобы получить новый знаменатель.

4. Решить.

а. 1 6 ÷ 2 =	б. 1 10 ÷ 2 =	с. 1 7 ÷ 3 =	г. 1 8 ÷ 5 =
e. 12 20 ÷ 2 =	ф. 1 2 ÷ 14 =	г. 8 5 ÷ 4 =	ч. 1 9 ÷ 9 =

5. Трое детей поровну распределяют 1/4 фунта шоколада.

а. Сколько каждая получает в фунтах?

г. В унциях?

6. Пол-литра сока равномерно налить в пять стаканов.

а. Сколько сока в литрах в каждом стакане?

г. Сколько миллилитров сока в каждом стакане?

7. Есть 12 стаканов с разным количеством масла. Линейный сюжет показывает, сколько масла
находится в каждом стакане, в чашках.

Если все масло в стаканах было слито вместе, а затем распределено равномерно в 12 стаканов,
сколько масла будет в каждом стакане?

8.Решать.

а. 2 9 ÷ 2 =	б. 1 9 ÷ 2 =	с. 14 20 ÷ 7 =	г. 8 11 ÷ 4 =
e. 6 9 ÷ 3 =	ф. 8 15 ÷ 4 =	г. 21 100 ÷ 3 =	ч. 1 11 ÷ 2 =

9. Решите обратную задачу: если каждый человек получил столько пирога, сколько было изначально?

а. ÷ 3 = 1 4

г. ÷ 2 = 2 5

г. ÷ 6 = 1 7

г. ÷ 3 = 3 10

10. Напишите задачу-рассказ, соответствующую каждому разделу, и решите.

а. 1 2 ÷ 3 =

г. 6 8 ÷ 2 =

г. 1 4 ÷ 2 =

11. Однажды утром контейнер Джошуа с бензином был заполнен только на 1/8.
Налил половину в его газонокосилку.

а. Насколько сейчас заполнен контейнер для бензина?

г. Если контейнер вмещает 3 галлона, какой количество оставшегося бензина в галлонах?

(Вызов) В квартах?

Наконец, мы разделим нескольких оставшихся кусочков пирога между определенное количество людей. Это немного сложнее, но я думаю, вы справитесь!

Когда 3/4 делится поровну между двумя человек, одну четвертую часть нужно разделить на два. Каждые человек получают 1/4 и 1/8. 3 4 ÷ 2 = 1 4 + 1 8 = 3 8

Другой способ решения той же проблемы является чтобы разделить каждую четвертую часть на 2.Это означает, что сначала мы меняем 3/4 на 6/8, а затем можем разделить равномерно на 2. 3 4 ÷ 2 ↓ 6 8 ÷ 2 = 3 8

12. Оставшийся пирог делится поровну. Сколько получает каждый человек? Напишите предложение о разделении.

а. Разделите 5/6 между двумя людьми. Сначала разделите каждую часть на 2 новых.	б. Разделите 2/3 между тремя людьми. Сначала разделите каждую часть на 3 новых.
г. Разделите 2/3 между четырьмя людьми.	г. Разделите 3/4 между четырьмя людьми.
e. Разделите 2/5 на троих. Сначала разделите каждую часть на 3.	ф. Разделите 4/5 между тремя людьми.

---

Этот урок взят из книги Марии Миллер Math Mammoth Fractions 2 и размещен на сайте www.