Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська моваУкраїнська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Как комбинировать квадратные корни и преобразовывать квадратные корни в экспоненты
Обновлено: 14.
07.2021
Линейная алгебра для чайников
Исследуйте книгу Купить на Amazon
Объединение квадратных корней
Квадратные корни, в которых используется подкоренной символ, — это небинарные операции — операции, включающие только одно число, — которые спрашивают вас: «На какое число, умноженное само на себя, вы получите это число под подкоренем?» Поиск квадратных корней — относительно распространенная операция в алгебре, но работа с корнями и их объединение не всегда так ясны. Выражения с радикалами можно умножать или делить, если степень корня или значение под корнем одинаковы. Выражения с радикалами нельзя складывать или вычитать, если степень корня и значение под радикалом не совпадают. Когда вы находите квадратные корни, символ этой операции называется радикалом. Сила корня относится к числу снаружи и в верхнем левом углу корня. Если числа нет, вы предполагаете, что степень корня равна 2.
Сложение и вычитание можно выполнять, если степени корня и значения под радикалом совпадают.
Примеры:
Эти радикалы не могут быть объединены, потому что операция сложения, а значение под радикалом не то же самое:
Эти радикалы можно комбинировать, потому что степень корня и числа под радикалом одинаковы:
Эти радикалы не могут быть объединены, потому что операция — вычитание, а степень корня не одинакова:
Умножение и деление можно выполнить, если степени корня одинаковы.
Примеры:
Эти радикалы можно комбинировать, потому что операция умножения, а степень корня одинакова:
Эти радикалы можно комбинировать, потому что операция деления и степень корня одинаковая:
Эти радикалы не могут быть объединены, потому что операция деления, а сила корня не одинакова:
Преобразование квадратных корней в экспоненты
Нахождение квадратных корней и преобразование их в степени — относительно распространенная операция в алгебре.
Квадратные корни, в которых используется подкоренной символ, — это небинарные операции — операции, включающие только одно число, — которые спрашивают вас: «На какое число, умноженное само на себя, вы получите это число под подкоренем?» Чтобы преобразовать квадратный корень в показатель степени, вы используете дробь в степени, чтобы указать, что это означает корень или радикал. Когда вы находите квадратные корни, символом этой операции является радикал, который выглядит следующим образом:При переходе от радикальной формы к дробной степени помните эти основные формы:
n -й корень из a может быть записан как дробная экспонента с a , возведенная в степень, обратную этой степени.
Когда n -й корень
Берется число, оно возводится в степень 1/ n . Когда степень возводится в другую степень, вы умножаете степени вместе, и, таким образом, м (иначе записывается как m /1) и 1/ n перемножаются.
Вот несколько примеров замены радикальных форм дробными показателями:
Возводя степень в степень, вы умножаете степени, но основания должны быть одинаковыми.Поскольку возведение степени в степень означает, что вы умножаете показатели степени (при условии, что основания одинаковы), вы можете упростить следующие выражения:
Оставьте показатель степени 9/4. Не записывайте его как смешанное число.
Следующий пример не может быть объединен, потому что основания не совпадают:
Об этой статье
Эту статью можно найти в категории:
- Алгебра ,
Как решить «$4\sqrt5$ такой же, как какой квадратный корень?»?
спросил
Изменено 7 лет, 3 месяца назад
Просмотрено 917 раз
$\begingroup$
Каков правильный метод решения такой задачи:
«$4\sqrt{5}$ равно квадратному корню?»
Возможные ответы:
- $\sqrt{20}$
- $\sqrt{10}$
- $\sqrt{40}$
- $\sqrt{80}$
Мне сообщили, что $\sqrt{80}$ является правильным ответом, но я не понимаю почему.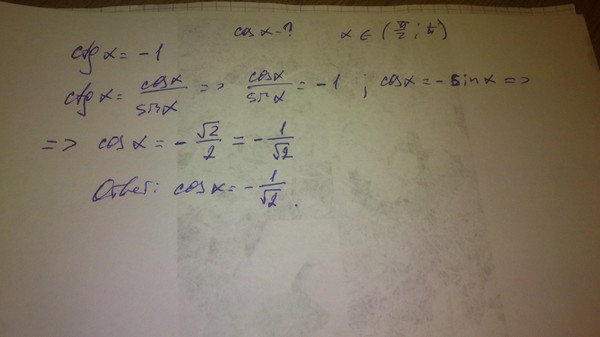
- квадратные числа
$\endgroup$
5
$\begingroup$
Потому что $4=\sqrt{16}$. Тогда $\sqrt{16}\cdot \sqrt{5} = \cdots$
$\endgroup$
3
$\begingroup$
Я предпочитаю этот состав, особенно для начинающих:
$x=4 \times \sqrt{5} = \sqrt{16} \times \sqrt{5} = \sqrt{16\times5} = \sqrt{80}$
Вот как я сделал это в своем голова при чтении вашего вопроса.
Это также хорошая практика для решения доказательств, когда вам нужно показаться , чтобы на мгновение пойти в неправильном направлении (делая $4$ лексически «больше», как $\sqrt{16}$), чтобы свести термины вместе.
$\endgroup$
2
$\begingroup$ 92b}$
Здесь $|a|$ — абсолютное значение $a$, так что $\dfrac{a}{|a|}= 1$, если $a>0$ и $\dfrac{a} {|a|}= -1$, если $a<0$.