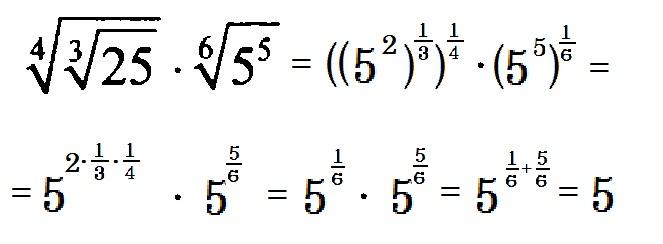математика — Корень из 2 в степени корень из 2 в степени корень из 2
Вопрос задан
Изменён 1 год 4 месяца назад
Просмотрен 1k раз
Есть число, которое можно представить так:
Решаю его так:
Но тогда подходят 2 корня: 2 и 4.
Единственное место, где, как мне кажется, мог ошибиться это переход между первой и второй строчкой решения. Но вроде же нормальный рекурсивный переход. Что в этом решение не так?
- математика
- рекурсия
- уравнения
14
Итак, рассмотрим ряд
с k возведениями в степень.
Теперь по индукции докажем, что последовательность возрастающая и ограничена сверху 2. Базу индукции мы только что записали.
А вот теперь, когда мы доказали, что ряд возрастающий и ограничен сверху, т.е. сходится, мы применяем ваш метод (имеем право!).
И находим, что корень 4 не годится, так как ряд ограничен сверху двойкой.
Значит, остается единственное решение — 2.
Оригинал тут.
Если честно, я не вижу причину для волнения.
С одной стороны, итерационный процесс x_{i+1} = ln(x_i)*2/ln(2) имеет две неподвижные точки: 2 и 4.
Но вы же ведёте итерацию не абы как, а начинаете её в точке x_0 = sqrt(2). Из этой точки итерация сходится к x = 2.
Кстати, к x = 4 никакая итерация сойтись не сможет, это неустойчивая неподвижная точка. Шаг влево — итерация сходится к 2. Шаг вправо — итерация уходит на бесконечность.
возможно у вас вот такой пример был:
x^x^x^x^.