Онлайн калькулятор степеней
Калькулятор степеней
Основание:Показатель степени:
Результат:
История вычислений:
Калькулятор степеней — это простое приложение, которое помогает вычислить результат возведения числа в степень. На странице калькулятора есть два поля ввода: в одно из них нужно ввести число, которое мы хотим возвести в степень, а в другое — значение степени. После нажатия на кнопку «Рассчитать» калькулятор выполнит операцию и отобразит результат на странице.
Кроме того, калькулятор имеет дополнительные функции, такие как проверка ввода на наличие ошибок и поддержка работы с дробными числами. Если пользователь вводит некорректные данные, калькулятор сообщит об ошибке вместо отображения результата.
Также в калькуляторе есть функция сохранения истории вычислений. Каждый раз, когда пользователь вводит новое выражение, его результат добавляется в список истории вычислений. Можно посмотреть историю предыдущих вычислений, которая отображается на странице в виде списка.
Наконец, в калькулятор добавлена возможность копировать результат и историю вычислений. Это удобно, если пользователь хочет сохранить результат или передать его кому-то еще.
Инструкция по заполнению формы калькулятора
Калькулятор степеней прост в использовании. Вот инструкции по заполнению формы:
Введите число, которое нужно возвести в степень, в поле «Основание». Например, если вы хотите вычислить 2 в степени 3, введите число 2 в поле «Основание».
Введите значение степени в поле «Показатель степени». Например, если вы хотите вычислить 2 в степени 3, введите число 3 в поле «Показатель степени».
Нажмите на кнопку «Рассчитать», чтобы выполнить операцию.
Результат операции будет отображен в поле «Результат». Если вы ввели некорректные данные, в поле «Результат» будет отображена ошибка.
Если вы хотите начать вычисление заново, нажмите кнопку «Сбросить», чтобы очистить поля ввода и результат.
Если вы хотите скопировать результат вычисления, нажмите кнопку «Копировать», чтобы скопировать результат в буфер обмена.
3 можно записать 2 * 2 * 2 или 2 в кубе. Это позволит легче воспринимать и работать со сложными выражениями.Не забывайте о дробных степенях. Они могут быть полезны во многих задачах, особенно в физике и инженерии.
Приводите числа к общему знаменателю, когда работаете с дробными степенями. Это поможет упростить вычисления и избежать ошибок.
Используйте калькулятор. Калькулятор степеней может быть очень полезным инструментом для вычисления значений в сложных выражениях. Он может также помочь проверить правильность вычислений, особенно при работе с большими числами.
Помните о порядке операций. При вычислении сложных выражений с несколькими степенями важно следовать правильному порядку операций. Обычно сначала выполняются операции в скобках, затем умножение и деление, а затем сложение и вычитание.
3 можно записать 2 * 2 * 2 или 2 в кубе. Это позволит легче воспринимать и работать со сложными выражениями.Надеемся, что эти советы и хитрости помогут вам лучше понять и работать со степенями!
Таблица степеней
Таблица степеней для чисел от 1 до 10:
| Число | Степень 2 | Степень 3 | Степень 4 | Степень 5 |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 8 | 16 | 32 |
| 3 | 9 | 27 | 81 | 243 |
| 4 | 16 | 64 | 256 | 1024 |
| 5 | 25 | 125 | 625 | 3125 |
| 6 | 36 | 216 | 1296 | 7776 |
| 7 | 49 | 343 | 2401 | 16807 |
| 8 | 64 | 512 | 4096 | 32768 |
| 9 | 81 | 729 | 6561 | 59049 |
| 10 | 100 | 1000 | 10000 | 100000 |
В этой таблице показаны результаты возведения чисел от 1 до 10 в степени 2, 3, 4 и 5.
(1/2) = √16 = 4
Таким образом, квадратный корень из числа 16 равен 4.
Дорогие пользователи, если вы использовали наш калькулятор степеней и хотите поделиться своим опытом или оставить отзыв, пожалуйста, не стесняйтесь оставить комментарий! Ваши отзывы и комментарии помогают нам улучшать качество наших услуг и сделать их более удобными и полезными для всех пользователей.
Вы можете написать о том, как вам понравился наш калькулятор, был ли он полезен для ваших вычислений, или какие еще функции вы хотели бы видеть в калькуляторе. Мы ценим ваше мнение и будем рады услышать от вас обратную связь.
Спасибо, что использовали наш калькулятор степеней!
Быстрое возведение в степень по модулю
УчебаМатематика
Калькулятор возводит большие числа в степень по модулю
Этот калькулятор можно использовать для возведения в степень целого числа по модулю. Калькулятор позволяет задать большие целые числа и в модуле, и в основании, и в показателе степени.
Используется быстрый алгоритм, описанный сразу за калькулятором.
Возведение в степень по модулю
Основание
Показатель
Модуль
Результат
Если применять наивный способ возведения в степень — просто перемножить p-1 раз основание, нам потребуется на единицу меньше умножений, чем показатель степени. Несмотря на всю мощь современных компьютеров, такой способ нам не подходит, так как мы собираемся использовать для показателя числа даже большие, чем стандартные 64-битные целые. Например, в простом числе Мерсена: 618970019642690137449562111, уменьшая на единицу которое мы используем как значение показателя степени по-умолчанию, насчитывается 89 двоичных разрядов (см. Сколько бит занимает число).
Чтобы оперировать подобными показателями требуются алгоритмы быстрого возведения в степень.
В калькуляторе Возведение полинома в степень мы уже задействовали один быстрый алгоритм возведения в степень, основанный на дереве степеней, который позволяет свести к минимуму число операций умножения.
Однако для огромных показателей реализация этого алгоритма с хранением в памяти всего дерева степеней не подходит из-за ограничений по ресурсам.
Поэтому в данном калькуляторе для вычисления степени мы применяем библиотеку bigInt, реализующую двоичный алгоритм, не требующий дополнительной памяти. Вариант этого алгоритма описан в той же статье, однако обработка двоичных разрядов показателя степени происходит там последовательно со старшего бита до младшего. В нашем случае это несколько неудобно, так как мы используем большие целые и не вдаваясь в реализацию хранилища целых, мы заранее не представляем, сколько разрядов они занимают в памяти.
Двоичный алгоритм возведения в степень справа налево
Поэтому алгоритм обрабатывает двоичное представление показателя степени начиная с младшего бита и кончая старшим (слева направо), согласно следующему алгоритму:
a //основание степени
e //показатель степени
m //модуль
//Вычисление степени
r ⟵ 1
while (e!=0) {
if (e mod 2 = 1) r ⟵ r * a mod m;
e ⟵ e / 2;
a = a*a mod m;
}
output ⟵ rСсылка скопирована в буфер обмена
Похожие калькуляторы
- • Модулярная арифметика
- • Решение сравнений по модулю
- • Обратный элемент в кольце по модулю
- • Простая дробь по модулю
- • Обратная матрица по модулю
- • Раздел: Математика ( 270 калькуляторов )
Математика модуль по модулю степень Теория чисел
PLANETCALC, Быстрое возведение в степень по модулю
Anton2020-11-10 14:37:45
‘; return ret; } }
Калькулятор градусов треугольника
Если вы хотите, чтобы 
Продолжайте читать, чтобы узнать, как вычислить степень треугольника для нескольких возможных сценариев, например,
- Когда известны три стороны;
- Когда известны два угла; и
- Когда известны две стороны и один угол
Вы также найдете пример того, как найти степень треугольника с помощью нашего инструмента.
Что такое треугольник?
Треугольник — это замкнутая кривая, имеющая три стороны (aaa, bbb и ccc на рис. 1). Он состоит из трех вершин и трех углов (∠α\угол \alpha∠α, ∠β\угол \beta∠β и ∠γ \угол \gamma∠γ).
В следующем разделе мы попробуем научиться вычислять степень треугольника.
Рис. 1: Треугольник со сторонами a,b,c и углами α, β, γКак вычислить степень треугольника
Чтобы вычислить степень треугольника, мы можем использовать один из следующих методов: 92)}{2аб}\право ]\\\\ \end{align*}αβγ=arccos[2bc(b2+c2−a2)]=arccos[2ac(a2+c2−b2)]=arccos[2ab(a2+b2−c2)]
Если известны два угла
Замечательное свойство трех углов треугольника состоит в том, что сумма трех углов треугольника составляет 180 градусов
Мы можем использовать это свойство, чтобы найти неизвестную степень треугольника, если известны два угла.α+β+γ=180°⟹α=180°−(β+γ)β=180°−(α+γ)γ=180°−(β+α)\footnotesize \альфа + \бета + \гамма = 180\градус \\ \начать{выравнивать*} \подразумевает \альфа & = 180\градус — (\бета + \гамма)\\ \бета & = 180\градус — ( \альфа + \гамма) \\ \гамма & = 180\градус — (\бета + \альфа) \end{align*}α+β+γ=180°⟹αβγ=180°−(β+γ)=180°−(α+γ)=180°−(β+α)
Если известны две стороны и один угол
Здесь снова мы можем использовать закон косинусов или закон синусов, чтобы найти известный градус. Например, если мы знаем значения сторон aaa, ccc и угла γ\gammaγ, по формуле закона синусов мы можем написать:
asin(α)=csin(γ)⟹α=arcsin[a⋅ sin(γ)c]β=180°−(α+γ)\footnotesize \frac{a}{\text{sin} (\alpha)} = \frac{c}{\text{sin} (\gamma)} \\ \начать{выравнивать*} \подразумевает \alpha &= \text{arcsin} \left[ \frac{a \cdot \text{sin} (\gamma)}{c} \right] \\ \бета &= 180\градус — ( \альфа + \гамма) \end{align*}sin(α)a=sin(γ)c⟹αβ=arcsin[ca⋅sin(γ)]=180°−(α+γ)
Если вы хотите узнать больше о треугольниках, рекомендуем воспользоваться нашим калькулятором углов треугольника.
Как пользоваться калькулятором градусов треугольника
Теперь давайте посмотрим, как найти градус треугольника, если каждая из его сторон равна 5 см.
В раскрывающемся меню выберите 3 стороны в качестве параметра заданного .
Введите размеры трех сторон , aaa, bbb и ccc, по 4 см каждая.
Инструмент отобразит градуса треугольника (∠α\угол \alpha∠α, ∠β\угол \beta∠β и ∠γ \угол \gamma∠γ) как 60°60\градус60°.
Вы также можете использовать этот калькулятор градусов треугольника, чтобы найти углы треугольника, если вы знаете либо два угла, либо один угол и две стороны.
FAQ
Как найти градус в прямоугольном треугольнике, если известен один из острых углов?
Чтобы найти градус в прямоугольном треугольнике, если известен один из острых углов, следуйте приведенным инструкциям:
В прямоугольном треугольнике один угол равен 90 градусов.
Следовательно, сумма двух других углов будет 90 градусов .Вычесть значение известного угла из 90 градусов .
Поздравляем! Вы нашли градус неизвестного угла.
Следовательно, сумма двух других углов будет 90 градусов .В какой степени сумма углов в треугольнике?
Согласно свойству суммы углов треугольника, три внутренних угла треугольника в сумме дают 180 градусов .
Чему равен третий угол треугольника, если два его угла равны 80° и 45°?
Третий угол равен 55° . Чтобы получить этот ответ, выполните следующие действия:
Найдите сумму двух известных углов
Вычесть результат из 180° , т. е. 180° — 125° = 55°.
Вы получите 55°, градус третьего угла.
Калькулятор градусов, градиента и уклона
Наклон или уклон линии описывает направление и крутизну линии.
Уклон может быть выражен в углах, градиентах или градусах.
наклон, выраженный как угол
S Угол = TAN -1 (Y / X) (1)
, где
S Угла
S Угла
S .0158 = угол (рад, градусы (°))
x = горизонтальная длина (м, футы ..)
y = вертикальная высота (м, футы …)
Пример — уклон как угол
Уклон как угол для высоты 1 м на расстоянии 2 м можно рассчитать как
S угол = tan -1 ((1 м)/(2 м))
= 26,6 °
Уклон, выраженный в виде уклона
S класс (%) = (100%) y / x (2)
, где
S Сравнение (%) = класс (%)
Пример — Слоп
2
2
2
2 уклон для отметки 1 м на расстоянии 2 м можно рассчитать как %)
Уклон и уклон крыши
Уклон крыши – это уклон, создаваемый стропилами.
Вы можете найти шаг крыши в виде x:12, например, 4/12 или 9/12. (3)
S класс (%) = (100 %) 4 / 12
= 33,3 %0005 S angle = tan -1 (x / 12) (3b) S angle = tan -1 ( 4 / 12) = 18,4 ° Расчет угловых градусов, уклона и длины уклона. x — горизонтальная длина (м, футы, дюймы….) y — высота над уровнем моря (м, футы, дюймы….) (включить всплывающее окно) Используйте эту таблицу для оценки наклона или уклона. Измерьте горизонтальный ход и вертикальный подъем и начертите линии на графике, чтобы оценить наклон. Загрузите и распечатайте таблицу уклонов/наклонов Example — Roof Picth 4/12 as Angle
Калькулятор наклона или уклона
Таблица наклона или уклона
Уклоны, уклоны, уклоны в процентах
Slope Angle
(degrees) Gradient Grade
(%) Y X 0.1 1 573.0 0.17 0.2 1 286.5 0.35 0.3 1 191.0 0.52 0.4 1 143.2 0.70 0.5 1 114.6 0.87 0.57 1 100 1 0.6 1 95.49 1.05 0. 
7 1 81.85 1.22 0.8 1 71.62 1.40 0.9 1 63.66 1.57 1 1 57.29 1.75 2 1 28.64 3.49 3 1 19.08 5.24 4 1 14.30 6.99 5 1 11.43 8.75 5.71 1 10 10 6 1 9.514 10.5 7 1 8.144 .0325 10 1 5.671 17.6 11 1 5. 
145 19.4 12 1 4.705 21.3 13 1 4.331 23.1 14 1 4.011 24.9 15 1 3.732 26.8 16 1 3.487 28.7 17 1 3.271 30.6 18 1 3.078 32.5 19 1 2.904 34.4 20 1 2.747 36.4 21 1 2.605 38.4 22 1 2.475 40.4 23 1 2.356 42.4 24 1 2.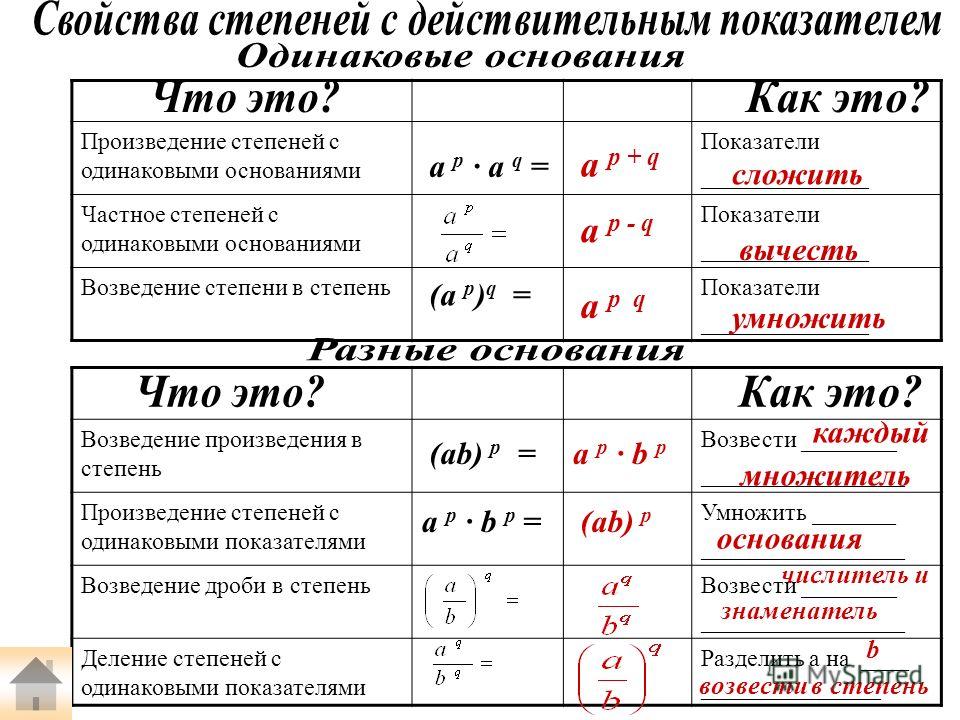 
246 44.5 25 1 2.145 46.6 26 1 2.050 48.8 27 1 1.963 51.0 28 1 1.881 53.2 29 1 1.804 55.4 30 1 1.732 57.7 31 1 1.664 60.1 32 1 1.600 62.5 33 1 1.540 64.9 34 1 1.483 67.5 35 1 1.428 70.0 36 1 1.376 72.7 37 1 1. 
327 75.4 38 1 1.280 78.1 39 1 1.235 81.0 40 1 1.192 83.9 41 1 1.150 86.9 42 1 1.111 90.0 43 1 1.072 93.3 44 1 1.036 96.6 45 1 1.000 100.0 46 1 0.9657 103.6 47 1 0.9325 107.2 48 1 0.9004 111.1 49 1 0,8693 115,0 50 1 . 
0328 51 1 0.8098 123.5 52 1 0.7813 128.0 53 1 0.7536 132.7 54 1 0.7265 137.6 55 1 0.7002 142.8 56 1 0.6745 148.3 57 1 0.6494 154.0 58 1 0.6249 160.0 59 1 0.6009 166.4 60 1 0.5774 173.2 61 1 0.5543 180.4 62 1 0.5317 188.1 63 1 0. 
5095 196.3 64 1 0.4877 205.0 65 1 0.4663 214.5 66 1 0.4452 224.6 67 1 0.4245 235.6 68 1 0.4040 247.5 69 1 0.3839 260.5 70 1 0.3640 274.7 71 1 0.3443 290.4 72 1 0.3249 307.8 73 1 0.3057 327.1 74 1 0.2867 348.7 75 1 0.2679 373. 
2 76 1 0.2493 401.1 77 1 0.2309 433.1 78 1 0.2126 470.5 79 1 0.1944 514.5 80 1 0.1763 567.1 81 1 0.1584 631.4 82 1 0.1405 711.5 83 1 0.1228 814.4 84 1 0.1051 951.4 85 1 0.08749 1143 86 1 0.06993 1430 87 1 0.05241 1908 88 1 0. 