2 Пи или не 2 Пи — вот в чём вопрос / Хабр
Перевод поста Giorgia Fortuna «2 Pi or Not 2 Pi?».
Выражаю огромную благодарность Кириллу Гузенко за помощь в переводе.
Три месяца назад мир (или по крайней мере мир гиков) праздновал день Пи (03.14.15…). Сегодня (6/28 — 28 июня 2015 г.) другой математический день — день 2π, или день Тау (2π = 6.28319…).
Некоторые говорят, что день тау действительно является днём для празднования, и что τ (= 2π), а не π, должен быть самой важной константой. Все началось в 2001 году со вступительного слова знаменитого эссе Боба Пале, математика из университета Юты:
“Я знаю, что некоторые сочтут это богохульством, но я считаю, что π — это ошибка”.
Это вызвало в некоторых кругах празднование дня тау — или, как многие говорят, единственного дня, в который можно съесть два пи(рога) (2pies≈2π — игра слов в англ.
Однако правда ли то, что τ — константа получше? В современном мире это довольно просто проверить, а Wolfram Language делает эту задачу ещё проще (действительно, недавний пост в блоге Майкла Тротта о датах в числе пи, вдохновлённый постом Стивена Вольфрама о праздновании векового дня числа пи, весьма активно задействовал Wolfram Language). Я начала с рассмотрения 320000 препринтов на arXiv.org чтобы посмотреть, сколько в действительности формул содержат 2π по сравнению с теми, что содержат просто π или π с другими сомножителями.
Вот облако из некоторых формул, построенное с помощью функции WordCloud, содержащих 2π:
Я обнаружила, что лишь 18% рассматриваемых формул содержат 2π, из чего следует, что перейти на использование τ — не лучший выбор.
Но почему тогда сторонники использования τ считают, что мы должны перейти к использованию этого нового символа? Одна из причин заключается в том, что использование τ должно сделать тригонометрию проще для изучения и понимания.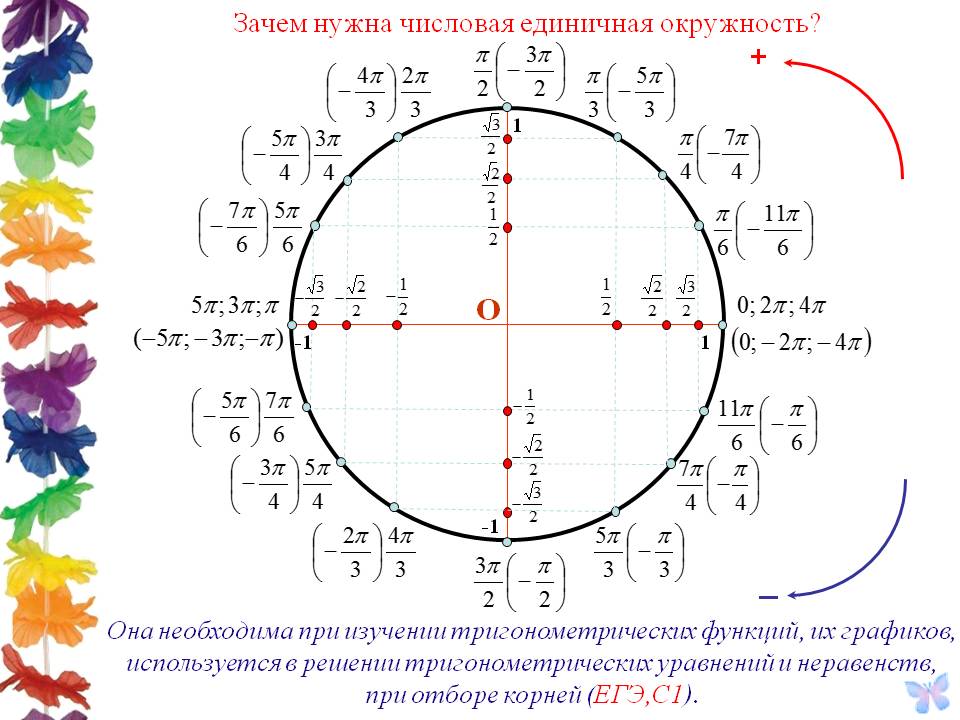 В конце концов, в тригонометрии мы используем не углы, а радианы, а в окружности содержится 2π радиан. Это означает, что четверти круга соответствует 1/2π радиан, или π/2, а не четверть чего-то! От этой несправедливости можно избавиться введением символа τ, и тогда каждой части окружности будет соответствовать такая же часть от τ. Например, четверти окружности соответствовал бы угол τ/4.
В конце концов, в тригонометрии мы используем не углы, а радианы, а в окружности содержится 2π радиан. Это означает, что четверти круга соответствует 1/2π радиан, или π/2, а не четверть чего-то! От этой несправедливости можно избавиться введением символа τ, и тогда каждой части окружности будет соответствовать такая же часть от τ. Например, четверти окружности соответствовал бы угол τ/4.
Лично у меня использование числа π не вызывает каких-то сильных негативных чувств, и честно говоря, я не думаю, что использование τ позволило бы студентам быстрее изучать тригонометрию. Давайте вспомним о двух самых важных тригонометрических функциях — синусе и косинусе. Пожалуй, самые важные в изучении тригонометрии формулы — sin= cos(2π) = 1, и sin() = cos(π) = –1. Я не только всегда предпочитала использовать косинус потому, что его значения легче запомнить (нет никаких дробных значений в π и 2π), но я и также всегда помнила, что синус и косинус отличаются тем, что одна функция принимает ненулевые значения в точках, кратных π, а другая принимает ненулевые значения в дробных частях π.
Учитывая вышесказанное, получается, что использование τ или π есть вопрос личного предпочтения. Это справедливое заключение, однако нам нужен более строгий подход для определения того, какая из констант более полезна.
Даже тот подход, которым я руководствовалась вначале, может привести к неправильным выводам. В Тау манифесте Майкл Хартл приводит некоторые примеры тех мест, где часто можно встретить 2π:
И в самом деле, все эти формулы выглядели бы проще, если бы мы использовали τ. Однако это всего лишь шесть формул из того огромного количества, которые ученые регулярно используют, и как я упоминала ранее, не так уж много математических выражений содержат 2π. Тем не менее, вполне возможно, что формулы, не содержащие 2π, будут более простыми, если будут записаны через τ. Например, выражение 4π² запишется просто как τ².
Поэтому я вернулась к научным статьям, чтобы выяснить, сделает ли использование τ вместо 2π (и τ/2 вместо π) формулы более простыми. Например, вот те, которые станут более простыми с использованием τ:
А вот некоторые из тех, которые не станут:
Позвольте объяснить, что я подразумеваю под более простой формой записи на примере: если я возьму часть, содержащую π в нижней левой формуле таблицы с формулами
Я могу заменить π на τ/2 с помощью функции ReplaceAll и получить:
Посмотрев на эти два выражения, можно увидеть, что второе проще. И дело здесь не в интуиции — во втором просто меньше символов. Для большей ясности можно рассмотреть соответствующие им древовидные графы посредством функции TreeForm:
Для получения численного представления их различия мы можем использовать количества ветвей дерева, которые соответствуют числу символов в исходных формулах:
Чтобы определить, упрощается ли формула в результате использования τ, я вычислила сложность каждой формулы (которая определяется количеством ветвей дерева), содержащей π, для формул из статей, в зависимости от того, какая из констант используется — π или τ. Для большей точности я сначала удалила все выражения, которые были равны или эквивалентны π или 2π. Я чувствовала, что будет несправедливо их учитывать, потому что они часто встречаются сами по себе, вне формул. Затем я сравнила случаи, когда использование τ упрощало формулу с теми, когда усложняло, и лишь 43% формул стали проще с использованием τ, то есть в более чем половине случаев использование τ усложняет формулу. Иными словами, из этого сравнения следует, что мы должны продолжать использовать π. Тем не менее, это не конец истории.
Для большей точности я сначала удалила все выражения, которые были равны или эквивалентны π или 2π. Я чувствовала, что будет несправедливо их учитывать, потому что они часто встречаются сами по себе, вне формул. Затем я сравнила случаи, когда использование τ упрощало формулу с теми, когда усложняло, и лишь 43% формул стали проще с использованием τ, то есть в более чем половине случаев использование τ усложняет формулу. Иными словами, из этого сравнения следует, что мы должны продолжать использовать π. Тем не менее, это не конец истории.
Я заметила вот что: если выражение становится более или менее сложным, то это значит, что количество ветвей у него менее 40. В самом деле, если посмотреть на процент формул, которые становятся проще при использовании π или τ и имеют количество ветвей меньше определённого значения, то вы увидите следующую картину:
Ось х представляет верхнюю границу количества ветвей. Из этого следует, что почти для всех формул их сложность зависит от выбора символа только в случае, если число ветвей меньше 50.
Более важное наблюдение заключается в том, что по мере роста сложности формулы ситуация резко меняется. Даже если выбрать формулы со сложностью большей, чем 3, как рассмотренная ранее формула , то тогда лишь 48% формул станут проще с использованием π против 52% для τ. Приведенные ниже графики показывают, как процентные отношения формул, которые проще с использованием π или τ, изменяются в зависимости от сложности:
Как можно заметить, при числе ветвей более 48 графики начинают вести себя хаотично. Это следствие того, что лишь 0,4% формул выборки имеют сложность более 50. Мы ничего особо конкретного не можем сказать о них, и прошлый опыт говорит нам о том, что это нам очень-то и не нужно.
И из этого графика также следует то, что в повседневной жизни и для каких-то выражений, которые сложнее чего-то наподобие , в целях упрощения выражений нам однозначно следует использовать τ. Но есть еще один момент, которого я не коснулась. Что насчёт различных областей приложений?
Возможно, в физике формулы будут проще выглядеть с τ, а в других областях — нет. Изначально я включила в поиск статьи из различных областей; однако, я не проверяла принадлежность формул, содержащих π, тем или иным областям знаний, а также то, принадлежат ли формулы, которые становятся проще с использованием τ, какому-то ограниченному подмножеству областей. В самом деле, если рассмотреть лишь математические статьи, то результат окажется следующим:
Изначально я включила в поиск статьи из различных областей; однако, я не проверяла принадлежность формул, содержащих π, тем или иным областям знаний, а также то, принадлежат ли формулы, которые становятся проще с использованием τ, какому-то ограниченному подмножеству областей. В самом деле, если рассмотреть лишь математические статьи, то результат окажется следующим:
Получается, что лишь 23% всех формул становятся проще с использованием τ, да и то лишь для довольно сложных выражений. Вот что-то наподобие этого:
можно проще записать через τ, однако большинство подобных выражений встречается весьма редко. Получается, что либо учёные из различных областей должны использовать различные соглашения в зависимости от специфичных для своих областей формул, либо все должны перейти на использование

Тем не менее, вышеуказанная формула содержит ещё кое-что, на чём я бы хотела заострить внимание. Так она выглядит с τ:
Пускай выражение действительно проще записывается через τ, однако подобное улучшение столь незначительно, что становится пренебрежимо малым. Рассмотрим, например, эти два выражения вместе с количествами их ветвей:
И соответствующие им выражения в τ:
Первая формула проще в τ
, но количество ветвей становится лишь на 1/13 меньше по сравнению с первоначальным количеством, в то время как второе выражение проще записывается в π, а после замены его сложность возрастает на 1/6. Другими словами, улучшение в первом случае составило 1/13, а во втором -1/6 (знак минус означает ухудшение). Среднее значение вектора составляет -0.044 — отрицательное число, что означает, что использование τ в этих двух выражениях делает общий вектор на 0,044 хуже.Подобный векторный подход отличается от ранее использованного подхода, при котором не учитывался размер уравнения. В нём считается количество улучшений, а не количество упрощенных выражений, и это переворачивает с ног на голову предыдущие выводы. Я получила эти векторы для формул, в которых сложность ограничена снизу — всё так же, как и в предыдущем примере. Получается, что общее улучшение при замене π на τ уменьшается с увеличением сложности:
В нём считается количество улучшений, а не количество упрощенных выражений, и это переворачивает с ног на голову предыдущие выводы. Я получила эти векторы для формул, в которых сложность ограничена снизу — всё так же, как и в предыдущем примере. Получается, что общее улучшение при замене π на τ уменьшается с увеличением сложности:
а наименьшее ухудшение -0,04 достигается при сложности 5. Как можно заметить, общее улучшение всегда отрицательно; это означает, что пусть и большее количество формул имеют более короткую запись через τ (в зависимости от области), но в целом сумма всех «упрощений» формул перевешивается всеми «усложнениями».
В итоге всего этого исследования у меня сформировалась такая позиция: думаю, нам стоит быть довольными нашим старым другом π и не переходить на использование τ.
У меня есть два заключительных замечания. Первое заключается в том, что если бы мы жили в мире, где активнее используется τ, то вывод был бы полностью противоположным. Если бы наши выражения уже записывались бы через τ, и мы исследовали бы вопрос о переходе на использование π и вопросы упрощения, то наш график сумм векторов выглядел бы следующим образом:
Если бы наши выражения уже записывались бы через τ, и мы исследовали бы вопрос о переходе на использование π и вопросы упрощения, то наш график сумм векторов выглядел бы следующим образом:
Подобное различие объясняется тем, что векторы, которые используются для построения графиков, зависят от исходных сложностей, и потому меняются при изменении оных.
Из этого следует, что для большинства формул, которые имеют сложность больше двух и меньше 18, улучшение от замены τ на π будет отрицательным. К сожалению для сторонников τ, мы живем всё таки в мире π.
Второе замечание, на которое навёл меня Майкл Тротт, заключается в том, что 2/3 из формул, указанных в Тау манифесте (зеленая таблица в начале поста), содержат не просто 2π, а комплексное выражение 2πi. Это говорит о том, что, возможно, сама постановка вопроса, на который я пыталась ответить, является некорректной. Быть может, лучшей будет следующая формулировка: будет ли смысл ввести новый символ τ для комплексного числа 2πi?
Это новое обозначение потребует также замены πi на τ/2, но это не повлияет на сложность πi. В общем, формулы, содержащие πi, либо уменьшат, либо сохранят свою сложность. Вот облако формул, которые станут проще:
В общем, формулы, содержащие πi, либо уменьшат, либо сохранят свою сложность. Вот облако формул, которые станут проще:
Так они станут выглядеть после подстановки 2πi на τ:
Можно было бы возразить, что процент улучшения формул не будет достаточно высоким, и переход от 2πi к τ неоправданным. Однако факты говорят обратное: из всех формул, содержащих πi, 75% станут проще, а остальные 25% сохранят свой уровень сложности — то есть ни одна формула не станет сложнее. Это весомый аргумент, но я не в том положении, чтобы претворить эту идею; однако, полагаю, что равенство τ = 2πi перспективнее (и менее исторически сложно), чем τ = 2π.
Независимо от вашего мнения касательно τ, надеюсь, что вы прекрасно провели день Тау. Наслаждайтесь сегодняшним днём двух пи(рогов) — мнимых или каких бы то ни было.
Как сделать 2 pi r на калькуляторе? – Обзоры Вики
Отсюда, как рассчитывается pi r? Пи иногда присваивается значение 22 больше 7, что примерно равно 3. 14. Для более точного приближения на вашем калькуляторе должна быть кнопка Пи. Формула для площадь равна пи, умноженному на квадрат радиуса, R обозначает радиус окружности. Таким образом, формула: площадь равна пи R в квадрате.
14. Для более точного приближения на вашем калькуляторе должна быть кнопка Пи. Формула для площадь равна пи, умноженному на квадрат радиуса, R обозначает радиус окружности. Таким образом, формула: площадь равна пи R в квадрате.
Что такое пи р 2р? В геометрии, площадь, заключенная в круг радиуса r, равна u03c0r2. Здесь греческая буква u03c0 представляет постоянное отношение длины окружности любого круга к его диаметру, примерно равное 3.1416.
Что такое формула площади?
Для прямоугольника длиной l и шириной w формула для вычисления площади имеет следующий вид: A = lw (прямоугольник). То есть площадь прямоугольника — это длина, умноженная на ширину. В качестве особого случая, поскольку l = w в случае квадрата, площадь квадрата со стороной s определяется по формуле: A = s2 (площадь).
В качестве особого случая, поскольку l = w в случае квадрата, площадь квадрата со стороной s определяется по формуле: A = s2 (площадь).
Что такое пи*д? Чай Длина окружности круга или сферы равен диаметру, умноженному на 3.1416. Окружность = 3.1416 ⋅ Диаметр. C = π ⋅ D. Рисунок №4. Длина окружности равна пи × диаметр.
Каково уравнение цилиндра? Формула объема цилиндра V = Bh или V = πr2h. Радиус цилиндра 8 см, высота 15 см. Подставим 8 вместо r и 15 вместо h в формуле V = πr2h.
Каково значение числа пи?
Вкратце, «пи» — это греческая буква, обозначающая «р» или «π», — это отношение длины окружности любого круга к диаметру этого круга. Независимо от размера круга это отношение всегда будет равно пи. В десятичной форме значение пи равно приблизительно 3.14.
Как вы решаете для области?
com/embed/cx2DzSSMg5E» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Как вычислить площадь и объем? В то время как основная формула площади прямоугольной формы – длина × ширина, основная формула объема – длина × ширина × высота.
Как использовать формулу площади?
Пирог — настоящее число?
Пи — иррациональное число, что означает, что это действительное число, которое не может быть выражено простой дробью. … Начиная с математики, ученики знакомятся с числом «пи», равным 3.14 или 3.14159. Хотя это иррациональное число, некоторые используют рациональные выражения для оценки пи, например, 22/7 из 333/106.
Является ли Pir 2 таким же, как pi D? 2*pi*r и pi*d — одно и то же.. Общепринято, что мы пишем первое вместо второго. Кроме того, при выводе (с использованием дифференциальных уравнений) длина окружности получается как 2*pi*r. Надеюсь это поможет.
Кроме того, при выводе (с использованием дифференциальных уравнений) длина окружности получается как 2*pi*r. Надеюсь это поможет.
Какова ценность пирога? В десятичной форме значение числа пи равно приблизительно 3.14. Но пи — иррациональное число, а это означает, что его десятичная форма не заканчивается (например, 1/4 = 0.25) и не повторяется (например, 1/6 = 0.166666…).
Как найти объем цилиндра калькулятор?
Рассчитайте объем цилиндра: V = πr2h.
Как найти площадь цилиндра? Формула для расчета общей площади поверхности цилиндра дается как общая площадь поверхности цилиндра = 2πr (h + r), в то время как площадь криволинейной поверхности цилиндра формула, площадь криволинейной / боковой поверхности цилиндра = 2πrh, где ‘r’ — радиус основания, а ‘h’ — высота цилиндра.
Как вы рассчитываете объем?
В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема: длина × ширина × высота.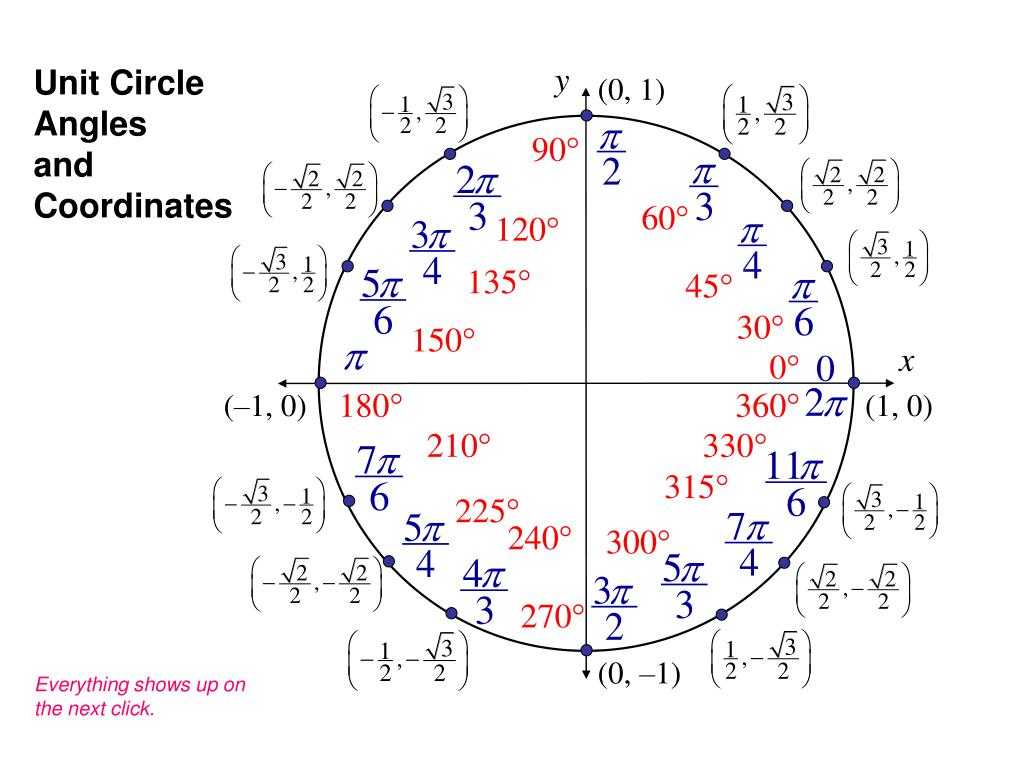
Почему число 3.14 называется числом пи? Только в 18 веке — примерно через два тысячелетия после того, как Архимед впервые вычислил значение числа 3.14 — имя «пи» впервые было использовано для обозначения числа. … «Он использовал его потому что греческая буква Пи соответствует букве «П»… А число «пи» находится по периметру круга ».
Чему равно число пи на 2?
Радианы и градусы
| Степени | Радианы (точно) | Радианы (приблизительно) |
|---|---|---|
| 30° | π / 6 | 0.524 |
| 45° | π / 4 | 0.785 |
| 60° | π / 3 | 1.047 |
| 90° | π / 2 | 1.571 |
Почему число пи 22 делится на 7? Дробное значение числа Пи равно 22/7. Так как пи является иррациональным числом, т.е. цифры после запятой никогда не заканчиваются и не заканчиваются, т.е. 3. 1415926 … и так далее. Вот почему 22/7 используется для расчетов.
1415926 … и так далее. Вот почему 22/7 используется для расчетов.
Как написать пи на компьютере?
Нажмите ctrl+shift+u, затем введите ноль-три-C-ноль, затем нажмите Enter и вы получите символ пи. Как мне ввести символ Pi в Windows 10, если у меня нет блокировки NUM? Вам не нужна блокировка NUM; вместо этого просто удерживайте клавишу Alt и введите 227.
Что это за символ р? Rho (верхний/нижний регистр P ρ) 17-я буква греческого алфавита. Он используется для обозначения звука «р» в древнегреческом и новогреческом языках. В системе греческих цифр имеет значение 100.
Кто отец Пи?
Первый расчет π был произведен Архимед Сиракузский (287–212 до н.э.), один из величайших математиков древнего мира.
Формулы площади круга и расчет онлайн. Площадь круга по диаметру расчет онлайн
| Справочник по математике | Геометрия (Планиметрия) | Окружность и круг |
Основные определения и свойства. Число π Число π |
| Формулы для площади круга и его частей |
| Формулы для длины окружности и ее дуг |
| Площадь круга |
| Длина окружности |
| Длина дуги |
| Площадь сектора |
| Площадь сегмента |
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Окружность и круг — в чём отличие?
Часто понятия круг и окружность путают, хотя это разные вещи. Окружность — это замкнутая линия, а круг — это плоская фигура, ограниченная окружностью. Таким образом, гимнастический обруч или колечко — это окружности, а монета или вкусный блин — это круги.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от одной заданной точки — центра окружности.
Круг — бесконечное множество точек на плоскости, которые удалены от заданной точки, называемой центром круга, на значение, не превышающее заданного неотрицательного числа, называемого радиусом этого круга.
Таблица диаметров и сечения проводов
Формула для расчёта диаметра достаточно проста и выдаёт стандартные значения для конкретного диаметра. Поэтому часто можно увидеть в продаже соответствующие таблицы площадей круга.
Поэтому часто можно увидеть в продаже соответствующие таблицы площадей круга.
Таким способом можно пользоваться в том случае, если под рукой оказался стандартный проводник, указанный в ГОСТ. Например — при диаметре сердечника 2.8 мм площадь его сечения составит 6 мм2.
Прочитав эту статью, любой человек сможет самостоятельно рассчитать площадь поперечного сечения провода или кабеля. Это пригодится при замене старой проводки или при монтаже новой кабельной линии. Главное условия подбора – повышенная точность, так как идеального соотношения качества, простоты установки, безопасности и оптимальной цены можно добиться только после проведения кропотливых замеров.
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат: r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
r2 = (x – a)2 + (y – b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
| { | x = a + r cos t |
| y = b + r sin t |
Таблица с формулами площади круга
| Радиус круга r | |
| Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно | |
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула |
| 1 | радиус | |
| 2 | диаметр | |
| 3 | длина окружности | |
| 4 | сторона квадрата вписанного в круг | |
| 5 | сторона квадрата, в который вписан круг | |
| 6 | стороны треугольника | где |
| 7 | сторона равностороннего треугольника | |
| 8 | высота равностороннего треугольника | |
| 9 | боковая сторона и основание равнобедренного треугольника | |
| 10 | стороны при прямом угле треугольника | |
| 11 | боковая сторона и основание равнобедренного треугольника | |
| 12 | боковые стороны равнобедренного треугольника и угол между ними | |
| 13 | стороны прямоугольного треугольника | |
| 14 | сторона и угол при основании треугольника | |
| 15 | сторона равностороннего треугольника | |
| 16 | сторона и угол при основании трапеции | |
| 17 | боковые стороны и диагональ трапеции | где |
| 18 | стороны прямоугольника | |
| 19 | сторона и количество сторон многоугольника | |
| 20 | сторона шестиугольника |
Что такое площадь поперечного сеченья
Если провод разрезать строго перпендикулярно его длине, чтобы металлические сердечники имели форму правильного круга, то несложно будет измерить диаметр этих жил и определить их площадь с использованием стандартной формулы.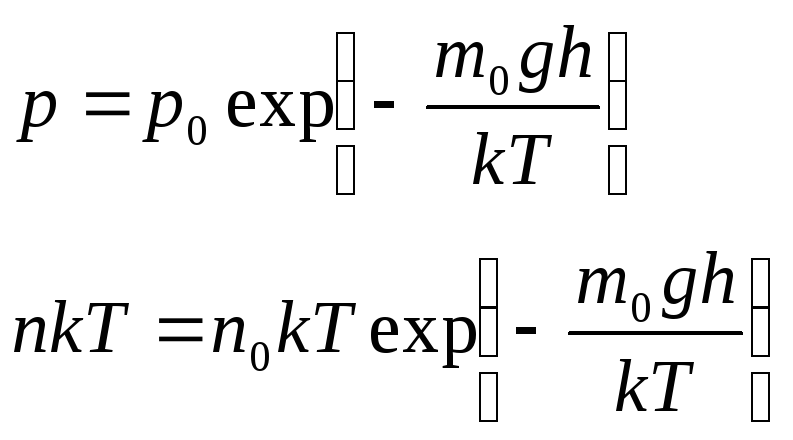
Важно! До недавнего времени опытные электрики могли определить этот параметр на глаз, но сегодня даже они вынуждены измерять провода, и проводить вычисления. Во времена Советского Союза все провода и кабели выпускались по единому ГОСТу, который и нормировал стандартные сечения. Если это 2.5 мм2, то электрик сразу мог отличить его от близких параметров 2 мм2 или 3 мм2. Сегодня производством кабельной продукции занимаются различные компании, которые могут сознательно уменьшать сечение провода и экономить на этом деньги. Вместо заявленных 2.5 мм2 в продажу может поступить провод 2,2 мм2, а это может иметь серьезные последствия и закончиться выгоранием проводки.
Длина окружности круга
Множество точек удаленных от центра круга на расстояние, не превышающее радиус круга, называется кругом. Отношение длины любой окружности C
к ее диаметру
d
всегда будет равно одному и тому же числу. Это число – всем известное число
π
(«пи»), которое примерно равно 3,14. Так же, справедлива формула определения числа
Так же, справедлива формула определения числа
π
, как отношение длины окружности
C
к двум ее радиусам
r
. Исходя из этого, выводится формула длины окружности
C
, которая равна произведения числа
π
и диаметра
d
окружности или 2-м ее радиусам
r
.
С=2πr
С=
πd
π=C/d
Для примера
решим простую задачу, где нужно найти длину окружности, у которой известен радиус
r
=2 см.
C= πd
d=2r=4 см
С=4*3,14=12,56
Подставляем известные данные в формулу длины окружности и получаем, что длина окружности примерно равна 12,56 см.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).
Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса.
Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: отсюда . После того, как найдем диагональ – мы сможем рассчитать радиус: . И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Рассмотрим пример расчета площади круга, описанного вокруг квадрата. Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности. Для начала рассчитаем длину диагонали d. Теперь подставляем данные в формулу
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
Рис.4
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Определение площади поперечного сечения ствола
Для определения объема ствола или его части нужно знать не только длину ствола, но и площадь сечения g. Поперечное сечение ствола не является правильным кругом, поэтому его диаметр d чаще определяют как среднюю арифметическую величину из двух измерений — наибольшего и наименьшего. Площадь сечения ствола определяют по диаметру, используя формулу:
Поперечное сечение ствола не является правильным кругом, поэтому его диаметр d чаще определяют как среднюю арифметическую величину из двух измерений — наибольшего и наименьшего. Площадь сечения ствола определяют по диаметру, используя формулу:
где d — диаметр ствола, принимаемый за диаметр круга.
Так как сечение ствола не является правильным кругом, то такой способ измерения диаметра приводит к некоторой ошибке при вычислении площади сечения. Кроме того, на величину ошибки вычисления площади сечения в коре влияет строение коры: при гладкой коре ошибка меньше, при трещиноватой ‑ больше.
Влияние ошибки в диаметре на точность вычисления объема и площади сечения.
При измерении толщины ствола или его части исправной мерной вилкой всегда возникает случайная ошибка, которая приводит к неточным вычислениям площади сечения и объема. Процент ошибки в диаметре определяется по обычной формуле процентов, т.е.
Если в диаметре допущена та или иная ошибка, то это приведет к ошибке при определении площади сечения и объема. Эти ошибки выражаются такими формулами:
Эти ошибки выражаются такими формулами:
— процент ошибки в объеме:
— процент ошибки площади сечения:
Из приведенных формул можно сделать следующие выводы:
1. Ошибка в диаметре, выраженная в процентах, вызывает двойную ошибку в объеме и площади сечения с тем же знаком.
2. Тонкие стволы и отрезки нужно измерять с большей точностью, т.е. более мелкими ступенями, так как при одной и той же величине ошибки, полученной при измерении и тонкого и толстого ствола или отрезка, относительная ошибка в диаметре, площади сечения и объеме будет большей.
Для уменьшения величины ошибок при измерении толщины ствола
или его отрезка мерной вилкой необходимо выполнять следующие требования:
1) место измерения необходимо очистить от мха и лишайника;
2) если в месте, где надо измерить диаметр, находятся утолщения, необходимо измерить диаметр выше и ниже на одно и то же расстояние (за зоной влияния утолщения) и из двух измерений взять среднее арифметическое;
3) мерную вилку следует накладывать на ствол или на отрезок при большом растворе подвижной ножки, причем так, чтобы мерная линейка касалась ствола;
4) плоскость, проходящая через мерную линейку и обе ножки, должна быть перпендикулярна оси ствола;
5) отсчет следует делать, не отнимая вилки от ствола.
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:
- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.

- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
Источники
- https://tokar.guru/hochu-vse-znat/raschet-ploschadi-poperechnogo-secheniya-kruga.html
- https://mnogoformul.ru/formuly-ploshhadi-kruga-i-raschet-onlayn
- https://www.calc.ru/ploshchad-kruga.html
- https://ru.onlinemschool.com/math/formula/circle/
- https://allcalc.ru/node/18
- https://minus-procentov-online.ru/krug/diametr/
- https://doza.pro/art/math/geometry/area-circle
- https://zen.yandex.ru/media/studystudent/dlina-okrujnosti-i-ploscad-kruga-formuly-i-primery-5e9d7c122517bd2ed0b40460
- https://2mb.
 ru/matematika/geometriya/ploshhad-kruga/
ru/matematika/geometriya/ploshhad-kruga/
Примеры из реальной жизни
DVD-диск
Сегодня DVD-диски утратили звание самого популярного носителя информации, но это не мешает нам измерить площадь болванки. Стандартный диск имеет отверстие диаметром 15 мм, а сама болванка имеет диаметр 120 мм. Таким образом, площадь диска Sd составит:
Sd = Sb – So,
где So – площадь пустого отверстия.
Введем данные в форму онлайн-калькулятора и получим такие результаты:
Sb = 376,9 и So = 47,12
Выполняем несложный расчет и получаем:
Sd = 376,9 — 47,12 = 328,79
Таким образом, площадь стандартного DVD-диска составляет 328,79 квадратных миллиметров.
Основание конуса
Все мы знаем, что в основании объемного конуса лежит круг. Коническую форму имеют многие реальные объекты, к примеру, обычный дорожный конус. Если вы хотите узнать площадь основания такой фигуры, то вам достаточно замерить радиус конуса и ввести эти данные в форму калькулятора. Допустим, радиус выбранной фигуры составляет 15 см. Тогда площадь круга, лежащего в основании, будет равна:
Допустим, радиус выбранной фигуры составляет 15 см. Тогда площадь круга, лежащего в основании, будет равна:
S =94,24
Это означает, что площадь основания дорожного конуса составляет 94,24 квадратных сантиметров.
| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | Найти объем | сфера (4) | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | 2 1/2÷22000000 | |
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | Перевести в процентное соотношение | 3/9 | |
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Формула площади круга
- Главная
- Справочник
- Геометрия
- Формулы площади
- Формула площади круга
Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус). {2} }{4} \]
{2} }{4} \]
где \(d=2r\) – диаметр.
Расчитать площадь фигуры онлайн
Калькулятор: Площадь круга
Входные данные
rD
через радиус r через диаметр D
Радиус
Количество знаков после запятой в результате вычислений 1234567
Результат
Площадь геометрической фигуры, или площадь фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади фигуры выражается числом заключающихся в него квадратных единиц.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Формулы площади Площадь Формулы Геометрия 4305
Пример 1
Площадь • Формулы • Геометрия
Дан квадрат, вписанный в круг. 2}=625 \]
2}=625 \]
625 кв.ед.
Уровень5 класс ПредметГеометрия СложностьПростая
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Формула площади треугольника
Площадь треугольника равна произведению половины основания треугольника (a) на его высоту (h)
Формулы площади Площадь Формулы Геометрия
Формула площади прямоугольного треугольника
Площадь прямоугольного треугольника равна половине произведения катетов треугольника
Формулы площади Площадь Формулы Геометрия
Формула площади равнобедренного треугольника
Площадь равнобедренного треугольника равна произведению половины основания треугольника на его высоту
Формулы площади Площадь Формулы Геометрия
Формула площади равностороннего треугольника
Площадь равностороннего треугольника — половина произведения его основания на высоту
Формулы площади Площадь Формулы Геометрия
Формула площади трапеции
Площадь трапеции равна произведению полусуммы ее оснований (a, b) на высоту (h)
Формулы площади Площадь Формулы Геометрия
Формула площади параллелограмма
Площадь параллелограмма равна произведению его основания (a) на высоту (h)
Формулы площади Площадь Формулы Геометрия
Формула площади прямоугольника
Площадь прямоугольника равна произведению его сторон
Формулы площади Площадь Формулы Геометрия
Формула площади ромба
Площадь ромба равна произведению длины его стороны на высоту (a, h), или половине произведения его диагоналей.

Формулы площади Расчёт Площадь Формулы Геометрия Фигуры
Сложение и вычитание векторов
Суммой двух векторов a и b называется третий вектор c, проведенный из начала a к концу b, если начало вектора b совпадает с концом вектора a. Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Что такое Вольт
1 Вольт равен электрическому напряжению, вызывающему в электрической цепи постоянный ток силой 1 ампер при мощности 1 ватт.
Электротехника Формулы Физика Теория Электричество
Закон Кулона
Сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними.
Законы Формулы Физика Теория Электричество Закон
Процент / доля от числа
Арифметика Калькулятор Расчёт Проценты
Как собрать кубик Рубика 3х3.
 Самая легкая схема для начинающих
Самая легкая схема для начинающихИнструкции
Сколько соток, квадратных метров, километров и аров в одном гектаре земли? Метры, сотки, ары, гектары: значение, таблица. Как рассчитать, сколько гектаров в одной сотке или в одном квадратном метре, аре: перевод соток в гектары
Гектар — это площадь квадрата со стороной 100 м. Ар — площади квадрата со стороной в 10 м. 1 сотка это 100 квадратных метров
Площади и объемы Площадь Математика Формулы Геометрия
Размеры форматов листов А5, А4, А3, А2, А1, А0 в миллиметрах и мегабайтах
Разное Размеры
Как перевести число из десятичной системы в двоичную
Основы Расчёт Справочник Информатика Программирование
Формула рассчитать отверстия по окружности. Как рассчитать длину окружности, если не указан диаметр и радиус круга
И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.
Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
D = 2 * (S / Пи) * (1 / 2)
S — в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Описания фигуры
Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:
- Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом. Диаметр данной фигуры равен длине рассматриваемого отрезка.
- Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице. Если это условие не соблюдается, то это не окружность.
- Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.
Терминология
Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Основные формулы
Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:
- Длина равна произведению числа π и диаметра. Формулу обычно записывают следующим образом: C = π*D.
- Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
- Диаметр равен частному от деления длины окружности на π или удвоенному радиусу.
 Формула является достаточно простой и выглядит так: D = C/π = 2*R.
Формула является достаточно простой и выглядит так: D = C/π = 2*R. - Площадь круга равна произведению числа π и квадрата радиуса. Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Как найти длину окружности по диаметру
Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором. Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Длина через радиус
Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Примеры задач
Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности. Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Решение примера
Для начала запишем, что нам дано: C = 26 см, π = 3,14. Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Не так страшен зверь, как его малюют
Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.
Для любой точки L , лежащей на окружности, действует равенство OL=R . (Длина отрезка OL равняется радиусу окружности).
Отрезок, который соединяет две точки окружности, является ее хордой .
Хорда, проходящая прямо через центр окружности, является диаметром этой окружности (D)
. {\circ}}
{\circ}}
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
AN\cdot NB = CN \cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей .
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. {\circ}
{\circ}
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr ,
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p} ,
где p = \frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника . {\circ}
{\circ}
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.

- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
2 Пи или не 2 Пи?—Wolfram Blog
Три месяца назад мир (или, по крайней мере, мир гиков) праздновал День Пи века (14.03.15…). Сегодня (28.06) очередной математический день: 2π-день, или день Тау (2π = 6,28319…).
Некоторые говорят, что День Тау — это действительно день, который нужно праздновать, и что самой заметной константой должно быть τ(=2π), а не π. Все началось в 2001 году со знаменитой вступительной строки эссе Боба Пале, математика из Университета штата Юта:
: «Я знаю, что некоторые назовут это богохульством, но я считаю, что число π неверно».
Который породил в некоторых кругах празднование Дня Тау — или, как говорят многие, дня, когда разрешается съесть два пирога.
Но правда ли, что τ лучшая константа? В современном мире это довольно легко тестировать, а Wolfram Language значительно упрощает эту задачу. (Действительно, недавняя запись в блоге Майкла Тротта о датах в числах числа пи, вдохновленная публикацией Стивена Вольфрама «День века числа пи», широко использовала язык Wolfram Language.) Я начал с просмотра 320 000 препринтов с arXiv.org, чтобы увидеть на практике, как многие формулы включают 2π, а не только π или другие кратные π.
(Действительно, недавняя запись в блоге Майкла Тротта о датах в числах числа пи, вдохновленная публикацией Стивена Вольфрама «День века числа пи», широко использовала язык Wolfram Language.) Я начал с просмотра 320 000 препринтов с arXiv.org, чтобы увидеть на практике, как многие формулы включают 2π, а не только π или другие кратные π.
Вот WordCloud некоторых формул, содержащих 2π:
Я обнаружил, что только 18% рассмотренных формул включают 2π, предполагая, что τ, в конце концов, не лучший выбор.
Но тогда почему сторонники τ считают, что мы должны перейти на этот новый символ? Одна из причин заключается в том, что использование τ облегчило бы понимание и изучение геометрии и тригонометрии. Ведь когда мы изучаем тригонометрию, мы измеряем углы не в градусах, а в радианах, а в окружности 2π радиан. Это значит, что 1/4 окружности соответствует 1/2 π радиан, или π/2, а не четверти чего-то! Это противоречащее здравому смыслу безумие можно разрешить с помощью символа τ, потому что каждому соотношению круга соответствует отношение τ. Например, 1/4 будет иметь угол τ/4.
Например, 1/4 будет иметь угол τ/4.
У меня лично нет сильных чувств против π, и, честно говоря, я не думаю, что студенты быстрее освоили бы тригонометрию, если бы использовали τ. Подумайте о двух самых важных тригонометрических функциях, синусе и косинусе. Полезнее всего помнить о них то, что sin = cos(2 π) = 1, а sin = cos(π) = –1. Я не только всегда предпочитал косинус просто потому, что его легче запомнить (в числах π и 2 π нет дробей), я также всегда признавал, что синус и косинус различны, потому что один отличен от нуля при целых числах, кратных π, а другой равен нулю. отличны от нуля на некоторых его долях. При использовании τ эта симметрия была бы потеряна, и мы остались бы с равенствами sin = cos(τ) = 1 и sin = cos = –1.
Учитывая эти наблюдения, кажется, что выбор τ или π является личным выбором. Это справедливо, но это не строгий подход к определению того, какая константа более полезна.
Даже тот подход, который у меня был в начале, мог привести к неверному выводу. Манифест Тау , написанный Майклом Хартлом, приводит несколько примеров мест, где чаще всего используется 2π:
Манифест Тау , написанный Майклом Хартлом, приводит несколько примеров мест, где чаще всего используется 2π:
И действительно, все эти формулы были бы проще, если бы мы использовали τ. Однако это всего лишь шесть из огромного числа формул, которые регулярно используют ученые, и, как я уже упоминал ранее, не так много математических выражений включают 2π. Тем не менее могло случиться так, что формулы, не содержащие 2π, были бы еще проще, если бы были записаны через τ. Например, выражение 4 π² просто станет (τ²).
По этой причине я просмотрел научные статьи, чтобы посмотреть, упростит ли их формулы использование τ вместо 2π (и τ/2 вместо π). Например, вот некоторые, которые были бы проще в τ:
А вот некоторые, которые не были бы:
Позвольте мне теперь попытаться объяснить, что я имею в виду под проще, на примере: если я возьму термин содержащий π в нижней левой формуле таблицы уравнений Tau Manifesto :
Я могу заменить π на τ/2 с помощью команды ReplaceAll и получить:
Просто взглянув на эти два выражения, вы увидите, что второе проще.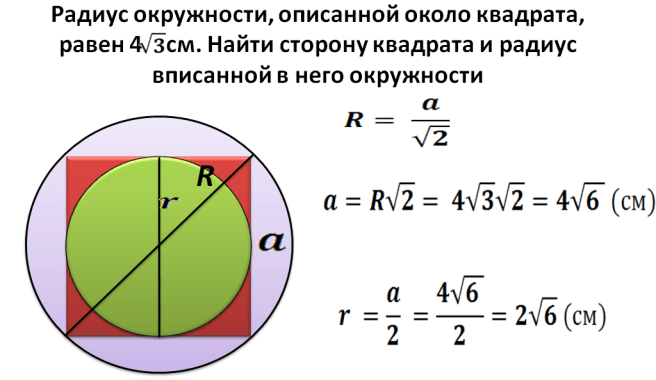 Это говорит вам не только ваша интуиция; видно, что в заменяемом выражении меньше символов и констант. Мы можем посмотреть на соответствующие им TreeForms, чтобы продемонстрировать это явно:
Это говорит вам не только ваша интуиция; видно, что в заменяемом выражении меньше символов и констант. Мы можем посмотреть на соответствующие им TreeForms, чтобы продемонстрировать это явно:
Чтобы получить числовую разницу, мы можем посмотреть на количество листьев (количество листьев на деревьях), которые соответствуют количеству символов и констант в оригинале. формулы:
Чтобы увидеть, оказывает ли τ общее упрощающее влияние, я вычислил сложность каждой формулы (определяемой как их количество листьев, как вычислено выше), включающей π, которая появлялась в статьях при использовании π и τ. Точнее, я сначала удалил все формулы, которые были либо равны π, либо 2 π. Я чувствовал, что было бы несправедливо рассматривать и их, потому что очень часто, если они появляются сами по себе, они не обозначают формул. Затем я сравнил, сколько раз формулы τ были лучше, с тем, сколько раз они не были лучше, и только 43% формул, сложность которых вообще изменилась, были на самом деле лучше, а это означает, что использование τ заставило бы более половины из них выглядеть лучше.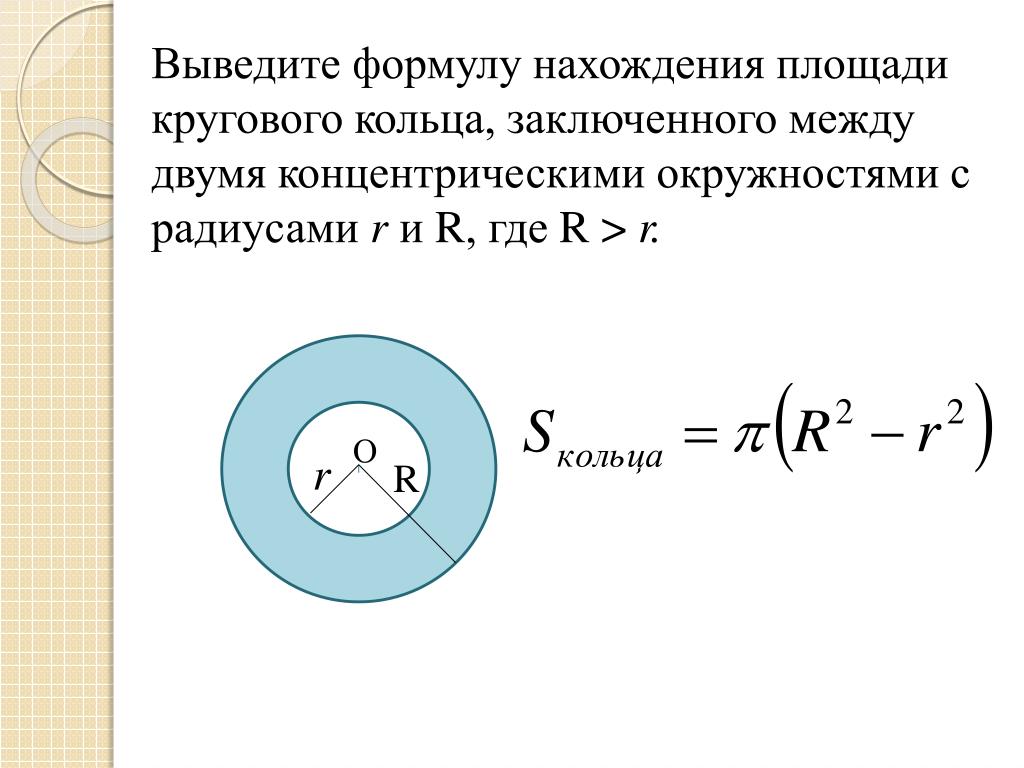 сложный. Другими словами, исходя из этого сравнения, мы должны продолжать использовать π. Однако это не конец истории.
сложный. Другими словами, исходя из этого сравнения, мы должны продолжать использовать π. Однако это не конец истории.
Одно наблюдение, которое я сделал, заключается в том, что если выражение становится более или менее сложным, оно, вероятно, будет иметь количество листьев меньше 40. На самом деле, если вы посмотрите на процент формул, которые лучше при использовании π или τ и у которых количество листьев меньше фиксированного числа, вы получите следующую картину:
, где ось x представляет верхнюю границу количества листьев. Это говорит о том, что почти все упрощающиеся формулы имеют сложность менее 50, независимо от выбранного нами символа.
Более важным наблюдением является то, что ситуация резко меняется по мере увеличения сложности формул. Уже при рассмотрении только формул со сложностью выше 3, как и ранее, только 48% проще в π против 52%, которые проще в τ. На приведенном ниже графике показано, как процент формул, которые лучше по π или τ, меняется в зависимости от сложности:
Как видите, когда количество листьев превышает 48, ситуация становится хаотичной. Это связано с тем, что только 0,4% формул имеют сложность выше 50. Их недостаточно, чтобы мы могли вывести о них что-либо стабильное и разумное, а предыдущее наблюдение говорит нам, что нам в любом случае не следует сильно беспокоиться о них.
Это связано с тем, что только 0,4% формул имеют сложность выше 50. Их недостаточно, чтобы мы могли вывести о них что-либо стабильное и разумное, а предыдущее наблюдение говорит нам, что нам в любом случае не следует сильно беспокоиться о них.
Этот график говорит мне, что в повседневной жизни и для чего-то более сложного, чем довольно простые выражения, такие как , мы действительно должны использовать τ для простоты. Но есть еще кое-что, что я не учел. А разные предметы?
Возможно, формулы в физике выглядят проще в τ, но формулы в других предметах — нет. Первоначальный поиск, который я сделал, включал статьи из разных тем; однако я изначально не проверял, были ли большинство π-содержащих формул из ограниченного подмножества этих предметов, или те, которые стали проще с τ, были в основном из ограниченного подмножества. На самом деле, если я просто ограничу анализ статьями по математике, ситуация станет следующей:
По сути, только 23% формул выигрывают от использования τ, и эти преимущества проявляются только при достаточно высокой сложности. Например, что-то вроде:
Например, что-то вроде:
было бы выражением, которое было бы проще в τ, и вы, вероятно, не видели многих выражений такого типа. Это говорит о том, что либо ученые в разных предметах должны использовать разные соглашения в зависимости от формул, специфичных для их области, либо что все научные дисциплины должны перейти на τ, даже если для некоторых из них это не имеет смысла. Ведь при демократии побеждает большинство, и угодить всем невозможно.
Однако приведенная выше формула показывает еще кое-что, на что я хочу обратить внимание. С τ получается так:
И это не очень большое улучшение: хотя выражение может быть проще в τ, улучшение может быть настолько небольшим, что оно не имеет значения. Рассмотрим, например, эти два выражения вместе с их количеством листьев:
И соответствующие выражения в τ:
Первая формула проще в τ, но количество листьев всего на 1/13 меньше исходной сложности, тогда как второе выражение проще в π, а замененное выражение на 1/6 выше исходной сложности. Другими словами, улучшение в первом случае составило 1/13, а во втором -1/6 (знак минус указывает на отрицательное улучшение, так как выражение в τ было хуже). Среднее значение вектора равно –0,044, отрицательное число, что означает, что использование τ в этих двух выражениях ухудшает весь вектор на 0,044, хотя π и τ улучшают одну формулу.
Другими словами, улучшение в первом случае составило 1/13, а во втором -1/6 (знак минус указывает на отрицательное улучшение, так как выражение в τ было хуже). Среднее значение вектора равно –0,044, отрицательное число, что означает, что использование τ в этих двух выражениях ухудшает весь вектор на 0,044, хотя π и τ улучшают одну формулу.
Этот векторный подход отличается от метода «один счет на уравнение», который я использовал ранее. Он рассматривает количество улучшений, а не просто бинарный вариант «или/или», и полностью переворачивает предыдущие выводы. Я вычислил эти векторы для формул, имеющих ограниченную снизу сложность, так же, как и в предыдущем примере. Я заметил, что общее улучшение при переходе от π к τ, вычисленное как среднее значение этих векторов, по мере увеличения сложности выглядит следующим образом:
, где наименьшее ухудшение, -0,04, достигается при сложности 5. Как видите, улучшение все время остается ниже 0, а это означает, что, хотя большее количество формул может быть короче с τ (в зависимости от поле), в среднем эти сокращения длины перевешиваются увеличением длины в формулах, которые становятся длиннее.
В заключение этого научного исследования: я думаю, мы должны быть довольны нашим старым другом π и не переключаться на τ.
У меня есть два последних замечания. Во-первых, если бы мы уже жили в мире τ, вывод был бы другим, и мы предпочли бы придерживаться τ. Если бы наши выражения уже были в τ и мы исследовали, упростит ли их переход на π, наш векторный график выглядел бы так: первоначальные сложности, и поэтому меняются, когда меняется оригинал.
Это показывает, что для формул, имеющих сложность больше 2 (большинство из них имеют) и для которых сложность не всегда больше 18, улучшение перехода от τ к π снова будет отрицательным, что предполагает, что мы не должны принять переключатель. К сожалению для сторонников τ, мы живем не в τ-мире.
Второе наблюдение, которое сообщил мне Майкл Тротт, состоит в том, что 2/3 формул, показанных в Манифесте Тау (зеленая таблица в начале), содержат не только 2π, но и комплекс число 2π и . Это говорит о том, что, возможно, вопрос, на который я пытался ответить, неверен. Лучше было бы так: есть ли смысл использовать новый символ τ для комплексного числа 2π i ?
Лучше было бы так: есть ли смысл использовать новый символ τ для комплексного числа 2π i ?
Это новое соглашение также потребует замены π i на τ/2, но это не повлияет на сложность π i . В общем, формулы, содержащие член π i внутри, либо упрощаются, либо сохраняют свою сложность. Чтобы дать вам представление, вот облако слов формул, которые станут проще:
Которые после замены τ= 2π i становятся такими:
Можно возразить, что процент улучшенных формул может быть недостаточно высоким, и переход от 2π i к τ не стоит усилие. Однако данные свидетельствуют об обратном: из всех формул, имеющих член π i , 75 % будут проще, а оставшиеся 25 % сохранят свою первоначальную сложность — ни одна из них не ухудшится. Это важное замечание, и я не в состоянии это сделать, но я думаю, что равенство τ = 2π i выглядит более многообещающе (и менее разрушительно с исторической точки зрения), чем τ = 2π.
Каким бы ни было ваше мнение о τ, я желаю вам прекрасного Дня Тау. Пожалуйста, насладитесь сегодня двумя пи (е) — воображаемыми или нет.
Как найти длину окружности — PSAT Math
Все математические ресурсы PSAT
10 Диагностические тесты 421 практический тест Вопрос дня Карточки Learn by Concept
Справка по математике PSAT » Геометрия » Плоская геометрия » Круги » Радиус » Как найти длину окружности
Если площадь круга равна , какова длина окружности круга?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула площади круга: πr 2 . Площадь этого конкретного круга равна 81π, поэтому 81π = πr 2 . Разделите обе части на π, и у нас останется r 2 = 81. Извлеките квадратный корень из обеих сторон, чтобы найти r=9. Формула длины окружности: 2πr = 2π(9) = 18π. Правильный ответ: 18π.
Извлеките квадратный корень из обеих сторон, чтобы найти r=9. Формула длины окружности: 2πr = 2π(9) = 18π. Правильный ответ: 18π.
Сообщить об ошибке
Окружность площадью 13 π в 2 с центром в точке C . Чему равна окружность этого круга?
Возможные ответы:
2√13 π
√26 π
13 π
√13 π 9003 9002 26
√13 π 9003 9002 26
√13 π 9003 9002 26
a 2√13 π
Объяснение:
Формула площади круга: A = πr 2 .
Нам дана площадь, и подстановкой мы знаем, что 13 π = πr 2 .
Разделим π и получим 13 = r 2 .
Извлекаем квадратный корень из r , чтобы найти, что r = √13.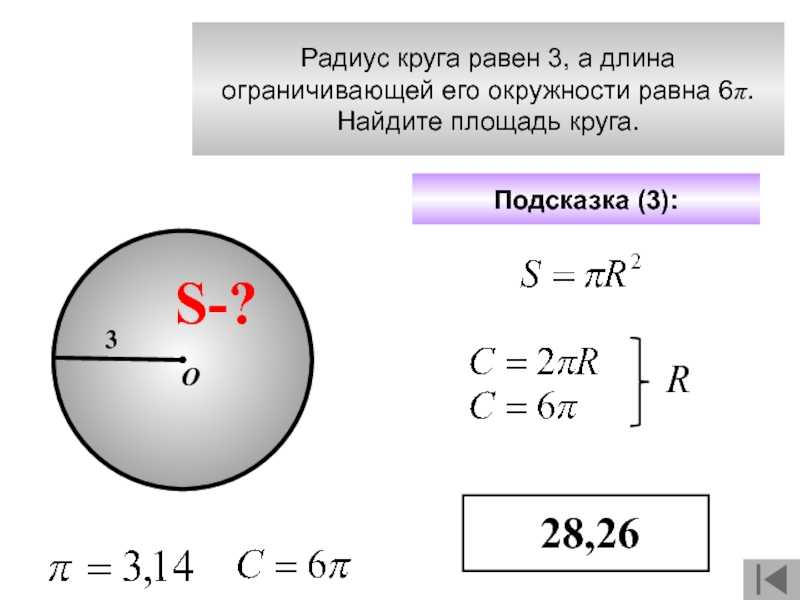
Находим длину окружности по формуле C = 2 πr .
Затем мы подставляем наши значения, чтобы найти C = 2√13 π .
Сообщить об ошибке
Прямоугольник 6 на 8 вписан в окружность. Какова окружность круга?
Possible Answers:
12 π
25 π
10 π
6 π
8 π
Correct answer:
10 №
Пояснение:
Сначала вы должны нарисовать схему. Диагональ прямоугольника также является диаметром круга. Диагональ является гипотенузой, кратной 2 треугольника 3,4,5, и, следовательно, равна 10.
Сообщить об ошибке
Садовник хочет построить забор вокруг своего сада, показанного ниже. Сколько метров ограждения им понадобится, если длина стороны прямоугольника 12, а ширина 8?
Возможные ответы:
8π +
40 Ft.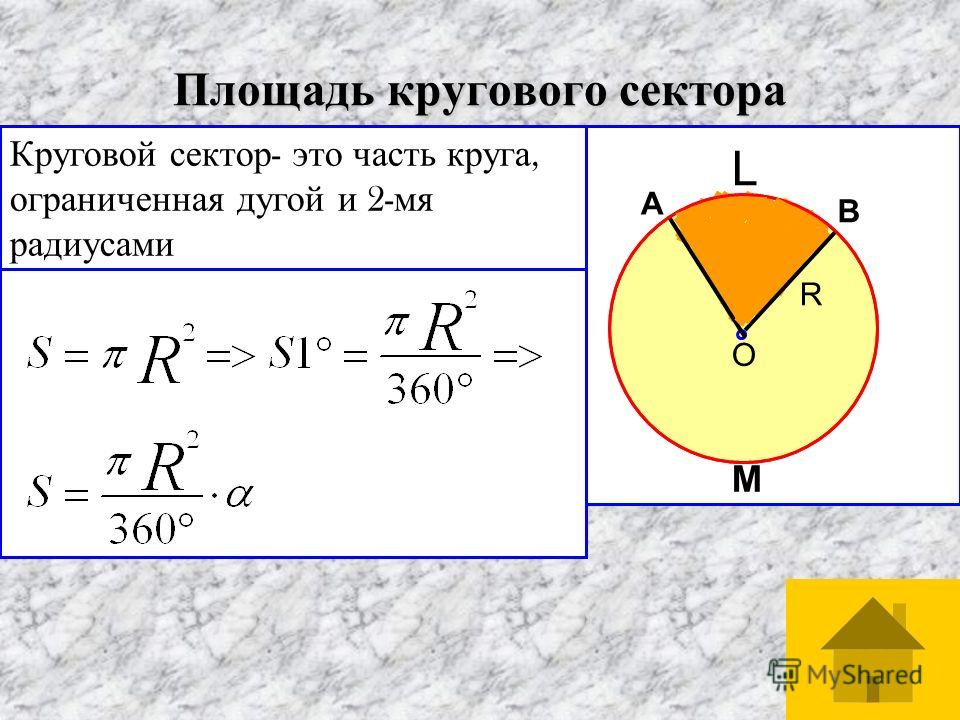
96 FT
4 24
. Пояснение:
Форма сада состоит из прямоугольника и двух полукругов. Поскольку они строят забор, нам нужно найти периметр. Периметр длины прямоугольника равен 24. Периметр или длину окружности можно найти с помощью уравнения C=2π(r), где r= радиус окружности. Поскольку у нас есть две полуокружности, мы можем найти длину окружности одной полной окружности с радиусом 4, что будет равно 8π.
Сообщить об ошибке
Диаметр круга определяется двумя точками (2,5) и (4,6). Чему равна окружность этого круга?
Возможные ответы:
π√5
5π
π√2.5
Ни один из других ответов
2,5π
Правильный ответ:
π√5
. Объяснение: Сначала мы должны вычислить расстояние между этими двумя точками. Напомним, что формула расстояния: √((x 2 — х 1 ) 2 + (у 2 — у 1 ) 2 )
Напомним, что формула расстояния: √((x 2 — х 1 ) 2 + (у 2 — у 1 ) 2 )
Следовательно, для нас: — 5) 2 ) = √((2) 2 + (1) 2 ) = √(4 + 1) = √5
Если d = √5, длина окружности равна πd, или π√5.
Сообщить об ошибке
Автомобильная шина имеет радиус 18 дюймов. Когда шина сделала 200 оборотов, какое расстояние проехала машина в футах?
Возможные ответы:
500π
600π
300π
3600π
Правильный ответ:
600π 3
3 Объяснение:
Если радиус равен 18 дюймам, диаметр равен 3 футам. Таким образом, длина окружности шины равна 3π на C=d(π). После 200 оборотов шина и автомобиль прошли 3π x 200 = 600π футов.
Сообщить об ошибке
Круг имеет приведенное ниже уравнение. Какова окружность круга?
Какова окружность круга?
( x – 2) 2 + ( y + 3) 2 = 9
Возможные ответы:
Объяснение:
Радиус равен 3. Получается длина окружности .
Сообщить об ошибке
Если окружность (показана выше) с площадью разделена на 6 равных частей, какова длина дуги одной из частей?
Примечание. Приведенный выше рисунок не обязательно выполнен в масштабе.
Возможные ответы:
Правильный ответ:
Пояснение:
Начните с вычисления длины окружности. Используйте полученную площадь круга и уравнение площади круга, чтобы определить радиус круга:
=
Разделите обе стороны на .
=
Найдите:
Радиус круга равен 6. Теперь найдите длину окружности.
Теперь найдите длину окружности.
Окружность равна удвоенному радиусу, умноженному на .
Теперь, когда у нас есть длина окружности, разделите ее на 6, чтобы найти длину одной из частей окружности:
Длина дуги одной из частей окружности равна .
Сообщить об ошибке
В квартире Эшли есть квадратная комната площадью 81 кв. фут. Какова окружность самого большого круглого коврика, который она может поместить в этом пространстве?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить этот вопрос, сначала рассчитайте длину каждой стороны комнаты.
Длина каждой стороны комнаты также равна длине диаметра самого большого круглого ковра, который может поместиться в комнате. Так как длина окружности равна просто
Сообщить об ошибке
Уведомление об авторских правах
Все математические ресурсы PSAT
10 диагностических тестов 421 практический тест Вопрос дня Карточки Learn by Concept
Sin 2pi — Найдите значение Sin 2pi
Перед тем, как перейти к нахождению значения sin 2pi, давайте вспомним значения функции синуса различных стандартных углов из тригонометрической таблицы.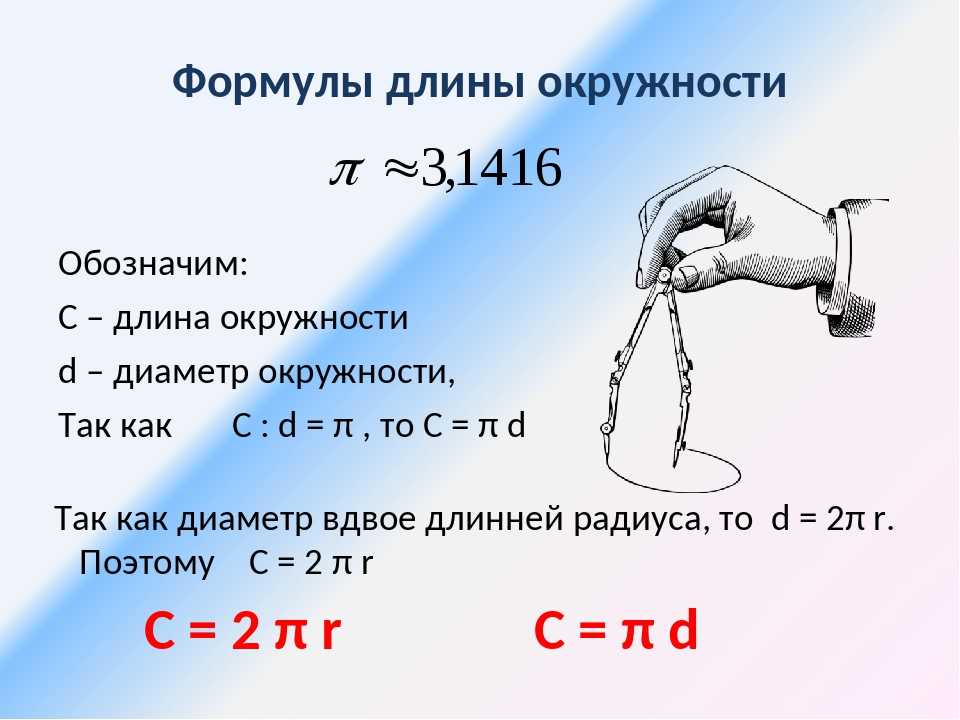 sin 0 = 0, sin π/6 = 1/2, sin π/4 = √2/2, sin π/3 = √3/2 и sin π/2 = 1. Конечно, эта таблица не включает значение sin 2pi в нем. Мы обнаружим, что sin 2pi равен 0, используя здесь различные методы. Кроме того, мы решим некоторые примеры задач, используя это.
sin 0 = 0, sin π/6 = 1/2, sin π/4 = √2/2, sin π/3 = √3/2 и sin π/2 = 1. Конечно, эта таблица не включает значение sin 2pi в нем. Мы обнаружим, что sin 2pi равен 0, используя здесь различные методы. Кроме того, мы решим некоторые примеры задач, используя это.
| 1. | Что такое Sin 2pi? |
| 2. | Синус 2pi с использованием формулы двойного угла |
| 3. | Синус 2pi с использованием опорных углов |
| 4. | Синус 2pi с использованием единичного круга |
| 5. | Часто задаваемые вопросы о Sin of 2pi |
Что такое Sin 2pi?
Значение sin 2pi равно 0. т. е. sin 2π = 0. Из тригонометрической таблицы мы знаем тригонометрические отношения стандартных углов 0, π/6, π/4, π/3 и π/2. Таким образом, эта таблица не дает нам значения sin 2pi. Обычно, чтобы найти значение любого тригонометрического отношения нестандартного угла, мы используем исходные углы и квадрант, в котором лежит угол. Мы можем сделать то же самое, чтобы найти грех 2pi также. Значение sin 2pi можно легко найти, используя несколько других методов, таких как 9.0003
Мы можем сделать то же самое, чтобы найти грех 2pi также. Значение sin 2pi можно легко найти, используя несколько других методов, таких как 9.0003
- Используя формулу двойного угла
- Использование опорного угла
- Использование единичной окружности
Мы докажем, что sin 2π = 0 в каждом из этих методов.
Синус 2pi с использованием формулы двойного угла
Мы можем найти значение sin 2pi, используя формулу двойного угла для синуса: sin 2x = 2 sin x cos x. Поскольку нам нужно найти значение sin(2π), мы должны заменить x = π в приведенной выше формуле. Тогда получаем:
sin 2π = 2 sin π cos π … (1)
Так как π также является нестандартным углом, найдем значения sin π и cos π по формулам суммы и разности. Тогда мы получаем
sin π = sin (π/2 + π/2) = sin π/2 cos π/2 + cos π/2 sin π/2 = (1)(0) + (0)(1) = 0
потому что π = потому что (π/2 + π/2) = потому что π/2 потому что π/2 — sin π/2 sin π/2 = (0)(0) — (1)(1) = -1
Подставьте эти значения в (1),
sin 2π = 2 (0) (-1) = 0
Следовательно, sin 2pi = 0,
Синус 2pi с использованием эталонных углов
Если мы переведем 2π в градусы, мы получим 360°.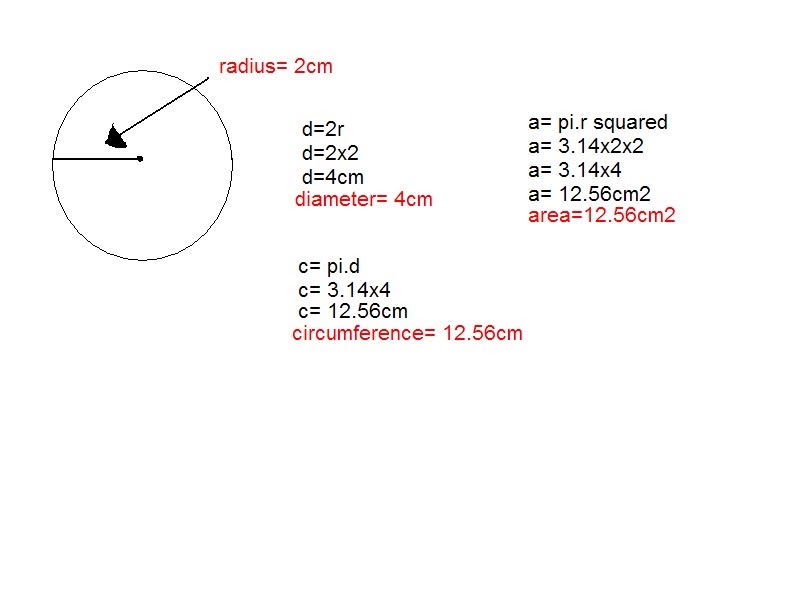 Поскольку 360° лежит в интервале [0°, 360°], сам его котерминальный угол является опорным углом. Чтобы найти его котерминальный угол, мы вычитаем из него 360°. Тогда мы получаем 360° — 360° = 0°. Таким образом, котерминальный угол 360° равен 0°. Кроме того, мы знаем, что 360° означает один полный оборот и, таким образом, происходит либо в первом квадранте, либо в четвертом квадранте. Рассмотрим оба случая.
Поскольку 360° лежит в интервале [0°, 360°], сам его котерминальный угол является опорным углом. Чтобы найти его котерминальный угол, мы вычитаем из него 360°. Тогда мы получаем 360° — 360° = 0°. Таким образом, котерминальный угол 360° равен 0°. Кроме того, мы знаем, что 360° означает один полный оборот и, таким образом, происходит либо в первом квадранте, либо в четвертом квадранте. Рассмотрим оба случая.
- Первый квадрант: Мы знаем, что в первом квадранте грех положителен.
Тогда sin 360° = + sin 0° = 0 (поскольку sin 0° = 0) - Четвертый квадрант: Мы знаем, что в четвертом квадранте грех отрицателен.
Тогда sin 360° = — sin 0° = 0 (поскольку sin 0° = 0)
В обоих случаях sin 360° = sin 2π = 0,
Следовательно, sin 2π = 0,
Синус 2pi с использованием единичного круга
Прежде чем найти значение sin 2pi с помощью единичной окружности, вспомним несколько моментов, касающихся единичной окружности.
- Единичная окружность — это окружность радиусом с центром в начале координат.
- Каждая точка на единичной окружности соответствует углу.
- Этот угол образован линией, соединяющей начало координат и точку с положительным направлением оси x против часовой стрелки.
- Если P(x, y) соответствует некоторому углу θ, то x = cos θ и y = sin θ. т. е. координата y точки представляет собой синус соответствующего угла.
Поскольку 2π (что есть не что иное, как 360°) представляет один полный оборот, это не что иное, как угол между осью x и, таким образом, он эквивалентен 0° на единичной окружности. Мы также знаем, что 0° соответствует точке (1, 0) на единичной окружности (поскольку это точка на единичной окружности на оси x). Таким образом,
sin 2π = sin 0° = координата y (1, 0) = 0.
Следовательно, sin 2π = 0.
Вы можете представить это на следующем рисунке.
Важные примечания:
Вот несколько важных примечаний, связанных с грехом 2pi.
- грех 2π = 0
- потому что 2π = 1
- тангенс 2π = 0
- sin любого кратного π равен 0, т. е. sin nπ = 0 для любого целого числа n.
Например, sin(-2π) = 0, sin π = 0,
Связанные темы:
Вот некоторые темы, связанные с грехом 2pi.
- Тригонометрические отношения
- Тригонометрические формулы
- Закон синусов
- Закон косинусов
Примеры использования Sin 2pi
Пример 1. Найдите значение cos 2pi, используя тот факт, что sin 2pi = 0.
Решение:
Используя тригонометрическое тождество,
sin 2 x + 8 1
Замените x = 2π здесь,
sin 2 2π + cos 2 2π = 1
Мы знаем, что sin 2π = 0. Замените его здесь,
0 2 + cos 2 2π = 1
COS 2 2π = 1
Cos 2π = ± ± ± 1 000 = ± 1 000 = ± 1 000 = ± 1 000 = ± 1 000 = ± 1 000 = ± 1 000 = ± 1000 2 Cos = ± ± 1000 2
.

Но 2π находится в первом или четвертом квадранте, и в каждом из случаев cos положителен.
Таким образом, cos 2π = 1.
Ответ: cos 2π = 1.
Пример 2: Найдите значение sin 4pi, используя тот факт, что sin 2pi = 0,
Решение:
Используя формулу двойного угла для sin,
sin 2x = 2 sin x cos x
Подставим здесь x = 2π, sin 4π = 2 (0) cos 2π (поскольку sin 2π = 0)
sin 4π = 0
Ответ: sin 4π = 0.
Пример 3: Найдите значение sin 5π/2, используя формулы суммы и разности.
Решение:
Используя формулы суммы и разности,
sin (A + B) = sin A cos B + cos A sin B
Подставьте здесь A = 2π и B = π/2,
sin (2π + π/ 2) = sin 2π cos π/2 + cos 2π sin π/2
Мы знаем, что sin 2pi = 0 и cos 2pi = 1. Кроме того, sin π/2 = 1 и cos π/2 = 0. Таким образом, ,
sin 5π/2 = (0)(0) + (1) (1) = 1.

Ответ: sin 5π/2 = 1.
перейти к слайдуперейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по Sin of 2pi
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о Sin of 2pi
Что такое грех 2pi?
Значение sin 2 пи равно 0. Это потому, что 2π — это не что иное, как 0 градусов на единичной окружности. Таким образом, sin 2π = sin 0 = 0,92(пи/2)?
Мы знаем, что sin π/2 = 1. Итак, sin 2 π/2 = (sin π/2) 2 = 1 2 = 1.
Является ли Sin 2pi неопределенным?
Нет, sin(2π) НЕ является неопределенным, вместо этого sin(2π) = 0. Это связано с тем, что котерминальный угол 2π равен 0, из этого мы можем сделать вывод о значении sin 2pi, поскольку sin 2π = sin 0 = 0.
Почему Sin 2pi равен нулю?
Поскольку 2π — это угол, который находится в интервале [0, 2π], его опорный угол есть не что иное, как его котерминальный угол, равный 0. Таким образом, sin 2pi может быть задан как sin 2π = sin 0 = 0.
Как доказать, что Sin 2pi равен 0?
На единичной окружности 2π — это один полный оборот, и, следовательно, 2π эквивалентно углу 0 радиан. Мы знаем, что 0 радиан на единичной окружности соответствуют точке (1, 0). Таким образом, sin 2π = sin 0 = y-координата (1, 0) = 0. Следовательно, sin 2π = 0.
Каково значение cos(-2pi)?
Мы знаем, что cos (-x) = cos x. Итак, cos (-2π) = cos 2π. На единичной окружности cos 2π совпадает с cos 0 и, следовательно, равен 1. Таким образом, cos(-2pi) = 1,
Как найти значение Sin 2pi, используя формулу двойного угла?
У нас есть sin 2x = 2 sin x cos x. Подставьте x = π в приведенную выше формулу. Тогда для греха 2pi мы получаем: sin 2π = 2 sin π cos π … (1).
Теперь,
- sin π = sin (π/2 + π/2) = sin π/2 cos π/2 + cos π/2 sin π/2 = (1)(0) + (0)( 1) = 0
- cos π = cos (π/2 + π/2) = cos π/2 cos π/2 — sin π/2 sin π/2 = (0)(0) — (1)(1) = -1
Подставьте эти значения в (1),
sin 2π = 2 (0) (-1) = 0
Следовательно, sin 2π = 0.
Что такое Tan 2π с использованием Sin 2pi?
Мы знаем, что sin 2pi равен нулю, т. е. sin(2π) = 0. Также мы знаем, что tan x = (sin x) / (cos x) для любого x. Таким образом, tan(2π) = [sin(2π)] / [cos(2π)] = (0) / [cos(2π)] = 0. Следовательно, tan(2π) = 0,
Каково значение Грех 2пи/3?
Переведем 2π/3 в градусы. Тогда мы получаем 2π/3 = 120°. Используя единичный круг, sin 120° = √3/2. Таким образом, sin 2pi/3 = √3/2.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист по тригонометрии
PI
| ИП |
| (Математика | Разное | Константы | ИП) |
Пи — это отношение длины окружности
круга к диаметру. Это означает, что для любого круга можно разделить
окружность (расстояние по окружности) на диаметр и
всегда получают точно такое же число. Неважно, большой или маленький
круг есть, Пи остается прежним. Пи часто пишут с помощью символа
и произносится
«пирог», как и десерт.
Это означает, что для любого круга можно разделить
окружность (расстояние по окружности) на диаметр и
всегда получают точно такое же число. Неважно, большой или маленький
круг есть, Пи остается прежним. Пи часто пишут с помощью символа
и произносится
«пирог», как и десерт.
История | Пи веб-сайты| Сделай сам Пи |Цифры| Формулы
Краткая история числа Пи
Древние цивилизации знали, что существует фиксированное отношение длины окружности
до диаметра, который был примерно равен трем. Греки усовершенствовали
процесс, и Архимеду приписывают первый теоретический расчет
числа Пи.
В 1761 году Ламберт доказал, что Пи иррационально, т. е. что его нельзя записать как отношение целых чисел.
В 1882 году Линдеман доказал трансцендентность Пи, т.
состоит в том, что Pi не является корнем любого алгебраического уравнения с рациональными коэффициентами. Это открытие доказало, что нельзя «квадратировать круг».
была проблема, которая занимала многих математиков до того времени. (Более
информация о возведении в квадрат
круг.)
Это открытие доказало, что нельзя «квадратировать круг».
была проблема, которая занимала многих математиков до того времени. (Более
информация о возведении в квадрат
круг.)
Сколько цифр? Это когда-нибудь закончится?
Поскольку число Пи известно как иррациональное, это означает, что цифры
никогда не заканчиваться и не повторяться каким-либо известным образом. Но вычисление цифр Пи
на протяжении всей истории привлекала математиков.
Некоторые всю жизнь вычисляли числа Пи, но до появления компьютеров
было рассчитано менее 1000 цифр. В 1949, компьютер вычислил
2000 цифр, и гонка началась. Миллионы цифр вычислены,
с рекордом (по состоянию на сентябрь 1999 г.) суперкомпьютера на
Токийский университет, который подсчитал 206 158 430 000 цифр. (первый
1000 цифр)
Подробнее об истории числа Пи можно найти в архивах Mac Tutor Math History.
Аппроксимация Пи
Архимед подсчитал, что Пи было между 3 10/71 и 3 1/7 (также пишется 223/71 < 22/7 ).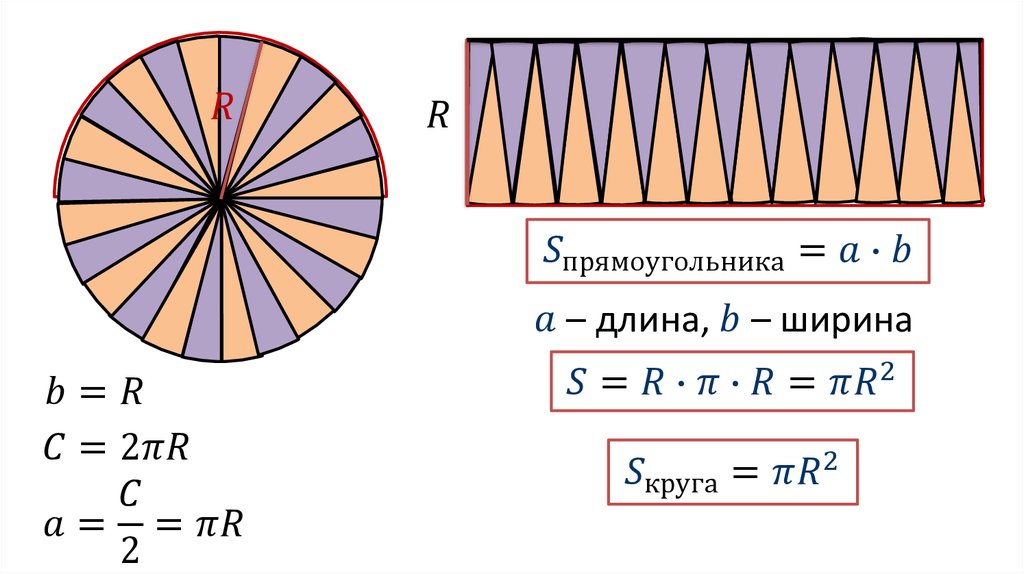 22/7 по-прежнему является хорошим приближением. 355/113 лучше.
22/7 по-прежнему является хорошим приближением. 355/113 лучше.
Веб-сайты Pi
Пи продолжает привлекать внимание многих людей во всем мире. если ты
заинтересованы в получении дополнительной информации, существует множество веб-сайтов, посвященных
число Пи. Есть сайты, которые предлагают тысячи, миллионы или миллиарды
числа, пи-клубы, пи-музыка, люди, которые считают цифры, люди, которые
запоминать цифры, эксперименты с числом Пи и многое другое. Проверьте это Yahoo
страницу для полного списка.
Крутой эксперимент с числом пи
Один из самых интересных способов узнать больше о числе чисел — это провести эксперименты с числами числа.
самим собой. Вот знаменитая игла Бюффона .
В эксперименте с иглой Бюффона вы можете бросить иглу на
разлинованный лист бумаги. Если вы следите за тем, сколько раз игла
приземляется на линию, оказывается, что она напрямую связана со значением числа Пи.
Буффон
Апплет моделирования иглы (Майкл Дж. Хурбен)
Буффон
Игла (Джордж Риз, Управление математики, науки и технологий
Образование Университет Иллинойса (Шампейн-Урбана)
Цифры числа Пи
Первые 100 знаков после запятой
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 …
Первые 1000 знаков после запятой
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164
0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172
5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975
6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482
1339360726 02473 7245870066 0631558817 4881520920 9628292540
26 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 766
5
миллион, 10 миллионов, 100 миллионов и 200 миллионов цифр
Формулы для Пи
Более сложный формулы и выводы
Формула Виеты
2/PI = 2/2 * ( 2 + 2 )/2 * (2 + ( ( 2 + 2) ) )/2 * ...с
Формула Лейбница
PI/4 = 1/1 — 1/3 + 1/5 — 1/7 + …
Продукт Уоллис
PI/2 = 2/1 * 2/3 * 4/3 * 4/5 * 6/5 * 6/7 * …2/PI = (1 — 1/2 2 )(1 — 1/4 2 )(1 — 1/6 2 )…
Формула лорда Брункера
4/ПИ = 1 + 1
----------------
2 + 3 2
------------
2 + 5 2
---------
2 + 7 2 ...
(PI 2 )/8 = 1/1 2 + 1/3 2 + 1/5 2 + …
(PI 2 )/24 = 1/2 2 + 1/4 2 + 1/6 2 + …
Формула Эйлера
(PI 2 )/6 = (n = 1..) 1/n 2 = 1/1 2 + 1/2 2 + 1/3 2 + ...
(или вообще…)
(n = 1..) 1/n (2k) = (-1) (k-1) PI (2k) 2 (2k) В (2к) / ( 2(2к)!)B (k) = k th число Бернулли. например. В 0 =1 В 1 =-1/2 В 2 =1/6 В 4 =-1/30 В 6 =1/42 В 8 =-1/30 В 10 =5/66. Дальнейшие числа Бернулли определяется как (n 0)B 0 + (n 1)B 1 + (n 2)B 2 + … + (n (n-1))B (N-1) = 0 при условии, что все нечетные числа Бернулли > 1 = 0. (n k) = биномиальный коэффициент = n!/(k!(n-k)!)
См. Power Summations #2 для упрощенные выражения (без обозначений Бернулли) этих сумм для заданных значений k.
Вычисление числа Пи (π) — Карьера в математике
В некотором смысле число Пи (π) является очень простым: для вычисления числа Пи просто нужно взять любой круг и разделить его длину окружности на диаметр.
С другой стороны, число Пи (π) — это первое число, которое мы изучаем в школе, где мы не можем записать его в виде точной десятичной дроби. тысячи лет.
Мы узнаем, что можем начать записывать Пи (π) = 3,141592653589….. но никогда не сможем это закончить. Число Пи (π) бесконечно, и его цифры не повторяются — это то, что называется иррациональным числом. На самом деле, если вы будете искать достаточно долго среди цифр числа Пи (π), вы сможете найти любое число, включая дату вашего рождения.
Пи (π) — тоже очень полезное число. Он появляется повсюду в математике, а также имеет бесчисленное количество применений в технике и науке. Многие вещи круглые, и всякий раз, когда что-то круглое, значение Пи (π) обычно становится важным. Например, если инженер хочет рассчитать объем водопроводной трубы, он будет использовать следующую формулу для цилиндра:
(Где радиус трубы и высота трубы.)
Вычисление числа Пи (π)
Поскольку число Пи (π) имеет так много важных применений, мы должны иметь возможность начать вычислите его, по крайней мере, с точностью до нескольких знаков после запятой.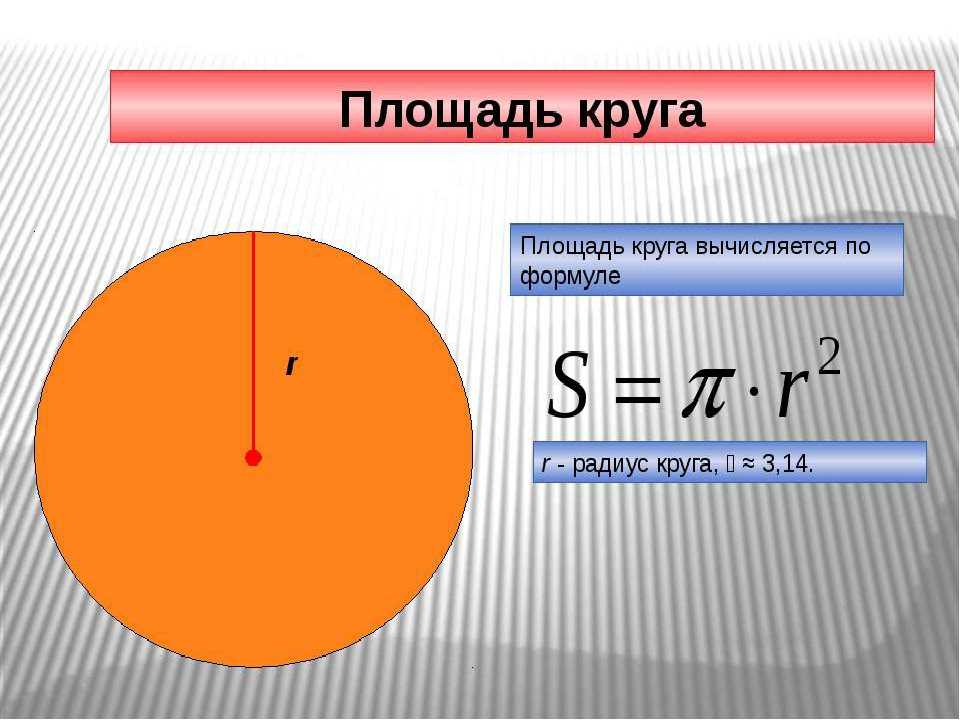 Кто-то должен был придумать приблизительное значение числа Пи (π), которое появляется на вашем калькуляторе — оно не попало туда по волшебству!
Кто-то должен был придумать приблизительное значение числа Пи (π), которое появляется на вашем калькуляторе — оно не попало туда по волшебству!
Измерение кругов
Первый и самый очевидный способ вычислить число Пи (π) — это взять самый совершенный круг, какой только сможете, а затем измерить его окружность и диаметр, чтобы вычислить число Пи (π). Это то, что сделали бы древние цивилизации, и именно так они впервые осознали, что внутри каждого круга скрыто постоянное соотношение. Проблема с этим методом заключается в точности — можете ли вы доверять своей рулетке, чтобы получить число Пи (π) с точностью до 10 или более знаков после запятой?
Использование многоугольников для приближения числа Пи (π)
Древнегреческий математик Архимед изобрел оригинальный метод приближенного вычисления числа Пи (π). Архимед начал с того, что вписал правильный шестиугольник внутрь круга, а затем описал другой правильный шестиугольник вне того же круга. Затем он смог рассчитать точные длины окружностей и диаметры шестиугольников и, следовательно, получить грубое приближение числа Пи (π), разделив длину окружности на диаметр.
Затем Архимед нашел способ удвоить количество сторон своих шестиугольников. Затем он мог найти более точную аппроксимацию числа Пи (π), используя многоугольники с большим количеством сторон, которые были ближе к окружности. Он сделал это четыре раза, пока не стал использовать 96-сторонние полигоны. Архимед точно вычислил длину окружности и диаметр и, следовательно, смог приблизить число Пи (π) к значению между и . С тех пор дробь остается одним из самых популярных и запоминающихся приближений числа Пи (π).
Примерно через 600 лет после Архимеда китайский математик Цзу Чунчжи использовал аналогичный метод для вписания правильного многоугольника с 12 288 сторонами. Это дало приближение Пи (π), которое правильно до шести знаков после запятой. Прошло еще почти 600 лет, прежде чем был разработан совершенно новый метод, который улучшил это приближение.
Вычисление числа Пи (π) с использованием бесконечного ряда
В конце концов математики обнаружили, что на самом деле существуют точные формулы для вычисления числа Пи (π). Единственная загвоздка в том, что каждая формула требует, чтобы вы делали что-то бесконечное количество раз. (Что имеет смысл, учитывая, что цифры числа Пи (π) продолжаются бесконечно.) Одна из удивительных вещей, которая интересует людей в отношении числа Пи (π), заключается в том, что для людей существует не одна формула, а множество различных. учиться.
Единственная загвоздка в том, что каждая формула требует, чтобы вы делали что-то бесконечное количество раз. (Что имеет смысл, учитывая, что цифры числа Пи (π) продолжаются бесконечно.) Одна из удивительных вещей, которая интересует людей в отношении числа Пи (π), заключается в том, что для людей существует не одна формула, а множество различных. учиться.
Один из самых известных и красивых способов вычисления числа Пи (π) — использовать ряд Грегори-Лейбница:
Если бы вы продолжали этот шаблон вечно, вы могли бы вычислить точно, а затем просто умножить его на 4. чтобы получить .. Если, однако, вы начнете складывать первые несколько членов, вы начнете получать приближение для Pi (π). Проблема с приведенным выше рядом заключается в том, что вам нужно сложить множество членов, чтобы получить точное приближение числа Пи (π). Вам нужно сложить более 300 терминов, чтобы получить число Пи (π) с точностью до двух знаков после запятой!
Еще одна серия, которая сходится быстрее, — это серия Нилаканта, которая была разработана в 15 -м -м веке. Сходится быстрее означает, что вам нужно выработать меньше терминов, чтобы ваш ответ стал ближе к Pi (π) .
Сходится быстрее означает, что вам нужно выработать меньше терминов, чтобы ваш ответ стал ближе к Pi (π) .
Nilacantha Series:
Математики также нашли другие более эффективные ряды для вычисления Пи (π). Компьютерные программы могут добавлять все больше и больше терминов, вычисляя число Пи (π) с необычайной степенью точности. В 2014 году был установлен мировой рекорд: компьютер вычислил число Пи (π) с точностью до 13 300 000 000 000 9.0165
знаков после запятой.До появления компьютеров вычислить число Пи (π) было намного сложнее. В 19 -м -м веке Уильяму Шэнксу потребовалось 15 лет, чтобы вычислить число Пи (π) с точностью до 707 знаков после запятой. К сожалению, позже выяснилось, что он ошибся и был прав только до 527 знаков после запятой! Девять или 10 цифр числа Пи (π), которые вы видите на своем калькуляторе, известны, вероятно, с 1400 года.
Теперь, когда вы знаете, как вычислять число Пи (π), вы всегда можете попробовать свои силы в запоминании десятичных знаков числа Пи (π). Самая последняя запись была создана в День числа Пи в 2019 году.Google, который рассчитал число Пи с точностью до 31,4 триллиона знаков после запятой!. С другой стороны, вы можете просто использовать следующую мнемонику для изучения первых шести десятичных знаков числа Пи (π): «Как бы я хотел вычислить число Пи»
Самая последняя запись была создана в День числа Пи в 2019 году.Google, который рассчитал число Пи с точностью до 31,4 триллиона знаков после запятой!. С другой стороны, вы можете просто использовать следующую мнемонику для изучения первых шести десятичных знаков числа Пи (π): «Как бы я хотел вычислить число Пи»
Длина каждого слова соответствует цифре числа Пи (π) .
| Как | я | желание | я | банка | вычислить | Пи |
| 3 | 1 | 4 | 1 | 5 | 9 | 2 |
Статья Хейзел Льюис
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желто-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найдите точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек (45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы | 45 | |
| 33 | Найти точное значение | соз(45) | |
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. |


 Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
 ru/matematika/geometriya/ploshhad-kruga/
ru/matematika/geometriya/ploshhad-kruga/
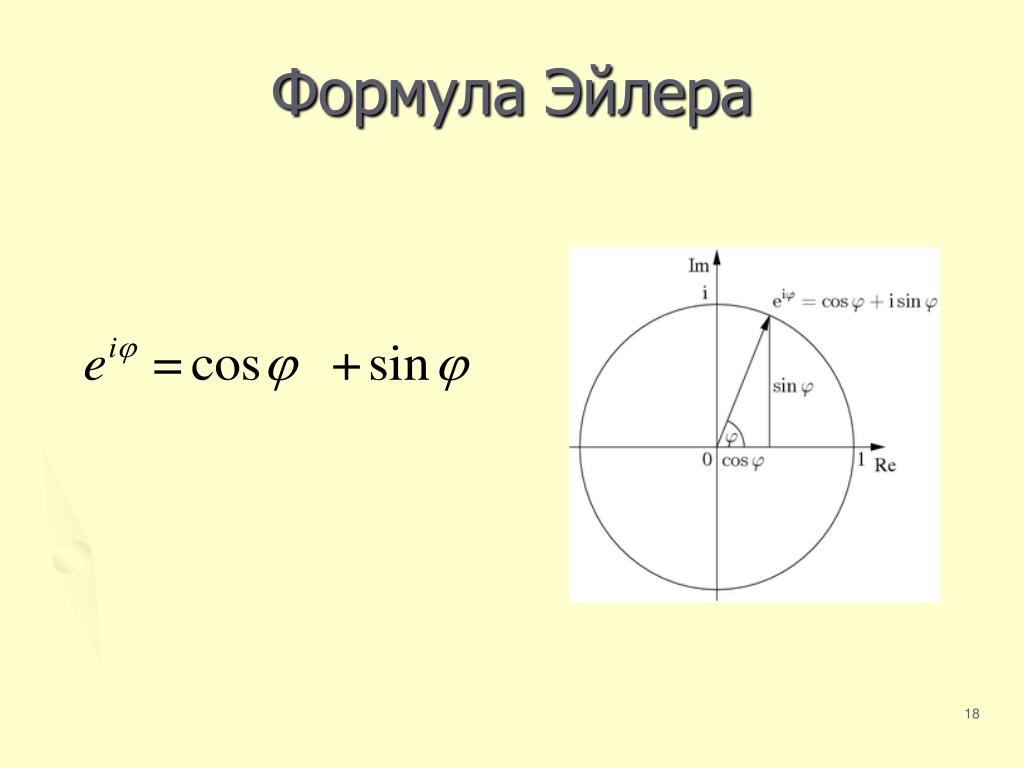 Самая легкая схема для начинающих
Самая легкая схема для начинающих Формула является достаточно простой и выглядит так: D = C/π = 2*R.
Формула является достаточно простой и выглядит так: D = C/π = 2*R.


 ..с
..с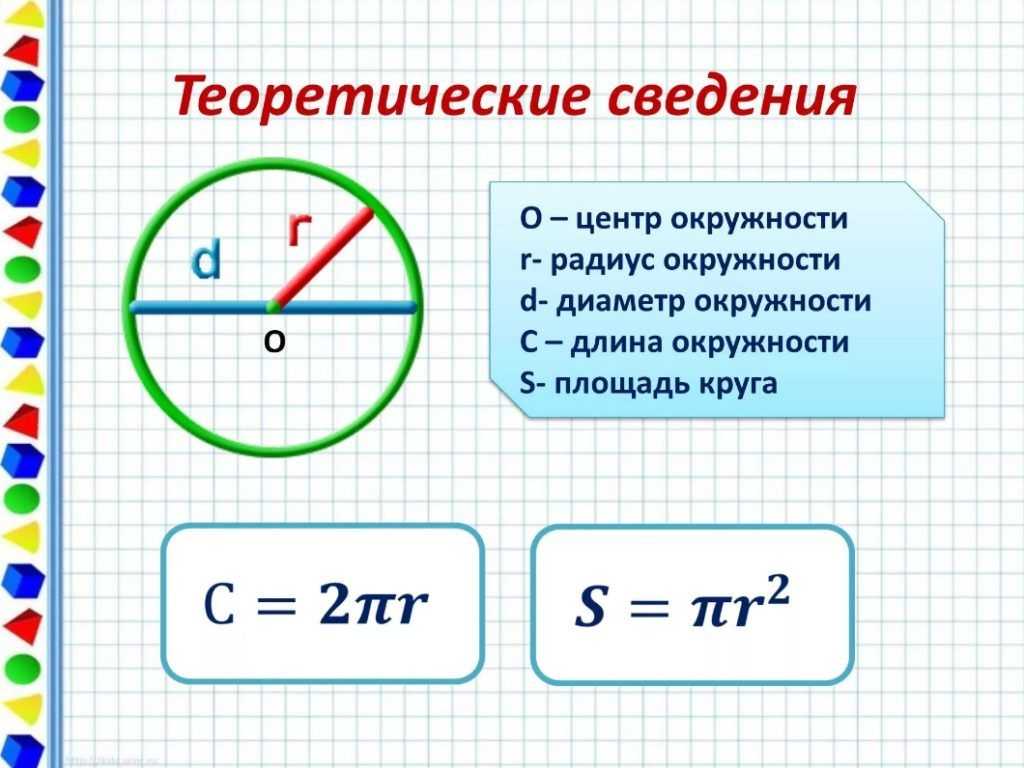 ..
..