Второй и третий признаки равенства треугольников 7 класс онлайн-подготовка на Ростелеком Лицей
Повторение понятия «равные треугольники», первого признака равенства треугольников
Для начала вспомним из материалов предыдущих уроков, что две фигуры называются равными, если их можно совместить наложением. На рисунке указаны два равных отрезка и два равных угла.
Рис. 1. Углы А и А1 равны, АВ = CD
Доказательство признаков равенства треугольников
Рассмотрим теперь равенство треугольников. Треугольники называются равными, если их можно совместить наложением. В таком случае совместятся все стороны и углы треугольников.
Рис. 2. Равные треугольники АВС и А1В1С1
Теперь мы готовы сформулировать и доказать второй признак равенства треугольников.
Второй признак равенства треугольников:
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, такие треугольники равны.
Теорема: Дано . Доказать: АВС и .
Доказательство: Выполним наложение данных в условии фигур. В результате данного действия вершины А и А1, , отрезки АС и А1С1 совпадают. Если рассматривать треугольники в целом, то совпадет с .
Теорема доказана.
Рис. 3. Равные треугольники АВС и А1В1С1
Третий признак равенства треугольников:
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Теорема: Дано . Доказать: АВС и .
Доказательство: Выполним наложение данных в условии фигур. В результате
данного действия имеем три случая:
1. Луч СС1 внутри .
Рис. 4. Равные треугольники АВС и А1В1С1
В таком случае по первому признаку.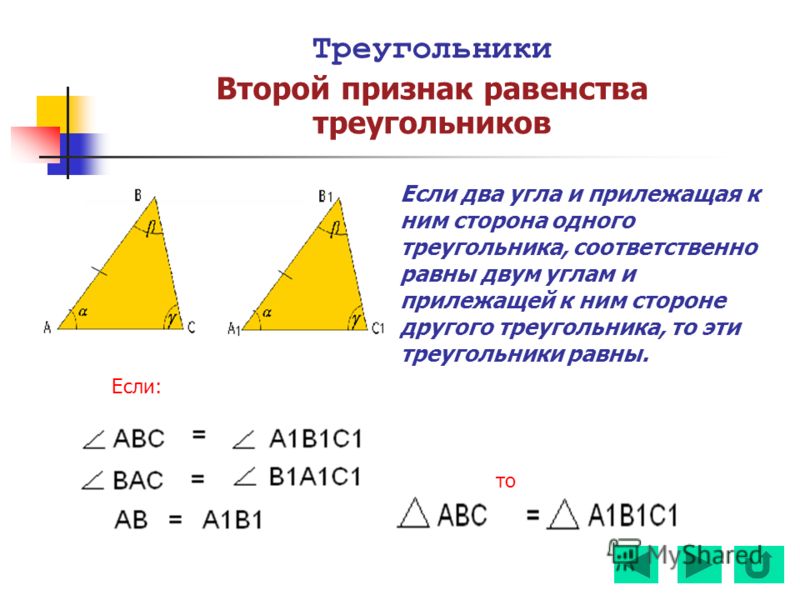
1. Луч СС1 совпадает с одной из сторон .
2. Луч СС1 лежит вне угла .
Рис. 5. Равные треугольники АВС и А1В1С1. Случаи 2, 3
Случаи 2 и 3 предлагаем рассмотреть самостоятельно.
Теорема доказана.
Рис. 6. Третий признак равенства треугольников
Решение задач
Рассмотрим некоторые задачи, чтобы закрепить пройденный материал.
Пример 1: Известно, что . Найти стороны АВ и ВС.
Решение: Выполним пояснительный рисунок к задаче.
Рис. 7. Чертеж к примеру 1
Поскольку , то треугольники АВС и ADC равны по второму признаку. Из равенства треугольников следует, что .
Ответ: 11 см, 19 см.
Пример 2: В изображенных треугольниках , , и медианы ВМ и ВМ1 тоже равны.
Доказать равенство треугольников: .
Рис. 8
Доказательство:
Вследствие того, что М и М1 – середины равных отрезков, то А1М1 = АМ. , ВМ = ВМ1 (по условию). Следовательно, по третьему признаку. Из равенства треугольников следует равенство углов .
, (по условию), (по доказанному). Следовательно, по первому признаку.
Что и требовалось доказать.
Рекомендованные ссылки на интернет-ресурсы
- Математика (Источник).
- School.xvatit.com (Источник).
Рекомендованное домашнее задание
1. № 37. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.
2. На рисунке РC = QR, CR = QP. Докажите, что ∠CQP = ∠QCR.
3.
4. Докажите перпендикулярность прямых СQ и BА, если AC = BC, а OA = OB.
Второй признак равенства треугольников
Если сторона и прилегающие к ней углы одного треугольника соответственно равна стороне и прилегающим к ней углам другого треугольника другого треугольника, то такие треугольники равны
\( 1)\:\:AC=A_1C_1\)
\( 2)\:\:∡A=∡A_1\)
\( 3)\:\:∡C=∡C_1\)
\(\Rightarrow ΔABC=ΔA_1B_1C_1\) по второму признаку.
1. В треугольниках \(ABH и BHC \:\: ∡ABH=∡HBC и ∡AHB=∡BHC\) . Доказать равенство треугольников \(ABH и BHC\).
Показать подсказку Показать решение Видеорешение
\(BH\) общая
Дано: \(∡AHB=∡BHC , \: ∡ABH=∡HBC\)
Доказать: \(ΔABH=ΔBHC\)
Доказательство:
\( 1)\:\: ∡AHB=∡BHC \) (по условию)
2) \(∡ABH=∡HBC (по условию) \)
3) \(BH\) общая
\(\Rightarrow ΔABH=ΔBHC\) по второму признаку.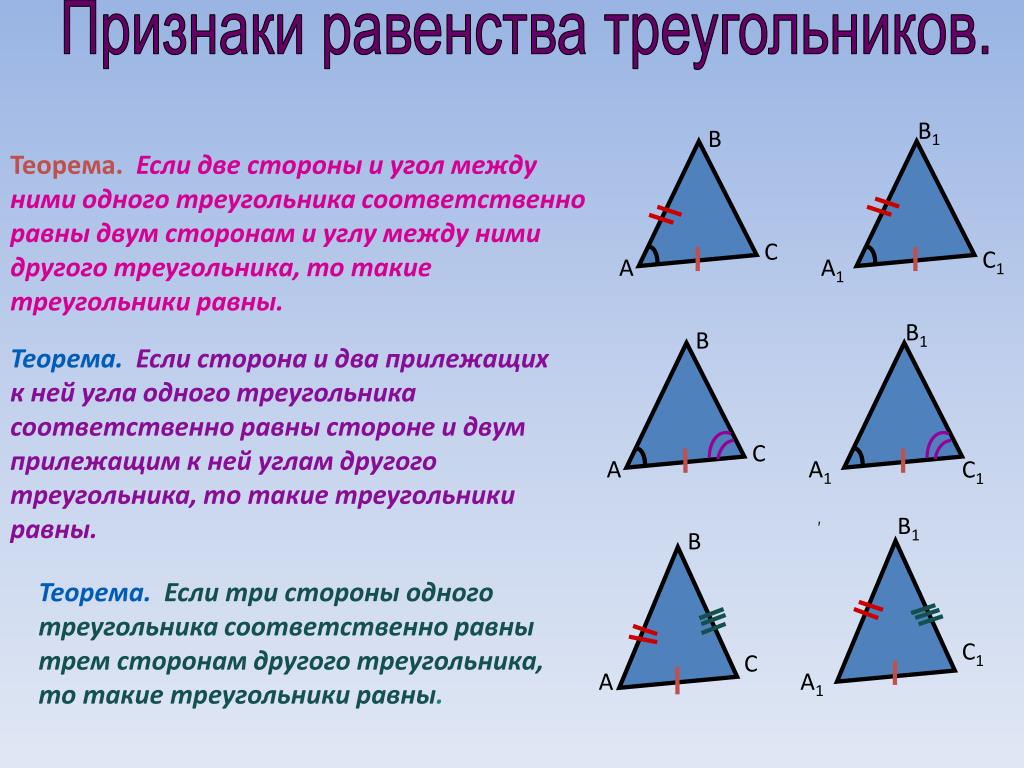
2. \( BO=OC \:\: ∡ABO=∡OCD \) . Доказать равенство треугольников \(ABO и COD\).
Показать подсказку Показать решение Видеорешение
\( ∡AOB=∡COD \) (Так как они вертикальные)
Дано: \(BO=OC , \: ∡ABO=∡OCD\)
Доказать: \( ΔABO = ΔCOD \)
Доказательство:
\( 1)\:\: BO=OC \) (по условию)
2) \( ∡ABO=∡OCD \) (по условию)
3) \( ∡AOB=∡COD \) (Так как они вертикальные)
\(\Rightarrow ΔABO = ΔCOD\) по второму признаку.
3.
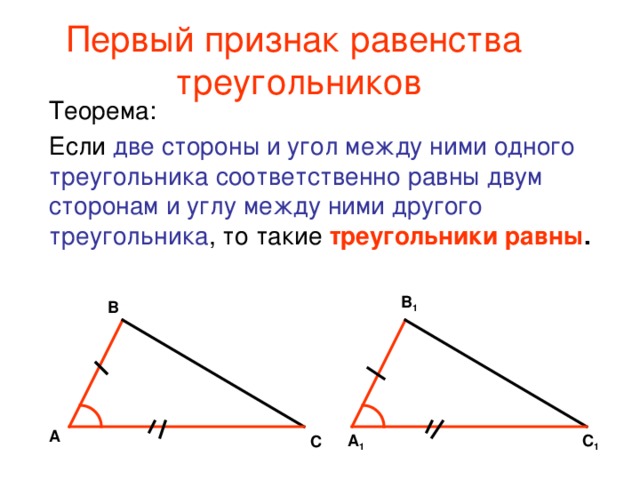\( ∡ADB=∡BDC \:\: ∡ABD=∡CBD \) . Доказать равенство треугольников \(ADB и BDC \).
Показать подсказку Показать решение Видеорешение
\( BD Общая \)
Дано: \(∡ADB=∡BDC , \: ∡ABD=∡CBD \)
Доказать: \( ΔADB = ΔBDC \)
Доказательство:
\( 1)\:\: ∡ADB=∡BDC \) (по условию)
2) \( ∡ABD=∡CBD \) (по условию)
3) \( BD \) (Общая)
\(\Rightarrow ΔADB = ΔBDC \) по второму признаку.
4. Отрезки \(AB и CD \) пересекаются в середине \(O\) отрезка \(CD \;\; , ∡ACO=∡BDO \) . Доказать равенство треугольников \(ACO и BDO \).
Показать подсказку Показать решение Видеорешение
\( ∡AOC=∡BOD \) (Так как они вертикальные)
Дано: \(∡ACO=∡BDO \)
\(O\) середина отрезка \(CD \)
Доказать: \( ΔACO = ΔBDO \)
Доказательство:
\( 1)\:\: ∡ACO=∡BDO \) (по условию)
2) \( CO=OD \) (так как точка \(O \) середина \(CD \) )
3) \( ∡AOC=∡BOD \) (Так как они вертикальные)
\(\Rightarrow ΔAOC = ΔBDO \) по второму признаку.
0 \) (так как \(BH\) высота )
2) \(∡ABH=∡HBC \) (так как \(BH\) биссектриса )
3) \(BH\) общая
\(\Rightarrow ΔABH=ΔBHC\) по второму признаку.
В треугольнике \(ABH\;\; AB \) лежит против прямого угла \( AHB \),
а в треугольнике \(BHC\)
\(BC\) лежит против прямого угла \( BHC \)
В равных треугольниках против равных углов лежат равные стороны, значит:
\(AB=BC, а ΔABC-равнобедренный\)
Объяснение урока: Равенство площадей двух треугольников
В этом объяснении мы научимся определять треугольники, у которых одной и той же площади, когда их основания равны по длине, а вершины противоположны эти основания находятся на параллельной им прямой.
Чтобы понять, почему этот результат верен, рассмотрим следующий сценарий.
У нас есть две параллельные линии, ⃖⃗𝐴𝐵 и ⃖⃗𝐶𝐷, и два треугольника с общим основанием, △𝐴𝐵𝐶 и △𝐴𝐵𝐷. Докажем, что площади этих треугольников равны. вспомнив сначала, что площадь треугольника равна половине длина его основания, умноженная на его перпендикулярную высоту. Так, добавим перпендикулярные линии из точек 𝐶 и 𝐷, чтобы найти перпендикулярные высоты каждого треугольника.
Мы будем называть точки пересечения этих перпендикулярных линий и параллельные прямые ⃖⃗𝐴𝐵 и ⃖⃗𝐶𝐷 𝐸 и 𝐹, как показано. Мы можем отметить, что все углы в 𝐸𝐶𝐷𝐹 прямые, так как ∠𝐸 и ∠𝐹 прямые углы и ⃖⃗𝐶𝐷⫽⃖⃗𝐴𝐵. Таким образом, 𝐸𝐶𝐷𝐹 — прямоугольник. Следовательно, длины 𝐶𝐸 и 𝐷𝐹 равны. Теперь мы можем показать, что площади треугольников равны, найдя выражения по своим направлениям: площадь△𝐴𝐵𝐶=12(𝐴𝐵)(𝐶𝐸),△𝐴𝐵𝐷=12(𝐴𝐵)(𝐷𝐹).
Поскольку 𝐶𝐸=𝐷𝐹, имеем площадьплощадь△𝐴𝐵𝐶=△𝐴𝐵𝐷.
Мы доказали следующий результат.
Теорема: Равенство площадей треугольников на параллельных прямых
Если два треугольника имеют общее основание и вершины, противоположные этому основанию, лежат на прямой прямые параллельны основанию, то их площади равны.
Теперь рассмотрим пример применения этой теоремы для нахождения треугольников. с равными площадями.
Пример 1. Нахождение площадей треугольников между параллельными прямыми
Что из следующего имеет ту же площадь, что и △𝐷𝐸𝐵?
- △𝐸𝐷𝐶
- △𝐹𝐵𝐶
- △𝐸𝐹𝐶
- 𝐴𝐷𝐹𝐸 90 026
- 𝐷𝐵𝐶𝐸
Ответ
Мы можем ответить на этот вопрос, вспомнив, что два треугольника, имеющие общую
основание, а вершина, противоположная основанию, лежит на прямой, параллельной
к основанию будут иметь равные площади. Тогда мы можем отметить, что
⃖⃗𝐷𝐸⫽⃖⃗𝐵𝐶,
поэтому любой треугольник с основанием 𝐷𝐸
и конечная вершина на ⃖⃗𝐵𝐶 будет иметь
равно площади △𝐷𝐸𝐵.
В частности, △𝐸𝐷𝐶 разделяет базу 𝐷𝐸 с △𝐷𝐸𝐵 и его вершина 𝐶 лежит на 𝐵𝐶, поэтому он имеет ту же площадь, что и △𝐷𝐸𝐵, который является вариантом A.
В нашем следующем примере нам нужно будет применить эту теорему, чтобы определить площадь треугольника.
Пример 2. Нахождение площадей треугольников между параллельными прямыми
Учитывая, что площадь △𝑌𝐴𝐵=568см, найдите площадь △𝑋𝐶𝐷.
Ответить
Начнем с того, что пометим данный треугольник и треугольник, чей площадь, которую мы хотим найти на данной диаграмме.
Мы можем разделить каждый из этих треугольников на два меньших треугольника вдоль строку 𝑋𝑌, чтобы получить следующее.
Сначала рассмотрим два верхних треугольника, как показано на рисунке.
Заметим, что эти треугольники имеют общее основание,
𝑋𝑌 и их противоположные вершины
𝐴 и 𝐷 оба лежат на прямой, параллельной
база.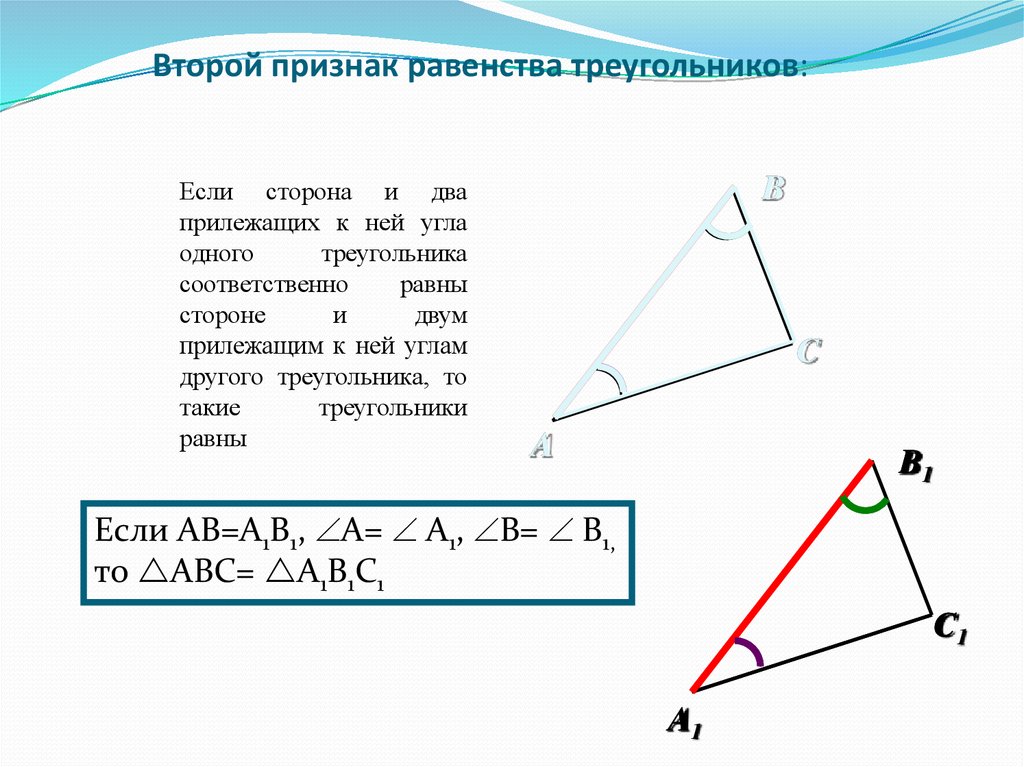
Отсюда мы знаем, что эти треугольники имеют одинаковую площадь.
Теперь рассмотрим два нижних треугольника, как показано на рисунке.
Мы можем еще раз отметить, что эти два треугольника имеют общее основание, 𝑋𝑌, и их противоположные вершины 𝐵 и 𝐶 оба лежат на прямой, параллельной основанию. Следовательно, мы знаем что эти треугольники имеют равные площади.
Так как эти треугольники имеют одинаковые площади и в сумме образуют большие треугольники, 𝑌𝐴𝐵 и 𝑋𝐶𝐷, также должны иметь одинаковую площадь.
Следовательно, площадь треугольника 𝑋𝐶𝐷 равна 568 см 2 .
В нашем следующем примере мы покажем, что если два треугольника лежат на двух параллельных прямые и у них основания одинаковой длины, то они имеют одинаковую площадь.
Пример 3. Определение треугольников с равными площадями между параллельными прямыми
Учитывая, что △𝑁𝑀𝐾?
- 𝐻𝑁𝐾𝐶
- 𝑍𝑂𝑋𝐻
- △𝐶𝑍𝐻
- △𝐻𝑁𝑍 9 0026
- △𝐶𝑁𝐻
Ответить
Нам дана пара параллельных прямых, поэтому мы можем использовать тот факт, что если две
треугольники имеют общее основание и вершины, противоположные этому основанию, лежат на прямой
прямые параллельны основанию, то их площади равны.
Если мы выберем
𝑀𝑁 в качестве основания треугольника, то мы можем выбрать любую точку на
⃖⃗𝐷𝐾 в качестве конечной вершины треугольника, чтобы найти треугольник равной площади
△𝑁𝑀𝐾. Следовательно,
△𝑁𝑀𝐾,
△𝑁𝑀𝐶,
△𝑁𝑀𝑍,
△𝑁𝑀𝑂 и △𝑁𝑀𝐷 все имеют
тот же район. Однако ни один из них не является вариантом ответа на этот вопрос.
Вместо этого воспользуемся тем фактом, что площадь треугольника равна половине длина его основания, умноженная на его перпендикулярную высоту. Мы выбираем 𝑀𝑁 в качестве основания треугольника и можно добавить перпендикулярную высоту ℎ к диаграмме, как показано на рисунке.
Следовательно, площадь△𝑁𝑀𝐾=12(𝑀𝑁)×ℎ.
Мы можем использовать тот же метод для определения площадей △𝐶𝑍𝐻 и △𝑂𝐷𝑋.
Складываем перпендикулярные линии из оснований в вершину и замечаем, что
все зеленые линии параллельны. Заметим, что поскольку каждый из них является
пересекая параллельные прямые, они также пересекают ⃖⃗𝑀𝑋 под прямым углом.
Таким образом,
все они образуют прямоугольники с сечениями ⃖⃗𝑀𝑋
и ⃖⃗𝐷𝐾, поэтому каждый перпендикуляр
линия имеет ту же длину, что и ℎ. Поэтому,
площадьплощадь△𝐶𝑍𝐻=12(𝐶𝑍)×ℎ,△𝑂𝐷𝑋=12(𝑂𝐷)×ℎ.
Наконец, поскольку 𝑀𝑁, 𝐶𝑍, и 𝑂𝐷 у всех есть одинаковой длины, мы можем заключить, что треугольники △𝑁𝑀𝐾, △𝐶𝑍𝐻 и △𝑂𝐷𝑋 все имеют одинаковую площадь.
Следовательно, △𝐶𝑍𝐻 имеет ту же площадь, что и △𝑁𝑀𝐾, что является вариантом C.
В предыдущем примере мы показали следующее свойство.
Свойство: равенство площадей треугольников на параллельных прямых
Если два треугольника лежат на двух параллельных прямых и имеют основания одинаковой длины, тогда они имеют одинаковую площадь.
В нашем следующем примере мы рассмотрим, как разбивается медиана треугольника. площадь исходного треугольника.
Пример 4. Нахождение площадей треугольников с конгруэнтными основаниями
Если площадь △𝐷𝐸𝐶=6,99 см,
найдите площадь △𝐴𝐵𝐶.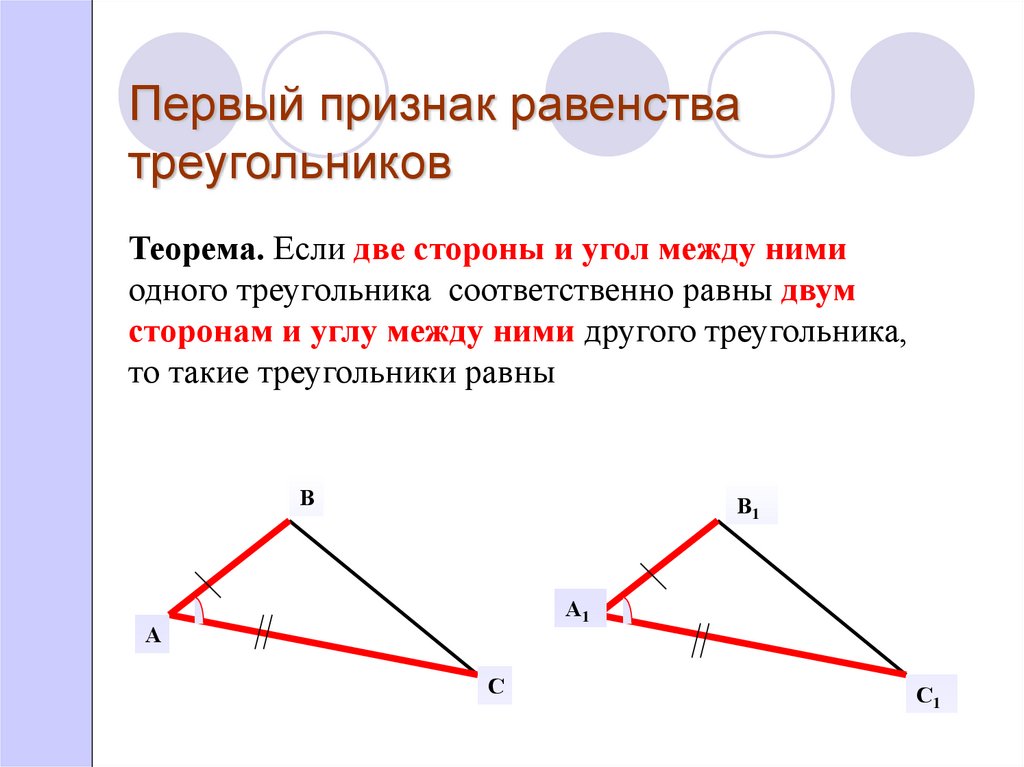
Ответ
Мы хотим определить площадь △𝐴𝐵𝐶 и для этого нам дана площадь из △𝐷𝐸𝐶. Это означает, что мы хотим сравнить площади некоторых треугольников с площадями треугольников. △𝐷𝐸𝐶. Для этого вспомним, что площадь треугольника равно половине длины его основания, умноженной на его перпендикулярная высота. Если мы выберем 𝐶𝐸 быть основанием этого треугольника, мы получаем следующее.
Точку на перпендикуляре мы называем 𝐹; тогда мы можем увидеть, что площадь△𝐷𝐸𝐶=12(𝐶𝐸)(𝐷𝐹).
Из диаграммы видно, что 𝐴𝐸=𝐶𝐸. На самом деле это говорит нам о том, что 𝐷𝐸 — медиана треугольника △𝐴𝐶𝐷. Поскольку треугольники △𝐷𝐴𝐸 и △𝐷𝐸𝐶 имеют одинаковую длину основания, мы можем проверить, имеют ли они одинаковую высоту перпендикуляра.
Выбрав 𝐴𝐸 в качестве основания, перпендикуляр из 𝐷 к
⃖⃗𝐴𝐸 также пересекутся в 𝐹, поэтому
площадь△𝐷𝐴𝐸=12(𝐴𝐸)(𝐷𝐹)=12(𝐶𝐸)(𝐷𝐹)=△𝐷𝐸𝐶.
Так как эти треугольники вместе составляют △𝐴𝐶𝐷, у нас есть площадьсм△𝐴𝐶𝐷=6,99+6,99=13,98.
Мы можем применить те же самые рассуждения, чтобы показать, что △𝐴𝐶𝐷 и △𝐴𝐷𝐵 имеют одинаковую площадь. Мы видим что оба треугольника имеют одинаковую длину основания, так как 𝐶𝐷=𝐷𝐵, и эти основания лежат на одной прямой. Наконец, они имеют общую точку вершины 𝐴, поэтому перпендикулярное расстояние от основания до 𝐴 будет одинаковым для обоих треугольники.
Следовательно, их площади одинаковы и поэтому площадьсм△𝐴𝐵𝐷=13,98.
С △𝐴𝐵𝐶 является комбинацией этих треугольников, мы имеем areaareaareacm△𝐴𝐵𝐶=△𝐴𝐵𝐷+△𝐴𝐶𝐷=13,98+13,98=27,96.
В нашем предыдущем примере мы показали два полезных результата. Во-первых, мы увидели, что
медиана треугольника разделит треугольник на два треугольника с одинаковыми
область. Во-вторых, мы видели, что два треугольника с конгруэнтными основаниями на одной и той же
прямая линия, имеющая общую противоположную вершину, будет иметь одинаковую площадь, так как
их перпендикулярные высоты равны.
Мы можем записать эти результаты формально
следующее.
Свойство: Равенство площадей треугольников с конгруэнтными основаниями
Любая медиана треугольника разделит треугольник на два треугольника с одинаковой площадью.
Любые два треугольника с конгруэнтными основаниями, лежащие на одной прямой и имеют общую вершину, противоположную основанию, имеют одинаковую площадь.
В нашем следующем примере мы применим это свойство для нахождения равнобедренных треугольников. площадь данного треугольника.
Пример 5. Определение треугольников с одинаковой площадью между Параллельные линии
Площадь какого треугольника равна △𝐿𝐵𝐶?
Ответ
Заметим, что нам дано, что 𝐵𝐶=𝐷𝑋; тогда мы можем вспомнить, что любые два
треугольники с равными основаниями, лежащие на одной прямой и
имеют общую вершину, противоположную основанию, имеют одинаковую площадь. Следовательно,
△𝐿𝐵𝐶 и △𝐷𝑋𝐿
имеют одинаковую площадь.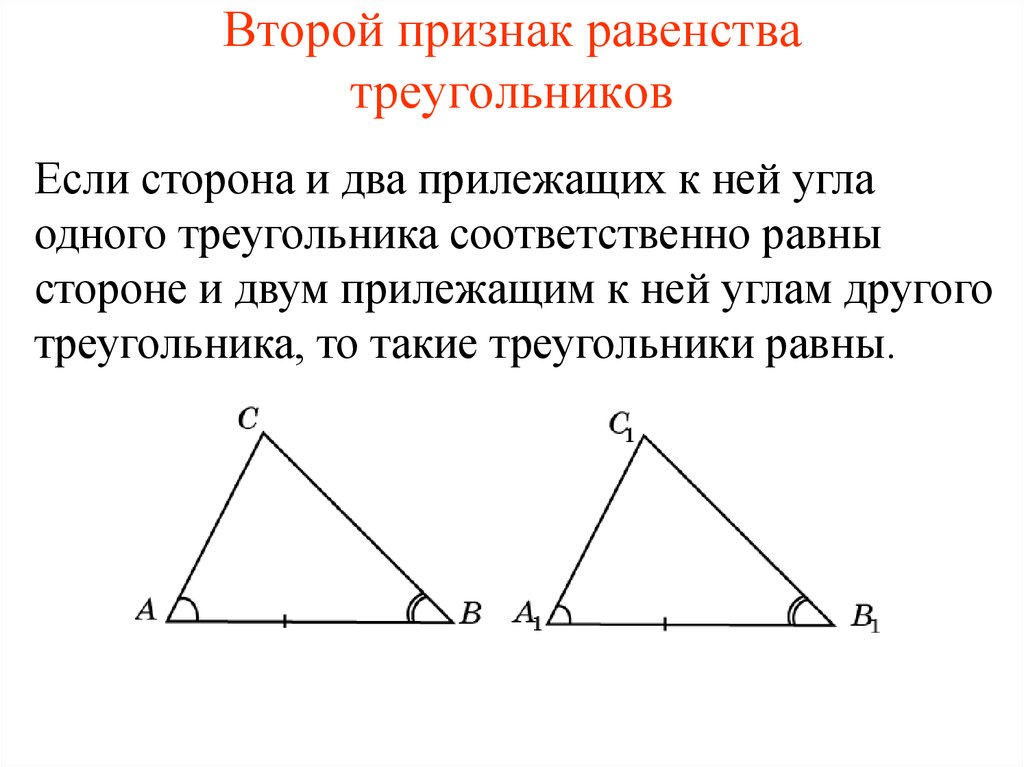
До сих пор мы концентрировались на поиске треугольников с равными площадями заданному треугольник или используя эти результаты для определения площадей. Однако мы также можем задать те же вопросы наоборот. Например, если два треугольника одинаковой площади имеют общую основание и их вершины, противоположные основанию, лежат на одной стороне, что уж говорить об этих вершинах?
Чтобы помочь нам понять ситуацию, давайте сначала набросаем эту информацию.
Мы знаем, что △𝐴𝐵𝐶 и △𝐴𝐵𝐷 иметь одинаковую площадь; мы можем найти выражения для площади каждого треугольника используя половину длины основания, умноженную на высоту перпендикуляра. Добавление перпендикуляров к диаграмме дает нам следующее.
Теперь у нас есть площадь△𝐴𝐵𝐶=12(𝐴𝐵)(𝐶𝐹),△𝐴𝐵𝐷=12(𝐴𝐵)(𝐷𝐺).
Так как площади треугольников равны, мы должны иметь, что
𝐶𝐹=𝐺𝐷. Далее заметим, что эти прямые перпендикулярны
⃖⃗𝐺𝐹 и имеют одинаковую длину; следовательно, мы должны иметь это
𝐶𝐷𝐺𝐹 — прямоугольник и, в частности, это означает, что
⃖⃗𝐶𝐷⫽⃖⃗𝐺𝐹.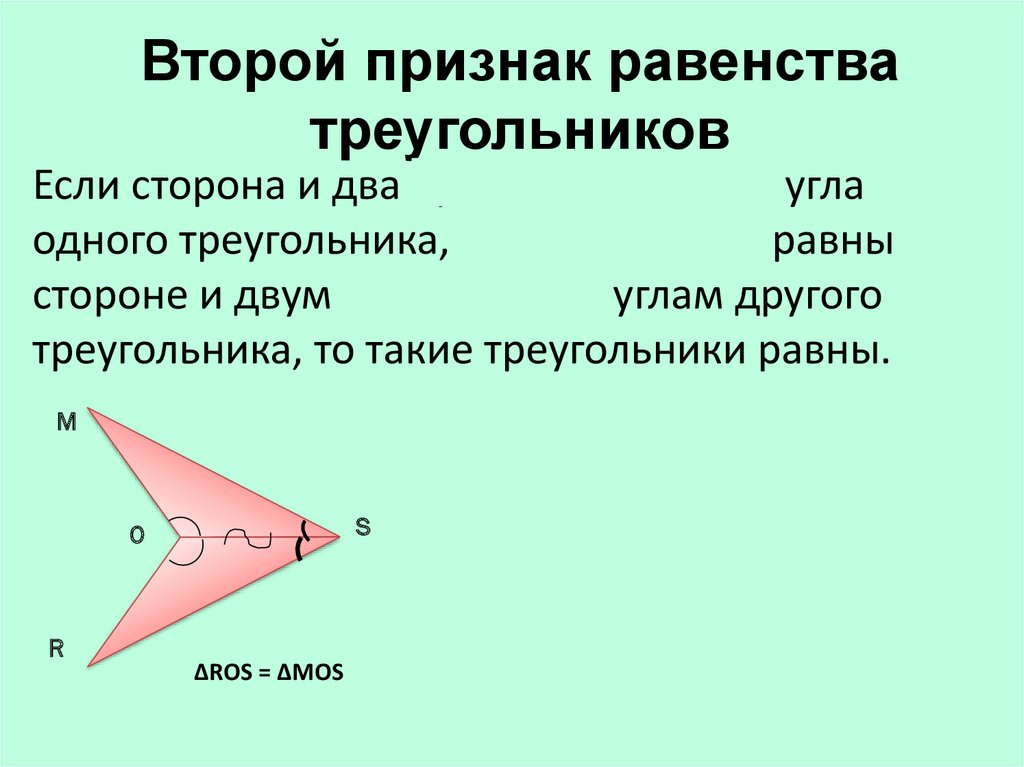
Мы доказали следующий результат.
Теорема: Вершины равновеликих треугольников, имеющих общее основание, параллельны Их общее основание
Если два треугольника имеют общее основание и равные площади, а вершины противоположны основание лежит по одну сторону от основания, то эти вершины лежат на одной прямой параллельно основанию.
Стоит отметить, что этот результат также верен, если треугольники равны основания на одной линии. Формально это можно записать следующим образом.
Теорема: Вершины равновеликих треугольников с конгруэнтными основаниями выровнены параллельно к их общему основанию
Если два треугольника имеют конгруэнтные основания на прямой линии и имеют равные площади а вершины, противоположные основанию, лежат по одну сторону от основания, то эти вершины лежат на прямой, параллельной основанию.
Давайте теперь рассмотрим пример применения этой теоремы для идентификации
геометрическое свойство по диаграмме.
Пример 6. Треугольники между параллельными прямыми и общим основанием
Если районы △𝐿𝑁𝐴 и △𝑌𝐴𝐺 одинаковы, что из следующего должно быть правдой?
- 𝑌𝐿=𝑁𝐺
- 𝑌𝐺⫽𝑁𝐿
- 𝑌𝐺=𝑁𝐿
- 𝐴𝑁= 𝐴𝐺
- 𝑌𝐿⫽𝑁𝐺
Ответ
Начнем с того, что заметим, что каждый из треугольников △𝐿𝑁𝐴 а △𝑌𝐴𝐺 состоит из двух меньших треугольников; мы можем сравнить площади этих меньших треугольников. Начнем с сравнивая треугольники △𝐴𝐺𝐸 и △𝐴𝐷𝑁; мы можем сделать это, добавив расстояние по перпендикуляру от 𝐴 до ⃖⃗𝐺𝑁 к схеме, как показано на рисунке.
Напомним, что любые два треугольника с конгруэнтными основаниями, лежащие на одной прямой и имеют общую вершину, противоположную основанию. тот же район. Следовательно, площадьплощадь△𝐴𝐺𝐸=△𝐴𝐷𝑁.
Комбинируя этот результат с тем фактом, что треугольники △𝐿𝑁𝐴 и
△𝑌𝐴𝐺 имеют одинаковую площадь означает, что
треугольники △𝑌𝐺𝐸 и
△𝐿𝑁𝐷 также должны иметь одинаковую площадь.
Вспомним, что если два треугольника имеют конгруэнтные основания на прямой прямой и имеют равные площади, а вершины, противоположные основанию, лежат на одной стороне основания, то эти вершины лежат на прямой, параллельной к базе.
Следовательно, 𝑌𝐿⫽𝑁𝐺, что является вариантом E.
В нашем последнем примере мы применим эти теоремы и свойства для определения геометрическое свойство из данной диаграммы.
Пример 7. Определение геометрического свойства при условии, что площади двух треугольников равны
Точки 𝑍, 𝐻 и 𝐷 коллинеарный. Если площади △𝑍𝐶𝐻 и △𝐶𝐻𝐷 одинаковы, что из следующего должно быть правдой?
- 𝐶𝐻=𝐻𝐷
- 𝐶𝐻⫽𝐹𝐷
- 𝐶𝐻=𝐷𝐶
- 𝐶𝐻=𝐹𝐻
Ответ
Сначала отметим, что ⃖⃗𝐻 𝐹 параллельно
⃖⃗𝐶𝑍 и ⃖⃗𝐻𝑍
параллелен ⃖⃗𝐶𝐹. Таким образом,
𝐶𝑍𝐻𝐹 — параллелограмм. Следовательно, его диагональ
𝐶𝐻, разбивает параллелограмм на два
равновеликие треугольники, △𝑍𝐶𝐻 и
△𝐶𝐻𝐹.
Также стоит отметить, что сказать, что три точки лежат на одной прямой, означает, что все они лежат на одной прямой.
линия.
Следовательно, поскольку площадьплощадь△𝑍𝐶𝐻=△𝐶𝐻𝐷, мы можем заключить, что площадь△𝐶𝐻𝐷=△𝐶𝐻𝐹.
Мы также можем отметить, что эти треугольники имеют одно и то же основание, 𝐶𝐻.
Тогда мы можем вспомнить, что если два треугольника имеют общее основание и равны площади и вершины, противоположные основанию, лежат по одну сторону от основания, то эти вершины лежат на прямой, параллельной основанию.
Так как треугольники △𝐶𝐻𝐷 и △𝐶𝐻𝐹 имеют одинаковую площадь, делят базу 𝐶𝐻 и иметь вершины по одну сторону от основания, мы можем сделать вывод, что основание параллельно линии между противоположными вершинами база. То есть 𝐶𝐻⫽𝐹𝐷, что является вариантом B.
В предыдущем примере существует множество различных способов определения
результат.
Например, мы могли бы использовать тот факт, что если площади
△𝑍𝐶𝐻 и △𝐶𝐻𝐷 одинаковы, то их основания, лежащие на одной прямой, конгруэнтны, что приводит к 𝐻𝐷=𝑍𝐻=𝐹𝐶, а так как
𝐻𝐷⫽𝐹𝐶, так что
𝐻𝐷𝐹𝐶 — параллелограмм.
Давайте закончим, повторив некоторые важные моменты из этого объяснитель.
Ключевые точки
- Если два треугольника имеют общее основание и вершины, противоположные этому основанию, лежат на прямой прямые параллельны основанию, то их площади равны.
- Если два треугольника лежат на двух параллельных прямых и имеют одинаковую длину основания, тогда они имеют одинаковую площадь.
- Медиана треугольника делит его на две равные по площади части.
- Треугольники с конгруэнтными основаниями на одной прямой и общие вершины, противоположные основаниям, равны по площади.
- Если два треугольника имеют общее основание и равные площади, а вершины противоположны
основания лежат по одну сторону от основания, то эти вершины лежат на
прямая, параллельная основанию.
Как определить конгруэнтность треугольников
Два треугольника равны, если они имеют:
Но нам не обязательно знать все три стороны и все три угла… обычно достаточно трех из шести . |
Есть пять способов определить конгруэнтность двух треугольников: SSS , SAS , ASA , AAS и HL .
1. SSS
(боковой, боковой, боковой)SSS означает «сторона, сторона, сторона» и означает, что у нас есть два треугольника, у которых все три стороны равны.
Например:
| соответствует: |
(дополнительную информацию см.
в разделе Решение треугольников SSS)
Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
2. SAS
(сторона, угол, сторона)SAS означает «сторона, угол, сторона» и означает, что у нас есть два треугольника, в которых мы знаем, что две стороны и угол между ними равны.
Например:
| соответствует: |
(дополнительную информацию см. в разделе Решение треугольников SAS)
Если две стороны и угол между ними одного треугольника равны соответствующим сторонам и углу другого треугольника, то такие треугольники равны.
3. ASA
(угол, сторона, угол) ASA означает «угол, сторона, угол» и означает, что у нас есть два треугольника, в которых мы знаем, что два угла и сторона равны.
Например:
| соответствует: |
(дополнительную информацию см. в разделе Решение треугольников ASA)
Если два угла и прилежащая к ним сторона одного треугольника равны соответствующим углам и стороне другого треугольника, то такие треугольники равны.
4. AAS
(угол, угол, сторона)AAS означает «угол, угол, сторона» и означает, что у нас есть два треугольника, в которых мы знаем, что два угла и не включенная сторона равны.
Например:
| соответствует: |
(дополнительную информацию см. в разделе Решение треугольников AAS)
Если два угла и сторона, не входящая в один треугольник, равны соответствующим углам и стороне другого треугольника, то такие треугольники равны.
5. HL
(гипотенуза, катет)Это относится только к прямоугольным треугольникам!
| или |
HL означает « H ypotenuse, L eg», потому что самая длинная сторона прямоугольного треугольника называется гипотенузой, а две другие стороны называются катетами.
Значит у нас есть два прямоугольных треугольника с
- одинаковая длина гипотенузы и
- такой же длины для одной из двух других ножек .
Неважно, какая сторона, так как треугольники можно вращать.
Например:
| соответствует: |
(дополнительную информацию см.