2 x гипербола: Построить график функций y=2/x — ответ на Uchi.ru

alexxlab / / Разное

Mathway | Популярные задачи

1Оценить с использованием заданного значенияквадратный корень из 50
2Оценить с использованием заданного значенияквадратный корень из 45
3Вычислить5+5
4Вычислить7*7
5Разложить на простые множители24
6Преобразовать в смешанную дробь52/6
7Преобразовать в смешанную дробь93/8
8Преобразовать в смешанную дробь34/5
9Графикy=x+1
10Оценить с использованием заданного значенияквадратный корень из 128
11Найти площадь поверхностисфера (3)
12Вычислить54-6÷2+6
13Графикy=-2x
14Вычислить8*8
15Преобразовать в десятичную форму 5/9
16Оценить с использованием заданного значенияквадратный корень из 180
17Графикy=2
18Преобразовать в смешанную дробь7/8
19Вычислить9*9
20Risolvere per CC=5/9*(F-32)
21Упростить1/3+1 1/12
22Графикy=x+4
23Графикy=-3
24Графикx+y=3
25Графикx=5
26Вычислить6*6
27Вычислить2*2
28Вычислить4*4
29Вычислить1/2+(2/3)÷(3/4)-(4/5*5/6)
30Вычислить1/3+13/12
31Вычислить5*5
32Risolvere per d2d=5v(o)-vr
33Преобразовать в смешанную дробь3/7
34Графикy=-2
35Определить наклонy=6
36Перевести в процентное соотношение9
37Графикy=2x+2
38Графикy=2x-4
39Графикx=-3
40Решить, используя свойство квадратного корняx^2+5x+6=0
41Преобразовать в смешанную дробь1/6
42Преобразовать в десятичную форму9%
43Risolvere per n12n-24=14n+28
44Вычислить16*4
45Упроститькубический корень из 125
46Преобразовать в упрощенную дробь43%
47Графикx=1
48Графикy=6
49Графикy=-7
50Графикy=4x+2
51Определить наклонy=7
52Графикy=3x+4
53Графикy=x+5
54График3x+2y=6
55Решить, используя свойство квадратного корняx^2-5x+6=0
56Решить, используя свойство квадратного корняx^2-6x+5=0
57Решить, используя свойство квадратного корняx^2-9=0
58Оценить с использованием заданного значенияквадратный корень из 192
59Оценить с использованием заданного значенияквадратный корень из 25/36
60Разложить на простые множители14
61Преобразовать в смешанную дробь7/10
62Risolvere per a(-5a)/2=75
63Упроститьx
64Вычислить6*4
65Вычислить6+6
66Вычислить-3-5
67Вычислить-2-2
68Упроститьквадратный корень из 1
69Упроститьквадратный корень из 4
70Найти обратную величину1/3
71Преобразовать в смешанную дробь11/20
72Преобразовать в смешанную дробь7/9
73Найти НОК11 , 13 , 5 , 15 , 14 , , , ,
74Решить, используя свойство квадратного корняx^2-3x-10=0
75Решить, используя свойство квадратного корняx^2+2x-8=0
76График3x+4y=12
77График3x-2y=6
78Графикy=-x-2
79Графикy=3x+7
80Определить, является ли полиномом2x+2
81Графикy=2x-6
82Графикy=2x-7
83Графикy=2x-2
84Графикy=-2x+1
85Графикy=-3x+4
86Графикy=-3x+2
87Графикy=x-4
88Вычислить(4/3)÷(7/2)
89График2x-3y=6
90Графикx+2y=4
91Графикx=7
92Графикx-y=5
93Решить, используя свойство квадратного корняx^2+3x-10=0
94Решить, используя свойство квадратного корняx^2-2x-3=0
95Найти площадь поверхностиконус (12)(9)
96Преобразовать в смешанную дробь3/10
97Преобразовать в смешанную дробь7/20
98Преобразовать в смешанную дробь2/8
99Risolvere per wV=lwh
100Упростить6/(5m)+3/(7m^2)

Mathway | Популярные задачи

1Множительx^2-4
2Множитель4x^2+20x+16
3Графикy=-x^2
4Вычислить2+2
5Множительx^2-25
6Множительx^2+5x+6
7Множительx^2-9
8Множительx^3-8
9Вычислитьквадратный корень из 12
10Вычислитьквадратный корень из 20
11Вычислитьквадратный корень из 50
12Множительx^2-16
13Вычислитьквадратный корень из 75
14Множительx^2-1
15Множительx^3+8
16Вычислить-2^2
17Вычислитьквадратный корень из (-3)^4
18Вычислитьквадратный корень из 45
19Вычислитьквадратный корень из 32
20Вычислитьквадратный корень из 18
21Множительx^4-16
22Вычислитьквадратный корень из 48
23Вычислитьквадратный корень из 72
24Вычислитьквадратный корень из (-2)^4
25Множительx^3-27
26Вычислить-3^2
27Множительx^4-1
28Множительx^2+x-6
29Множительx^3+27
30Множительx^2-5x+6
31Вычислитьквадратный корень из 24
32Множительx^2-36
33Множительx^2-4x+4
34Вычислить-4^2
35Множительx^2-x-6
36Множительx^4-81
37Множительx^3-64
38Вычислить4^3
39Множительx^3-1
40Графикy=x^2
41Вычислить2^3
42Вычислить(-12+ квадратный корень из -18)/60
43Множительx^2-6x+9
44Множительx^2-64
45Графикy=2x
46Множительx^3+64
47Вычислить(-8+ квадратный корень из -12)/40
48Множительx^2-8x+16
49Вычислить3^4
50Вычислить-5^2
51Множительx^2-49
52Вычислить(-20+ квадратный корень из -75)/40
53Множительx^2+6x+9
54Множитель4x^2-25
55Вычислитьквадратный корень из 28
56Множительx^2-81
57Вычислить2^5
58Вычислить-8^2
59Вычислить2^4
60Множитель4x^2-9
61Вычислить(-20+ квадратный корень из -50)/60
62Вычислить(-8+ квадратный корень из -20)/24
63Множительx^2+4x+4
64Множительx^2-10x+25
65Вычислитьквадратный корень из -16
66Множительx^2-2x+1
67Вычислить-7^2
68Графикf(x)=2^x
69Вычислить2^-2
70Вычислитьквадратный корень из 27
71Вычислитьквадратный корень из 80
72Множительx^3+125
73Вычислить-9^2
74Множитель2x^2-5x-3
75Вычислитьквадратный корень из 40
76Множительx^2+2x+1
77Множительx^2+8x+16
78Графикy=3x
79Множительx^2+10x+25
80Вычислить3^3
81Вычислить5^-2
82Графикf(x)=x^2
83Вычислитьквадратный корень из 54
84Вычислить(-12+ квадратный корень из -45)/24
85Множительx^2+x-2
86Вычислить(-3)^3
87Множительx^2-12x+36
88Множительx^2+4
89Вычислитьквадратный корень из (-8)^2
90Множительx^2+7x+12
91Вычислитьквадратный корень из -25
92Множительx^2-x-20
93Вычислить5^3
94Множительx^2+8x+15
95Множительx^2+7x+10
96Множитель2x^2+5x-3
97Вычислить квадратный кореньквадратный корень из 116
98Множительx^2-x-12
99Множительx^2-x-2
100Вычислить2^2

Гиперболы:

Гиперболы:

Гипербола – это множество точек, абсолютное значение разности между двумя фиксированными точками, называемыми фокусами, является постоянной ценность.

 

Гиперболы имеют две симметричные половины. У них есть два вершины, которые являются наиболее внутренними точками. Они имеют два очага, как указано в определение, и у них есть две асимптоты, которые пересекаются в центре гиперболы.

 

Если гипербола открывается в горизонтальном направлении, уравнение гиперболы в стандартной форме выглядит как

Обратите внимание на вычитание между условия. Если срок y после вычитания гипербола открывается в стороны.

 

Если гипербола открывается вверх и вниз, стандартная форма уравнения

. x -член сейчас вычитается.

 

Внутри гиперболы находится прямоугольник. асимптоты пересекают углы этого прямоугольника. Вы найдете эту коробку по двигаясь влево и вправо от центра a расстояние от до и вверх и вниз от центра на расстоянии b . Центр гиперболы является центром этого прямоугольника. прямоугольник имеет размеры 2 a на 2 b .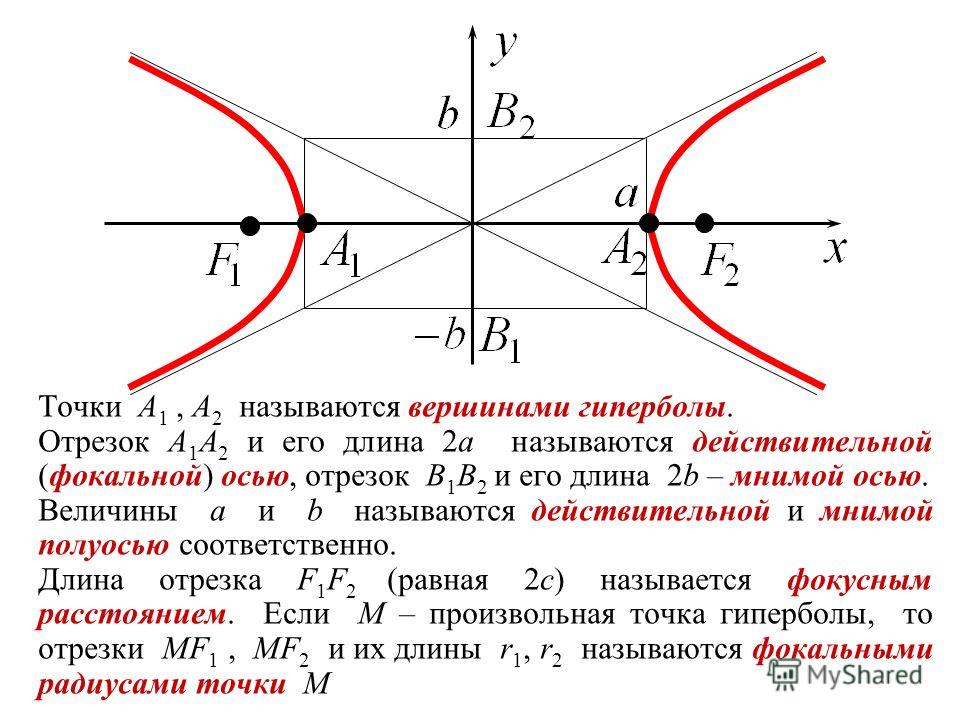

 

с 2 = а 2 + б 2 для гиперболы, где a, b и c относятся к фокусам и вершинам.

 

Самая базовая гипербола равна x 2 y 2 = 1 или y 2 x 2 = 1. Центр находится в точке (0,0).

 

Эксцентриситет гиперболы — это эксцентриситет = c/a, а эксцентриситет на больше, чем 1 для гиперболы. Чем больше эксцентриситет, тем шире гипербола.

 

Еще раз заполнив квадрат, можно написать уравнения гиперболы в стандартную форму, чтобы легко определить ее график и связанные с ним точки и асимптоты.

Пример:

Обратите внимание. боком. Термин x 2 равен положительный.

 

Существует прямоугольник с центр гиперболы как ее центр. Длина стороны прямоугольника в направлении x равна 2(5) = 10. Длина стороны по у направление равно 2(12) = 24.

 

Диагональные линии, проходящие через центр гиперболы и углы прямоугольника являются асимптотами кривая гиперболы. Эти строки y = 12x/5 и y = -12x/5.

 

в 2 = а 2 + б 2 = 25 + 144 = 169 с = 13. Вы перемещаетесь на 13 клеток вправо и влево от центра, чтобы найти фокусы. Фокусы (-13, 0) и (13, 0).

 

В общем виде эта гипербола имеет уравнение вида 144x 2 25y 2 3600 = 0. Обратите внимание, что коэффициенты x 2 и y 2 имеют противоположные знаки, в отличие от эллипсы и круги.

Другой Пример:

 

 

Обратите внимание, что эта гипербола открывается вверх. и вниз. Термин x 2 равен отрицательный.

 

Имеется прямоугольник с центр гиперболы как ее центр. Длина стороны прямоугольника в направлении x равна 2(3) = 6. Длина стороны в направлении Y равно 2(3).

 

Диагональные линии, проходящие через центр гиперболы и углы прямоугольника являются асимптотами гиперболы изгиб. Эти строки

y = (3x)/3 и y = — (3x)/3.

 

В общем виде эта гипербола имеет уравнение вида 9y 2 x 2 9 = 0. Обратите внимание, что коэффициенты равны x 2 . и y 2 имеют противоположные знаки, в отличие от эллипсов и окружностей.

 

Другой Пример:

 

или в общем виде x 2 16y 2 6x 32y 21 = 0

 

центр равен (3, -1) a 2 = 16 a = 4 , б 2 = 1, б = 1

 

в 2 = а 2 + б 2 = 17 c = 17

 

 

Теперь вы практикуете:

 

1.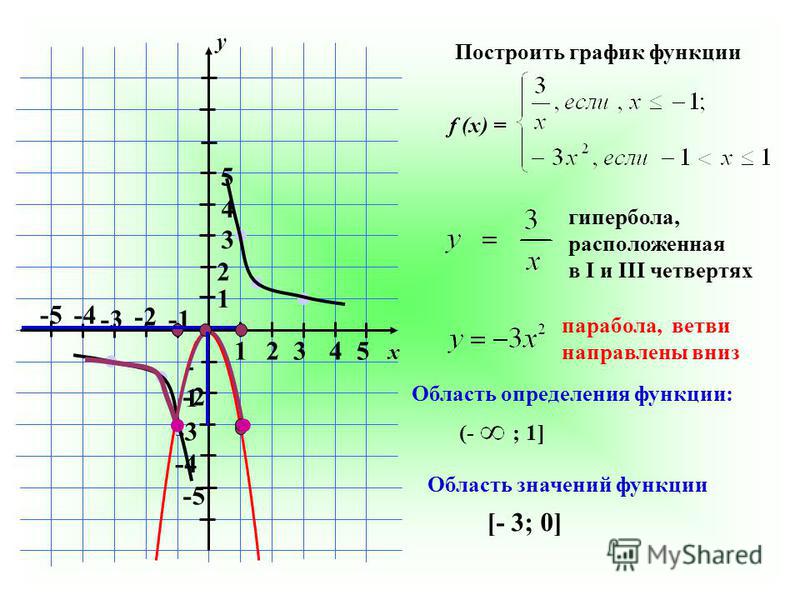 По заданному найти следующее элементы этой гиперболы и нарисуйте график, обозначив все важные элементы.

 

Найти: a. Центр б. главные вершины c. Углы внутренний прямоугольник e. асимптоты ф. Фокусы

 

2. По заданным найти следующее элементы этой гиперболы и нарисуйте график, обозначив все важные элементы.

 

Найти: a. Центр б. главные вершины c. Углы внутренний прямоугольник e. асимптоты ф. Фокусы

3. Дано х 2 у 2 = 1 найти следующие элементы этой гиперболы и построить график, маркировка всех важных элементов.

 

Найти: a. Центр б. главные вершины c. Углы внутренний прямоугольник e. асимптоты ф. Очаги

 

 

4. Заполните квадрат, чтобы переписать эту гиперболу в стандартную форма

 

. Затем найдите центр, главные вершины, углы внутренний прямоугольник, асимптоты и фокус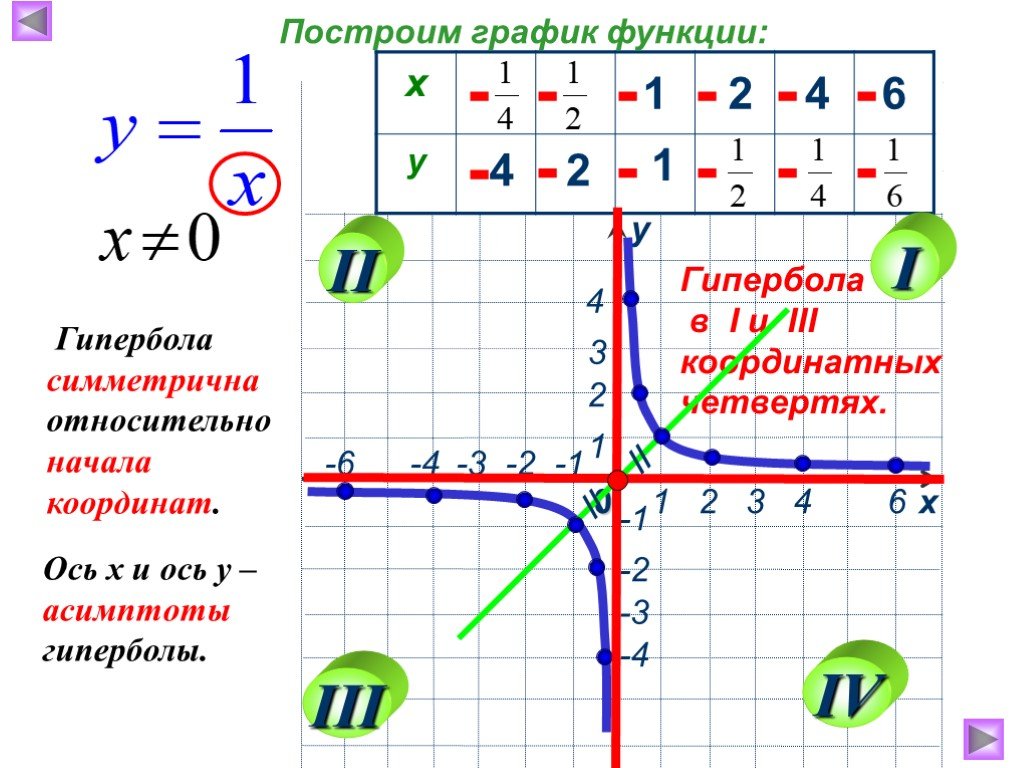ы. Нарисуйте график, обозначающий важные элементы.

 

5 лет 2 — 2x 2 + 50y + 4x + 73 = 0

 

5. Заполните квадрат, чтобы переписать эту гиперболу в стандартную форма

 

. Затем найдите центр, главные вершины, углы внутренний прямоугольник, асимптоты и фокусы. Нарисуйте график, обозначающий важные элементы.

 

72x 2 у 2 +16y 100 = 0

 

6. Решите относительно y, чтобы получить верхняя и нижняя функции, представляющие эту параболу. Нарисуйте их на своем калькулятор для проверки вашего графика на 1.

 

7. Что такое домен и диапазон верхнюю функцию в 6.

 

8. Решить относительно y, чтобы получить верхняя и нижняя функции, представляющие эту параболу. Нарисуйте их на своем калькулятор для проверки вашего графика на 2.

 

9. Укажите домен и диапазон нижняя функция в 8.

 

10. Решите x 2

y 2 = 1 для y, чтобы получить верхнюю и нижние функции, представляющие эту параболу. Нарисуйте их на своем калькуляторе, чтобы проверьте свой график для 2.

 

11. Укажите домен и диапазон нижняя функция в 10.

 

12. Для каждого приведенного ниже уравнения укажите представляет ли он круг, эллипс, параболу или гиперболу.

 

а. 9x 2 15 лет 2 +7x 3y + 20 = 0

 

б. х 2 + 4 года 2 12x + 9y + 14 = 0

 

c. у 2 -4,5у + 3х 2,5 = 0

 

д. х 2 + у 2 19x + 25y + 4 = 0

 

e. 2x 2 + 2 года 2 5x 9y + 3 = 0

 

f. х 2 у 2 8x 2y + 8 = 0

 

13. Заполните страницы с 1 по 6 551

 

14. Заполните #7, стр. 551

 

15.

Заполните #10, стр. 551

 

16. Заполните #35 и #36, стр. 552 900

05

17. Заполните № 40 Стр. 552

18. Заполните #52 Page 552

Включите домашнее задание:

2., 3., 5., 8. ., 12., 15., and 17.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Уравнение гиперболы — гиганты

в математике, гипербола, конечно, не является важной склонной секцией, которая формируется, когда поверхность плоскости пересекает двойную кону, но не а не в центр. В результате пересечения двойного конуса и плоской поверхности образуются две неограниченные кривые, являющиеся зеркальным отражением друг друга. Гипербола симметрична относительно сопряженной оси и во многом напоминает эллипс. Гипербола — это геометрическое место точек, разность расстояний которых от двух фокусов является фиксированной величиной.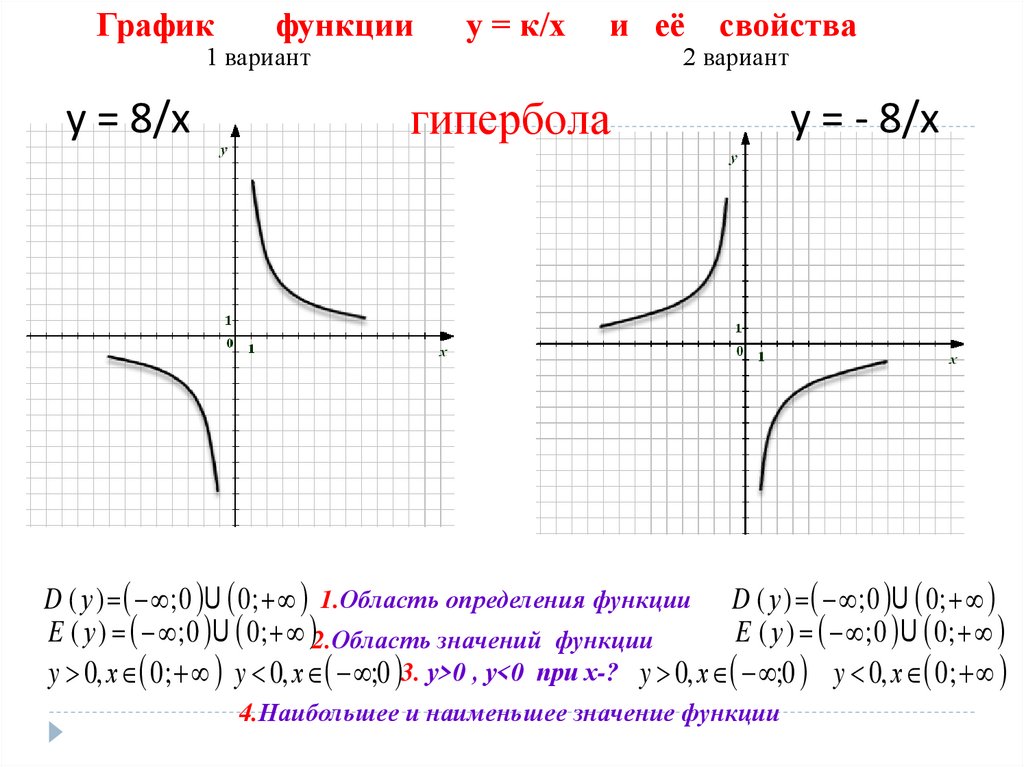 Эта разница получается путем вычитания расстояния до ближнего фокуса из расстояния до дальнего фокуса. Если P (x, y) — точка на гиперболе и F, F’ — два фокуса, то геометрическое место гиперболы равно PF-PF’ = 2a.

Уравнение гиперболы

Стандартные уравнения гиперболы:

(или)

Гипербола имеет два стандартных уравнения. Эти уравнения гиперболы основаны на ее поперечной оси и сопряженной оси.

  • Стандартное уравнение гиперболы: [(x 2 /a 2 ) – (y 2 /b 2 )] = 1, где ось X является поперечной осью, а ось Y -ось — сопряженная ось.
  • Кроме того, другое стандартное уравнение гиперболы [(y 2 /a 2 )- (x 2 /b 2 )] = 1, где ось Y является поперечной осью, а Ось X является сопряженной осью.
.0547

Координаты центра: (0, 0)

Координаты вершины: (а, 0) и (-а, 0)

Координаты очагов: (с, 0) и (-с, 0)

Длина поперечной оси = 2a

Длина сопряженной оси = 2b

Длина широкой прямой кишки = 2b 2 /a

Уравнения асимптот: 

y = (b/a) x и y = -(b/a) x

Эксцентриситет (e) = √[1 + (b 2 /a 2 )]

 

Координаты центра: (0, 0)

Координаты вершины: (0, а) и (0, -а)

Координаты ) и (0, -c)

Длина поперечной оси = 2b

Длина сопряженной оси = 2a

Длина широкой прямой кишки = 2b 2 /a

Уравнения асимптот:

y = (a/b) x и y = -(a/b) x

Эксцентриситет (e) = √[1 + (b 2 /a 2 )]

  • Стандартное уравнение гиперболы с центром (h, k) и осью X в качестве поперечной оси и осью Y в качестве сопряженной оси:

  • Кроме того, другое стандартное уравнение гиперболы с центром (h, k) и осью Y в качестве поперечной оси и осью X в качестве сопряженной оси:

    Уравнение гиперболы

    Hyperbola

    Formulae of parameters of a hyperbola

     

    Coordinates of the center: (h, k)

    Coordinates of the vertex: 

    (h + a, k) и (h – a, k)

    Координаты очагов: (h + c, k) и (h – c, k)

    Длина поперечной оси = 2a

    Длина сопряженной оси = 2b

    Длина широкой прямой кишки = 2b 2 /a

    Уравнения асимптот:

    y = (b/a) (x – h) + k и

    y = -(b/a) (x – h) + k

     

    Координаты центра: (h, k)

    Координаты вершины:

    (h, k + a) и (h, k – a) h, k + c) и (h, k – c)

    Длина поперечной оси = 2a

    Длина сопряженной оси = 2b

    Длина широкой прямой кишки = 2b 2 /a

    Уравнения асимптот:

    y = (a/b) (x – h) + k и

    y = -(a/b) (x – h) + k

    Вывод уравнения гиперболы

    Рассмотрим точку P на гиперболе с координатами (x, y). Из определения гиперболы мы знаем, что разница между расстоянием точки Р от двух фокусов F и F’ равна 2а, т. е. PF’-PF = 2а.

    Пусть координаты фокусов равны F(c, o) и F'(-c, 0).

     

    Теперь, используя формулу координатного расстояния, мы можем найти расстояние от точки P (x, y) до фокусов F (c, 0) и F’ (-c, 0).

    ⇒ √[(x + c) 2 + (y – 0) 2 ] – √[(x – c) 2 + (y – 0) 2 ] = 2a

    −

    √ [(x + c) 2 + y 2 ] = 2a + √[(x – c) 2 + y 2 ] 

    Теперь, возведя в квадрат обе стороны, мы получим

    ⇒ (х + с) 2 + у 2 = 4а 2 + (х – с) 2 + у 2 + 4а√[(7 – с) 0 4 2 2 ]

    ⇒ 4CX — 4A 2 = 4A√ [(x — c) 2 + y 2 ]

    ⇒ Cx — A 2 = A√ [(x — c) 2 + y 2 ] 

    Теперь, возводя в квадрат с обеих сторон и упрощая, получаем

    ⇒ [(x 2 /a 2 ) – (y 2 4c 2 2 ))] = 1

    Имеем c 2 = a 2 + b 2 , поэтому, подставив это в приведенное выше уравнение, мы получим

    ⇒ x 2 8 – y 2 /b 2 = 1

    Отсюда выводится стандартное уравнение гиперболы.

    Аналогично можно вывести стандартные уравнения другой гиперболы, т.е.0493

    В аналитической геометрии гипербола — это коническое сечение, которое получается, когда плоскость пересекает двойной прямой круговой конус под таким углом, что обе половины конуса соединяются. Гипербола может быть описана с использованием таких понятий, как фокусы, директриса, широкая прямая кишка и эксцентриситет.

    Давайте проверим несколько важных терминов, относящихся к различным параметрам гиперболы.

    • Фокусы: Гипербола имеет два фокуса с координатами F(c, o) и F'(-c, 0).
    • Центр гиперболы: Центр гиперболы — это середина линии, соединяющей два фокуса.
    • Большая ось : Длина большой оси гиперболы составляет 2а единиц.
    • Малая ось: Длина малой оси гиперболы составляет 2b единиц.
    • Вершины: Точки пересечения гиперболы с осью называются вершинами. (а, 0) и (-а, 0) — вершины гиперболы.
    • Широкая прямая кишка гиперболы : Широкая прямая кишка гиперболы — это линия, проходящая через любой из фокусов гиперболы и перпендикулярная поперечной оси гиперболы. Концы широкой прямой кишки лежат на гиперболе, а ее длина равна 2b 2 /a.

     

    • Поперечная ось: Поперечная ось гиперболы — это линия, проходящая через два фокуса и центр гиперболы.
    • Сопряженная ось: Сопряженная ось гиперболы — это прямая, проходящая через центр гиперболы и перпендикулярная поперечной оси.
    • Асимптоты: Гипербола имеет пару асимптот, где асимптота — это прямая линия, приближающаяся к гиперболе на графике, но никогда не касающаяся ее.

    Уравнения асимптот пары асимптот гиперболы: y = (b/a) x и y = -(b/a) x

    • Директриса: Директриса гиперболы – это фиксированная прямая линия, перпендикулярная оси гиперболы.
    • Эксцентриситет гиперболы:  Эксцентриситет гиперболы — это отношение расстояния точки от фокуса до ее перпендикулярного расстояния от директрисы. Эксцентриситет гиперболы больше 1, т. е. e > 1.

    Эксцентриситет гиперболы (e) = √[1 + (b 2 /a 2 )]

    Гипербола представляет собой незамкнутую кривую, каждая из которых имеет две ветви, которые выглядят как зеркальные отражения каждой другой . Для любой точки на любой из ветвей абсолютная разница между точкой и фокусами постоянна и равна 2а, где а — расстояние ветви от центра. Формула гиперболы помогает нам найти различные параметры и связанные части гиперболы, такие как уравнение гиперболы, большая и малая оси, эксцентриситет, асимптоты, вершина, фокусы и полуширокая прямая кишка

    Sample Problems

    Problem 1: Determine the eccentricity of the hyperbola x 2 /64 – y 2 /36 = 1.

    Solution:

    Given,

    The equation of the гипербола равна x 2 /64 – y 2 /36 = 0

    Сравнивая данное уравнение со стандартным уравнением гиперболы x 2 /a 2 – y 2 /b 24 8 = 1, получаем

    a 2 = 64, b 2 = 36

    ⇒ a = 8, b = 6

    Имеем,

    Эксцентриситет гиперболы (e) = √(1 + b 2 /a 5) 0

    0 2 0

    ⇒ e = √(1 + 6 2 /8 2 )

    ⇒ e = √(1 + 36/64)

    ⇒ e = √(64 + 36)/64) = √(100/100/100 64)

    ⇒ e = 10/8 = 1,25

    Следовательно, эксцентриситет данной гиперболы равен 1,25.

    Задача 2: Если уравнение гиперболы имеет вид [(x-4) 2 /25]-[(y-3) 2 /9] = 1, найдите длины большой оси, малой оси и широкой прямой кишки.

    Решение:

    Дано,

    Уравнение гиперболы: [(x-4) 2 /25]-[(y-3) 2 /9] сравнивая данное уравнение со стандартным уравнением гиперболы, (x – h) 2 /a 2 – (y – k) 2 /b 2 = 1

    Здесь x = 4 большая ось, а y = 3 — малая ось.

    a 2 = 25 ⇒ a = 5

    b 2 = 9 ⇒ b = 3

    Длина большой оси = 2a = 2 × (5) = 10 единиц

    Длина малой ось = 2b = 2 × (3) = 6 ед.

    Длина широкой прямой кишки = 2b 2 /a = 2(3) 2 /5 = 18/5 = 3,6 ед.

    Задача 3 : Найдите вершину, асимптоту, большую ось, малую ось и директрису, если уравнение гиперболы имеет вид [(x-6) 2 /7 2 ]-[(y-2) 2 /4 2 ] = 1.

    Решение:

    Дано,

    Уравнение гиперболы [(x-6) 2 89048] y-2) 2 /4 2 ] = 1

    Сравнивая данное уравнение со стандартным уравнением гиперболы, (x – h) 2 /a 2 – (y – k) 2 /b 2 = 1

    h = 6, k = 2, a = 7, b = 4

    Вершина гиперболы: (h + a, k) и (h – a, k) = (13, 2) и (-1, 2)

    Большая ось гиперболы: x = h ⇒ x = 6

    Малая ось гиперболы: y = k ⇒ y = 2

    Уравнения асимптот гиперболы:

    y = k − (b / a)x + (b / a)h и y = k+ (b / a)x — (b / a)h

    ⇒ y = 2 — (4/7)x + (4/7)6 и y = 2 + (4/7)x – (4/7)6

    ⇒ y = 2 – 0,57x + 3,43 и y = 2 + 0,57x – 3,43

    ⇒ y = 5,43 – 0,57x и y = -1,43 + 0,57x

    Уравнение директрисы гиперболы: x = ± a 2 /√ (A 2 + B 2 )

    ⇒ x = ± 7 2 /√ (7 2 + 4 2 ) = ± 49 /√65

    ⇒ x = x = x = x = x = x = x = x = x = x = x = x = x = x = x = x = x = ± 6,077

    Задача 4. Найдите эксцентриситет гиперболы, широкая прямая кишка которой составляет половину сопряженной оси.

    Решение:

    Дано,

    Длина широкой прямой кишки составляет половину ее сопряженной оси.

    Пусть уравнение гиперболы будет [(x 2 / a 2 ) – (y 2 / b 2 )] = 1

    Тогда сопряженная ось = 2b

    Длина широкой прямой кишки = (2b 2 / a)

    5 90 Из приведенных данных, (2b 2 / a) = (1/2) × 2b

    ⇒ 2b = a

    Имеем,

    Эксцентриситет гиперболы (e) = √[1 + (b 2 /a 2 )]

    Теперь подставим a = 2b в формулу эксцентриситета

    ⇒ e = √[1 + (b 2 /(2b) 2 ]

    ⇒ e = √[1 + (b 2 /4b 2 )] = √(5/4) 

    ⇒ e = √5/2

    Следовательно, требуемый эксцентриситет равен √5/2.

    Задача 5. Найдите вершину, фокусы и уравнения асимптот, если уравнение гиперболы имеет вид [y 2 /25]-[x 2 /9] = 1.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *