Филиппов § 11. Линейные уравнения с постоянными коэффициентами
Бесплатные решения из сборника задач по дифференциальным уравнениям А.Ф. Филиппова. Решения дифференциальных уравнений в данном разделе доступны в режиме онлайн без регистрации.
§ 11. Линейные уравнения с постоянными коэффициентами
511. Решить уравнение: y» + y’ — 2y = 0.
512. Решить уравнение: y» + 4y’ + 3y = 0.
513. Решить уравнение: y» — 2y’ = 0.
514. Решить уравнение: 2y» — 5y’ + 2y = 0.
515. Решить уравнение: y» — 4y’ + 5y = 0.
516. Решить уравнение: y» + 2y’ + 10y = 0.
517. Решить уравнение: y» + 4y = 0.
518. Решить уравнение: y»’ — 8y = 0.
519. Решить уравнение: yIV — y = 0.
520. Решить уравнение: yIV + 4y = 0.
521. Решить уравнение: yVI + 64y = 0.
522. Решить уравнение: y» — 2y’ + y = 0.
523. Решить уравнение: 4y» + 4y’ + y = 0.
524. Решить уравнение: yV — 6yIV + 9y»’ = 0.
525. Решить уравнение: yV — 10y»’ + 9y’ = 0.
526. Решить уравнение: yIV + 2y» + y = 0.
527. Решить уравнение: y»’ — 3y» + 3y’ — y = 0.
528. Решить уравнение: y»’ — y» — y’ + y = 0.
529. Решить уравнение: yIV — 5y» + 4y = 0.
530. Решить уравнение: yV + 8y»’ + 16y’ = 0.
531. Решить уравнение: y»’ — 3y’ + 2y = 0.
532. Решить уравнение: yIV + 4y» + 3y = 0.
533. Решить уравнение: y» — 2y’ — 3y = e4x.
534. Решить уравнение: y» + y = 4xex.
535. Решить уравнение: y» — y = 2ex — x2.
536. Решить уравнение: y» + y’ — 2y = 3xex.
537. Решить уравнение: y» — 3y’ + 2y = six x.
538. Решить уравнение: y» + y = 4 sin x.
539. Решить уравнение: y» — 5y’ + 4y = 4x2e2x.
540. Решить уравнение: y» — 3y’ + 2y = x cos x.
541. Решить уравнение: y» + 3y’ — 4y = e-4x + xe-x.
542. Решить уравнение: y» + 2y’ — 3y = x2ex.
543. Решить уравнение: y» — 4y’ + 8y = e2x + sin 2x.
544. Решить уравнение: y» — 9y = e3x cos x.
545. Решить уравнение: y» — 2y’ + y = 6xex.
546. Решить уравнение: y» + y = x sin x.
547. Решить уравнение: y» + 4y’ + 4y = xe2x.
548. Решить уравнение: y» — 5y’ = 3×2 + sin 5x.
549. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» — 2y’ + 2y = ex + x cos x.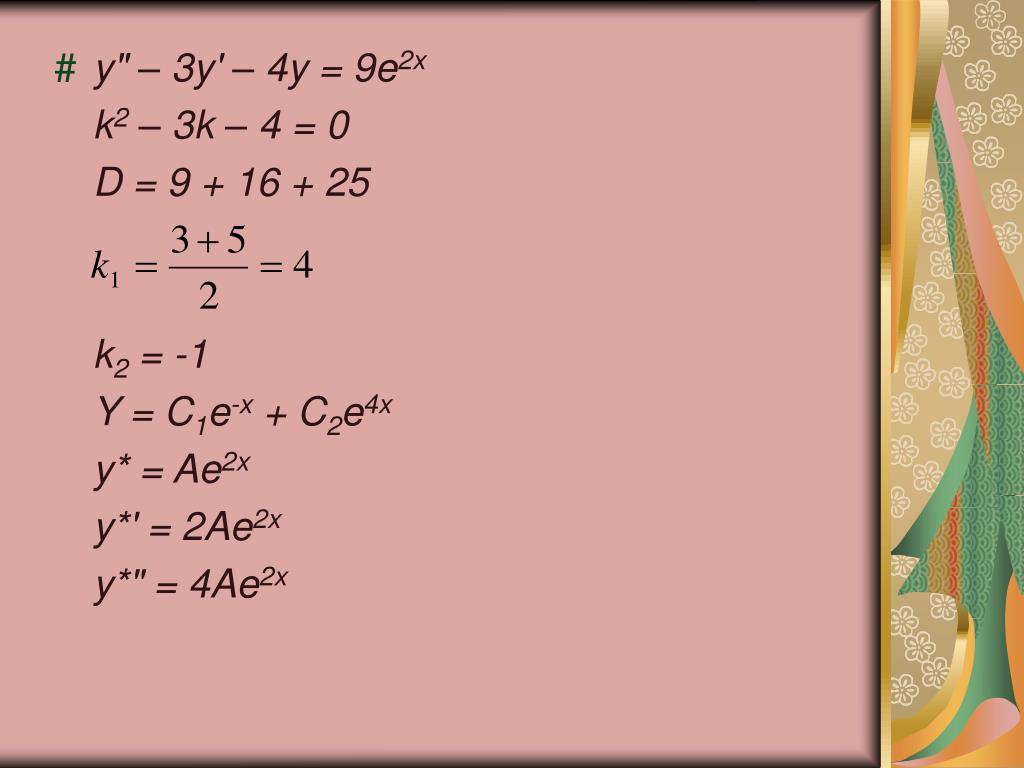
550. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» + 6y’ + 10y = 3xe-3x — 2e3x cos x.
552. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» + 7y’ + 10y = xe-2x cos 5x.
553. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» — 2y’ + 5y = 2xex + ex sin 2x.
554. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» — 2y’ + y = 2xex + ex sin 2x.
555. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» — 8y’ + 17y = e4x(x2 — 3x sin x).
556. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y»’ + y’ = sin x + x cos x.
557. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y»’ — 2y» + 4y’ — 8y = e2x sin 2x + 2×2.
558. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» — 6y’ + 8y = 5xe2x + 2e4x sin x.
559. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» + 2y’ + y = x(e-x — cos x).
560. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y»’ — y» — y’ + y = 3ex + 5x sin x.
562. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» — 9y = e-3x(x2 + sin 3x).
563. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): yIV + y» = 7x — 3 cos x.
564. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» + 4y = cos x * cos 3x.
566. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» — 4y’ + 5y = e2x sin2 x.
568. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» — 2y’ + 2y = (x + ex)sin x.
569. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): yIV + 5y» + 4y = sin x * cos 2x.
570. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» — 3y’ + 2y = 2x.
572. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» + 4y’ + 3y = ch x.
573. Написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить): y» + 4y = sh x * sin 2x.
575. Решить дифференциальное уравнение способом вариации постоянных: y» — 2y’ + y = ex/x.
576. Решить дифференциальное уравнение способом вариации постоянных: y» + 3y’ + 2y = 1/(ex + 1).
577. Решить дифференциальное уравнение способом вариации постоянных: y» + y = 1/sin x.
578. Решить дифференциальное уравнение способом вариации постоянных: y» + 4y = 2 tg x.
579. Решить дифференциальное уравнение способом вариации постоянных: y» + 2y’ + y = 3e-x sqrt(x + 1).
580. Решить дифференциальное уравнение способом вариации постоянных: y» + y = 2 sec3 x.
581. Решить дифференциальное уравнение способом вариации постоянных: x3(y» — y) = x2 — 2.
582. Найти решение уравнения, удовлетворяющее указанным начальным условиям: y» — 2y’ + y = 0; y(2) = 1, y'(2) = -2.
583. Найти решение уравнения, удовлетворяющее указанным начальным условиям: y» + y = 4ex; y(0) = 4, y'(0) = -3.
584. Найти решение уравнения, удовлетворяющее указанным начальным условиям: y» — 2y’ = 2ex; y(1) = -1, y'(1) = 0.
585. Найти решение уравнения, удовлетворяющее указанным начальным условиям: y» + 2y’ + 2y = xe-x; y(0) = y'(0) = 0.
586. Найти решение уравнения, удовлетворяющее указанным начальным условиям: y»’ — y’ = 0; y(0) = 3, y'(0) = -1, y»(0) = 1.
587. Найти решение уравнения, удовлетворяющее указанным начальным условиям: y»’ — 3y’ — 2y = 9e2x; y(0) = 0, y'(0) = -3, y»(0) = 3.
588. Найти решение уравнения, удовлетворяющее указанным начальным условиям: yIV + y» = 2 cos x; y(0) = -2, y'(0) = 1, y»(0) = y»'(0) = 0.
589. Решить уравнение Эйлера: x2y» — 4xy’ + 6y = 0.
590. Решить уравнение Эйлера: x2y» — xy’ — 3y = 0.
591. Решить уравнение Эйлера: x3y»’ + xy’ — y = 0.
592. Решить уравнение Эйлера: x2y»’ = 2y’.
593. Решить уравнение Эйлера: x2y» — xy’ + y = 8×3.
594. Решить уравнение Эйлера: x2y» + xy’ + 4y = 10x.
595. Решить уравнение Эйлера: x3y» — 2xy = 6 ln x.
597. Решить уравнение Эйлера: x2y» — 6y = 5×3 + 8×2.
598. Решить уравнение Эйлера: x2y» — 2y = sin ln x.
599. Решить уравнение Эйлера: (x — 2)2y» — 3(x — 2)y’ + 4y = x.
600. Решить уравнение Эйлера: (2x + 3)3y»’ + 3(2x + 3)y’ — 6y = 0.
601. Применяя различные методы, решить уравнения 601–611: y» + 2y’ + y = cos ix.
602. Применяя различные методы, решить уравнения 601–611: y» — 2y’ + y = xex sin2 ix.
603. Применяя различные методы, решить уравнения 601–611: y» + 2iy = 8ex sin x.
604. Применяя различные методы, решить уравнения 601–611: y» + 2iy’ — y = 8 cos x.
610.
Применяя различные методы, решить уравнения 601–611: x2y» — xy’ + y = ln x/x + x/ln x.
612. Какие условия достаточно наложить на функцию f(x), чтобы все решения уравнения задачи 611 (y» + y = f(x)) оставались ограниченными при x → +∞?
613. Построить линейное однородное дифференциальное уравнение с постоянными коэффициентами (возможно более низкого порядка), имеющее данное частное решение: y1 = x2ex…
615. Построить линейное однородное дифференциальное уравнение с постоянными коэффициентами (возможно более низкого порядка), имеющее данное частное решение: y1 = x sin x.
616. Построить линейное однородное дифференциальное уравнение с постоянными коэффициентами (возможно более низкого порядка), имеющее данное частное решение: y1 = xex…
617. Построить линейное однородное дифференциальное уравнение с постоянными коэффициентами (возможно более низкого порядка), имеющее данные частные решения: y1 = xex,.
..
618. Построить линейное однородное дифференциальное уравнение с постоянными коэффициентами (возможно более низкого порядка), имеющее данные частные решения: y1 = x, y2…
619. При каких a и b все решения уравнения y» + ay’ + by = 0 ограничены на всей числовой оси -∞ < x < +∞?
620. При каких a и b все решения уравнения y» + ay’ + by = 0 стремятся к нулю при x → +∞?
623. При каких a и b каждое решение уравнения y» + ay’ + by = 0 обращается в нуль на бесконечном множестве точек x?
624. При каких a и b все решения уравнения y» + ay’ + by = 0 удовлетворяют соотношению y = o(e-x) при x → +∞?
625. Для заданного b > 0 подобрать такое a, при котором решение уравнения y» + ay’ + by = 0 с начальными условиями y(0) = 1, y'(0) = 0 возможно быстрее стремится к нулю при x →…
628. Найти периодическое решение уравнения x» + x’ + 4x = eiωt и на комплексной плоскости начертить кривую, которую пробегает амплитудный множитель этого решения при изменении.
..
629. Дано уравнение y» + ay’ + by = f(x), причем |f(x)| ≤ m (-∞ < x < ∞), а корни характеристического уравнения λ2 < λ1 <…
634. Частица массы m движется по оси Ox, отталкиваясь от точки x = 0 с силой 3mr0 и притягиваясь к точке x = 1 с силой 4mr1, где r0 и r1 –…
635. Электрическая цепь состоит из последовательно включенных источника постоянного тока, дающего напряжение V, сопротивления R, самоиндукции L и выключателя, который включается при t =…
639. Последовательно включены источник тока, напряжение которого меняется по закону E = V sin ωt, сопротивление R и самоиндукция L. Найти силу тока в цепи (установившийся режим).
обыкновенных дифференциальных уравнений — как решить $y»+2y’-3y=0$?
Итак, мы видим, что у нас есть Линейное дифференциальное уравнение второго порядка . Существует несколько разновидностей
методов для решения этого типа уравнений, некоторые из которых перечислены, но я думаю, что этот метод является наиболее прямым и не требует особых хитростей или сообразительности, это довольно
шаг пошаговый процесс.
ПОДСКАЗКА: $~~$ Мы знаем, что для этого типа уравнений должно выполняться следующее: 9{2}+2r-3$$
ПРИМЕЧАНИЕ: Всю работу, которую мы проделали для получения нашего характеристического многочлена , можно сохранить в будущем всякий раз, когда у нас есть ОДУ с постоянным коэффициентом, потому что начальное предположение всегда будет делиться в конце. Вот в чем хитрость.
1.) Соблюдайте порядок ОДУ (а именно, старшую производную в уравнении).
2.) Начните с наибольшей производной и двигайтесь вниз к наименьшему члену (а именно, к постоянным терминам). 92-4ac}}{2a}.$$
3) Если оба вышеперечисленных варианта невозможны (обычно для кубических или более высоких степеней), то используется деление в длинное/синтетическое деление и обычно помогает сначала построить уравнение в виде графика и найти хотя бы одно ноль и используйте этот коэффициент, возьмите исходный полином и попробуйте деление в длину/синтетическое деление.
Так, например, если вы нашли $2$ в качестве нуля полинома, то вы должны использовать $(r-2)$, чтобы попытаться уменьшить полином до квадратного, если это возможно, или до чего-то, что можно разложить на множители. 9{nd}$ Порядок линейных уравнений с постоянными коэффициентами однородных обыкновенных дифференциальных уравнений, и то же самое относится к более высокому порядку.
Есть и другие случаи помимо этого одного из реальных различных корней . Теперь мы рассмотрим, что представляют собой эти другие случаи.
Другая ситуация, с которой вы можете столкнуться, — это когда у вас есть действительных неразличимых корней (т. е. кратность двух и более). Теперь для слова множественность все, что это означает, просто следующее: если вы получаете некоторые числа, которые появляются более одного раза (это означает, что они точно такие же). 9{2}+6r+9=0$,
наши корни к этому многочлену будут следующими: $r=-3,~r=-3$. Это яркий пример того, что означает множественность.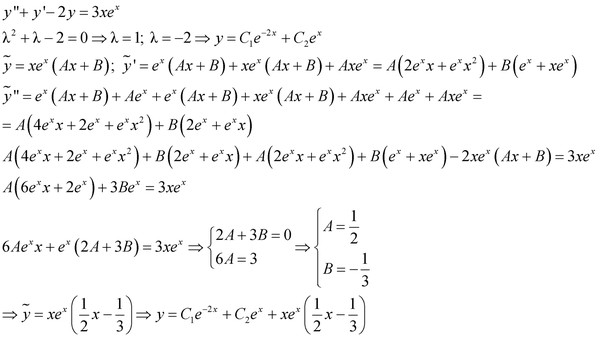
Наши корни будут $r=-3$ (с кратностью 2), потому что один и тот же корень встречается дважды, это означает необходимость умножения линейной комбинации решения на соответствующее количество степеней $’x’$ или $’t ‘$ в зависимости от вашей независимой переменной в ODE. Давайте рассмотрим еще несколько примеров.
$\underline{Пример~2:}$ Если бы у нас был этот характеристический полином 9{3}=0$, наши корни для этого конкретного полинома будут следующими: $r=0,~r=0,~r=0,~r=-\dfrac{3}{5}$
Это еще один отличный пример того, когда мы делаем вывод, что у нас снова есть повторяющиеся корни, равные $r=0$ (теперь с кратностью 3). Опять же, вам придется умножить независимые однородные решения на соответствующую степень вашей независимой переменной, которую в нашем случае мы используем $’x’$. Давайте рассмотрим еще один пример упражнений, чтобы лучше понять эту идею. Кроме того, во что бы то ни стало, пожалуйста, найдите время, если можете, и проверьте эти 9{2}+4r=0$, наши корни для этого конкретного полинома будут следующими: $r=0,~r=-\dfrac{2}{3},~r=-\dfrac{2}{3} $.