Найдите значения выражения 3 косинус в квадрате минус 1,6 Если синус в квадрате равен 0,2 — Знания.site
Ответы 1
ОТТ:
Ответ 0,8
Знаешь ответ? Добавь его сюда!
Последние вопросы
Физика
2 часа назад
Помоги, пожалуйста, прорешать оба варианта. Нужно к среде (3 мая) ЗАДАНИЯ ВНИЗУ!!!!
Математика
3 часа назад
4,8у+3,7у=11,9 Ачимы помогити🥰🥰🥰🥰 Решить уравнение
Математика
3 часа назад
5.8*(4.5-x) решите уравнение пожайлуста!
Математика
5 часов назад
Вычислите удобный способом
15/29*(19/25*7/9)*5/7
История
6 часов назад
Помогите пожалуйста
История
6 часов назад
Рассмотрите репродукцию картины художника В.
 В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура
В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура1.Используя сюжет картины и пункт 1 &26, составьте перечень качеств, которыми обладал Тимур.
2.Как объясняют спасение русской земли от тимура современные учёные?
3.Как объясняли это современники событий?
История
6 часов назад
рассказ от имени путешественника или первопроходца (цель, участники, маршрут). по теме Русские путешественники и первопроходцы XVII
Другие предметы
7 часов назад
можно ли на др маме подарить отчима?
Математика
8 часов назад
помогите якласс
Математика
8 часов назад
помогите якласс
Математика
9 часов назад
В магазине продавалось w книг русских писателей и на d книг больше зарубежных писателей.
 Сколько всего книг было в магазине?
Сколько всего книг было в магазине?Мальвина и Пьеро вместе собирали голубику и собрали v штук. А Артемон собрал в k раз больше. Сколько всего голубики собрали Мальвина, Пьеро и Артемон?
В x группах занимается по w девочек, а в одной группе — p мальчиков.
Во сколько раз больше занимается мальчиков, чем девочек?
В у группах занимается по х мальчиков, а в одной группе — r девочек.
Во сколько раз меньше занимается мальчиков, чем девочек
Русский язык
14 часов назад
Произведите синтаксический разбор предложений, и составте схемы.
1) Гвардия уже вышла из Петербурга 10-го августа, и сын, оставшийся для обмундирования вМоскве, должен был догнать ее по дороге в Радзивилов.
2) У Ростовых были именинницы Натальи, мать и меньшая дочь.
3) Графиня с красивой старшею дочерью и гостями, не перестававшими сменять один другого, сидели в гостиной.

4) Граф встречал и провожал гостей, приглашая всех к обеду.
5) Проводив одного гостя, граф возвращался к тому или той, которые еще были в гостиной.
Математика
1 день назад
ужас мне так лень сюда заходить
Химия
1 день назад
Визначте масу калій гідроксиду ,що реагує з 5,6 л сульфур(IV) оксиду (н.у.).
Алгебра
1 день назад
Найди первые пять членов геометрической прогрессии bn
= 256•(1/2).n
How much to ban the user?
1 hour 1 day 100 years
Функция синус-квадрата — исчисление
Эта статья о конкретной функции из подмножества действительных чисел в действительные числа.В статье представлена информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференцированию и интегрированию.
Посмотреть полный список конкретных функций на этой вики
Содержание
- 1 Определение
- 2 Ключевые данные
- 3 личности
- 4 График
- 5 Дифференциация
- 5.1 Первая производная
- 5.2 Вторая производная
- 5.3 График функции с производной
- 6 Точки и интервалы интереса
- 6.1 Критические точки
- 6.2 Интервалы увеличения и уменьшения
- 6.3 Локальные экстремальные значения
- 6.4 Интервалы подбарабанья вверх и вниз
- 6.5 Точки перегиба
- 7 Интеграция
- 7.1 Первая первообразная
- 7.1.1 Использование формулы косинуса двойного угла
- 7.1.2 Использование интегрирования по частям
- 7.
 2 График функции с первообразной
2 График функции с первообразной - 7.3 Определенные интегралы
- 7.4 Модифицированные версии
- 7.5 Высшие производные
- 7.1 Первая первообразная
- 8 Серия Power и серия Taylor
- 8.1 Расчет ряда мощностей
- 8.2 Полиномы Тейлора как аппроксимации
- 9 Предельные вычисления
- 9.1 Нулевой порядок
- 9.2 Пределы высшего порядка
Определение
Эта функция, обозначенная , определяется как композиция функции квадрата и функции синуса. В явном виде это карта:
Для краткости пишем как .
Ключевые данные
| Элемент | Значение |
|---|---|
| Домен по умолчанию | все действительные числа, т. е. все |
| диапазон | , то есть абсолютное максимальное значение: 1, абсолютное минимальное значение: 0 |
| период | , т. е. |
| локальное максимальное значение и точки достижения | Все локальные максимальные значения равны 1 и достигаются при нечетных целых кратных . |
| локальное минимальное значение и точки достижения | Все локальные минимальные значения равны 0 и достигаются при целых кратных . |
| точки перегиба (обе координаты) | нечетных кратных , со значением 1/2 в каждой точке. |
| производная | , то есть функция синуса двойного угла. |
| вторая производная | |
| производная | раз выражение, которое равно или , в зависимости от остатка по модулю |
| первообразная | |
| среднее значение за период | 1/2 |
| выражение как синусоидальная функция плюс постоянная функция | |
| важные симметрии | четная функция (следует из комбинации четной функции с нечетной функцией четной, функция квадрата четная, а функция синуса нечетная) в более общем смысле, зеркальная симметрия относительно любой вертикальной линии формы , целое число. 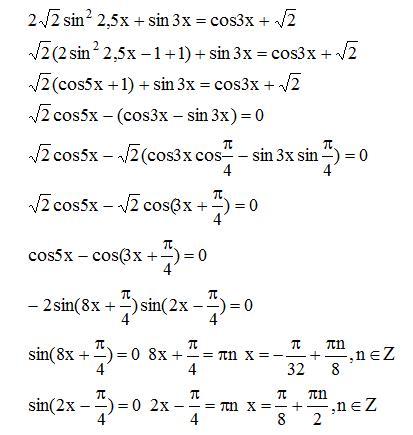 Также полуоборотная симметрия относительно всех точек формы . |
| Описание интервала на основе увеличения/уменьшения и вогнутости вверх/вниз | Для каждого целого числа интервал от до подразделяется на четыре части: : возрастание и вогнутость вниз : уменьшение и вогнутость вниз, : уменьшение и вогнутость вверх |
| серия Power и серия Taylor | Степенной ряд около 0 (который, следовательно, также является рядом Тейлора) равен Это глобально сходящийся степенной ряд. |
Личности
У нас есть следующие важные личности с участием:
- , связывая это с функцией квадрата косинуса.
- или эквивалентно .
График
Вот график на интервале , выполненный в масштабе:
Вот увеличенный вид графика между и . Пунктирная горизонтальная линия указывает среднее значение:
Точки с красными точками обозначают точки перегиба, а точки с черными точками обозначают локальные экстремальные значения.
Вот изображение, показывающее функцию (синяя) и функция квадрата косинуса (фиолетовая) с пунктирной линией. На картинке показано, что:
Дифференцирование
Первая производная
ЧТО МЫ ИСПОЛЬЗУЕМ : цепное правило для дифференцирования, правило дифференцирования для степенных функций, функция синуса # Первая производная, формула двойного косинуса угла
У нас есть:
Мы можем сделать это двумя способами.
Используя цепное правило для дифференцирования, мы имеем:
По формуле двойного синуса угла это то же самое, что и .
В качестве альтернативы, используя формулу двойного косинуса угла, мы перепишем:
Дифференцируя, получаем:
Вторая производная
Снова продифференцировав производную, получим:
График функции с производной
Заполните позже
Точки и интервалы интереса
Критические точки
Рассмотрим .
Это равно нулю именно в точках, где , поэтому . Другими словами, критические точки возникают при целых кратных .
Интервалы возрастания и убывания
Функция положительна при , при и отрицательна при , при . Делим на 2, получаем:
- возрастает на интервалах вида , .
- убывает на интервалах вида , .
Локальные экстремальные значения
Из информации об интервалах возрастания и убывания делаем вывод, что:
- достигает своих локальных максимальных значений в точках вида , и все значения равны 1.
- достигает своих локальных минимальных значений в точках вида , , и все значения равны 0.
Интервалы вогнутости вверх и вниз
Вторая производная есть функция . Это положительно для и отрицательно для , где . Таким образом, мы получаем:
- вогнут на промежутках вида , с .
- вогнуто вниз на интервалах вида , с .
Точки перегиба
Из определения интервалов, где вогнутость вверх и вогнутость вниз, мы обнаруживаем, что точками перегиба являются точки с -координатой, нечетно кратной . Значение функции во всех этих точках равно .
Значение функции во всех этих точках равно .
- В точках с функция переходит от вогнутости вверх (слева) к вогнутости вниз (справа).
- В точках с функция переходит от вогнутой вниз (слева) к вогнутой вверх (справа).
Интегрирование
Первая первообразная
ЧТО ИСПОЛЬЗУЕМ : формула косинуса двойного угла, рекурсивная версия интегрирования по частям, интегрирование линейного преобразования функции
Использование формулы косинуса двойного угла
900 05Теперь мы можем сделать интеграция:
Для интегрирования используем метод интегрирования линейного преобразования функции для получения . Подключив его, мы получим:
Использование интегрирования по частям
Переписываем и используем интегрирование по частям в его рекурсивной версии:
Теперь перепишем и получим:
Установив выбор первообразной таким образом, чтобы вышеприведенное выполнялось без каких-либо свободно плавающих констант, мы получаем:
Переставляя, получаем:
Это дает:
Итак, общая первообразная:
Используя формулу синуса двойного угла, мы можем убедиться, что это соответствует предыдущему ответу.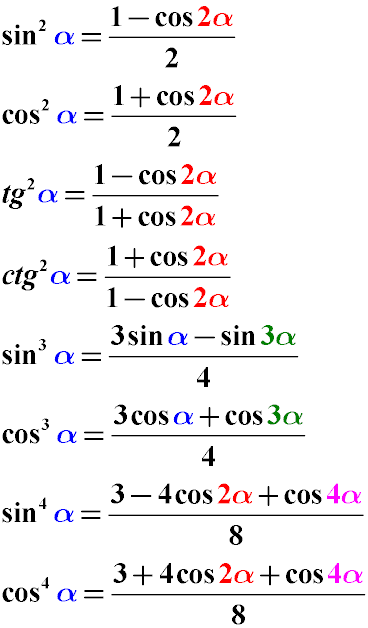
Для заданной непрерывной функции на связном множестве первообразные, полученные разными методами, должны отличаться на константу . В некоторых случаях первообразные могут быть точно равными, но это не обязательно вообще .
См. Нулевая производная подразумевает локальную постоянную
График функции с первообразной
На рисунке ниже мы изображаем (синий) и функцию (фиолетовый). Это уникальная первообразная, которая принимает значение 0 в 0. Остальные первообразные можно получить, сдвинув фиолетовый график по вертикали:
Черные точки соответствуют локальным экстремумам для , а красные точки соответствуют точкам перегиба первообразной. Как и следовало ожидать, каждая черная точка находится на той же вертикальной линии, что и красная точка, поскольку точки перегиба первообразной соответствуют локальным экстремальным значениям исходной функции. Дальше:
- Первообразная везде возрастает, потому что везде неотрицательна и равна нулю только в изолированных точках.

- Первообразная вогнута на тех интервалах, где является возрастающей, т. е. на интервалах вида as изменяется по целым числам.
- Первообразная вогнута вниз на тех интервалах, где убывающая, т. е. на интервалах вида as меняется по целым числам.
Определенные интегралы
Часть в первообразной означает, что линейная часть первообразной имеет наклон , а это связано с тем, что имеет среднее значение на любом интервале длины, равной периоду. На самом деле ясно, что функция является синусоидальной функцией относительно .
Итак, имеем:
где целое число.
Среднее значение для интервала длины, равного кратному периоду, равно . Таким образом, для очень больших интервалов среднее значение очень близко к 1/2, даже если оно не обязательно должно быть ровно 1/2. Конкретно:
Преобразованные версии
На основе интегрирования мы можем также интегрировать квадрат любой синусоидальной функции, используя интегрирование линейного преобразования функции:
Таким образом, мы видим, что среднее значение этой функции также на любом интервале длины, кратной периоду. Также на достаточно большом интервале среднее значение близко к 1/2:
Также на достаточно большом интервале среднее значение близко к 1/2:
Высшие первообразные
Можно проводить антидифференцировку более одного раза. Первообразная представляет собой сумму многочлена степени и тригонометрической функции с периодом .
Степенной ряд и ряд Тейлора
Расчет степенного ряда
Мы можем использовать идентификатор:
вместе со степенным рядом функции косинуса, чтобы найти степенной ряд для .
Степенной ряд функции косинуса везде сходится к функции и равен:
Серия мощности для:
Серия мощности для:
Разделив на 2, получим степенной ряд для:
Вот еще одна формулировка, в которой первые несколько терминов написаны более явно:
Полиномы Тейлора как аппроксимации
Обратите внимание, что, поскольку это четная функция, все ее полиномы Тейлора также являются четными полиномами. На рисунке ниже мы рассматриваем графики и его второй, четвертой и шестой тейлоровских аппроксимаций.
- Второй полином Тейлора , равный третьему полиному Тейлора , равен .
- Четвертый полином Тейлора , который равен пятому полиному Тейлора , равен .
- Шестой полином Тейлора , который равен седьмому полиному Тейлора , равен .
Предельные вычисления
Порядок нуля
Из степенного ряда получаем следующий предел:
Таким образом, порядок нуля в нуле равен 2, а остаток равен 1.
Этот лимит можно вычислить разными способами:
| Наименование метода расчета предела | Подробнее |
|---|---|
| Простая манипуляция с использованием | |
| Использование правила Лопиталя | |
| Использование серии Power | Имеем , значит получаем . Принимая предел как дает 1. |
Пределы высшего порядка
У нас есть предел:
Этот лимит можно вычислить разными способами:
| Наименование метода расчета предела | Подробнее |
|---|---|
| Использование и | У нас есть . Первый предел равен, а второй предел равен 2 из заданных данных. Получаем таким образом. |
| Использование правила Лопиталя | . |
| Использование серии Power | У нас есть , значит , значит предел равен 1/3. |
Функция синус-квадрат — Исчисление
Эта статья о конкретной функции от подмножества действительных чисел до действительных чисел. В статье представлена информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференцированию и интегрированию.
Посмотреть полный список конкретных функций на этой вики
Содержание
- 1 Определение
- 2 Ключевые данные
- 3 личности
- 4 График
- 5 Дифференциация
- 5.1 Первая производная
- 5.2 Вторая производная
- 5.3 График функции с производной
- 6 Точки и интервалы интереса
- 6.
 1 Критические точки
1 Критические точки - 6.2 Интервалы увеличения и уменьшения
- 6.3 Локальные экстремальные значения
- 6.4 Интервалы подбарабанья вверх и вниз
- 6.5 Точки перегиба
- 6.
- 7 Интеграция
- 7.1 Первая первообразная
- 7.1.1 Использование формулы косинуса двойного угла
- 7.1.2 Использование интегрирования по частям
- 7.2 График функции с первообразной
- 7.3 Определенные интегралы
- 7.4 Модифицированные версии
- 7.5 Высшие первообразные
- 7.1 Первая первообразная
- 8 Серия Power и серия Taylor
- 8.1 Расчет ряда мощностей
- 8.2 Полиномы Тейлора как аппроксимации
- 9 Предельные вычисления
- 9.1 Нулевой порядок
- 9.2 Пределы высшего порядка
Определение
Эта функция, обозначенная , определяется как композиция функции квадрата и функции синуса. В явном виде это карта:
Для краткости пишем как .
Ключевые данные
| Элемент | Значение |
|---|---|
| Домен по умолчанию | все действительные числа, т. е. все |
| диапазон | , то есть абсолютное максимальное значение: 1, абсолютное минимальное значение: 0 |
| период | , т. е. |
| локальное максимальное значение и точки достижения | Все локальные максимальные значения равны 1 и достигаются при нечетных целых кратных . |
| локальное минимальное значение и точки достижения | Все локальные минимальные значения равны 0 и достигаются при целых кратных . |
| точек перегиба (обе координаты) | нечетных кратных , со значением 1/2 в каждой точке. |
| производная | , то есть функция синуса двойного угла. |
| вторая производная | |
| производная | раз выражение, которое равно или , в зависимости от остатка по модулю |
| первообразная | |
| среднее значение за период | 1/2 |
| выражение как синусоидальная функция плюс постоянная функция | |
| важные симметрии | четная функция (следует из комбинации четной функции с нечетной функцией четной, функция квадрата четной, функция синуса нечетной) в более общем смысле, зеркальная симметрия относительно любой вертикальной линии формы , целое число.  Также полуоборотная симметрия относительно всех точек формы . |
| Описание интервала на основе увеличения/уменьшения и вогнутости вверх/вниз | Для каждого целого числа интервал от до подразделяется на четыре части: : возрастание и вогнутость вверх : возрастание и вогнутость вниз : уменьшение и вогнутость вниз, : уменьшение и вогнутость вверх |
| Степенной ряд около 0 (который, следовательно, также является рядом Тейлора) равен Это глобально сходящийся степенной ряд. |
Личности
У нас есть следующие важные личности с участием:
- , связывая это с функцией квадрата косинуса.
- или эквивалентно .
График
Вот график на интервале , выполненный в масштабе:
Вот увеличенный вид графика между и . Пунктирная горизонтальная линия указывает среднее значение:
Точки с красными точками обозначают точки перегиба, а точки с черными точками обозначают локальные экстремальные значения.
Вот изображение, показывающее функцию (синяя) и функция квадрата косинуса (фиолетовая) с пунктирной линией. На картинке показано, что:
Дифференциация
Первая производная
ЧТО МЫ ИСПОЛЬЗУЕМ : цепное правило для дифференцирования, правило дифференцирования для степенных функций, функция синуса # Первая производная, формула двойного косинуса угла
У нас есть:
Мы можем сделать это двумя способами.
Используя цепное правило для дифференцирования, мы имеем:
По формуле двойного синуса угла это то же самое, что и .
В качестве альтернативы, используя формулу двойного косинуса угла, мы перепишем:
Дифференцируя, получаем:
Вторая производная
Снова продифференцировав производную, получим:
График функции с производной
Заполните позже
Точки и интервалы интереса
Критические точки
Рассмотрим . Как было подсчитано ранее, имеем:
Как было подсчитано ранее, имеем:
Это равно нулю именно в точках, где , поэтому . Другими словами, критические точки возникают при целых кратных .
Интервалы возрастания и убывания
Функция положительна при , при и отрицательна при , при . Делим на 2, получаем:
- возрастает на интервалах вида , .
- убывает на интервалах вида , .
Локальные экстремальные значения
Из информации об интервалах возрастания и убывания делаем вывод, что:
- достигает своих локальных максимальных значений в точках вида , и все значения равны 1.
- достигает своих локальных минимальных значений в точках вида , , и все значения равны 0.
Интервалы вогнутости вверх и вниз
Вторая производная есть функция . Это положительно для и отрицательно для , где . Таким образом, мы получаем:
- вогнут на промежутках вида , с .
- вогнуто вниз на интервалах вида , с .
Точки перегиба
Из определения интервалов, где вогнутость вверх и вогнутость вниз, мы обнаруживаем, что точками перегиба являются точки с -координатой, нечетно кратной . Значение функции во всех этих точках равно .
Значение функции во всех этих точках равно .
- В точках с функция переходит от вогнутости вверх (слева) к вогнутости вниз (справа).
- В точках с функция переходит от вогнутой вниз (слева) к вогнутой вверх (справа).
Интегрирование
Первая первообразная
ЧТО ИСПОЛЬЗУЕМ : формула косинуса двойного угла, рекурсивная версия интегрирования по частям, интегрирование линейного преобразования функции
Использование формулы косинуса двойного угла
Теперь мы можем выполнить интеграцию:
Для интегрирования используем метод интегрирования линейного преобразования функции для получения . Подключив его, мы получим:
Использование интегрирования по частям
Переписываем и используем интегрирование по частям в его рекурсивном варианте:
Теперь перепишем и получим:
Установив выбор первообразной таким образом, чтобы вышеприведенное выполнялось без каких-либо свободно плавающих констант, мы получаем:
Переставляя, получаем:
Это дает:
Итак, общая первообразная:
Используя формулу синуса двойного угла, мы можем убедиться, что это соответствует предыдущему ответу.
Для заданной непрерывной функции на связном множестве первообразные, полученные разными методами, должны отличаться на константу . В некоторых случаях первообразные могут быть точно равны, но это вообще не надо .
См. Нулевая производная подразумевает локальную постоянную
График функции с первообразной
На рисунке ниже мы изображаем (синий) и функцию (фиолетовый). Это уникальная первообразная, которая принимает значение 0 в 0. Остальные первообразные можно получить, сдвинув фиолетовый график по вертикали:
Черные точки соответствуют локальным экстремумам для , а красные точки соответствуют точкам перегиба первообразной. Как и следовало ожидать, каждая черная точка находится на той же вертикальной линии, что и красная точка, поскольку точки перегиба первообразной соответствуют локальным экстремальным значениям исходной функции. Дальше:
- Первообразная везде возрастает, потому что везде неотрицательна и равна нулю только в изолированных точках.

- Первообразная вогнута на тех интервалах, где является возрастающей, т. е. на интервалах вида as изменяется по целым числам.
- Первообразная вогнута вниз на тех интервалах, где убывающая, т. е. на интервалах вида as меняется по целым числам.
Определенные интегралы
Часть в первообразной означает, что линейная часть первообразной имеет наклон , и это связано с тем, что имеет среднее значение на любом интервале длины, равной периоду. На самом деле ясно, что функция является синусоидальной функцией относительно .
Итак, имеем:
где целое число.
Среднее значение для интервала длины, равного кратному периоду, равно . Таким образом, для очень больших интервалов среднее значение очень близко к 1/2, даже если оно не обязательно должно быть ровно 1/2. Конкретно:
Преобразованные версии
На основе интегрирования мы можем также интегрировать квадрат любой синусоидальной функции, используя интегрирование линейного преобразования функции:
Таким образом, мы видим, что среднее значение этой функции также на любом интервале длины, кратной периоду . Также на достаточно большом интервале среднее значение близко к 1/2:
Также на достаточно большом интервале среднее значение близко к 1/2:
Высшие первообразные
Можно проводить антидифференцировку более одного раза. Первообразная представляет собой сумму многочлена степени и тригонометрической функции с периодом .
Степенной ряд и ряд Тейлора
Расчет степенного ряда
Мы можем использовать тождество:
вместе со степенным рядом функции косинуса, чтобы найти степенной ряд для .
Степенной ряд функции косинуса везде сходится к функции и равен:
Серия мощности для:
Серия мощности для:
Разделив на 2, получим степенной ряд для:
Вот еще одна формулировка, в которой первые несколько терминов написаны более явно:
Полиномы Тейлора как аппроксимации
Обратите внимание, что, поскольку это четная функция, все ее полиномы Тейлора также являются четными полиномами. На рисунке ниже мы рассматриваем графики и его второй, четвертой и шестой тейлоровских аппроксимаций.

 В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура
В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура Сколько всего книг было в магазине?
Сколько всего книг было в магазине?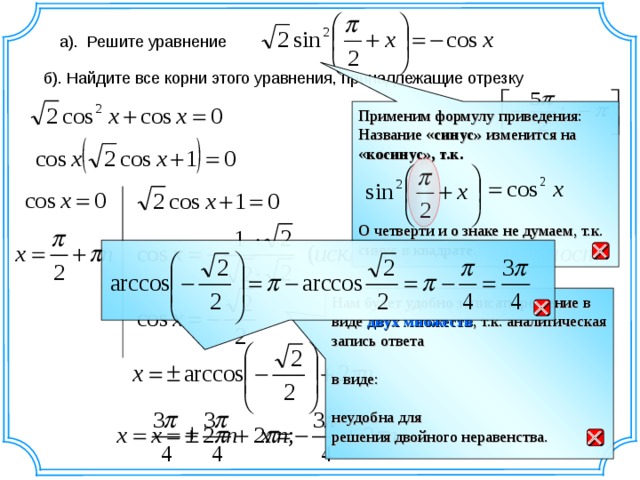
 В статье представлена информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференцированию и интегрированию.
В статье представлена информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференцированию и интегрированию.  2 График функции с первообразной
2 График функции с первообразной
 1 Критические точки
1 Критические точки