3 корень из i: Извлечение корня из комплексного числа онлайн

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )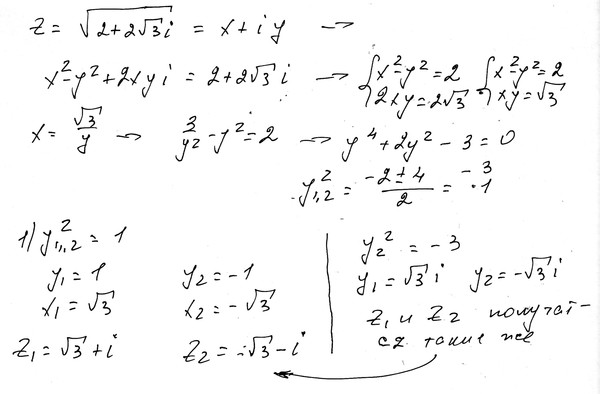
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значение
cos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )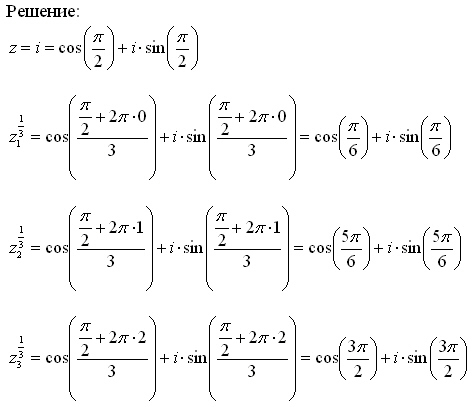
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )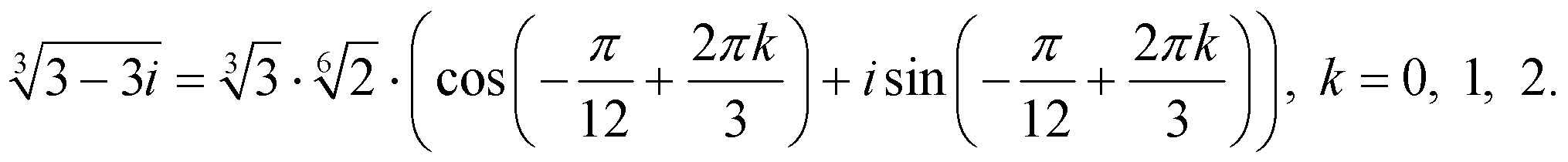
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значение sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )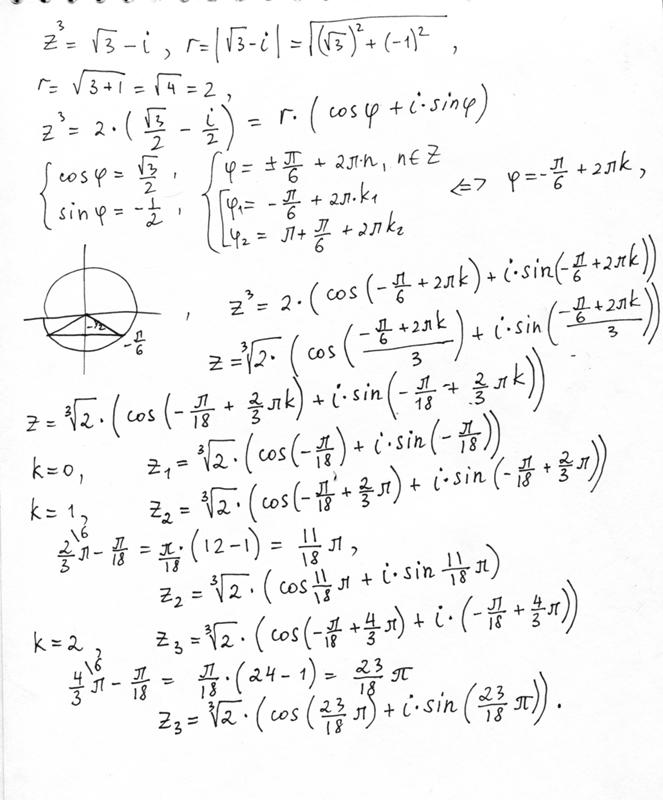
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы
88 град.

Алгебра

Алгебра
  

Ленг С. Алгебра. — М.: Мир, 1968.

Автор книги, видный американский математик, профессор Колумбийского университета С. Ленг, хорошо знаком советскому читателю по двум вышедшим ранее монографиям «Алгебраические числа» и «Введение в теорию дифференцируемых многообразий» (издательство «Мир», 1966 и 1967). В книге рассмотрены все основные разделы современной алгебры (группы, кольца, модули, теория полей, линейная и полилинейная алгебра, представления грунп). Читатель найдет здесь также первоначальные сведения по гомологической алгебре и алгебраической геометрии.

Книга отражает изменения, происшедшие в алгебре за последние два десятилетия, и дает читателю возможность основательно познакомиться с областями алгебры, ставшими уже классическими. Язык категорий и функторов связывает воедино разрозненные ранее понятия и результаты.

Книга будет весьма полезной математикам различных специальностей, студентам, аспирантам и научным работникам. Она может служить основой специальных курсов по алгебре.



Оглавление

От редактора перевода
Предисловие
Предварительные сведения
Литература
Часть первая. ГРУППЫ, КОЛЬЦА И МОДУЛИ
§ 1. Моноиды
§ 2. Группы
§ 3. Циклические группы
§ 4. Нормальные подгруппы
§ 5. Действие группы на множестве
§ 6. Силовские подгруппы
§ 7. Категории и функторы
Произведения и копроизведения
§ 8. Свободные группы
§ 9. Прямые суммы и свободные абелевы группы
§ 10. Конечно порожденные абелевы группы
§ 11. Дуальная группа
УПРАЖНЕНИЯ
Глава II. Кольца
§ 1. Кольца и гомоморфизмы
§ 2. Коммутативные кольца
§ 3. Локализация
§ 4. Кольца главных идеалов
УПРАЖНЕНИЯ
Глава III. Модули
§ 2. Группа гомоморфизмов
§ 3. Прямые произведения и суммы модулей
§ 4. Свободные модули
§ 5. Векторные пространства
§ 6. Дуальное пространство
УПРАЖНЕНИЯ
Глава IV. Гомологии
§ 1. Комплексы
§ 2. Гомологическая последовательность
§ 3. Эйлерова характеристика
§ 4. Теорема Жордана — Гёльдера
УПРАЖНЕНИЯ
Глава V. Многочлены
§ 1. Свободные алгебры
§ 2. Определение многочленов
§ 3. Элементарные свойства многочленов
§ 4. Алгоритм Евклида
§ 5. Простейшие дроби
§ 6. Однозначность разложения на простые множители многочленов от нескольких переменных
§ 7. Критерии неприводимости
§ 8. Производная и кратные корни
§ 9. Симметрические многочлены
§ 10. Результант
УПРАЖНЕНИЯ
Глава VI. Нётеровы кольца и модули
§ 1. Основные критерии.
§ 2. Теорема Гильберта
§ 3. Степенные ряды
§ 4. Ассоциированные простые идеалы
§ 5. Примарное разложение
УПРАЖНЕНИЯ
Часть вторая. ТЕОРИЯ ПОЛЕЙ
§ 1. Конечные и алгебраические расширения
§ 2. Алгебраическое замыкание
§ 3. Поля разложения и нормальные расширения
§ 4. Сепарабельные расширения
§ 5. Конечные поля
§ 6. Примитивные элементы
§ 7. Чисто несепарабельные расширения
УПРАЖНЕНИЯ
Глава VIII. n – a = 0
§ 10. Когомологии Галуа
§ 11. Алгебраическая независимость гомоморфизмов
§ 12. Теорема о нормальном базисе
УПРАЖНЕНИЯ
Глава IX. Расширения колец
§ 1. Целые расширения колец
2. Целые расширения Галуа
§ 3. Продолжение гомоморфизмов
УПРАЖНЕНИЯ
Глава X. Трансцендентные расширения
§ 1. Базисы трансцендентности
§ 2. Теорема Гильберта о нулях
§ 3. Алгебраические множества
§ 4. Теорема Нётера о нормализации
§ 5. Линейно свободные расширения
§ 6. Сепарабельные расширения
§ 7. Дифференцирования
УПРАЖНЕНИЯ
Глава XI. Вещественные поля
§ 1. Упорядоченные поля
§ 2. Вещественные поля
§ 3. Вещественные нули и гомоморфизмы
УПРАЖНЕНИЯ
Глава XII. Абсолютные значения
§ 1. Определения, зависимость и независимость
§ 2. Пополнения
§ 3. Конечные расширения
§ 4. Нормирования
§ 5. Пополнения и нормирования
§ 6. Дискретные нормирования
§ 7. Нули многочленов в полных полях
УПРАЖНЕНИЯ
Часть третья. ЛИНЕИНАЯ АЛГЕБРА И ПРЕДСТАВЛЕНИЯ
§ 1. Матрицы
§ 2. Ранг матрицы
§ 3. Матрицы и линейные отображения
§ 4. Определители
§ 5. Двойственность
§ 6. Матрицы и билинейные формы
§ 7. Полуторалинейная двойственность
Терминология
УПРАЖНЕНИЯ
Глава XIV. Структура билинейных форм
§ 1. Предварительные сведения, ортогональные суммы
§ 2. Квадратичные отображения
§ 3. Симметрические формы, ортогональные базисы
§ 4. Гиперболические пространства
§ 5. Теорема Витта
§ 6. Группа Витта
§ 7. Симметрические формы над упорядоченными полями
§ 8. Алгебра Клиффорда
§ 9. Знакопеременные формы
§ 10. Пфаффиан
§ 11. Эрмитовы формы
§ 12. Спектральная теорема (эрмитов случай)
§ 13. Спектральная теорема (симметрический случай)
УПРАЖНЕНИЯ
Глава XV. Представление одного эндоморфизма
§ 2. Модули над кольцами главных идеалов
§ 3. Разложение над одним эндоморфизмом
§ 4. Характеристический многочлен
УПРАЖНЕНИЯ
Глава XVI. Полилинейные произведения
§ 1. Тензорное произведение
§ 2. Основные свойства
§ 3. Расширение основного кольца
§ 4. Тензорное произведение алгебр
§ 5. Тензорная алгебра модуля
§ 6. Знакопеременные произведения
§ 7. Симметрические произведения
§ 8. Кольцо Эйлера — Гротендика
§ 9. Некоторые функториальные изоморфизмы
УПРАЖНЕНИЯ
Глава XVII. Полупростота
§ 1. Матрицы и линейные отображения над некоммутативными кольцами
§ 2. Условия, определяющие полупростоту
§ 3. Теорема плотности
§ 4. Полупростые кольца
§ 5. Простые кольца
§ 6. Сбалансированные модули
УПРАЖНЕНИЯ
Глава XVIII. Представления конечных групп
§ 1. Полупростота групповой алгебры
§ 2. Характеры
§ 3. Одномерные представления
§ 4. Пространство функций классов
§ 5. Соотношения ортогональности
§ 6. Индуцированные характеры
§ 7. Индуцированные представления
§ 8. Положительное разложение регулярного характера
§ 9. Сверхразрешимые группы
§ 10. Теорема Брауэра
§ 11. Поле определения представления
УПРАЖНЕНИЯ
Добавление
Предварительное вычисление алгебры

— Как найти кубические корни $i$?

спросил

Изменено 5 лет, 3 месяца назад

Просмотрено 33 тысячи раз

$\begingroup$

Я пытаюсь выяснить, какие три возможности $z$ таковы, что 93 = i$, тогда $$z = \exp\left[ i \left(\frac{\pi}{6}+\frac{2n\pi}{3}\right)\right]$$ для всех целых чисел $n$.

$\endgroup$

1

$\begingroup$

Я полагаю, что ваш «полиномиальный» подход также сработал бы, если бы вы имели в виду это:

[При этом мы предполагаем, что ничего не знали о «тождестве Эйлера», теореме Де Муавра или корнях единства, всех из них обеспечивают достаточно эффективные устройства] 92 \ = \ \ frac {3} {4} \ \ \ Rightarrow \ \ a \ = \ \ pm \ frac {\ sqrt {3}} {2} \ \ \ Rightarrow \ \ z \ = \ \ frac {\ sqrt{3}}{2} + \frac{1}{2}i \ , \ -\frac{\sqrt{3}}{2} + \frac{1}{2}i \\ . $$

Мы нашли три комплексных решения уравнения. Как говорит Дэн , (одна из форм) Фундаментальная теорема алгебры утверждает, что этот многочлен третьей степени с комплексными коэффициентами имеет всего три корня (с учетом кратностей, каждая из которых здесь равна 1).

Мы, вероятно, не хотели бы использовать этот метод для более высоких степеней, поскольку алгебраическое решение стало бы более сложным. Методы, описанные на других плакатах, используются гораздо чаще. 93, 3\тета)$. Кубические корни $(r, \theta)$ равны $\left(\sqrt[3]{r}, \frac{\theta}{3}\right)$, $\left(\sqrt[3]{ r}, \frac{\theta+2\pi}{3}\right)$ и $\left(\sqrt[3]{r}, \frac{\theta+4\pi}{3}\right) $ (напомним, что добавление $2\pi$ к аргументу не меняет число). Другими словами, чтобы найти кубический корень комплексного числа, возьмите кубический корень из абсолютного значения (радиуса) и разделите аргумент (угол) на 3.

$i$ находится под прямым углом от $1$ : $i = \left(1, \frac{\pi}{2}\right)$. Графически:

Кубический корень из $i$ равен $A = \left(1, \frac{\pi}{6}\right)$. Два других: $B = \left(1, \frac{5\pi}{6}\right)$ и $\left(1, \frac{9\pi}{6}\right) = -i$ .

Вспоминая основы тригонометрии, прямоугольные координаты $A$ равны $\left(\cos\frac{\pi}{6}, \sin\frac{\pi}{6}\right)$ (треугольник OMA равен прямоугольник в М). Таким образом, $A = \cos\frac{\pi}{6} + i \sin\frac{\pi}{6} = \frac{\sqrt{3}}{2} + i\frac{1}{ 2}$.

Если вы не помните значения $\cos\frac{\pi}{6}$ и $\sin\frac{\pi}{6}$, вы можете найти их с помощью геометрии. Треугольник $OAi$ имеет две равные стороны $OA$ и $Oi$, поэтому он равнобедренный: углы $OiA$ и $OAi$ равны. Сумма углов треугольника равна $\pi$, и мы знаем, что третий угол $iOA$ равен $\frac{\pi}{2} — \frac{\pi}{6} = \frac{\ пи{3}$; поэтому $OiA = OAi = \dfrac{\pi — \frac{pi}{3}}{2} = \dfrac{\pi}{3}$. Итак, $OAi$ — равносторонний треугольник, а высота AN также является медианой, поэтому N — середина треугольника $[Oi]$: $\sin\frac{\pi}{6} = AM = ON = \frac{ 1}{2}$. 2} = \dfrac{\sqrt{3}}{2}$. 93 = i = 0 + 1i$, это означает, что $\cos(3\theta) = 0$ и $\sin(3\theta) = 1$. Решение этой системы дает $3\theta = \frac{\pi}{2} + 2\pi n$ или $\theta = \frac{\pi}{6} + \frac{2 \pi n}{3} $ для любого $n \in \mathbb{Z}$.

Подстановка нескольких значений для $n$ дает:

  • $n = 0$ → $\theta = \frac{\pi}{6}$ → $z = \frac{\sqrt{3}}{ 2} + \frac{1}{2} i$
  • $n = 1$ → $\theta = \frac{5\pi}{6}$ → $z = \frac{-\sqrt{3}}{2} + \frac{1}{2} i$
  • $n = 2$ → $\theta = \frac{3\pi}{2}$ → $z = -i$ 92=0$      $⟹ a=±b\sqrt {3}$

    Установив значение $a$ в (ii), мы получаем,

    Если $a=0$,      $b=-1$

    Если $a=±b\sqrt {3}$,      $ b=1/2$

    Тогда $a=±b\sqrt {3}=±(1/2)\sqrt {3}=±\ sqrt {3}/2$

    Итак, $(a,b)=(0,-1),(±\sqrt {3}/2,1/2)$

    Теперь есть 3 значения $ з$.

    (1) $\sqrt [3] {i} =a+bi= 0+(-1)i= -i$

    (2) $\sqrt [3] {i} =a+bi= \ dfrac {\ sqrt {3}} {2}+\ dfrac {i} {2} $

    (3) $\sqrt [3] {i} =a+bi= -\dfrac {\sqrt {3}}{2}+\dfrac {i}{2}$

    $\endgroup$

    комплексных чисел — Показать, что $\frac{-1+\sqrt{3}i}{2}$ является кубическим корнем из 1?

    спросил

    Изменено 5 лет, 9 месяцев назад

    Просмотрено 4к раз

    $\begingroup$

    Я знаю, как напрямую доказать, что комплексное число является одним из кубических корней из 1.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *