Алгоритм построения графика функции: Алгоритмы построения графиков функции. 8–9-й класс

alexxlab / / Разное

Содержание

Алгоритмы построения графиков функции. 8–9-й класс

Урок алгебры в 9 классе по теме «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины» был построен на основе компьютерных технологии, применяя исследовательскую деятельность обучения.

Цели урока: Обучающая: Наглядно продемонстрировать учащимся возможности использования компьютера при построении графиков функции с модулями; для самоконтроля, экономии времени при построении графиков функций вида у=f |(х)| , у = | f (х)| , у=|f |(х)| |.

Развивающая: Развитие интеллектуальных умений и мыслительных операций — анализ и синтез сравнение, обобщение. Формирование ИКТ компетентности учащихся.

Воспитывающая: Воспитание познавательного интереса к предмету путем введения новейших технологий обучения. Воспитание самостоятельности при решении учебных задач.

Оборудование: Оборудование: компьютерный класс, интерактивная доска, презентация на тему «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины», раздаточный материал: карточки для работы с графической моделью функций, листы для фиксирования результатов исследования функций, персональные компьютеры.

Лист самоконтроля.

Программное обеспечение: презентация Microsoft PowerPoint «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины»

Ход урока

1. Организационный момент

2. Повторение, обобщение и систематизация. Это этап урока сопровождается компьютерной презентацией.

Слайд 2.

График функции у=f |(х)|

у=f |(х)| — четная функция, т.к. | х | = | -х |, то f |-х| = f | х |

График этой функции симметричен относительно оси координат.

Следовательно, достаточно построить график функции у=f(х) для х>0,а затем достроить его левую часть, симметрично правой относительно оси координат.

Например, пусть графиком функции у=f(х) является кривая, изображенная на рис.1, тогда графиком функции у=f |(х)| будет кривая, изображенная на рис.2.

Рис.1

Рис.2

1. Исследование графика функции у= |х|

  1. Если х 0, то |х| =х и наша функция у=х, т.е. искомый график совпадает с биссектрисой первого координатного угла.
  2. Если х<0, то |х|= -х и у= -х. При отрицательных значениях аргумента х график данной функции - прямая у= -х, т.е. биссектриса второго координатного угла.

Таким образом, искомый график есть ломанная, составленная из двух полупрямых. (Рис.3)

Рис. 3

Из сопоставления двух графиков: у=х и у= |х|, учащиеся сделают вывод, что второй получается из первого зеркальным отображением относительно ОХ той части первого графика, которая лежит под осью абсцисс. Это положение вытекает из определения абсолютной величины.

Из сопоставления двух графиков: у = х и у = -х, сделают вывод: функции у = f(|х|) получается из графика у = f (x) при х 0 симметричным отображением относительно оси ОУ.

Можно ли применять этот метод построения графиков для любой функции, содержащей абсолютную величину?

Слайд 3 и 4.

1. Построите график функции у=0,5 х

2 — 2|х| — 2,5

1) Поскольку |х| = х при х 0, требуемый график совпадает с параболой у=0,5 х2 — 2х — 2,5 . Если х<0, то поскольку х2 = |х|2, |х|=-х и требуемый график совпадает с параболой у=0,5 х2 + 2х — 2,5.

2) Если рассмотрим график у=0,5 х2 -2х — 2,5 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график.

Можно ли применять этот метод построения графиков дл квадратичной функции, для графиков обратной пропорциональности, содержащие абсолютную величину?

2. Например: у=х2 — |х| -3

1) Поскольку |х| = х при х 0, требуемый график совпадает с параболой у=0,25 х2 — х — 3.

Если х<0, то поскольку х2 = |х|2, |х|=-х и требуемый график совпадает с параболой у=0,25 х2 + х — 3.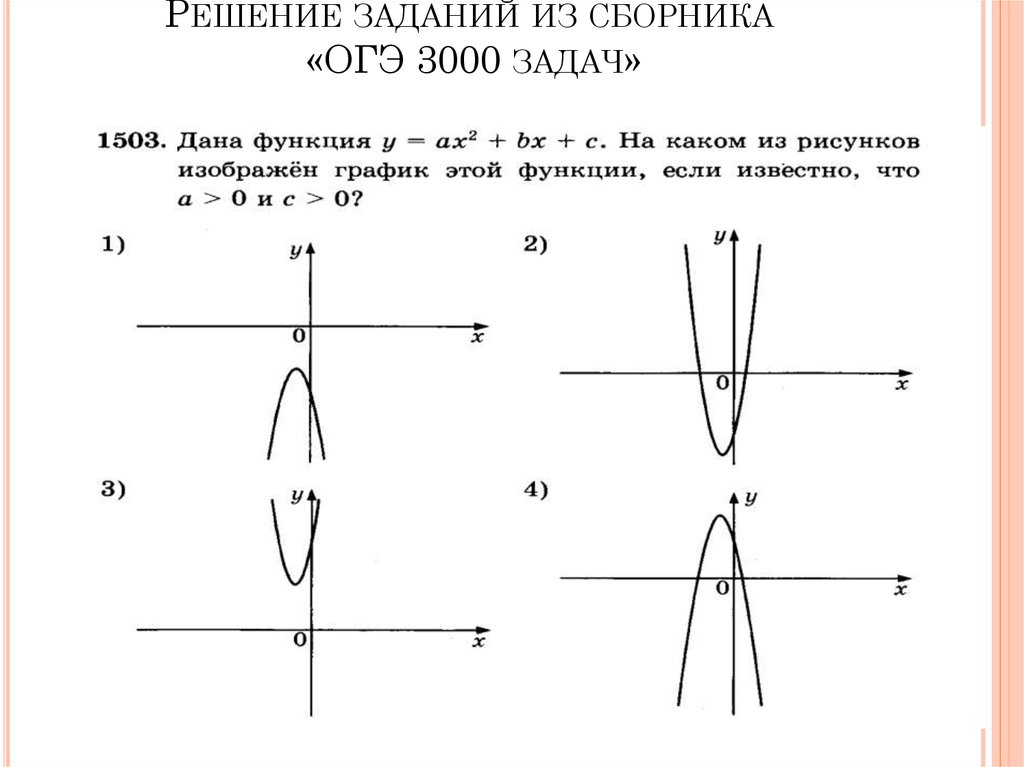

2) Если рассмотрим график у=0,25 х2 — х — 3 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график.

(0; — 3) координаты точки пересечения графика функции с осью ОУ.

у =0, х2 -х -3 = 0

х2 -4х -12 = 0

Имеем, х1= — 2; х2 = 6.

(-2; 0) и (6; 0) — координаты точки пересечения графика функции с осью ОХ.

Если х<0, ордината точки требуемого графика такая же, как и у точки параболы, но с положительной абсциссой, равной |х|. Такие точки симметричны относительно оси ОУ(например, вершины (2; -4) и -(2; -4).

Значит, часть требуемого графика, соответствующая значениям х<0, симметрична относительно оси ОУ его же части, соответствующей значениям х>0.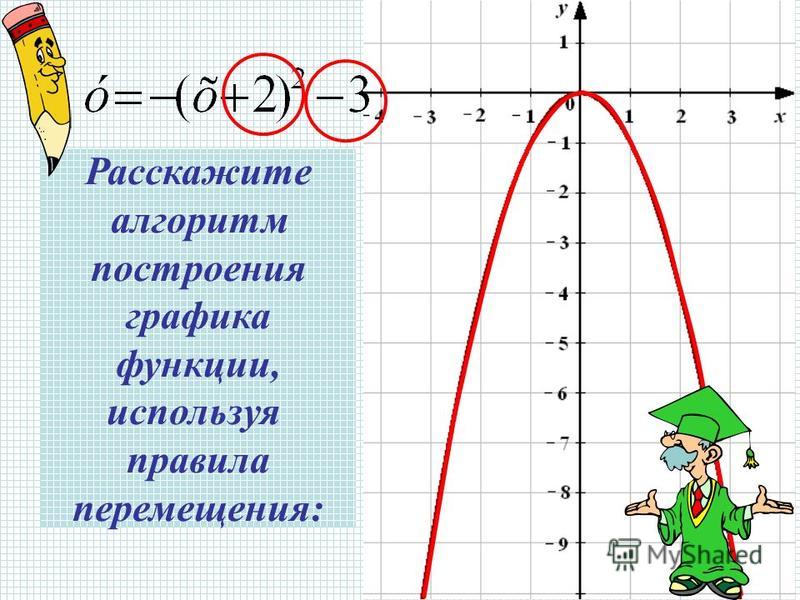

б) Поэтому достраиваю для х<0 часть графика, симметричную построенной относительно оси ОУ.

Рис. 4

На тетрадях ученики доказывают, что график функции у = f |(х)| совпадает с графиком функции у = f (х) на множестве неотрицательных значений аргумента и симметричен ему относительно оси ОУ на множестве отрицательных значений аргумента.

Доказательство: Если х  0, то f |(х)|= f (х), т.е. на множестве неотрицательных значений аргумента графики функции у = f (х) и у = f |(х)| совпадают. Так как у = f |(х)| — чётная функция, то её график симметричен относительно ОУ.

Таким образом, график функции у = f |(х)| можно получить из графика функции у = f (х) следующим образом:

1. построить график функции у = f(х) для х>0;

2. Для х<0, симметрично отразить построенную часть относительно оси ОУ.

Вывод: Для построения графика функции у = f |(х)|

1. построить график функции у = f(х) для х>0;

2. Для х<0, симметрично отразить построенную часть

относительно оси ОУ.

Слайд 5

4. Исследовательская работа по построению графика функции у = | f (х)|

Построить график функции у = |х2 — 2х|

Освободимся от знака модуля по определению

Если х2 — 2х0, т.е. если х 0 и х2, то |х2 - 2х|= х2 — 2х

Если х2 — 2х<0, т.е. если 0<х< 2, то |х2 — 2х|=- х2 + 2х

Видим, что на множестве х 0 и х2 графики функции

у = х2 — 2х и у = |х2 — 2х|совпадают, а на множестве (0;2)

графики функции у = -х2 + 2х и у = |х2 — 2х| совпадают. Построим их.

График функции у = | f (х)| состоит из части графика функции у = f(х) при у ?0 и симметрично отражённой части у = f(х) при у <0 относительно оси ОХ.

Слайд 6

Построить график функции у = |х2 — х —6|

1) Если х2 — х -6 0, т.е. если х-2 и х3, то |х2 — х -6|= х2 — х -6.

Если х2 — х -6<0, т.е. если -2<х< 3, то |х2 — х -6|= -х2 + х +6.

Построим их.

2) Построим у = х2 — х -6 . Нижнюю часть графика

симметрично отбражаем относительно ОХ.

Сравнивая 1) и 2), видим что графики одинаковые.

Работа на тетрадях.

Докажем, что график функции у = | f (х)| совпадает с графиком функции у = f (х) для f(х) >0 и симметрично отражённой частью у = f(х) при у <0 относительно оси ОХ.

Действительно, по определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий:

у = f(х), если f(х) 0; у = — f(х), если f(х) <0

Для любой функции у = f(х), если f(х) >0, то

| f (х)| = f(х), значит в этой части график функции

у = | f (х)| совпадает с графиком самой функции

у = f(х).

Если же f(х) <0, то | f (х)| = — f(х),т.е. точка (х; — f(х)) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ «отрицательную» часть графика у = f(х).

Слайд 7

Вывод: действительно для построения графика функции у = |f(х) | достаточно:

1.Построить график функции у = f(х) ;

2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс. (Рис.5)

Рис.5

Вывод: Для построения графика функции у=|f(х) |

1.Построить график функции у=f(х) ;

2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, строим кривые, симметричные построенным графикам относительно оси абсцисс.

(Рис.6, 7.)

Слайды 8-13.

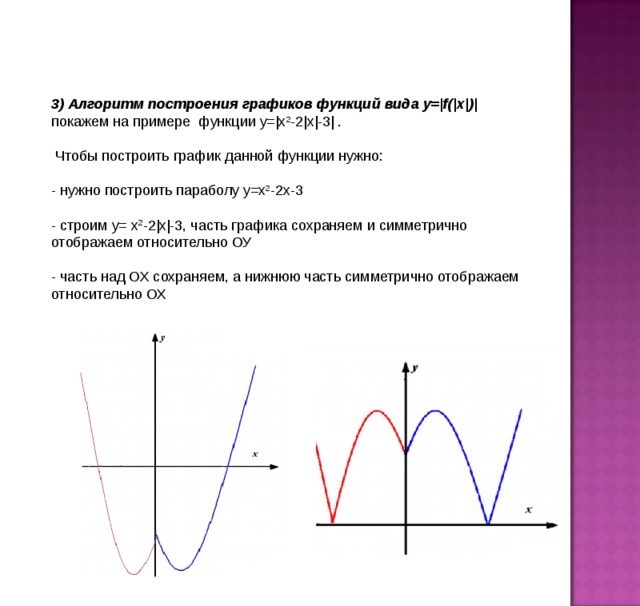
5. Исследовательская работа по построению графиков функции у=|f |(х)| |

Применяя определение абсолютной величины и ранее рассмотренные примеры, построим графиков функции:

у = |2|х| — 3|

у = |х2 — 5|х||

у = | |х2| — 2| и сделал выводы.

Для того чтобы построить график функции у = | f |(х)| надо:

1. Строить график функции у = f(х) для х>0.

2. Строить вторую часть графика, т. е. построенный график симметрично отражать относительно ОУ, т.к. данная функция четная.

3. Участки получившегося графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.

Построить график функции у = | 2|х | — 3| (1-й способ по определению модуля)

1. Строим у = 2|х | — 3 , для 2 |х| — 3 > 0 , |х |>1,5 т.е. х< -1,5 и х>1,5

а) у = 2х — 3 , для х>0

б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.

2. Строим у = —2 |х| + 3, для 2|х | — 3 < 0. т.е. -1,5<х<1,5

а) у = —2х + 3, для х>0

б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.

У = | 2|х | — 3|

1) Строим у = 2х-3, для х>0.

2) Строим прямую, симметричную построенной относительно оси ОУ.

3) Участки графика, расположенные в нижней полуплоскости, отображаю симметрично относительно оси ОХ.

Сравнивая оба графика, видим, что они одинаковые.

2.

у = | х2 — 5|х| |

1. Строим у = х2 — 5 |х|, для х2 — 5 |х| > 0 т.е. х >5 и х<-5

а) у = х2 — 5 х, для х>0

б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.

2. Строим у = — х2 + 5 |х| , для х2 — 5 |х| < 0. т.е. -5х5

а) у = — х2 + 5 х , для х>0

б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.

У = | х2 — 5|х| |

а) Строим график функции у = х2 — 5 х для х>0.

Б) Строим часть графика, симметричную построенной относительно оси ОУ

в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ.

Сравнивая оба графика, видим что они одинаковые. (Рис.9)

3. у =| |х|2 — 2 |

1). Строим у = |х|2 — 2 , для |х|2 — 2 > 0, x> и x< —

а) у = х2 — 2, для х>0

б) для х<0, симметрично отражаю построенную часть относительно оси ОУ.

2). Строим у = — |х|2 + 2 , для |х|2 — 2 < 0. т.е. — < x<

а) у = —х2 + 2 , для х>0

б) для х<0, симметрично отражаю построенную часть относительно оси ОУ.

У = ||х|2 — 2 |

а) Строим у = х2 -2 для х > 0.

Б) Строим часть графика, симметричную построенной относительно оси ОУ

в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ.

Сравнивая оба графика, видим что они одинаковые. (Рис.10)

3. Подведение итогов урока.

14,15 слайды.

Алгоритм построения графика функции у=f |(х)|

1.Построить график функции у=f(х) для х>0;

2.Построить для х<0 часть графика, симметричную построенной относительно оси ОУ.

Алгоритм построения графика функции у=|f(х) |

1.Построить график функции у=f(х) ;

2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, строить кривые, симметричные построенным графикам относительно оси абсцисс.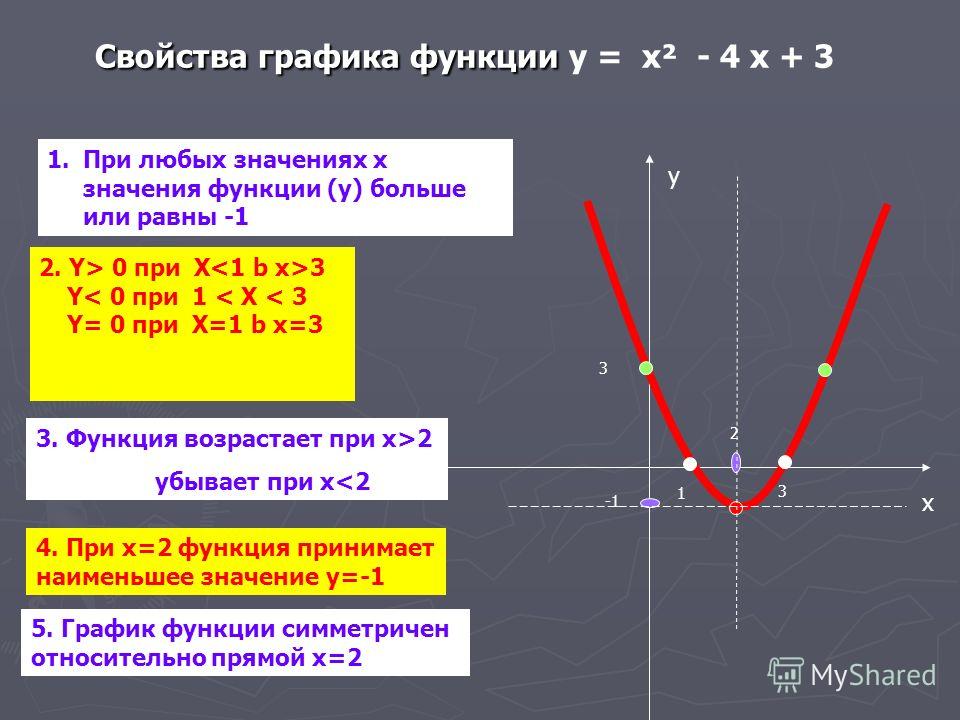

Алгоритм построения графика функции у=|f |(х)| |

1. Построить график функции у=f(х) для х>0.

2. Построить кривую графика, симметричную построенной относительно оси ОУ, т.к. данная функция четная.

3. Участки графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.

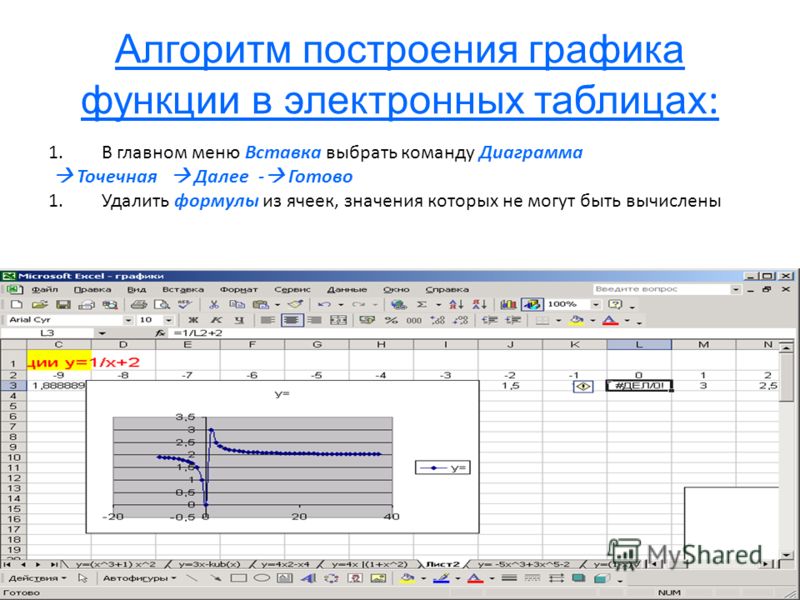
Алгоритм построения графика функции — Информатика, информационные технологии

1 Вызываем Мастер диаграмм.

В окне первого шага выбираем Тип диаграммы – График, вид графика – график с маркерами, помечающими точки данных.

2 В поле Диапазон, переключившись на вкладку Ряд ® Добавить. В появившемся окне ввести в поле Значение ссылку на диапазон В3 : В13, а в поле Подписи по оси Х ссылку на диапазон А3:А13. Для ввода ссылок минимизировать диалоговое окно (щелчок мыши по кнопке – минимизация, находящейся в правой части поля, после чего выделить диапазоны).

3 На вкладке Заголовки заполняем поля: Название диаграммы, Ось Х (категорий), Ось Y (значений). На вкладке Линии сетки устанавливаем флажок Основные линии для оси Х, а на вкладке Легенда снимаем флажок Добавить легенду.

4 Размещаем диаграмму на имеющемся листе.

После появления диаграммы форматируем область построения диаграммы, установив для нее цвет заливки – белый (выбрать в списке Элементы диаграммы панели диаграммы значение область построения диаграммы и нажав кнопку Формат области построения, устанавливаем в диалоговом окне прозрачный тип заливки).

Аналогично форматируем Ось категорий, установив на вкладке Вид переключатель метки делений в положении внизу.

Форматирование элемента Ряд 1 сводится к установке на вкладке Вид флажка Сглаженная линия.

В результате этих действий получится график функции, показанный на рисунке 4.40.

Рисунок 4.40 – График функции

Расчет минимального и максимально значений функции

Установив курсор на требуемую ячейку вызываем функцию Мин, используя Мастер функций (Мастер функций ® Математические ® МИН). В появившемся диалоговом окне указываем ссылку на диапазон В3 : В13. После нажатия клавиши ОК в ячейке появляется минимальное значение функции.

Аналогичные действия проделываем для нахождения максимального значения используя функцию =МАКС().

Полученные результаты и лист с формулами отображены на рисунках 4.41, 4.42.

Рисунок 4.41 – Лист с расчетами

Рисунок 4.42 – Лист с формулами

Построение линии тренда

Задание: Аппроксимировать приведенные ниже статистические данные, используя пять стандартные функции тренда. Выбрать среди них функцию, наилучшим образом описывающую исходные данные.

Последовательность действий:

1 Занесите в столбец В значения X из таблицы, а в столбец С –значения Y. Измените название листа Лист1 на Данные(рис. 4.43).

Рисунок 4.43

2 Пользуясь этими данными, постройте график. При построении графика укажите тип диаграммы Точечная и поместите график на отдельном листе.

3 Наведите курсор мыши на любую точку построенного графика, дождитесь появления всплывающей подсказки с параметрами этой точки и нажмите правую клавишу мыши. 2) в положение включено и нажмите на кнопку OK.

5 Переместите уравнение на свободное место диаграммы, подберите размер шрифта.

6 Сформируйте заголовок диаграммы Линейная и назовите лист с диаграммой Линейная, так как показано на рисунке 4.44.

Рисунок 4.44 – Диаграмма с линейной аппроксимацией

7 Выполните еще раз пункты 2, 3, 4, 5 и постройте на отдельном листе график со степенной аппроксимацией. Сформируйте заголовок диаграммы Степенная и назовите лист с диаграммой Степенная, так как показано на рисунке 4.45.

Рисунок 4.45 – Диаграмма со степенной аппроксимацией

8 Выполните еще раз пункты 2,3,4,5 и постройте на отдельном листе график с логарифмической аппроксимацией. Сформируйте заголовок диаграммы Логарифмическая и назовите лист с диаграммой Логарифмическая, так как показано на рисунке 4.46.

Рисунок 4.46 – Диаграмма с логарифмической аппроксимацией

9 Выполните еще раз пункты 2, 3, 4, 5 и постройте на отдельном листе график с экспоненциальной аппроксимацией.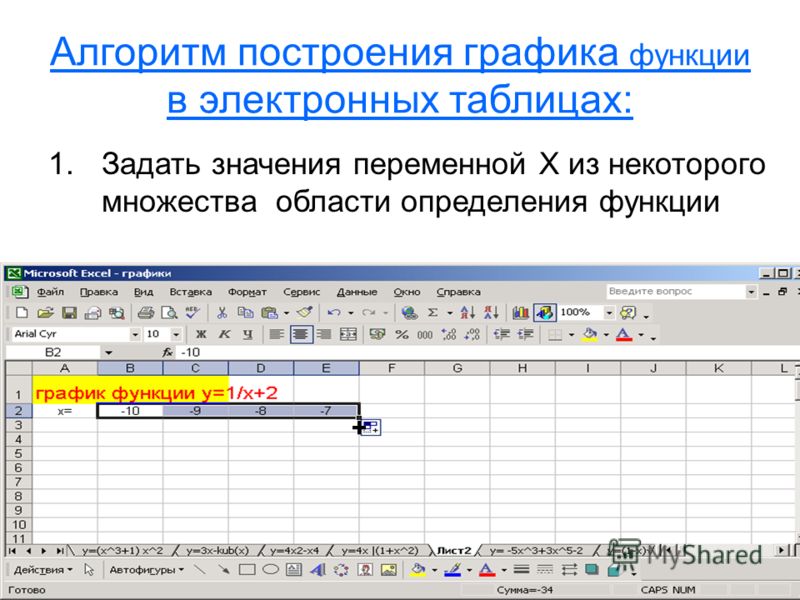 2) для нее наибольшая: R2 = 0,8465.

Статьи к прочтению:
  • Алгоритм разветвляющегося вычислительного процесса. привести пример.
  • Алгоритм реализации проекта

Общая схема исследования функции и построение ее графика


Похожие статьи:

  • Построение двух графиков в рамках одного окна

    Приведем пример скрипта для построения двух графиков в рамках одного окна в MATLAB: % скрипт, строящий два графика в рамках одного окна %координаты точек…

  • Построение диаграмм и графиков. в программе excel термин диаграмма используется для обозначения всех видов графического представления числовых данных

    В программе Excel термин диаграмма используется для обозначения всех видов графического представления числовых данных. Построение графического…

10 графических алгоритмов с визуальным объяснением | by Vijini Mallawaarachchi

Краткое введение в 10 основных графических алгоритмов с примерами и визуализациями

Графики стали мощным средством моделирования и сбора данных в реальных сценариях, таких как социальные сети, веб-страницы, ссылки и местоположения. и маршруты в GPS. Если у вас есть набор объектов, связанных друг с другом, вы можете представить их с помощью графа.

Изображение автора

В этой статье я кратко объясню 10 основных алгоритмов работы с графами, которые очень полезны для анализа и их применения.

Во-первых, давайте представим график.

Граф состоит из конечного набора вершин или узлов и набора ребер , соединяющих эти вершины. Две вершины называются смежными , если они соединены друг с другом одним и тем же ребром.

Некоторые основные определения, относящиеся к графикам, приведены ниже. Вы можете обратиться к рисунку 1 для примеров.

  • Порядок: Количество вершин в графе
  • Размер: Количество ребер в графе
  • Степень вершины: Количество ребер, инцидентных вершине
  • : Изолированные Вершина, не соединенная с другими вершинами графа
  • Самостоятельная петля : Ребро из вершины в себя
  • Направленный граф: Граф, в котором все ребра имеют направление, указывающее начало вершина и что является конечной вершиной
  • Неориентированный граф: Граф с ребрами, не имеющими направления
  • Взвешенный граф: Ребра графа имеют веса
  • Невзвешенный граф: Ребра графа не имеют весов
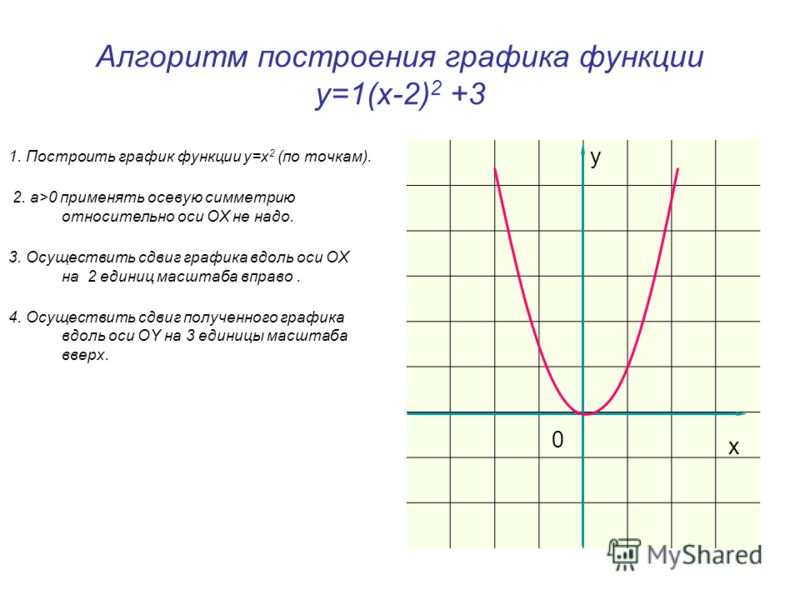Визуализация терминологии Рис. 1. of Graphs (Image by Author)Рис. 2. Анимация BFS обхода графа (Image by Author)

Обход или поиск является одной из фундаментальных операций, которые можно выполнять на графах. В поиск в ширину (BFS), мы начинаем с определенной вершины и исследуем всех ее соседей на текущей глубине, прежде чем перейти к вершинам следующего уровня. В отличие от деревьев, графы могут содержать циклы (путь, первая и последняя вершины которого совпадают). Следовательно, мы должны отслеживать посещенные вершины. При реализации BFS мы используем структуру данных очереди.

На рис. 2 показана анимация обхода BFS примера графа. Обратите внимание, как вершины обнаруживаются (желтые) и посещаются (красные).

Приложения

  • Используется для определения кратчайших путей и минимальных остовных деревьев.
  • Используется сканерами поисковых систем для создания индексов веб-страниц.
  • Используется для поиска в социальных сетях.
  • Используется для поиска доступных соседних узлов в одноранговых сетях, таких как BitTorrent.
Рис. 3. Анимация обхода графа DFS (изображение автора) ). В DFS мы также должны отслеживать посещенные вершины. При реализации DFS мы используем структуру данных стека для поддержки поиска с возвратом.

На рис. 3 показана анимация обхода в глубину того же примера графа, что и на рис. 2. Обратите внимание, как он перемещается вглубь и возвращается назад.

Приложения

  • Используется для поиска пути между двумя вершинами.
  • Используется для обнаружения циклов на графике.
  • Используется в топологической сортировке.
  • Используется для решения головоломок, имеющих только одно решение (например, лабиринты)
Рис. 4. Анимация, показывающая кратчайший путь из вершины 1 в вершину 6 (Изображение автора)

Кратчайший путь из одной вершины в другую — это такой путь в графе, что сумма весов ребер, по которым нужно пройти, минимальна.

На рис. 4 показана анимация, в которой кратчайший путь определяется из вершины 1 в вершину 6 графа.

Алгоритмы

  1. Алгоритм кратчайшего пути Дейкстры
  2. Алгоритм Беллмана-Форда

Приложения

  • Используется для поиска направления движения из одного места в другое в картографическом программном обеспечении, таком как карты Google или Apple.
  • Используется в сети для решения проблемы пути с минимальной задержкой.
  • Используется в абстрактных машинах для определения вариантов достижения определенного целевого состояния путем перехода между различными состояниями (например, может использоваться для определения минимально возможного количества ходов для победы в игре).
Изображение Daniel Dino-Slofer с PixabayРис. 5. Цикл (изображение автора)

Цикл — это путь в графе, первая и последняя вершины которого совпадают. Если мы начинаем с одной вершины, идем по пути и заканчиваем в начальной вершине, то этот путь является циклом.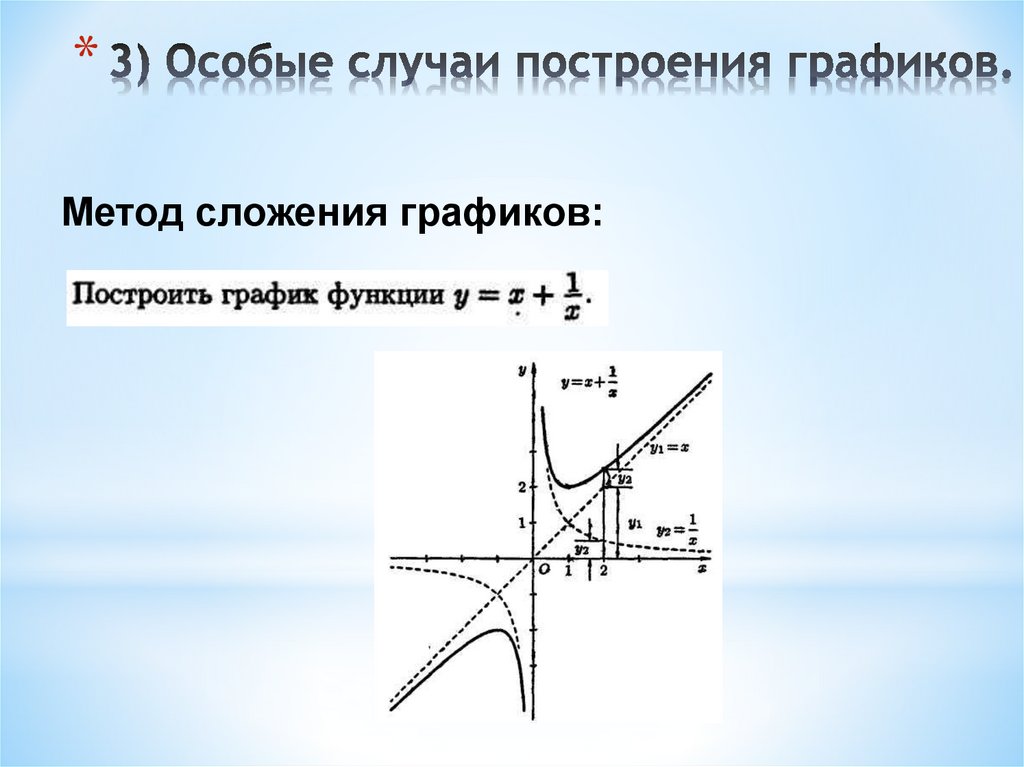 Обнаружение циклов — это процесс обнаружения этих циклов. На рис. 5 показана анимация обхода цикла.

Алгоритмы

  1. Алгоритм обнаружения цикла Флойда
  2. Алгоритм Брента

Приложения

  • Используется в алгоритмах на основе распределенных сообщений.
  • Используется для обработки крупномасштабных графов с использованием системы распределенной обработки в кластере.
  • Используется для обнаружения взаимоблокировок в параллельных системах.
  • Используется в криптографических приложениях для определения ключей сообщения, которые могут сопоставить это сообщение с тем же зашифрованным значением.
Рис. 6. Анимация, показывающая минимальное остовное дерево (изображение автора)

минимальное остовное дерево — это подмножество ребер графа, которое соединяет все вершины с минимальной суммой весов ребер и состоит из циклы.

На рис. 6 показана анимация, показывающая процесс получения минимального остовного дерева.

Алгоритмы

  1. Алгоритм Прима
  2. Алгоритм Крускала

Приложения

  • Используется для построения деревьев для вещания в компьютерных сетях.
  • Используется в графическом кластерном анализе.
  • Используется при сегментации изображения.
  • Используется при районировании социально-географических районов, когда регионы группируются в смежные регионы.
Рис. 7. Сильно связанные компоненты (изображение автора)

Граф называется сильно связный , если каждая вершина графа достижима из любой другой вершины.

На рис. 7 показан пример графа с тремя сильно связанными компонентами, вершины которых окрашены в красный, зеленый и желтый цвета.

Алгоритмы

  1. Алгоритм Косараджу
  2. Алгоритм компонентов сильной связности Тарьяна

Приложения

  • Используется для вычисления разложения Дульмажа–Мендельсона, которое представляет собой раздельную классификацию ребер двудольного графа.
  • Используется в социальных сетях для поиска группы людей, тесно связанных между собой, и предоставления рекомендаций на основе общих интересов.
Изображение Gerd Altmann с сайта PixabayРис. 8. Топологическое упорядочение вершин в графе (Изображение автора)

Топологическая сортировка графа представляет собой линейное упорядочение его вершин так, что для каждого направленного ребра (u, v ) в упорядочении вершина u предшествует v.

На рис. 8 показан пример топологического упорядочения вершин (1, 2, 3, 5, 4, 6, 7, 8). Вы можете видеть, что вершина 5 должна идти после вершин 2 и 3. Точно так же вершина 6 должна идти после вершин 4 и 5.

Алгоритмы

  1. Алгоритм Кана
  2. Алгоритм, основанный на поиске в глубину

Приложения

  • Используется при планировании инструкций.
  • Используется при сериализации данных.
  • Используется для определения порядка выполнения задач компиляции в make-файлах.
  • Используется для разрешения зависимостей символов в компоновщиках.
Рис. 9. Окраска вершин (Изображение автора)

Окраска графа присваивает цвета элементам графа при соблюдении определенных условий. Раскраска вершин — наиболее часто используемый метод раскраски графов. При раскрашивании вершин мы пытаемся раскрасить вершины графа, используя k цветов, и любые две соседние вершины не должны иметь одинаковый цвет. Другие методы окрашивания включают окрашивание краев и окрашивание лиц .

Хроматическое число графа — это наименьшее количество цветов, необходимое для раскрашивания графа.

На рис. 9 показана раскраска вершин примера графа с использованием 4 цветов.

Алгоритмы

  1. Алгоритмы, использующие поиск в ширину или поиск в глубину
  2. Жадная раскраска

Приложения

  • Используется для планирования расписания.
  • Используется для присвоения частот мобильной радиосвязи.
  • Используется для моделирования и решения таких игр, как судоку.
  • Используется для проверки двудольности графа.
  • Используется для раскрашивания географических карт стран или штатов, где соседние страны или штаты окрашены в другой цвет.
Изображение TheAndrasBarta с PixabayРис. 10. Определение максимального потока (Изображение автора)

Мы можем смоделировать граф как сеть потока с весами ребер в качестве пропускной способности. В задаче максимального потока мы должны найти путь потока, который может обеспечить максимально возможный расход.

На рис. 10 показан анимированный пример определения максимального потока сети и определения конечного значения потока.

Алгоритмы

  1. Алгоритм Форда-Фалкерсона
  2. Алгоритм Эдмондса-Карпа
  3. Алгоритм Диника

Приложения

  • Используется в расписании авиакомпаний для составления расписания полетов.
  • Используется при сегментации изображения для поиска фона и переднего плана в изображении.
  • Используется для устранения бейсбольных команд, которые не могут выиграть достаточно игр, чтобы догнать текущего лидера в своем дивизионе.
Рис. 11. Сопоставление двудольного графа (изображение автора)

A сопоставление в графе — это множество ребер, не имеющих общих вершин (т. е. никакие два ребра не имеют общей вершины). Сопоставление называется максимальным паросочетанием , если оно содержит максимально возможное количество ребер, соответствующих как можно большему количеству вершин.

На рис. 11 показана анимация получения полного соответствия двудольного графа с двумя наборами вершин, обозначенными оранжевым и синим цветом.

Алгоритмы

  1. Алгоритм Хопкрофта-Карпа
  2. Венгерский алгоритм
  3. Алгоритм цветения

Приложения

  • Используется в сватовстве для подбора женихов и невест (задача стабильного брака).
  • Используется для определения покрытия вершин.
  • Используется в теории транспорта для решения задач распределения ресурсов и оптимизации путешествий.

Я надеюсь, что вы нашли эту статью полезной как простое и обобщенное введение в алгоритмы графов. Я хотел бы услышать ваши мысли. 😇

Вы можете ознакомиться с реализациями графовых алгоритмов, найденными в networkx и igraph модули python. Вы можете прочитать о python-igraph в моей предыдущей статье «Руководство для новичков по Python-igraph».

Руководство для новичков по Python-igraph

Простое руководство по распространенным функциям python-igraph с примерами и кодом

в направлении datascience.com

Вы также можете ознакомиться с моими предыдущими статьями о структурах данных.

8 общих структур данных, которые должен знать каждый программист

Структуры данных — это специализированные средства организации и хранения данных в компьютерах таким образом, чтобы мы могли выполнять…

по направлению datascience. com

Структуры данных в C++. Часть 1

Реализация общих структур данных на C++

по направлению к datascience.com

из 8 различных древовидных структур данных

в направлении datascience.com

Самобалансирующиеся бинарные деревья поиска 101

Введение в самобалансирующиеся бинарные деревья поиска

в направлении datascience.com

Большое спасибо за прочтение. 😊

Ура! 😃

Как использовать графовые алгоритмы

Главная/Блог/Учебники и руководства/Алгоритмы 101: Как использовать графовые алгоритмы

17 декабря 2020 г. — 11 мин чтения на собеседованиях по кодированию. Чтобы получить преимущество на собеседованиях, важно хорошо знать лучшие алгоритмы и их реализации.

В сегодняшнем уроке мы будем изучать алгоритмы графа . Мы начнем с введения в теорию графов и алгоритмы графов. Далее мы узнаем, как реализовать график. Наконец, мы рассмотрим распространенные проблемы с графами, с которыми вы можете столкнуться на собеседовании по программированию.

Сегодня мы узнаем:

  • Что такое графовые алгоритмы?
  • Свойства графа
  • Как представить графики в коде
  • Как реализовать обход в ширину
  • Как реализовать обход в глубину
  • Как удалить край
  • Дополнительные вопросы для интервью

Простой способ подготовиться к вопросам алгоритма

Этот кураторский путь проведет вас через все, что вам нужно знать, чтобы уверенно проходить собеседования по Python.

Ace the Python Coding Interview

Что такое графовые алгоритмы?

Алгоритм — это математический процесс решения задачи с использованием четко определенного или оптимального количества шагов. Это просто базовая техника, используемая для выполнения конкретной работы.

Граф — это абстрактное обозначение, используемое для представления связи между всеми парами объектов. Графы представляют собой широко используемые математические структуры, визуализируемые двумя основными компонентами: узлов и ребер .

Алгоритмы графов используются для решения проблем представления графов в виде сетей, таких как рейсы авиакомпаний, способы подключения к Интернету или подключение к социальным сетям на Facebook. Они также популярны в НЛП и машинном обучении для формирования сетей.

Некоторые из лучших алгоритмов графа включают:

  • Реализовать обход в ширину
  • Реализовать обход в глубину
  • Подсчитать количество узлов на уровне графа
  • Найти все пути между двумя узлами
  • Найти все компоненты связности графа
  • Алгоритм Дейкстры для поиска кратчайшего пути в данных графа
  • Удалить край

Хотя графы составляют неотъемлемую часть дискретной математики, они также находят практическое применение в компьютерных науках и программировании, в том числе в следующих областях:

  • Отношения между вызывающим и вызываемым абонентом в компьютерной программе, представленные в виде графа
  • Структура ссылок веб-сайта может быть представлена ​​ориентированным графом
  • Нейронные сети

Свойства графа

Граф, обозначенный G, представлен набором из вершин (V) или узлов, связанных ребрами (E) .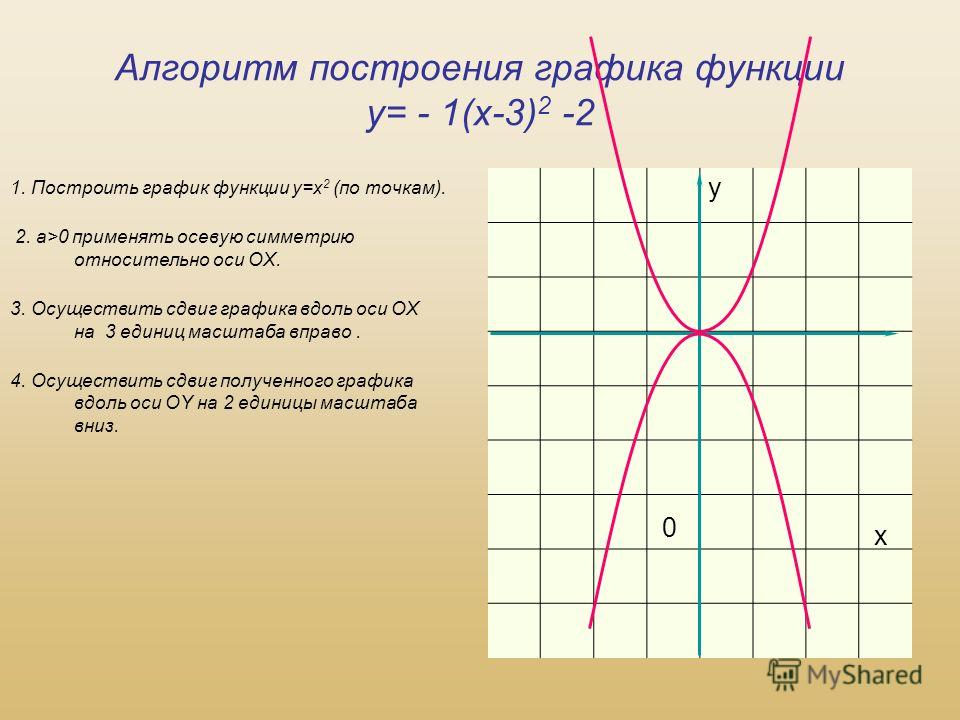 Количество ребер, которые у вас есть, зависит от вершин. Ребра могут быть направленными или ненаправленными.

В ориентированный граф , узлы связаны в одном направлении. Ребра здесь показывают одностороннюю связь.

В неориентированном графе ребра являются двунаправленными, показывая двустороннюю связь.

Пример: Хорошим примером использования неориентированного графа является алгоритм предложения друзей Facebook. Пользователь (узел) имеет ребро, идущее к другу A (другому узлу), который, в свою очередь, подключен (или имеет бегущее ребро) к другу B. Затем пользователю предлагается друг B.

Существует много других сложных типов графиков, которые попадают в разные подмножества. Ориентированный граф, например, имеет компоненты сильной связности, когда каждая вершина достижима из любой другой вершины.


Вершина

Вершина — это точка пересечения нескольких линий. Его еще называют узлом.


Ребро

Ребро — это математический термин, используемый для обозначения линии, соединяющей две вершины. Из одной вершины может быть образовано множество ребер. Однако без вершины невозможно сформировать ребро. Для каждого ребра должны быть начальная и конечная вершины.


Путь

Путь в графе G=(V,E)G = (V,E)G=(V,E) — это последовательность вершин v1, v2, …, vk, обладающая тем свойством, что являются ребрами между vivivi и vi+1vi+1vi+1. Мы говорим, что путь идет от v1v1v1 до vkvkvk.

Последовательность 6,4,5,1,26,4,5,1,2 определяет путь от узла 6 к узлу 2.

Подобным образом другие пути могут быть созданы путем обхода ребер графа. Путь называется простым, если все его вершины различны.


Обход

Обход — это путь, но он не требует последовательности отдельных вершин.


Связный граф

Граф является связным, если для каждой пары вершин uuu и vvv существует путь из uuu в vvv.


Цикл

Циклом называется путь v1, v2, …, vk, для которого верно следующее:

  • k>2k>2k>2k>2k>2k>2
  • Все первые k−1k−1k−1 вершин разные
  • v1=vkv1=vkv1=vk

Дерево

Дерево — это связный граф, не содержащий цикла.


Петля

В графе ребро, проведенное из вершины к самой себе, называется петлей. На рисунке V — это вершина, ребро которой (V, V) образует петлю.


Как представлять графы в коде

Прежде чем мы перейдем к решению задач с использованием графовых алгоритмов, важно сначала узнать, как представлять графы в коде. Графы могут быть представлены в виде матрицы смежности или списка смежности.


Матрица смежности

Матрица смежности — это квадратная матрица, помеченная вершинами графа и используемая для представления конечного графа. Элементы матрицы указывают, является ли пара вершин смежной или нет в графе.

В представлении матрицы смежности вам нужно будет перебрать все узлы, чтобы определить соседей узла.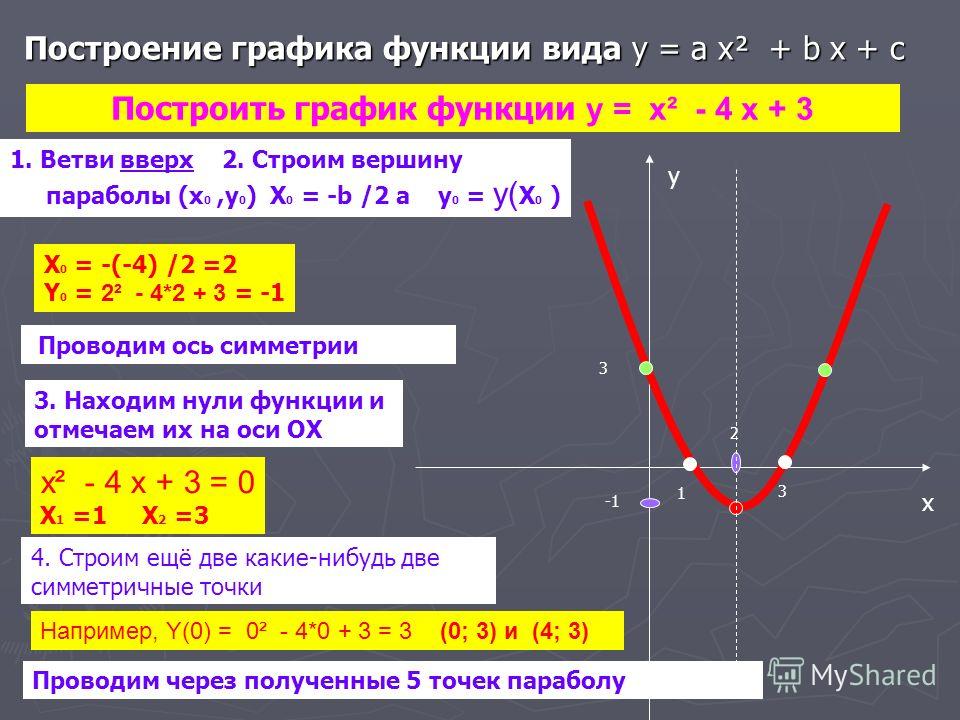

 а б в г д
а 1 1 - - -
б - - 1 - -
в - - - 1 -
г - 1 1 - -

Список смежности

Список смежности используется для представления конечного графа. Представление списка смежности позволяет легко перебирать соседей узла. Каждый индекс в списке представляет вершину, а каждый узел, связанный с этим индексом, представляет соседние с ним вершины.

 1 а -> {а б }
2б -> {с}
3 с -> { д }
4 д -> {б в }

Для класса базового графа, приведенного ниже, мы будем использовать реализацию списка смежности, так как она работает быстрее для решений алгоритмов, описанных далее в этой статье.


Класс графа

Требования к нашей реализации графа довольно просты. Нам потребуются два члена данных: общее количество вершин в графе и список для хранения смежных вершин . Нам также нужен метод для добавления ребер или набора ребер.

 
 class AdjNode: 
 
 """ 
 
 Класс для представления списка смежности узла 
 
 """ 
 
 def __init__(self, data): 
 
 5 900 
5 Constructor 02: параметр data : vertex 
 
 """ 
 
 self. vertex = data 
 
 self.next = None 
 
 class Graph: 
 
 """ 
 
 Graph Class ADT 
 
 """ 
5 _selfinit, def 
5 вершины ): 
 
 """ 
 
 Конструктор 
 
 :param vertices : Всего вершин в графе ребро в неориентированном графе 
 
 def add_edge(self, source, target): 
 
 """ 
 
 добавить ребро 
 
 :param source: Исходная вершина 
 
 :param назначение: Destination Vertex 
 
 """ 
5 
5 # Добавление узла к исходному узлу 
 
 node = AdjNode(destination) 
 
 node.next = self.graph[source] 
 
 self.graph[source] = node 
 
 # Добавление исходного узла к целевому, если неориентированный граф 
 
 # Намеренно закомментировал строки 
 
 #node = AdjNode(source) 
 
 #node.next = self.graph[destination] 
 
 #self.graph[destination] = узел 
 
 def print_graph(self): 
 
 """ 
 
 Функция распечатать график 
 
 """ 
 
 для i в диапазоне (self.V): 
 
 print("Список смежности вершин {}\n head". format(i), end="") 
 
 temp = self.graph[i] 
 
 while temp: 
 
 print(" -> {} ".format(temp.vertex), end="") 
 
 temp = temp.next 
 
 print(" \n") 
 
 # Основная программа 
 
 if __name__ == "__main__": 
 
 V = 5 # Всего вершин 
 
 g = Graph(V) 
 
 g.add_edge(0, 1) 
 
 g.add_edge(0, 4) 
 
 g.add_edge(1, 2) 
 
 g.add_edge(1, 3) ) 
 
 g.add_edge(1, 4) 
 
 g.add_edge(2, 3) 
 
 g.add_edge(3, 4) 
 
 g.print_graph()

В приведенном выше примере мы видим Python граф класса . Мы заложили основу нашего графового класса. Переменная V содержит целое число, указывающее общее количество вершин.


Продолжайте учиться.

Подготовьтесь к собеседованию по Python, не просматривая видео или документацию. Текстовые курсы Educative легко просматриваются и включают живую среду кодирования, что делает обучение быстрым и эффективным.

Интервью с первоклассным программистом на Python


Как реализовать обход в ширину

Имея граф, представленный в виде списка смежности и начальной вершины, ваш код должен вывести строку, содержащую вершины графа, перечисленные в правильном порядке обхода. Когда вы проходите граф от начальной вершины, вы должны сначала вывести правый потомок каждого узла, а затем левый.

Чтобы решить эту проблему, уже добавлен ранее реализованный класс Graph.

Ввод: Граф, представленный в виде списка смежности и начальной вершины

Вывод: Строка, содержащая вершины графа, перечисленные в правильном порядке обхода

Пример результата: 4 = «02143» или результат = «01234»

Посмотрите и разработайте пошаговый алгоритм, прежде чем переходить к реализации. Попробуйте сначала решить ее самостоятельно. Если вы застряли, вы всегда можете обратиться к решению, представленному в разделе решений.

 
 def bfs(graph, source): 
 
 """ 
 
 Функция для печати BFS графа 
 
 :param graph: Граф 
 
 :param source: начальная вершина 
 
 :return: 
5 "" " 
 
 # Напишите здесь свой код! 
 
 проход


Решение 

 
 def bfs(my_graph, source): 
 
 """ 
 
 Функция для печати BFS графика 
 :5 param00 График: 02 : источник параметра: запуск вершина 
 
 :return: 
 
 """ 
 
 # Отметить все вершины как не посещенные 
 
 посещенные = [False] * (len(my_graph. graph)) 
 
 # Создать очередь для BFS 
 
 queue = [] 
 
 # Строка результата 
 
 result = "" 
 
 # Пометить исходный узел как 
 
 # Посещенный и поставить его в очередь Удалите вершину из очереди 
 
 # и распечатайте ее 
 
 source = queue.pop(0) 
 
 result += str(source) 
 
 # Получить все смежные вершины 
 
 # источника исключенных из очереди вершин. Если соседний 
 
 # не был посещен, то отметьте его 
 
 # посещенным и поставьте в очередь 
 
, пока my_graph.graph[source] не None: 
 
 data = my_graph.graph[source].vertex 
 
 если нет посещено[данные]: 
 
 очередь.добавить(данные) 
 
 посещено[данные] = True 
 
 my_graph.graph[источник] = my_graph.graph[источник].next 
 
 вернуть результат 
 
 # Main для тестирования вышеуказанной программы 
 
 if __name__ == "__main__": 
 
 V = 5 
 
 g = Graph(V) 
 
 g.add_edge(0, 1) 
5 . add_edge(0, 2) 
 
 g.add_edge(1, 3) 
 
 g. add_edge(1, 4) 
 
 print(bfs(g, 0))

Мы начинаем с выбранного узла и пересекаем граф по слоям. Исследуются все соседние узлы. Затем мы переходим на следующий уровень. Мы проходим по графику горизонтально, то есть по каждому слою.

Граф может содержать циклы. Чтобы избежать повторной обработки одного и того же узла, мы можем использовать логический массив, который помечает посещенные массивы. Вы можете использовать очередь для хранения узла и пометить его как посещенный. Очередь должна следовать методу формирования очереди «первым пришел – первым обслужен» (FIFO).


Как реализовать обход в глубину

В этой задаче вам нужно реализовать обход в глубину. Для решения этой проблемы уже предусмотрен реализованный ранее класс графа.

Входные данные: Граф, представленный в виде списка смежности и начальной вершины

Выходные данные: Строка, содержащая вершины графа, перечисленные в правильном порядке обхода 01342″ или результат = «02143»

Посмотрите и разработайте пошаговый алгоритм, прежде чем переходить к реализации. Попробуйте сначала решить ее самостоятельно. Если вы застряли, вы всегда можете обратиться к решению, представленному в разделе решений.

 
 def dfs(graph, source): 
 
 """ 
 
 Функция для печати DFS графа 
 
 :param graph: Граф 
 
 :param source: начальная вершина 
 
 ""  
25 " 
 
 # Напишите здесь свой код! 
 
 проход


Решение 

 
 def dfs(my_graph, source): 
 
 """ 
 
 Функция для печати DFS графика 
 :9000: График 
 :
 График 002 :параметр источник: запуск вершина 
 
 :return: возвращает обход в виде строки 
 
 """ 
 
 # Отметить все вершины как не посещенные 
 
 посещенные = [False] * (len(my_graph.graph)) 
 
 # Создать стек для DFS 
 
 stack = [] 
 
 # Строка результата 
 
 result = "" 
 
 # Поместить исходный код 
 
 stack.append(source) 
 
 while stack: 
 
 # Извлечь вершину из стека 
5 90.002 pop() 
 
, если не посещали [источник]: 
 
 result += str(source) 
 
 visit[source] = True 
 
 # Получить все смежные вершины извлеченного источника вершин. 
 
 # Если соседний не был посещен, то нажать его 
 
 пока my_graph.graph[source] не None: 
 
 data = my_graph.graph[source].vertex 
 
 если не посещен[data]: 
 
 stack.append(data) 
 
 my_graph.graph[source] = my_graph.graph[source].next 
 
 return result 
 
 # Main для тестирования вышеуказанной программы 
 
 if __name__ == "__main__": 
 
 V = 5 
 
 g = Graph(V) 
 
 g.add_edge(0, 1) 
 
 g.add_edge(0, 2) 
 
 g.ad , 3) 
 
 g.add_edge(1, 4) 
 
 print(dfs(g, 0))

Алгоритм поиска в глубину использует идею поиска с возвратом. Здесь «возврат» означает двигаться вперед, пока на текущем пути больше нет узлов, а затем двигаться назад по тому же пути, чтобы найти узлы для прохождения.


Как удалить край

В этой задаче вы должны реализовать функцию remove_edge , которая принимает источник и место назначения в качестве аргументов. Если между ними существует ребро, оно должно быть удалено.

Ввод: Граф, источник (целое число) и пункт назначения (целое число)

Вывод: Обход BFS графа с удаленным ребром между источником и местом назначения

Сначала закройте рассмотрите эту проблему и разработайте пошаговый алгоритм, прежде чем переходить к реализации. Попробуйте сами, прежде чем проверять решение!

 
 def remove_edge(graph, source, target): 
 
 """ 
 
 Функция для удаления ребра 
 
 :param graph: График 
 
 :param source: Исходная вершина 
 
 :param destination: Целевая вершина 
 
 """ 
 
 # Напишите здесь свой код! 
 
 пройти

Решение

Эта задача очень похожа на удаление в связанном списке, если вы с ней знакомы.

Наши вершины хранятся в связанном списке. Сначала мы получаем доступ к источника связанный список. Если головной узел исходного связанного списка содержит удаляемый ключ, мы сдвигаем головку на один шаг вперед и возвращаем граф.

Если ключ, который нужно удалить, находится в середине связанного списка, мы отслеживаем предыдущий узел и соединяем предыдущий узел со следующим узлом при встрече с пунктом назначения.


Дополнительные вопросы для интервью

Ниже приведены другие вопросы для интервью, которые вы можете попробовать решить:

  • Проверить, является ли граф сильно связным.
  • Подсчитать все возможные пути между двумя вершинами.
  • Подсчет количества узлов на заданном уровне в дереве с использованием поиска в ширину (BFS)
  • Подсчитайте количество деревьев в лесу.
  • Обнаружить цикл на графике.
  • Найти материнскую вершину в графе.
  • Найти K ядер неориентированного графа.
  • Найдите путь в прямоугольнике с кругами.
  • Использовать минимальное остовное дерево для проектирования сети
  • Найдите кратчайший путь от одного простого числа к другому, меняя по одной цифре за раз.
  • Найдите наименьшую двоичную цифру, кратную заданному числу.
  • Высота универсального дерева от родительского массива.
  • Итеративный поиск в глубину (DFS).
  • Используйте алгоритм Крускала, чтобы найти минимальный остовный лес неориентированного графа, взвешенного по ребрам
  • Использовать жадный алгоритм минимального связующего дерева Prim (MST)
  • Минимальное количество начальных вершин для обхода всей матрицы с заданными условиями.
  • Использовать алгоритм Беллмана-Форда для вычисления кратчайших путей от вершины к другим вершинам во взвешенном графе
  • Транспонировать график.
  • Проблема с кувшином для воды при использовании BFS.

Что предстоит узнать

Поздравляем, вы дошли до конца. Вы должны понимать, что такое графы в Python, и понимать, что нужно подготовить к вопросам на интервью по кодированию, связанным с графами.

Если вы хотите узнать больше об алгоритмах в Python, ознакомьтесь с планом обучения Educative 9.0013 Интервью по кодированию на Python .

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *