Преобразование графиков тригонометрических функций — презентация онлайн
Похожие презентации:
Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций
Преобразования графиков тригонометрических функций
Преобразование графиков тригонометрических функций и их свойства
Построение графика функции у=mf(x)
Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций
Преобразование графиков функции
1. Преобразование графиков тригонометрических функций
2. Цели урока
Обобщение и систематизация знания по данной теме.Закрепление знаний, полученных при изучении данной
темы.
Формирование навыков построения графиков
тригонометрических функций.
Формирование логического и алгоритмического
мышления
Формирование интереса к предмету
Развитие познавательной активности
3.
 Идите, идите вперед, уверенность придет к Вам позже… Д , Ламбер
Идите, идите вперед, уверенность придет к Вам позже… Д , Ламбер4. Алгоритм построения графика функции y=mf(x)
Если m>01.
2.
3.
Построить график функции
y=f(x)
Осуществить его растяжение
от оси х с коэффициентом m,
если m>1
Осуществить его сжатие к
оси х с коэффициентом
1/m,если 0<m<1
Если m<0
1.
2.
3.
4.
Построить график функции
y=f(x)
Осуществить его растяжение
от оси х с положительным
коэффициентом lml, если lml
>1
Осуществить его сжатие к
оси х с коэффициентом
1/lml,если 0< lml <1
Подвергнуть график
преобразованию симметрии
относительно оси х
5. Вопрос:
Что вы можете сказать онулях функции y=f(x) при
таком преобразованиии ?
6. Подберите коэффициенты a и b так, чтобы на данном рисунке был изображен график функции y=asinx+b или y=acosx+b
А7. Подберите коэффициенты a и b так, чтобы на данном рисунке был изображен график функции y=asinx+b или y=acosx+b
Б8.
_6.png) Подберите коэффициенты a и b так, чтобы на данном рисунке был изображен график функции y=asin(x+b) или y=acos(x+b)В
Подберите коэффициенты a и b так, чтобы на данном рисунке был изображен график функции y=asin(x+b) или y=acos(x+b)В9. Подберите коэффициенты a и b так, чтобы на данном рисунке был изображен график функции y=asin(x+b) или y=acos(x+b)
Г10. Алгоритм построения графика функции y=f(kx)
Если k>01.
2.
3.
Построить график функции
y=f(x)
Осуществить его сжатие к
оси у с коэффициентом k,
если k>1
Осуществить его растяжение
от оси y с коэффициентом
1/k,если 0<k<1
Если k<0
1.
2.
3.
4.
Построить график функции
y=f(x)
Осуществить его сжатие к
оси y с положительным
коэффициентом lkl, если lkl
>1
Осуществить его растяжение
от оси y с коэффициентом
1/lkl,если 0< lkl <1
Подвергнуть график
преобразованию симметрии
относительно оси y
11. Вопрос:
Что вы можете сказать о точкепересечения графика
функции y=f(x) с осью у при
таком преобразованиии ?
12.
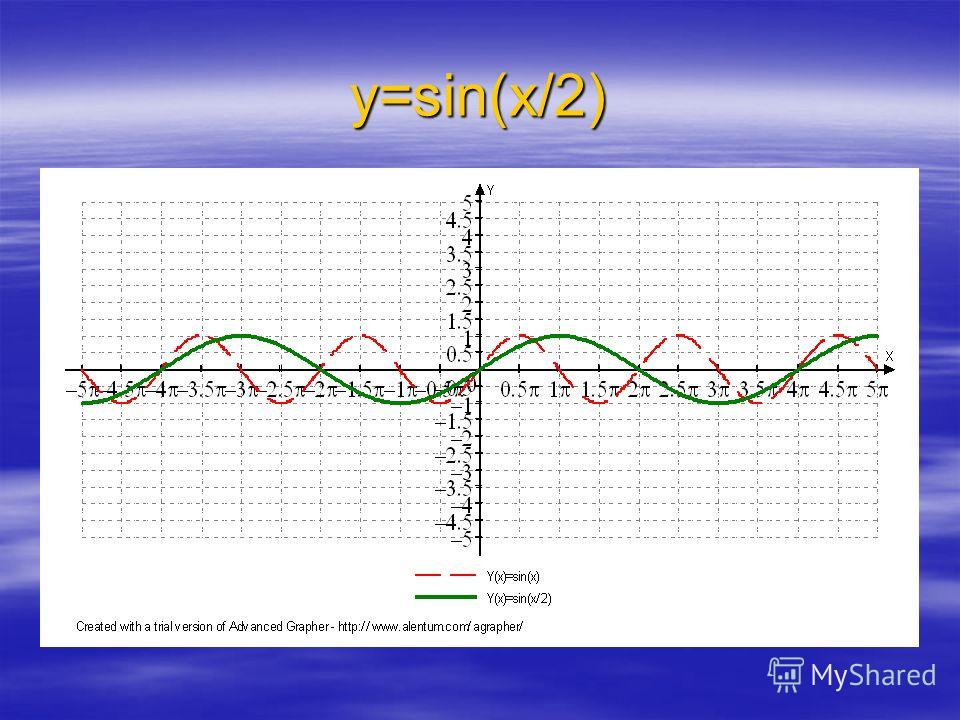 Подберите коэффициенты a,b и c так, чтобы на данном рисунке был изображен график функции y=asinbx+c или y=acosbx+cД
Подберите коэффициенты a,b и c так, чтобы на данном рисунке был изображен график функции y=asinbx+c или y=acosbx+cД13. Подберите коэффициенты a,b и c так, чтобы на данном рисунке был изображен график функции y=asinbx+c или y=acosbx+c
Е14. Составьте алгоритмы построения графиков функций
Вариант 1Составьте алгоритмы
построения графиков
функций:
1) y=3sinx
2) y= — 1/3cosx – 1
3) y= — 4cos(3x – π/2)
Вариант 2
Составьте алгоритмы
построения графиков
функций:
1) y= — 1/2cosx
2) y=4sin(x – π/6)
3) y=1/2sin(x/2 + π/3)
15. Проверьте:
Вариант 11) y=3sinх
Построить график функции y=sinx
Осуществить растяжение от оси х с
коэффициентом 3
2)y=-1/3cosx-1
Построить график функции y=cosx
Осуществить cжатие к оси х с
коэффициентом 3
Подвергнуть график
преобразованию симметрии
относительно оси х
Вариант 2
Осуществить сдвиг вдоль оси у на
1 единицу масштаба вниз
1)y=-1/2cosx
Построить график функции y=cosx
Осуществить cжатие к оси х с
коэффициентом 2
Подвергнуть график
преобразованию симметрии
относительно оси х
2)y=4sin(x-π/6)
Построить график функции y=sinx
Осуществить сдвиг вдоль оси x на
π/6 единиц масштаба вправо
Осуществить растяжение от оси х с
коэффициентом 4
16.
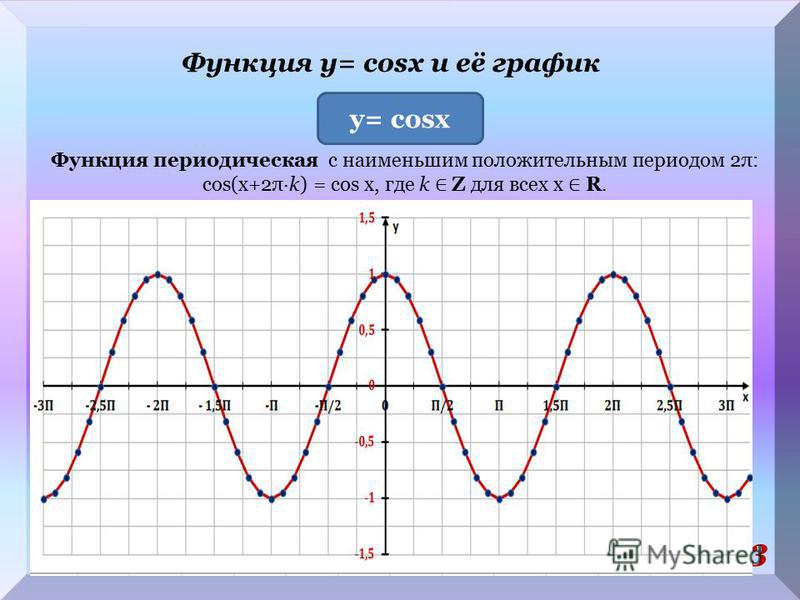 Самостоятельная работаВариант 1
Самостоятельная работаВариант 1Вариант 2
(работа в тетрадях)
(работа за компьютером)
1.Постройте график функции:
y=2sin(x+π/3).
По графику найдите:
а) область значений
функции;
б)промежутки
монотонности функции.
2.Постройте график функции:
y=cos2x+3
1.Постройте график функции:
y= — 3sin2x
По графику найдите:
а) область значений
функции;
2.Постройте график функции:
y=4cos2x-1
3.Постройте график функции:
y=3sinlxl
17. Самостоятельная работа
Вариант 1Вариант 2
(работа за компьютером)
(работа в тетрадях)
1.Постройте график функции:
y= 3cosx-2
По графику найдите:
а) область значений
функции;
2.Постройте график функции:
y= -sinx/2+1
3.Постройте график функции:
y=2lcosxl
1.Постройте график функции:
y=1/2cos(x-π/6)
2.Постройте график
функции: y= -sinx/2-2
По графику найдите:
а) область значений
функции;
б)промежутки
монотонности функции.

18. Итоги урока
Повторили алгоритмы построенияграфиков функций
Составляли алгоритмы построения
графиков и строили графики
тригонометрических функций
Проверили свои знания по данной теме,
оценивая свою работу на каждом этапе
урока
19. Домашнее задание:
№17.8(б), №17.9(г),№18.7(в), №19.4(г)
English Русский Правила
Контрольная работа по теме «Исследование функции с помощью производной»
Контрольная работа по теме «Исследование функции с помощью производной»
Вариант № 1
1. Найти промежутки возрастания и убывания функции f(х) = х3 – 3х?
2. Найти точки экстремума функции f(х) = х
3. Чему равно наибольшее и наименьшее значение функции у = – х2 + 4х + 2 на промежутке [0;4]
4. Напишите уравнение касательной к графику функции f(х) = х3– 1 в точке с абсциссой х0 = — 1
5. Найдите точку перегиба к графику функции а)у = х3 — 3х2 +1; б) y=2cos2x
Найдите точку перегиба к графику функции а)у = х3 — 3х2 +1; б) y=2cos2x
6. Исследовать с помощью производной функцию и постройте график
а) f(х) =2– 3х2 – х3 ; б) f(х) =
Вариант № 2
1. Найти промежутки возрастания и убывания функции f(х) = х3 – 3х2?
2. Найти точки экстремума функции f(х) = х3 – 6х2 + 9х
3. Чему равно наибольшее и наименьшее значение функции у = 2х2 — 8х + 11 на промежутке [0;4]
4. Напишите уравнение касательной к графику функцииf(х) = х 3 — 2х + 1 в точке с абсциссой х0 = 2
5. Найдите точку перегиба к графику функции а) у = — 3х3 +4,5х2 + 1; ; б) y=3sin2x
6. Исследовать с помощью производной функцию и постройте график
а) f(х) =2х3 -3 х2 — 4 f(х) =
Контрольная работа по теме «Исследование функции с помощью производной»
Вариант № 1
1. Найти промежутки возрастания и убывания функции f(х) = х3 – 3х?
Найти промежутки возрастания и убывания функции f(х) = х3 – 3х?
2. Найти точки экстремума функции f(х) = х3 – 9х2 + 15х
3. Чему равно наибольшее и наименьшее значение функции у = – х2 + 4х + 2 на промежутке [0;4]
4. Напишите уравнение касательной к графику функции f(х) = х3– 1 в точке с абсциссой х0 = — 1
5. Найдите точку перегиба к графику функции а)у = х3 — 3х2 +1; б) y=2cos2x
6. Исследовать с помощью производной функцию и постройте график
а) f(х) =2– 3х2 – х3 ; б) f(х) =
Вариант № 2
1. Найти промежутки возрастания и убывания функции f(х) = х3 – 3х2?
2. Найти точки экстремума функции f(х) = х3 – 6х2 + 9х
3. Чему равно наибольшее и наименьшее значение функции у = 2х2 — 8х + 11 на промежутке [0;4]
4. Напишите уравнение касательной к графику функцииf(х) = х3 — 2х + 1 в точке с абсциссой х0 = 2
5.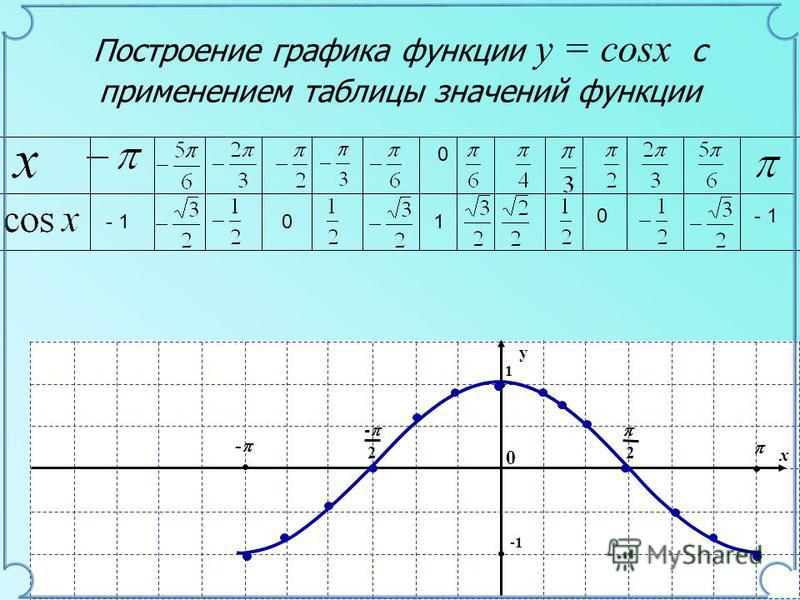 Найдите точку перегиба к графику функции а) у = — 3х3 +4,5х2 + 1; ; б) y=3sin2x
Найдите точку перегиба к графику функции а) у = — 3х3 +4,5х2 + 1; ; б) y=3sin2x
6. Исследовать с помощью производной функцию и постройте график
а) f(х) =2х3
-3 х2 — 4 f(х) =Контрольная работа по теме «Исследование функции с помощью производной»
Вариант № 1
1. Найти промежутки возрастания и убывания функции f(х) = х3 – 3х?
2. Найти точки экстремума функции f(х) = х3 – 9х2 + 15х
3. Чему равно наибольшее и наименьшее значение функции у = – х2 + 4х + 2 на промежутке [0;4]
4. Напишите уравнение касательной к графику функции f(х) = х3– 1 в точке с абсциссой х0 = — 1
5. Найдите точку перегиба к графику функции а)у = х3 — 3х2 +1; б) y=2cos2x
6. Исследовать с помощью производной функцию и постройте график
а) f(х) =2– 3х2 – х3 ; б) f(х) =
Вариант № 2
1.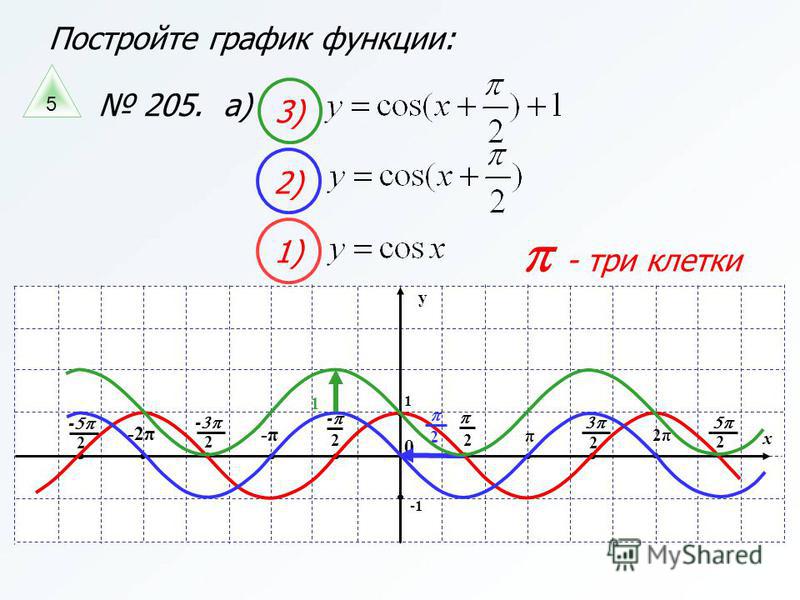 Найти промежутки возрастания и убывания функции f(х) = х
Найти промежутки возрастания и убывания функции f(х) = х
2. Найти точки экстремума функции f(х) = х3 – 6х2 + 9х
3. Чему равно наибольшее и наименьшее значение функции у = 2х2 — 8х + 11 на промежутке [0;4]
4. Напишите уравнение касательной к графику функцииf(х) = х3 — 2х + 1 в точке с абсциссой х0 = 2
5. Найдите точку перегиба к графику функции а) у = — 3х3 +4,5х2 + 1; ; б) y=3sin2x
6. Исследовать с помощью производной функцию и постройте график
а) f(х) =2х3 -3 х2 — 4 f(х) =
Чтобы изучить y=3cos2x-3sin2x, посмотрите на график, созданный Вольфрам Альфа на интервале [-пи, пи]. 2. Обратите внимание на наименьший фазовый сдвиг, учитывая косинусоидальную волну. паттерн представляет собой сдвиг влево на ок. пи/8. Используйте этот сдвиг и Амплитуда период (так что В = ) Отсюда видно, что y = 3cos2x −3sin 2x можно записать у = AcosB (х + пи / 8) 3.
 Вставьте свои значения для A и B, как указано выше, и напишите
уравнение в более традиционной форме
у = Acos(Bx+C)
4. Обратите внимание, что в нашем первом примере y=acosBx-bsinBx a=b=3
Также обратите внимание, что прямоугольный треугольник с катетами a и b будет иметь
гипотенуза 3sqrt2 ок. равно 4.2 Каковы отсутствующие меры угла в радианах?
Вставьте свои значения для A и B, как указано выше, и напишите
уравнение в более традиционной форме
у = Acos(Bx+C)
4. Обратите внимание, что в нашем первом примере y=acosBx-bsinBx a=b=3
Также обратите внимание, что прямоугольный треугольник с катетами a и b будет иметь
гипотенуза 3sqrt2 ок. равно 4.2 Каковы отсутствующие меры угла в радианах?Вопрос
Пошаговый ответ
AI Рекомендуемый ответ:
1. Определите функцию и область ее применения.
y=acosBx-bsinBx
2. Найдите график y=acosBx-bsinBx.
Рекомендация видео с лучшим совпадением:
Решено проверенным экспертом
У нас нет заданного вами вопроса, но вот рекомендуемое видео, которое может помочь. 9{\ circ} $ $ (ГРАФИК НЕ КОПИРУЕТСЯ)
Рекомендуемые видео
Стенограмма
Все в порядке. Я нарисовал грубую картину того, как выглядит график после того, как мне дали график. Первое, что нас просят сделать, это найти уравнение для графика. Ладно, давай уберем это с дороги. Мы можем использовать знак или сознак. Я вижу, что это начинается здесь и идет вниз и вокруг, пока не закончится здесь. Я вижу это как график сознаков. Это то, что я собираюсь использовать. Мы должны проработать это немного в обратном направлении. В части B сказано давать период сдвига фаз и сонь. Я собираюсь сделать часть B и ответить на часть A для этих вещей. Это только половина дистанции от макса до мужчин. Максимальный возраст для мужчин — 12 лет. Мы сократили его вдвое. У нас есть число шесть. Так что шесть. Это перед знаком? Дистанция 200-20м. Помните, что период отображается и рассчитывается по уравнению. Мы знаем, что это 180 больше b. Мы можем понять, что B тоже с небольшим количеством математики. Мы знаем, что период равен 180. Мы это тоже знаем. Является ли это фактором смещения фаз? Эта точка должна быть здесь. К 20 она смещена вправо. У нас фазовый сдвиг равен 20. Когда мы вычислим тета минус постоянная, мы назовем это x.
Первое, что нас просят сделать, это найти уравнение для графика. Ладно, давай уберем это с дороги. Мы можем использовать знак или сознак. Я вижу, что это начинается здесь и идет вниз и вокруг, пока не закончится здесь. Я вижу это как график сознаков. Это то, что я собираюсь использовать. Мы должны проработать это немного в обратном направлении. В части B сказано давать период сдвига фаз и сонь. Я собираюсь сделать часть B и ответить на часть A для этих вещей. Это только половина дистанции от макса до мужчин. Максимальный возраст для мужчин — 12 лет. Мы сократили его вдвое. У нас есть число шесть. Так что шесть. Это перед знаком? Дистанция 200-20м. Помните, что период отображается и рассчитывается по уравнению. Мы знаем, что это 180 больше b. Мы можем понять, что B тоже с небольшим количеством математики. Мы знаем, что период равен 180. Мы это тоже знаем. Является ли это фактором смещения фаз? Эта точка должна быть здесь. К 20 она смещена вправо. У нас фазовый сдвиг равен 20. Когда мы вычислим тета минус постоянная, мы назовем это x.

Поделиться вопросом
Добавить в плейлист
Хммм, кажется, у вас нет плейлистов. Пожалуйста, добавьте свой первый плейлист.
`
Эскиз графика и области состояний, диапазона, амплитуды, периода и фазового сдвига, если необходимо. у=3sin2x
Цитата страницы Начать эссе значок-вопрос Спросите репетитора Начать бесплатную пробную версию Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяСсылайтесь на эту страницу следующим образом:
«Нарисуйте график и область состояния, диапазон, амплитуду, период и фазовый сдвиг, если необходимо. y = 3sin2x» Редакционная статья eNotes , 15 февраля 2013 г., https://www.enotes.com/homework-help/sketch-graph- диапазон-амплитуда-период-384777.
По состоянию на 15 февраля 2023 г.
y = 3sin2x» Редакционная статья eNotes , 15 февраля 2013 г., https://www.enotes.com/homework-help/sketch-graph- диапазон-амплитуда-период-384777.
По состоянию на 15 февраля 2023 г.
Вам нужно найти область определения функции `y = 3sin 2x`, следовательно, `x in R`.
Вам нужно найти диапазон функции, такой что:
`-1*3 <= 3sin2x <= 1*3 => -3 <= 3sin 2x <= 3 => y in [-3,3] `
Вам нужно найти амплитуду, поэтому `a = 3` .
Фазовый сдвиг отсутствует, и, поскольку функция растянута по горизонтали на 2, получается, что вы можете оценить период таким образом, что:
`T = (2pi)/2 => T = pi` функции дает `x в R`, диапазон функции `y в [-3,3]`, амплитуда функции `a = 3`, период функции `T = pi` фазового сдвига нет.
Набросок графика, выходы:
Утверждено редакцией eNotes
Математика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 Ответы воспитателя
Математика
Последний ответ опубликован 07 октября 2013 г. в 20:13:27.
Как определить, является ли это уравнение линейной или нелинейной функцией?
84 Ответы воспитателя
Математика
Последний ответ опубликован 09 октября 2017 г. в 00:54:39
Добавьте 1 плюс 2 плюс 3 плюс 4. . . вплоть до 100.
3 Ответы воспитателя
Математика
Последний ответ опубликован 25 февраля 2016 г. в 18:48:45.
Сколько времени (в часах) займет ваше путешествие, если вы проедете 350 км со средней скоростью 80 км/ч? Какова формула с данными: время, расстояние, скорость или скорость?
1 Ответ учителя
Математика
Последний ответ опубликован 15 мая 2012 г.
