1. 5x + 4 = x + 12 2. 13 – 5y = 8 – 2y 3. 5x + (3x – 7) = 9 4. 3y – (5 – y) = 11 5. (7a + 1) – ( 6a + 3) = 5 6. (8s + 11) – 13 = 9s– 5 7. (5x – 3)+(7x – 4) = 8 – (15 – 11x) 8. (7 – 5k) – (8 – 4k) + (5k + 6) = 8 9. 2x + 5 = 2(x + 1) + 11 10. 15(v + 2) – 30 = 15v 11. 5(3x + 1,2) + x = 6,8 12. 0,4b + 3 = 0,2(3b + 1) – b 13. 6(x – 1) = 9,4 – 1,7x 14. 3,5 – 9a = 2(0,5a – 4) 15. 3(2,4 – 1,1m) = 2,7m + 3,2 16. 3(x – 1) = 2(2 – x) + 6 17. 4(3 – h) – 11 = 7(2h– 5) 18. –3(3y + 4) + 4(2y – 1) = 0 19. 0,3(5x – 7) = 3(0,2x + 3,2) 20. 4(1,2b + 3,7) – 2,8 = 5,2b 21. 0,9(4y – 2) = 0,5(3y – 4) + 4,4 22. 4(0,2x – 7) – 5(0,3x + 6) = 5 1. 8x – 5 = x – 40 2. 9 + 13y = 35 + 26y 3. 6s+ (3s – 2) = 14 4. 8y – (7y – 142) = 51 5. (6x + 1) – (3 – 2x) = 14 6. (6 – 2c) + 4 = – 5c – 3 7. (10x–3) + (14x–4) = 8 – (15 – 22x) 8. (7–10k) – (8–8k) + (10k + 6) = – 8 9. 6y – 20 = 2(5y – 10) – 4y 10. 6(1 + 5v) = 5(1 + 6v) 11. 4(x + 3,6) = 3x – 1,4 12. 3,4 – 0,6b= 2b – (0,4b+ 1) 13.
– 3(y + 2,5) = 6,9 – 4,2y 14. 0,5y + 7 = 5(0,2 + 1,5y) 15. 4(x – 0,8) = 3,8x – 5,8 16. 4(1 – 0,5a) = – 2(3 + 2a) 17. 2(h – 3) = 3(4 – h) + 5 18. 3x + 2(2x – 3) = 8 – 7(x + 2) 19. 0,7(5z – 3) = 5(0,1 + 0,5z) 20. 4(3 – 2x) + 24 = 2(3 + 2x) 21. 0,2(5y – 2) = 0,3(2y –1) – 0,9 22. 3(0,4x + 7) – 4(0,8x – 3) = 2 1. 1,3p – 11 = 0,8p + 5 2. 0,71x – 13 = 10 – 0,29x 3. 8c + 0,73 = 4,61 – 8c 4. 13 – (5x + 11) = 6x 5. 2 = (3x – 5) – (7 – 4x) 6. 8x + 5 = 119 + (7 – 3x) 7. (4y + 3) – (10y + 11) = 7 + (13 – 4y) 8. (3 – 2x) + (4 – 3x) + (5–5x) = 12 + 7x 9. 3y – (y – 19) = 2y 10. 3y + (y – 2) = 2(2y – 1) 11. 13 – 4,5a = 2(3,7 – 0,5a) 12. 0,8x – (0,7x + 0,36) = 7,1 13. 7(x – 8,2) = 3x + 19 14. 0,2(5x – 6) + 2x = 0,8 15. – (7y + 0,6) = 3,6 – y 16. 5(x + 2) = 4(3 – x) + 7 17. – 3(5 – 2x) + 4x = 5(x – 3) + 27 18. 0,4(6x – 7) = 0,5(3x + 7) 19. 7(1,4y + 1,8) – 27,6 = 10,1y 20. 3(5 – x) + 13 = 4(3x – 8) 21. 0,7(6y – 5) = 0,4(y – 3) – 1,16 22. – 7(0,3x – 8) + 3( 0,4x + 5) = 8 1. 0,3p – 5 = 6 – 0,7p 2. 9c + 2,65 = 36,85 – 9c 3.
5 = – 1 – (3 – 9x) 4. – 9 – (8x – 11) = 12 5. 12 = (7x – 9) – (11 – x) 6. 11x + 103 = 1 + (12x – 31) 7. (2x + 3) – (5x + 11) = 7 + (13 – 2x) 8. (2x + 3) + (3x + 4) + (5x + 5)=12 –7x 9. 6x = 1 – (4 – 6x) 10. 6y – (y – 4) = 4 + 5y 11. 5,6 – 7y = – 4(2y – 0,9) + 2,4 12. x – 0,5 = 2(0,3x – 0,2) 13. 3(2,5 – 2x) = 13,5 – 14x 14. 0,6y – 1,5 = 0,3(y – 4) 15. 0,5(4 – 2a) = a – 1,8 16. 7(3 + x) = 2(x – 5) + 8 17. – 0,2(5 – 0,7x) + 0,02 = 1,4(x – 1,6) 18. 1,2(3b + 5) = 2(2,4b – 3,6) 19. 3,2(5x – 1) = 3,6x – 9,4 20. 8(0,7x – 4) – 2(0,2x – 3) = – 39 21. – 3(2,1z – 4) – 4,2 = 1,2(– 5z + 0,5) 22. 6,4(2 – 3y) = 6(0,8y – 1) + 6,8Опубликовано 3 года назад по предмету Математика от Olga831106
Русский язык — 2 года назад
В каком из предложений пропущена одна (только одна!) запятая?1.она снова умолкла, точно некий внутренний голос приказал ей замолчать и посмотрела в зал.
2.и он понял: вот что неожиданно пришло к нему, и теперь останется с ним, и уже никогда его не покинет. 3.и оба мы немножко удовлетворим свое любопытство.4.впрочем, он и сам только еле передвигал ноги, а тело его совсем застыло и было холодное, как камень. 5.по небу потянулись облака, и луна померкла.
| 1 | Найти том | сфера (5) | | |
| 2 | Найти площадь | круг (5) | | |
| 3 | Найдите площадь поверхности | сфера (5) | | |
| 4 | Найти площадь | круг (7) | | |
| 5 | Найти площадь | круг (2) | | |
| 6 | Найти площадь | круг (4) | | |
| 7 | Найти площадь | круг (6) | | |
| 8 | Найти том | сфера (4) | | |
| 9 | Найти площадь | круг (3) | | |
| 10 9(1/2) | ||||
| 11 | Найти простую факторизацию | 741 | ||
| 12 | Найти том | сфера (3) | | |
| 13 | Оценить | 3 квадратный корень из 8*3 квадратный корень из 10 | ||
| 14 | Найти площадь | круг (10) | | |
| 15 | Найти площадь | круг (8) | | |
| 16 | Найдите площадь поверхности | сфера (6) | | |
| 17 | Найти простую факторизацию | 1162 | ||
| 18 | Найти площадь | круг (1) | | |
| 19 | Найдите окружность | круг (5) | | |
| 20 | Найти том | сфера (2) | | |
| 21 | Найти том | сфера (6) | | |
| 22 | Найдите площадь поверхности | сфера (4) | | |
| 23 | Найти том | сфера (7) | | |
| 24 | Оценить | квадратный корень из -121 | ||
| 25 | Найти простую факторизацию | 513 | ||
| 26 | Оценка | квадратный корень из 3/16* квадратный корень из 3/9 | ||
| 27 | Найти том | коробка (2)(2)(2) | | |
| 28 | Найдите окружность | круг (6) | | |
| 29 | Найдите окружность | круг (3) | | |
| 30 | Найдите площадь поверхности | сфера (2) | | |
| 31 | Оценить | 2 1/2÷22000000 | ||
| 32 | Найдите Том | коробка (5)(5)(5) | | |
| 33 | Найти том | коробка (10)(10)(10) | | |
| 34 | Найдите окружность | круг (4) | | |
| 35 | Преобразование в проценты | 1,7 | ||
| 36 | Оценить | (5/6)÷(4/1) | ||
| 37 | Оценить | 3/5+3/5 | ||
| 38 | Оценить | ф(-2) | 92 | |
| 40 | Найти площадь | круг (12) | | |
| 41 | Найти том | коробка (3)(3)(3) | | |
| 42 | Найти том | коробка (4)(4)(4) | 92-4*-1+2||
| 45 | Найти простую факторизацию | 228 | ||
| 46 | Оценить | 0+0 | ||
| 47 | Найти площадь | круг (9) | | |
| 48 | Найдите окружность | круг (8) | | |
| 49 | Найдите окружность | круг (7) | | |
| 50 | Найти том | сфера (10) | | |
| 51 | Найдите площадь поверхности | сфера (10) | | |
| 52 | Найдите площадь поверхности | сфера (7) | | |
| 53 | Определить, является простым или составным | 5 | ||
| 60 | Преобразование в упрощенную дробь | 2 1/4 | ||
| 61 | Найдите площадь поверхности | сфера (12) | | |
| 62 | Найти том | сфера (1) | | |
| 63 | Найдите окружность | круг (2) | | |
| 64 | Найти том | коробка (12)(12)(12) | | |
| 65 | Добавить | 2+2= | ||
| 66 | Найдите площадь поверхности | коробка (3)(3)(3) | | |
| 67 | Оценить | корень пятой степени из 6* корень шестой из 7 | ||
| 68 | Оценить | 7/40+17/50 | ||
| 69 | Найти простую факторизацию | 1617 | ||
| 70 | Оценить | 27-(квадратный корень из 89)/32 | ||
| 71 | Оценить | 9÷4 | ||
| 72 | Оценка 92 | |||
| 74 | Оценить | 1-(1-15/16) | ||
| 75 | Преобразование в упрощенную дробь | 8 | ||
| 76 | Оценка | 656-521 | 9-2 | |
| 79 | Оценить | 4-(6)/-5 | ||
| 80 | Оценить | 3-3*6+2 | ||
| 81 | Найдите площадь поверхности | коробка (5)(5)(5) | | |
| 82 | Найдите площадь поверхности | сфера (8) | | |
| 83 | Найти площадь | круг (14) | | |
| 84 | Преобразование в десятичное число | 5 ноября | ||
| 85 9-2 | ||||
| 88 | Оценить | 1/2*3*9 | ||
| 89 | Оценить | 4/4-17/-4 | ||
| 90 | Оценить | 11. 02+17.19 | ||
| 91 | Оценить | 3/5+3/10 | ||
| 92 | Оценить | 4/5*3/8 | ||
| 93 | Оценить | 6/(2(2+1)) | ||
| 94 | Упростить | квадратный корень из 144 | ||
| 95 | Преобразование в упрощенную дробь | 725% | ||
| 96 | Преобразование в упрощенную дробь | 6 1/4 | ||
| 97 | Оценить | 7/10-2/5 | ||
| 98 | Оценить | 6÷3 | ||
| 99 | Оценить | 5+4 | ||
| 100 | Оценить | квадратный корень из 12- квадратный корень из 192 |
Решить {l}{2x+3y=19}{x-2y=-1} | Microsoft Math Solver.
\begin{array} { l } { 2 x + 3 y = 19 } \\ { x — 2 y = — 1 } \end{array} \right.Аналогичные задачи из веб-поиска
Поделиться
Скопировано в буфер обмена
2x+3y=19,x-2y=-1
Чтобы решить пару уравнений с помощью подстановки, сначала решите одно из уравнений для одного из переменные. Затем подставьте результат этой переменной в другое уравнение.
2x+3y=19
Выберите одно из уравнений и решите его относительно x, выделив x слева от знака равенства.
2x=-3y+19
Вычтите 3y из обеих частей уравнения.
x=\frac{1}{2}\left(-3y+19\right)
Разделите обе части на 2.
x=-\frac{3}{2}y+\frac{19}{ 2}
Умножьте \frac{1}{2} на -3y+19.
-\frac{3}{2}y+\frac{19}{2}-2y=-1
Подставьте \frac{-3y+19}{2} вместо x в другое уравнение, x-2y= -1.
-\frac{7}{2}y+\frac{19}{2}=-1
Добавьте -\frac{3y}{2} к -2y.
-\frac{7}{2}y=-\frac{21}{2}
Вычтите \frac{19}{2} из обеих частей уравнения.
y=3
Разделите обе части уравнения на -\frac{7}{2}, что равносильно умножению обеих частей на обратную дробь.
x=-\frac{3}{2}\times 3+\frac{19}{2}
Подставьте 3 вместо y в x=-\frac{3}{2}y+\frac{19}{ 2}. Поскольку результирующее уравнение содержит только одну переменную, вы можете найти x напрямую.
x=\frac{-9+19}{2}
Умножить -\frac{3}{2} на 3.
x=5
Добавить \frac{19}{2} к -\frac {9}{2} путем нахождения общего знаменателя и сложения числителей. Затем уменьшите дробь до меньших членов, если это возможно.
x=5,y=3
Теперь система решена.
2x+3y=19,x-2y=-1
Приведите уравнения к стандартной форме, а затем используйте матрицы для решения системы уравнений.
\left(\begin{matrix}2&3\\1&-2\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin {матрица} 19\\-1\end{matrix}\right)
Запишите уравнения в матричной форме.
обратная (\ левая (\ начало {матрица} 2 и 3 \\ 1 и -2 \ конец {матрица} \ правая)) \ левая (\ начало {матрица} 2 и 3 \\ 1 & -2 \ конец {матрица} \ правая) \ влево (\ начало {матрица} х \\ у \ конец {матрица} \ вправо) = обратное (\ влево (\ начало {матрица} 2 и 3 \\ 1 и -2 \ конец {матрица} \ вправо)) \ влево (\ начало {matrix}19\\-1\end{matrix}\right)
Слева умножьте уравнение на обратную матрицу \left(\begin{matrix}2&3\\1&-2\end{matrix}\right).
\left(\begin{matrix}1&0\\0&1\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin {матрица}2&3\\1&-2\конец{матрица}\справа))\влево(\начало{матрица}19\\-1\end{matrix}\right)
Произведение матрицы и ее обратной является единичной матрицей.
\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}2&3\\1&-2\end{matrix}\right))\left (\begin{matrix}19\\-1\end{matrix}\right)
Умножьте матрицы слева от знака равенства.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{-2}{2\left(-2\right)-3} &-\frac{3}{2\left(-2\right)-3}\\-\frac{1}{2\left(-2\right)-3}&\frac{2}{2\ влево(-2\вправо)-3}\конец{матрица}\вправо)\влево(\начать{матрица}19\\-1\end{matrix}\right)
Для матрицы 2\times 2 \left(\begin{matrix}a&b\\c&d\end{matrix}\right) обратная матрица равна \left(\ begin{matrix}\frac{d}{ad-bc}&\frac{-b}{ad-bc}\\\frac{-c}{ad-bc}&\frac{a}{ad-bc} \end{matrix}\right), поэтому матричное уравнение можно переписать как задачу на умножение матриц.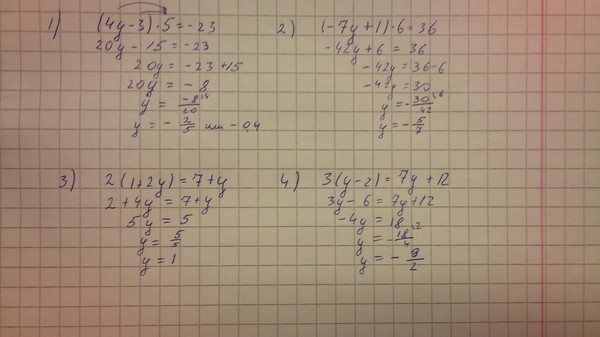
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{2}{7}&\frac{3}{7}\\ \frac{1}{7}&-\frac{2}{7}\end{matrix}\right)\left(\begin{matrix}19\\-1\end{matrix}\right)
Выполните арифметические действия.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{2}{7}\times 19+\frac{3}{7 }\left(-1\right)\\\frac{1}{7}\times 19-\frac{2}{7}\left(-1\right)\end{matrix}\right)
Умножить матрицы.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}5\\3\end{matrix}\right)
Выполните арифметические действия.
x=5,y=3
Извлечь элементы матрицы x и y.
2x+3y=19,x-2y=-1
Чтобы решить методом исключения, коэффициенты одной из переменных должны быть одинаковыми в обоих уравнениях, чтобы переменная сокращалась при вычитании одного уравнения из другого.
2x+3y=19,2x+2\влево(-2\вправо)y=2\влево(-1\вправо)
Чтобы сделать 2x и x равными, умножьте все члены с каждой стороны первого уравнения на 1 и все члены по обе стороны от второго на 2.
2x+3y=19,2x-4y=-2
Упростить.
2x-2x+3y+4y=19+2
Вычтите 2x-4y=-2 из 2x+3y=19, вычитая одинаковые члены по обе стороны от знака равенства.
3y+4y=19+2
Прибавьте 2x к -2x. Члены 2x и -2x сокращаются, оставляя уравнение только с одной переменной, которую можно решить.
7 лет=19+2
Добавить 3 года к 4 годам.
7y=21
Прибавьте 19 к 2.
y=3
Разделите обе части на 7.
x-2\times 3=-1
Подставьте 3 вместо y в x-2y=-1. Поскольку результирующее уравнение содержит только одну переменную, вы можете найти x напрямую. 9{ 2 } — 4 x — 5 = 0
Тригонометрия
4 \sin \theta \cos \theta = 2 \sin \theta
Линейное уравнение
y = 3x + 4
Арифметика
90Матрица
\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin {array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{массив} \right]
Одновременное уравнение
\left.