где применяется и как построить
Что это такое? Диаграмма Эйлера кажется чем-то очень сложным на первый взгляд. Однако на самом деле это круги, накладываемые друг на друга при решение определенных задач. Их применяют в алгебре, информатике и даже в жизни, столкнувшись с каким-то выбором.
Как строить? Для начала нужно представить универсальное множество в виде прямоугольника. Внутри него будут эллипсы или круги, которые могут пересекаться, а могут и нет. Их можно дополнять, объединять, пересекать. Давайте рассмотрим все это на примере ниже.
В статье рассказывается:
- Что собой представляет диаграмма Эйлера
- Разница между диаграммой Эйлера и диаграммой Эйлера-Венна
- Задачи, решаемые диаграммой Эйлера
- Принцип построения диаграммы
- Применение диаграмм для доказательства логических равенств
-
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.
Бесплатно от Geekbrains
Что собой представляет диаграмма Эйлера
Так называется геометрическое изображение, которое используют, чтобы смоделировать множества и схематично отразить отношения между ними. На диаграмме Эйлера наглядно показаны утверждения о данных множествах.
При этом универсальное множество обозначено прямоугольником, а подмножества изображены в виде кругов. Поэтому диаграмму называют также «круги Эйлера». Такое схематичное изображение применяют при решении математических и логических задач, а также в менеджменте и различных прикладных целях.
Автор этого способа – математик XVIII века Леонард Эйлер, который хотел таким образом помочь размышлениям. Автором кругов является известный математик Леонард Эйлер, который считал, что они необходимы, чтобы облегчить размышления человека. Диаграмма Эйлера стала признанным методом с момента своего появления.
Что собой представляет диаграмма ЭйлераБиография Леонарда Эйлера связана со Швейцарией, Пруссией и Россией. {n}} комбинаций π{\displaystyle n} свойств, то есть конечную булеву алгебру. При π = 3 диаграмма Эйлера-Венна обычно выглядит как три круга, имеющих одинаковый радиус, их центры совпадают с вершинами равностороннего треугольника, стороне которого приблизительно равны радиусы.
{n}} комбинаций π{\displaystyle n} свойств, то есть конечную булеву алгебру. При π = 3 диаграмма Эйлера-Венна обычно выглядит как три круга, имеющих одинаковый радиус, их центры совпадают с вершинами равностороннего треугольника, стороне которого приблизительно равны радиусы.
Если определённая комбинация свойств соответствует пустому множеству, на схеме эту область закрашивают. Диаграммы Эйлера могут быть не типичны, а иногда эквивалентны диаграммам Венна. Закрашенный участок схемы указывает на то, что это множество не содержит элементов, то есть пустое.
Задачи, решаемые диаграммой Эйлера
Прикладное значение, которое имеет диаграмма Эйлера: задачи на соотношение множеств в математике, логике, информатике, статистике становятся понятнее при её использовании. Круги Эйлера можно применять и в жизни, находя с их помощью взаимосвязи и отвечая на возникающие насущные вопросы.
Задачи, решаемые диаграммой ЭйлераКруги Эйлера можно разделить на такие группы:
- равнозначные;
- пересекающиеся;
- подчиненные;
- соподчиненные;
- противоречащие;
- противоположные.

Выполняя упражнения на развитие мышления, чаще всего можно столкнуться с двумя их видами:
- Круги, изображающие объединяющиеся понятия и вложенные один в другой, чтобы это показать.
- Круги, иллюстрирующие пересечения различных множеств, которые имеют те или иные общие признаки.
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
pdf 3,7mb
doc 1,7mb
Уже скачали 20496
Приведём пример использования кругов при выборе профессии. Можно перебирать варианты, обдумывая наиболее подходящий, а можно начертить схему, изобразив в виде кругов то, что вам нравится делать, что вы умеете, и что хорошо оплачивается.
Метод прост в применении и подходит для всех. Его используют и при работе с дошкольниками в детском саду с 4-5 лет, и при обучении студентов (например, можно увидеть подобные задачи в ЕГЭ по информатике), и в научной среде.
Принцип построения диаграммы
При построении диаграммы Эйлера сначала рисуют большой прямоугольник, обозначающий универсальное множество U. Внутри этого прямоугольника располагают фигуры, которые являются изображением множеств: круги (если их не больше трёх) или круги и эллипсы (когда множеств четыре и больше). Фигуры пересекаются различными способами, в зависимости от условий задачи.
Допустим, у нас имеется выражение А. Изображаем на диаграмме круг, обозначающий множество А. Пространство внутри круга показывает значения, при которых выражение А будет истинным, а область снаружи обозначает ложь. Чтобы отобразить на схеме логическую операцию, заштрихуем те части диаграммы, в которых значения истинны.
Можно доказать любой закон алгебры, представив его в виде графической схемы при помощи диаграммы Эйлера. Алгоритм действий таков:
- Сначала чертим диаграмму и заштриховываем все множества, которые находятся с левой стороны от знака «равно».
- Затем нужно начертить другую диаграмму и на ней заштриховать множества, находящиеся справа от знака равенства.
- Если на диаграммах окажется заштрихованной одна и та же область, тождество будет истинным.
Сильнее углубимся в тему.
Дополнение множества
Дополнением к множеству A будет множество Его элементы не относятся к множеству А.
= {x | x ∉ A}
Но в включаются не все элементы, не относящиеся к А. По условиям применения диаграммы Эйлера, все множества, о которых идёт речь в задаче, будут включены в универсальное множество U, то есть являются его подмножествами. С учётом этого дополнение будет определяться так:
=U∖A
Объединение множеств
Объединением двух множеств (назовём их А и В) будет множество A ∪ B, состоящее из элементов, которые включаются хотя бы в одно из них.
Это можно записать так:
A ∪ B={x |x ∈ A или x ∈ B}
Пересечение множеств
Пересечение множеств A и B это множество A ∩ B. Оно состоит из элементов, которые входят и в множество А, и в то же время в множество В.
Только до 24.04
Скачай подборку тестов, чтобы определить свои самые конкурентные скиллы
Список документов:
Тест на определение компетенций
Чек-лист «Как избежать обмана при трудоустройстве»
Инструкция по выходу из выгорания
Чтобы получить файл, укажите e-mail:
Подтвердите, что вы не робот,
указав номер телефона:
Уже скачали 7503
Записывается пересечение множеств так:
A ∩ B = {x | x ∈ A и x ∈ B}
Симметричная разность множеств
Симметричная разность – это множество A \ B, в которое включаются элементы, которые входят только в одно из множеств А и В, но не в оба сразу.
Запись симметричной разности выглядит таким образом:
A △ B = (A ∖ B) ∪ (B ∖ A)
Разность множеств
Разностью A \ B являются элементы множества A, не входящие в B.
Записанная разность множеств выглядит так:
A ∖ B = {x | x ∈ A и x ∉ B}
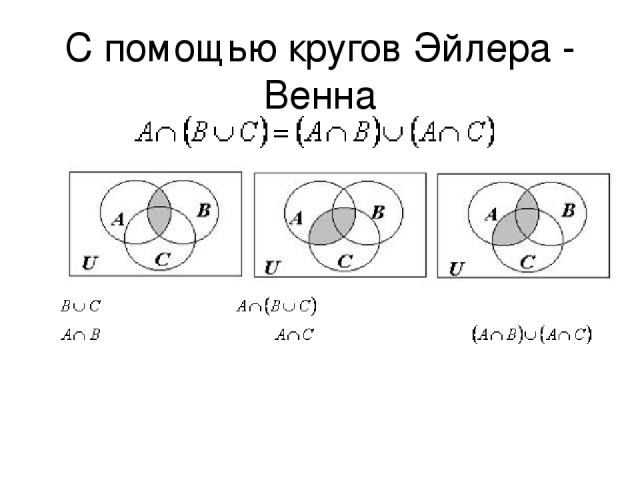
Применение диаграмм для доказательства логических равенств
Давайте рассмотрим, как применяется диаграмма Эйлера на примере доказательства логического равенства.
Применение диаграмм для доказательства логических равенствПредставим, что мы имеем конъюнкцию множеств A ∧ B.
Сначала работаем с левой частью равенства. Нужно с помощью диаграммы Эйлера построить множества А и В, заштриховать оба круга цветом и таким образом выделим дизъюнкцию.
Дальше нужно показать инверсию с помощью штриховки области за пределами этих множеств.
Теперь переключаемся на правую часть равенства. Сперва показываем цветной штриховкой за пределами круга А инверсию этого множества.
То же самое действие выполняем для множества В.
Штрихуем чёрным цветом все области пересечения и получаем графическое отображение конъюкции инверсий множеств А и В.
Сравнивая области, отображающие правую и левую части равенства, убеждаемся, что они равны. Таким образом, истинность логического равенства доказана при помощи диаграммы Эйлера.
Пример решения задачи с помощью кругов Эйлера
В демонстрационном тесте ЕГЭ по информатике и ИКТ была представлена задача, которую мы решим с применением этого метода.
Условия задачи:
В языке запросов поискового применяется символ «|» для логической операции «или» и символ «&», чтобы обозначить логическую операцию «и».
Таблица, приведённая ниже, отражает запросы в некотором сегменте сети Интернет и количество найденных страниц по этим запросам.
| Запрос | Найдено страниц (в тысячах) |
| Крейсер | Линкор | 7000 |
| Крейсер | 4800 |
| Линкор | 4500 |
Вопрос: какое количество страниц (в тысячах) найдётся, если запрос будет сформулирован в виде Крейсер & Линкор?
Принимаем версию, что все запросы выполняются в один отрезок времени, поэтому набор страниц, которые включают искомые слова, остался неизменным.
Решение:
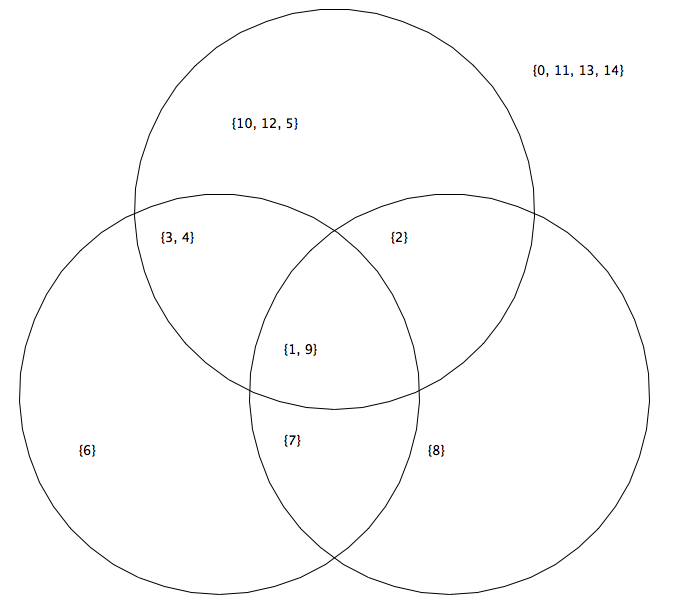
Покажем условие задачи при помощи диаграммы Эйлера. Используем цифры 1, 2 и 3 для обозначения полученных областей.
Используя условия задачи, составляем уравнения:
- Крейсер | Линкор: 1 + 2 + 3 = 7000
- Крейсер: 1 + 2 = 4800
- Линкор: 2 + 3 = 4500
Искомая область Крейсер & Линкор обозначенная на чертеже цифрой 2, находится путём подстановки уравнения (2) в уравнение (1). Получаем следующее:
4800 + 3 = 7000, откуда получаем область 3, равную 2200.
Полученный результат мы подставляем в уравнение (3). Получаем результат:
Область 2 + 2200 = 4500, значит, она равна 2300.
Ответ: будет найдено 2300 страниц по запросу Крейсер & Линкор.
Этот пример показывает, что можно решать с помощью диаграммы Эйлера задачи, являющиеся достаточно сложными или запутанными.
Пример решения задачи с помощью кругов ЭйлераМожно сделать вывод, что круги Эйлера не просто занимательный, но и полезный в плане решения учебных и бытовых задач метод. Многие вещи можно представить в виде множеств, а поможет наглядно представить их пересечение или объединение диаграмма Эйлера.
Многие вещи можно представить в виде множеств, а поможет наглядно представить их пересечение или объединение диаграмма Эйлера.
Любопытно, что современная массовая культура применяет круги Эйлера для создания мемов, а также их можно встретить в таких сериалах, как «Теория большого взрыва» и «4исла».
Советуем применять этот метод для решения задач и непременно поделитесь этим полезным и наглядным способом с друзьями.
Рейтинг: 5
( голосов 2 )
Поделиться статьей
Круги Эйлера | Обучонок
Леонард Эйлер — математик, механик, физик и астроном.
Леонард Эйлер за свою долгую жизнь (он родился в 1707 г., а умер в 1783 г.) написал более 850 научных работ. В одной из них и появились эти круги, ставшие в один ряд с остальными интересными фактами в области математики.
Круги Эйлера – это геометрическая схема, которая помогает находить или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.
Например, на рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал.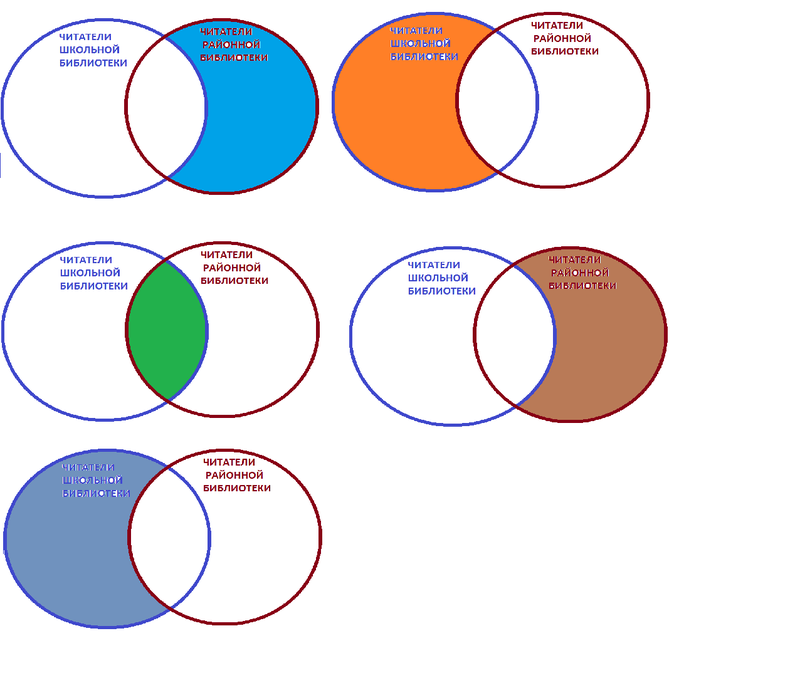
Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому для них нужен отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.
Итак, мы видим, что круги Эйлера – это тот метод, который наглядно демонстрирует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ. Сам Леонард Эйлер так и говорил о названных его именем схемах: «
Например, если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет вам определиться с выбором:
Возможно, чертеж вроде этого поможет вам определиться с выбором:
Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.
Другой пример, доказывающий прикладное значение кругов Эйлера: Каждый из 35 девятиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и поселковой. Из них 25 человек берут книги в школьной библиотеке, 20 – в поселковой.
Сколько девятиклассников:
- Являются читателями обеих библиотек;
- Не являются читателями районной библиотеки;
- Не являются читателями школьной библиотеки;
- Являются читателями только районной библиотеки;
- Являются читателями только школьной библиотеки?
Заметим, что первый вопрос является ключевым для понимания и решения данной задачи. Ведь не сразу сообразишь, как получается 20 + 25 = 45 из 35. В первом вопросе звучит подсказка к пониманию условия: есть ученики, которые посещают обе библиотеки. А если условие задачи изобразить на схеме, то ответ на первый вопрос становится очевидным.
А если условие задачи изобразить на схеме, то ответ на первый вопрос становится очевидным.
Всего 35 девятиклассников
Решение:
1. 20 + 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.
2. 35 – 20 = 15 (человек) – не являются читателями районной библиотеки. (На схеме левая часть левого круга)
3. 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки. (На схеме правая часть правого круга)
4. 35 – 25 = 10 (человек) – являются читателями только районной библиотеки. (На схеме правая часть правого круга)
5. 35 – 20 = 15 (человек) – являются читателями только школьной библиотеки. (На схеме левая часть левого круга).
Очевидно, что 2 и 5, а также 3 и 4– равнозначны и ответы на них совпадают.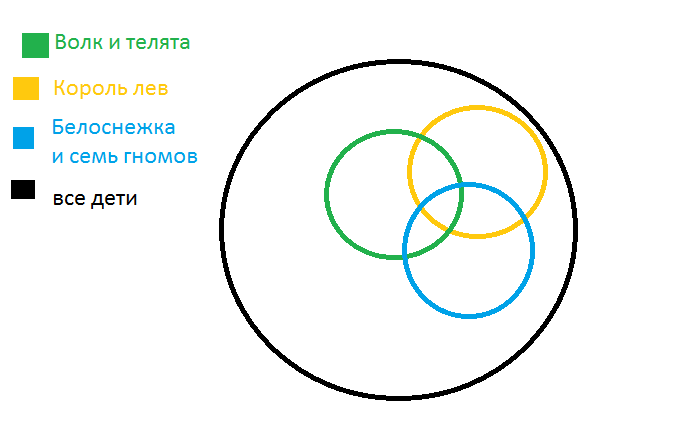
Ещё один пример: В туристической группе из 100 человек 75 человек знают немецкий язык, 65 человек-английский язык, а 10 человек — не знают ни немецкого, ни английского языка. Сколько туристов знают два языка?
Решение: Изобразим условие задачи в виде кругов Эйлера. В большом круге, изображающем 100 туристов, поместим 2 меньших круга, изображающих знатоков английского и немецкого языков. Легко видеть, что 90 туристов (100-10) знают хотя бы один язык; 15 туристов (90-75) знают только английский язык, 65-15=50 – туристов знают оба языка.
Ответ: 50 туристов.
Таким образом, круги Эйлера имеют большое прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте.
Автор: Уразов Роберт, 9 «Б» класс.
Руководитель: учитель математикиНовосельцева Ольга Альбертовна
МБОУ «Новоаганская ОСШ №1»
Если страница Вам понравилась, поделитесь в социальных сетях:
eulerAPE: Рисование трехмерных диаграмм Венна, пропорциональных площади, с использованием эллипсов
Рисунок 1.

Примеры пропорциональных площади трехмерных диаграмм Венна, нарисованных кругами (A – C) и многоугольниками (D – F) в литературе.
(A) Сравнение клеточного типа дифференциально регулируемых генов после лечения противораковыми препаратами [11]. Метод, использованный для построения диаграммы, не указан. Эта диаграмма является перепечаткой рисунка 3B из [11], опубликованного ранее под лицензией CC BY. (B) Суммирование прогностических показателей тяжелой малярии [12]. Метод, использованный для построения диаграммы, не указан. Эта диаграмма является перепечаткой рис. 3 из [12] (с N и проценты в круглых скобках удалены), ранее опубликованный под лицензией CC BY. (C) Анализ различий и сходств между идентифицированным протеомом белка куриного яйца в трех разных исследованиях [13]. Нарисовано с помощью плоттера диаграмм Венна [http://omics.pnl.gov/software/VennDiagramPlotter.php]. Эта диаграмма является перепечаткой рисунка 2А из [13], опубликованного ранее под лицензией CC BY. (D) Анализ перекрытий между генными библиотеками [14]. Нарисовано с помощью DrawVenn [5]. Эта диаграмма является перепечаткой рисунка 4B в [14] по лицензии CC BY, с разрешения John Wiley and Sons, оригинальное авторское право 2009 г.. (E) Изучение изменчивости транскриптома различных типов тканей самца полевого сверчка, а именно семенников, добавочной железы и остальной части тела [15]. Нарисовано с помощью Convex Venn-3 [51]. Эта диаграмма является перепечаткой рисунка 1 (слева) в [15] под лицензией CC BY, с разрешения Натана Бейли, оригинальное авторское право 2013 г. (F) Суммирование генов, влияющих на индуцированное Top1 повреждение ДНК, выявленное в трех разных исследованиях [16] . Нарисовано с помощью DrawEuler [55]. Эта диаграмма является перепечаткой рисунка 3А в [16] (с добавленными числовыми метками, указывающими количественные данные, которые в соответствии со статьей должен представлять каждый регион на диаграмме), ранее опубликованного по лицензии CC BY.
(D) Анализ перекрытий между генными библиотеками [14]. Нарисовано с помощью DrawVenn [5]. Эта диаграмма является перепечаткой рисунка 4B в [14] по лицензии CC BY, с разрешения John Wiley and Sons, оригинальное авторское право 2009 г.. (E) Изучение изменчивости транскриптома различных типов тканей самца полевого сверчка, а именно семенников, добавочной железы и остальной части тела [15]. Нарисовано с помощью Convex Venn-3 [51]. Эта диаграмма является перепечаткой рисунка 1 (слева) в [15] под лицензией CC BY, с разрешения Натана Бейли, оригинальное авторское право 2013 г. (F) Суммирование генов, влияющих на индуцированное Top1 повреждение ДНК, выявленное в трех разных исследованиях [16] . Нарисовано с помощью DrawEuler [55]. Эта диаграмма является перепечаткой рисунка 3А в [16] (с добавленными числовыми метками, указывающими количественные данные, которые в соответствии со статьей должен представлять каждый регион на диаграмме), ранее опубликованного по лицензии CC BY.
Подробнее »
РасширятьФигура 2.

Точные пропорциональные площади 3-диаграммы Венна, нарисованные с помощью эллипсов и Эйлера APE для данных на рисунке 1.
Каждая из этих диаграмм изображает наборы и количественные данные, обозначенные числовыми метками в областях соответствующей диаграммы на рисунке 1. Эти диаграммы были нарисованы с помощью euler APE , но метки были добавлены вручную.
Подробнее »
РасширятьРисунок 3.
Диаграммы, созданные различными методами рисования для одних и тех же медицинских данных из журнальной статьи.
Все диаграммы предназначены для отображения ω = { A = 0,25, B = 0,01, C = 0,11, AB = 7 029,
7 AC 0 БК
= 0,03, ABC = 0,15}, что представляет собой результаты медицинского обследования из журнальной статьи [37], в которую также включена диаграмма D для ω . Диаграммы, созданные для ω с использованием методов рисования на основе кругов, отмечены как C, диаграммы с использованием методов на основе многоугольников отмечены как P, а единственная диаграмма с эллипсами, созданная Эйлером APE , — E. Зеленый цвет указывает на точные диаграммы. с diagError ≤10 −6 . Красным цветом отмечены диаграммы с неточными или отсутствующими областями. D представляет собой перерисовку рисунка 5 (внизу) в [37], ранее опубликованного по лицензии CC BY.
Диаграммы, созданные для ω с использованием методов рисования на основе кругов, отмечены как C, диаграммы с использованием методов на основе многоугольников отмечены как P, а единственная диаграмма с эллипсами, созданная Эйлером APE , — E. Зеленый цвет указывает на точные диаграммы. с diagError ≤10 −6 . Красным цветом отмечены диаграммы с неточными или отсутствующими областями. D представляет собой перерисовку рисунка 5 (внизу) в [37], ранее опубликованного по лицензии CC BY.Подробнее »
РасширятьРисунок 4.
Метод построения пропорциональной площади трехмерной диаграммы Венна с использованием окружностей.
(A) Количественные значения в каждом регионе указывают требуемые площади региона, для которых должна быть построена пропорциональная площади 3-диаграмма Венна. (B) Первый шаг построения, посредством которого рисуются три точные 2-диаграммы Венна.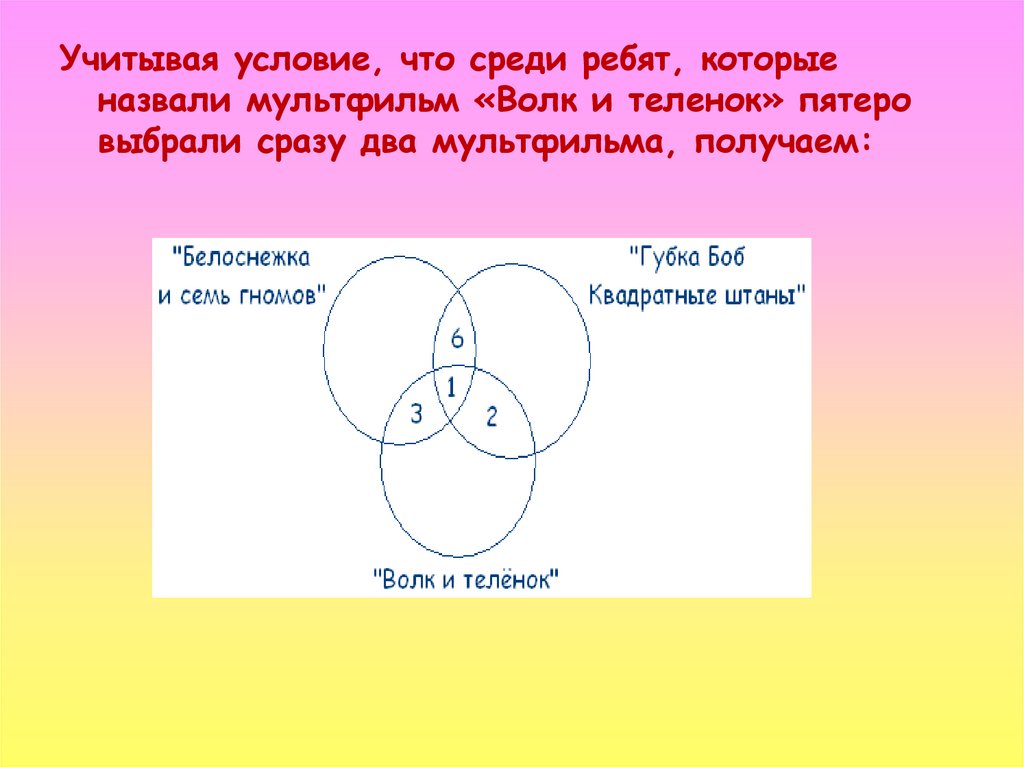 (C) Второй шаг построения, при котором идентичные копии круга с номером c повернуты таким образом, что они полностью перекрываются, и виден только один круг, помеченный c . (D) Случай, когда видны только три круга, так что получаются области 3-диаграммы Венна. (E) Фактическая площадь областей на построенной диаграмме D, которые, как и в большинстве случаев, когда эти диаграммы рисуются кружками, не соответствуют искомым значениям в A. Числовая метка в каждой области этой диаграммы указывает на Фактическая площадь регионов.
(C) Второй шаг построения, при котором идентичные копии круга с номером c повернуты таким образом, что они полностью перекрываются, и виден только один круг, помеченный c . (D) Случай, когда видны только три круга, так что получаются области 3-диаграммы Венна. (E) Фактическая площадь областей на построенной диаграмме D, которые, как и в большинстве случаев, когда эти диаграммы рисуются кружками, не соответствуют искомым значениям в A. Числовая метка в каждой области этой диаграммы указывает на Фактическая площадь регионов.
Подробнее »
РасширятьРисунок 5.
Генератор начальной диаграммы делит интервал пополам вдоль линии биссектрисы, чтобы расположить третий эллипс.
Центр эллипса e 3 является точкой на прямой L , делящей пополам угол ψ между двумя касательными T 1 8 и 078 . Метод деления пополам применяется в интервале, обозначенном блеклыми синими кружками вдоль л . Полученный центр должен минимизировать несовпадение требуемой и действительной площадей области ровно в три эллипса.
Метод деления пополам применяется в интервале, обозначенном блеклыми синими кружками вдоль л . Полученный центр должен минимизировать несовпадение требуемой и действительной площадей области ровно в три эллипса.
Подробнее »
РасширятьРисунок 6.
Различные способы изменения свойств эллипсов в процессе поиска оптимизации.
На каждой итерации алгоритма оптимизации центр (A), полуоси (B) и угол поворота (C) каждого эллипса соответственно модифицируются параметрами pγ , pαβ и pθ в поисках других решений. (A) Серые точки обозначают новые центры, которые получаются, когда одна или обе координаты центра эллипса (сплошной черный цвет) увеличиваются или уменьшаются на pγ . (B) Метка + pαβ означает, что эта полуось была увеличена на процент pαβ , а — pαβ означает, что эта полуось была уменьшена на процент pαβ . Пунктирные эллипсы показывают, как изменяется эллипс (сплошной черный), когда: (сверху слева) только большая полуось увеличивается или уменьшается на рαβ ; (вверху справа) только полуминор увеличивается или уменьшается на pαβ ; (внизу слева) обе полуоси увеличены или обе уменьшены на pαβ ; (внизу справа) одна из полуосей увеличена, а другая уменьшена на pαβ . (C) Пунктирные эллипсы показывают, как меняется эллипс (сплошной черный) при увеличении или уменьшении его угла поворота на pθ .
Пунктирные эллипсы показывают, как изменяется эллипс (сплошной черный), когда: (сверху слева) только большая полуось увеличивается или уменьшается на рαβ ; (вверху справа) только полуминор увеличивается или уменьшается на pαβ ; (внизу слева) обе полуоси увеличены или обе уменьшены на pαβ ; (внизу справа) одна из полуосей увеличена, а другая уменьшена на pαβ . (C) Пунктирные эллипсы показывают, как меняется эллипс (сплошной черный) при увеличении или уменьшении его угла поворота на pθ .
Подробнее »
РасширятьРисунок 7.
Количество повторных запусков для создания хорошей диаграммы для 61 элемента данных в L1.
Количество повторных прогонов (1–10), которые потребовались euler APE для создания хорошей диаграммы для 61 элемента данных в L1, для которых во время первого запуска была сгенерирована неправильная диаграмма.
Подробнее »
РасширятьРисунок 8.
Время и общее количество итераций для создания хороших диаграмм для данных в L1.
Журнал 10 ( время в секундах ) и журнал 10 ( общее количество итераций ) для создания хороших диаграмм для 9939 первых элементов данных в L10 10,0 помечены как « Run 1 ») и для 61 из 10 000 элементов данных в L1 во время любого из них до максимум 10 повторов (помечены как « Reruns »).
Подробнее »
РасширятьРисунок 9.
Примеры хороших диаграмм, сгенерированных после первого прогона для данных в L1.
(A) и (B) иллюстрируют ( i ) хорошую диаграмму, которая была найдена с использованием ( ii ) начальной диаграммы, сгенерированной для элемента данных в L1 ({ a = 2273, b = 24458 , c = 44454, ab = 7116, ac = 740, bc = 18807, abc = 12092} для A и { a 9170383 =0007 b = 6248, c = 16230, ab = 615, ac = 289, bc = 840, abc = 922} для множества B) iii ) случайно сгенерированная трехмерная диаграмма Венна.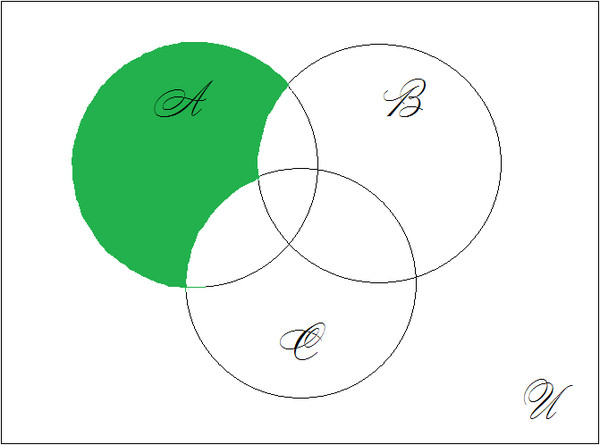
Подробнее »
РасширятьРисунок 10.
Примеры хороших диаграмм, сгенерированных после первого повторного запуска для данных в L1.
(A) Пример ( i ) неправильная диаграмма с очень низким diagError (6,51×10 −4 ), сгенерированная во время первого запуска, и ( ii ) хорошая диаграмма, сгенерированная во время первого повторного запуска для данных ({ a = 10018, b = 27132, c = 39737, ab = 9567, ac = 11454, bc = 3,
7 abc) в L 6 6,
8 abc) получено от ( iii ) случайная диаграмма. Хорошая диаграмма в ii была сгенерирована за 1,2 секунды и 86 итераций (включая первый прогон и один повтор). (Б) Пример ( i ) неправильная диаграмма с низким diagError (8,38×10 −3 ), сгенерированная во время первого запуска, и ( ii ) хорошая диаграмма, сгенерированная во время первого повторного запуска для данных ({ a = 53804, б = 39550, в = 1256, аб = 15606, а. с. получено из ( iii ) случайная диаграмма. Хорошая диаграмма в ii была сгенерирована в 2.9секунд и 367 итераций (включая первый запуск и один повторный запуск).
с. получено из ( iii ) случайная диаграмма. Хорошая диаграмма в ii была сгенерирована в 2.9секунд и 367 итераций (включая первый запуск и один повторный запуск). Подробнее »
Расширять Рисунок 11.
Примеры диаграмм, созданных venneuler и euler APE (круги и эллипсы) для данных в L2.
Примеры диаграмм, созданных с помощью ( i ) кругов Веннелера, ( ii ) кругов Эйлера APE и ( iii ) эллипсов Эйлера APE для случайных 3-х наборов данных в L2. (A) Диаграммы, построенные для данных { a = 3491, b = 3409, c = 3503, ab = 120, ac = 114, bc 0 0 0 9 0 2 0 9 = 0 0 8 = 126} . i отсутствует область abc и имеет напряжение = 5,69×10 −4 и diagError = 1,16×10 −2 . A ii и A iii имеют необходимые области, по одной для каждого отношения набора данных. А ii имеет напряжений = 8,36×10 −3 и diagError = 2,63×10 −2 . A iii имеет напряжение = 3,96×10 −12 и diagError = 6,55×10 −7 . (B) Диаграммы, построенные для данных { a = 45910, b = 3261, c = 45467, ab = 58845, ac = 3028, 9006, 70007 bc = 100008 азбука = 18496} . B i отсутствует регион ac и имеет стресс = 3,17×10 −3 и diagError = 2,07×10 −2 . В B i есть две области, изображающие только b . B ii и B iii имеют необходимые области, по одной для каждого отношения набора данных. B ii имеет напряжений = 2,13×10 −2 и diagError = 4,36×10 −2 . B iii имеет напряжение = 3,43×10 −12 и diagError = 6,85×10 −7 .
A ii и A iii имеют необходимые области, по одной для каждого отношения набора данных. А ii имеет напряжений = 8,36×10 −3 и diagError = 2,63×10 −2 . A iii имеет напряжение = 3,96×10 −12 и diagError = 6,55×10 −7 . (B) Диаграммы, построенные для данных { a = 45910, b = 3261, c = 45467, ab = 58845, ac = 3028, 9006, 70007 bc = 100008 азбука = 18496} . B i отсутствует регион ac и имеет стресс = 3,17×10 −3 и diagError = 2,07×10 −2 . В B i есть две области, изображающие только b . B ii и B iii имеют необходимые области, по одной для каждого отношения набора данных. B ii имеет напряжений = 2,13×10 −2 и diagError = 4,36×10 −2 . B iii имеет напряжение = 3,43×10 −12 и diagError = 6,85×10 −7 . (C) Диаграммы, построенные для данных { a = 3664, b = 46743, c = 59811, ab = 1742, ac = 2099, 90907 ab 9002 с = 24504} . C i , C ii и C iii имеют обязательные области, по одной для каждого отношения набора данных. C i имеет напряжений = 4,27×10 −3 и diagError = 2,30×10 −2 . C ii имеет стресс = 8,31×10 −3 и diagError = 2,44×10 −2 . C iii имеет напряжения = 1,13×10 −12 и diagError = 4,03×10 −7 .
(C) Диаграммы, построенные для данных { a = 3664, b = 46743, c = 59811, ab = 1742, ac = 2099, 90907 ab 9002 с = 24504} . C i , C ii и C iii имеют обязательные области, по одной для каждого отношения набора данных. C i имеет напряжений = 4,27×10 −3 и diagError = 2,30×10 −2 . C ii имеет стресс = 8,31×10 −3 и diagError = 2,44×10 −2 . C iii имеет напряжения = 1,13×10 −12 и diagError = 4,03×10 −7 .
Подробнее »
Расширять Рисунок 12.
Stress и diagError всех диаграмм, сгенерированных venneuler и eiler APE (круги и эллипсы).
(A) напряжение и (B) diagError всех диаграмм, созданных с помощью кругов Веннелера, с кругами Эйлера APE и с эллипсами Эйлера APE для 10 000 3-х наборов данных в L2 . 10 000 диаграмм, созданных Веннелером с помощью кругов, имели напряжений дюймов [3,77×10 −5 , 6,14×10 −1 ] с медианой 3,04×10 −2 и средним значением 6,41×10
3 −2 , а diagError в [1,56×10 −3 , 2,46×10 −1 ] с медианой 4,56×10 −2 и средним значением 5,73×10 −2 . 10 000 диаграмм, созданных с помощью окружностей с помощью euler APE , имели напряжений дюймов [1,91×10 −10 , 7,79×10 −1 ] с медианой 7,00×10× −5 30 и средним значением 1,13. и diagError в [3,30×10 −6 , 3,31×10 −1 ] с медианой 6,28×10 −2 и средним значением 6,73×10 −2 . 10 000 диаграмм, созданных Эйлером 9 с помощью эллипсов.0007 APE имел напряжение в [3,98×10 -14 , 2,24×10 -1 ] с медианой 7,59×10 -12 и средним значением 1,17×10 -7 diag 0 9005 и 08 в [ 6,00×10 −8 , 1,39×10 −1 ] с медианой 8,00×10 −7 и средним значением 2,94×10 −3 .
10 000 диаграмм, созданных Эйлером 9 с помощью эллипсов.0007 APE имел напряжение в [3,98×10 -14 , 2,24×10 -1 ] с медианой 7,59×10 -12 и средним значением 1,17×10 -7 diag 0 9005 и 08 в [ 6,00×10 −8 , 1,39×10 −1 ] с медианой 8,00×10 −7 и средним значением 2,94×10 −3 . Подробнее »
Расширять Рисунок 13.
Фигура в статье в медицинском журнале и фигура, воссозданная с помощью Эйлера 9.0015 АПЕ .
(A) Рисунок с двумя диаграммами Венна, нарисованными кружками, в статье в медицинском журнале [37]. Это перерисовка рисунка 5 из [37], опубликованного ранее под лицензией CC BY. (B) Фигура, как она выглядела бы, если бы диаграммы были нарисованы эллипсами с помощью euler APE . Метки для диаграмм euler APE были добавлены вручную.
Подробнее »
Расширять Знакомство с eulerr
Знакомство с eulerr Йохан Ларссон
09.12.2022
Мотивация
eulerr создает диаграммы Эйлера, пропорциональные площади, которые отображают заданные отношения (пересечения, объединения и непересекающиеся) с помощью окружностей или эллипсов. Диаграммы Эйлера — это диаграммы Венна, не требующие наличия всех взаимодействий множеств (независимо от того, пусты они или нет). То есть, в зависимости от ввода, eulerr иногда будет создавать диаграммы Венна, а иногда нет.
R содержит несколько пакетов для создания диаграмм Эйлера; некоторые из наиболее известных (на CRAN)
- ЭВенн,
- Диаграмма Венна
- Венн
- красочный VennPlot и
- продавец.
Последний из них ( venneuler ) был основным источником вдохновения для этого пакета, наряду с уточнениями, которые Фредриксон представил в своем блоге и сделал доступным в своем javascript venn. js. eulerAPE, которая была первой программой, использующей эллипсы вместо кругов, также сыграла важную роль в разработке eulerr . Недостатки eulerAPE заключается в том, что он обрабатывает только три набора, которые все должны пересекаться.
js. eulerAPE, которая была первой программой, использующей эллипсы вместо кругов, также сыграла важную роль в разработке eulerr . Недостатки eulerAPE заключается в том, что он обрабатывает только три набора, которые все должны пересекаться.
venneuler , с другой стороны, будет принимать любое количество наборов (теоретически), но, как известно, дает несовершенные решения для конфигураций наборов, которые имеют идеальные такие. И в отличие от eulerAPE , он ограничен кругами (как и venn.js ).
Введите eulerr
eulerr основан на улучшениях venneuler, которые Бен Фредриксон представил в venn.js , но был запрограммирован с нуля, использует различные оптимизаторы и возвращает статистику, представленную в venneuler и eulerAPE , а также допускает ряд различных входных данных и обусловливает дополнительные переменные. Более того, он может моделировать отношения множеств с помощью эллипсов для любого числа вовлеченных множеств.
Более того, он может моделировать отношения множеств с помощью эллипсов для любого числа вовлеченных множеств.
Входные данные
На момент написания можно обеспечить входные данные для eulerr как
- именованный числовой вектор с комбинациями наборов как непересекающиеся комбинации наборов или объединения (в зависимости от того, как аргумент
тип устанавливается в euler() ), - матрица или структура логических данных со столбцами, представляющими наборы, и строками, представляющими отношения наборов для каждого наблюдения,
- список примеров пространств или
- стол.
библиотека (эйлерр)
# Ввод в виде именованного числового вектора
fit1 <- euler(c("A" = 25, "B" = 5, "C" = 5,
«А&В» = 5, «А&В» = 5, «В&В» = 3,
"А&В&С" = 3))
# Ввод в виде матрицы логических
set.seed(1)
мат <- cbind(
A = образец (с (ИСТИНА, ИСТИНА, ЛОЖЬ), 50, ИСТИНА),
B = образец (с (ИСТИНА, ЛОЖЬ), 50, ИСТИНА),
C = образец (с (ИСТИНА, ЛОЖЬ, ЛОЖЬ, ЛОЖЬ), 50, ИСТИНА)
)
fit2 <- эйлер(мат) Мы проверяем наши результаты, печатая объект Эйлера
fit2
#> исходные подогнанные остатки regionError
#> А 13 13 0 0,008
#> В 4 4 0 0,002
#> С 0 0 0 0. 000
#> А и В 17 17 0 0,010
#> АиК 5 5 0 0,003
#> B&C 1 0 1 0,024
#> A&B&C 2 2 0 0,001
#>
#> ошибка диагностики: 0.024
#> напряжение: 0,002
000
#> А и В 17 17 0 0,010
#> АиК 5 5 0 0,003
#> B&C 1 0 1 0,024
#> A&B&C 2 2 0 0,001
#>
#> ошибка диагностики: 0.024
#> напряжение: 0,002
или получить прямой доступ и нанести на график остатки.
# Кливленд Точечный график остатков
библиотека (решетка)
dotplot (остатки (fit2), xlab = "",
панель = функция(...) {
панель.abline(v = 0, lty = 2)
панель.dotplot(...)
}) Остатки для диаграммы соответствия.
Мы также можем использовать eulerr встроенную функцию error_plot() для диагностики соответствия.
error_plot(fit2)
График из error_plot() .
Это показывает нам, что пересечение несколько чрезмерно представлено в . Однако, учитывая, что эти остатки находятся в масштабе первоначальных значений, остатки, возможно, не представляют большого интереса.
В качестве альтернативы мы могли бы построить круги в другой программе, получив их координаты и радиусы.
коэфф(fit2)
#> h k a b phi
#> А -0,531 -0,2496 3,432 3,432 2,5
#> В 1,112 -0,2496 2,706 2,706 2,5
#> С -1,507 1,4108 1,492}
\] , где \(\hat{y}_i\) — обычная оценка методом наименьших квадратов из регрессии подогнанных областей по исходным областям, которая исследуется во время оптимизации,
и статистика diagError из eulerAPE (Микалеф и Роджерс, 2014 г.):
\[
\max_{i = 1, 2, \dots, n} \left| \frac{y_i}{\сумма y_i} -
\ гидроразрыва {\ шляпа {у} _i} {\ сумма \ шляпа {у} _i} \ справа |
\]
В нашем примере ошибка диагностики равна 0,002, а напряжение равно 0,002, что позволяет предположить, что подгонка является точной.
Теперь мы можем быть уверены, что eulerr обеспечивает разумное представление нашего ввода с помощью кругов. В противном случае мы могли бы попытаться использовать эллипсы вместо этого. (Wilkinson 2012) представляет собой сложную комбинацию, которую удается подогнать с достаточно небольшой ошибкой; однако с eulerr мы можем полностью избавиться от этой ошибки.
wilkinson2012 <- c(A = 4, B = 6, C = 3, D = 2, E = 7, F = 3,
"A&B" = 2, "A&F" = 2, "B&C" = 2, "B&D" = 1,
"Б&Ф" = 2, "К&Д" = 1, "Д&Э" = 1, "Э&Ф" = 1,
"A&B&F" = 1, "B&C&D" = 1)
fit3 <- euler(wilkinson2012, shape = "эллипс")
сюжет(fit3) Сложная комбинация из Wilkinson 2012.
Если после того, как мы попробовали использовать эллипсы, нам все еще не хватает хорошей подгонки, нам лучше остановиться здесь и поискать другой способ визуализации наших данных. (Я предлагаю отличный пакет UpSetR.)
Визуализация
Нет, мы подошли к самой интересной части: построению нашей диаграммы. Это легко, а также легко настраивается с помощью eulerr . Параметры по умолчанию можно легко изменить в соответствии с потребностями любого пользователя.
сюжет(fit2)
В eulerr легко настроить графики Эйлера.
# Удалите заливку, измените границы, отобразите количество и переключите шрифт. сюжет (подгонка2,
количества = ИСТИНА,
заполнить = "прозрачный",
лт = 1:3,
labels = list(font = 4))
сюжет (подгонка2,
количества = ИСТИНА,
заполнить = "прозрачный",
лт = 1:3,
labels = list(font = 4))
Настройка графиков Эйлера в eulerr очень проста.
Построение графиков осуществляется с помощью специального метода построения графиков, основанного на превосходных возможностях, предоставляемых базовым пакетом R grid . Цветовая палитра eulerr по умолчанию выбрана так, чтобы не нарушать цветовой баланс.
Благодарности
eulerr были бы невозможны без работы Бена Фредриксона над venn.js или работы Леланда Уилкинсона venneuler .
Ссылки
Микаллеф, Луана и Питер Роджерс. 2014. «eulerAPE: Рисование пропорциональных площадям 3-диаграмм Венна с использованием эллипсов». PLOS ONE 9 (7): e101717. https://doi.org/10.1371/journal.pone.0101717.
Уилкинсон, Л. 2012. «Точные и приблизительные круговые диаграммы Венна и Эйлера, пропорциональные площади».
 A ii и A iii имеют необходимые области, по одной для каждого отношения набора данных. А ii имеет напряжений = 8,36×10 −3 и diagError = 2,63×10 −2 . A iii имеет напряжение = 3,96×10 −12 и diagError = 6,55×10 −7 . (B) Диаграммы, построенные для данных { a = 45910, b = 3261, c = 45467, ab = 58845, ac = 3028, 9006, 70007 bc = 100008 азбука = 18496} . B i отсутствует регион ac и имеет стресс = 3,17×10 −3 и diagError = 2,07×10 −2 . В B i есть две области, изображающие только b . B ii и B iii имеют необходимые области, по одной для каждого отношения набора данных. B ii имеет напряжений = 2,13×10 −2 и diagError = 4,36×10 −2 . B iii имеет напряжение = 3,43×10 −12 и diagError = 6,85×10 −7 .
A ii и A iii имеют необходимые области, по одной для каждого отношения набора данных. А ii имеет напряжений = 8,36×10 −3 и diagError = 2,63×10 −2 . A iii имеет напряжение = 3,96×10 −12 и diagError = 6,55×10 −7 . (B) Диаграммы, построенные для данных { a = 45910, b = 3261, c = 45467, ab = 58845, ac = 3028, 9006, 70007 bc = 100008 азбука = 18496} . B i отсутствует регион ac и имеет стресс = 3,17×10 −3 и diagError = 2,07×10 −2 . В B i есть две области, изображающие только b . B ii и B iii имеют необходимые области, по одной для каждого отношения набора данных. B ii имеет напряжений = 2,13×10 −2 и diagError = 4,36×10 −2 . B iii имеет напряжение = 3,43×10 −12 и diagError = 6,85×10 −7 . (C) Диаграммы, построенные для данных { a = 3664, b = 46743, c = 59811, ab = 1742, ac = 2099, 90907 ab 9002 с = 24504} . C i , C ii и C iii имеют обязательные области, по одной для каждого отношения набора данных. C i имеет напряжений = 4,27×10 −3 и diagError = 2,30×10 −2 . C ii имеет стресс = 8,31×10 −3 и diagError = 2,44×10 −2 . C iii имеет напряжения = 1,13×10 −12 и diagError = 4,03×10 −7 .
(C) Диаграммы, построенные для данных { a = 3664, b = 46743, c = 59811, ab = 1742, ac = 2099, 90907 ab 9002 с = 24504} . C i , C ii и C iii имеют обязательные области, по одной для каждого отношения набора данных. C i имеет напряжений = 4,27×10 −3 и diagError = 2,30×10 −2 . C ii имеет стресс = 8,31×10 −3 и diagError = 2,44×10 −2 . C iii имеет напряжения = 1,13×10 −12 и diagError = 4,03×10 −7 .

 js. eulerAPE, которая была первой программой, использующей эллипсы вместо кругов, также сыграла важную роль в разработке eulerr . Недостатки eulerAPE заключается в том, что он обрабатывает только три набора, которые все должны пересекаться.
js. eulerAPE, которая была первой программой, использующей эллипсы вместо кругов, также сыграла важную роль в разработке eulerr . Недостатки eulerAPE заключается в том, что он обрабатывает только три набора, которые все должны пересекаться. Более того, он может моделировать отношения множеств с помощью эллипсов для любого числа вовлеченных множеств.
Более того, он может моделировать отношения множеств с помощью эллипсов для любого числа вовлеченных множеств. тип устанавливается в euler() ),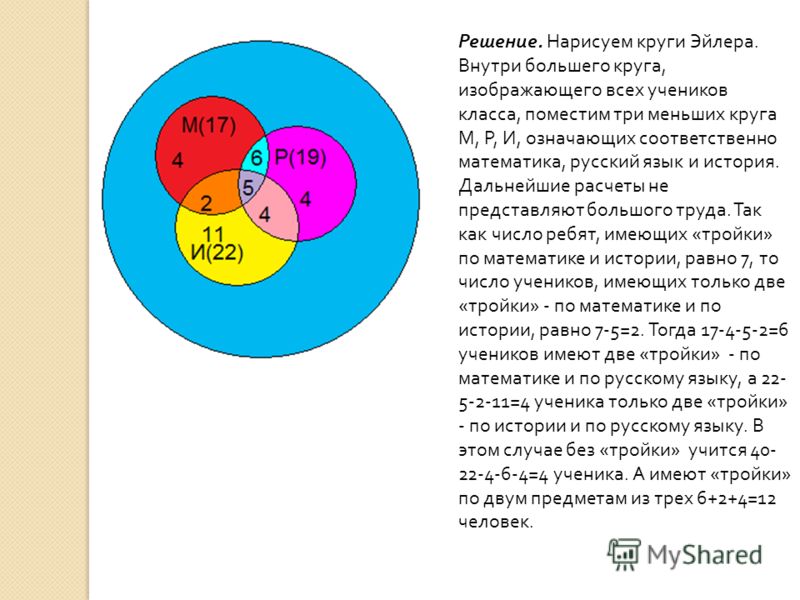 000
#> А и В 17 17 0 0,010
#> АиК 5 5 0 0,003
#> B&C 1 0 1 0,024
#> A&B&C 2 2 0 0,001
#>
#> ошибка диагностики: 0.024
#> напряжение: 0,002
000
#> А и В 17 17 0 0,010
#> АиК 5 5 0 0,003
#> B&C 1 0 1 0,024
#> A&B&C 2 2 0 0,001
#>
#> ошибка диагностики: 0.024
#> напряжение: 0,002 error_plot() для диагностики соответствия. error_plot() .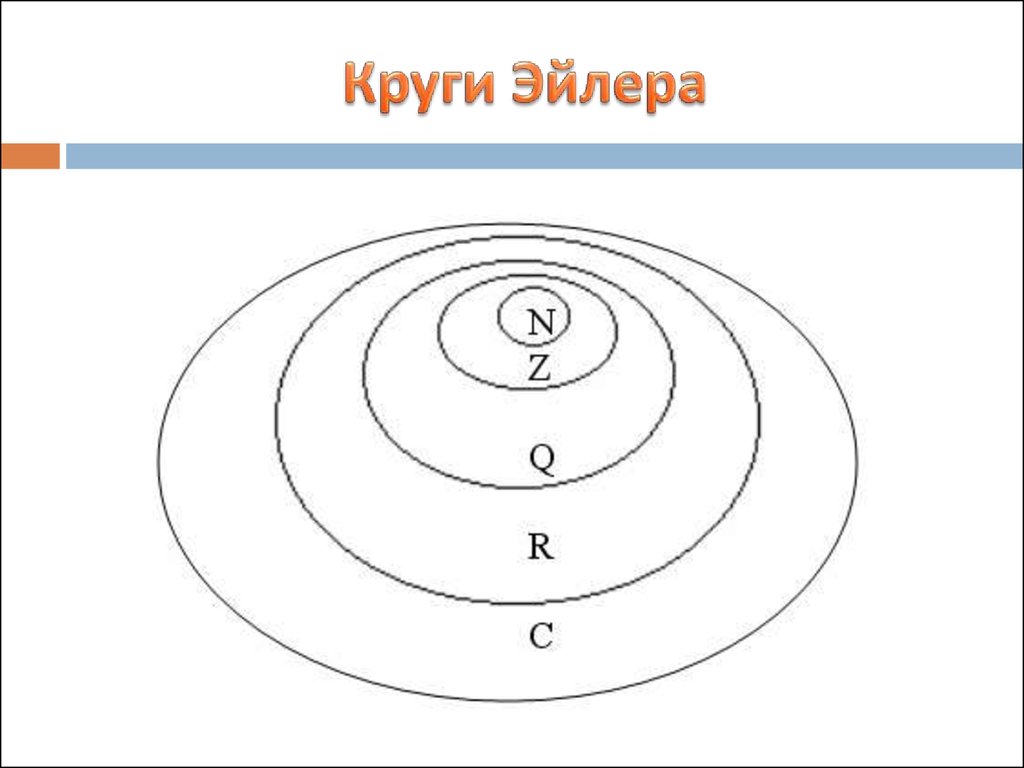
, где \(\hat{y}_i\) — обычная оценка методом наименьших квадратов из регрессии подогнанных областей по исходным областям, которая исследуется во время оптимизации,
и статистика diagError из eulerAPE (Микалеф и Роджерс, 2014 г.):
\[ \max_{i = 1, 2, \dots, n} \left| \frac{y_i}{\сумма y_i} - \ гидроразрыва {\ шляпа {у} _i} {\ сумма \ шляпа {у} _i} \ справа | \]
В нашем примере ошибка диагностики равна 0,002, а напряжение равно 0,002, что позволяет предположить, что подгонка является точной.
Теперь мы можем быть уверены, что eulerr обеспечивает разумное представление нашего ввода с помощью кругов. В противном случае мы могли бы попытаться использовать эллипсы вместо этого. (Wilkinson 2012) представляет собой сложную комбинацию, которую удается подогнать с достаточно небольшой ошибкой; однако с eulerr мы можем полностью избавиться от этой ошибки.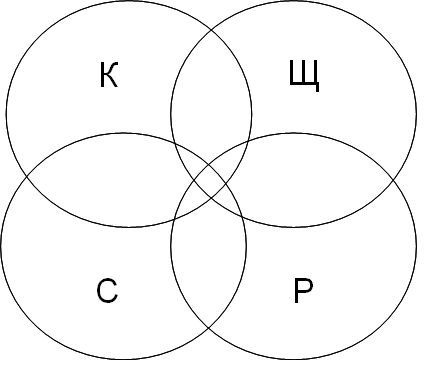
wilkinson2012 <- c(A = 4, B = 6, C = 3, D = 2, E = 7, F = 3,
"A&B" = 2, "A&F" = 2, "B&C" = 2, "B&D" = 1,
"Б&Ф" = 2, "К&Д" = 1, "Д&Э" = 1, "Э&Ф" = 1,
"A&B&F" = 1, "B&C&D" = 1)
fit3 <- euler(wilkinson2012, shape = "эллипс")
сюжет(fit3) Сложная комбинация из Wilkinson 2012.
Если после того, как мы попробовали использовать эллипсы, нам все еще не хватает хорошей подгонки, нам лучше остановиться здесь и поискать другой способ визуализации наших данных. (Я предлагаю отличный пакет UpSetR.)
Визуализация
Нет, мы подошли к самой интересной части: построению нашей диаграммы. Это легко, а также легко настраивается с помощью eulerr . Параметры по умолчанию можно легко изменить в соответствии с потребностями любого пользователя.
сюжет(fit2)
В eulerr легко настроить графики Эйлера.
# Удалите заливку, измените границы, отобразите количество и переключите шрифт.сюжет (подгонка2, количества = ИСТИНА, заполнить = "прозрачный", лт = 1:3, labels = list(font = 4))
Настройка графиков Эйлера в eulerr очень проста.
Построение графиков осуществляется с помощью специального метода построения графиков, основанного на превосходных возможностях, предоставляемых базовым пакетом R grid . Цветовая палитра eulerr по умолчанию выбрана так, чтобы не нарушать цветовой баланс.
Благодарности
eulerr были бы невозможны без работы Бена Фредриксона над venn.js или работы Леланда Уилкинсона venneuler .
Ссылки
Микаллеф, Луана и Питер Роджерс. 2014. «eulerAPE: Рисование пропорциональных площадям 3-диаграмм Венна с использованием эллипсов». PLOS ONE 9 (7): e101717. https://doi.org/10.1371/journal.pone.0101717.
Уилкинсон, Л. 2012. «Точные и приблизительные круговые диаграммы Венна и Эйлера, пропорциональные площади».


 с. получено из ( iii ) случайная диаграмма. Хорошая диаграмма в ii была сгенерирована в 2.9секунд и 367 итераций (включая первый запуск и один повторный запуск).
с. получено из ( iii ) случайная диаграмма. Хорошая диаграмма в ii была сгенерирована в 2.9секунд и 367 итераций (включая первый запуск и один повторный запуск).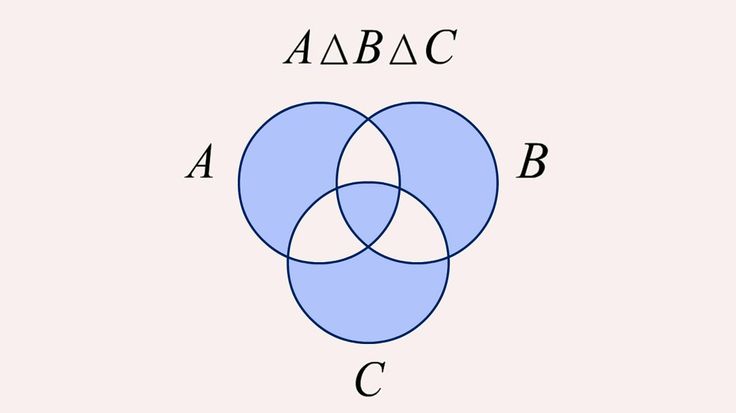 10 000 диаграмм, созданных Эйлером 9 с помощью эллипсов.0007 APE имел напряжение в [3,98×10 -14 , 2,24×10 -1 ] с медианой 7,59×10 -12 и средним значением 1,17×10 -7 diag 0 9005 и 08 в [ 6,00×10 −8 , 1,39×10 −1 ] с медианой 8,00×10 −7 и средним значением 2,94×10 −3 .
10 000 диаграмм, созданных Эйлером 9 с помощью эллипсов.0007 APE имел напряжение в [3,98×10 -14 , 2,24×10 -1 ] с медианой 7,59×10 -12 и средним значением 1,17×10 -7 diag 0 9005 и 08 в [ 6,00×10 −8 , 1,39×10 −1 ] с медианой 8,00×10 −7 и средним значением 2,94×10 −3 . сюжет (подгонка2,
количества = ИСТИНА,
заполнить = "прозрачный",
лт = 1:3,
labels = list(font = 4))
сюжет (подгонка2,
количества = ИСТИНА,
заполнить = "прозрачный",
лт = 1:3,
labels = list(font = 4))