4 на 4 равно: Задача «4 4 4 4 4 = 15, 40, 80, 160», как знаки поставить?

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значение tan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95		Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Размер кластера по умолчанию для файловых систем FAT, NTFS и exFAT

Windows 10 Pro released in July 2015 Windows Server 2008 Datacenter without Hyper-V Windows Server 2008 Enterprise without Hyper-V Windows Server 2008 for Itanium-Based Systems Windows Server 2008 Standard without Hyper-V Windows Server 2008 Datacenter Windows Server 2008 Enterprise Windows Server 2008 Standard Windows Vista Enterprise 64-bit Edition Windows Vista Home Basic 64-bit Edition Windows Vista Home Premium 64-bit Edition Windows Vista Ultimate 64-bit Edition Windows Vista Business 64-bit Edition Windows Vista Enterprise Windows Vista Home Basic Windows Vista Home Premium Windows Vista Starter Windows Vista Ultimate Microsoft Windows XP Home Edition Microsoft Windows XP Professional Microsoft Windows XP Starter Edition Windows Server 2008 R2 Datacenter Windows Server 2008 R2 Enterprise Windows Server 2008 R2 for Itanium-Based Systems Windows Server 2008 R2 Foundation Windows Server 2008 R2 Standard Windows 7 Enterprise Windows 7 Home Basic Windows 7 Home Premium Windows 7 Professional Windows 7 Starter Windows 7 Ultimate Windows 8 Windows 8 Enterprise Windows 8 Pro Windows Server 2012 Datacenter Windows Server 2012 Essentials Windows Server 2012 Foundation Windows Server 2012 Standard Еще.

..Меньше

Аннотация

Во всех файловых системах, используемых Windows, дисковое пространство организовывается с учетом размера кластеров (или размера единицы распределения). Размер кластера — минимальный объем дискового пространства, который может быть выделен для хранения файла. Таким образом, если размер файла не кратен размеру кластера, для его хранения необходимо использовать дополнительное пространство (кратное размеру кластера). При обычном разделении пространства на жестком диске средний объем памяти, потерянной в таком случае, можно рассчитать по формуле (размер кластера)/2 * (количество файлов).

Если размер кластера не задан во время форматирования раздела, используются значения по умолчанию, зависящие от размера раздела. Эти значения выбираются с учетом оптимального соотношения теряемого объема и числа кластеров в разделе. 

Дополнительная информация

Раздел (том) жесткого диска можно отформатировать под файловую систему NTFS, FAT или exFAT. В зависимости от метода форматирования раздела в Windows могут использоваться следующие значения по умолчанию.

  • С помощью команды FORMAT без указания размера кластера.

  • С помощью программы Windows Explorer, когда в поле Единица размещения в диалоговом окне Формат оставлено значение Стандартный размер размещения.


По умолчанию размер кластера для файловой системы NTFS в Windows NT 4.0 и более поздних версий равен 4 КБ. Это обусловлено тем, что сжатие файлов в NTFS невозможно для дисков с большим размером кластера. Команда форматирования не использует размер кластера больше 4 КБ, кроме случая, когда пользователь переопределяет значения по умолчанию. Вы можете сделать это, используя /А: переключение вместе с командой Format или с помощью указания большего размера кластера в соответствующем поле при форматировании с помощью проводника. 

При использовании программы Convert.exe для преобразования раздела FAT в NTFS всегда используется исходный размер кластера FAT в качестве размера кластера NTFS, если он не превышает 4 КБ. Если размер кластера FAT больше 4 КБ, то кластеры преобразовываются к размеру 4 КБ в NTFS/ Это объясняется тем, что структуры файловой системы FAT ориентированы на пределы кластера, и следовательно, установка любого большего размера кластера не позволяет выполнить преобразование. При форматировании раздела с помощью программы установки Windows NT 3.5, 3.51 и 4.0 , он сначала форматируется в FAT, а затем преобразуется в NTFS, а значит, в этом случае размер кластера всегда будет таким, каким был указан ранее при форматировании раздела в Настройках.

Размеры кластера по умолчанию для файловой системы NTFS

В следующей таблице описаны размеры кластера по умолчанию для NTFS.

Размер тома

Windows NT 3.51

Windows NT 4.0

Windows 7, Windows Server 2008 R2, Windows Server 2008, Windows Vista, Windows Server 2003, Windows XP и Windows 2000

7 МБ — 512 МБ

512 байт

4 КБ

4 КБ

512 МБ — 1 ГБ

1 МБ

4 КБ

4 КБ

1 ГБ —2 ГБ

2 ГБ

4 КБ

4 КБ

2 ГБ —2 ТБ

4 КБ

4 КБ

4 КБ

2 ТБ —16 ТБ

Не поддерживается*

Не поддерживается*

4 КБ

16 ТБ —32 ТБ

Не поддерживается*

Не поддерживается*

8 ГБ

32 ТБ —64 ТБ

Не поддерживается*

Не поддерживается*

16 ГБ

64 ТБ —128 ТБ

Не поддерживается*

Не поддерживается*

32 ГБ

128 ТБ —256 ТБ

Не поддерживается*

Не поддерживается*

64 ГБ

> 256 TB

Не поддерживается

Не поддерживается

Не поддерживается


Примечание . Звездочка (*) означает, что он не поддерживается из-за ограничений записи главной загрузки (MBR).

Размер кластера по умолчанию для FAT16

В приведенной ниже таблице указаны значения размеров кластеров по умолчанию для файловой системы FAT16.

Размер тома

Windows NT 3.51

Windows NT 4.0

Windows 7, Windows Server 2008 R2, Windows Server 2008, Windows Vista, Windows Server 2003, Windows XP и Windows 2000

7 МБ —8 МБ

Не поддерживается

Не поддерживается

Не поддерживается

8 МБ —32 МБ

512 байт

512 байт

512 байт

32 МБ —8 МБ

1 МБ

1 МБ

1 МБ

64 ТБ —128 ТБ

2 ГБ

2 ГБ

2 ГБ

128 ТБ —256 ТБ

4 КБ

4 КБ

4 КБ

256 МБ —512 МБ

8 ГБ

8 ГБ

8 ГБ

512 МБ — 1 ГБ

16 ГБ

16 ГБ

16 ГБ

1 ГБ —2 ГБ

32 ГБ

32 ГБ

32 ГБ

2 ГБ —4 ГБ

64 ГБ

64 ГБ

64 ГБ

4 ГБ —8 ГБ

Не поддерживается

128 КБ*

Не поддерживаются

8 ГБ —16 ГБ

Не поддерживается

256 KB*

Не поддерживаются

> 16 ГБ

Не поддерживаются

Не поддерживается

Не поддерживается

Примечание. Символ «*» означает доступность только для носителей с размером сектора, превышающим 512 байт.

Размер кластера по умолчанию для FAT32

В приведенной ниже таблице указаны значения размеров кластеров по умолчанию для файловой системы FAT32.

Размер тома

Windows NT 3.51

Windows NT 4.0

Windows 7, Windows Server 2008 R2, Windows Server 2008, Windows Vista, Windows Server 2003, Windows XP и Windows 2000

7 МБ — 16 МБ

Не поддерживается

Не поддерживается

Не поддерживается

16 МБ —32 МБ

512 байт

512 байт

Не поддерживается

32 МБ —8 МБ

512 байт

512 байт

512 байт

64 МБ —128 МБ

1 МБ

1 МБ

1 МБ

128 ТБ —256 ТБ

2 ГБ

2 ГБ

2 ГБ

256 МБ — 8 ГБ

4 КБ

4 КБ

4 КБ

8—16 ГБ

8 ГБ

8 ГБ

8 ГБ

16 ТБ —32 ТБ

16 ГБ

16 ГБ

16 ГБ

32 ГБ — 2 ТБ

32 ГБ

Не поддерживается

Не поддерживается

> 2 ТБ

Не поддерживаются

Не поддерживается

Не поддерживается

Размер кластера по умолчанию для exFAT

В приведенной ниже таблице указаны значения размеров кластеров по умолчанию для файловой системы exFAT.

Размер тома

Windows 7, Windows Server 2008 R2, Windows Server 2008, Windows Vista, Windows Server 2003 и Windows XP

7 МБ — 256 МБ

4 КБ

256 МБ — 1 ГБ

32 ГБ

32 ГБ — 256 ТБ

128 МБ.

> 256 TБ

Не поддерживаются

Чему равно «8 ÷ 2(2 + 2)»? Объяснение вирусного математического твита

31 июля 2019, 17:18 | Обновлено: 28 августа 2019, 14:28

Сэм Пранс

@samprance

Математическое уравнение «8 ÷ 2(2 + 2)» стало вирусным, потому что люди получают два разных ответа.

Сбор матлетов. Новая математическая сумма стала вирусной. Все бьются над ответом на вопрос «8 ÷ 2(2 + 2)».

Время от времени Интернет заставляет вас сомневаться в том, что вы делаете, не задумываясь. В январе нас всех заставили пересмотреть то, как мы пишем букву «х». По-видимому, существует восемь различных способов. В мае нас спросили, моем ли мы ноги. Слишком многие из вас этого не делают. Затем в июне мы были вынуждены задуматься о том, как мы складываем числа в уме. Существуют сотни способов вычислить такую ​​простую сумму, как «27+48». Все, что мы думали, что знали, было ложью.

ПОДРОБНЕЕ: Лучшие мемы 2019 года (на данный момент)
ПОДРОБНЕЕ: Как сложить «27+48»? Интернет потерял сознание из-за этого вирусного математического твита

Теперь Интернет ломает другое уравнение, потому что никто не знает, чему равно «8 ÷ 2(2 + 2)».

Каков фактический ответ на «8 ÷ 2(2 + 2)»?

Чему равно «8 ÷ 2(2+2)»? Вирусная математическая сумма объяснена.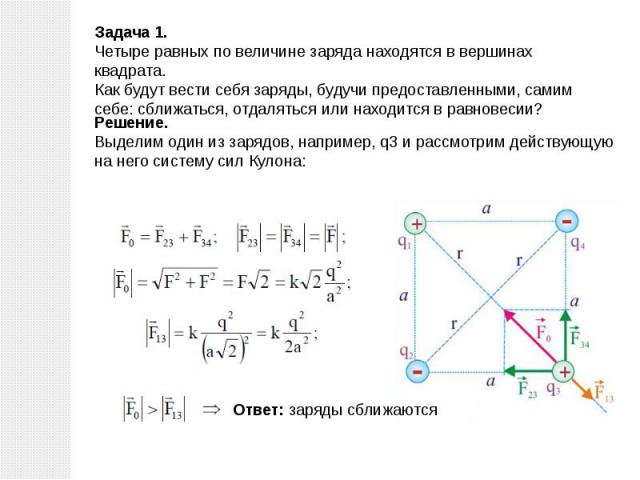 Картина: Paramount Pictures // TV Globo

Вчера этот вопрос стал вирусным, когда @pjmdolI написал в Твиттере: «Умфи решают это» вместе с изображением суммы «8 ÷ 2(2 + 2)». Твит сразу же получил тысячи ответов и ретвитов с людьми с математическими степенями. другой ответил: «Взял 3 класса математики, дифференциальные уравнения и линейную алгебру, это 16, братан». Хотя кто прав?

Люди, получившие 1, считают, что сначала нужно разобраться со всеми скобками. Итак, вы делаете «2 + 2», и сумма упрощается до «8 ÷ 2 (4)». Затем у вас все еще есть скобки, поэтому вам нужно сделать «2 x 4», прежде чем продолжить. Это дает вам «8 ÷ 8», что равно 1.

Однако те, у кого получилось 16, считают, что когда вы дойдете до ‘8 ÷ 2(4)’, вы сначала сделаете ‘8 ÷ 2’, потому что они оба находятся за скобками. Это дает вам 4 (4), что равно 16. Это становится очень запутанным, верно?

умфи решают это pic.twitter.com/0RO5zTJjKk

— em ♥︎ (@pjmdolI) 28 июля 2019 г.

1. Количество людей, говорящих, что 16 человек должны пересдать математику 😭

— JKOurEuphoria (@JungKookQueen97) 28 июля 2019 г.

взял 3 класса по математике, дифференциальным уравнениям и линейной алгебре, это 16 бро

— Джейк Чилленхол (@corynhendrix) 30 июля 2019 г.

у меня 2 степени по математике это 1

— laur♏️ (@lauram_williams) 30 июля 2019

Проблема в том, что люди думают, что PEMDAS является последовательным, и не понимают, что умножение и деление, а затем сложение и вычитание являются ПАРАМИ, то есть перемещение слева направо в зависимости от того, что идет ПЕРВЫМ в каждой паре, выполняется первым. Ответ — 16. pic.twitter.com/vycgWRvrmM

— Вато (@trillxfaded) 30 июля 2019 г.

(2+2) 4
8/2(4)
Согласно PEMDAS, сначала нужно избавиться от скобок, поэтому
2(4)=8
8/8=1 ответ равен единице.

— koook (@SoWhAT9000) 28 июля 2019 г.

8/2(2+2)
8/2(4)
Да, вы используете PEMDAS, но поскольку в этом уравнении первым идет деление, вы делите первым.
4(4)
16

— Наоми (@mikrogguki) 29 июля 2019 г.
Чему равно «8 ÷ (2 x 4)»? Вирусный математический опрос. Картина: @neworlean через Twitter

Некоторые люди используют метод PEMDAS (в США это означает скобки, возведение в степень, умножение, деление, сложение, вычитание), а другие используют BODMAS (в Великобритании это означает скобки, порядок, деление, умножение, сложение, вычитание). Оба метода означают одно и то же, потому что деление и умножение связаны друг с другом. Сложение и вычитание также сочетаются друг с другом. По сути, PEMDAS также является PEDMSA, а BODMAS также является BOMDSA.

К сожалению, правильный ответ буквально зависит от того, как вас учили, и все сводится к тому, считаете ли вы, что должны решить сначала «2(4)» или «8 ÷ 2».

Если вы введете сумму в Google, она скажет, что ответ равен 16, но в опросе более 234 000 человек в Твиттере 59% проголосовали за «1». Некоторые калькуляторы говорят 16. Другие говорят 1. По словам анонимного профессора Оксфордского университета, который говорил с The Mirror: «Нет ни одного правильного ответа. Уравнение было написано неоднозначно, что оставляет его открытым для интерпретации».

По сути, когда Кэди Херон заявила в серии «Дрянные девчонки », что любит математику, потому что «она одинакова во всех странах», она солгала.

Что вы думаете? Вы команда 1 или команда 16?

Решить линейные уравнения с одним неизвестным k-3/4=10 Решатель алгебры тигра

Переставить:

Переставить уравнение, вычитая то, что находится справа от знака равенства из обеих частей уравнения:

                     k-3/ 4-(10)=0

Пошаговое решение :

Шаг 1 : 

 3
 Упростить —
            4
Уравнение в конце шага 1 : 
 3
  (к — —) — 10 = 0
        4

Шаг 2 :

Преобразование целого в виде эквивалентной дроби:

 2. 1   Вычитание дроби из целого

Преобразование целого в виде дроби с использованием 4 в качестве знаменателя:

 k k • 4
     к = — = —————
          1 4

Эквивалентная дробь: Полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое число

Общий знаменатель: Эквивалентная дробь и другая дробь, участвующая в вычислении, имеют один и тот же знаменатель знаменатель

Объедините числители, подставьте сумму или разность к общему знаменателю, затем приведите к наименьшему члену, если возможно:

 k • 4 - (3) 4k - 3
 знак равно
      4 4
Уравнение в конце шага 2 : 
 (4k – 3)
  ———————— - 10 = 0
     4
 Шаг 3
    10 = —— = ——————
          1 4
Сложение дробей, имеющих общий знаменатель:

 3.2       Сложение двух эквивалентных дробей 

 (4к-3) - (10 • 4) 4к - 43
 знак равно
         4 4
Уравнение в конце шага 3 : 
 4k - 43
  ——————— = 0
     4

Шаг 4 :

Когда дробь равна нулю: 
  4.
No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *