Игры с природой онлайн
Назначение сервиса. Данный тип задач относится к задачам принятия решений в условиях неопределенности. С помощью сервиса можно выбрать оптимальную стратегию, используя:- критерий минимакса, критерий максимакса, критерий Байеса, критерий Вальда, критерий Сэвиджа, критерий Лапласа, критерий Ходжа-Лемана;
- критерий Гурвица, обобщенный критерий Гурвица с расчетом эффективности;
- множество Паретто.
- Шаг №1
- Шаг №2
- Видеоинструкция
Инструкция. Для выбора оптимальной стратегии в онлайн режиме необходимо задать размерность матрицы. Затем в новом диалоговом окне выбрать необходимые критерии и коэффициенты. Также можно вставить данные из Excel.
Размерность платежной матрицы (целевая функция ЗПР в условиях неопределенности)
Примечание: Сначала, если возможно, упрощают матрицу, вычеркивая невыгодные стратегии A.
Стратегии природы вычеркивать нельзя, т. к. каждое из состояний природы может наступить случайным образом, независимо от действий A.
Любую хозяйственную деятельность человека можно рассматривать как игру с природой. В широком смысле под «природой» понимается совокупность неопределенных факторов; влияющих на эффективность принимаемых решений. Безразличие природы к игре (выигрышу) к возможность получения экономистом (статистиком) дополнительной информации о ее состоянии отличают игру экономиста с природой от обычной матричной игры, в которой принимают участие два сознательных игрока.
Пример. Предприятие может выпускать 3 вида продукции А1, А2 и А3, получая при этом прибыль, зависящую от спроса, который может быть в одном из 4-х состояний (В 1, В2, В3, В4). Элементы платежной матрицы характеризуют прибыль, которую получат при выпуске i-й продукции при j-м состоянии спроса.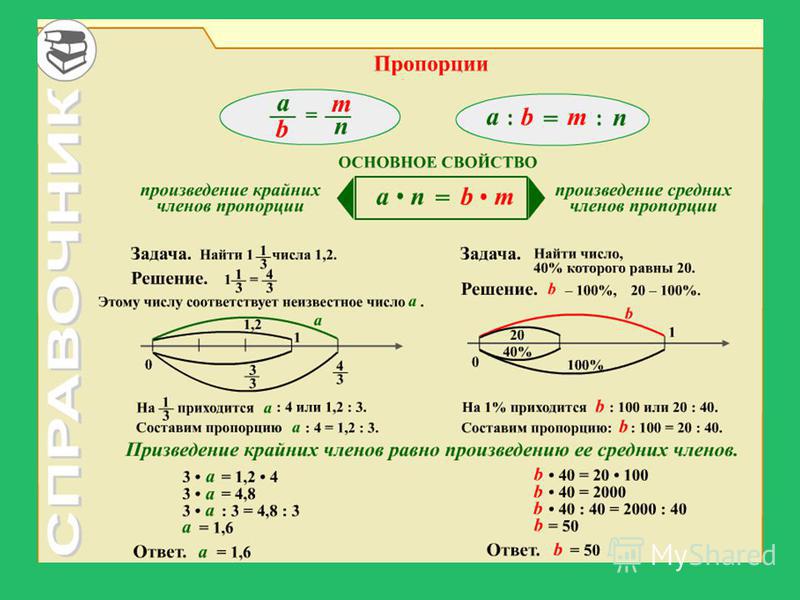
Игра предприятия А против спроса В задана платежной матрицей:
| В1 | В2 | В3 | В4 | |
| А1 | 2 | 7 | 8 | 6 |
| А2 | 2 | 8 | 7 | 3 |
| А3 | 4 | 3 | 4 | 2 |
Решение.
Критерий максимакса
| Ai | П1 | П2 | П3 | П4 | max(aij) |
| A1 | 2 | 7 | 8 | 6 | 8 |
| A2 | 2 | 8 | 7 | 3 | 8 |
| A3 | 4 | 3 | 4 | 2 | 4 |
Вывод: выбираем стратегию N=1.
Критерий Лапласа.
| Ai | П1 | П2 | П3 | П4 | ∑(aij) |
| A1 | 0.5 | 1.75 | 2 | 1.5 | 5.75 |
| A2 | 0.5 | 2 | 1.75 | 0.75 | 5 |
| A3 | 1 | 0.75 | 1 | 0.5 | 3.25 |
| pj | 0.25 | 0.25 | 0.25 | 0.25 |
Вывод: выбираем стратегию N=1.
Критерий Вальда.
| Ai | П1 | П2 | П3 | П4 | min(aij) |
| A1 | 2 | 7 | 8 | 6 | 2 |
| A2 | 2 | 8 | 7 | 3 | 2 |
| A3 | 4 | 3 | 4 | 2 | 2 |
Вывод: выбираем стратегию N=1.
Критерий Севиджа.
Находим матрицу рисков.
Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце bj = max(aij) характеризует благоприятность состояния природы.
1. Рассчитываем 1-й столбец матрицы рисков.
r11 = 4 — 2 = 2; r21 = 4 — 2 = 2; r31 = 4 — 4 = 0;
2. Рассчитываем 2-й столбец матрицы рисков.
r12 = 8 — 7 = 1; r22 = 8 — 8 = 0; r32 = 8 — 3 = 5;
3. Рассчитываем 3-й столбец матрицы рисков.
r13 = 8 — 8 = 0; r23 = 8 — 7 = 1; r33 = 8 — 4 = 4;
4. Рассчитываем 4-й столбец матрицы рисков.
r14 = 6 — 6 = 0; r24 = 6 — 3 = 3; r34 = 6 — 2 = 4;
| Ai | П1 | П2 | П3 | П4 |
| A1 | 2 | 1 | 0 | 0 |
| A2 | 2 | 0 | 1 | 3 |
| A3 | 0 | 5 | 4 | 4 |
| Ai | П1 | П2 | П3 | П4 | max(aij) |
| A1 | 2 | 1 | 0 | 0 | 2 |
| A2 | 2 | 0 | 1 | 3 | 3 |
| A3 | 0 | 5 | 4 | 4 | 5 |
Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A1.
Пример. Предлагается три проекта инвестиций и прогноз получения доходов за год (дивиденды и повышение стоимости капитала) при различных возможных исходах.
| Проект инвестиций 1 возможные исходы: | Проект инвестиций 2 возможные исходы: | Проект инвестиций 3 возможные исходы: | ||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 40 | 40 | 20 | 30 | 20 | 30 | 20 | 30 | 20 |
Пропорции тест (6 класс) по математике онлайн
Последний раз тест пройден более 24 часов назад.
Для учителя
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Верно ли утверждение 3 : 3,6 = 5 : 6?
Да
Нет
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 2 из 10
Найдите произведение средних членов пропорции 3 : 5 = 15 : 25
75
135
45
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 3 из 10
Решите уравнение 6,4 : 0,16 = 4 : у
10
2,5
0,1
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 4 из 10
Какая из данных пропорций неверна?
5 : 2 = 15 : 6
3 : 9 = 12 : 37
2 : 39 = 4 : 78
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 5 из 10
Решите пропорцию 42 : (4 * х) = 21 : 4
4
2
3
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 6 из 10
Найдите произведение крайних членов пропорции 2 : 7 = 12 : 42
84
24
294
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 7 из 10
Решите уравнение 0,75 : 1,5 = 5 : х
2,5
0,1
10
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 8 из 10
Верно ли утверждение 4 : 0,2 = 280 : 13?
Да
Нет
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 9 из 10
Деревянный брусок объемом 4 куб.
см весит 36 г. Сколько грамм весит брусок объемом 5 куб. см?36
45
25
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 10 из 10
Запишите пропорцию: 5 так относится к 7 как 25 к 35:
5 : 7 = 25 : 35
7 : 5 = 25 : 35
Правильный ответ
Неправильный ответ
В вопросе ошибка?
см весит 36 г. Сколько грамм весит брусок объемом 5 куб. см?Доска почёта
Чтобы попасть сюда — пройдите тест.
Тест «Пропорции» (6 класс) рассчитан на учеников средних классов, которые хотят оценить или закрепить свои знания по теме. Вопросы проверяю теорию, а также умение решать пропорции. Задания теста проверяют все необходимые аспекты раздела, поэтому являются прекрасным помощников для экспресс-подготовки к контрольной работе.
Задания удобно просматривать в онлайн режиме с любого доступного устройства.
Тест по математике «Пропорции» – это один из самых эффективных методов самооценивания и самоподготовки к занятиям.
Рейтинг теста
3.9
Средняя оценка: 3.9
Всего получено оценок: 1592.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Multi step proportion calculator
- Expression
- Equation
- Inequality
- Contact us
- Simplify
- Factor
- Expand
- GCF
- LCM
- Solve
- Graph
- System
- Решение
- График
- Система
- Математический решатель на вашем сайте
Наши пользователи:
Сначала я был в замешательстве, покупать это программное обеспечение или нет. Но за пять дней я более чем доволен Алгебратором. Я боролся с квадратными уравнениями и неравенствами.
Логический и пошаговый подход к решению задач оказался для меня благом, и теперь я люблю решать эти уравнения.
Виктория Хилл, Колорадо
Я просто хотел сказать вам, что я только что купил вашу программу, и это невероятно! Большое спасибо за разработку такой программы. Кстати, недавно я отправил вам электронное письмо, в котором сообщал, что купил PAT (персональный репетитор по алгебре) и очень им недоволен.
Мария Чавес, Техас
Огромное спасибо! Кому пришла в голову идея изобрести такую полезную алгебру-сифтвару — она меня спасла, теперь я ее действительно понимаю.
Джефф Плай, CO
Это программное обеспечение является лучшим в своем роде. Объяснения каждого шага превосходны и просты для понимания. Незаменимая вещь для родителей детей старшего школьного возраста. Отличная работа.
Линда Ховард, Джорджия
Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение спасает им жизнь.
Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою? Поисковые фразы, использованные 09.01.2013:
- algebarator
- метод квадратного корня
- формула сложения и вычитания положительных и отрицательных чисел
- бесплатный онлайн-репетитор по решению неравенств
- как использовать вход на ти-83
- алан тест-практика
- скачать бесплатные электронные книги по бухгалтерскому учету
- буквальные игры евкации
- метод дроби квадратичный
- факторинг числа в кубе
- как решать одновременные уравнения с 3 неизвестными
- Дробная экспонента
- факторинговый калькулятор трехчленов
- Квадратные уравнения Word задачи
- рассчитать погонный метр
- ответы на практические вопросы по алгебре 2 с отличием
- преобразовать смешанную дробь в десятичную
- легкая алгебра cd
- алгебраические неравенства для чайников
- Калькулятор дробей для деления рациональных выражений
- Решатель уравнений второго класса
- glencoe предварительная алгебра ответы
- Задачи по алгебре онлайн
- Рабочий лист решения тригонометрических уравнений
- программное обеспечение
- ДОМАШНИЕ ЗАДАНИЯ ПО МАТЕМАТИКЕ
- дополнительные факты 7-9 рабочий лист c Лог решения
- с ti-83
- рабочие листы уравнения сложения
- научный калькулятор онлайн Ти-84 апплет
- наибольший общий целочисленный делитель Matlab
- ЖК рабочий лист
- Десятичные выражения и уравнения
- задачи на умножение и деление дробей
- o уровень прошлого бумаги mcqs биология
- рабочие листы по делению десятичных дробей
- думмит глава 7 решения
- онлайн калькулятор для упорядочивания дробей от наименьшей до наибольшей
- Бесплатная помощь с домашним заданием по алгебре: Rational Exponents 9Код 0003 для нахождения суммы ряда квадратов чисел в java
- Продам рабочую тетрадь и заметки по алгебре thinkwell
- алгебраический расчет Шпаргалка по формуле вероятности
- головоломок
- бесплатных рабочих листа по графическим системам неравенств
- бесплатный онлайн учебник по техасской геометрии
- диапазон доменов ti-83
- листа по базовой алгебре
- решение одношаговых уравнений рабочий лист
- печатных рабочих листа калькулятора
- ти-84 плюс графические трюки
- рабочий лист по симметрии первый класс
- преобразование десятичного квадрата в недесятичный квадрат Рабочий лист одновременных уравнений
- коммутативное свойство сложения печатных листов
- комбинированный решатель
- 8 класс без калькулятора, рабочий лист
- РЕШЕНИЕ НЕРАВЕНСТВ 7 КЛАСС РАБОТЫ ДЛЯ ПЕЧАТИ
- онлайн калькулятор подстановок с дробями
- Математические задачи 7-го класса — умножение и деление целых чисел
- скачать Книга о количественных способностях, глава 2
- программа уравнений
- помощь по продвинутой алгебре
- Банк вопросов для теста способностей скачать бесплатно
- уравнение в кубе
- решить квадратные практические задачи
- для печати ti 84 деятельности
- темы исследовательские проекты по математике
- ti 84 скачать
- «Десятичное число» + «рабочие листы»
- радикальное решение проблем
- алгоритм java «упрощение радикалов»
- факторинговые параболы
- java пример суммы чисел
- лозунги для показателей и квадратных корней
- Рабочие листы по умножению и делению рациональных чисел
- умножить на дробную степень
- прошлые экзамены по английскому языку 11 лет
- базовая алгебра помощь видео решение задач
- ЖК-решатель
- определения пятого класса
- наименьший общий делитель чисел 20, 40 и 50
- бесплатных печатных рабочих листа для ks3
- записать как экспоненциальное выражение
- математических стихотворения из 30 слов
- решатель радикальных математических уравнений
- Базовая математика в колледже, ключ ответа Игнасио Белло
- Уравнения с кубическим корнем в Java
| Предыдущая | Далее |
Доля населения — размер выборки
Используйте этот калькулятор, чтобы определить подходящий размер выборки для оценки доли населения, которое обладает определенным свойством (например, им нравится ваш продукт, они владеют автомобилем или они могут говорить на втором языке).
язык) с заданной погрешностью. Если вы собираетесь задать более одного вопроса, используйте самый большой размер выборки для всех вопросов. Обратите внимание, что если не все вопросы имеют только два действительных ответа (например, да или нет), а включают один или несколько дополнительных ответов (например, «не знаю»), вам понадобится другой калькулятор размера выборки.
Какая погрешность вам нужна? 5 % — обычный выбор | % | Погрешность — это требуемый уровень точности. Это диапазон, в котором оценивается истинная пропорция, и ее следует выражать в процентных пунктах (например, ±2%). Более низкая погрешность требует большего размера выборки. |
Какой уровень уверенности вам нужен? Типичные варианты: 90 %, 95 % или 99 % | % | Уровень достоверности определяет степень неопределенности, связанную с вашей оценкой. Более высокий уровень достоверности требует большего размера выборки. |
Насколько велико население? Если вы не знаете, введите 100 000 | Сколько человек входит в совокупность, из которой вы делаете выборку? Размер выборки не сильно меняется для населения, превышающего 100 000 человек. | |
Какова, по вашему мнению, вероятная доля выборки? Если вы не уверены, оставьте значение 50% | % | Какой вы ожидаете пропорцию выборки? Часто это можно определить, используя результаты предыдущего опроса или проведя небольшое пилотное исследование. |
Это вероятность того, что предел погрешности будет содержать истинную пропорцию.
| Размер выборки | |||
| Ваша погрешность будет | 9,79% | 3,08% | 0,93% |
| С погрешностью | % | % | % |
| Размер вашей выборки будет | 8763 | 2345 | 383 |
| С доверительной вероятностью | % | % | % |
| Размер вашей выборки будет | 270 | 383 | 660 |
| При численности населения | человек|||
| Размер вашей выборки будет | 80 | 278 | 370 |
| С долей выборки | % | % | % |
| Размер вашей выборки будет | 139 | 288 | 246 |
Рабочий пример
Если розничный продавец хочет оценить долю своих клиентов, которые купили товар после просмотра их веб-сайта в определенный день с 9Уровень достоверности 5% и допустимая погрешность 5%, сколько клиентов они должны контролировать? Учитывая, что их веб-сайт имеет в среднем 10 000 просмотров в день, и они не уверены в своем текущем коэффициенте конверсии, им потребуется отобрать 370 клиентов.
Если, однако, они знают из предыдущих исследований, что они ожидают коэффициента конверсии 5%, то размера выборки 73 будет достаточно.
Формула
Этот калькулятор использует следующую формулу для размера выборки n:
n = N*X / (X + N – 1),
где,
X = Z α/2 2 *p*(1-p) / МОЕ 2 ,
и Z α/2 — критическое значение нормального распределения при α/2 (например, для уровня достоверности 95 % α равно 0,05, а критическое значение равно 1,96), MOE — предел погрешности, p — доля выборки, а N — численность населения. Обратите внимание, что к формуле размера выборки была применена поправка на конечную совокупность.
В следующей ссылке объясняется, как FPC используется для корректировки оценки дисперсии при выборке без замены (см. стр. 141–142).
Дэниел В.В. (1999 г.). Биостатистика: основа для анализа в области медицинских наук. 7 -е издание . Нью-Йорк: Джон Уайли и сыновья.
Обсуждение
Приведенный выше калькулятор размера выборки предоставляет рекомендуемое количество выборок, необходимое для оценки истинного среднего значения доли с требуемой погрешностью и уровнем достоверности.
Вы можете использовать Альтернативные сценарии, чтобы увидеть, как изменение четырех входных данных (предел погрешности, уровень достоверности, размер совокупности и пропорция выборки) влияет на размер выборки. Наблюдая за тем, что происходит с альтернативными сценариями, вы можете увидеть, как каждый ввод связан с размером выборки и что произойдет, если вы не будете использовать рекомендуемый размер выборки. Чем больше размер выборки, тем больше вы можете быть уверены в том, что оценки отражают генеральную совокупность, и тем уже доверительный интервал. Однако зависимость не является линейной, например, удвоение размера выборки не уменьшает вдвое доверительный интервал.
Дополнительную информацию см. в записи нашего блога «Важность и влияние размера выборки».
Определения
Погрешность
Погрешность — это требуемый уровень точности. Это положительное или отрицательное число, которое часто сообщается с оценочной долей и также называется доверительным интервалом. Это диапазон, в котором оценивается истинная доля населения, который часто выражается в процентных пунктах (например, ± 2%). Обратите внимание, что фактическая точность, достигнутая после того, как вы соберете свои данные, будет больше или меньше этого целевого количества, потому что она будет основана на пропорции, оцененной на основе данных, а не на вашей ожидаемой пропорции выборки.
Уровень достоверности
Доверительный уровень — это вероятность того, что предел погрешности содержит истинную пропорцию. Если бы исследование повторялось и каждый раз рассчитывался диапазон, можно было бы ожидать, что истинное значение будет лежать в пределах этих диапазонов в 95% случаев. Чем выше уровень достоверности, тем больше вы можете быть уверены, что интервал содержит истинную пропорцию.